SPA Attack on NTRU Protected Implementation with Sparse
Representation of Private Key
Tom
´
a
ˇ
s Rabas
a
, Ji
ˇ
r
´
ı Bu
ˇ
cek
b
and R
´
obert L
´
orencz
c
Faculty of Information Technology, Czech Technical University in Prague, Th
´
akurova, Prague, Czech Republic
Keywords:
NTRU, Simple Power Analysis, Post-Quantum Cryptography, Sparse Representation.
Abstract:
NTRU is a post-quantum public-key, lattice-based cryptosystem. Several suggested implementations claim to
be simple-power analysis resistant. One of these implementations was described in (An et al., 2018) using a
sparse representation of a private key and a new design of an algorithm for the multiplication of polynomials.
We show that it is still vulnerable. We theoretically explain a vulnerability in the algorithm description that
could potentially lead to a single-trace attack. We practically perform the attack on two targets with different
architectures: an 8-bit microcontroller of the AVR family and a 32-bit microcontroller ARM Cortex-M0.
Statistical analysis performed on the second target, measured by the ChipWhisperer platform, shows that with
a chance of 91.0% we get the correct key just from one measured trace. Ability to get two measurements raises
our probability of a successful attack up to 99.6%.
1 INTRODUCTION
Current standardized public-key cryptosystems are
based on the assumed difficulty of factorizing inte-
gers or computing discrete logarithms. If quantum
computers of sufficient size are built, these cryp-
tosystems will all be insecure (Chen et al., 2016).
In order to provide algorithms which are based on
different assumptions, while being secure in the
presence of quantum computers, the National Insti-
tute of Standards and Technology (NIST) has ini-
tiated a process to solicit, evaluate, and standard-
ize one or more quantum-resistant public-key cryp-
tographic algorithms. NTRU was one of the round
3 finalists. In the category of public-key encryp-
tion and key-establishment algorithms, these were
Classic McEliece, CRYSTALS-KYBER, NTRU, and
SABER. So far, only CRYSTALS-KYBER was cho-
sen as a future standard while NTRU did not.
In the third round, NIST asked for more focus on
side-channel attacks including power-measuring at-
tacks (Alagic et al., 2020). Especially implementa-
tions on embedded devices tend to be more vulnera-
ble to these attacks as they are more likely to be used
in an environment where the attacker has full access
a
https://orcid.org/0000-0002-0924-359X
b
https://orcid.org/0000-0003-1359-4285
c
https://orcid.org/0000-0001-5444-8511
to the device.
1.1 Previous Work
In 2008 researchers from Leuven published the first
article (Atici et al., 2008) about NTRU implemen-
tation and power analysis. The work presented a
compact and low-power implementation suitable for
RFID and performed differential power analysis us-
ing 25 000 measurements to recover the key from an
FPGA device. In 2010 an article was published de-
scribing three countermeasures against power anal-
ysis attacks on NTRU (randomization of ciphertext,
temporary array or encoding of private key). They
presented a thorough theoretical discussion and their
experimental results.
Another paper from 2013 showed that all previ-
ous countermeasures can be overcome by first-order
collision attacks (Zheng et al., 2013) and suggested
other countermeasures (dummy operations, timing
noise, mathematical randomization/random key rota-
tion) that should help with resistance to power attacks.
Countermeasure random key rotation is revisited
in the paper (Wang et al., 2017) and implementation
schemes in software and hardware are suggested.
In the paper (An et al., 2018), which is our main
focus, authors provide two single trace attacks on two
implementations and suggest new protected imple-
mentations that should prevent all current first-order
Rabas, T., Bu
ˇ
cek, J. and Lórencz, R.
SPA Attack on NTRU Protected Implementation with Sparse Representation of Private Key.
DOI: 10.5220/0011729200003405
In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 135-143
ISBN: 978-989-758-624-8; ISSN: 2184-4356
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
135

power attacks.
Paper (Schamberger et al., 2019) revisits previous
works, does some experiments and provides a new ef-
ficient implementation of NTRU with masking.
Together with the NIST Post-Quantum Cryptog-
raphy (PQC) competition, most papers concerning
public-key cryptosystems and side-channel attacks
changed their focus on the referenced or optimized
C/assembly implementation given at NIST’s website
(e.g. NTRU submission from NIST Round-3 software
packages). That is also the case in the following two
articles.
Paper (Askeland and Rønjom, 2021) presented a
single trace attack on the implementation submitted
to NIST. It identifies two strong sources of leakage in
the unpacking of the secret key. The larger portion
of the secret key is recovered by exploiting these two
leakages. The remaining parts are found by lattice
reduction techniques.
Paper (Karabulut et al., 2021) focuses on the gen-
eration of the private key. They reveal that the sorting
implementation in NTRU/NTRU Prime and the shuf-
fling in CRYSTALS-DILITHIUM’s polynomial sam-
pling process leak information about the −1, 0, or +1
assignments made to the coefficients.
Paper (Ravi et al., 2021) proposes several
novel ciphertext-chosen attacks combined with side-
channel leakage using few thousand chosen ciphertext
queries to successfully recover the private key.
1.2 Our Approach
In our work, we concentrate on simple power analy-
sis following the idea that protection against statisti-
cal methods using thousands of traces can be achieved
on a higher abstract level using an appropriate proto-
col that forces the device to change keys more often.
Also, we do not target key generation as in (Karabulut
et al., 2021) or unpacking the key as in (Askeland and
Rønjom, 2021), but rather focus on the implementa-
tion of a commutative multiplication of polynomials
itself. In the end, we focus on implementations that
intend to protect themselves against power analysis.
Let us stress that this is not the case for implementa-
tions referred by NIST on their websites. These im-
plementations are not trying to achieve any protec-
tion against power analysis (in contrast to timing at-
tacks). Our aim is to attack the protected implemen-
tation with countermeasure for the polynomial mul-
tiplication presented in (An et al., 2018), which was
supposed to be resistant against current power attacks.
Organization of the Paper. In section 2, we give
the necessary background on the NTRU algorithm.
Section 3 describes the target implementation of
NTRU. In section 4, we present the attack with its
assumptions and its model in Python. Section 5 de-
scribes a realization of the attack on concrete architec-
tures. In section 6, we describe possible mitigations
and countermeasures. Finally, section 7 concludes the
paper.
2 NTRU ALGORITHM
We use the notation R = Z[x]/(x
N
− 1) for the poly-
nomial ring used in NTRU. It consists of all polyno-
mials with degree less than N and coefficients in Z.
An element f ∈ R can be written as f =
∑
N−1
i=0
f
i
x
i
.
Let d
f
and d
g
be some fixed integer parameters.
We define L
f
as a set of polynomials from R that have
exactly d
f
+ 1 coefficients equal to 1 and d
f
coeffi-
cients equal to -1. We define B
g
as a set of polynomi-
als from R that have d
g
coefficients equal to 1 and -1.
We say that polynomials from L
f
and B
g
are ternary
polynomials meaning their coefficients are just 0,1 or
−1.
We will also use two integers p and q as mod-
uli. They must be coprime (gcd(p,q) = 1) and p <<
q. Then, we define f
p
to be a polynomial from
Z
p
[x]/(x
N
− 1) constructed from a polynomial f ∈ R
by reducing its coefficients modulo p. We denote the
inverse of f
p
∈ Z
p
[x]/(x
N
− 1) as f
−1
p
. Similarly, we
define f
q
and f
−1
q
for the modulus q.
Key Generation. The algorithm generates the pri-
vate and public keys as follows. The private key is
a ternary polynomial f selected from L
f
. The public
key is then constructed as h = p f
−1
q
g (mod q),g ∈ B
g
.
Encryption. In order to encrypt plaintext m, we first
choose a random polynomial r ∈ R with d
r
coeffi-
cients equal to 1 and -1. Then, we compute the cipher-
text by multiplying r with public key h together with
adding our plaintext m, i.e. e = rh + m (mod q).
Decryption. is done in two steps. First we compute
intermediate result a = e f (mod q) and then we re-
cover the plaintext as m = a f
−1
p
(mod p).
Correctness of the decryption can be seen in the
following equations:
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
136

a = e f (mod q)
= rh f + m f (mod q)
= r p f
−1
q
g f + m f (mod q)
= r pg + m f (mod q)
a f
−1
p
= (r pg + m f ) f
−1
p
(mod p)
= 0 + m f f
−1
p
(mod p)
= m (mod p)
Thanks to an optimization of choosing f as pF + 1
where F ∈ L
f
, then f
−1
p
is equal to 1 modulo p so
the second computation is trivial. This optimization
is also used in our case.
Note that the private key is used just in one multi-
plication with ciphertext. This multiplication will be
our target for the power analysis attack.
3 IMPLEMENTATION
One can store the private key in a dense or sparse
representation. Even though the referenced and op-
timized implementations given on NIST’s website
use a dense representation, our target implementation
uses a sparse representation as the original one, de-
noted by (An et al., 2018) as ”NTRU Open Source”,
that our target implementation is based on.
It first stores degrees of all monomials whose co-
efficient is 1 in increasing order into an array. Then,
it concatenates the array with degrees of all monomi-
als whose coefficient is −1 in increasing order. For
example, if f = 1 − x
1
+ x
2
+ x
3
− x
4
+ x
7
− x
8
, then
we encode it as [0,2, 3,7,1, 4,8]. Let us denote this
representation of the private key as b.
General polynomial (e.g. ciphertext) is stored in
dense representation with increasing order of degrees,
meaning that polynomial e = 3x
4
− x
2
+ 9x − 5 is
stored as [−5,9,−1, 0,3].
3.1 Algorithm 4 – Countermeasure of
NTRU Open Source
Here we will describe the supposedly safe implemen-
tation of polynomial multiplication in NTRU against
simple power analysis from (An et al., 2018). You can
see the implementation in Fig. 1. We will refer to it as
Algorithm 4 (as numbered in the original paper).
The implementation uses a temporary array t for
storing intermediate results. In the end, this array
stores the final product of the multiplication. Instead
of initializing it to zeroes, the algorithm uses a ran-
dom number r as a protection against some power at-
tacks (lines 1 – 3). In the end, it removes the same
value r from t so that the result is still correct (lines
27 – 29).
In a nutshell, the algorithm itself goes through
array b and for each element does the following: it
stores the value of the current element of b into vari-
able k, then, it goes through the whole temporary ar-
ray t and takes those elements of ciphertext e that
should be added to t. Exactly which elements of e
are added to which element of t is influenced by the
current value of k – it simply tells us the offset size
we need to apply.
Notice that since the coefficients of the private key
are 1 or −1, adding/subtracting the appropriate ele-
ments of ciphertext e to temporary array t is sufficient
and no multiplication by the coefficients of the private
key is needed (contrary to standard multiplication).
The algorithm first goes through the second half of
the array b, i.e. elements {b
d
f
+1
,..., b
2d
f
} that corre-
sponds to coefficients −1 (lines 4 to 13). It flips a sign
of the temporary array t (lines 14 to 16), and then, it
goes through the first half of the array b, i.e. elements
{b
0
,..., b
d
f
} (lines 17 to 26).
For better understanding, we show a visualization
of Algorithm 4 in Fig. 2
3.2 Bugs in Algorithm 4
During our analysis, we found a few bugs in the im-
plementation that we must describe and correct in or-
der to be able to show the attack.
3.2.1 Parity of N
In several places in the code, the algorithm uses an
index of an array equal to both N/2 and (N − 1)/2.
Note that it is not possible to use both at the same
time. It depends on the parity of N. If N is odd, the
algorithm should call index (N − 1)/2. If N is even,
the algorithm should call index N/2. Otherwise, we
will use a non-integer index of an array.
To ensure that the algorithm would be correct if N
is both odd and even, we will preferably use bN/2c.
3.2.2 Final Subtraction of R
Algorithm 4 in the beginning initializes all elements
of an array t by random value r instead of just zero. In
the end, r is subtracted away from the array t. Unfor-
tunately, since we change the sign of t in the middle
of the algorithm (lines 14 and 15 in 1), this is not what
we want. In order to reverse the influence of r on out-
SPA Attack on NTRU Protected Implementation with Sparse Representation of Private Key
137

Algorithm 4: Countermeasure of NTRU Open Source
Project.
Require: cipher-text polynomial e ∈ R and coefficient loca-
tion indices of private key b
Ensure: H = F ·e (mod q)
1. for i = 0;i < N;i++ do
2. t
i
← r B r is a random value
3. end for
4. for j = d
f
+ 1; j < 2d
f
+ 1; j++ do
5. k ← b
j
6. x ←
N−1
2
− k, y ← N − k
7. t
N−1
2
← t
N−1
2
+ e
x
8. x ← x + 1
9. for i = 0; i <
N−1
2
;i++,x++,y++ do
10. t
N
2
+i+1
← t
N
2
+i+1
+ e
x
11. t
i
← t
i
+ e
y
12. end for
13. end for
14. for i = 0;i < N;i++ do
15. t
i
← −t
i
16. end for
17. for j = 0; j < d
F
+ 1; j++ do
18. k ← b
j
19. x ←
N−1
2
− k, y ← N − k
20. t
N−1
2
← t
N−1
2
+ e
x
21. x ← x + 1
22. for i = 0; i <
N−1
2
;i++,x++,y++ do
23. t
N
2
+i+1
← t
N
2
+i+1
+ e
x
24. t
i
← t
i
+ e
y
25. end for
26. end for
27. for i = 0;i < N;i++ do
28. H
i
← t
i
− r (mod q)
29. end for
30. return H
Figure 1: Description of algorithm 4 from (An et al., 2018)
as it is.
Figure 2: Visualization of algorithm 4.
put, we must as a matter of fact add r to the t in the
end.
3.2.3 Indices Out of Range
The most problematic issue, also concerning power
analysis, is that the index variables in the algorithm
are out of range of the intended arrays.
Variable k is assigned value b
j
in Line 5 of 1.
Note that b
j
can take values in range from 0 to N.
Then, variables x and y are assigned values
N−1
2
− k
and N − k respectively on line 6. Therefore, variable
x is initialized as a value in the range from −
N−1
2
to
N−1
2
, similarly variable y is initialized as a value in the
range from 0 to N. Since we iterate variables x and y
from the initialized value increasingly up to the next
N−1
2
values, see line 9, the variable x can range from
−
N−1
2
to N and similarly variable y ranges from 0 to
N +
N−1
2
. Let us remind that variables x and y are used
as index variables for array e with ciphertext that has
exactly N elements. We can see, that both variables
run out of the index range. There is no straightforward
correction of this bug that would not leak information
about the private key by power analysis.
3.3 Modified Implementation
Our suggested modification, see Figure 3 includes a
concatenation of the ciphertext with itself construct-
ing a twice as long array e := e||e allowing to go
outside of the boundaries of the original ciphertext.
We also simplify the computation using just one in-
dex variable y and omitting variable x, which makes
Algorithm 4 and the attack easier to understand. Nev-
ertheless, the attack would work to the version with
two index variables x and y as well.
Visualization of the modified version can be seen
in Figure 4.
4 OUR METHOD
For our attack to be successful, we assume that our
target leaks the hamming weight (HW) or hamming
distance (HD) of the operands of addition (steps 8, 18
in 3). This means that it is possible to distinguish the
cases when the added number (e
y
) is zero from the
cases it is non-zero.
We divide our attack into two cases. First, we
choose the input as a zero followed by high hamming
weight values (e.g. 255), i.e. we assume the cho-
sen ciphertext model. In the second case, we restrict
ourselves just to random input, i.e. we assume only
known ciphertext model.
In the case of chosen ciphertext model, we have
the privilege to have high hamming weight (HW) dif-
ferences that are directly visible in the trace. That
allows us to simply look for the minimum from a cor-
rectly chosen set of points in the trace. That gives sur-
prisingly good results. In the case of known cipher-
text model, i.e. we encounter only random cipher-
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
138

Correction of Algorithm 4.
Require: cipher-text polynomial e ∈ R and encoding b of
private key F
Ensure: H = F ·e (mod q)
1. for i = 0;i < N;i++ do
2. t
i
← r B r is a random value
3. end for
4. for j = d
f
+ 1; j < 2d
f
+ 1; j++ do
5. k ← b
j
6. y ← N − k
7. for i = 0; i < N;i++,y++ do
8. t
i
← t
i
+ e
y
9. end for
10. end for
11. for i = 0;i < N;i++ do
12. t
i
← −t
i
13. end for
14. for j = 0; j < d
F
+ 1; j++ do
15. k ← b
j
16. y ← N − k
17. for i = 0; i < N;i++,y++ do
18. t
i
← t
i
+ e
y
19. end for
20. end for
21. for i = 0;i < N;i++ do
22. H
i
← t
i
+ r (mod q)
23. end for
24. return H
Figure 3: Correction of Algorithm 4 from (An et al., 2018).
Figure 4: Visualization of modified Algorithm 4.
texts, such approach appeared to be ill-suited, since
the HW differences were very small and the influence
of other phenomena prevailed. We found better re-
sults with least-square method where we were look-
ing for rotation of set of points with the least sum of
squares of their differences. Such method is used to
obtain results in subsection 6.4.
If we do not state otherwise, in the rest of the paper
we assume the chosen ciphertext model. We argue
that in most practical scenarios, this ability is given to
the attacker or the attacker is effectively able to obtain
it.
4.1 Attack Description
Let us note that the attack is possible due to the sparse
representation of the private key and the high-level
description of the multiplication of polynomials in the
corresponding ring suggested by (An et al., 2018).
We will try to exploit operation t
i
→ t
i
+ e
y
that
happens on lines 8 and 18 in Fig. 3. If e
y
is zero,
then the value t
i
remains the same and the hamming
distance between the old and the new value is zero.
When updating the temporary array t on lines 7 – 9,
we can measure each addition and find out when we
will add this zero value.
Observe that the addition of the concrete zero
value will keep happening later and later depending
on the key value. To see that, let us repeat that our pri-
vate key is encoded in a sparse representation with in-
creasing degrees of coefficients – first 1 and then −1,
i.e. if the private key is 1 − x
1
+ x
2
+ x
3
− x
4
+ x
7
− x
8
we encode it as [0,2, 3,7,1, 4,8]. Therefore, values in
variable k assigned on line 5 will be continuously in-
creasing for the second half of the array b and then for
the first half of the array b (let us remind that the al-
gorithm first process the second half of b). We iterate
in for-cycle (lines 7-9) over all the ciphertext values
starting from value N − k.
We can see that the offset depends on the differ-
ence b
j+1
− b
j
for corresponding j and we can ob-
serve the corresponding offset by locating the addi-
tion of the zero in the ciphertext. For visualization
see Fig. 5.
At the end of the algorithm, we should know all
the differences b
1
− b
0
, b
2
− b
1
, . . . , b
2d
f
− b
2d
f
−1
.
Then, we can proceed with brute-force attack by try-
ing all N possible values of b
0
. Similar approach was
also used in (Lee et al., 2010) to attack another imple-
mentation of NTRU.
4.2 Attack Simulation
We implemented the target in Python and sim-
ulated the attack in the same programming lan-
guage. You can see a plot from the result in
Fig. 6 for values N = 31,q = 128,d
f
= 7, b =
[0,2,5, 7,9, 12,15,18, 1,3,6, 10,14, 16,17].
In the plot you can see 15 traces corresponding to
15 elements of b. Each trace contains N peaks cor-
responding to N additions t
i
→ t
i
+ e
y
in line 8. The
height of the peak corresponds to the Hamming dis-
tance between t
i
and t
i
+ e
y
.
Black arrows in the plot point on zero peaks (peak
of the height zero that corresponds to the addition of
the zero element of the ciphertext). Then, all the dif-
ferences b
j+1
− b
j
are visible from the plot by count-
SPA Attack on NTRU Protected Implementation with Sparse Representation of Private Key
139

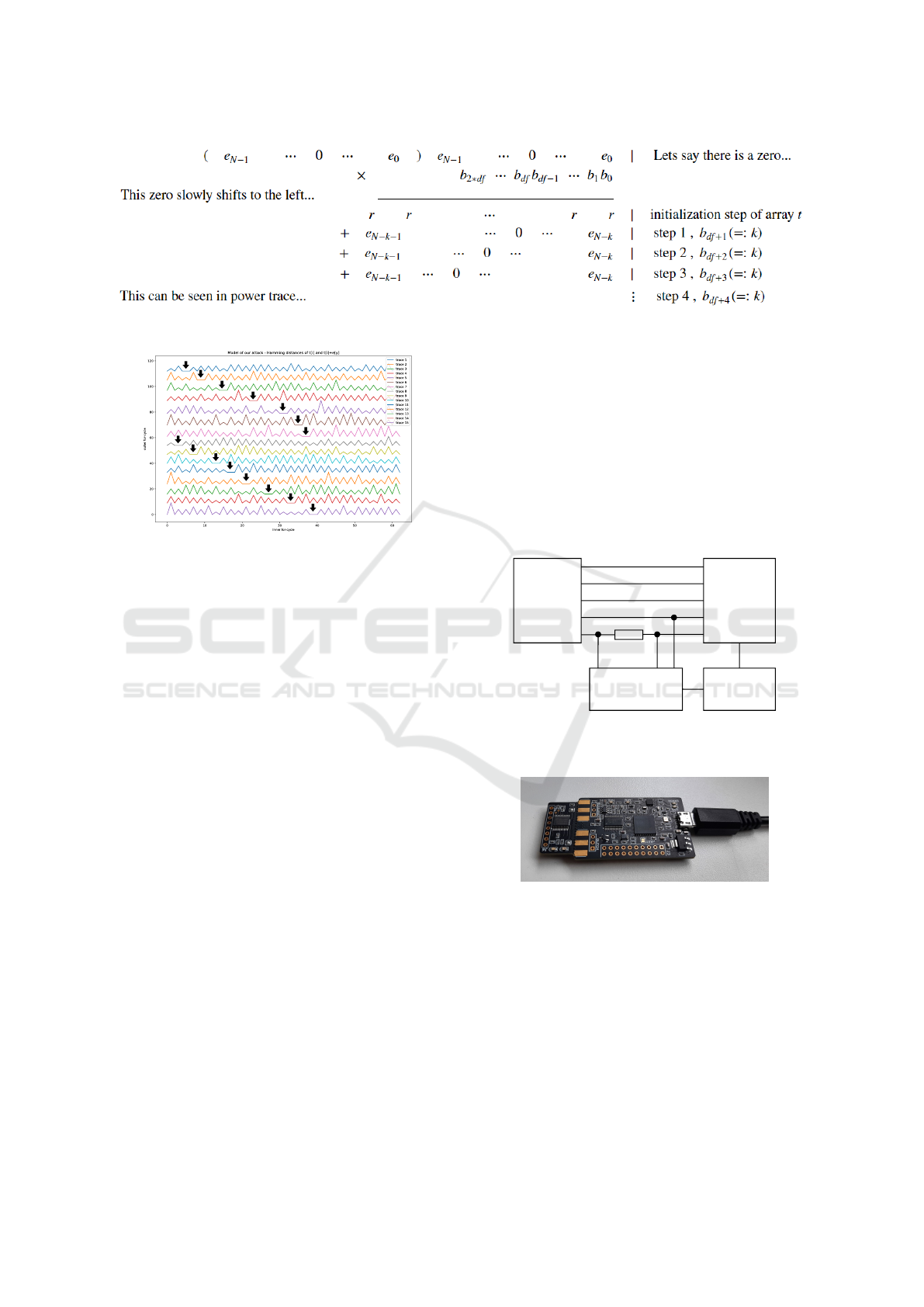
Figure 5: Visualization of the attack assuming we have zero in ciphertext.
Figure 6: Results of our simulation of the attack for
b = [0,2,5,7,9,12,15, 18, 1, 3, 6, 10, 14, 16, 17] and a ran-
dom ciphertext with a zero on the second position.
ing how many peaks are between the zero peaks in
j-th trace and the zero peak on ( j + 1)-th trace.
5 REALIZATION OF THE
ATTACK
We did two distinct experiments on different targets
to show the soundness of our attack and its indepen-
dence on concrete architecture. In both experiments,
we implemented the NTRU decryption algorithm in a
reduced form: we included only the polynomial mul-
tiplication function according to the Correction of Al-
gorithm 4. (Fig. 3). Furthermore, we chose the NTRU
instance with same parameters as in the previous sec-
tion, i.e. N = 31,q = 128, d
f
= 7.
In the first experiment, the target is an 8-bit mi-
crocontroller (Microchip AVR ATmega32A) mounted
on a smart card printed circuit board. The microcon-
troller was connected to a smart card reader through
a measurement adapter, see Fig. 7. The power con-
sumption signal was measured on a 50Ω series resis-
tor using a standard passive oscilloscope probe. We
used a Keysight DSOX3024T oscilloscope connected
to the controlling PC via USB. In this case, we per-
formed trace compression by averaging selected sam-
ples from the first half of each clock cycle of the mi-
crocontroller (after the rising edge of the microcon-
troller’s clock signal) to get a compressed trace sig-
nal.
In the second experiment, the target is a 32-bit mi-
crocontroller of the family ARM Cortex-M0, namely
STM32F0. The target is part of the development
board and kit - ARM ChipWhisperer-Nano, NAE-
CW1101-04, from NewAE Technology Inc., see Fig.
8. The second experiment allows us to do more mea-
surements and a more robust analysis of the success-
rate of the attack due to flexibility and simplicity of
the overall ChipWhisperer framework.
USB
USB PC
Control
GNDVtrace
Smart Card
Reader
DUT
ATmega32A
CLK
IO
VCC
Trigger
Oscilloscope
DSOX3024T
R = 50 Ω
Figure 7: Schematic diagram of measurement in the first
experiment – 8-bit AVR.
Figure 8: Setup in the second experiment – ChipWhisperer-
Nano (target and measurement sections) connected to the
PC via USB.
5.1 First Experiment – 8-bit
Microcontroller AVR
In order to improve signal quality, we performed 100
measurements of the same decryption run and aver-
aged a selected amount of traces (1 to 100). It turned
out that averaging already between 5 – 10 traces gave
us 100% probability of successful attack, as you can
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
140

see in Figure 9. Thus, the initial choice of perform-
ing 100 measurements proved to be superfluous. We
repeated this for several runs with different values
for the private key and ciphertext, which again con-
firmed the practicability of the attack. Nevertheless, a
more profound analysis with a larger data set was still
needed. We provide such analysis in subsection 5.2.
Figure 9: First experiment – 8-bit AVR: average trace of
polynomial multiplication (10 traces). The element b
10
= 2
of the private key is visible as a lowest value of the points
marked by circles.
5.2 Second Experiment – 32-bit
Microcontroller ARM Cortex-M0
We did a more robust analysis in the second exper-
iment with the ChipWhisperer platform and the tar-
get ARM Cortex-M0. We expected the leakage to be
lower, and we would get slightly worse results since
the target has a 32-bit architecture. Surprisingly, we
got even better results than in experiment 1, mean-
ing the success rate and necessary amount of traces
for a successful attack without any mistakes was even
lower. We presume it is an effect of a more precise
measurement method due to lower noise of the Chip-
Whisperer platform.
Statistics. For 5000 random keys, we measured 10
traces with chosen-ciphertext containing zero in the
beginning and coefficients with high hamming dis-
tance in the rest, namely 0xFF. That gave us data for
the following statistical analysis. Due to our chosen
parameters, each key is in the implementation rep-
resented as 15 coefficients. Our attack provides us
with guesses for each of these coefficients. Then we
count how many of them are different from the origi-
nal key. We see in Table 1 that our attack is in 91.0%
cases successful (with no wrong coefficients) using
just one measured trace. For example, if we measure
decryption of the same chosen ciphertext 3-times with
the same key and perform our attack on the averaged
trace, we get a 99.9% success rate.
Table 1: Second Experiment: Success rate for 5000 keys
with chosen ciphertext described in relative frequencies of
0, 1 or more than 1 wrong coefficients.
# of wrong coeff’s 0 1 ≥2
1 trace 91.0% 8.5% 0.4%
avg of 2 traces 99.6% 0.4% 0%
avg of 3 traces 99.9% 0.1% 0%
6 POSSIBLE MITIGATIONS AND
COUNTERMEASURES
6.1 Random Pre-Charging
One of the ways how to mitigate the leakage of the
hamming weight of one of the operands of the addi-
tion could be to randomly precharge the target register
holding the variable called t by adding a random value
before adding the array a and then subtracting the ran-
dom value away. You can see our implementation of
such mitigation using Extended Asm here, where t is
a temporary array with N elements, a is an input array
with 2N elements containing 2xciphertext, and rtmp
is an array with N random elements:
for (i = 0; i < N; ++i, ++y)
{
asm(
" ldrh r6, %[ti]\n\t"
" add r6, %[r]\n\t"
" add r6, %[ay]\n\t"
" strh r6, %[ti]\n\t"
// t[i] = t[i] + rtmp[i] + a[y];
" add r6, %[nr]\n\t"
" strh r6, %[ti]"
// t[i] = t[i] + (-rtmp[i])
: [ti] "=m" (t[i])
: [ay] "r" (a[y]), [r] "r" (rtmp[i]),
[nr] "r" (-rtmp[i])
: "r6"
);
}
Nevertheless, the influence of such mitigation ap-
peared to be questionable since results showed that it
gives on average one more wrong coefficient of the
key than in the case where we attack the implementa-
tion without this mitigation.
6.2 Randomization of the Temporary
Array
The paper (Lee et al., 2010) concludes that random
initialization of the temporary array t should be a suf-
ficient countermeasure against simple-power analy-
sis. This is true in the case of their implementation.
Unfortunately, because of changes the authors did in
SPA Attack on NTRU Protected Implementation with Sparse Representation of Private Key
141

(An et al., 2018), this countermeasure is no longer
sufficient.
Let us note that article (Lee et al., 2010) from
2010 states that the initialization of t as [r,r,.. .,r]
is not sufficient since an attacker could potentially
do a brute force attack trying all possible choices
for r (that should depend on concrete architecture).
Therefore, they suggest random initialization of t as
[r
1
,r
2
,..., r
N
].
Nevertheless, neither of these countermeasures
mitigates our attack, since it exploits different ham-
ming weights in the ciphertext (not in the target reg-
ister, which starts to be quite random during a normal
computation itself).
6.3 Random Key Rotation
(Wang et al., 2017) argues that a combination of ran-
dom initialization of t with a new protection called
random key rotation is secure against the first-order
power analysis.
The idea behind random key rotation is the follow-
ing: instead of straightforwardly multiplying cipher-
text with secret key e f (mod q), we choose random
i ∈ {0,.. .,N − 1}, then we compute f x
i
and ex
N−i
,
and finally, we multiply them getting the intended cor-
rect result ex
N−i
f x
i
= e f (mod q).
Random key rotation helps against statistical anal-
ysis methods, but it does not provide protection
against single-trace power analysis. Since our attack
on ChipWhisperer platform gave us around 90% ac-
curacy with just one trace, this mitigation is therefore
questionable, even so, if real-world cryptography will
use NTRU only in ephemeral usage.
6.4 Blinding Ciphertext
A possible countermeasure, originally against corre-
lation power analysis (CPA), is blinding the cipher-
text. It appeared to be also effective against simple
power analysis.
We can blind the ciphertext with an array [r, .. .,r],
or with [r
1
,..., r
N
] := R as described in (Lee et al.,
2010). Then we compute (e + R) f − R f . This coun-
termeasure would provide the same protection against
our attack as we would hypothetically get by limiting
the enemy to a ciphertext known model since in that
case the ciphertext can be assumed to be random. Re-
sults of carrying out the attack on random ciphertext
are shown in table 2.
Needless to say that this countermeasure is quite
expensive since it doubles the computational cost.
Table 2: Second Experiment: statistical results for 2000
keys with random ciphertext described in relative frequen-
cies of 0, 1, 2 or more than 2 wrong coefficients.
# of wrong coeff. 0 1 2 ≥3
1 trace 61.1% 28.6% 8.6% 1.7%
avg of 2 traces 97.9% 2.1% 0% 0%
avg of 3 traces 99.8% 0.2% 0% 0%
6.5 Randomization of Private Key B
A promising and low-cost countermeasure that had
the potential to affect our attack was the randomiza-
tion of b from (Lee et al., 2010). The implementation
stores the private key so that the elements of b are
in increasing order (separated in two halves). This is
not necessary. In fact, we can randomly permute the
first and the second half of the coefficients separately,
and the result would be the same. This can be done
before every decryption and it would make any sta-
tistical method significantly more difficult, e.g. cor-
relation power analysis or differential power analysis.
Although the paper (Lee et al., 2010) states that it is
not clear how much resistance it provides against sim-
ple power analysis.
We simulated this countermeasure to protect our
target implementation, but we concluded that it is still
vulnerable to our attack with modification. The im-
portant observation is that we can actually find the
original b that has increasing coefficients by exploit-
ing all the iterations of the outer for-cycle at once.
Randomization of b means just reordering of the rows
in Fig. 6.
7 CONCLUSION
We have closely studied one implementation of
NTRU that was supposed to provide protection
against simple power analysis by (An et al., 2018).
Unfortunately, their proposed implementation had
several bugs, so we needed to address them first.
Then, we theoretically explained an attack that re-
covers the secret key using few traces of decrypting
ciphertext that contains zero on target that complies
with hamming weight or hamming distance model.
We first simulated our theoretical attack on a model
in Python language for convenience. Then, we did
first practical experiment on 8-bit microcontroller of
the Microchip AVR family, namely ATmega32A, as
a proof of concept. Then we did a more profound
statistical analysis with 32-bit microcontroller ARM
Cortex-M0 as the target. This analysis showed that
with probability of 91% our attack is successful just
with a single trace assuming the attacker is able to
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
142

choose the decrypting ciphertext. If the attacker
acquires just one trace with random ciphertext, its
chance of success reduces to 61.1%. Potential future
work would be to use advantage of partial guessing
entropy and combine our side-channel attack together
with classical cryptoanalysis.
ACKNOWLEDGEMENTS
We would like to thank Michal Mar
ˇ
s
´
alek, with whom
the beginning of the research was carried out in
NCISA of the Czech Republic.
The authors also acknowledge the sup-
port of the OP VVV MEYS funded project
CZ.02.1.01/0.0/0.0/16 019/ 0000765 ”Research
Center for Informatics”, and the support by the Grant
Agency of the Czech Technical University in Prague,
grant No. SGS21/142/OHK3/2T/18.
REFERENCES
Alagic, G., Alperin-Sheriff, J., Apon, D., Cooper, D., Dang,
Q., Kelsey, J., Liu, Y.-K., Miller, C., Moody, D., Per-
alta, R., et al. (2020). Status report on the second
round of the NIST post-quantum cryptography stan-
dardization process. US Department of Commerce,
NIST.
An, S., Kim, S., Jin, S., Kim, H., and Kim, H. (2018). Single
trace side channel analysis on NTRU implementation.
Applied Sciences, 8(11):2014.
Askeland, A. and Rønjom, S. (2021). A side-channel as-
sisted attack on NTRU. Cryptology ePrint Archive.
Atici, A. C., Batina, L., Gierlichs, B., and Verbauwhede, I.
(2008). Power analysis on NTRU implementations for
RFIDs: First results.
Chen, L., Chen, L., Jordan, S., Liu, Y.-K., Moody, D., Per-
alta, R., Perlner, R., and Smith-Tone, D. (2016). Re-
port on post-quantum cryptography, volume 12. US
Department of Commerce, National Institute of Stan-
dards and Technology.
Karabulut, E., Alkim, E., and Aysu, A. (2021). Single-
Trace Side-Channel Attacks on ω-Small Polynomial
Sampling: With Applications to NTRU, NTRU Prime,
and CRYSTALS-DILITHIUM. In 2021 IEEE Inter-
national Symposium on Hardware Oriented Security
and Trust (HOST), pages 35–45. IEEE.
Lee, M.-K., Song, J. E., Choi, D., and Han, D.-G. (2010).
Countermeasures against power analysis attacks for
the NTRU public key cryptosystem. IEICE transac-
tions on fundamentals of electronics, communications
and computer sciences, 93(1):153–163.
Ravi, P., Ezerman, M. F., Bhasin, S., Chattopadhyay, A.,
and Roy, S. S. (2021). Will you cross the threshold for
me?-Generic side-channel assisted chosen-ciphertext
attacks on NTRU-based KEMs. Cryptology ePrint
Archive.
Schamberger, T., Mischke, O., and Sepulveda, J. (2019).
Practical evaluation of masking for ntruencrypt on
ARM cortex-m4. In International Workshop on Con-
structive Side-Channel Analysis and Secure Design,
pages 253–269. Springer.
Wang, A., Wang, C., Zheng, X., Tian, W., Xu, R., and
Zhang, G. (2017). Random key rotation: side-channel
countermeasure of NTRU cryptosystem for resource-
limited devices. Computers & Electrical Engineering,
63:220–231.
Zheng, X., Wang, A., and Wei, W. (2013). First-order colli-
sion attack on protected NTRU cryptosystem. Micro-
processors and Microsystems, 37(6-7):601–609.
SPA Attack on NTRU Protected Implementation with Sparse Representation of Private Key
143