Leveraging Explainability with K-Fold Feature Selection

Artur J. Ferreira

1,2,3 a

and M

ario A. T. Figueiredo

1,2,3 b

ISEL, Instituto Superior de Engenharia de Lisboa, Instituto Polit

ecnico de Lisboa, Portugal

IST, Instituto Superior T

ecnico, Universidade de Lisboa, Portugal

Instituto de Telecomunicac¸

oes, Lisboa, Portugal

ﬁ

Keywords:

Cancer Detection, Classiﬁcation, k-Fold Data Split, Explainability, Feature Selection, Leave-One-Out.

Abstract:

Learning with high-dimensional (HD) data poses many challenges, since the large number of features often

yields redundancy and irrelevance issues, which may decrease the performance of machine learning (ML)

methods. Often, when learning with HD data, one resorts to feature selection (FS) approaches to avoid the

curse of dimensionality. The use of FS may improve the results, but its use by itself does not lead to explain-

ability, in the sense of identifying the small subset of core features that most inﬂuence the prediction of the

ML model, which can still be seen as a black-box. In this paper, we propose k-fold feature selection (KFFS),

which is a FS approach to shed some light into that black-box, by resorting to the k-fold data partition proce-

dure and one generic unsupervised or supervised FS ﬁlter. KFFS ﬁnds small and decisive subsets of features

for a classiﬁcation task, at the expense of increased computation time. On HD data, KFFS ﬁnds small subsets

of features, with dimensionality small enough to be analyzed by human experts (e.g, a medical doctor in a

cancer detection problem). It also provides classiﬁcation models with lower error rate and fewer features than

those provided by the use of the individual supervised FS ﬁlter.

1 INTRODUCTION

The use of machine learning (ML) techniques has

been proven successful for different problems. How-

ever, there are still many challenges and open prob-

lems. One that is worthy of attention is feature selec-

tion (FS), which is to ﬁnd the best set of features for a

given ML model and task (Guyon et al., 2006; Guyon

and Elisseeff, 2003). Despite its long research his-

tory and the emergence of deep learning techniques,

which minimize the need to perform a separate fea-

ture extraction and selection phase, many efforts still

continue within the research for adequate FS tech-

niques (Alipoor et al., 2022; Chamlal et al., 2022;

Huynh-Cam et al., 2022; Jeon and Hwang, 2023; Xu

et al., 2022). When learning with high-dimensional

(HD) data, performing FS becomes a challenge, due

to the curse of dimensionality (Bishop, 1995). The use

of FS improves the results, but its standard use may

not be enough to achieve explainability, in the sense

of identifying the smallest subset of features that most

inﬂuence the prediction results of the ML model, on a

given task.

As ML models become more complex, the re-

https://orcid.org/0000-0002-6508-0932

https://orcid.org/0000-0002-0970-7745

search community has gained interest in their ex-

plainability (Hanif et al., 2021; Tjoa and Guan, 2021;

Xu et al., 2019). Explainable artiﬁcial intelligence

(XAI)-based methods are growing in popularity. In

this work, explainability refers to the identiﬁcation of

the subset of features that is the most decisive for a su-

pervised classiﬁcation task. The interpretation, that is

the determination of the connection between the cause

(the feature) and the effect (the prediction), is left to

the human expert on the ﬁeld of the dataset (for in-

stance, a medical doctor for cancer detection).

In this paper, we propose k-fold feature selection

(KFFS), a FS ﬁlter approach to leverage the results

of any unsupervised or supervised FS ﬁlter. We re-

sort to the k-fold data partition procedure to assess

which features are chosen more often. KFFS shows

improvement as compared to the use of the individual

FS ﬁlter. The remainder of this paper is organized as

follows. In Section 2, we overview the state-of-the-

art in FS techniques and explainability on supervised

classiﬁcation. The proposed approach is described in

Section 3. The experimental evaluation is reported in

Section 4. Finally, Section 5 ends the paper with some

concluding remarks and directions of future work.

458

Ferreira, A. and Figueiredo, M.

Leveraging Explainability with K-Fold Feature Selection.

DOI: 10.5220/0011744400003411

In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 458-465

ISBN: 978-989-758-626-2; ISSN: 2184-4313

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 RELATED WORK

In this section, we review related work on the key as-

pects of FS techniques over the past years, as well

as some existing approaches to provide explainability

for classiﬁcation models. In Subsection 2.1, we de-

scribe the key notation followed in this paper. Subsec-

tion 2.2 overviews the ﬁlter FS technique addressed in

the experimental evaluation. Finally, Subsection 2.3

refers to recent works on explainable models.

2.1 Notation and Terminology

Let X = {x

,... ,x

} be a dataset, with n pat-

terns/instances/examples, on a n × d matrix, in which

the rows hold the patterns and the columns are the

features. Each pattern x

is a d−dimensional vector,

where d is the number of features/attributes/variables,

designated as X

, with i ∈ {0, .. ., d − 1}. Let

C denote the number of distinct class labels, with

∈ {1,. .. ,C} denoting the class of pattern i and

y = {c

,. .. ,c

} is the set of class labels correspond-

ing to the n patterns.

2.2 Feature Selection Filters

It is well-known that the use of FS techniques usu-

ally improves the accuracy of a classiﬁer learnt from

data and allows for faster training. Another beneﬁt

of FS is that it mitigates the effects of the curse of di-

mensionality. Over the past decades, researchers have

come up with many different FS algorithms, which

are usually placed into one of four categories (Guyon

et al., 2006): wrappers; embedded; ﬁlters; hybrid.

For recent surveys on FS techniques see the publica-

tions by Remeseiro and Bolon-Canedo (2019),Pudji-

hartono et al. (2022), and Dhal and Azad (2022).

In this work, we focus on ﬁlter methods which as-

sess the goodness of a given subset of features using

characteristics of that subset, without resorting to a

speciﬁc learning algorithm. These approaches keep

some features and discard others, based on some cri-

terion, which is independent of the subsequent learn-

ing algorithm. Filters are the simplest and fastest

approach, thus one would expect that these meth-

ods would perform worse than the other approaches.

However, in many big-data and HD scenarios, ﬁlter

approaches are often the only applicable choice.

Some successful FS ﬁlters follow the relevance-

redundacy (RR) framework (Yu and Liu, 2003). In a

nutshell, the RR framework is based on the idea that a

dataset is composed by (weakly or strongly) relevant,

redundant, and non-redundant features. The FS meth-

ods aim to ﬁnd the most relevant and non-redundant

features. In this work, we consider the use of the fast

correlation-based ﬁlter (FCBF), proposed by Yu and

Liu (2003, 2004). FCBF computes feature-class and

feature-feature correlations. It starts by selecting a

set of features that is highly correlated with the class,

with a correlation value above some threshold set by

the user. The features with higher correlation with

the class are called predominant, in the ﬁrst step. This

correlation is assessed by the symmetrical uncertainty

(SU) (Yu and Liu, 2003) measure, deﬁned as

SU(X

) =

2I(X

)

H(X

) + H(X

)

, (1)

where H(.) denotes the Shannon entropy and I(.)

denotes the mutual information (MI) (Cover and

Thomas, 2006). The SU is zero for independent ran-

dom variables and equal to one for deterministically

dependent random variables, i.e., if one is a bijective

function of the other. In the second step, a redundancy

detection procedure ﬁnds redundant features among

the predominant ones. The set of redundant features is

further split in order to remove the redundant ones and

keep those that are the most relevant to the class. In

order to remove the redundant features, three heuristic

criteria are applied.

2.3 Explainability and Interpretability

In recent years, there has been interest in addressing

techniques to provide explainability and interpretabil-

ity (Lou et al., 2013; Ribeiro et al., 2016; Bastani

et al., 2017; Kim et al., 2018; Mothilal et al., 2020;

Lakkaraju and Bastani, 2020). This interest has in-

creased mainly due to the need to interpret deep learn-

ing models, due to their size, complexity, and opacity.

One famous approach is SHapley Additive ex-

Planations (SHAP), a game-theoretic method to ex-

plain the output of any ML model. It connects op-

timal credit allocation with local explanations using

Shapley values, a notion imported from cooperative

game theory. The SHAP values provide insights into

the importance of each feature. A general method

to obtain representative SHAP values was proposed

by Scheda and Diciotti (2022), using nested cross-

validation (CV).

Another approach is local interpretable model-

agnostic explanations) (LIME) (Ribeiro et al., 2016),

which explains the predictions of any classiﬁer with

an interpretable model, locally around the prediction.

The explainable boosting machine (EBM) (Lou et al.,

2013) is a tree-based, cyclic gradient boosting gener-

alized additive model with automatic interaction de-

tection. An EBM model is often as accurate as state-

of-the-art black-box models, while remaining com-

pletely interpretable. Although EBM are often slower

Leveraging Explainability with K-Fold Feature Selection

459

to train than other algorithms, they are extremely

compact and fast at prediction time.

Regarding cancer detection explainability Moor-

thy and Mohamad (2011) proposed a random forest

(RF) method that performs both FS and classiﬁcation

of microarray data. It aims to ﬁnd the smallest pos-

sible sets of genes (features) with lowest error rates.

Rostami et al. (2022) introduced a FS method that in-

tegrates the concept of node centrality and commu-

nity detection. That method selects a subset of genes

with the lowest similarity and highest dependency,

showing improvement as compared to previous ap-

proaches.

Another approach for explainability is knowledge

distillation (KD), which transfers knowledge from a

large model to a smaller one (Bastani et al., 2017).

The large model acts as the black-box or teacher. The

smaller model is the explainer or student. Thus, the

student model is learned to imitate the behavior of the

teacher, while being interpretable.

The hybrid FS algorithm ﬁlter-dominating hybrid

sequential forward ﬂoating search (FDHSFFS) was

proposed by Gan et al. (2014). Qi et al. (2019)

use FDHSFFS embedded with CV methods on four

datasets with dimensionality ranging from 32 to 528

features. They found large differences in the resulting

feature subspace dimensionality, concluding that 2-

fold CV and leave-one-out (LOO) CV are more suit-

able for evaluation with low-dimensional and small

sample datasets, and 10-fold nested CV and 10-fold

CV are more adequate for HD datasets.

In recent work, Szepannek and L

ubke (2022) ad-

dress the partial dependence plots (PDP), which is a

model-agnostic assessment of each feature effect on

the model response. The authors address the degree of

model explainability in a forensic problem extending

the concept of explainability to the multiclass case.

3 PROPOSED APPROACH

In this section, we describe our proposed approach.

First, we state the key ideas that are the basis of

our proposal and then we present it in an algorithmic

style. For a dataset with n instances and d features,

these key ideas are as follows:

• Use of the k-fold data partition procedure with

varying values of k, which can be taken into the

extreme value of n instances, yielding a leave-

one-out (LOO) data partition.

• Apply a generic unsupervised or supervised FS

ﬁlter k times (once per fold, on the training data

subset).

• Set an array of d global counters (one per feature)

with the number of times that each feature is cho-

sen on the k folds.

• Keep the features with counters above some

threshold T

and discard the others.

• The importance of a feature is proportional to the

number of times it is chosen, on the k folds, by the

FS ﬁlter.

We expect that different samplings of the training data

with a FS ﬁlter may identify the features that provide

explainability of the data. Features that are chosen

more often will have more impact on the average ML

model performance. Algorithm 1 details KFFS.

4 EXPERIMENTAL EVALUATION

In this section, we report the experimental evaluation

of the proposed method. Subsection 4.1 describes

the public domain datasets along with their respective

tasks as well as the experimental settings. In Sub-

section 4.2, we analyze the behavior of KFFS as a

function of its parameters. Subsection 4.3 reports ex-

perimental results for explainability with cancer de-

tection datasets, while in Subsection 4.4 we address

all the datasets. Finally, Subsection 4.5 discusses the

key ﬁndings of the experimental evaluation.

4.1 Datasets and Settings

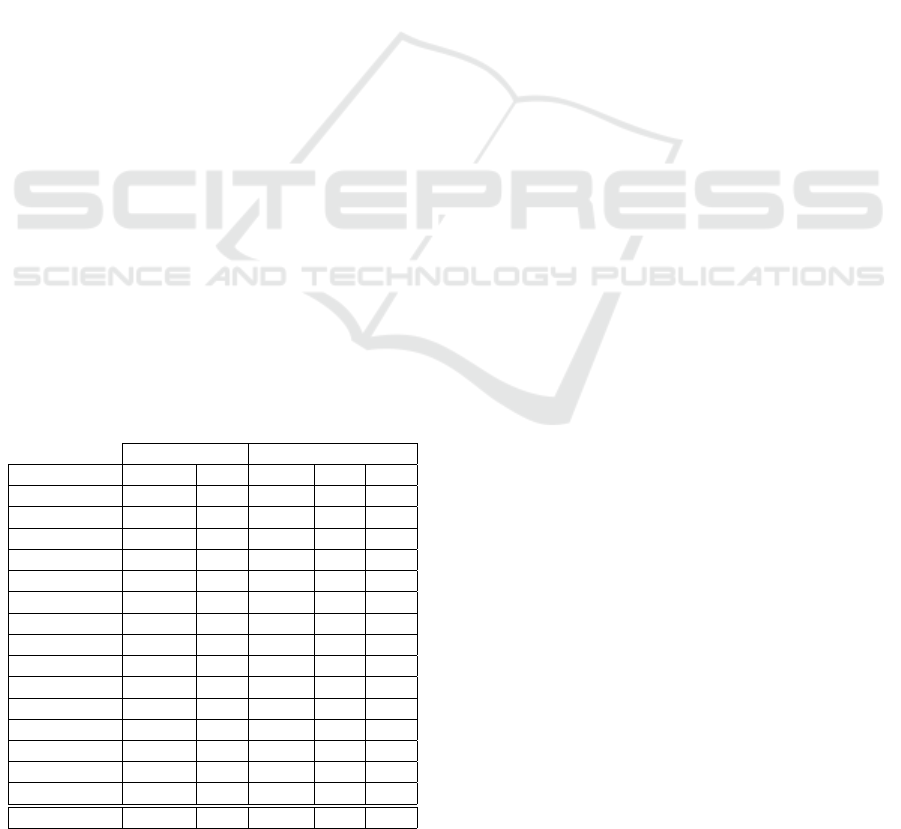
Table 1 summarizes the main characteristics of the

microarray datasets used in this work. In this table,

we have gathered datasets from different problems,

some with low-dimensionality and the majority with

high-dimensionality. We have included many cancer

detection datasets, since this is an application sce-

nario in which the proposed approach can be poten-

tially most useful. These datasets can be obtained

from different public repositories, such as the Uni-

versity of California at Irvine (UCI) https://archive.

ics.uci.edu/ml/index.php, knowledge extraction evo-

lutionary learning (KEEL), https://sci2s.ugr.es/keel/

datasets.php, and https://csse.szu.edu.cn/staff/zhuzx/

Datasets.html.

Many of these datasets have more features than

instances, that is, n ≪ d, leading to challenging situ-

ations for ML techniques (Bishop, 1995), which are

the ones that we intend to address with KFFS. We

use the FCBF implementation of the Arizona State

University (ASU) repository, https://jundongl.github.

io/scikit-feature/ with its default parameters. The lin-

ear support vector machines (SVM) and the na

ıve

Bayes (NB) classiﬁers from the Waikato environment

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

460

Algorithm 1: k-Fold Feature Selection (KFFS) for unsupervised or supervised FS.

Input: X: n × d matrix, n patterns of a d-dimensional dataset.

@ f ilter : a FS ﬁlter (unsupervised or supervised).

k : an integer stating the number of folds (k ∈ {2,. . .,n}).

: a threshold (percentage) to chose the number of features.

y : n× 1 class label vector (necessary only in case of a FS supervised ﬁlter).

Output: idx: m−dimensional vector with the indexes of the selected features.

1: Allocate the feature counter vector (FCV ), with dimensions 1 × d, such that each position refers to a speciﬁc feature.

2: Initialize FCV

= 0, with i ∈ {0,.. .,d − 1}.

3: Compute the k data folds in the dataset (different splits into training and test data).

4: For each fold, apply @ f ilter on the training data and update FCV

with the number of times @ f ilter selects feature i.

5: After the k data folds are processed, convert FCV to percentage: FCVP ← FCV/k.

6: Keep the indexes of the features that have been selected at least T

times (expressed in percentage), idx ← FCVP ≥ T

7: Return idx (the vector with the indexes of the selected features that have been selected at least T

times).

for knowledge analysis (WEKA) tool are used in the

experiments. The evaluation metrics are the test-set

error rate, using LOOCV and the running time of the

FS algorithms. We also perform some statistical sig-

niﬁcance tests to the error rate.

The experiments were carried out in MATLAB

R2018a, on a laptop computer running Windows 10

(64 bit), with 16 GB of RAM and a CPU with 1.7

GHz clock frequency.

4.2 Sensitivity Analysis

In this subsection, we analyze the behavior of KFFS

as functions of its parameters. First, we analyze the

percentage of the number of times a feature is cho-

sen on the LOO procedure by the FCBF ﬁlter. Fig-

ure 1 shows these values for the Dermatology and

Colon datasets. On the Dermatology dataset, we ob-

Table 1: Datasets with n instances, d features, and C classes.

Name n d C Problem

Brain-Tumor-1 90 5920 5 Cancer detection

Brain-Tumor-2 50 10367 4 Cancer detection

CLL-SUB-11 111 11340 3 Leukemia detection

Colon 62 2000 2 Cancer detection

Dermatology 358 34 6 Skin disease detection

DLBCL 77 5469 2 Detect B-cell malignancies

GLA-BRA-180 180 49151 4 Glioma grade analysis

GLI-85 85 22283 2 Glioma detection

Hepatitis 155 19 2 Hepatitis survival

Ionosphere 351 34 2 Radio detection

Leukemia 72 7129 2 Leukemia detection

Leukemia-1 72 5328 3 Leukemia detection

Leukemia-2 72 11226 3 Leukemia detection

Libras 360 90 15 Hand movement type

Lymphoma 96 4026 9 Lymphoma detection

Prostate-Tumor 102 10509 2 Prostate tumor detection

SMK-CAN-187 187 19993 2 Lung cancer detection

Sonar 208 60 2 Distinguish sonar signals

SRBCT 83 2308 4 Cancer detection

TOX-171 171 5748 4 Brain tumor detection

Wine 178 13 3 Three wine cultivars

serve that FCBF never selects 13 features in any of the

n = 358 folds. On the n folds, FCBF has selected at

least once 21 features. However, some of these fea-

tures have a small percentage of choice over all the

folds (say, for instance features 9 and 22). For the

Colon dataset, on the n = 62 folds, FCBF selects at

least once 62 features and never selects 1938 features.

We now check the impact of changing the thresh-

old T

, for ﬁxed k = n. Figure 2 shows on the left yy-

axis the test-set error rate as a function of the thresh-

old T

for the DLBCL dataset, with the SVM classi-

ﬁer. We display the baseline error (no FS, Err=2.60%)

and the error rate attained by FCBF (Err=2.60%) as

well as the average number of features per fold, m =

66. For KFFS, we have considered T

∈ {1, .. ., 100}

with @ﬁlter=FCBF and k = n. This ﬁgure also shows

the average number of selected features m for KFFS,

as functions of the threshold, on the right yy-axis.

As expected, as the threshold increases KFFS selects

fewer features. For T

= 80, KFFS attains lower error

rate than the baseline, using m = 48 features. Thus, it

is able to reduce the dimensionality from d = 5469 to

m = 48, with lower error rate and fewer features, as

compared to the single use of FCBF.

We now check on the effect of the choice of the

number of folds k used by KFFS, with threshold T

40. The range of values considered is k ∈ {2, .. ., 10},

with independent tests for each value of k. Figure 3

(top) shows the test set error rate attained by baseline,

FCBF, and KFFS with FCBF and the number of fea-

tures m per fold, on the Prostate-Tumor dataset. On

the bottom of the ﬁgure, we display the running time

of KFFS as a function of k. Regarding the error rate,

using different values of k leads to adequate values,

since there we ﬁnd several values of k that yield bet-

ter results than those of the baseline and FCBF meth-

ods. The increase of k leads to a linear increase on the

running time, as expected.

Leveraging Explainability with K-Fold Feature Selection

461

Figure 1: Percentage of choice for each feature by FCBF with the LOO procedure on the Dermatology and Colon datasets.

Figure 2: Test set error rate for baseline (no FS), FCBF, and

KFFS (with @ﬁlter=FCBF and k = n) with the SVM classi-

ﬁer on the DLBCL dataset (left yy-axis) as a function of the

threshold T

∈ {1,..., 100}. Number of selected features,

m, as a function of the threshold (right yy-axis).

4.3 Cancer Detection and Explainability

Using KFFS with FCBF we apply Algorithm 1, with

k = n, and varying threshold values in the range of

the integers from 1 to 100, to identify the smallest

subset of features with the lower error for cancer de-

tection. For each one of the outputs provided by Al-

gorithm 1 (the idx vector), we use the SVM classiﬁer

with LOOCV and evaluate the generalization error.

Then, we identify the threshold that leads to the low-

est Err using fewer features. The experimental results

are reported in Table 2 and show that, when time is

not a constraint, KFFS ﬁnds quite small subsets of

features to provide explainability for cancer detection

data. For all datasets, except Leukemia-1 and TOX-

171, the error rate decreases with the KFFS algorithm.

For all datasets, we get a large decrease on the dimen-

sionality, leading to a human-manageable number of

features. In many cases, the generalization error on

the reduced subspace is much lower than on the orig-

Figure 3: On top, the test set error rate (Err, in %) for

baseline, FCBF, KFFS (with @ﬁlter=FCBF and T

= 40)

with the SVM classiﬁer on the Prostate-Tumor dataset, for

k ∈ {2, ..., 10}. On bottom, the running time of KFFS in

seconds, as a function of k.

inal space, leveraging the explainability of the data.

The human experts will then provide interpretability

on the causes (features) that lead to a given conse-

quence regarding the presence/absence of cancer and

the type of cancer (classiﬁcation).

4.4 Evaluation with All Datasets

In this subsection, we report the experimental results

of KFFS with the FCBF ﬁlter and k = n, that is, Algo-

rithm 1 with the LOO procedure. Table 3 presents,

for each dataset, the estimates of the error rate of

the linear SVM classiﬁer for the baseline case (no

FS) and for the FCBF use. We also apply KFFS us-

ing FCBF with threshold T

∈ {40,50, 60,70, 80}.

In most cases, KFFS yields an improvement of the

results of the FCBF ﬁlter. In many cases, the use

of FCBF under the KFFS framework leads to a sig-

niﬁcant reduction on the dimensionality of the data.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

462

For instance, with T

= 60 on the Leukemia-2 dataset

(which has d = 11226), we get m = 61 with Err=0%.

These 61 features would serve to explain leukemia de-

tection and to distinguish between different types of

leukemia (for this dataset, c = 3). These experimental

results also show that the KFFS approach seems to be

preferable for HD datasets. In terms of average error

rate for all datasets, the KFFS algorithm with FCBF

and T

= 40 achieves the best results.

Table 4 reports a similar test as in Table 3, now us-

ing the NB classiﬁer. Again, using the NB classiﬁer,

we observe a dramatic reduction on the dimensional-

ity and a statistical signiﬁcant decrease on the clas-

siﬁcation error. In terms of average error rate for all

datasets, the KFFS algorithm with FCBF and T

= 40

achieves the best results.

4.5 Discussion

We have found that the output of KFFS is sensitive to

the setting of the threshold parameter. In many HD

datasets, by choosing appropriate thresholds, KFFS

can lead to smaller subsets of features with lower er-

ror than both the baseline version and the one pro-

vided by the use of FCBF. Regarding the number of

folds, k, we have found that the running time of the

algorithm increases linearly with it. For k = 10, i.e.

feature assessment with 10-fold CV in KFFS, we at-

tain adequate results with many datasets. Even with

Table 2: The lower Err (with LOOCV) with fewer features

(m) and the best threshold T

found by KFFS (with k = n

and @ f ilter =FCBF), on cancer detection datasets. The

evaluation is performed with the SVM classiﬁer, with vary-

ing thresholds T

∈ {1,2, . ..,100}. For the error rates,

the Friedman test p-value is p = 0.0075 (≤ 0.05), and the

paired-sample t-test is t = 0.0013 (≤ 0.05), thus having sta-

tistical signiﬁcance.

Baseline SVM KFFS (FCBF, k = n)

Dataset d Err Best T

m Err

Brain-Tumor-1 5920 10.00 20 132 5.56

Brain-Tumor-2 10367 22.00 78 32 10.00

CLL-SUB-11 11340 18.92 17 125 5.41

Colon 2000 17.74 83 9 12.90

DLBCL 5469 2.60 89 36 0.00

GLA-BRA-180 49151 27.22 93 24 17.78

GLI-85 22283 8.24 99 9 3.53

Leukemia 7129 1.39 88 24 0.00

Leukemia-1 5327 2.78 2 157 4.17

Leukemia-2 11225 4.17 87 36 0.00

Lymphoma 4026 4.17 82 177 2.08

Prostate-Tumor 10509 8.82 100 11 3.92

SMK-CAN-187 19993 27.27 54 39 20.32

SRBCT 2308 0.00 87 42 0.00

TOX-171 5748 0.00 1 291 1.17

Average 11519.67 10.35 – 76.27 5.79

values lower than 10, KFFS yields adequate results in

some datasets, with fast computation time. In generic

terms, as k tends to n, we assure the best results to-

wards the joint minimization of the size of the sub-

set of features and the generalization error rate, at the

expense of additional computation time. For cancer

detection datasets, our approach is able to ﬁnd small

subsets of features with very low generalization er-

ror. The resulting size of these subsets allows them to

be interpreted and analyzed by humans. In this case,

time is not the key factor to be considered, since the

aim is to identify the features that explain cancer clas-

siﬁcation. On the evaluation of the methods, we also

have found that the use of LOOCV provides better

estimates than those with 10-fold CV.

5 CONCLUSIONS

Learning with high-dimensional data is a challenging

task. High-dimensional feature spaces pose many dif-

ﬁculties that can be mitigated by using feature selec-

tion techniques. In some problems, it is important to

achieve accuracy in classiﬁcation but it is also impor-

tant to provide means to explain and interpret the de-

cisions taken by the learned models.

In this paper, we proposed a technique that is

able to successfully perform feature selection on high-

dimensional data and to signiﬁcantly reduce its di-

mensionality. The technique ﬁnds feature subspaces

small enough to be interpreted by a human user (e.g.

a clinical expert, for cancer detection). We resort to

a feature selection ﬁlter and the k-fold data partition

procedure. After the k-fold procedure is carried out,

we analyze the fraction of times that each feature is

chosen. The larger this fraction, the more important

that feature is ranked. As compared to the standard

use of one ﬁlter, our approach can be seen as adding

counters to the selection of each feature, and then

post-processing those counters to ﬁnd values above

a threshold to output the ﬁnal subset of features.

The experimental results on a large number of

datasets with different problems, show that the pro-

posed approach can leverage the results of one sin-

gle ﬁlter, by choosing an appropriate threshold, at the

expense of computation time. The extra time taken

in our procedure is the trade-off to ﬁnd these human

manageable and interpretable feature subsets.

As future work, we intend to compare our pro-

posal with the permutation feature importance tech-

nique. We also plan to combine different ﬁlters to ex-

plore the use of union and intersection of the feature

subspaces, provided by each ﬁlter.

Leveraging Explainability with K-Fold Feature Selection

463

Table 3: The average number of features (m) and the average test error rate (Err, %) with the linear SVM classiﬁer with

LOOCV, using FCBF and KFFS, with thresholds T

∈ {40, 50,60,70,80}. The best result (lower Err with fewer features,

m) in bold face. Regarding the error rates, the Friedman test p-value is p = 9.3161 × 10

−8

(≤ 0.05), thus having statistical

signiﬁcance.

KFFS using FCBF (k = n)

Baseline SVM FCBF only T

= 40 T

= 50 T

= 60 T

= 70 T

= 80

Dataset d Err m Err m Err m Err m Err m Err m Err

Brain-Tumor-1 5920 10.00 108.8 15.56 107.0 6.67 101.0 6.67 95.0 7.78 72.0 8.89 51.0 11.11

Brain-Tumor-2 10367 22.00 76.1 20.00 69.0 10.00 62.0 8.00 51.0 8.00 40.0 6.00 31.0 12.00

CLL-SUB-11 11340 18.92 79.9 32.43 76.0 9.91 63.0 13.51 52.0 16.22 44.0 12.61 41.0 14.41

Colon 2000 17.74 14.7 17.74 16.0 9.68 14.0 11.29 12.0 12.90 12.0 12.90 10.0 12.90

Dermatology 34 2.51 14.1 3.91 14.0 3.07 14.0 3.07 14.0 3.07 14.0 3.07 14.0 3.07

DLBCL 5469 2.60 66.5 2.60 63.0 2.60 61.0 2.60 58.0 2.60 56.0 2.60 44.0 2.60

GLA-BRA-180 49151 27.22 173.4 32.22 167.0 21.11 139.0 22.22 112.0 22.78 92.0 22.22 62.0 20.00

GLI-85 22283 8.24 132.6 11.76 132.0 3.53 116.0 4.71 103.0 5.88 88.0 5.88 72.0 5.88

Hepatitis 19 24.52 6.9 20.00 7.0 19.35 7.0 19.35 7.0 19.35 7.0 19.35 7.0 19.35

Ionosphere 34 11.97 4.1 16.81 4.0 16.81 4.0 16.81 4.0 16.81 4.0 16.81 4.0 16.81

Leukemia 7129 1.39 50.6 2.78 51.0 1.39 49.0 1.39 47.0 1.39 44.0 0.00 35.0 1.39

Leukemia-1 5327 2.78 50.4 8.33 48.0 5.56 43.0 5.56 42.0 5.56 37.0 6.94 27.0 5.56

Leukemia-2 11225 4.17 81.3 2.78 83.0 0.00 75.0 0.00 61.0 0.00 53.0 1.39 42.0 1.39

Libras 90 26.67 9.9 42.78 10.0 41.67 10.0 41.67 10.0 41.67 10.0 41.67 10.0 41.67

Lymphoma 4026 4.17 273.7 4.17 272.0 2.08 256.0 3.13 238.0 3.13 218.0 3.13 188.0 2.08

Prostate-Tumor 10509 8.82 71.8 7.84 73.0 5.88 61.0 6.86 55.0 6.86 52.0 5.88 45.0 7.84

SMK-CAN-187 19993 27.27 49.9 32.09 51.0 22.99 41.0 20.32 34.0 25.13 30.0 22.99 26.0 24.60

Sonar 60 22.60 10.0 22.60 12.0 22.12 10.0 21.63 8.0 25.00 8.0 25.00 8.0 25.00

SRBCT 2308 0.00 79.3 0.00 82.0 0.00 78.0 0.00 74.0 0.00 68.0 0.00 59.0 0.00

TOX-171 5748 0.00 83.7 8.77 85.0 4.68 76.0 4.09 67.0 4.68 58.0 4.68 51.0 7.60

Wine 13 1.12 10.0 0.56 10.0 0.56 10.0 0.56 10.0 0.56 10.0 0.56 10.0 0.56

Average 8240.24 11.65 68.94 14.56 68.19 9.98 61.43 10.16 54.95 10.92 48.43 10.60 39.86 11.23

Table 4: The average number of features (m) and the average test error rate (Err, %) with the NB classiﬁer with LOOCV,

using FCBF and KFFS, with thresholds T

∈ {40,50,60,70,80}. Best result (lower Err with fewer features, m) in bold face.

Regarding the error rates, the Friedman test p-value is p = 2.2414 × 10

−6

(≤ 0.05), thus having statistical signiﬁcance.

KFFS using FCBF (k = n)

Baseline NB FCBF only T

= 40 T

= 50 T

= 60 T

= 70 T

= 80

Dataset d Err m Err m Err m Err m Err m Err m Err

Brain-Tumor-1 5920 10.00 108.8 15.56 107.0 8.89 101.0 8.89 95.0 10.00 72.0 10.00 51.0 13.33

Brain-Tumor-2 10367 30.00 76.1 30.00 69.0 12.00 62.0 12.00 51.0 12.00 40.0 16.00 31.0 14.00

CLL-SUB-11 11340 32.43 79.9 28.83 76.0 14.41 63.0 14.41 52.0 13.51 44.0 14.41 41.0 15.32

Colon 2000 41.94 14.7 22.58 16.0 16.13 14.0 16.13 12.0 14.52 12.0 14.52 10.0 14.52

Dermatology 34 2.51 14.1 3.91 14.0 3.63 14.0 3.63 14.0 3.63 14.0 3.63 14.0 3.63

DLBCL 5469 18.18 66.5 6.49 63.0 3.90 61.0 3.90 58.0 3.90 56.0 3.90 44.0 2.60

GLA-BRA-180 49151 32.22 173.4 33.33 167.0 19.44 139.0 21.11 112.0 19.44 92.0 20.00 62.0 18.33

GLI-85 22283 17.65 132.6 17.65 132.0 5.88 116.0 5.88 103.0 7.06 88.0 4.71 72.0 4.71

Hepatitis 19 15.48 6.9 16.13 7.0 16.77 7.0 16.77 7.0 16.77 7.0 16.77 7.0 16.77

Ionosphere 34 17.38 4.1 11.11 4.0 10.26 4.0 10.26 4.0 10.26 4.0 10.26 4.0 10.26

Leukemia 7129 0.00 50.6 4.17 51.0 0.00 49.0 0.00 47.0 0.00 44.0 0.00 35.0 1.39

Leukemia-1 5327 4.17 50.4 4.17 48.0 4.17 43.0 4.17 42.0 4.17 37.0 4.17 27.0 4.17

Leukemia-2 11225 6.94 81.3 4.17 83.0 1.39 75.0 1.39 61.0 2.78 53.0 2.78 42.0 2.78

Libras 90 35.83 9.9 36.67 10.0 35.56 10.0 35.56 10.0 35.56 10.0 35.56 10.0 35.56

Lymphoma 4026 23.96 273.7 19.79 272.0 14.58 256.0 14.58 238.0 13.54 218.0 13.54 188.0 14.58

Prostate-Tumor 10509 37.25 71.8 7.84 73.0 7.84 61.0 6.86 55.0 6.86 52.0 6.86 45.0 5.88

SMK-CAN-187 19993 39.57 49.9 32.09 51.0 25.13 41.0 26.20 34.0 24.06 30.0 21.93 26.0 23.53

Sonar 60 32.69 10.0 28.85 12.0 31.73 10.0 28.85 8.0 32.69 8.0 32.69 8.0 32.69

SRBCT 2308 0.00 79.3 1.20 82.0 1.20 78.0 1.20 74.0 1.20 68.0 1.20 59.0 1.20

TOX-171 5748 22.81 83.7 22.22 85.0 6.43 76.0 8.77 67.0 10.53 58.0 12.28 51.0 13.45

Wine 13 2.25 10.0 2.25 10.0 2.25 10.0 2.25 10.0 2.25 10.0 2.25 10.0 2.25

Average 8240.24 20.16 68.94 16.62 68.19 11.50 61.43 11.56 54.95 11.65 48.43 11.78 39.86 11.95

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

464

REFERENCES

Alipoor, G., Mirbagheri, S., Moosavi, S., and Cruz, S.

(2022). Incipient detection of stator inter-turn short-

circuit faults in a doubly-fed induction generator using

deep learning. IET Electric Power Applications.

Bastani, O., Kim, C., and Bastani, H. (2017). Interpret-

ing blackbox models via model extraction. ArXiv,

abs/1705.08504.

Bishop, C. (1995). Neural Networks for Pattern Recogni-

tion. Oxford University Press.

Chamlal, H., Ouaderhman, T., and Rebbah, F. (2022). A hy-

brid feature selection approach for microarray datasets

using graph theoretic-based method. Information Sci-

ences, 615:449–474.

Cover, T. and Thomas, J. (2006). Elements of information

theory. John Wiley & Sons, second edition.

Dhal, P. and Azad, C. (2022). A comprehensive survey on

feature selection in the various ﬁelds of machine learn-

ing. Applied Intelligence, 52(4):4543–45810.

Gan, J. Q., Awwad Shiekh Hasan, B., and Tsui, C. S. L.

(2014). A ﬁlter-dominating hybrid sequential forward

ﬂoating search method for feature subset selection in

high-dimensional space. International Journal of Ma-

chine Learning and Cybernetics, 5(3):413–423.

Guyon, I. and Elisseeff, A. (2003). An introduction to vari-

able and feature selection. Journal of Machine Learn-

ing Research (JMLR), 3:1157–1182.

Guyon, I., Gunn, S., Nikravesh, M., and Zadeh (Editors), L.

(2006). Feature extraction, foundations and applica-

tions. Springer.

Hanif, A., Zhang, X., and Wood, S. (2021). A survey

on explainable artiﬁcial intelligence techniques and

challenges. In IEEE 25th International Enterprise

Distributed Object Computing Workshop (EDOCW),

pages 81–89.

Huynh-Cam, T.-T., Nalluri, V., Chen, L.-S., and Yang, Y.-

Y. (2022). IS-DT: A new feature selection method for

determining the important features in programmatic

buying. Big Data and Cognitive Computing, 6(4).

Jeon, Y. and Hwang, G. (2023). Feature selection with

scalable variational gaussian process via sensitivity

analysis based on L2 divergence. Neurocomputing,

518:577–592.

Kim, B., Wattenberg, M., Gilmer, J., Cai, C., Wexler, J.,

egas, F., and Sayres, R. (2018). Interpretability

beyond feature attribution: Quantitative testing with

concept activation vectors (tcav). In Dy, J. G. and

Krause, A., editors, ICML, volume 80 of Proceedings

of Machine Learning Research, pages 2673–2682.

PMLR.

Lakkaraju, H. and Bastani, O. (2020). How do I fool you?

manipulating user trust via misleading black box ex-

planations. Proceedings of the AAAI/ACM Conference

on AI, Ethics, and Society, pages 79–85.

Lou, Y., Caruana, R., Gehrke, J., and Hooker, G. (2013).

Accurate intelligible models with pairwise interac-

tions. In Dhillon, I. S., Koren, Y., Ghani, R., Sen-

ator, T. E., Bradley, P., Parekh, R., He, J., Gross-

man, R. L., and Uthurusamy, R., editors, The 19th

ACM SIGKDD International Conference on Knowl-

edge Discovery and Data Mining, KDD, Chicago, IL,

USA, pages 623–631. ACM.

Moorthy, K. and Mohamad, M. (2011). Random forest

for gene selection and microarray data classiﬁcation.

Bioinformation, 7(3):142–146.

Mothilal, R., Sharma, A., and Tan, C. (2020). Explain-

ing machine learning classiﬁers through diverse coun-

terfactual explanations. In Proceedings of the 2020

Conference on Fairness, Accountability, and Trans-

parency, pages 607–617. ACM.

Pudjihartono, N., Fadason, T., Kempa-Liehr, A., and

O’Sullivan, J. (2022). A review of feature selection

methods for machine learning-based disease risk pre-

diction. Frontiers in Bioinformatics, 2:927312.

Qi, C., Diao, J., and Qiu, L. (2019). On estimating model in

feature selection with cross-validation. IEEE Access,

7:33454–33463.

Remeseiro, B. and Bolon-Canedo, V. (2019). A review

of feature selection methods in medical applications.

Computers in Biology and Medicine, 112:103375.

Ribeiro, M. T., Singh, S., and Guestrin, C. (2016). Why

should I trust you? explaining the predictions of any

classiﬁer. In HLT-NAACL Demos, pages 97–101. The

Association for Computational Linguistics.

Rostami, M., Forouzandeh, S., Berahmand, K., Soltani, M.,

Shahsavari, M., and Oussalah, M. (2022). Gene se-

lection for microarray data classiﬁcation via multi-

objective graph theoretic-based method. Artiﬁcial In-

telligence in Medicine, 123:102228.

Scheda, R. and Diciotti, S. (2022). Explanations of machine

learning models in repeated nested cross-validation:

An application in age prediction using brain complex-

ity features. Applied Sciences, 12(13).

Szepannek, G. and L

ubke, K. (2022). Explaining artiﬁcial

intelligence with care. KI - K

unstliche Intelligenz.

Tjoa, E. and Guan, C. (2021). A survey on explainable ar-

tiﬁcial intelligence (xai): Toward medical xai. IEEE

transactions on neural networks and learning systems,

32(11):4793—4813.

Xu, F., Uszkoreit, H., Du, Y., Fan, W., Zhao, D., and Zhu,

J. (2019). Explainable ai: A brief survey on history,

research areas, approaches and challenges. In Natural

Language Processing and Chinese Computing.

Xu, Y., Liu, Y., and Ma, J. (2022). Detection and de-

fense against DDoS attack on SDN controller based

on feature selection. In Chen, X., Huang, X., and

Kutyłowski, M., editors, Security and Privacy in So-

cial Networks and Big Data, pages 247–263, Singa-

pore. Springer Nature Singapore.

Yu, L. and Liu, H. (2003). Feature selection for high-

dimensional data: a fast correlation-based ﬁlter solu-

tion. In Proceedings of the International Conference

on Machine Learning (ICML), pages 856–863.

Yu, L. and Liu, H. (2004). Efﬁcient feature selection via

analysis of relevance and redundancy. Journal of Ma-

chine Learning Research (JMLR), 5:1205–1224.

Leveraging Explainability with K-Fold Feature Selection

465