Machine Fault Classification Using Hamiltonian Neural Networks
Jeremy Shen
1
, Jawad Chowdhury
2
, Sourav Banerjee
3
and Gabriel Terejanu
2
1
Dept. of Electrical and Computer Engineering, University of Michigan, Ann Arbor, MI, U.S.A.
2
Dept. of Computer Science, University of North Carolina at Charlotte, Charlotte, NC, U.S.A.
3
Dept. of Mechanical Engineering, University of South Carolina, Columbia, SC, U.S.A.
Keywords:
Physics-Informed Neural Networks, Supervised Learning, Energy Conservation, Dynamical Systems.
Abstract:
A new approach is introduced to classify faults in rotating machinery based on the total energy signature
estimated from sensor measurements. The overall goal is to go beyond using black-box models and incorporate
additional physical constraints that govern the behavior of mechanical systems. Observational data is used to
train Hamiltonian neural networks that describe the conserved energy of the system for normal and various
abnormal regimes. The estimated total energy function, in the form of the weights of the Hamiltonian neural
network, serves as the new feature vector to discriminate between the faults using off-the-shelf classification
models. The experimental results are obtained using the MaFaulDa database, where the proposed model yields
a promising area under the curve (AUC) of 0.78 for the binary classification (normal vs abnormal) and 0.84
for the multi-class problem (normal, and 5 different abnormal regimes).
1 INTRODUCTION
A cost-effective method for ensuring component re-
liability is to enhance the current schedule-based
maintenance approach with deterministic component
health and usage data to inform selective and targeted
maintenance activities. Condition monitoring and
fault diagnosis systems are required to guard against
unexpected failures in safety-critical and production
applications. Early fault detection can reduce un-
planned failures, which will in turn reduce life cy-
cle costs and increase readiness and mission assur-
ances. Irrespective of different machinery, manufac-
turing tools like CNC machines, heavy equipment,
aircraft, helicopters, space vehicles, car engines, and
machines generate vibrations. The analysis of these
vibration data is the key to detecting machinery degra-
dation before the equipment or the structure fails. Ma-
chine faults usually leave key indications of its in-
ternal signature through the changes in modal pa-
rameters. For example, they may change the natu-
ral frequency of the system, generate unique damping
characteristics, degradation in stiffness, generation of
acoustic frequencies, etc. The defects and faults in the
system may also generate a different form of energy
transduction from mechanical to electrical or to elec-
tromagnetic energy, which leaves unique signatures.
The statistical features of vibration signals in the time,
frequency, and time-frequency domains each have
different strengths for detecting fault patterns, which
has been thoroughly studied (Nayana and Geethan-
jali, 2017; Van et al., 2020; Li et al., 2016). Vari-
ous approaches have been proposed to extract features
from these vibration signals using time-domain and
frequency-domain analysis (Lei et al., 2008), Fourier
and wavelet transform (Li et al., 2013), and manifold
learning (Jiang et al., 2009). It is also shown that in-
tegration and hybridization of feature extraction al-
gorithms can yield synergies that combine strengths
and eliminate weaknesses (Usamentiaga et al., 2013;
Rizzo and di Scalea, 2006). Most of the work done
in this area is based on data collected from vibration
sensors (Yen and Lin, 2000; Seshadrinath et al., 2014;
Bellini et al., 2008), which are cheap and enable non-
intrusive deployments. However, they generate huge
datasets. As these data sets are very big in nature find-
ing the above-mentioned unique features, and their
respective paraxial contributions are extremely chal-
lenging. Hence, recently several feature extraction-
driven machine learning algorithms are deployed to
solve this challenge (Amin et al., 2015; Wei et al.,
2019; Caggiano et al., 2019; Yin et al., 2019).
One of the challenges with building and deploying
machine learning models to support decision-making
is achieving a level of generalization that allows us
to learn on one part of the data distribution and pre-
dict on another. This challenge is amplified when
learning using data from physical systems, as ma-
474
Shen, J., Chowdhury, J., Banerjee, S. and Terejanu, G.
Machine Fault Classification Using Hamiltonian Neural Networks.
DOI: 10.5220/0011746800003411
In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 474-480
ISBN: 978-989-758-626-2; ISSN: 2184-4313
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

chine learning models such as neural networks (NN)
capture an approximation of the underlying physi-
cal laws. Recently, new approaches have emerged
under the umbrella of physics-informed neural net-
works (PINN) (Karniadakis et al., 2021) to train NN
that not only fit the observational data but also re-
spect the underlying physics. This work leverages the
Hamiltonian neural network (HNN) (Greydanus et al.,
2019) to learn the Hamiltonian equations of energy-
conserving dynamical systems from noisy data.
HNNs are used to characterize the total energy of
rotating machinery, which is part of a wide range of
applications such as power turbines, helicopters, and
CNC machines just to name a few. In Ref. (Ribeiro
et al., 2017), the authors proposed a similarity-based
model to calculate the similarity score of a signal with
a set of prototype signals that characterize a target
operating condition. These similarity score features
are used in conjunction with time and spectral do-
main features to classify the behavior of the system
using off-the-shelf classification models, such as ran-
dom forests.
The main contribution of this work is to be inten-
tional with respect to the underlying physics of the ro-
tating machinery when generating discriminatory fea-
tures. Namely, the conservation of energy is used as
an inductive bias in the development and training of
the HNN. While these mechanical systems are dissi-
pative in nature, we assume that for short periods of
time, the energy of the system is conserved due to the
energy injected by the motor. The features derived
by our approach are in the form of the weights of the
HNN, which characterize the total energy of the sys-
tem. In other words, we attempt to identify the operat-
ing regime based on the energy function. As with the
previous approaches, these physics-informed features
are then used to train off-the-shelf classifiers, such
as logistic regressions and random forests to predict
the condition of the mechanical system. The experi-
mental results are performed on the Machinery Fault
Database (MaFaulDa)
1
from the Federal University of
Rio de Janeiro. The proposed system yields a promis-
ing area under the curve (AUC) of 0.78 for both the
binary classification (normal vs abnormal) and 0.84
for the multi-class problem (normal, and 5 different
abnormal regimes).
This paper is structured as follows: Section 2 in-
troduces the background on the HNN and MaFaulDa
dataset. Section 3 presents our proposed approach to
derive physics-informed features to classify operating
conditions. Section 4 shows the empirical evaluations
and Section 5 summarizes our findings.
1
http://www02.smt.ufrj.br/
∼
offshore/mfs/page 01.html
2 BACKGROUND
2.1 Hamiltonian Neural Networks
The Hamiltonian equations of motion, Eq. 1, describe
the mechanical system in terms of canonical coordi-
nates, position q and momentum p, and the Hamilto-
nian of the system H .
dq
dt
=
∂H
∂p
,
dp
dt
= −
∂H
∂q
(1)
Instead of using neural networks to directly learn the
Hamiltonian vector field

∂H
∂p
, −
∂H
∂q

, the approach
used by Hamiltonian neural networks is to learn a
parametric function in the form of a neural network
for the Hamiltonian itself (Greydanus et al., 2019).
This distinction accounts for learning the exact quan-
tity of interest and it allows us to also easily obtain
the vector field by taking the derivative with respect
to the canonical coordinates via automatic differenti-
ation. Given the training data, the parameters of the
HNN are learned by minimizing the following loss
function, Eq. 2.
L =




∂H
∂p
−
dq
dt




2
+




∂H
∂q
+
dp
dt




2
(2)
2.2 Machinery Fault Database
(MaFaulDa)
A comprehensive set of machine faults and vi-
bration data was needed for the development and
testing of the Hamiltonian-based feature extraction
and classification of different operating states with
damage/defects. The Machinery Fault Database
(MaFaulDa) consists of a comprehensive set of vi-
bration data from a SpectraQuest Alignment-Balance-
Vibration System, which includes multiple types of
faults, see Fig. 1. The equipment has two shaft-
supporting bearings, a rotor, and a motor. Accelerom-
eters are attached to the bearings to measure the vi-
bration in the radial, axial, and tangential directions
of each bearing. In addition, measurements from a
tachometer (for measuring system rotation frequency)
and a microphone (for capturing sound during sys-
tem operation) are also included in the database. The
database includes 10 different operating states and a
total of 1951 sets of vibration data: (1) normal op-
eration, (2) rotor imbalance, (3) underhang bearing
fault: outer track, (4) underhang bearing fault: rolling
elements, (5) underhang bearing fault: inner track,
(6) overhang bearing fault: outer track, (7) overhang
bearing fault: rolling elements, (8) overhang bearing
fault: inner track, (9) horizontal shaft misalignment,
(10) vertical shaft misalignment.
Machine Fault Classification Using Hamiltonian Neural Networks
475

Figure 1: SpectraQuest System: Alignment-Balance-Vibration.
Normal Operation. There are 49 sets of data from
the system operating under normal conditions with-
out any fault, each with a fixed rotating speed within
the range from 737 rpm to 3686 rpm with steps of
approximately 60 rpm.
Rotor Imbalance. To simulate different degrees of
imbalanced operation, distinct loads of (6, 10, 15, 20,
25, 30, 35) g were coupled to the rotor. The database
includes a total of 333 different imbalance-operation
scenarios with combinations of loads and rotation fre-
quencies.
Bearing Faults. As one of the most complex el-
ements of the machine, the rolling bearings are the
most susceptible elements to fault occurrence. Three
defective bearings, each one with a distinct defec-
tive element (outer track, rolling elements, and inner
track), were placed one at a time in each of the bear-
ings. The three masses of (6, 10, 20) g were also
added to the rotor to induce a combination of rotor im-
balance and bearing faults with various rotation fre-
quencies. There is a total of 558 underhang bearing
fault scenarios and 513 overhang bearing fault sce-
narios.
Horizontal Shaft Misalignment. Horizontal shaft
misalignment faults were induced by shifting the mo-
tor shaft horizontally of (0.5, 1.0, 1.5, 2.0) mm. The
database includes a total of 197 different scenarios
with combinations of horizontal shaft misalignment
and rotation frequencies.
Vertical Shaft Misalignment. Vertical shaft mis-
alignment faults were induced by shifting the motor
shaft vertically of (0.51, 0.63, 1.27, 1.4, 1.78, 1.9)
mm. The database includes a total of 301 differ-
ent scenarios with combinations of vertical shaft mis-
alignment and rotation frequencies.
3 METHODOLOGY
The approach proposed to identify the operating state
of the rotating machinery is to learn the total energy of
the system from vibration data using HNN and use the
parameters of the Hamiltonian as discriminating fea-
tures. The intuition is that the total energy signature
is different under various faults. The main assump-
tion that we make is that the energy of the system is
conserved for short periods of time thanks to the en-
ergy injected by the motor, which allows us to use the
HNN (Greydanus et al., 2019). The overall model ar-
chitecture is shown in Fig. 2.
The first step is to develop a set of generalized
coordinates from the raw vibration data using an au-
toencoder trained only on the data from normal con-
ditions. The encoder NN is then used to generate a
low dimensional representation (2D in our case) from
the 8 vibration measurements taken in any operating
regime. This approach in developing arbitrary coor-
dinates has been proposed in the original HNN pa-
per (Greydanus et al., 2019).
Using the newly developed coordinates, the sec-
ond step is to train an HNN for each sequence of data
generated at 50 kHz sampling rate during 5 s. The
parameters θ of the Hamiltonian H
θ
fully character-
ize the energy function of the operating state and they
can be used to train a classifier.
The parameterization of the Hamiltonian is high-
dimensional (41, 200 weights in our case) as it de-
pends on the number of layers and hidden neurons per
layer chosen in HNN. As a result, we have chosen to
reduce its dimension using principal component anal-
ysis (PCA) before training a classifier as a random
forest in the last modeling step.
ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods
476

Figure 2: The proposed fault classification model.
4 NUMERICAL RESULTS
The proposed fault classification system has been
used with the MaFaulDa dataset and a 70 : 30 split
into train and test data. Given the imbalance of col-
lected data, namely 49 datasets recorded for normally
operating motors vs. 1800+ datasets recorded for all
faulty operating motors, we have used the synthetic
minority over-sampling technique (SMOTE) (Chawla
et al., 2002) to create synthetic data points for the mi-
nority class. The PyCaret
2
framework was used to
develop the classifiers and preprocess the HNN fea-
tures.
Two different tasks are considered. The first is the
binary classification where we are discriminating be-
tween normal and abnormal conditions using a ran-
dom forest, and the second is the multi-class problem
where we are discriminating using a logistic regres-
sion between the classes listed in Table 1, where class
0 is the normal regime.
2
https://pycaret.org
Table 1: Pairwise classification - results on testing set.
Class normal vs X AUC F1-score
1 horizontal-misalign. 0.59 0.80
2 imbalance 0.92 0.95
3 overhang 0.85 0.85
4 underhang 0.80 0.88
5 vertical-misalign. 0.91 0.92
The receiver operating characteristic (ROC)
curves are provided for both tasks in Figs. 3 and 4
respectively. The macro-averaged AUC calculated on
the test data is 0.78 for the binary classification and
0.84 for the multi-class problem and the F1 score is
0.96 and 0.51 respectively, which demonstrates the
viability of physics-informed features from HNN to
capture the state of the system. These classification
problems are imbalanced due to the skewed distribu-
tion of examples across the classes and as a result,
we have chosen not to report the accuracy as it was
reported in prior work (Ribeiro et al., 2017; Marins
et al., 2018). We note however that Ref.(Ribeiro et al.,
2017) reports an F1-score of 0.99 on a 10-fold cross-
Machine Fault Classification Using Hamiltonian Neural Networks
477

validation exercise, which is higher that the 0.96 on
our binary classification, and that our multiclass F1-
score is lower due to the aggregation of bearing fault
classes.
Table 1 shows the AUC for pairwise classifica-
tion between each unique defective operating condi-
tion and the normal condition. Fig. 6 shows the phase
spaces of 10 different operating conditions (1 normal
and 9 faulty). Interestingly, among all the pairwise
comparisons, the model finds the discrimination be-
tween normal and horizontal-misalignment regimes
rather challenging, which we plan to further explore
in future studies. We do expect that the faults intro-
duced generate slight changes in the phase portraits of
various regimes, see Fig. 6. However, we find qual-
itatively that the phase portrait of overhang/ball-fault
is significantly different than the rest, which suggests
that the sub-classes of overhang, namely ball-fault,
cage-fault, and outer-race should be treated as classes
on their own.
Figure 3: Results on test set - binary classification.
Figure 4: Results on test set - multi-class problem.
Discussion on the Effect of Rotation Frequency
on the Hamiltonian. Fig. 5 shows the Hamiltonian
of normally operating motors operating at different
speeds. Interestingly, even though this has not been
enforced, the general structure of the Hamiltonian
vector field remains largely the same across various
speeds, while the magnitude of the Hamiltonian in-
creases at higher speeds as expected. It can be con-
cluded in this case that the vector field is dependent
on the operating condition, and the magnitude is de-
pendent on the operating speed.
Discussion on HNN on Dissipative Systems. The
HNN has the ability to learn the total energy of a num-
ber of systems (Greydanus et al., 2019), including an
ideal mass-spring system. Although the HNN is de-
signed to conserve energy, it is interesting to consider
what the HNN learns from dissipative systems. We
believe that the methodology is more broadly appli-
cable and it applies also when this assumption does
not hold.
We have used a mass-spring-damper to experi-
ment with the behavior of HNN for dissipative sys-
tems. This is a non-conservative system and the
Hamiltonian formulated by the HNN is not a con-
ventional solution to the mass-spring-damper system,
the conserved quantity is not the total energy, and the
generalized coordinates are not position and momen-
tum defined by classical mechanics. Nevertheless, a
qualitative analysis of the trajectories shows that the
HNN creates unique solutions for each value of the
damping ratio, see Fig. 7. While we are unable to use
conventional physics to understand the results of the
HNN on the mass-spring-damper system, it is evident
that the results can be used to discriminate between
the different systems.
5 CONCLUSIONS
A novel predictive model is introduced to discrimi-
nate between normal and abnormal operating regimes
of rotating machinery. The model is based on the total
energy signature of the system learned using a Hamil-
tonian Neural Network. The performance measures
obtained from the experimental data suggest that the
proposed physics-informed features are an excellent
candidate for machine fault classification.
ACKNOWLEDGEMENT
Research was sponsored by the National Institute of
Food and Agriculture under Grant Number 2017-
67017-26167 and by the Army Research Office un-
der Grant Number W911NF-22-1-0035. The views
and conclusions contained in this document are those
of the authors and should not be interpreted as rep-
resenting the official policies, either expressed or im-
ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods
478

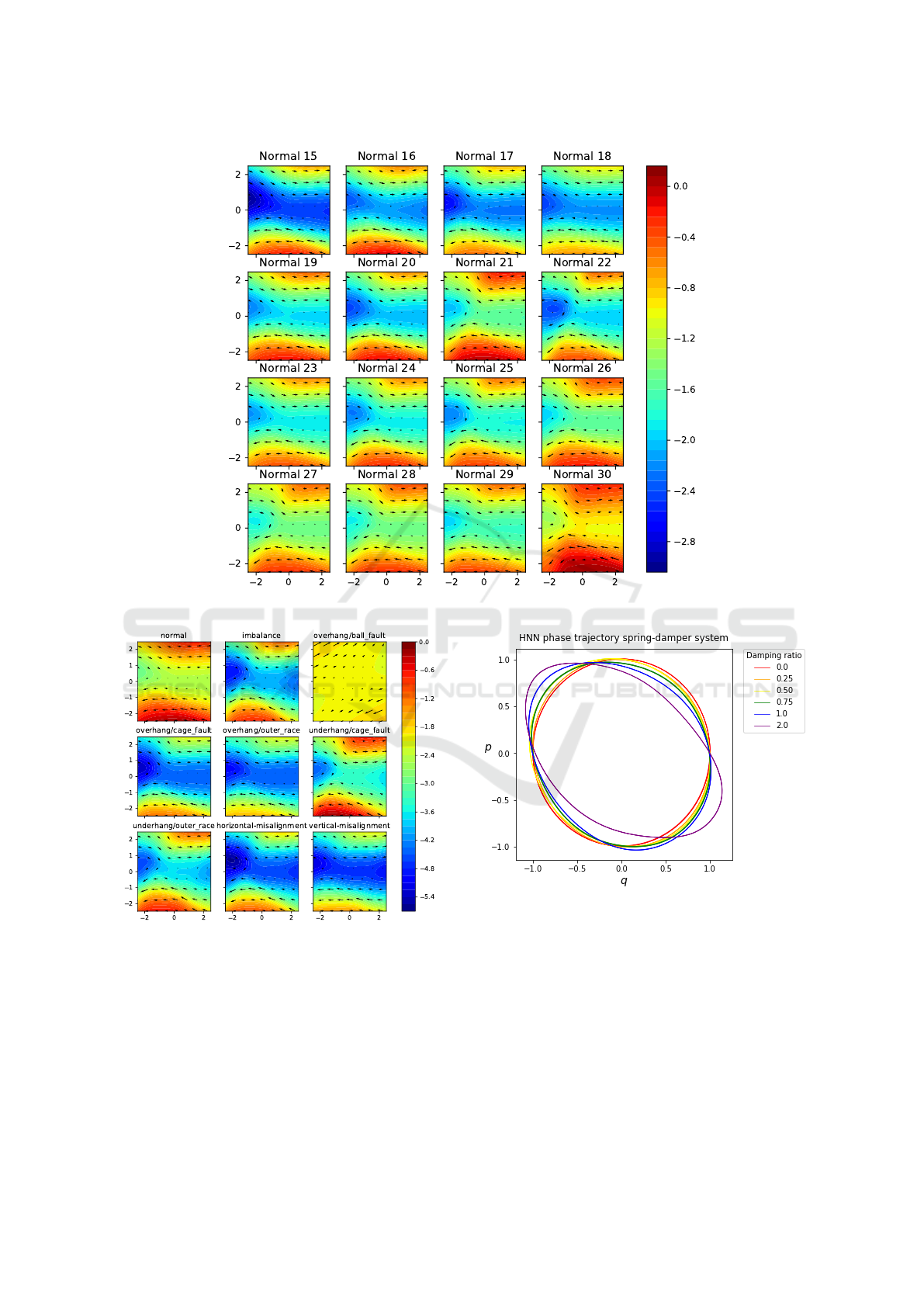
Figure 5: The effect of rotation frequency on the Hamiltonian.
Figure 6: Phase portraits of various operating conditions.
plied, of the Army Research Office, the National In-
stitute of Food and Agriculture, or the U.S. Govern-
ment. The U.S. Government is authorized to repro-
duce and distribute reprints for Government purposes
notwithstanding any copyright notation herein.
Figure 7: HNN results on variable damping ratios.
REFERENCES
Amin, H. U., Malik, A. S., Ahmad, R. F., Badruddin, N.,
Kamel, N., Hussain, M., and Chooi, W.-T. (2015).
Feature extraction and classification for eeg signals
using wavelet transform and machine learning tech-
niques. Australasian Physical & Engineering Sci-
ences in Medicine, 38(1):139–149.
Bellini, A., Immovilli, F., Rubini, R., and Tassoni, C.
(2008). Diagnosis of bearing faults of induction ma-
Machine Fault Classification Using Hamiltonian Neural Networks
479

chines by vibration or current signals: A critical com-
parison. In 2008 IEEE Industry Applications Society
Annual Meeting, pages 1–8.
Caggiano, A., Zhang, J., Alfieri, V., Caiazzo, F., Gao, R.,
and Teti, R. (2019). Machine learning-based image
processing for on-line defect recognition in additive
manufacturing. CIRP Annals, 68(1):451–454.
Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,
W. P. (2002). Smote: synthetic minority over-
sampling technique. Journal of artificial intelligence
research, 16:321–357.
Greydanus, S. J., Dzumba, M., and Yosinski, J. (2019).
Hamiltonian neural networks. In 33rd Conference
on Neural Information Processing Systems (NeurIPS),
Vancouver, Canada.
Jiang, Q., Jia, M., Hu, J., and Xu, F. (2009). Machinery fault
diagnosis using supervised manifold learning. Me-
chanical systems and signal processing, 23(7):2301–
2311.
Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris,
P., Wang, S., and Yang, L. (2021). Physics-informed
machine learning. Nature Reviews Physics, 3(6):422–
440.
Lei, Y., He, Z., and Zi, Y. (2008). A new approach to in-
telligent fault diagnosis of rotating machinery. Expert
Systems with applications, 35(4):1593–1600.
Li, C., S
˜
A¡nchez, R.-V., Zurita, G., Cerrada, M., and Cabr-
era, D. (2016). Fault diagnosis for rotating machinery
using vibration measurement deep statistical feature
learning. Sensors, 16(6).
Li, P., Kong, F., He, Q., and Liu, Y. (2013). Multiscale slope
feature extraction for rotating machinery fault diagno-
sis using wavelet analysis. Measurement, 46(1):497–
505.
Marins, M. A., Ribeiro, F. M., Netto, S. L., and da Silva,
E. A. (2018). Improved similarity-based modeling for
the classification of rotating-machine failures. Journal
of the Franklin Institute, 355(4):1913–1930. Special
Issue on Recent advances in machine learning for sig-
nal analysis and processing.
Nayana, B. R. and Geethanjali, P. (2017). Analysis of sta-
tistical time-domain features effectiveness in identifi-
cation of bearing faults from vibration signal. IEEE
Sensors Journal, 17(17):5618–5625.
Ribeiro, F., Marins, M., Netto, S., and da Silva, E. (2017).
Rotating machinery fault diagnosis using similarity-
based models. In XXXV Simp
´
osio Brasileiro de
Telecomunicac¸
˜
oes e Processamento de Sinais, S
˜
ao Pe-
dro, Brasil.
Rizzo, P. and di Scalea, F. L. (2006). Feature extraction for
defect detection in strands by guided ultrasonic waves.
Structural Health Monitoring, 5(3):297–308.
Seshadrinath, J., Singh, B., and Panigrahi, B. K. (2014).
Investigation of vibration signatures for multiple fault
diagnosis in variable frequency drives using complex
wavelets. IEEE Transactions on Power Electronics,
29(2):936–945.
Usamentiaga, R., Venegas, P., Guerediaga, J., Vega, L., and
L
´
opez, I. (2013). Feature extraction and analysis for
automatic characterization of impact damage in car-
bon fiber composites using active thermography. NDT
& E International, 54:123–132.
Van, B., Van Hoa, N., Nguyen, H., and Jang, Y. M. (2020).
Statistical feature extraction in machine fault detec-
tion using vibration signal. In International Confer-
ence on Information and Communication Technology
Convergence (ICTC), pages 666–669.
Wei, J., Chu, X., Sun, X.-Y., Xu, K., Deng, H.-X., Chen,
J., Wei, Z., and Lei, M. (2019). Machine learning in
materials science. InfoMat, 1(3):338–358.
Yen, G. and Lin, K.-C. (2000). Wavelet packet feature ex-
traction for vibration monitoring. IEEE Transactions
on Industrial Electronics, 47(3):650–667.
Yin, L., Ye, B., Zhang, Z., Tao, Y., Xu, H., Salas Avila,
J. R., and Yin, W. (2019). A novel feature extraction
method of eddy current testing for defect detection
based on machine learning. NDT & E International,
107:102108.
ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods
480