Bayesian Iterative Closest Point for Shape Analysis of Brain Structures
Mauricio Casta
˜
no-Aguirre
1,2 a
, Hernan F. Garcia
3,1 b
,
´
Alvaro A. Orozco
2 c
,
Gloria Liliana Porras-Hurtado
1 d
and David A. C
´
ardenas-Pe
˜
na
2 e
1
Salud Comfamiliar, Comfamiliar Risaralda, Pereira, Colombia
2
Automatics Research Group, Universidad Tecnol
´
ogica de Pereira, Pereira, Colombia
3
SISTEMIC Research Group, Universidad de Antioquia, Medell
´
ın, Colombia
Keywords:
Bayesian Optimization, Gaussian Processes, Iterative closest-Point, Point Cloud Alignment, Shape Analysis.
Abstract:
Machine learning in medical image analysis has proved to be a strategy that solves many problems emerging
from the variability in the physician’s outlines and the amount of time each physician spends analyzing each
image. One of the most critical medical image analysis approaches is Medical Image Registration which has
been a topic of active research for the last few years. In this paper, we proposed a Bayesian Optimization
framework for Point Cloud Registration for shape analysis of brain structures. Here, we rely on a modified
version of the Iterative Closest Point (ICP) algorithm. This approach built a black box function that receives
input parameters for performing an Point Cloud transformation. Then, we used a similarity metric that shows
the performance of the transformation. With this similarity metric, we built a function to define a Bayesian
strategy that allows us to find the global optimum of the similarity metric-based function. To this end, we
used Bayesian Optimization, which performs global optimization of unknown functions making observations
and performing probabilistic calculations. This model considers all the previous observations, which prevents
the strategy from falling into an optimal local, as often happens in strategies based on classical optimization
approaches such as Gradient Descent. Finally, we evaluate the model by performing a point cloud registration
process corresponding to brain structures at different time instances. The experimental results show a faster
convergence towards the global optimum and building. Besides, the proposed model evidenced robust opti-
mization results for registration strategies in point clouds.
1 INTRODUCTION
Image registration is the preferred technique in medi-
cal image applications and has been a topic of active
research over decades. Medical image registration
techniques serve as the fundamental basis for proce-
dures such as image-guided radiation therapy, image-
guided radiation surgery, and image-guided mini-
mally invasive treatments (Wang et al., 2014; Jaffray
et al., 2007; Sadozye and Reed, 2012). Intuitively, the
registration process finds an optimal transformation
that aligns an image in the input data and is a crucial
step for image analysis; in which valuable informa-
tion is conveyed in more than one image (i.e., images
acquired at different times). Therefore, accurate inte-
a
https://orcid.org/0000-0002-2811-7847
b
https://orcid.org/0000-0002-2814-8838
c
https://orcid.org/0000-0002-1167-1446
d
https://orcid.org/0000-0003-1193-7184
e
https://orcid.org/0000-0002-0522-8683
gration of relevant information from two or more im-
ages is very important (Oliveira and Tavares, 2014).
In the context of registration processes, fixed image
remains unchanged, and the moving image is trans-
formed using the fixed Image as a reference (Oliveira
and Tavares, 2014).
Most of the works currently carried out in medical
image registration are based on deep learning strate-
gies. However, these approaches are time-consuming
and lack interpretability. Since the discovery of
deep learning applications in the context of segmen-
tation and classification tasks, new applications have
emerged; for example, a Deep Learning Image Reg-
istration framework for unsupervised affine and de-
formable image registration is proposed (Vos et al.,
2019). In this framework, a convolutional neural net-
work (ConvNet) is trained for image registration by
exploiting image similarity analogous to conventional
intensity-based image registration. After the ConvNet
has been trained, it can register pairs of unseen images
920
Castaño-Aguirre, M., Garcia, H., Orozco, Á., Porras-Hurtado, G. and Cárdenas-Peña, D.
Bayesian Iterative Closest Point for Shape Analysis of Brain Structures.
DOI: 10.5220/0011747200003411
In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 920-925
ISBN: 978-989-758-626-2; ISSN: 2184-4313
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

in one shot. Similarly, other strategies (Mansilla et al.,
2020) build a function to model images as a deforma-
tion field that aligns multivariate views. This model is
a fast learning-based framework for deformable, pair-
wise medical image registration. In addition, the strat-
egy rapidly computes a deformation field by directly
evaluating the function (Mansilla et al., 2020).
Although most deformable image registration
strategies use deep learning-based image registration
methods (Balakrishnan et al., 2019; Krebs et al.,
2019; Lau et al., 2020; Mansilla et al., 2020; Vos
et al., 2019; Zhao et al., 2019) achieving state-of-the-
art performances. However, The proper interpretabil-
ity of the deformation process is still an open gap in
the image registration field. Similarly, this model re-
quires a time-consuming training phase and a large
amount of data to perform well in the validation. Con-
sequently, the model leads to problems in which there
is insufficient sample quantity in the input data. Re-
gardless, local pixel-level loss functions do not con-
sider the global context and might produce similar
values for anatomically plausible, and non-plausible
segmentation. Also, these strategies rely on 2D ap-
proaches in which each slice of the medical image
is processed, restraining the correspondence informa-
tion between shapes.
Point cloud registration methods such as Iterative
Closest Points (ICP) have been successfully applied
in numerous real-world tasks (Garc
´
ıa et al., 2016;
Besl and McKay, 1992; Chen and Medioni, 1991; Liu
et al., 2016; Oomori et al., 2016; Umeyama, 1991;
Zhang, 2005; Zhang et al., 2022; Li et al., 2022;
Bouaziz et al., 2013). This strategy is known for
its susceptibility to local minima problems and re-
quires adequate model initialization and manual hy-
perparameter tuning. Therefore, a proper model opti-
mization is required to perform accurately.
In (Garc
´
ıa et al., 2016) the use of optimization
models to fit 3D brain structures based on Bayesian
optimization has been explored. However, due to
emerging problems related to the classical Bayesian
optimization approach such as misspecified models
and covariate shift we can identify a need to de-
fine optimization strategies that allow us to deal
with these problems. Bayesian Optimization (BO)
reaches global optima in many challenging optimiza-
tion benchmark functions (Jones, 2001). BO states
that the objective function is sampled from a Gaussian
Process, maintaining the posterior distribution for this
function as observations. Recently, new strategies
have improved Bayesian Optimization by reducing
the iterations required for the convergence by adding
stopping criteria for the searching process (Dai et al.,
2019; Stanton et al., 2022; Fong and Holmes, 2021),
which makes this type of strategy even more efficient
for global optimization processes.
This paper proposes a point cloud registration ap-
proach to building a black box function based on
an point cloud transformation optimization within a
Bayesian framework. Here, we use Bayesian opti-
mization to find the optimal parameters that align the
point clouds accurately. Our key contribution is based
on the Bayesian optimization strategy that computes
the model parameters for controlling the alignment of
the point cloud registration process in a probabilis-
tic way. The rest of the paper proceeds as follows.
Section 2 provides a detailed discussion of materi-
als and methods. Section 3 presents the experimen-
tal results and some discussions about the proposed
method. The paper concludes in Section 4, with some
insights about the proposed framework.
2 MATERIALS AND METHODS
2.1 Datasets
For the input data, we use two databases. The
first is the Tosca dataset (Bronstein et al., 2006), a
dataset with Hi-resolution three-dimensional nonrigid
shapes. The database contains 80 objects, including
11 cats, 9 dogs, 3 wolves, 8 horses, 6 centaurs, 4 go-
rillas, 12 female figures, and two different male fig-
ures, containing between 7 and 20 poses (Bronstein
et al., 2007). Furthermore, the second one comes
from Magnetic Resonance Images (MRI) from pa-
tients with perinatal asphyxia acquired during early
childhood in a medical center in Colombia called
Brain Asphyxia Dataset. The MRI images are then
converted into 3D point cloud data using the infant
Free Surfer framework (Fischl, 2012). Then, we ob-
tain segmentations of 20 different neuroanatomical
regions relevant in the context of perinatal asphyxia
(Satheesan et al., 2020), (Miller et al., 2005). After
this process, the anatomy of a subject is represented
by a collection of m (m = 20 brain structures) point
clouds S = {P
0
;P
1
;. . . ;P
m
}, where each point cloud
represents a brain structure. A point cloud is de-
fined as a set of n points P = [P
0
;P
1
;. . . ;P
n
], where
each point is a vector of coordinates P
i
= (x, y, z)
(Guti
´
errez-Becker and Wachinger, 2018).
We test our approach in 20 different point clouds
for the Tosca data sets. In this data set, we ap-
plied a rigid random transformation to evaluate if the
model can find rigid transformations on point clouds
with significant variability. For the perinatal asphyxia
dataset, we test our model with MRI acquired at dif-
ferent times related to the same patient (i.e., to evalu-
Bayesian Iterative Closest Point for Shape Analysis of Brain Structures
921

ate the clinical outcome). Each patient has 20 differ-
ent neuroanatomical structures at different ages (e.g.,
at birth and one year). Among these structures, we
have left and right white matter, caudate nucleus,
putamen, and thalamus.
2.2 Transformations for 3D Point
Clouds
As for the implementation of the registration al-
gorithm, we rely on the ICP algorithm used in
(Rusinkiewicz, 2001). Then, we build a function to
model variables for translational and rotational pa-
rameters.
We must define the constraints of the transforma-
tion function to guarantee an optimal grid search. For
the rotational parameters, we define constraints from
−2π to 2π, and the translations parameters are given
by,
α = {α ∈ R| − 2π ≤ α ≤ 2π} (1)
β = {β ∈ R| − 2π ≤ β ≤ 2π} (2)
γ = {γ ∈ R| − 2π ≤ γ ≤ 2π} (3)
t
x,y,z
= {t ∈ R}. (4)
Then, the transformation matrix with rotational
parameters α,β,γ and the translations for each axis
t
x,y,z
are,
T =




cosαcosβ cos α sin β sin γ − sin α cos γ cosαsinβcosγ+ sin α sin γ t
x
sinαcosβ sinαsinβsinγ + cosαcosγ sin α sin β cos γ −cos α sin γ t
y
−sinβ cosβsinγ cosβcosγ t
z
0 0 0 1




(5)
2.3 Performance Metric
To set the optimization process, we need to use a per-
formance metric that measures the similarity or the
differences between the objects to be aligned. We use
Root Mean Square Error and Normalized Mutual In-
formation (MI). MI measures objects’ information, as
shown in equation 6,
I(P
A
, P
B
) = D
KL
(P
(A,B)
∥P
A
⊗ P
B
), (6)
where D
KL
is the Kullback–Leibler divergence
(Williams and Maybeck, 2006). If this information is
zero, it means that knowledge on B does not give any
information about A (i.e., two partitions have nothing
to do with each other). The larger the two partitions
are, the larger I(P
A
, P
B
). However, this is still not an
ideal metric for evaluating. Thus, we choose to nor-
malize it as in H(P
A
) + H(P
B
) (see (Zhang, 2015) for
further details). The Normalized Mutual Information
can be written as
NMI(P
A
, P
B
) =
2I(P
A
, P
B
)
H(P
A
) + H(P
B
)
(7)
In this context A and B represents the fixed and
the moving point cloud respectively.
2.4 Conformal Bayesian Optimization
with Gaussian Process Priors
Our goal is to minimize the distance between the
fixed and moving point cloud which is referred to
as the cost function f (x) on some bounded set X
that controls the model parameters. To this end,
Bayesian optimization builds a probabilistic frame-
work for f (x) with the aim to exploit this model to
make predictions about the transformation parameters
X = {α, β, γ, t
x,y,z
} (Snoek et al., 2012).
The main components of the Bayesian opti-
mization framework are the prior function to op-
timize and the acquisition function that will al-
low us to determine the next point to evaluate
the cost function (Rasmussen and Williams, 2005).
We use a Gaussian process prior due to its flex-
ibility and tractability. A Gaussian Process (GP)
is an infinite collection of scalar random variables
indexed by an input space such that for any fi-
nite set of inputs X = {x
1
, x
2
, ··· , x
n
}, the ran-
dom variables f
∆
= [ f (x
1
), f (x
2
), ··· , f (x
n
)] are dis-
tributed according to a multivariate Gaussian distri-
bution f(X) = GP(m(x), k(x, x
′
)). A GP is com-
pletely specified by a mean function m(x) = E [ f (x)]
(usually defined as the zero function) and a posi-
tive definite covariance function given by k(x, x
′
) =
E
h
( f (x) − m(x))( f (x
′
) − m(x
′
)
T
)
i
(see (Snoek et al.,
2012) for further details). Let us assume that f (x)
is drawn from a Gaussian process prior and that
our observations are set as
{
x
n
, y
n
}
N
n=1
, where y
n
∼
N ( f (x
n
), ν) and ν is the noise variance. The acqui-
sition function is denoted by a : X → R
+
and estab-
lishes the point in X that is evaluated in the optimiza-
tion process as x
next
= argmax
x
a(x). Since the acqui-
sition function depends on the GP hyperparameters,θ,
and the predictive mean function µ(x;{x
n
, y
n
}, θ) (as
well as the predictive variance function), the best cur-
rent value is then x
best
= arg min
x
n
f (x
n
).
Since the discovery of the problems encountered
in the classical Bayesian optimization models like
model missespecification and covariate shift. It is
necessary to find strategies that try to solve this
problem as it does Conformal Bayesian Optimization
(Fong and Holmes, 2021). Conformal prediction is
an uncertainty quantification method with coverage
guarantees even for misspecified models and a simple
mechanism to correct for covariate shift. A confor-
ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods
922

mal prediction set is defined as C
α
(x) ⊂ Y is a set of
possible labels for a test point x
n
Candidate labels y
′
are included in C
α
(x) if the
resulting pair (x
n
, y
′
) is sufficiently similar to actual
examples seen in the past. The degree of similar-
ity is measured by a score function s and importance
weights w, and the similarity threshold is determined
by the miscoverage tolerance α (see (Stanton et al.,
2022) for further details).
2.5 Optimized Transformations with
Bayesian Optimization
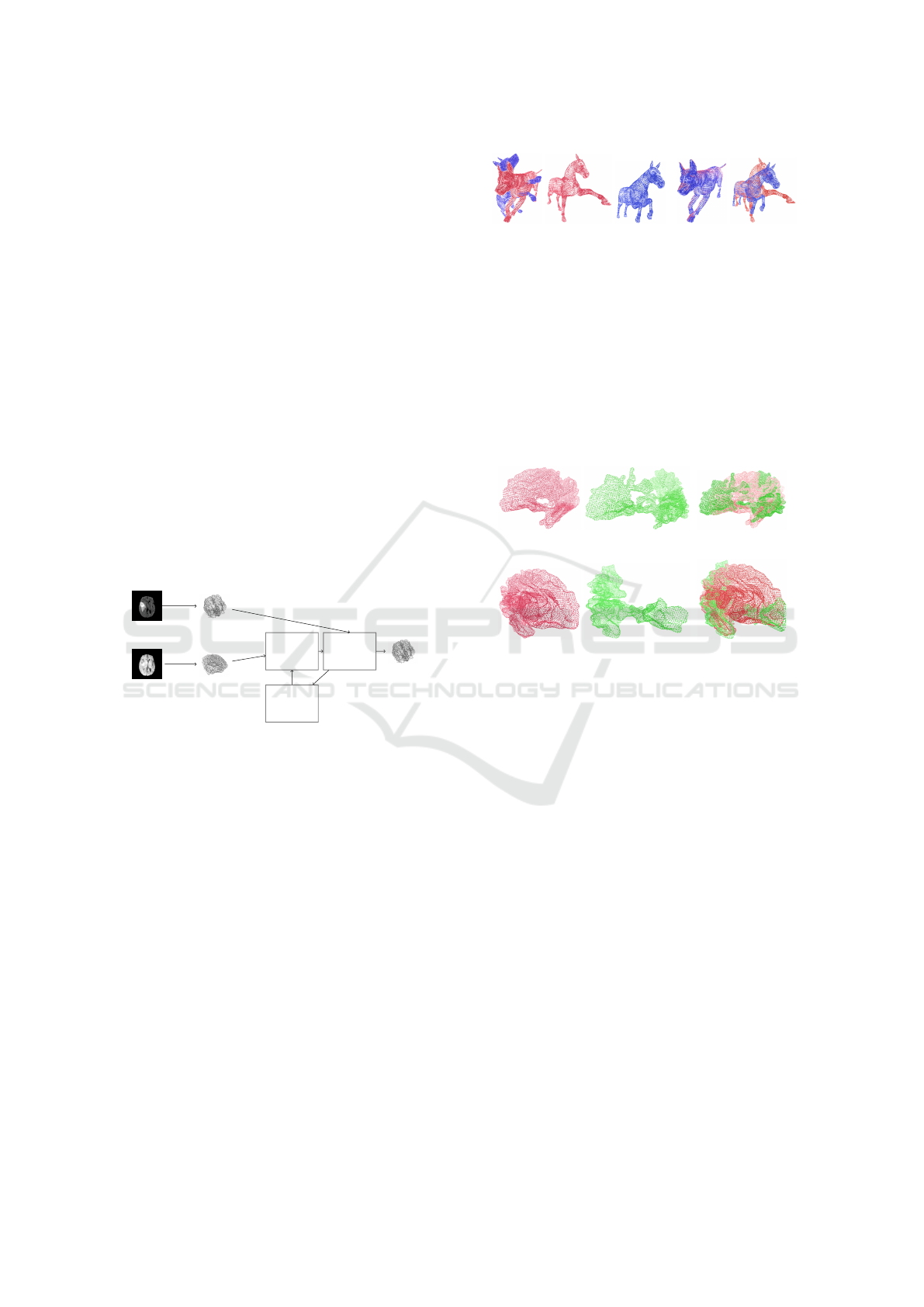
Figure 1 shows the proposed approach. We define
three components: the optimization function, the per-
formance metric, and the model parameters. Besides,
we used the transformation matrix to set the opti-
mization function (see section 2.2) and the perfor-
mance metric. Finally, a Gaussian process was se-
lected and tested with different acquisition functions
in the Bayesian optimizer block. Our goal is to sam-
ple the transformation parameters of the registration
process by using the posterior distribution over the ac-
quisition function.
Fixed image Fixed Point Cloud
Moving image Moving Point Cloud
Transforma-
tion
Function
Bayesian
Opti-
mization
Performance
metric
Moved Point Cloud
Figure 1: Proposed Approach for optimizing the hyperpa-
rameters of an affine transformation function. The model
finds the hyperparameters that optimize a performance met-
ric to align the Moving point cloud to the Fixed point cloud.
3 RESULTS AND DISCUSSIONS
Figure 2 shows some point clouds alignment using
the Tosca dataset (Bronstein et al., 2006; Bronstein
et al., 2007). The results show that Bayesian optimiz-
ers can accurately compute affine transformation pa-
rameters. For instance, figure 2a and figure 2b show
how the model aligns the blue shapes with the red
ones. Hence, we can analyze the changes produced
from the fixed point cloud to the moving one (i.e., legs
and head of the horse).
Besides, the model was also tested with the brain
structure dataset as shown in figure 3. Figure 3b and
3d show the resulting shape alignment for two neu-
rodevelopmental cases. We matched both left and
right white matter structures at two different times.
(a) Before registration (b) After registration
Figure 2: Example of our method with rigid transforma-
tions in some point clouds available in Tosca dataset. We
analyzed the results of point clouds that present different
poses.
As a consequence, significant loss of white matter can
be noted when comparing the first and second brain
structures (i.e., red and green shapes). Thus, Bayesian
optimization computes robust transformation param-
eters allowing accurate matches and resulting in rel-
evant neurodevelopmental tools for shape quantifica-
tion.
(a) (b)
(c) (d)
Figure 3: Shape alignment examples for two neurodevelop-
mental cases. We define the red point clouds as fixed and
the green point clouds as the moving ones. The brain struc-
tures are left (a-b) and right white matter (c-d).
Figure 4a and figure 4b show the convergence of
the Bayesian optimization process for left and right
white matter, respectively. The red plots show the
distance between the hyperparameters for each iter-
ation. It can be seen in figure 4 the exploration and
exploitation behavior during the hyperparameter tun-
ing. Exploration means that the model is sampling the
hyperparameters from broad bounded regions. Also,
small distances between consecutive hyperparameters
indicate the exploitation stage where the fine-tuning is
performed. Besides, the blue plots show the minimum
error obtained for each iteration. Thus, we analyze
how the model initiates a grid search that estimates an
optimal solution by performing probabilistic model-
ing.
Table 1 and 2 show the quantitative results of the
alignment process for the two datasets. We report
both NMI and RMSE metrics for comparison where
the Least-squares estimation (Umeyama, 1991), ICP
Employing K-D Tree optimization (Liu et al., 2016),
and Point Cloud matching using singular value de-
Bayesian Iterative Closest Point for Shape Analysis of Brain Structures
923

composition (Oomori et al., 2016) are also tested
1
.
In table 1, we evaluate the ability of our model to
align point clouds with different poses in the Tosca
dataset. Besides, table 2 shows the performance of
the methods using the Brain Asphyxia dataset. The
results show that ICP-based methods fail on some
point clouds making a qualitatively incorrect point
cloud alignment as shown in figure 5. The results
show that our model outperforms other registration
strategies even for large iteration experiments. Con-
sequently, the results show that a Bayesian optimiza-
tion strategy does not fall into local minima due to its
capability of a trade-off between exploitation and ex-
ploration, which is controlled by the acquisition func-
tion. Hence the compared models lack robustness and
exhibitin local minima convergences and inaccurate
matches.
(a) (b)
Figure 4: Convergence of the Bayesian Optimization pro-
cess. The figures show the distance between values of x
selected consecutively (red plot), and the minimum value
of the performance index obtained in each iteration (blue
plot).
Table 1: Comparison with different ICP algorithms. We re-
port Root Mean Square Error (RMSE x10
−3
) and Normal-
ized Mutual Information (NMI) using the Tosca dataset
Method RMSE ↓ NMI ↑
Least-squares Estimation of
transformation Parameters
Between Two Point
Patterns(Umeyama, 1991)
4.86e
−7
±4.39e
−7
0.99±9.04e
−5
ICP Employing K-D
Tree Optimization (Liu et al., 2016)
21.58±32.49 0.76±0.29
Point cloud matching
using singular value
decomposition (Oomori et al., 2016)
20.60±33.29 0.81±0.28
Our approach 4.20±2.64 0.88±0.08
Table 2: Comparison with different ICP algorithms using
the Brain Structure dataset.
Method RMSE-BS ↓ NMI-BS ↑
Least-squares Estimation of
transformation Parameters
Between Two Point
Patterns(Umeyama, 1991)
76.81±5.21 0.14±0.01
ICP Employing K-D
Tree Optimization (Liu et al., 2016)
67.88±8.21 0.21±0.02
Point cloud matching
using singular value
decomposition (Oomori et al., 2016)
45.29±5.01 0.24±4.12e
−3
Our approach 32.29±2.21 0.78±0.05
1
All the mentioned methods were implemented to be
tested in the specific datasets of this work, The cuantita-
tive results was obtained using all the brain structures of the
Brain Asphyxia Dataset
(a) Initial (b) Others (c) Ours
(d) Initial (e) Others (f) Ours
Figure 5: Some alignment processes for both datasets (b)
(Liu et al., 2016; Oomori et al., 2016) and (e) (Liu et al.,
2016; Oomori et al., 2016; Umeyama, 1991) with the com-
pared approaches. The other methods have problems align-
ing some point clouds correctly, indicating local optima
problems. For instance, figure b and e show moved shapes
rotated with respect to the fixed ones (red).
4 CONCLUSIONS
This paper presented a Bayesian Optimization frame-
work for probabilistic 3D shape registration pro-
cesses. Our method seeks to find the optimal parame-
ters that align point clouds data in a probabilistic way.
The experimental results showed that our approach
aligns point clouds properly by solving problems usu-
ally found in common ICP strategies such as local
optima. This approach is relevant for aligning point
clouds that are non-rigid, as shown in point clouds of
Brain Structures, which allows us to make a more ex-
haustive analysis of the neurodevelopmental changes
that appeared in perinatal asphyxia.
For future works, we plan to analyze to extend this
framework on non-rigid shape matching. The motiva-
tion for this research line is based on the need to ac-
curately quantify plausible elastic changes related to
neurodevelopmental clinical outcomes.
ACKNOWLEDGEMENTS
We thank the Ministry of Sciences of Colombia for
financing the project with CTO 897-2021. Also ac-
knowledges to the master’s degree in electrical engi-
neering, vice-rectorate of research, innovation and ex-
tension of the technological university of Pereira for
its funding with code E6-23-1.
REFERENCES
Balakrishnan, G., Zhao, A., Sabuncu, M., Guttag, J.,
and Dalca, A. V. (2019). Voxelmorph: A learning
ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods
924

framework for deformable medical image registration.
IEEE Transactions on Medical Imaging, 38:1788–
1800.
Besl, P. J. and McKay, N. D. (1992). A method for registra-
tion of 3-d shapes. IEEE Trans. Pattern Anal. Mach.
Intell., 14:239–256.
Bouaziz, S., Tagliasacchi, A., and Pauly, M. (2013). Sparse
iterative closest point. Computer Graphics Forum, 32.
Bronstein, A. M., Bronstein, M. M., and Kimmel, R.
(2006). Efficient computation of isometry-invariant
distances between surfaces. SIAM J. Sci. Comput.,
28:1812–1836.
Bronstein, A. M., Bronstein, M. M., and Kimmel, R.
(2007). Calculus of nonrigid surfaces for geometry
and texture manipulation. IEEE Transactions on Visu-
alization and Computer Graphics, 13:902–913.
Chen, Y. and Medioni, G. (1991). Object modeling by reg-
istration of multiple range images. Proceedings. 1991
IEEE International Conference on Robotics and Au-
tomation, pages 2724–2729 vol.3.
Dai, Z., Yu, H., Low, K. H., and Jaillet, P. (2019). Bayesian
optimization meets bayesian optimal stopping. In
ICML.
Fischl, B. R. (2012). Freesurfer. NeuroImage, 62:774–781.
Fong, E. and Holmes, C. C. (2021). Conformal bayesian
computation. In NeurIPS.
Garc
´
ıa, H.,
´
Alvarez, M. A., and Orozco,
´
A. (2016).
Bayesian optimization for fitting 3d morphable mod-
els of brain structures. In CIARP.
Guti
´
errez-Becker, B. and Wachinger, C. (2018). Deep
multi-structural shape analysis: Application to neu-
roanatomy. In MICCAI.
Jaffray, D. A., Kupelian, P. A., Djemil, T., and Macklis,
R. (2007). Review of image-guided radiation therapy.
Expert Review of Anticancer Therapy, 7:103 – 89.
Jones, D. R. (2001). A taxonomy of global optimiza-
tion methods based on response surfaces. Journal of
Global Optimization, 21:345–383.
Krebs, J., Delingette, H., Mailh
´
e, B., Ayache, N., and
Mansi, T. (2019). Learning a probabilistic model
for diffeomorphic registration. IEEE Transactions on
Medical Imaging, 38:2165–2176.
Lau, T. F., Luo, J., Zhao, S., Chang, E., and Xu, Y. (2020).
Unsupervised 3d end-to-end medical image registra-
tion with volume tweening network. IEEE Journal of
Biomedical and Health Informatics, 24:1394–1404.
Li, J., Hu, Q., Zhang, Y., and Ai, M. (2022). Robust sym-
metric iterative closest point. ISPRS Journal of Pho-
togrammetry and Remote Sensing, 185:219–231.
Liu, J., Zhu, J., Yang, J., Meng, X., and Zhang, H. (2016).
Three-dimensional point cloud registration based on
icp algorithm employing k-d tree optimization. In In-
ternational Conference on Digital Image Processing.
Mansilla, L., Milone, D. H., and Ferrante, E. (2020). Learn-
ing deformable registration of medical images with
anatomical constraints. Neural networks : the official
journal of the International Neural Network Society,
124:269–279.
Miller, S. P., Ramaswamy, V., Michelson, D. J., Barkovich,
A. J., Holshouser, B. A., Wycliffe, N., Glidden, D. V.,
Deming, D. D., Partridge, J. C., Wu, Y. W., Ashwal,
S., and Ferriero, D. M. (2005). Patterns of brain in-
jury in term neonatal encephalopathy. The Journal of
pediatrics, 146 4:453–60.
Oliveira, F. P. M. and Tavares, J. (2014). Medical image
registration: a review. Computer Methods in Biome-
chanics and Biomedical Engineering, 17:73 – 93.
Oomori, S., Nishida, T., and Kurogi, S. (2016). Point cloud
matching using singular value decomposition. Artifi-
cial Life and Robotics, 21:149–154.
Rasmussen, C. E. and Williams, C. K. I. (2005). Gaussian
Processes for Machine Learning (Adaptive Computa-
tion and Machine Learning). The MIT Press.
Rusinkiewicz, M. L. (2001). Efficient variants of the icp
algorithm. Proc. 3rd Int. Conf. 3D Digital Imaging
and Modeling, pages 145–152.
Sadozye, A. H. and Reed, N. S. (2012). A review of re-
cent developments in image-guided radiation therapy
in cervix cancer. Current Oncology Reports, 14:519–
526.
Satheesan, A. P., Chinnappa, A. R., Goudar, G., and
Raghoji, C. R. (2020). Correlation between early mag-
netic resonance imaging brain abnormalities in term
infants with perinatal asphyxia and neuro develop-
mental outcome at one year. International Journal of
Contemporary Pediatrics.
Snoek, J., Larochelle, H., and Adams, R. P. (2012). Prac-
tical bayesian optimization of machine learning algo-
rithms. In Pereira, F., Burges, C. J. C., Bottou, L., and
Weinberger, K. Q., editors, Advances in Neural In-
formation Processing Systems 25, pages 2951–2959.
Curran Associates, Inc.
Stanton, S., Maddox, W. J., and Wilson, A. G. (2022).
Bayesian optimization with conformal coverage guar-
antees. ArXiv, abs/2210.12496.
Umeyama, S. (1991). Least-squares estimation of transfor-
mation parameters between two point patterns. IEEE
Trans. Pattern Anal. Mach. Intell., 13:376–380.
Vos, B. D., Berendsen, F., Viergever, M., Sokooti, H., Star-
ing, M., and Isgum, I. (2019). A deep learning frame-
work for unsupervised affine and deformable image
registration. Medical Image Analysis, 52:12X143.
Wang, L., Gao, X., Zhou, Z., and Wang, X. (2014). Eval-
uation of four similarity measures for 2d/3d registra-
tion in image-guided intervention. Journal of Medical
Imaging and Health Informatics, 4:416–421.
Williams, J. L. and Maybeck, P. (2006). Cost-function-
based hypothesis control techniques for multiple hy-
pothesis tracking. Math. Comput. Model., 43:976–
989.
Zhang, J., Yao, Y., and Deng, B. (2022). Fast and robust
iterative closest point. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 44:3450–3466.
Zhang, P. (2015). Evaluating accuracy of community detec-
tion using the relative normalized mutual information.
In Journal of Statistical Mechanics: Theory and Ex-
periment.
Zhang, Z. (2005). Iterative point matching for registration
of free-form curves and surfaces. International Jour-
nal of Computer Vision, 13:119–152.
Zhao, S., Dong, Y., Chang, E., and Xu, Y. (2019). Recur-
sive cascaded networks for unsupervised medical im-
age registration. 2019 IEEE/CVF International Con-
ference on Computer Vision (ICCV), pages 10599–
10609.
Bayesian Iterative Closest Point for Shape Analysis of Brain Structures
925