Modelling Spatial Connectivity of Forest Harvest Areas: Exact and

Heuristic Approaches

Pete Bettinger

Warnell School of Forestry and Natural Resources, University of Georgia, 180 E. Green Street, Athens, Georgia, U.S.A.

Keywords: Connectivity, Spatial Analysis, Land Management, Forestry, Natural Resource Management.

Abstract: A forest management planning process can involve the development of a tactical plan that illustrates for a

land manager where to go and what to do within a specific period of time, acknowledging and satisfying all

recognized management constraints. More often these days, forest management constraints address the size,

timing, and placement of management activities. The optimization methods used to mathematically develop

a forest plan, and to integrate spatial constraints into planning efforts are often referred to as exact and heuristic

approaches. This paper describes how one might model spatial connectivity of forest harvest areas as

constraints under both approaches, using two different representations of connectivity, the unit restriction

model and the area restriction model. The heuristic approach to the latter has until now only been described

using scientific notation. Here, we provide guidance for the programming logic.

1 INTRODUCTION

Forest management is an important aspect of modern

society. Nations around the world act in various ways

to address the use of these renewable resources, to

balance the demand for wood and paper products with

the demand for other ecosystem services such as the

development and maintenance of recreational spaces

and wildlife habitat, and the provisioning of water and

sequestered carbon. Knowledge of the potential

location of future forest management activities can

help forest managers better account for spatial

management restrictions and wildlife habitat

concerns, and thus allow appropriate decisions to be

made. In some cases the rules for the management of

forests are embedded in laws and regulations (e.g.,

Maine Forest Service, 2017). In the absence of these,

forest management may be influenced by the desires

of certification programs (e.g., Forest Stewardship

Council-US, 2019) or simply by the desires of the

forest landowner.

Over the last three decades, the use of spatial

dependencies for analysing appropriate actions has

been increasingly suggested in the functional

relationships that connect proposed management

activities to economic, ecologic, or social outcomes.

https://orcid.org/0000-0002-5454-3970

In the field of forestry, the use of a geographic

concept, adjacency, has become an important method

for assessing spatial dependencies, and the outcomes

of these assessments subsequently are used to control

(constrain) the assignment of management activities

to forest areas.

There are many reasons why a specific forest

landowner would want to develop a forest plan that

addresses spatial issues such as adjacency of

management activities, from concern over the

cumulative effects of the management of their lands

to compliance with laws and regulations (Bettinger

and Sessions, 2003). Landowners often develop a

forest plan to guide the implementation of

management activities by forest managers. The closer

a plan models the real world system in which the

forest managers operate, the more likely the outcomes

of forest management can trusted. However, forest

planning problems with spatial connectivity

constraints can be difficult to mathematically model.

Often the number of spatial relationships that are

needed to represent connectivity of management

activities or the impact of management on wildlife

habitat components increase exponentially as

management unit size decreases and the scope of

local analysis rules increase. Some examples include

the examination of wildlife habitat conditions within

136

Bettinger, P.

Modelling Spatial Connectivity of Forest Harvest Areas: Exact and Heuristic Approaches.

DOI: 10.5220/0011761600003473

In Proceedings of the 9th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2023), pages 136-143

ISBN: 978-989-758-649-1; ISSN: 2184-500X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

a certain distance of a proposed timber harvest, and

the impact of that proposed harvest on minimum

habitat suitability constraints (Bettinger and Boston,

2008), and the evaluation of the average size of a

forest openings caused by proposed timber harvest

activities, and the impact of that proposed harvest on

constraints that limit maximum average opening sizes

(SFI USA, 2022). The mathematical approaches that

might be used to represent important spatial

relationships within a forest planning or optimization

context may overwhelm both the planner and the data

development processes employed.

This paper describes the common ways in which

adjacency of planned management activities is

modeled in quantitative processes that lead to the

development of a formal forest plan. The methods are

aimed at the integration of these ideas as constraints

with exact approaches to optimization of a forest plan

through mixed integer programming, and with

heuristic approaches to combinatorial optimization

through processes such as simulated annealing,

threshold accepting, or tabu search.

2 METHODS

The concepts described here refer to the development

of a tactical forest plan (where to go, and what to do

during specific periods of time). A mathematical

recognition and acknowledgement that two proposed

forest management activities are adjacent, in time and

space, can be used as a constraint that limits one of

them from being implemented through the tactical

forest plan. The feasibility of forest plans, which

guide the activities implemented by forest managers,

should be sound, providing forest managers an

opportunity to avoid mistakenly transforming the

condition of a landscape to a state that may be not

only undesirable, but also difficult to remedy in a

short amount of time.

Management units (i.e., stands, polygons) are

defined in modern times through the development of

a geographic information system (GIS) database.

These are contiguous areas of land that will be

managed in the same way through time. They often

include resources (e.g., trees) that have similarities or

are managed similarly. One example would be an area

of planted pine trees, where all of the trees are the

same species and age, and thus managed as an even-

aged system. Another example may be an area

containing a collection of heterogeneous tree species

and tree ages that are managed together as an uneven-

aged system. Adjacency refers to the proximity of

each management unit. In forest management, the

most common type of adjacency relationship between

two management units is that they share a side (or in

GIS, a line). However, an adjacency relationship may

suggest that two management units (a) only share a

point (vertex) in geographical space, of (b) share not

even a single vertex but have polygon vertices that are

within some assumed distance (e.g., less than 100 m

apart in geographical space).

Described below are methods for addressing

constraints of an optimization process. Constraints

control the amount, timing, and placement of

management activities when one seeks to minimize or

maximize some objective function (e.g., maximize

revenue). Two types of adjacency relationships are

commonly recognized in forest management

planning to control the timing and placement of final

forest harvests (clearcuts): the unit restriction model

and the area restriction model (Murray 1999).

2.1 Unit Restriction Adjacency

The concept of unit restriction adjacency in forest

and natural resource management is often used within

mathematical processes related to the development of

a tactical forest plan (where to go, and what to do

during specific periods of time). Unit restriction

adjacency constraints would prevent the assignment

of similar activities to two adjacent management units

during a specific period of time. For example, if the

final felling of trees in two management units were

under consideration, a unit restriction adjacency

constraint would prevent the assignment of the

fellings to occur during the same period of time. The

period of time is also referred to the green-up period,

which denotes the amount of time that the regenerated

forest in one management unit (the one whose trees

have been previously harvested) to grow to a desired

height (hence green up). In the northwestern United

States, the green-up period is often assumed to be 5

years on private lands, yet it can be much longer on

public lands. The length of the green-up period is

often defined by law or by policy.

2.1.1 Exact Approach

When employing unit restriction adjacency of forest

management activities and using an exact approach

suitable for mixed integer programming optimization

techniques (branch and bound, cutting plane, etc.),

one would develop pairwise constraints that limit the

ability of the process from selecting for management

two adjacent neighbours during the same time period

or green-up period. For example, to prevent the trees

in both management unit 1 and management unit 2,

Modelling Spatial Connectivity of Forest Harvest Areas: Exact and Heuristic Approaches

137

which are physically adjacent, from being harvested

during the same period of time (e.g., time period 1) a

constraint would be developed:

MU1P1 + MU2P1 <= 1

(1)

Here, the decision variable MU1P1 represents the

potential harvest of trees in management unit 1 during

time period 1. This approach assumes that the

decision variables are assigned only integer values,

where 1 = yes, harvest the trees in the management

unit, and 0 = no, do not harvest the trees in the

management unit. Obviously, only one of the two

choices would be possible with this constraint. For

multiple time periods (a green-up period that is longer

than a single time period), multiple pairwise

constraints may be necessary.

MU1P1 + MU2P1 <= 1

(2)

MU1P1 + MU2P2 <= 1

(3)

MU1P1 + MU2P3 <= 1

(4)

In the example above, if the trees in management

unit 1 are scheduled for harvest during time period 1

(e.g., MU1P1 = 1), then the trees in management unit

2 are not allowed to be harvested during time periods

1, 2, and 3.

What may not be obvious in this approach is that

the equations reflecting the constraints must be

constructed prior to solving the problem with an

optimization technique. If the green-up period

changes (lengthens or shortens), or the rules for

defining adjacent land areas change, the equations

would need to be re-developed.

2.1.2 Heuristic Approach

When a forest planning problem is being solved

(attempted to be optimized) with a heuristic approach,

computer logic (If-Then-Else statements, For-Next

loops, etc.) is used to assess constraints in real time.

For example, if a heuristic is attempting to schedule a

final harvest for management unit 1, it assesses all of

the potential constraint violations prior to formally

assigning the harvest period to that management unit.

To enable the assessment of adjacency constraints

within a heuristic, a list of the adjacency relationships

among the management units is often held in memory

of the computer program, and this list is accessed

when it is needed. The list may be as simple as:

1,2

1,3

1,4

2,1

2,12

3,1

3,4

...

This adjacency list suggests that management unit

1 is adjacent (however defined) to management units

2, 3, and 4. The list is redundant, as it also indicates

that in addition to management unit 1 being adjacent

to management unit 2, management unit 2 is adjacent

to management unit 1. To improve the efficiency of

this process, the list of adjacency relationships might

be sorted by management unit number, and pointers

might be developed to quickly access the beginning

and ending set related to a specific management unit.

For example, the pointers for management unit 2 are

4 (beginning line number) and 5 (ending line

number). This structure might be composed of a

single column vector once the beginning and ending

points for each management unit are known.

As an example of how a heuristic process would

assess the unit restriction adjacency constraint,

imagine that the trees in management unit 2 are

potentially being scheduled for final harvest during

time period 1. The logic within a heuristic would

check all of the neighbours of management unit 2 to

determine whether their trees are currently scheduled

for harvest during the same period of time.

Constraint violation = 0

For a = Beginning pointer (Management

Unit 2) to Ending pointer (Management

unit 2)

If (Potential harvest period

(Management unit 2) = Scheduled

harvest period (Adjacency list (a)))

Then

Constraint violation = 1

End If

Next a

Here, potential harvest period (Management unit 2)

is time period 1, and the scheduled harvest periods of

neighbours are determined by understanding who the

neighbours are from the adjacency list. In this

approach, there would be no need to re-develop

equations to assess the adjacency relationships. One

would only need the assumption of the green-up

period length to enable the logic to work during the

heuristic search process. If the green-up period were

longer than one time period within the time horizon,

the logic would expand to:

LowerPeriod = Potential harvest period

(Management unit 2)

- (Greenup window -

UpperPeriod = Potential harvest period

(Management unit 2)

+ (Greenup window -

GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management

138

Constraint violation = 0

For a = Beginning pointer (Management

Unit 2) to Ending pointer (Management

unit 2)

If (Scheduled harvest period

(Adjacency list (a)) >= LowerPeriod

AND Scheduled harvest period

(Adjacency list (a)) <= UpperPeriod)

Then

Constraint violation = 1

End If

Next a

Here, LowerPeriod and UpperPeriod represent

the bounds on the green-up period, or the time periods

that represent the beginning and ending of the green-

up period with respect to the potential schedule of a

harvest in Management unit 2 during time period 1.

Of course, some minor additional logic would be

necessary to ensure that LowerPeriod and

UpperPeriod are reasonable (i.e., greater than 0 and

less than or equal to the total number of time periods).

One advantage to the heuristic approach is that the

entire set of equations that define the adjacency

relationships need not be pre-defined, as the

relationships are assessed in real time, when needed.

2.2 Area Restriction Adjacency

The concept of area restriction adjacency in forest

and natural resource management is also used within

mathematical processes related to the development of

a tactical forest plan. In fact, this model of controlling

adjacent management activities is more closely

associated with common practice than the unit

restriction model, as management units defined in a

geographic information system may be of various

sizes, and combining them for on-site management

may be more practical than managing them

separately.

Area restriction adjacency constraints would

allow the assignment of similar activities to two or

more adjacent management units during a specific

period of time, as long as the total size of the

contiguous set of activities does not exceed some

maximum, assumed size. For example, if the final

felling of trees in two management units were under

consideration, an area restriction adjacency constraint

would allow the assignment of the fellings to occur

during the same period of time only if their total size

did not exceed some assumed maximum size.

Depending on the size of management units

(polygons) developed within a geographic

information system, and the assumed maximum size,

this collection of adjacent management units with

similar activities assigned can be brief (2 or 3

management units) or extensive (many management

units). For final harvests, the complicating factor is

the green-up period, and therefore here, the constraint

needs to be assessed from the perspective of each

management unit within the collection of adjacent

management units.

2.2.1 Exact Approach

Several methods for developing the equations that

would allow multiple forest management units that

are connected to be managed during a common period

of time have been described in the literature (e.g.,

Meneghin et al. 1998, Murray and Church 1996). For

this illustration we use the path model that was

described by McDill et al. (2002), as it concisely

illustrates an exact approach for modelling area

restriction adjacency.

Imagine that there are a collection of forest

management units of various sizes, and that there is

some assumed maximum area size (A) for final

harvests of the trees. Beginning with any two adjacent

pairs of management units, if the combined area of

these exceeds A, then a pairwise adjacency constraint

can be developed to prevent both of the management

units from being scheduled for harvest during a

specific period of time (i.e., the length of the green-

up period), just as we noted earlier. However, if the

combined size of the two management units is less

than A, it is possible that both can be scheduled for

harvest during the same period of time. In this latter

case, an examination of all of the adjacent neighbours

to these two management units would be made to

define the clusters of management units whereby the

last one added would force the total size of the cluster

to exceed A.

For example, assume management units 1-4 are

adjacent in one form or another. Assume the areas of

these management units are respectively 10 ha, 12 ha,

15 ha, and 10 ha. If A = 40 ha, then all four

management units should not be scheduled for a final

harvest during a period of time defined by the green-

up period. The exact approach constraints developed

to prevent scheduling all four during time period 1 of

a planning process would be devised in this manner

MU1P1 + MU2P1 + MU3P1 + MU4P1 <= 3

)

which allows up to three of the management units to

be scheduled for a harvest during time period 1, but

not all four of them. In other words, from none to any

three of the management units can be scheduled for

harvest during time period 1 based on their adjacency

relationships.

Modelling Spatial Connectivity of Forest Harvest Areas: Exact and Heuristic Approaches

139

The "path" in the path model reflects the

connectivity of management units. Some

management units in the resulting cluster may not be

themselves adjacent, yet a cluster is formed that

connects all of those considered. All possible paths

that originate from each management unit, that relate

to the possible final harvest of the trees in that

management unit during different periods of time,

must be assessed to develop these constraints.

Further, redundant and dominated constraints (made

ineffective based on other constraints) should

preferably be avoided, which may add considerable

time to the development of the set of exact approach

constraints.

As with the unit restriction model, equations

reflecting the constraints must be constructed prior to

solving the problem. If the green-up period changes

(lengthens or shortens) the equations would need to

be re-developed. The larger the A (maximum size)

and the longer the green-up period, the larger

becomes the set of constraints needed. This

development and management of constraint

equations to represent the adjacency relationships is

perhaps the most important disadvantage of using an

exact approach to model spatial connectivity.

2.2.2 Heuristic Approach

As an example of how a heuristic process would

assess the area restriction adjacency constraint,

imagine that the trees in management unit 2 are

potentially being scheduled for final harvest during

time period 1. The logic within a heuristic would

check all of the neighbours and place them in a set of

management units that forms a harvest block, as long

as the trees within the neighbouring management

units are already scheduled for harvest within the

green-up period, and as long as the total size of the

harvest block is less than the maximum size (A)

allowed. The example below begins with

management unit 2, and illustrates the building of

harvest block based on the prior harvest schedules

assigned to nearby neighbouring management units.

Constraint violation = 0

Block size = Size (Management Unit 2)

Queued (1) = Management Unit 2

Do While Queued (1) > 0

For a = Beginning pointer (Queued (1))

to Ending pointer (Queued (1))

If (Potential harvest period

(Queued (1)) = Scheduled harvest

period (Adjacency list (a))) Then

Place Adjacency list (a), the

adjacent neighbour, in the next

empty cell of the Queued array.

Block size = Block size + Size

(Adjacency list (a))

If (Block size > A) Then

Constraint violation = 1

Exit Loop

End If

Next a

"Seated" Management unit = Queued (1),

remembering member(s) of the harvest

block

The Queued array is then adjusted,

moving neighbouring management units

up 1 place

Loop

In addition to this abbreviated process, several

additional checks and balances may be needed. For

example, when neighbouring management units are

identified, they are ignored if they are already present

in the Queued array or if they are "Seated" as part of

the harvest block. If the logic suggests a constraint

violation has occurred, the resulting harvest block is

too large, and the proposed management activity

originally under consideration (in this case, the

harvest of trees in management unit 2 during time

period 1) is disallowed. However, if the resulting

harvest block does not exceed the maximum allowed

size, the proposed management activity may be

allowed to be scheduled within the framework of a s-

metaheuristic (e.g., simulated annealing, tabu search),

assuming the solution is feasible with respect to all

other constraints and other heuristic rules allow the

change to be made to the current feasible solution.

The main disadvantage of this heuristic approach

to modelling spatial connectivity is the programming

logic needed to efficiently and correctly represent the

development of a sprawling harvest block. Further,

when the green-up period is longer than one time

period, the assignment of harvest period to the focal

management unit in the process (the management unit

in position Queued(1)) defines the LowerPeriod and

UpperPeriod that were mentioned earlier. These

periods of time only relate to management unit 1, and

subsequently they need to be adjusted to assess

constraint violations related to all of the management

units in the Queued array (making them temporarily

the focal unit in this process).

2.3 Case Study

The application of unit restriction and area restriction

adjacency constraints is applied to a forested tract of

land situated in the western United States. The

management plan devised for this property has a 30-

year time horizon that consists of six, 5-year time

GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management

140

periods. The goal of the planning process is to provide

a guide to the forest managers, suggesting which

management units to harvest trees in each of the six

time periods, while minimizing deviations from a pre-

defined sustainable flow of wood products (13,950

thousand board feet

of wood per 5-year time period).

When the area restriction adjacency constraint is

employed, the maximum size was assumed to be 48.6

hectares (120 acres).

The exact approach described for the URM case

was formulated as a mixed integer programming

model and solved using Lingo Extended 19.0 (Lindo

Systems Inc., 2022). The heuristic approaches that are

described here for both the URM and ARM cases

embedded into a threshold accepting heuristic model

that employed search reversion and 2-opt moves

(Bettinger et al., 2015). The exact model produced the

optimal solution to the problem, while the heuristic

model produced the near-optimal solutions to the

associated problems.

2.3.1 Landscape Data

The case study forest (1,841.5 hectares) is contiguous

(Figure 1) and composed of 87 management units that

contain Douglas-fir (Pseudotsuga menziesii) and

western hemlock (Tsuga heterophylla) trees of

various ages. This case study forest has been

employed in several other research studies regarding

optimization methods for developing forest plans

(Akbulut et al., 2017, Bettinger et al., 2015, Restrepo

et al., 2022).

3 RESULTS

For the case study landscape described above, the

exact method for developing a forest plan that

accommodates unit restriction adjacency constraints

for final harvests requires 1,260 non-redundant

pairwise adjacency constraints when the green-up

period is one time period. As the size of the green-up

periods increases, the number of pairwise constraints

for this case study forest increases: 3,360 pairwise

constraints for two-period green-up, 5,040 pairwise

constraints for three-period green-up, 6,300 pairwise

constraints for four-period green-up, and so on. The

increase is not linear, as the green-up period extends

beyond the last period of time horizon (for

UpperPeriod), or before the first period of the

time horizon (for LowerPeriod), fewer pairwise

a board foot is 1 inch thick × 1 foot tall × 1 foot wide, or

2.54 cm thick × 30.48 cm tall × 30.48 cm wide.

Figure 1: The contiguous case study forest area.

constraints are necessary. The heuristic method

requires no pre-defined adjacency constraints, as it

checks the constraint violations with each attempted

adjustment to feasible solutions in real time as the

optimization problem is being solved. The logic

required to assess the constraints within a heuristic

can be as simple as the six lines of code noted above,

however, additional logic would be required to read

and store the adjacency list, and to create the pointers

for each stand to efficiently access the adjacency list.

An example forest plan, or coloured graph, that

represents the planned harvest period for each

management unit, recognizing unit restriction

constraints, is illustrated in Figure 2.

The exact method for developing a forest plan that

accommodates area restriction adjacency constraints

for final harvests requires 2,046 non-redundant, non-

dominated adjacency constraints when the green-up

period is one time period. As the number of green-up

periods increases, the number of constraints for this

case study forest increases substantially: 22,040

constraints for two-period green-up, 74,988

constraints for three-period green-up, and 146,238

constraints for four-period green-up. Like the

Modelling Spatial Connectivity of Forest Harvest Areas: Exact and Heuristic Approaches

141

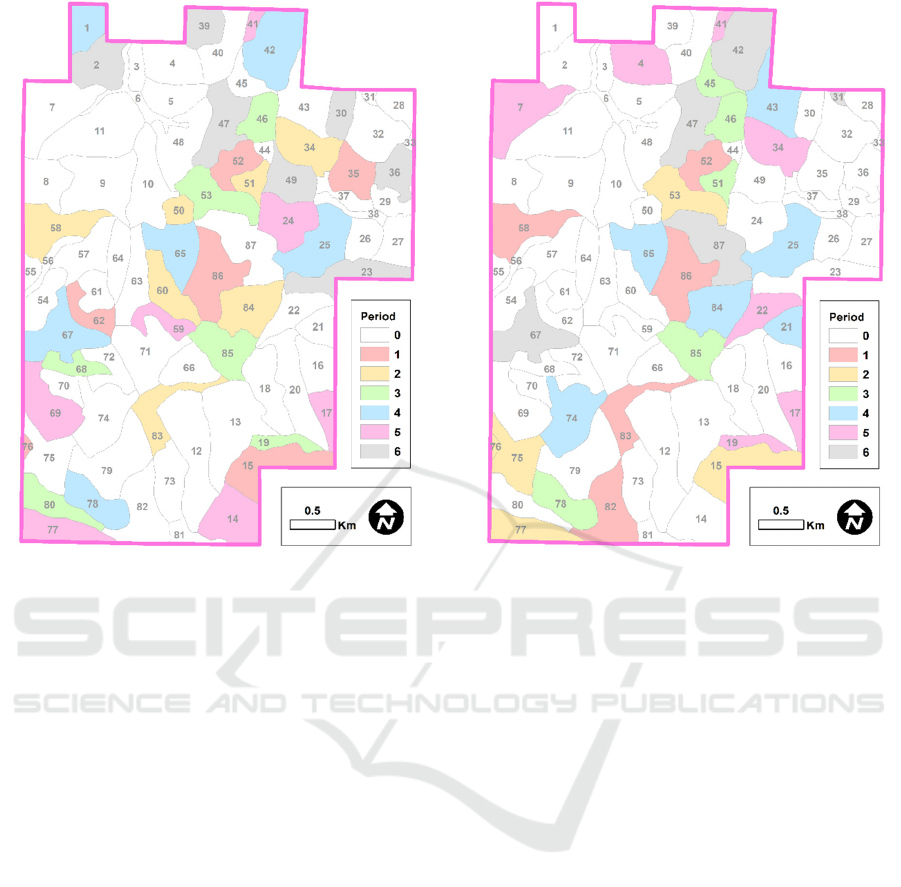
Figure 2: A forest plan that indicates the time period to

harvest the trees in each management unit, while

accommodating unit restriction adjacency constraints with

a green-up length of one time period.

previous case, the increase is not linear, but is it

certainly more substantial.

The combinations of management units that just

exceed the maximum area size, as the last one is

added, can be large when the management units are

small relative to the maximum area size. For this case

study landscape, one non-dominated area restriction

constraint contained six management unit decision

variables when the maximum area size was 48.6 ha,

and 8 non-dominated area restriction constraints

contained five management unit decision variables.

An example forest plan, or coloured graph, that

represents the planned harvest period for each

management unit, recognizing area restriction

constraints, is illustrated in Figure 3.

As suggested earlier, when it is necessary, removing

the redundant and the dominated constraints can be

cumbersome. For example, the constraint

MU1P1 + MU2P1 + MU3P1 + MU4P1 <= 3

(6)

is dominated by

MU1P1 + MU2P1 + MU4P1 <= 2

(7)

since if the latter is true, then the former must also be

true.

Figure 3: A forest plan that indicates the time period to

harvest the trees in each management unit, while

accommodating area restriction adjacency constraints with

a green-up length of one time period.

As noted earlier, one of the challenges when

utilizing an exact method for constraining the timing

and placement of forest management activities is in

reconstructing the area restriction model adjacency

constraints when the maximum area size or the green-

up period length changes. For example, a landowner

may wish to assess through modelling the impact of

various green-up or maximum final harvest size

policies on the production potential or economic

outcomes of a forest plan. For these purposes, the

development of adjacency constraints for an exact

method would likely require a separate computer

program to assess the relationships and remove the

redundant and dominated constraints.

As in the unit restriction case, the heuristic

method requires no pre-defined area restriction

adjacency constraints, as it checks in real time (during

the optimization process) the constraint violations

with each attempted adjustment to feasible solutions.

However, the logic required to assess the constraints

within a heuristic can require an extensive amount of

computer code to track the so-called queued and

seated management units noted earlier.

GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management

142

4 CONCLUSIONS

Described in this paper are methods for modelling the

connectivity of forest harvest areas, with particular

emphasis on the development of a tactical forest

management plan that prevents adjacent final

harvests of trees in management units located across

a forested area. Two common operations research

approaches for developing tactical forest

management plans that involve exact and heuristic

methods were described. The exact methods for

modelling unit restriction adjacency and area

restriction adjacency are well known within the

forestry community (e.g., McDill et al. 2002). The

heuristic method for assessing unit restriction

adjacency has been described in a number of

published papers over the last two decades (e.g.,

Akbulut et al., 2017, Bettinger et al. 2015, Bettinger

and Boston 2008). The logic for assessing area

restriction adjacency has only been described in a

theoretical sense in prior works, therefore the process

described here may be one of the first explicit

examples of how one might model area restriction

adjacency using computing logic.

As was illustrated in this paper, the number of a

priori defined constraints for exact URM and ARM

approaches that acknowledge and control the

adjacency of management activities can be quite

extensive, depending on the spatial management unit

size and the scope of local analysis rules. In contrast,

the heuristic approaches require only logic to assess

these relationships when they are needed during the

mathematical scheduling of management activities.

Regardless of the approach for developing a forest

plan or assessing the impact management activities

across a landscape, the exact and heuristic approaches

have both advantages and disadvantages that may be

of importance to scholars and practitioners. Future

work might involve studies designed to further

understand the time and effort needed to

accommodate these approaches as property size

increases and as spatial unit sizes change. These

investigations would advance our understanding how

the results from applying these methods may be

generalizable across different forest landscapes.

REFERENCES

Akbulut, R., Bettinger, P., Ucar, Z., Obata, S., Boston, K.,

Siry, J. (2017). Spatial forest plan development using

heuristic processes seeded with a relaxed linear

programming solution. Forest Science. 63(5): 518-528.

Bettinger, P., Boston, K. (2008). Habitat and commodity

production trade-offs in Coastal Oregon. Socio-

Economic Planning Sciences. 42(2): 112-128.

Bettinger, P., Demirci, M., Boston, K. (2015). Search

reversion within s-metaheuristics: Impacts illustrated

with a forest planning problem. Silva Fennica. 49(2):

article id 1232.

Bettinger, P., Sessions, J. (2003). Spatial forest planning:

To adopt or not to adopt? Journal of Forestry. 101(2):

24-29.

Forest Stewardship Council-US (2019). FSC-US Forest

Management Standard (V1.1), Complete with: Family

forest indicators and guidance and supplementary

requirements for lands managed by the USDA Forest

Service. Forest Stewardship Council US, Conifer, CO.

Lindo Systems Inc. (2022). LINGO Extended 19.0. Lindo

Systems Inc., Chicago, IL.

Maine Forest Service (2017). The forestry rules of Maine

2017, A practical guide for foresters, loggers and

woodlot owners, 2

edition. Maine Department of

Agriculture, Conservation & Forestry, Maine Forest

Service, Augusta, ME.

McDill, M.E., Rebain, S.A., Braze, J. (2002). Harvest

scheduling with area-based adjacency constraints.

Forest Science. 48(4): 631-642.

Meneghin, B.J., Kirby, M.W., Jones, G.J. (1988). An

algorithm for writing adjacency constraints efficiently

in linear programming models. U.S. Department of

Agriculture, Forest Service, Rocky Mountain Forest

and Range Experiment Station, Ft. Collins, CO.

General Technical Report RM-161. pp. 46-53.

Murray, A.T. (1999). Spatial restrictions in harvest

scheduling. Forest Science. 45(1): 45-52.

Murray, A.T., Church, R.L. (1996). Analyzing cliques for

imposing adjacency restrictions in forest models. Forest

Science. 42(2): 166-175.

Restrepo, H.I., Bettinger, P., Bullock, B.P. (2022). A

theoretical minimum solution for heuristics: The case

of the spatial timber harvest problem. Computers &

Operations Research. 143: Article 105792.

SFI USA. (2022). SFI 2022 forest management standard,

Section 2. SFI USA, Washington, D.C.

Modelling Spatial Connectivity of Forest Harvest Areas: Exact and Heuristic Approaches

143