Carbon-Box Testing

Sangharatna Godboley

, G. Monika Rani

and Sindhu Nenavath

Department of Computer Science and Engineering,

National Institute of Technology Warangal, Telangana, India

Keywords:

Random Testing, Dictionary Testing, Combinatorial Testing, Pairwise Testing, Branch Coverage.

Abstract:

Combinatorial testing tools can be used to generate test cases automatically. The existing methodologies such

as Random Testing etc. have always the scope of achieving better branch coverage. This is because most of

the time the boundary values which are corner cases have been ignored to consider, as a result, we achieve

low branch coverage. In this paper, we present a new type of testing type named Carbon-Box Testing. This

Carbon name justiﬁes the inﬂuence of Black-Box testing techniques we use with a lightweight White-Box

testing technique. We show the strength of our proposed method i.e. Dictionary Testing to enhance the branch

coverage. In Dictionary Testing, we trace the input variables and their dependent values statically and use

them as test inputs. This is a fact that utilizing the statically extracted values is insufﬁcient for achieving the

maximal Branch coverage, hence we consider Random Testing to generate the test inputs. The initial values

are the real-time Linux process ids, and then we perform mini-fuzzing with basic arithmetic operations to

produce more test inputs. Pairwise testing or 2-way testing in Combinatorial testing is a well-known black-

box testing technique. It requires a set of test inputs so that it can apply the mechanism to produce new test

inputs. Our main proposed approach involves the generation of test inputs for achieving Branch coverage from

Random testing values, Dictionary testing values, and a combination of both Random as well as Dictionary

values with and without pairwise testing values. We have evaluated the effectiveness of our proposed approach

using several experimental studies with baselines. The experimental results, on average, show that among all

the approaches, the fusion of Random and Dictionary tests with Pairwise testing has superior results. Hence,

this paper shows a new technique which is a healthy combination of two black-box and one white-box testing

techniques which leads to Carbon-Box Testing.

1 INTRODUCTION

Software testing and program analysis are the two

most basic concepts to ensure the quality of a pro-

gram or code. At least 50% of any project devel-

opment effort is taken by software testing. Among

all software testing techniques, Combinatorial testing

(Jun and Jian, 2009)(Dutta et al., 2019)(Calvagna and

Gargantini, 2009) is the stronger approach. In this

technique, test cases are generated by selecting values

for input variables (Lei et al., 2007) and then combin-

ing them with these parameter variables or parame-

ters. For example, consider a system with 6 inputs

or parameters, with each of them holding 10 values,

then the possible number of combinations or conﬁgu-

rations of values is 106. These generated 106 combi-

nations are termed as 106 test cases that are to be ex-

https://orcid.org/0000-0002-6169-6334

https://orcid.org/0000-0002-1662-5764

ecuted. It is difﬁcult to test all the test cases exhaus-

tively because of many reasons like time constraints

and lack of resources. The main problem here is to

reduce the number of conﬁgurations or combinations

such that the effectiveness of detecting errors/bugs is

not disturbed. To solve these kinds of problems, some

methods have been proposed. Pairwise testing(Feng-

an and Jian-hui, 2007) is one of the famous methods

which keeps a correct balance between the effective-

ness and quantity of combinations. It makes sure that

every combination of any two values is to be covered

by at least one test case.

Combinatorial testing uses automatic software

tools for the generation of combinatorial test cases to

determine the expected results for each set of test in-

put variables and values. Combinatorial testing aims

to ensure that the software product is error / bug-free

and can handle multiple cases or combinations of the

input conﬁguration values. Combinatorial testing is a

testing method where multiple combinations of input

314

Godboley, S., Rani, G. and Nenavath, S.

Carbon-Box Testing.

DOI: 10.5220/0011768900003464

In Proceedings of the 18th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2023), pages 314-321

ISBN: 978-989-758-647-7; ISSN: 2184-4895

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

parameter values are used to perform testing of the

software product.

In this paper, we use PICT (Czerwonka, 2010),

which is a publicly available tool. Any non-trivial

piece of software with a set of possible inputs is

too large to test. Some techniques like bound-

ary value analysis and equivalence partitioning(Reid,

1997) help to convert a large number of test case lev-

els into smaller test case levels with comparable de-

fect detection power. Exhaustive testing becomes im-

practical if the software under test (SUT)(Lei et al.,

2007) is inﬂuenced by such factors. Many combina-

torial techniques have been proposed and developed

over the years to assist testers in selecting subsets of

input conﬁgurations and combinations that would in-

crease the probability of identifying faults, as well as

t-wise testing Approaches, the most well-known of

which are pairwise testing.

The main advantage of combinatorial testing is to

reduce the number of test cases that are generated for

execution as compared to the exhaustive testing tech-

nique. Since the test cases are reduced, the cost of

execution time reduces due to its less size, and the

coverage is increased. If the selection of input vari-

able values is not done properly, then the resulting test

combinations and conﬁgurations are ineffective.

The problem statement is to generate a Test Suite

to overcome the disadvantages of using random val-

ues as a test suite. In the case of random test cases

or values, it is impossible to be speciﬁc about the ex-

pected results. The random values range is also larger

to explore. It is exhaustive to recreate the test if data

is not recorded which was used for testing. We gen-

erate Dictionary values for each variable used in the

program and then supply these as inputs in two ways

to generate branch coverage. The generation of dic-

tionary values is similar to that of boundary values

analysis. In boundary values analysis, the extreme

values are taken into consideration. However, in the

Dictionary values generation process, all the constant

operands that are present in the program are consid-

ered. When these values are combined with PICT

then the probability of the variables getting assigned

to its boundary values increases. Hence, this increase

is expected in the coverage as well. Using the Dic-

tionary Test Suite concept, A new Test suite is gen-

erated by the fusion of Random and Dictionary val-

ues (boundary values) of C program variables as in-

put to the PICT tool. This new Test Case Generation

increases the Line coverage, Branch coverage more

than the random test suite, and dictionary test suite

when supplied as input to Gcov

tool. It also reduces

the number of test cases that are generated for exe-

https://gcc.gnu.org/onlinedocs/gcc/Gcov.html

cution. Since the test cases are reduced, the cost of

execution time reduces due to its less size, and the

coverage is increased.

The rest of the paper is organized as follows. Sec-

tion 2 presents the basic concepts used in the pa-

per. Section 3 presents similar and related works

done in these ﬁelds. Section 4 presents our pro-

posed approach, we named it Fusion of Random and

Dictionary-based Test Case Generator (FRDTCG).

Section 5 explains the experimental results obtained

by the FRDTCG. Our work is concluded with future

insights in Section 6.

2 BASIC CONCEPT

In this section, we discuss important concepts which

are required to understand the work.

Pairwise Testing. Pairwise testing can be deﬁned as

follows: Let N independent test factors f

, f

... f

Let

be the possible levels for each f

Let R be the set

of tests produced for each factor at each level which

covers all possible pairs of test factor levels. It means

that for each ordered pair of factor levels with differ-

ent input parameters I

i, p

and I

j,q

where 1 ≤ p ≤ L

1 ≤ q ≤ L

, and i ̸= j there is at least one test case in

R which has both I

i, p

and I

j,q

This idea of test factor pairs at each level can be

expanded from all pairs to any feasible t-wise conﬁg-

urations or combinations where 1 ≤ t ≤ N (Maity and

Nayak, 2005). When ‘t’ equals to 1, the technique

becomes each-choice, and when ‘t’ equals N, the test

case suite becomes exhaustive.

Random Testing. The Random testing(Kelly J.

et al., 2001) is a black-box software testing technique,

which involves generating Random, independent in-

puts to test programs. To ensure that the test output

is pass or fail, the results are compared to software

speciﬁcations. In the lack of speciﬁcations, the lan-

guage’s exceptions are employed, which means that

if an exception occurs during test execution, the pro-

gram is defective; it is also used to avoid biased test-

ing. Random test cases are generated using the rand()

and srand() routines. We have developed our in-house

random test case generator that generates test cases,

and these test cases will be used for processing along

with other techniques.

Dictionary Testing. Dictionary Testing is a testing

technique that involves generating test inputs stati-

cally by extracting the boundary values of the pro-

gram. The boundary values i.e., Dictionary values

are meaningful when compared to the random values,

and hence help in effective testing. We have devel-

oped our in-house dictionary-based test case genera-

Carbon-Box Testing

315

tor that generates test cases, and these test cases will

be used for processing along with other techniques.

These dictionary values are supplied as input to the

PICT tool for generating possible combinations of

variables.

Line Coverage. The basic coverage metric used is

line coverage. Line coverage is a simple metric that

determines whether a line of program or code was ex-

ecuted or not. The number of executed lines divided

by the total number of lines is the Line Coverage of a

program. LineCoverage =

No. o f Executed Statements

Total No. o f Statements

Branch Coverage. The proportion of independent

code pieces that were executed is referred to as branch

coverage(Godboley et al., 2015). The term ”indepen-

dent code pieces” refers to segments of code that have

no branches leading into or out of them. To cover all

branches of the control ﬂow graph, the branch cover-

age method is implemented. At least, it covers all pos-

sible outcomes (true and false) once of each decision

point condition. The branch coverage is a white box

testing technique that guarantees that each decision

point’s branches are all tested. BranchCoverage =

No. o f Executed Branches

Total No. o f Branches

3 RELATED WORK

Over the past few years, many works have been pro-

posed in this domain. Below are some notable works

based on combinatorial testing.

Code coverage metrics like the decision, condi-

tion coverage, and Modiﬁed Condition / Decision

Coverage (MC/DC)(Awedikian et al., 2009)(Kelly J.

et al., 2001)(Godboley et al., 2018a) is enhanced by

combining the ideas of Concolic testing(Godboley

et al., 2018b) and Pairwise testing(Feng-an and Jian-

hui, 2007). Concolic Testing plus combinatorial test-

ing(Dutta et al., 2019) is proposed to evaluate the

effectiveness of Concolic testing tools. Maity et al.

(Maity and Nayak, 2005) demonstrate how ordered

designs and orthogonal arrays may be utilized to gen-

erate test cases for parameters with more than two

values. Czerwonka et al. (Czerwonka, 2010) focus

on how the pure pairwise testing approach must be

balanced in order to be practical, to aid the tester

who is attempting to apply pairwise testing in prac-

tice. Combinatorial Test Case generation for embed-

ded software using a search method to automatically

construct multi-dimensional parameters to cover the

high quality of test cases, and to extract the impor-

tant parameters for the combination test model(Zhou

et al., 2018).

Particle Swarm Optimization(Chen et al., 2010b),

a type of meta-heuristic search tool, is applied to pairs

testing in which test suites that cover all pair, triple,

and n-way combinations of factors with minimum

size are generated in order to determine the optimal

combinatorial test cases in the polynomial amount of

time. An extension to the white box which selects

additional test cases based on internal sub-operations

that are used in commercial tools and practical ap-

plications is proposed in (Kim et al., 2007). Test-

ing logical expressions(Ballance et al., 2012) in soft-

ware for fault simulation and fault evaluating appli-

cations proves that when paired-wise testing is com-

pared against random testing, the pairwise strategy is

found to be more effective.

Bell et al. (Bell and Vouk, 2005) addressed the

issues of random testing using N-way and enhanced

pairwise testing in order to reduce security failures

in network-centric software. The outcomes of ran-

dom testing of a simulation in which around 20% of

ﬂaws with probabilities of occurrence less than 50%

that are never exposed are also explained. Enhance-

ment of combinatorial testing(Li et al., 2019) and its

applications can detect faults that are caused by var-

ious inputs and their interactions. In this study, the

advancement of combinatorial testing research and

application in several sectors of application was ex-

plored, and potential application directions for the fu-

ture were given to provide ideas for its broad applica-

bility.

Bokil et al. (Bokil et al., 2009) provide a tool

AutoGen that reduces the cost and work by auto-

matically producing test data for C code. It is soft-

ware that can generate data for a variety of coverage

types, including MC/DC, and the experience of us-

ing it on real-world applications. The effort required

using the tool was one-third of the manual effort re-

quired. An improved distributed concolic testing ap-

proach(Godboley et al., 2016) which takes a remark-

able computational time for complex programs is a

more efﬁcient DCT method that improves the MC/DC

ratio while reducing computation time. Godboley

etal. (Godboley et al., 2017) introduced J

Model

for improved Modiﬁed Condition/Decision Coverage

analysis. The J

(JPCT, JCA, JCUTE) Model is pro-

posed to obtain a high MC/DC percentage, demon-

strating that the existing concolic testing technique

can be improved. In comparison to other transfor-

mation techniques, JPCT (Java Program Code Trans-

former) is a more efﬁcient version for program-to-

program transformation. JCA (Java Coverage Ana-

lyzer) is much more powerful than the existing cov-

erage analyzer for MC/DC since it is developed by

considering all MC/DC essential requirements.

Test case minimization approach (Ahmed, 2016)

using fault detection and combinatorial optimization

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

316

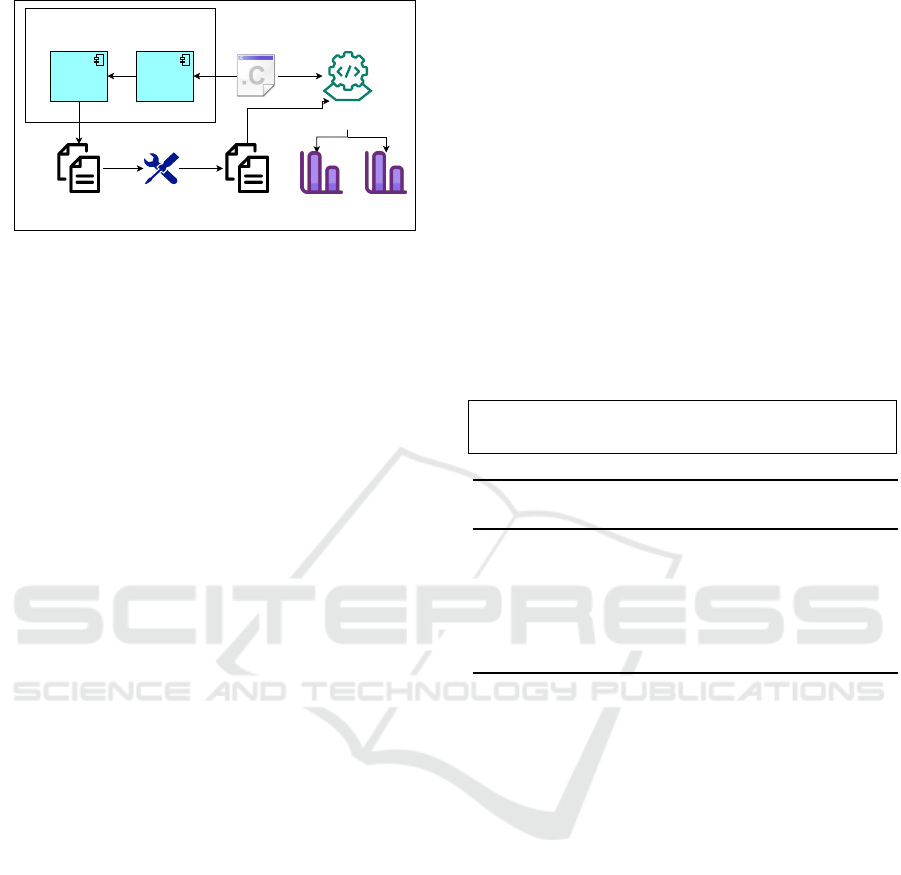
DTCG RTCG

FRDTCG

TS ETS

PICT

Gcov

LC BC

Figure 1: Framework for FRDTCG.

techniques for conﬁguration-aware structural testing

was proposed to reduce the number of test values.

Godefroid et al. (Godefroid et al., 2005) proposed

DART, which combines three techniques: (1) auto-

mated extraction of the interface of a program (2) au-

tomatic generation of a test driver that performs ran-

dom testing (3) dynamic analysis. Adaptive Random

Testing(Chen et al., 2010a) of test case diversity pro-

vides a summary of the most notable research ﬁndings

in the ﬁeld of ART Research which is applied in areas

of software testing. Kacker et al. (Kacker et al., 2013)

introduced Combinatorial testing for software which

is an adaptation of the design of experiments com-

binatorial t-way testing to detect software faults. In

this paper, Pairwise testing began using orthogonal ar-

rays rather than covering arrays. An Interleaving Ap-

proach to Combinatorial Testing and Failure-Inducing

Interaction Identiﬁcation that allows both generation

and identiﬁcation processes to interact has been dis-

cussed in (Niu et al., 2020). This methodology is

faster than previous approaches at identifying failure-

inducing interactions and requires fewer test cases.

Borazjany et al. (Borazjany et al., 2012) focused on

applying combinatorial testing to test a combinatorial

test generation tool called ACTS that is effective in

achieving high code coverage and fault detection.

4 PROPOSED APPROACH

In this section, we discuss the framework and algo-

rithm for our proposed approach. Fig. 1 presents

the framework of FRDTCG. The FRDTCG is imple-

mented by combining both RTCG (Random Test Case

Generation) and DTCG (Dictionary-based Test Case

Generation) along with the PICT tool.

The ﬂow starts with supplying a C program into

the FRDTCG component to generate Test Suite (TS).

The RTCG component involves generating random,

independent test cases to test the input C-program.

These random test cases are generated using the

rand() and srand() routines. The DTCG generates

Dictionary values i.e. statically extracts the values for

each input variable used in the program. The genera-

tion of dictionary values is similar to that of boundary

values analysis. In boundary values analysis, the ex-

treme values are taken into consideration. However,

in the dictionary values generation process, all the

constant operands that are present in the program are

considered. Next, the TS generated from FRDTCG

is supplied into the PICT tool to populate more test

cases. The additional test cases are added with TS and

called as Extended test Suite (ETS). These newly cre-

ated test cases have a high probability of the variables

getting assigned to their boundary values. Hence, this

high probability helps in achieving higher coverage as

well. To compute Line coverage and Branch Cover-

age we have used Gcov tool.

Listing 1: A sample Predicate from a C program.

if(((a230==10) && (a47==1) && (a56==1)

&& (a47!=1) && (a363==32) && (cf==1))){...}

Algorithm 1: Generation of Line coverage and Branch cov-

erage using FRDBTG.

Input: P

Output: LC, BC

1 TS ← FRDTCG(P);

2 ETS ← PICT(TS);

3 LC, BC ← Gcov(ETS);

4 return LC, BC;

Let us consider a sample predicate from a C pro-

gram as shown in Listing 1. We have extracted con-

stant operands from all the predicates in the program

and these constant values are taken in random i.e., not

as the exact order of the program. The constant values

in the below predicate are {10,1,32} which are bound-

ary values that, in turn, are considered as dictionary

values of the program. Now, we explain the algorith-

mic description of FRDTCG. We generate Random

values and Dictionary values for each variable used in

the program and then supply this as input in two ways

to generate branch coverage. In the ﬁrst way, we sup-

ply Random and Dictionary values as input to GCov

without using the PICT tool to generate coverage. The

second way is to supply Random and Dictionary val-

ues as input to the PICT tool and the output generated

is supplied to Gcov as input to generate coverage.

The Algorithm 1 shows the generation of a com-

bination of Random and Dictionary test cases by sup-

plying variables of the C program to FRDTCG. Line

2 in Algorithm 1 invocation of FRDTCG which is

a combination of Random and Dictionary-based test

cases i.e. TS. Line 2 in Algorithm 1 shows the invoca-

tion of the PICT tool by supplying TS, and outputting

Carbon-Box Testing

317

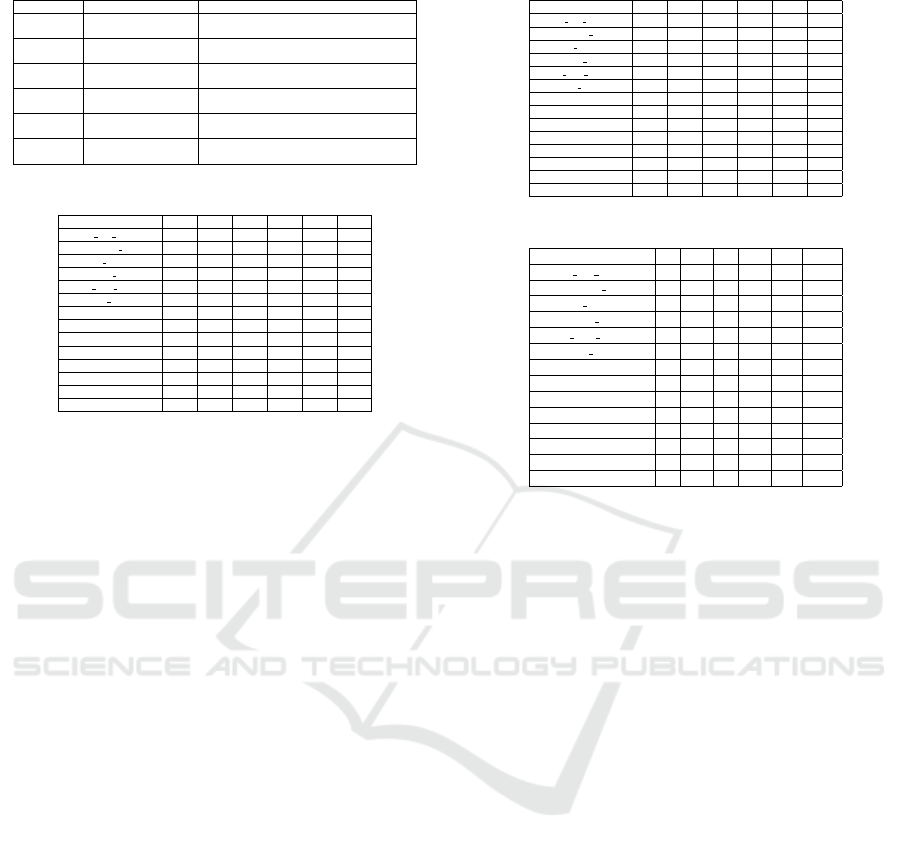
Table 1: Important nomenclatures with descriptions.

Abbreviation Component(s) Description

R RTCG

Test cases generated by

only random testing.

RP RTCG + PICT

Test cases generated by

random testing and pairwise testing.

D DTCG

Test cases generated by

only dictionary testing.

DP DTCG + PICT

Test cases generated by

dictionary testing and pairwise testing.

RD RTCG + DTCG

Test cases generated by fusion of

random testing and dictionary testing.

RDP RTCG + DTCG + PICT

Test cases generated by fusion of random

testing, dictionary testing, and pairwise testing.

Table 2: Consolidated Results of Line Coverage.

Programs R RP D DP RD RDP

Uninit var modiﬁed 24.14 24.14 57.47 57.47 57.47 57.47

Memory leak 12.15 12.15 77.57 77.57 77.57 77.57

Null pointer 19.44 19.44 41.67 41.67 59.72 59.72

Function pointer 10 10 83.08 83.08 83.08 83.08

Free null pointer 9.15 9.15 52.82 52.82 52.82 52.82

Num Rows 19.05 19.05 19.05 19.05 19.05 19.05

P2-L-T-R16 0.91 0.91 0.91 0.91 4.4 4.4

P7-L-T-R16 1.57 1.57 1.57 1.57 1.57 1.57

P8-L-T-R16 1.11 1.11 7.92 7.92 8.4 10.46

P10-L-T-R16 0.92 0.92 0.92 0.92 4.61 4.61

Wtest11-B15 33.72 33.72 36.74 40.93 36.74 41.40

Wtest31-B15 1.09 1.09 1.09 1.09 4.67 5.92

ZodiacandBirthstone 85.71 85.71 85.71 85.71 85.71 85.71

Prob1-IO-R14-B10 13.13 13.13 45.89 45.89 48.92 48.92

ETS. Line 3 in Algorithm 1 invokes the Gcov tool by

supplying ETS and produces LC and BC, which re-

turns at last.

5 EXPERIMENTAL RESULTS

In this section, we discuss the experimental results of

our proposed approach in detail.

5.1 Set Up

We performed the experiments on a 64-bit Ubuntu

machine with 8GB RAM and Intel (R) Core(TM)-i5

processor. For experimentation purposes, we consider

14 benchmark programs to generate the results. PICT

tool is used for enhancing the test cases generated by

the RTCG, DTCG and FRDTCG respectively. In or-

der to execute the test cases and to produce the line

and branch coverage reports, Gcov tool is used. Ta-

ble 1 shows the baselines and our proposed approach,

with their Abbreviation, Component(s) used and Brief

Description.

5.2 Results

In this section, we present the results of RTCG, DTCG

and FRDTCG approaches w.r.t., the total number of

test cases generated, line coverage, branch coverage

by both modes i.e., with and without using PICT tool.

It is observed that the results of generation of test

cases, line coverage, branch coverage using PICT tool

are useful. The consolidated results of all the three

approaches discussed so far are shown in TableS 2,

Table 3: Consolidated Results of Branch Coverage.

Programs R RP D DP RD RDP

Uninit var modiﬁed 74.36 74.36 79.49 79.49 84.62 84.62

Memory leak 46.51 46.51 83.7 83.7 87.5 87.5

Null pointer 71.43 71.43 71.43 71.43 87.5 87.5

Function pointer 38.1 38.1 89.52 89.52 89.52 89.52

Free null pointer 48.42 48.42 69.47 69.47 77.89 77.89

Num Rows 20 20 20 20 20 20

P2-L-T-R16 1.04 1.04 1.04 1.04 6.93 6.93

P7-L-T-R16 1 1 1 1 1 1

P8-L-T-R16 0.79 0.79 6.66 11.08 11.48 17.68

P10-L-T-R16 0.64 0.64 0.64 0.64 6.76 6.76

Wtest11-B15 32.03 32.03 52.11 61.52 52.11 60.04

Wtest31-B15 2.41 2.41 2.41 2.41 6.02 8.1

ZodiacandBirthstone 73.91 73.91 95.65 95.65 97.83 97.83

Prob1-IO-R14-B10 20.37 20.37 61.16 70.61 62.59 62.59

Table 4: Consolidated Results of Test Cases.

Programs R RP D DP RD RDP

Uninit var modiﬁed 15 403 15 403 30 1489

Memory leak 15 472 15 472 30 1730

Null pointer 15 416 15 416 30 1527

Function pointer 15 455 15 455 30 1677

Free null pointer 15 455 15 455 30 1617

Num Rows 15 268 15 268 30 1379

P2-L-T-R16 15 478 15 478 30 1757

P7-L-T-R16 15 455 15 455 30 1677

P8-L-T-R16 15 403 15 403 30 1489

P10-L-T-R16 15 472 15 472 30 1730

Wtest11-B15 15 416 15 416 30 1527

Wtest31-B15 15 403 15 403 30 1489

ZodiacandBirthstone 15 268 15 268 30 1022

Prob1-IO-R14-B10 15 806 15 806 30 2960

3 and 4. Table 2 illustrates line coverage results of

R, RP, D, DP, RD and RDP approaches. It can be

observed that there is a signiﬁcant difference in the

coverage results of R and D approaches when com-

pared to that of RD approach. Table 3 contains branch

coverage information for R, RP, D, DP, RD and RDP

approaches. These results almost show the trend un-

like the line coverage discussed. Table 4 presents the

total number of test cases generated in all of the ap-

proaches. We generated only 15 unique test cases us-

ing Random and Dictionary generators. We could test

for any number of test cases that we would like to

choose. The total number of test cases 15 is just a

random number we decided to take. It is to be noted

that we have considered equal quantities of test cases

i.e. 15, because the dictionary values which are ex-

tracted from the code are meaningful, whereas the

random values are uncertainty generated. Precisely,

we can say that with the same test suite size i.e., 15,

the effect of the dictionary values is clearly known

when compared with the random values. Thereafter,

these values are given as input to the PICT to generate

all of its combinations that correspond to RP and DP

columns in the table. The R and D generated test cases

are combined as RD and resulted in 30 unique test

cases. Thus, we can interpret that these values’ com-

binations are remarkably more in number when com-

pared to that of individual R and D approaches. From

the plotted graphs and tables, we can observe that the

line coverage and branch coverage for Random values

with and without PICT tool are equal for all the pro-

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

318

Table 5: Differences of Branch Coverages for all ap-

proaches with and without PICT.

Programs RP-R DP-D RDP-RD

Uninit var modiﬁed v15 0 0 0

Memory leak 0 0 0

Null pointer 0 0 0

Function pointer 0 0 0

Free null pointer 0 0 0

Num Rows 0 0 0

P2-L-T-R16 0 0 0

P7-L-T-R16 0 0 0

P8-L-T-R16 0 4.42 6.20

P10-L-T-R16 0 0 0

Wtest11-B15 0 9.41 7.93

Wtest31-B15 0 0 2.1

ZodiacandBirthstone 0 0 0

Prob1-IO-R14-B10 0 0 0

grams and there is no improvement in the line cover-

age and branch coverage using RTCG approach. For

a few programs, the line coverage and branch cover-

age for Dictionary values using PICT tool are greater

than or equal to line coverage and branch coverage

for dictionary values without using PICT tool. There-

fore, there is an improvement in the line coverage and

branch coverage using DTCG approach. For a few

more programs, the line coverage and branch cover-

age for Random and Dictionary values using the PICT

tool are greater than or equal to line coverage and

branch coverage for Random and Dictionary values

without using the PICT tool. Therefore, there is an

improvement in the line coverage and branch cover-

age using FRDTCG approach and the improvement

in coverage is also more than RTCG and DTCG ap-

proaches.

5.3 Analysis

In this section, the comparison of experimental results

is presented. The below Table 5 represents the differ-

ence in branch coverage between Random with PICT

and Random without PICT generated test cases, Dic-

tionary with PICT and Dictionary with PICT test

cases, Random and Dictionary without PICT and

Random and Dictionary without PICT generated test

cases. It can be observed that for very few pro-

grams only we have improvements in branch cover-

age when we use PICT and without PICT. Table 6

represents the difference in branch coverage between

Random test cases and Dictionary test cases with-

out PICT tool, Random test cases and Dictionary test

cases using the PICT tool. It can be observed from

the table that there is more increase in branch cov-

erage using DTCG approach than RTCG approach in

some programs. The difference in branch coverage

between the fusion of Random and Dictionary test

cases and Random test cases without combinatorial

testing i.e without using the PICT tool, a fusion of

Random and Dictionary test cases and Dictionary test

Table 6: RTCG vs. DTCG with and without PICT.

Programs D-R DP-RP

Uninit var modiﬁed v15 5.13 5.13

Memory leak 37.21 37.21

Null pointer 16.07 16.07

Function pointer 51.42 51.42

Free null pointer 21.05 21.05

Num Rows 0 0

P2-L-T-R16 0 0

P7-L-T-R16 0 0

P8-L-T-R16 5.87 10.29

P10-L-T-R16 0 0

Wtest11-B15 20.08 29.49

Wtest31-B15 0 0

ZodiacandBirthstone 21.74 21.74

Prob1-IO-R14-B10 40.79 40.79

Table 7: FRDTCG vs RTCG or DTCG.

Programs RD-R RD-D

Uninit var modiﬁed v15 10.26 5.13

Memory leak 40.99 3.78

Null pointer 16.07 0

Function pointer 51.42 0

Free null pointer 29.47 8.42

Num Rows 0 0

P2-L-T-R16 5.89 5.89

P7-L-T-R16 0 0

P8-L-T-R16 10.69 4.82

P10-L-T-R16 6.12 6.12

Wtest11-B15 20.08 0

Wtest31-B15 3.61 3.61

ZodiacandBirthstone 23.92 2.18

Prob1-IO-R14-B10 42.22 1.43

cases without combinatorial testing i.e without using

PICT tool are represented in Table 7. It is observed

that there is more improvement in FRDTCG vs RTCG

than FRDTCG vs DTCG approach. Table 8 represents

the difference in branch coverage between the com-

bination of Random and Dictionary test cases with

PICT tool and Random test cases without using PICT

tool, the combination of Random and Dictionary test

cases with PICT tool and Dictionary test cases with-

out using PICT tool. From all these tables, we can

incur that the proposed approach FRDTCG gives the

Table 8: FRDTCG vs RTCG or DTCG with and without

combinatorial testing.

Programs RDP-R RDP-D

Uninit var modiﬁed v15 10.26 5.13

Memory leak 40.99 3.78

Null pointer 16.07 0

Function pointer 51.42 0

Free null pointer 29.47 8.42

Num Rows 0 0

P2-L-T-R16 5.89 5.89

P7-L-T-R16 0 0

P8-L-T-R16 16.89 11.02

P10-L-T-R16 6.12 6.12

Wtest11-B15 28.01 7.93

Wtest31-B15 5.69 5.69

ZodiacandBirthstone 23.92 2.18

Prob1-IO-R14-B10 42.22 1.43

Carbon-Box Testing

319

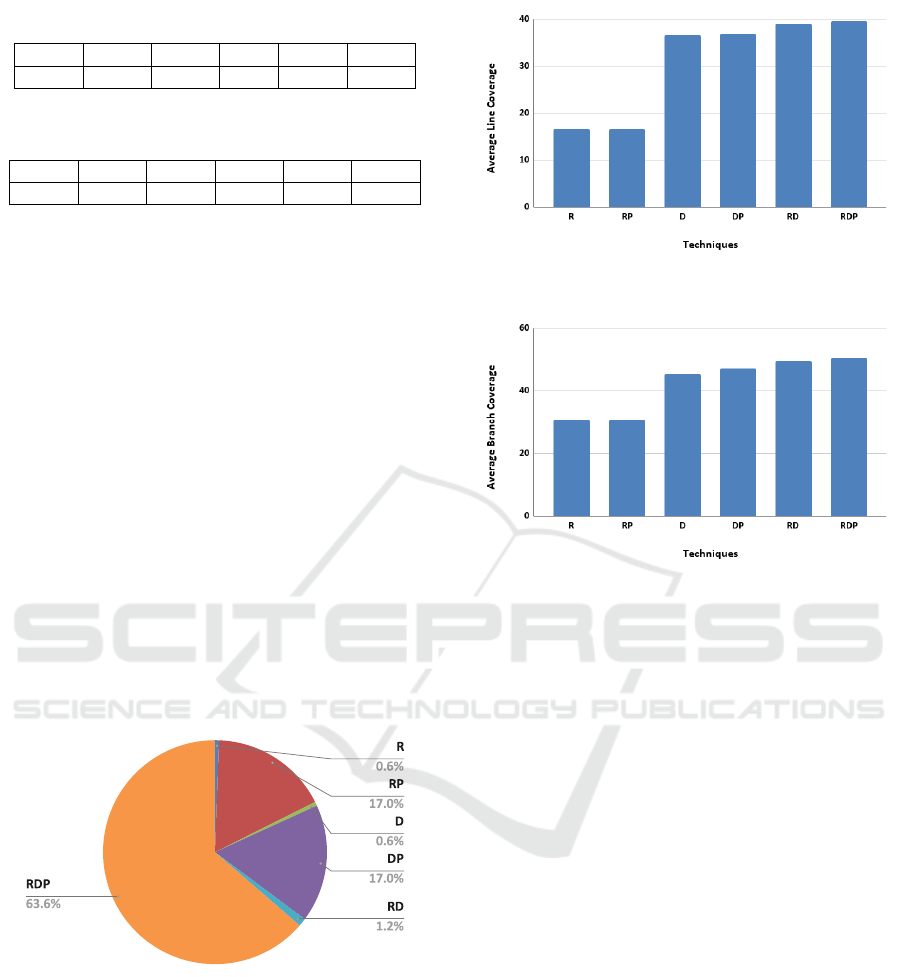
Table 9: Avg. Line Coverage results of all the approaches.

R RP D DP RD RDP

16.58 16.58 36.55 36.9 38.91 39.48

Table 10: Avg. Branch Coverage results of all the ap-

proaches.

R RP D DP RD RDP

30.79 30.79 45.31 46.97 49.41 50.57

best branch coverage among all other compared ap-

proaches. It is observed that there is an improvement

in FRDTCG vs RTCG than FRDTCG vs DTCG ap-

proach.

The Tables 9 and 10 represent the average line

and branch coverages results of R (Random without

PICT), RP (Random With PICT), D (Dictionary with-

out PICT), DP (Dictionary with PICT), RP (Random

and Dictionary without PICT) and RDP (Random and

Dictionary with PICT tool) i.e. the proposed approach

FRDTCG where a fusion of Random and Dictionary

values are supplied as input to PICT tool, gives the

best result. The average Test Cases generated for

each of the discussed approaches are plotted in Fig.

2. It can be observed that the RDP has the highest

(63.6%) test cases generation whereas R has the least

percentage i.e., 0.6%. Similarly, Fig. 3 and Fig. 4

represent the corresponding graphs of average branch

line and coverages for all the approaches where RDP

(fusion of Random and Dictionary with PICT tool)

gives the best branch coverage i.e. more branch cov-

erage when compared to other approaches.

Figure 2: Comparison of Avg. Test Cases generated for all

the three approaches.

6 CONCLUSION AND FUTURE

WORK

We propose a new testing type Carbon-Box Testing

which has features from both Black-Box and White-

Box testing techniques, but with more Black-Box in-

ﬂuence. We present a new technique for making com-

binatorial testing more robust by integrating pairwise

Figure 3: Comparison of Avg. line coverage for all the three

approaches.

Figure 4: Comparison of Avg. branch coverage for all the

three approaches.

testing to the test suite generated by random and dic-

tionary testing. We have discussed how to increase

branch coverage by taking random and dictionary val-

ues and combining them to generate a set of test

cases from the PICT tool. We have discussed Ran-

dom, Dictionary, and Random + Dictionary as in-

put to the PICT tool to show the improvements using

our work FRDTCG. To demonstrate the robustness of

Pairwise testing, we used the line and branch cover-

age as our parameters. Our research clearly demon-

strates the beneﬁts of combining RTCG and DTCG

with pairwise testing. To improve the effectiveness of

test cases created by combinatorial testing, we recom-

mend using pairwise testing with Random and Dictio-

nary values. We plan to expand this effort to incor-

porate t-way testing in the future. There is a need for

a detailed examination of the two-way to eight-way

levels, as several articles suggest such extensions. We

will make our proposed dictionary testing more robust

by introducing more stronger techniques.

REFERENCES

Ahmed, B. S. (2016). Test case minimization approach

using fault detection and combinatorial optimization

techniques for conﬁguration-aware structural testing.

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

320

Engineering Science and Technology, an International

Journal, 19(2):737–753.

Awedikian, Z., Ayari, K., and Antoniol, G. (2009). Mc/dc

automatic test input data generation. GECCO ’09,

page 1657–1664, New York, NY, USA. Association

for Computing Machinery.

Ballance, W. A., Vilkomir, S., and Jenkins, W. (2012).

Effectiveness of pair-wise testing for software with

boolean inputs. In 2012 IEEE Fifth International Con-

ference on Software Testing, Veriﬁcation and Valida-

tion, pages 580–586.

Bell, K. and Vouk, M. (2005). On effectiveness of pairwise

methodology for testing network-centric software. In

2005 International Conference on Information and

Communication Technology, pages 221–235.

Bokil, P., Darke, P., Shrotri, U., and Venkatesh, R. (2009).

Automatic test data generation for c programs. In

2009 Third IEEE International Conference on Se-

cure Software Integration and Reliability Improve-

ment, pages 359–368.

Borazjany, M. N., Yu, L., Lei, Y., Kacker, R., and Kuhn, R.

(2012). Combinatorial testing of acts: A case study.

In 2012 IEEE Fifth International Conference on Soft-

ware Testing, Veriﬁcation and Validation, pages 591–

600.

Calvagna, A. and Gargantini, A. (2009). Ipo-s: Incremental

generation of combinatorial interaction test data based

on symmetries of covering arrays. In 2009 Interna-

tional Conference on Software Testing, Veriﬁcation,

and Validation Workshops, pages 10–18.

Chen, T. Y., Kuo, F.-C., Merkel, R. G., and Tse, T. (2010a).

Adaptive random testing: The art of test case diversity.

Journal of Systems and Software, 83(1):60–66. SI:

Top Scholars.

Chen, X., Gu, Q., Qi, J., and Chen, D. (2010b). Apply-

ing particle swarm optimization to pairwise testing. In

2010 IEEE 34th Annual Computer Software and Ap-

plications Conference, pages 107–116.

Czerwonka, J. (2010). Pairwise testing, combinatorial test

case generation. 24th Paciﬁc Northwest Software

Quality Conference, 200.

Dutta, A., Kumar, S., and Godboley, S. (2019). Enhancing

test cases generated by concolic testing. In Proceed-

ings of the 12th Innovations on Software Engineering

Conference (Formerly Known as India Software Engi-

neering Conference), ISEC’19, New York, NY, USA.

Association for Computing Machinery.

Feng-an, Q. and Jian-hui, J. (2007). An improved test case

generation method of pair-wise testing. In 16th Asian

Test Symposium (ATS 2007), pages 149–154.

Godboley, S., Dutta, A., Mohapatra, D. P., and Mall, R.

(2017). J3 model: A novel framework for improved

modiﬁed condition/decision coverage analysis. Com-

puter Standards & Interfaces, 50:1–17.

Godboley, S., Dutta, A., Mohapatra, D. P., and Mall, R.

(2018a). Scaling modiﬁed condition/decision cover-

age using distributed concolic testing for java pro-

grams. Computer Standards & Interfaces, 59:61–86.

Godboley, S., Dutta, A., Mohapatra, D. P., and Mall, R.

(2018b). Scaling modiﬁed condition/decision cov-

erage using distributed concolic testing for java pro-

grams. Computer Standards & Interfaces, 59:61–86.

Godboley, S., Mohapatra, D., Das, A., and Mall, R. (2016).

An improved distributed concolic testing approach.

Software: Practice and Experience, 47.

Godboley, S., Sahani, A., and Mohapatra, D. P. (2015).

Abce: A novel framework for improved branch cov-

erage analysis. Procedia Computer Science, 62:266–

273. Proceedings of the 2015 International Confer-

ence on Soft Computing and Software Engineering

(SCSE’15).

Godefroid, P., Klarlund, N., and Sen, K. (2005). Dart:

Directed automated random testing. In Proceedings

of the 2005 ACM SIGPLAN Conference on Program-

ming Language Design and Implementation, PLDI

’05, page 213–223, New York, NY, USA. Association

for Computing Machinery.

Jun, Y. and Jian, Z. (2009). Combinatorial testing: Princi-

ples and methods. Journal of Software.

Kacker, R. N., Richard Kuhn, D., Lei, Y., and Lawrence,

J. F. (2013). Combinatorial testing for software: An

adaptation of design of experiments. Measurement,

46(9):3745–3752.

Kelly J., H., Dan S., V., John J., C., and Leanna K., R.

(2001). A practical tutorial on modiﬁed condition/de-

cision coverage. Technical report.

Kim, J., Choi, K., Hoffman, D. M., and Jung, G. (2007).

White box pairwise test case generation. In Seventh

International Conference on Quality Software (QSIC

2007), pages 286–291.

Lei, Y., Kacker, R., Kuhn, D. R., Okun, V., and Lawrence,

J. (2007). Ipog: A general strategy for t-way software

testing. In 14th Annual IEEE International Confer-

ence and Workshops on the Engineering of Computer-

Based Systems (ECBS’07), pages 549–556.

Li, Z., Chen, Y., Gong, G., Li, D., Lv, K., and Chen, P.

(2019). A survey of the application of combinato-

rial testing. In 2019 IEEE 19th International Con-

ference on Software Quality, Reliability and Security

Companion (QRS-C), pages 512–513.

Maity, S. and Nayak, A. (2005). Improved test generation

algorithms for pair-wise testing. In 16th IEEE Interna-

tional Symposium on Software Reliability Engineering

(ISSRE’05), pages 10 pp.–244.

Niu, X., Nie, C., Leung, H., Lei, Y., Wang, X., Xu, J., and

Wang, Y. (2020). An interleaving approach to combi-

natorial testing and failure-inducing interaction identi-

ﬁcation. IEEE Transactions on Software Engineering,

46(6):584–615.

Reid, S. (1997). An empirical analysis of equivalence parti-

tioning, boundary value analysis and random testing.

In Proceedings Fourth International Software Metrics

Symposium, pages 64–73.

Zhou, G., Cai, X., Hu, C., Li, J., Han, W., and Wang, X.

(2018). Research on combinatorial test case gener-

ation of safety-critical embedded software. In Qiao,

F., Patnaik, S., and Wang, J., editors, Recent Develop-

ments in Mechatronics and Intelligent Robotics, pages

204–209, Cham. Springer International Publishing.

Carbon-Box Testing

321