Towards Long-Term Continuous Tracing of Internet-Wide Scanning

Campaigns Based on Darknet Analysis

Chansu Han

1 a

, Akira Tanaka

, Jun’ichi Takeuchi

, Takeshi Takahashi

, Tomohiro Morikawa

and Tsung-Nan Lin

National Institute of Information and Communications Technology, Tokyo, Japan

Kyushu University, Fukuoka, Japan

University of Hyogo, Hyogo, Japan

National Taiwan University, Taipei, Taiwan, Republic of China

Keywords: Darknet Analysis, Scanning Campaign, Tracing, Non-Negative Matrix Factorization.

Abstract:

The darknet is an unused IP address space that can be an eﬀective resource for observing and analyzing global

indiscriminate scanning attacks. Scanning traﬃc on the darknet has expanded dramatically in recent years

and numerous constant scans for investigative purposes have been observed. This is problematic because the

investigative scans identiﬁed by naive rules account for about 60% of the total observed traﬃc. In earlier

work, we detected malware-caused indiscriminate scanning for attack purposes from darknet data by means

of anomaly detection methods, but the large amount of activity from investigation-purpose indiscriminate

scans led to false positives. We have therefore developed a new method for tracing scanning campaigns. By

distinguishing whether the campaign being traced is for attack or investigation purposes, we aim to reduce

the number of false positives and improve anomaly detection accuracy. We also intend to clarify the actual

state of constant scanner groups by tracing them. In this work, we describe the proposed method, implement

a prototype, and conduct experiments on real darknet data to investigate the feasibility of tracing scanning

campaigns.

1 INTRODUCTION

The number of indiscriminate cyberattacks and

Internet-wide scans reaching the darknet1, an unused

IP address space, has increased dramatically in re-

cent years. Our team monitors approximately 300K

IP addresses through NICTER2 , a large-scale darknet

observation system. Although analyzing darknet data

is eﬀective in terms of understanding global cyberat-

tack trends, the analysis is costly due to the diversity

and volume of observed packets. Furthermore, con-

stant scanning for investigative purposes has recently

emerged to form the majority of observed scans, which

creates noise that interferes with analyzing essential

threats (Endo et al., 2022).

https://orcid.org/0000-0002-1728-5300

1The term “darknet” is also known as a network tele-

scope and should not be confused with anonymous commu-

nication systems such as Tor.

2https://www.nicter.jp/

We previously developed a synchronization

anomaly detection framework called Dark-TRACER

with the goal of detecting malware-induced indis-

criminate scanning attack activities before an attack

goes viral (Han et al., 2022; Han et al., 2020). We

found that while Dark-TRACER detected threats an

average of 126.4 days earlier than when they were ﬁrst

observed and recognized by NICTER, it also detected

many false positive alerts that were unrelated to (or

had little to do with) attack activities.

In our experience, most false positive alerts are

anomalies detected due to synchronization by inves-

tigative scanners. Identifying whether an anomalous

alert is a campaign by investigative scanners unrelated

to an attack activity is challenging. Moreover, the

investigative scanner packets we identiﬁed in (Endo

et al., 2022) amounted to 50 to 60% of all packets,

even if we only naively examined them, and there

is a high possibility that there are more investigative

scanners in reality. Investigative scans have previ-

ously been ignored because of their small scale and

low resemblance to attack activities, but they have

Han, C., Tanaka, A., Takeuchi, J., Takahashi, T., Morikawa, T. and Lin, T.

Towards Long-Term Continuous Tracing of Internet-Wide Scanning Campaigns Based on Darknet Analysis.

DOI: 10.5220/0011769300003405

In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 617-625

ISBN: 978-989-758-624-8; ISSN: 2184-4356

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

617

now reached a point of systematic advancement and

are large-scale enough to hinder darknet analysis. It

is therefore vital to clarify the nature of investigative

scanners and reduce false positives by identifying the

causes of alerts.

To this end, conducting long-term, sequential anal-

ysis of temporal changes in analysis targets may be

more beneﬁcial than one-oﬀ analysis in terms of iden-

tifying and understanding the objectives of the target

scanner group’s activities. In this study, we present a

unique approach for tracing the activities of investiga-

tive and oﬀensive scanner groups and capturing the

actual status of constant scanner groups. Speciﬁcally,

we successively perform non-negative matrix factor-

ization (NMF) (Lee and Seung, 2000) for a short-term

period over time-series data while shifting the data

little by little. We restrict the decomposition results

to coinciding with overlapping intervals of preceding

and following time-series data; it should be possible

to trace analysis targets sequentially over long-term

time-series data.

There are three key advantages to our approach:

• Since the NMF is performed sequentially over a

long-term period while inheriting the decomposi-

tion results, bases are uniquely ﬁxed with respect

to the overlap period and do not change. A ‘ba-

sis’ here refers to a group of scanners that exhibit

similar temporal changes, and the number of bases

is a hyperparameter in the NMF. Therefore, trac-

ing can be ﬂexible even if there are changes to the

scanner speciﬁcations (scanner IP addresses, scan

frequency, etc.). This tracing ﬂexibility is nearly

impossible to achieve with other methods and thus

forms the most important element of our approach.

• Even if analysis targets are not speciﬁed in ad-

vance, the NMF decomposes scanner groups with

similar (synchronous) temporal patterns, which

enables us to trace scanner groups that behave sim-

ilarly. Of course, tracing a given set of targets in

advance is also possible.

• Since the NMF is relatively computationally in-

expensive, real-time tracing is possible for large-

scale darknet data.

In this work, we present the details of the proposed

method, discuss our prototype implementation, and

report the results of experiments on real darknet traﬃc

data to evaluate the feasibility of tracing. Our ﬁndings

demonstrate that the proposed method requires less

processing time than the original NMF and has fewer

deviations of decomposition results, and that judgment

of tracing success or failure is feasible.

2 TRACING TARGET

The ultimate goal of tracing in this study is to auto-

matically identify scanner groups that behave similarly

over the long-term and investigate their activities. For

this purpose, we need a ﬂexible tracing method that

can trace scanners even when their speciﬁcations (e.g.,

IP addresses or scanning frequency) change. Since

there are various potential tracing targets, it is diﬃcult

to deﬁne them, but here we describe a few speciﬁc

ones.

Hosts infected with the same worm-type malware

execute scans with similar temporal patterns over a

long-term period. We want to identify and trace

such similar infected hosts as a group campaign. In

addition to worms, we analyze systemized scanners

from Internet-wide scanning service providers such

as Shodan, Censys (Durumeric et al., 2015), Rapid7,

Onyphe, Shadowserver, and BinaryEdge3 , as well as

those from research institutions such as the University

of Michigan4 . Even if multiple scanner groups use

well-known scanning tools such as ZMap (Durumeric

et al., 2013), Masscan, or Nmap, we want to identify

and trace each as a distinct group rather than tracing

the scanning tools.

There are considered to be advanced scanning

tools/programs among the scanners. For example,

there are a random scan and a stealth scan. Are they

tracing targets in this study? First, the random scan

performs reconnaissance on random destination IP ad-

dresses. We have a worldwide network of darknet

observation nodes and monitor the large-scale dark-

net. Fast random scans show similar spatiotemporal

properties within a certain period in our large-scale

darknet. Thus, random scans fall within the scope of

our analysis target.

Next, the stealth scan performs slow and sporadic

reconnaissance to conceal its scanning activity. In

this case, stealth scan hosts may not scan with simi-

lar temporal patterns. However, their slowness makes

them unsuitable for malicious scanning activities that

require rapid scan execution (e.g., spreading malware

infections or probing for vulnerable devices). There-

fore, stealth scanners with malicious intent are consid-

ered to be scarce. On the other hand, stealth scanners

with benign intentions are considered small in scale

and do not cause problems in cyberspace. Although

stealth scanners are outside the scope of our analysis

target this time, groups of stealth scanners that do not

3From Shodan to BinaryEdge in order: https:

//www.shodan.io/, https://censys.io/, https://www.rapid7.

com/, https://www.onyphe.io/, https://www.shadowserver.

org/, and https://www.binaryedge.io/.

4https://cse.engin.umich.edu/about/resources/

connection-attempts/.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

618

Table 1: Notation of mathematical symbols.

Notation Description

𝑉 ∈ N

𝑛×𝑚

≥0

= {0, 1, 2, ·· · })

Long-term time-series data

matrix whose component

(𝑖, 𝑗 ) is the number of pack-

ets at time 𝑗 for host 𝑖

𝑉 [ 𝑗 : 𝑗

′

] ∈ N

𝑛× ( 𝑗

′

− 𝑗+1)

≥0

A submatrix of columns 𝑗

through 𝑗

′

of matrix 𝑉

𝑡 := [𝑠𝑡 + 1, 𝑠𝑡 + 𝑚

′

]

⊆ N

≥0

(𝑡 ∈ {0, 1, · · · })

The time width 𝑡 is deﬁned

as the interval from time

𝑠𝑡 + 1 to time 𝑠𝑡 + 𝑚

′

. The

width of sliding window is

𝑠, where 𝑚

′

is the width of

interval, satisfying 𝑠 < 𝑚

′

𝑉

𝑡

:= 𝑉 [𝑠𝑡 + 1 : 𝑠𝑡 + 𝑚

′

]

∈ N

𝑛×𝑚

′

≥0

(𝑡 ∈ {0, 1, · · · })

A submatrix of 𝑉 at a time

width 𝑡

emerge on the surface are interesting targets and are

the subject of future research. The proposed method

described in this paper may be able to trace stealth

scanners, but we do not evaluate this possibility.

We brieﬂy describe related works now. Conven-

tional studies (Mazel et al., 2017; Griﬃoen and Doerr,

2020; Tanaka et al., 2021) that identify scanners in

a rule-based manner are unable to analyze unknown

groups, perform ﬁne-grained groupings, and perform

long-term tracing. The clustering method of scanners

(Cohen et al., 2020) also cannot perform long-term

tracing of clusters when scanning hosts’ IP addresses

change. It was reported that when an infected device

sends many packets in the short term and becomes

overloaded, it repeatedly disconnects/reconnects PP-

PoE, causing a single host to change to multiple IP

addresses (Endo et al., 2022).

3 PROPOSED METHOD

In this section, we deﬁne the notation and then intro-

duce the proposed method and its pseudo-code.

3.1 Notation

Table 1 shows the notation used in this paper. Al-

though we consider darknet traﬃc data here, it is ap-

plicable to any general multivariate time-series data.

As a brief explanation of this notation, imagine a very

long horizontal time-series data matrix 𝑉 of length

𝑚 and many submatrices 𝑉

,𝑉

, · · · of width 𝑚

′

at each time width 𝑡, sliding by 𝑠-widths. Note that

the submatrices 𝑉

𝑡

and 𝑉

𝑡+1

at the time before and

after overlap the submatrix 𝑉



𝑠(𝑡 + 1) + 1 : 𝑠𝑡 + 𝑚

′



column length 𝑚

′

− 𝑠 (colored in red) and are exactly

equal, as shown in the following equation.

𝑉

𝑡

=𝑉 [𝑠𝑡 + 1 : 𝑠𝑡 + 𝑚

′

]



𝑉



𝑠𝑡 + 1 : 𝑠 (𝑡 + 1)





𝑉



𝑠 (𝑡 + 1) + 1 : 𝑠𝑡 + 𝑚

′





𝑉

𝑡+1

=𝑉 [𝑠 (𝑡 + 1) + 1 : 𝑠(𝑡 + 1) + 𝑚

′

]



𝑉



𝑠 (𝑡 + 1) + 1 : 𝑠𝑡 + 𝑚

′





𝑉



𝑠𝑡 + 𝑚

′

+ 1 : 𝑠(𝑡 + 1) + 𝑚

′





3.2 Proposed Method: LST-NMF

We call the proposed method long short-term non-

negative matrix factorization (LST-NMF) because it

performs the NMF (Lee and Seung, 2000) sequen-

tially by gradually sliding short-term data out of long-

term time-series data. The conventional NMF is a

one-shot analysis method in which the matrix 𝑉 is ap-

proximately decomposed by the multiplicative update

(MU) algorithm to obtain matrices 𝑊 and 𝐻 so that

𝑉 ≈ 𝑊 𝐻. For matrices 𝑊 and 𝐻, latent groups of fre-

quent patterns are obtained for the number of bases.

For instance, the NMF decomposition of matrix 𝑉

yields latent host groups of synchronized spatiotem-

poral patterns for a given number of bases.

However, it cannot successively analyze the tem-

poral dependencies of analysis targets, which is the

problem we are trying to solve. Therefore, we ﬁrst

consider how to address the problem without signiﬁ-

cantly modifying the original NMF algorithm.

We decompose the data matrix 𝑉

𝑡

at time width 𝑡

in NMF to be 𝑉

𝑡

≈ 𝑊

𝑡

𝐻

𝑡

, and then decompose the data

matrix 𝑉

𝑡+1

at the next time width using the decom-

position results 𝑊

𝑡

and 𝐻

𝑡

(𝑊

𝑡

∈ R

𝑛×𝑟

, 𝐻

𝑡

∈ R

𝑟 ×𝑚

′

Here, matrix 𝑊 denotes the spatial feature (scan host)

information, 𝐻 denotes the temporal feature infor-

mation, and 𝑟 denotes the number of bases (ranks).

The speciﬁc method of utilizing the decomposition

results 𝑊

𝑡

, 𝐻

𝑡

is that when decomposing matrix 𝑉

𝑡+1

the temporal feature matrix 𝐻

𝑡+1

is ﬁxed for the over-

lap period with 𝐻

𝑡

. In other words, multiplicative

update (MU) is performed with the condition that

𝐻

𝑡+1

[1 : 𝑚

′

− 𝑠] = 𝐻

𝑡

[𝑠 + 1 : 𝑚

′

]. The intuitive pic-

ture of the matrix decomposition at preceding and

following times can be interpreted as follows. The

submatrices highlighted in red are the blocks to be

ﬁxed.

𝑉

𝑡

𝑉

𝑡



1 : 𝑠





𝑉

𝑡



𝑠 + 1 : 𝑚

′



≈

𝑊

𝑡



𝐻

𝑡

[1 : 𝑠]



𝐻

𝑡

[𝑠 + 1 : 𝑚

′

]



𝑉

𝑡+1

𝑉

𝑡+1

[1 : 𝑚

′

− 𝑠]



𝑉

𝑡+1

[𝑚

′

− 𝑠 + 1 : 𝑚

′

]

≈

𝑊

𝑡+1



𝐻

𝑡+1

[1 : 𝑚

′

− 𝑠]



𝐻

𝑡+1

[𝑚

′

− 𝑠 + 1 : 𝑚

′

]



(1)

Towards Long-Term Continuous Tracing of Internet-Wide Scanning Campaigns Based on Darknet Analysis

619

We conﬁrmed that the original NMF is valid even

when the decomposition matrices 𝑊 and 𝐻 are up-

dated with some of their values ﬁxed. The conver-

gence of the NMF can be proved by using the auxil-

iary function method to show that the target function is

monotonically decreasing by a multiplicative update

(MU). The solutions of the auxiliary function and its

minimization problem are invariant regardless of the

ﬁxation. The update is performed only for the un-

ﬁxed elements of matrices 𝑊 and 𝐻. As a result, the

decomposition of matrix 𝑉

𝑡+1

in Eq. (1) is updated

only for the unﬁxed elements of matrices 𝑊

𝑡+1

and

𝐻

𝑡+1

[𝑚

′

− 𝑠 + 1 : 𝑚

′

] (colored in blue).

3.3 Problem Formulation

Here we formulate the problem in LST-NMF. Opti-

mization problems 𝑃

, 𝑃

, · · · are solved in order:

𝑃

: min

𝑊

,𝐻

| |𝑉

− 𝑊

𝐻

| |

𝐹

𝑃

: min

𝑊

,𝐻

| |𝑉

− 𝑊

𝐻

| |

𝐹

s.t. 𝐻

[1 : 𝑚

′

− 𝑠] = 𝐻

[𝑠 + 1 : 𝑚

′

𝑃

𝑡

: min

𝑊

𝑡

,𝐻

𝑡

| |𝑉

𝑡

− 𝑊

𝑡

𝐻

𝑡

| |

𝐹

s.t. 𝐻

𝑡

[1 : 𝑚

′

− 𝑠] = 𝐻

𝑡 −1

[𝑠 + 1 : 𝑚

′

where || · ||

𝐹

is the sum-of-squares error of the Frobe-

nius norm. Also, note that problem 𝑃

is not subject

to a ﬁxation condition statement.

3.4 Pseudo-Code

The pseudo-code of LST-NMF is provided in Algo-

rithm 1. The ﬁrst data matrix 𝑉

is decomposed using

the original NMF (line 1). After that, the data ma-

trix at the following time is sequentially decomposed

using the decomposition results of the preceding time.

The temporal feature matrix 𝐻

𝑡

is initially ﬁxed at

𝐻

𝑡

[1 : 𝑚

′

− 𝑠] ← 𝐻

𝑡 −1

[𝑠 + 1 : 𝑚

′

] (line 5), and only

unﬁxed blocks are updated in the update formula (lines

10–11). The spatial feature matrix 𝑊

𝑡

also uses the

decomposition result 𝑊

𝑡 −1

of the preceding time as

the initial value (line 6). The singular value decom-

position (SVD) is used for other blocks with no initial

values.

As a result, the number of iterations is reduced

because only a small number of elements in matrix

𝐻 are updated and the range to be updated is small.

Also, the decomposition result 𝑊

𝑡

is expected to be

a matrix with values close to 𝑊

𝑡 −1

. The smaller the

sliding width 𝑠 compared to the data interval width

𝑚

′

, the larger the expected eﬀect.

Algorithm 1: LST-NMF: Long Short-Term Non-negative

Matrix Factorization.

Require: A sequence of long-term time-series data matri-

ces V = (𝑉

,𝑉

, · · · ) (𝑉

𝑡

∈ N

𝑛×𝑚

′

≥0

rank parameter 𝑟 < min(𝑛, 𝑚

′

), thresholds 𝜖, 𝐿.

Ensure: Sequences of decomposed matrices

H = (𝐻

, 𝐻

, · · · ) and W = (𝑊

,𝑊

, · · · ).

(𝐻

𝑡

∈ R

𝑟 ×𝑚

′

, 𝑊

𝑡

∈ R

𝑛×𝑟

, 𝑉

𝑡

≈ 𝑊

𝑡

𝐻

𝑡

𝐻

𝑡

[1 : 𝑚

′

− 𝑠] = 𝐻

𝑡 −1

[𝑠 + 1 : 𝑚

′

])

/* Compute ﬁrst matrix 𝑉

with original NMF */

1: 𝐻

, 𝑊

← NMF(𝑉

,𝑟, 𝜖 , 𝐿)

/* Compute LST-NMF with ﬁxing duplicate block */

2: while 𝑡 ← 1, 2, 3, · · · do

3: ℓ, 𝑓 (0) ← 0

4: 𝐻

𝑡

← SVD(𝑉

𝑡

) // Initialization with SVD

5: 𝐻

𝑡

[1 : 𝑚

′

− 𝑠] ← 𝐻

𝑡 −1

[𝑠 + 1 : 𝑚

′

] // Initialization

6: 𝑊

𝑡

← 𝑊

𝑡 −1

// Initialization

7: 𝑉

′

𝑡

← 𝑉

𝑡

[𝑚

′

− 𝑠 + 1 : 𝑚

′

] // Obtain unﬁxed block

8: while 𝛿 < 𝜖 or ℓ ≥ 𝐿 do

9: 𝐻

′

𝑡

← 𝐻

𝑡

[𝑚

′

− 𝑠 + 1 : 𝑚

′

] // Obtain unﬁxed block

10: 𝐻

′

𝑡

← 𝐻

′

𝑡

𝑊

𝑡

𝑉

′

𝑡

𝑊

𝑡

𝑊

𝑡

𝐻

′

𝑡

// Update only unﬁxed block

11: 𝑊

𝑡

← 𝑊

𝑡

𝑉

𝑡

𝐻

𝑡

𝑊

𝑡

𝐻

𝑡

𝐻

𝑡

// Update only unﬁxed block

12: ℓ ← ℓ + 1

13: 𝑓 (ℓ) ← ||𝑉

𝑡

−𝑊

𝑡

𝐻

𝑡

𝐹

/(𝑛

𝑡

· 𝑚) // Norm

14: 𝛿 ← | 𝑓 (ℓ − 1) − 𝑓 (ℓ)| // Reduction in norm

15: end while

/* Normalization */

16: Λ ← diag(

𝑗

𝐻

𝑡

(𝑟, 𝑗 ))

17: 𝑊

𝑡

← 𝑊

𝑡

Λ, 𝐻

𝑡

← Λ

−1

𝐻

𝑡

18: end while

3.5 Normalization

Next, the normalization is performed in lines 16–17

of Algorithm 1. Since the values of matrices 𝑊, 𝐻

obtained by the NMF are not uniquely determined,

we normalize these matrices to align the value scales.

We update matrix 𝑊 to match its scale by summing

each row (basis) of matrix 𝐻 equal to 1. Expressed

in equations, the normalized matrices are

𝐻(𝑟, 𝑗) =

𝐻(𝑟, 𝑗)/

𝑗

𝐻(𝑟, 𝑗) and

𝑊 (𝑖, 𝑟) = 𝑊 (𝑖,𝑟) ·

𝑗

𝐻(𝑟, 𝑗).

If we set the diagonal matrix Λ = diag(

𝑗

𝐻(𝑟, 𝑗)), we

can easily calculate the normalization as

𝑊 = 𝑊Λ,

𝐻 =

−1

𝐻. The normalized value can then be interpreted

𝑊 (𝑖, 𝑟) packets observed in the temporal pattern

represented by the 𝑟-th row of

𝐻 from the 𝑖-th host.

The NMF computed with the rank parameter 𝑟 can

be expressed as 𝑉 (𝑖, 𝑗) ≈

𝑟

𝑊 (𝑖, 𝑟)

𝐻(𝑟, 𝑗). Summing

this expression in the column direction yields



𝑗

𝑉 (𝑖, 𝑗 ) ≈



𝑗





𝑟

𝑊 (𝑖, 𝑟 )

𝐻 (𝑟 , 𝑗 )





𝑟

𝑊 (𝑖, 𝑟 )





𝑗

𝐻 (𝑟 , 𝑗 )





𝑟

𝑊 (𝑖, 𝑟 ).

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

620

The total number of packets observed from the 𝑖-th

host equals the sum of

𝑊 in row 𝑖.

4 EVALUATION

In this section, we ﬁrst describe the experimental setup

and data preprocessing. We then present a compari-

son of the proposed LST-NMF and the original NMF.

Finally, we introduce a tracing method in LST-NMF

and report the results of the tracing.

4.1 Experimental Setup

In the actual implementation of the LST-NMF proto-

type, the data matrix 𝑉

𝑡

handles only the hosts that

appear in each time width to avoid unnecessary mem-

ory consumption. The initial value of matrix 𝑊

𝑡

line 6 of Algorithm 1 is initialized with 𝑊

𝑡 −1

only for

hosts that overlap with the preceding time, and SVD

is used for hosts that do not overlap with the preceding

time. Otherwise, Algorithm 1 remains unchanged.

We conducted experiments using real darknet traf-

ﬁc data, speciﬁcally, darknet sensor data of a subnet

/20 scale (approx. 4K IP addresses) for one day on

September 1, 2022. Only TCP-SYN packets, which

are indiscriminate scan attacks, were analyzed. This

dataset will be available on our website. This dataset

is available on our website5 .

The hyperparameters utilized in the experiments

are described below. The data matrix consisted of

30 minutes of data, counted in packets at 1-minute

intervals and sliding by 1 minute (i.e., 𝑚

′

= 30, 𝑠 = 1).

The rank parameter in LST-NMF was set to 𝑟 = 5, and

update stop thresholds were set to 𝜖 = 10

−5

, 𝐿 = 3, 000.

This hyperparameter setting is based on our previous

study with Dark-NMF (Han et al., 2021).

Experiments were performed on Ubuntu 18.04

with a Ryzen Threadripper 2990WX CPU and 128GB

memory.

4.2 Data Preprocessing

Before starting the experiment, we removed redundant

noise hosts (scanners) in the data as a preprocessing

step. The following hosts were excluded:

• A host 𝑖 with a low average number of pack-

ets per minute in the 30-minute data matrix 𝑉

𝑡

(

𝑗

𝑉

𝑡

(𝑖, 𝑗 )

𝑚

′

≤ 𝑎)

• A host 𝑖 with numerous packets per minute in the

entire data matrix 𝑉 (𝑉 (𝑖, 𝑗) ≥ 𝑏)

5https://csdataset.nict.go.jp/darknet-2022/

• A host 𝑖 with few destination IP addresses that sent

packets in the 30-minute data matrix 𝑉

𝑡

(ip.dst(𝑖) ≤

𝑐)

Most of the hosts in this dataset had a small number

of packets sent. In terms of computational reduction,

they were excluded as noise because their presence is

negligible and the reduction in the number of hosts

is signiﬁcant. Conversely, hosts with a large num-

ber of packets were excluded because they are greatly

aﬀected by large values when performing the approxi-

mated decomposition in NMF. Finally, hosts with few

destination IP addresses were excluded as noise be-

cause they are not considered scanners.

Histograms were calculated for the three prepro-

cessing rules described above, and the threshold val-

ues 𝑎, 𝑏, and 𝑐 were determined appropriately on the

basis of the overall data distribution. The number

of hosts in data matrix 𝑉

𝑡

per minute at each time

is shown in Fig. 1 after removing hosts by setting

𝑎 = 0.1, 𝑏 = 60, 𝑐 = 1. Consequently, the average host

reduction rate was 66.5% at each time point, and the

average number of duplicate hosts was about 97.8% at

each time point due to the preprocessing. The average

number of hosts after preprocessing at each time was

about 6,500, and the size of data matrix 𝑉

𝑡

was about

6500×30

≥0

(the average number of duplicate hosts was

about 6,300). The ﬂuctuation rate of duplicate hosts

at each time was not large (red line in Fig. 1b).

4.3 Comparative Evaluation of

LST-NMF and Original NMF

We computed LST-NMF and the original NMF on the

real darknet traﬃc data speciﬁed in Section 4.1 and

compared the results from the following four perspec-

tives:

• Iterations: the number of iterations at the end of

the algorithm

• Runtime: the time required to compute the algo-

rithm

• Approximation Error (||𝑉

𝑡

− 𝑊

𝑡

𝐻

𝑡

𝐹

): error at

the end of the algorithm. A large approximation

error indicates poor decomposition accuracy.

• Deviation (||𝑊

𝑡

𝐻

𝑡

−

𝑊

𝑡

𝐻

𝑡

𝐹

): deviation of the

approximate decomposition results between LST-

NMF (𝑊

𝑡

, 𝐻

𝑡

) and the original NMF (

𝑊

𝑡

𝐻

𝑡

). A

large deviation indicates a large gap between both

algorithms’ decomposition results.

First, our comparison of the number of iterations

showed that the average iteration ratio at each time

point was 4.21, with LST-NMF completing the cal-

culation in approximately four times fewer iterations.

Towards Long-Term Continuous Tracing of Internet-Wide Scanning Campaigns Based on Darknet Analysis

621

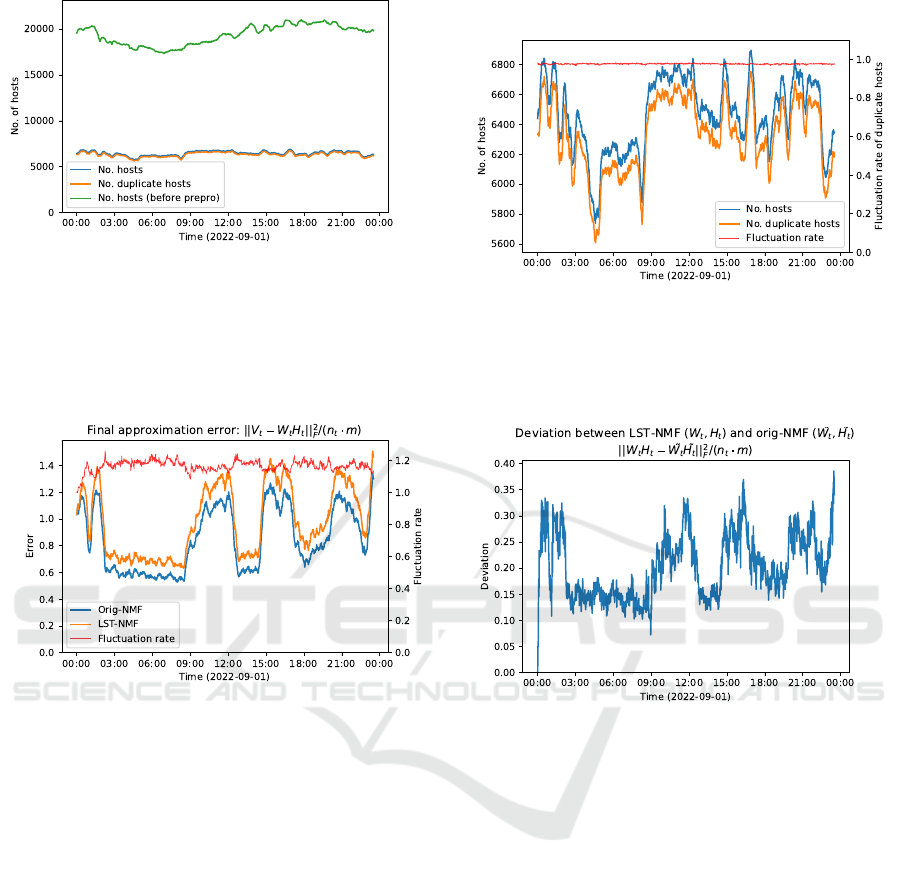
(a) Green: no. of hosts before preprocessing, blue: no. of

hosts after preprocessing, orange: no. of duplicate hosts

in the preceding and following data matrices.

The blue and orange lines are enlarged in Fig. 1b.

(b) Enlarged view of the number of hosts after preprocessing

in Fig. 1a (red: ﬂuctuation rate of duplicate hosts).

Figure 1: The number of hosts in data matrix 𝑉

𝑡

at each time (every minute) before and after preprocessing with

𝑗

𝑉

𝑡

(𝑖, 𝑗 )/𝑚

′

≤

0.1, 𝑉 (𝑖, 𝑗) ≥ 60, and ip.dst(𝑖) ≤ 1.

(a) Approximation errors (red: ﬂuctuation rate of both er-

rors). (b) Deviation between LST-NMF and original NMF.

Figure 2: Comparative evaluation of LST-NMF and original NMF.

The average iterations and standard deviations were

43.62 and 31.84 for LST-NMF and 130.47 and 51.27

for the original NMF, respectively. Similar to the

comparison of iterations, the average runtime ratio at

each time point was 6.23, with LST-NMF completing

processing about six times faster. The average run-

times and standard deviations were 0.19 and 0.14 s for

LST-NMF and 0.83 and 0.33 s for the original NMF,

respectively.

The LST-NMF had fewer iterations and shorter

runtimes than the original NMF because it utilizes the

preceding time’s decomposition result as the initial

value and keeps most of the values ﬁxed during the

iterative update.

Next, we compared the approximation error ||𝑉

𝑡

−

𝑊

𝑡

𝐻

𝑡

𝐹

and the deviation ||𝑊

𝑡

𝐻

𝑡

−

𝑊

𝑡

𝐻

𝑡

𝐹

between

LST-NMF (𝑊

𝑡

, 𝐻

𝑡

) and the original NMF (

𝑊

𝑡

𝐻

𝑡

). As

shown in Fig. 2, the average approximation error ra-

tio at each time point was 1.17, with the LST-NMF

showing an error approximately 17% larger than the

original NMF. The average approximation error and

standard deviation were 0.99 and 0.26 for LST-NMF

and 0.85 and 0.24 for the original NMF, respectively.

The average and std of the deviation between 𝑊 𝐻,

which approximates LST-NMF and the original NMF

to the original matrix 𝑉, were 0.2 and 0.06, respec-

tively.

Due to the iterative update with ﬁxed duplicate

blocks, the approximation error of LST-NMF was

about 17% worse than the original NMF. However,

the error did not increase with time, and there were

no intervals where the ﬂuctuation rate changed signif-

icantly (red line in Fig. 2a). The slightly higher loss

compared to the original NMF does not deteriorate the

performance of long-term tracing. Also, the deviation

was 4 to 5 times smaller than the approximation error,

indicating that the LST-NMF results were not far from

the original NMF results.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

622

(a) When threshold th = 1. (b) When threshold th = 2.

Figure 3: AS determination results for basis number 1. Blue: no. of all hosts, cyan: no. of packets in basis number 1

(

𝑖

𝑊

𝑡

(𝑖, 2)), other: no. of ASes per loose judgment 𝑋 (AH = AS, term = 𝑋).

(a) When threshold th = 1 and no loose AS judgment. (b) When the threshold th = 1 and loose AS judgment 𝑋 = 5.

Figure 4: AS ﬂuctuation indicator results for basis number 1.

4.4 Tracing Method and Result

LST-NMF enables us to analyze the temporal depen-

dence of analysis targets in long-term time-series data

sequentially over a long period. Here, we discuss a

method for tracing whether a target is observed over a

long-term period from the LST-NMF analysis results.

The LST-NMF analysis results for preceding and

following times are ﬁxed, so the bases are uniquely

ﬁxed and do not change. In other words, since the

bases are maintained, the long-term LST-NMF analy-

sis results for each basis enable us to identify scanner

groups whose packets are observed in a similar tempo-

ral pattern over a long period. The tracing procedure

is as follows:

1. Determine the active scanners (hereafter, ASes)

on each basis from the LST-NMF analysis results

at each time.

2. Judge the success or failure of tracing based on the

ﬂuctuation indicator of ASes on each basis.

3. Determine the primary ASes in the successfully

traced bases, and analyze the behavior of these

scanner groups.

Active scanners indicate scanners with (signiﬁcant)

activities on a basis. The thresholds for determining

the ASes (step 1) and setting the ﬂuctuation indicator

(step 2) are described in Section 4.4.1. By analyzing

the behavior of primary ASes, we can investigate the

cause and the purpose of the scanner group’s activities

and get a better understanding of the actual situation.

However, in this paper, we do not analyze the primary

AS, which is planned for future study.

4.4.1 Judgment Result of Active Scanner

Here we introduce the AS determination method and

AS ﬂuctuation indicator and investigate the feasibility

of determining whether or not the analysis target can

be successfully traced. First, ASes were determined by

setting a threshold value from the spatial feature matrix

𝑊

𝑡

at each time width. As explained in Section 3.5, the

normalized spatial feature matrix 𝑊 value represents

the number of packets observed from each host on

Towards Long-Term Continuous Tracing of Internet-Wide Scanning Campaigns Based on Darknet Analysis

623

each basis. Therefore, hosts with a value of less than 1

in the normalized 𝑊 can be interpreted as inactive on

the basis. Considering that the approximation error of

LST-NMF is close to 1, we decided to determine AS

by adopting a threshold value instead of just “less than

1”. In addition, as a consideration for hosts that did

not appear accidentally because the sliding width 𝑠 and

data interval width 𝑚

′

were too ﬁne for 1 minute and 30

minutes, we introduced the following loose judgment

method for AS: If a host is AS at least once in 𝑋

minutes before or after a certain time, it is considered

AS at that time.

Figure 3 shows the results of AS determination

for thresholds th = 1 and 2 and the loose judgments

𝑋 = 0, 5, 10, and 15. 𝑋 = 0 means no loose judgment.

Since not all ﬁve bases can be listed due to space

limitations, only the results for basis number 1 are in-

cluded. We found that the number of ASes decreased

when the threshold th increased, and the number of

ASes increased when the loose judgment 𝑋 increased.

Next, we utilized the AS ﬂuctuation indicator to

judge the success or failure of tracing. The Simp-

son coeﬃcient (aka overlap coeﬃcient) was utilized

as the AS ﬂuctuation indicator, and the results for ba-

sis number 1 are shown in Fig. 4. Let AS

𝑡

denote

the set of ASes at time width 𝑡. The AS ﬂuctua-

tion indicator (Simpson coeﬃcient) that compares the

set of ASes 𝑝 time width ahead was calculated as

|AS

𝑡

∩ AS

𝑡+𝑝

|/min(|AS

𝑡

|, |AS

𝑡+𝑝

|). The 𝑝 was set to

1 m, 30 m, 1 h, 4 h, and 6 h, and we checked the

ﬂuctuation of the AS set at each 𝑝. If the AS ﬂuctu-

ation indicator (Simpson coeﬃcient) is large, we can

assume that the ASes are successfully traced. Con-

versely, a small value indicates that the ASes have

changed signiﬁcantly, which can be interpreted as the

basis disappearing or changing its behavior.

As shown in Fig. 4a, the AS ﬂuctuation indica-

tor for 𝑝 = 1 was greatly blurred when there was no

loose AS judgment. In contrast, Fig. 4b shows that,

since the loose AS judgment at 𝑋 = 5 allowed for con-

sideration of hosts that did not appear accidentally,

there was less blurring of the AS ﬂuctuation indicator,

which continued to exhibit a high value. These results

demonstrate that tracing the success or failure can be

determined from this indicator.

Similar AS determinations and AS ﬂuctuation in-

dicator results were obtained for the other three bases,

except for one. The one-basis exception was almost

ten times larger than the others, and most hosts were

determined to be ASes. This may have been due to the

small number of bases 𝑟, so tuning will be performed.

5 DISCUSSION AND FUTURE

WORK

As stated in Section 1, the biggest advantage of LST-

NMF is that the bases do not change, which is a fac-

tor that cannot be achieved with the original NMF.

While it is also possible to analyze a long-term time-

series data matrix in one operation using the original

NMF, the matrix size would be huge and the process-

ing time would be extremely long. Moreover, local

events would likely not be detected due to the inability

to decompose the matrix into ﬁne units.

One concern with the current LST-NMF is that it

ﬁxes overlapping data at the time before and after the

decomposition, which may have a long-term eﬀect on

past decomposition results. In the future, we would

like to incorporate ﬂexibility by simultaneously de-

composing data matrices before and after times and

by approximating overlapping data at both times in-

stead of ﬁxing them.

We also plan to conduct a tracing case study by

analyzing the behavior of primary ASes. Since LST-

NMF can identify scanner groups that have been send-

ing packets with similar temporal patterns for a long-

term period, it is expected to be relatively convenient

to perform behavior analysis. Such analysis should

be able to capture distinctive behaviors based on the

statistics of destination port information, other header

information, and reverse lookup information of source

IP addresses.

We have been working on a platform for rapid

analysis and notiﬁcation of critical incidents in the

cybersecurity ﬁeld. We perform the cross-checking

analysis with the darknet and diﬀerent sources such as

honeypots, malware analysis, and cyber threat intelli-

gence (Takahashi et al., 2021). The results of scanner

groups with similar long-term behavior identiﬁed and

traced by LST-NMF will also be contributed to this

platform and deployed to the public.

6 CONCLUSION

In this paper, we proposed LST-NMF, a method for

tracing scanner group activities. Our experiments

showed that, compared to the original NMF, the pro-

cessing time of the proposed method was shorter and

there was only a small deviation of the decomposition

results. We also conﬁrmed the feasibility of tracing

success or failure. As this suggests that LST-NMF can

determine and distinguish investigative scanner activ-

ities, we should be able to signiﬁcantly reduce the

false positives from Dark-TRACER alerts that are not

related to true threats and thereby better understand

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

624

the actual status of scanners. In particular, if we can

ﬁlter out investigative scanners, it will be possible to

focus our analysis on only essential threats and scan-

ning activities. Moreover, LST-NMF can be applied

to multivariate time-series data in various ﬁelds and

extended to high-dimensional time-series tensors.

ACKNOWLEDGEMENTS

This research was conducted as part of the “MITI-

GATE” project in “Research and Development for

Expansion of Radio Wave Resources (JPJ000254)”,

which was supported by the Ministry of Internal Af-

fairs and Communications, Japan.

REFERENCES

Cohen, D., Mirsky, Y., Kamp, M., Martin, T., Elovici, Y.,

Puzis, R., and Shabtai, A. (2020). DANTE: A frame-

work for mining and monitoring darknet traﬃc. In

Computer Security – ESORICS 2020, pages 88–109.

Springer International Publishing.

Durumeric, Z., Adrian, D., Mirian, A., Bailey, M., and

Halderman, J. A. (2015). A search engine backed by

internet-wide scanning. In Proceedings of the 22nd

ACM SIGSAC Conference on Computer and Commu-

nications Security. ACM.

Durumeric, Z., Wustrow, E., and Halderman, J. A. (2013).

Zmap: Fast internet-wide scanning and its security

applications. In Proceedings of the 22th USENIX Se-

curity Symposium, pages 605–620.

Endo, Y., Mori, Y., and Kubo, M. (2022). NICTER statis-

tics – Q2, 2022, Cybersecurity Laboratory, National

Institute of Information and Communications Tech-

nology. https://blog.nicter.jp/2022/08/nicter

statistics

2022 2q/ (In Japanese).

Griﬃoen, H. and Doerr, C. (2020). Discovering collab-

oration: Unveiling slow, distributed scanners based

on common header ﬁeld patterns. In NOMS 2020

- 2020 IEEE/IFIP Network Operations and Manage-

ment Symposium. IEEE.

Han, C., Shimamura, J., Takahashi, T., Inoue, D., Takeuchi,

J., and Nakao, K. (2020). Real-time detection of global

cyberthreat based on darknet by estimating anomalous

synchronization using graphical lasso. IEICE Transac-

tions on Information and Systems, E103.D(10):2113–

2124.

Han, C., Takeuchi, J., Takahashi, T., and Inoue, D. (2021).

Automated detection of malware activities using non-

negative matrix factorization. In 2021 IEEE 20th Inter-

national Conference on Trust, Security and Privacy in

Computing and Communications (TrustCom). IEEE.

Han, C., Takeuchi, J., Takahashi, T., and Inoue, D. (2022).

Dark-TRACER: Early detection framework for mal-

ware activity based on anomalous spatiotemporal pat-

terns. IEEE Access, 10:13038–13058.

Lee, D. and Seung, H. S. (2000). Algorithms for non-

negative matrix factorization. In Advances in Neu-

ral Information Processing Systems, volume 13. MIT

Press.

Mazel, J., Fontugne, R., and Fukuda, K. (2017). Proﬁling

internet scanners: Spatiotemporal structures and mea-

surement ethics. In 2017 Network Traﬃc Measurement

and Analysis Conference (TMA). IEEE.

Takahashi, T., Umemura, Y., Han, C., Ban, T., Furumoto,

K., Nakamura, O., Yoshioka, K., Takeuchi, J., Murata,

N., and Shiraishi, Y. (2021). Designing comprehen-

sive cyber threat analysis platform: Can we orchestrate

analysis engines? In 2021 IEEE International Con-

ference on Pervasive Computing and Communications

Workshops and other Aﬃliated Events (PerCom Work-

shops). IEEE.

Tanaka, A., Han, C., Takahashi, T., and Fujisawa, K. (2021).

Internet-wide scanner ﬁngerprint identiﬁer based on

TCP/IP header. In 2021 Sixth International Conference

on Fog and Mobile Edge Computing (FMEC). IEEE.

Towards Long-Term Continuous Tracing of Internet-Wide Scanning Campaigns Based on Darknet Analysis

625