How to Select Quantum Compilers and Quantum Computers Before

Compilation

Marie Salm

, Johanna Barzen

, Frank Leymann

and Philipp Wundrack

University of Stuttgart, Institute of Architecture of Application Systems,

Universitätsstraße 38, Stuttgart, Germany

Keywords:

Quantum Computing, NISQ Analyzer, Decision Support, Machine Learning, Prediction.

Abstract:

Quantum computers might solve speciﬁc problems faster than classical computers in the future. But their

actual qubit numbers are small, and the error rates are high. However, quantum computers are already used in

various areas and a steadily increasing number is made available by cloud providers. To execute a quantum

circuit, it is mapped to the quantum computer’s hardware. The resulting compiled circuit strongly inﬂuences the

precision of the execution in terms of occurring errors caused by used qubits and quantum gates. Selecting an

optimal one is, therefore, essential. SDKs are used to implement circuits and differ in supported cloud providers

and programming languages. These differences complicate a change to other backends. In previous work, we

developed an automated framework to translate a given circuit and compile it on available quantum computers

using multiple compilers. The compilation results can be prioritized and executed. Nevertheless, the translation

and compilation with all compilers and quantum computers is resource-intensive and does not scale well with

further backends in the future. We, therefore, present an extension to automatically select suitable compiler and

quantum computer combinations based on the user’s needs, e.g., for short waiting times and precise results

based on past executions. To demonstrate and validate our approach, we show a prototype and case study.

1 INTRODUCTION

Quantum computing is often seen as a promising tech-

nology of the future (National Academies of Sciences,

Engineering, and Medicine, 2019). Several experi-

ments showed an advantage of quantum computers

compared to classical computers for speciﬁc prob-

lems (Arute et al., 2019; Zhong et al., 2020). However,

the current Noisy Intermediate-Scale Quantum (NISQ)

computers suffer from high error rates and offer only

a small number of qubits for computation (Preskill,

2018). Nevertheless, quantum computers are already

applied in different ﬁelds, such as ﬁnance, chemistry,

and computer science (Bova et al., 2021).

Cloud providers such as IBMQ and Google of-

fer access to steadily growing numbers of quantum

computers, also called Quantum Processing Units

(QPUs) (LaRose, 2019; Leymann et al., 2020; Buluta

et al., 2011). However, users of a growing community

often have to wait until their computations are exe-

https://orcid.org/0000-0002-2180-250X

https://orcid.org/0000-0001-8397-7973

https://orcid.org/0000-0002-9123-259X

https://orcid.org/0000-0001-7606-6936

cuted on available quantum computers as the access

is usually managed by the cloud providers using, e.g.,

queues or time slices to be booked (LaRose, 2019;

Vietz et al., 2021). Quantum computations for gate-

based quantum computers are described with quantum

circuits consisting of quantum gates and qubits, analo-

gous to classical circuits (Nielsen and Chuang, 2011).

Users implement quantum circuits by commonly us-

ing Software Development Kits (SDKs). Besides the

implementation, the SDKs also offer the compilation

for supported quantum computers and the subsequent

execution of circuits (LaRose, 2019). The compilation

with a quantum compiler is required to map the de-

signed qubits and gates of the circuit to the physical

qubits and gates of the speciﬁc quantum computer,

which is NP-hard (Siraichi et al., 2018; Leymann and

Barzen, 2020). Thereby, existing quantum computers

differ in the supported sets of gates, the qubit connec-

tivity, and the appearing error rates. The resulting com-

piled circuits, thus, differ between individual backends

and used compilation methods (Kharkov et al., 2022;

Salm et al., 2021). The number of required qubits, i.e.,

the width, the numbers of single- and multi-qubit gates,

and the number of sequentially executable gates, i.e.,

172

Salm, M., Barzen, J., Leymann, F. and Wundrack, P.

How to Select Quantum Compilers and Quantum Computers Before Compilation.

DOI: 10.5220/0011775300003488

In Proceedings of the 13th International Conference on Cloud Computing and Services Science (CLOSER 2023), pages 172-183

ISBN: 978-989-758-650-7; ISSN: 2184-5042

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

the depth of the compiled circuit, affects the quality,

i.e., the precision of the execution result (Leymann and

Barzen, 2020; Salm et al., 2020b): With each qubit and

gate further errors can be introduced to the computa-

tion leading to deviations from the actual result. Thus,

the circuits to be executed on today’s NISQ computers

should be as small as possible (Salm et al., 2020a).

In recent years, the number of SDKs has

grown (Gill et al., 2022). They differ in supported

cloud providers and, therefore, the set of accessible

quantum computers, programming languages to imple-

ment circuits, provided compilers, and gates (LaRose,

2019; Gill et al., 2022). This variety makes it difﬁcult

for the user to select an SDK for developing quan-

tum circuits. It complicates solving speciﬁc problems

using quantum computers that are suitable for the re-

quirements of the user, such as short waiting times and

precise execution results (Salm et al., 2022a,b).

In previous work, we developed an automated

framework that translates quantum circuits into several

programming languages (Salm et al., 2021). It enables

the exchange of circuits between different SDKs and

allows access to quantum computers offered by various

cloud providers. The compilation with several com-

pilers on available quantum computers is supported

to select optimal compilation results. Furthermore,

the executability regarding occurring errors is exam-

ined (Salm et al., 2020a). The executable compilation

results can be prioritized based on the requirements of

the user to ﬁnally execute selected ones on the suitable

quantum computers (Salm et al., 2022a,b).

However, the translation into the required program-

ming languages of supported SDKs and the compi-

lation with their various compilers on the available

quantum computers is resource-intensive. Moreover,

it gets more difﬁcult with the increasing amount of

upcoming SDKs, compilers, and quantum computers.

Therefore, the ﬁrst research question we want to tackle

with this work is the following:

RQ 1: How can quantum compilers and quantum

computers be automatically selected before the

translation and compilation of a given input circuit

targeting precise execution results of the future?

We extend the framework to (i) analyze the user’s

initial input circuit and (ii) select compilers and quan-

tum computers before the translation and compilation

based on prior execution results. We use machine learn-

ing (ML) algorithms and involve the user’s needs for

the selection. The extension reduces the number of

resources and improves the scalability of our approach.

Our second research question is, thereby, as follows:

RQ 2: Which quantum circuit and quantum com-

puter metrics are important to predict the precision

of future execution results for a given input circuit

before its translation and compilation?

Therefore, we present a (iii) prototype of the frame-

work and a (iv) case study. We compare the perfor-

mance and precision of various implementations of

several ML algorithms and examine the inﬂuence of

the input circuit and quantum computer properties,

i.e., metrics. We further investigate the runtime of our

pre-selection, compilation, and analysis approach.

The paper is structured as follows: Section 2

presents fundamentals about the selected ML algo-

rithms. Sect. 3 focuses on the extension of our ap-

proach. In Sect. 4, the system architecture and pro-

totype are presented and validated with a case study

in Sect. 5. Sect. 6 discusses limitations, and Sect. 7

presents related work. In Sect. 8, our paper is con-

cluded and future work is presented.

2 PREDICTING RESULTS

Selecting quantum computers and compilers for a non-

compiled input circuit aiming at precise executions

requires predicting the precision of future results for

the different combinations. For the prediction, met-

rics of prior executed circuits and the related quantum

computers, the precision of their results, and the in-

ﬂuence of the compilers must be considered. Salm

et al. (2022a) and Weder et al. (2021) collected sev-

eral circuit metrics describing its size, the numbers of

single- and multi-qubit gates, and measurement opera-

tions. Collected quantum computer metrics consider

the average error rates and times of supported gates,

measurement errors, and the decoherence times T1 and

T2, i.e., how long a speciﬁc quantum state is stable be-

fore getting too erroneous and ﬂipping to another state.

The results on a quantum computer are compared to

the optimal results using histogram intersection (Swain

and Ballard, 1991) to measure the precision of an exe-

cution (Salm et al., 2022a,b): The considered circuit

is also executed on a quantum simulator without the

occurrence of errors. The received results of both back-

ends are often represented as histograms, and the his-

togram intersection is calculated by superimposing

them (Swain and Ballard, 1991). A histogram inter-

section value of 1 means total congruence, whereas 0

means total difference. ML algorithms can be used to

learn the dependencies between past histogram inter-

section values, quantum computer and circuit metric

values, and compilers. The actual input circuit and

data provided on the quantum computer used serve

How to Select Quantum Compilers and Quantum Computers Before Compilation

173

as input. The given data, except for the compilers, is

quantitative. The output is continuous and given for

the training data input, thus, the prediction is a super-

vised regression problem (Schuld et al., 2016; James

et al., 2021). The compilers are nominal categorical

data and must be converted into numerical data in a

pre-processing step using one-hot encoding (Cerda

et al., 2018). The categories, i.e., the

compilers are

represented by

distinct binary feature vectors with

dimensions. The vector of the

-th category has a 1 at

the

-th dimension, 0 elsewhere with 0

≤ i ≤ n

. Various

ML algorithms exist. We selected multiple linear re-

gression, Support Vector Regression (SVR), K-Nearest

Neighbors regression (KNN regression), and decision

trees as their implemented variants delivered the best

predictions in Sect. 5. Our plug-in-based system can

support further ML and encoding algorithms. For the

following, the predictors are our metric values and

compilers, responses are the histogram intersection

values, and observations are the sample data points.

2.1 Multiple Linear Regression

Multiple linear regression estimates the regression

coefﬁcients of each predictor over all observations

such that the linear model suits well for the training

data (James et al., 2021). Thereby, predictors are as-

sumed to be linearly dependent on the observation. The

regression coefﬁcient of a predictor describes the rela-

tionship between the predictor and the response. The

estimated coefﬁcients can be applied to new predictors

to predict future responses.

2.2 Support Vector Regression

SVR bases on the Support Vector Machine

(SVM) (Vapnik, 1995) and is applicable for re-

gression problems (Awad and Khanna, 2015). SVR

forms a tube, serving as an error threshold around the

loss function to be estimated. Observations outside the

tube are punished, and those inside are ignored. The

goal of SVR is to ﬁnd a minimal loss function with a

tube as ﬂat as possible containing most of the given

data available for training.

2.3 K-Nearest Neighbors Regression

KNN regression is similar to KNN for classiﬁca-

tion (James et al., 2021). For a new observation from

the test data, the

observations from the training data

closest to the new one are considered.

is given. The

response of the new observation is estimated by aver-

aging all given responses of the K observations.

2.4 Decision Trees

By repeatedly dividing predictors of the training data

into two non-overlapping regions, an upside-down

tree is built (De’ath and Fabricius, 2000; James et al.,

2021). The mean of all contained responses deﬁnes

each region (De’ath and Fabricius, 2000). Starting

from the root, the predictors are step-wise compared

with the splitting points of the related regions and as-

signed to the ﬁtting region to predict an observation’s

response (James et al., 2021). At the bottom, the re-

sponse is determined as the mean value of the region.

3 APPROACH

To address RQ1, we present the extension of our ap-

proach from Salm et al. (2020a, 2021, 2022a,b) to

select quantum compilers and quantum computers be-

fore translating and compiling a given input circuit

based on prior execution results and the requirements

of the user, illustrated in Fig. 1.

3.1 Circuit Analysis

The input circuit of the user must be analyzed to select

available compilers and quantum computers based on

the user’s needs. In the (1) Circuit Analysis phase, the

user decides if they want to target precise execution

results, short waiting times until execution, or both in

combination. If the user desires a combination, they

can deﬁne the ratio between short waiting times and

precise execution results, e.g., 50:50 or 30:70. The

user can also specify a threshold how many compiled

circuits should at most be returned after compilation.

Afterward, the input circuit is analyzed based on the

circuit metrics collected by Salm et al. (2022a), such as

the number of operations, the number of single-qubit

gates, and the multi-qubit gate depth, i.e., the longest

path in the circuit only considering multi-qubit gates.

3.2 Compiler & QPU Pre-Selection

The analyzed metric values of the input circuit are

handed over to the (2) Compiler & QPU Pre-Selection

phase. In the ﬁrst step, the actual data of available

quantum computers is requested from the provenance

system QProv (Weder et al., 2021). QProv collects and

stores current data and metric values of available quan-

tum computers, such as the average gate errors and

times, and the average decoherence times. If the user

requires short waiting times until the execution, the

actual waiting times, e.g., queue lengths of the quan-

tum computers, are considered (Salm et al., 2022a).

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

174

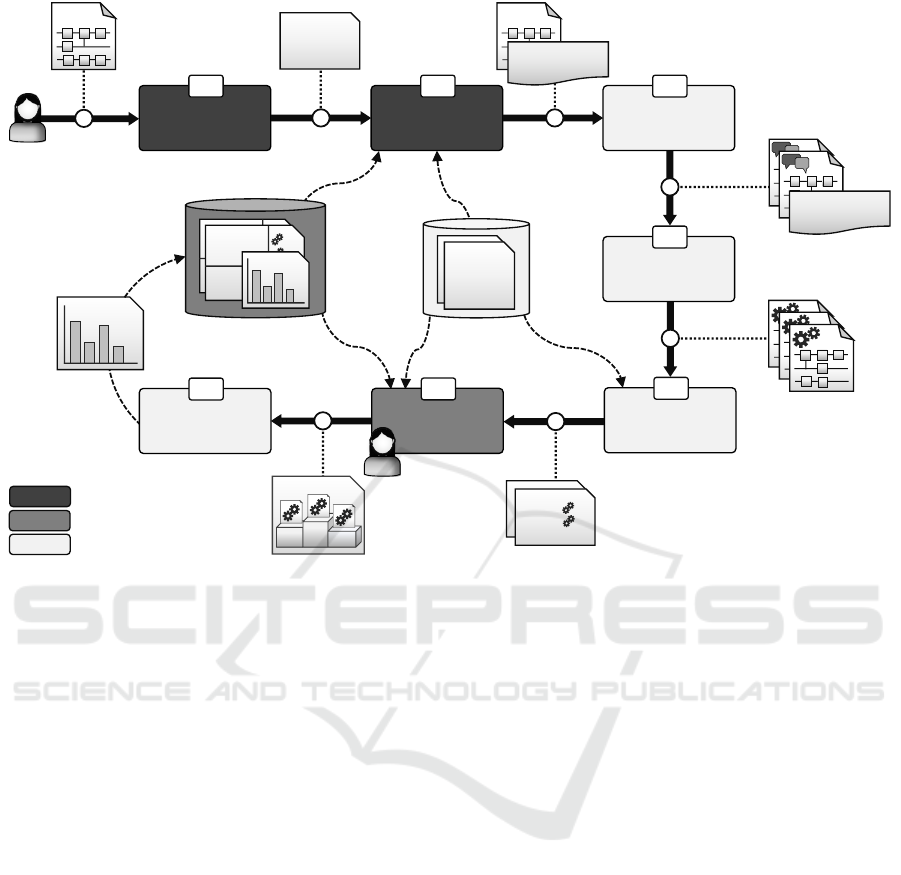
Depth 56

Width 5

... ...

Compiler & QPU

Pre-Selection

Circuit Analysis

Translation

Compilation

Compilation Result

Analysis

Prioritization

Execution

Compilers & QPUs

Translated Circuits,

Compiled Circuits

Circuit

Results

Measurement

t|ket⟩ + IBMQ_5

Qiskit + IBMQ_7

...

Compiled Circuits

Ranking of

Depth 23

Width 5

... ...

t|ket⟩ + IBMQ_5

Qiskit + IBMQ_7

...

Prior Metric Values

& Measurement Results

Depth 32 52

Width 5 5

... ... ...

T1 0.02

T2 0.04

... ...

Depth 32 52

Width 5 5

... ... ...

T1 0.02

T2 0.04

... ...

Circuit Metric

Values

Circuit, QPUs &

Compilers

Compiled Circuit

Metric Values

= old components

= adapted components

= new components

QProv

Depth 56

Width 5

... ...

T1 0.02

IBMQ_5

T2 0.04

... ...

Figure 1: Automated selection, translation, compilation, and prioritization for quantum circuits. Extending Salm et al. (2022b).

Next, each entity of a quantum computer is multiplied

by each entity of a compiler that natively supports the

quantum computer. The overall sum deﬁnes the num-

ber of all possible quantum computer and compiler

combinations. Then, the resulting combinations are

sorted ascending based on the queue length and short-

ened by the threshold the user deﬁned as the maximum

number of compilation results in Sect. 3.1.

If precise execution results are desired, the user

can choose between implementations of the ML al-

gorithms multiple linear regression, SVR, KNN re-

gression, and decision trees, described in Sect. 2, to

predict the precision of future results with the different

combinations. Decision trees are selected by default,

as they return the best results based on our case study,

see Sect. 5. The chosen ML algorithm accesses stored

metric values of all diverse input circuits executed in

the past, the used compilers, and the metric values of

the quantum computers on which they were executed.

Furthermore, the ML algorithm obtains the histogram

intersection values of the related past execution results.

If no prior data is available for learning, the (2) Com-

piler & QPU Pre-Selection phase targeting the desire

of precise execution results has to be skipped and all

available quantum computer and compiler combina-

tions are considered. In the other case, the prior metric

values and compilers serve as input, whereas the re-

lated histogram intersection values serve as a target to

train the ML algorithm, as described in Sect. 2. The

input values are normalized, and the objective is to

minimize the mean difference between the histogram

intersection values predicted by the ML algorithm and

the true histogram intersection values. The actual met-

ric values of the input circuit and the quantum com-

puters serve as input. The result is a list of predicted

histogram intersection values for the different quan-

tum computer and compiler combinations. It is sorted

descending by the histogram intersection values and

shortened by the threshold of the user from Sect. 3.1.

In the case the user requests estimations regarding

precise execution results and short waiting times, ﬁrst,

the sorted lists regarding waiting times and precise

execution results are created separately, as described

previously, but not yet shortened. Instead, the common

Borda count method is used to combine the two sorted

lists (B ˛aczkiewicz et al., 2021; Wang et al., 2009): For

each list, the quantum computer and compiler combi-

nation in the ﬁrst place gets

n −

1 points, in the sec-

ond place

n −

2 points, and so on, until the last place

gets 0 points, where

is the number of combinations.

Then, the received points for each combination are

summarized and based on the total points, a new list of

combinations in descending order is created. Suppose,

the user selected a ratio of precise execution results

and waiting times different to 50:50. In that case, the

assigned points for each combination on each list are

How to Select Quantum Compilers and Quantum Computers Before Compilation

175

multiplied by the related deﬁned percentage (Russell,

2007). For example, the user has chosen a ratio of

70:30 for precise results and waiting times. The points

on the ordered list regarding precise results are multi-

plied by 0.7, whereas the points on the list for waiting

times are multiplied by 0.3 and then summed up as

described. Finally, the new combined and ordered list

of quantum computer and compiler combinations is

shortened by the user’s threshold.

3.3 Translation

For the previously selected compilers, it is checked

if the programming language that was used to im-

plement the given input circuit is supported by their

SDKs (Salm et al., 2021). If it is not the case, the

circuit is automatically translated into the required

formats in the (3) Translation phase.

3.4 Compilation

The translated quantum circuits and the list of selected

quantum compiler and quantum computer combina-

tions is input for the (4) Compilation phase (Salm et al.,

2020a, 2021). The selected compilers map the related

translated circuits to the selected quantum computers.

One circuit is also compiled on an available quantum

simulator to later calculate the execution result without

the appearance of errors (Salm et al., 2022a).

3.5 Compilation Result Analysis

In the (5) Compilation Result Analysis phase, the com-

piled circuits are again analyzed based on the metrics

collected by Salm et al. (2022a). Their structures and

sizes commonly change with the mapping to the hard-

ware. The compilation results are selected based on

evaluating their executability on the target quantum

computers, as shown by Salm et al. (2020a). QProv is

invoked to gain the required quantum computer data.

3.6 Prioritization

The minimized list of pre-selected and executable com-

pilation results with their related quantum computers

is presented to the user. As described by Salm et al.

(2022b), in the (6) Prioritization phase, the user can

prioritize the list based on their own or pre-deﬁned

requirements, such as short waiting times and pre-

cise execution results. Based on the need for precise

future execution results, in comparison to Sect. 3.2,

the metric values of the remaining hardware-speciﬁc

compiled circuits ready to be executed are used to

calculate an accurate ranking. The metric values of

related quantum computers are received from QProv.

An optimizer calculates the relevance of the individual

metrics based on metric values and execution results

of prior compilation results and related quantum com-

puter data (Salm et al., 2022b). The resulting weights

determine the ranking via one of the supported multi-

criteria decision analysis methods (Salm et al., 2022a).

If the user requires a combination of short waiting

times and precise results, they can deﬁne the ratio

between both via weighted Borda count, described

in Sect. 3.1 and Sect. 3.2. The user can analyze the

sensitivity of the resulting ranking (Salm et al., 2022b).

3.7 Execution

In the (7) Execution phase, the user selects the priori-

tized compilation results to be executed (Salm et al.,

2020a). Besides executing the selected circuit on the

target quantum computer, one circuit is also executed

on a simulator if it offers enough resources for sim-

ulation. Suppose all execution results are received.

Then, the histogram intersection value is calculated

and stored with the compiler and the metric values of

the input circuit, the compiled circuit, and the quantum

computer for future selection and prioritization.

4 SYSTEM ARCHITECTURE &

PROTOTYPE

This section shows the system architecture and proto-

type of the approach we presented in Sect. 3.

4.1 System Architecture

Fig. 2 presents the overall system architecture (Salm

et al., 2020a, 2021, 2022a,b). The Predict & Prio Ser-

vice on the top left of Fig. 2 contains the Prediction

Algorithms, i.e., ML algorithms, explained in Sect. 2,

to estimate future execution results of a given input cir-

cuit based on prior data, as described in Sect. 3.2. Fur-

thermore, it applies the weighted Borda count method

to combine the diverse requirements of the user. The

HTTP REST API of the Predict & Prio Service is

adapted to support these new features. The service

also supports different methods to prioritize compiled

circuits, as described in previous work. The Translator

component in the bottom left of Fig. 2 translates the

input circuit into the required programming languages

of the selected compilers. The NISQ Analyzer UI and

the HTTP REST API of the NISQ Analyzer, in the

middle of Fig. 2, are extended to support the user in

deﬁning their needs for the pre-selection, compilation,

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

176

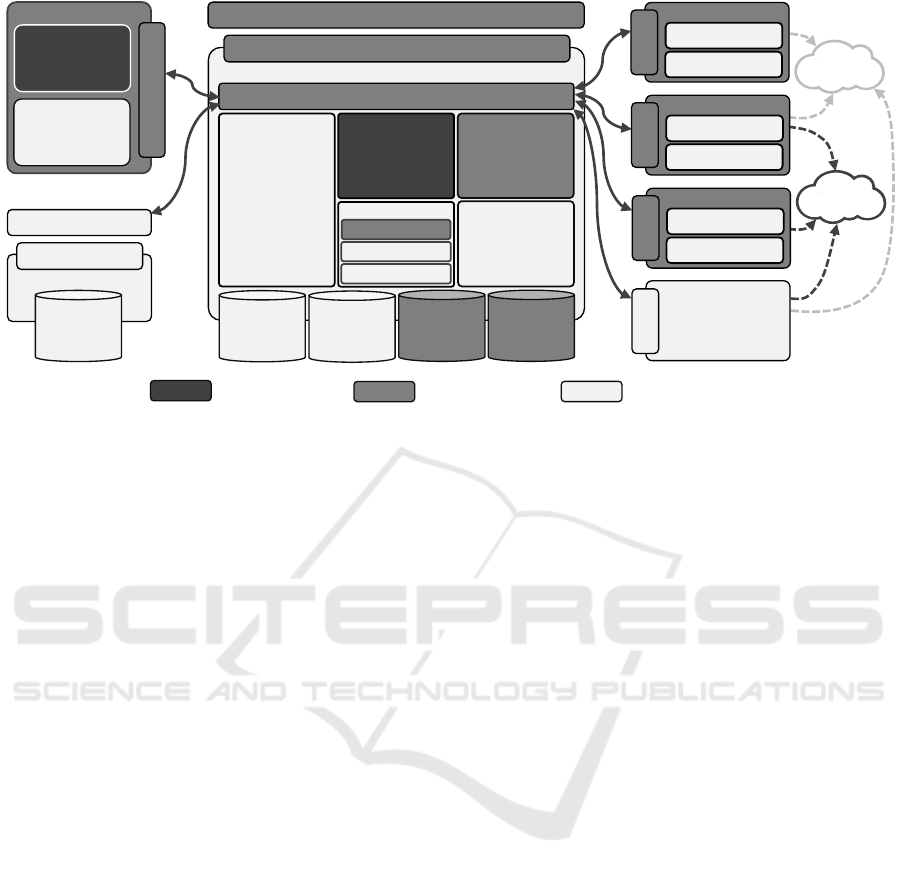
NISQ Analyzer

REST API

NISQ Analyzer UI

Connector

Rule Handler

Metrics,

Weights,

Rankings

Selector

Comp. Selector

QPU Selector

Impl. Selector

Performance

Extractor

Results

Algorithms,

Impl., SDKs

Selection

Rules

Rigetti

Forest Service

Quilc

Executor

REST API

QProv

REST API

pytket Service

t|ket⟩

Executor

REST API

IBMQ

REST API

Predict & Prio Service

Prioritization

Methods

Translator

REST API

Translator UI

Gate

Mappings

Transpiler

Executor

Qiskit Service

REST API

Prioritizer

Prediction

Algorithms

Pre-Selector

= old components

= adapted components

= new components

Figure 2: System architecture to select quantum computers and compilers. Extending Salm et al. (2022b).

prioritization, and execution of quantum computers.

The Pre-Selector coordinates the collection of the ac-

tual input circuit and quantum computer metric val-

ues by invoking QProv and the SDK Services (Fig. 2,

right). The SDK Services wrap supported SDKs and

uniformly offer their compilers and execution func-

tionalities. They are extended to enable the analysis

of non-compiled input circuits. The Pre-Selector also

collects prior input circuit and quantum computer met-

ric values and sends the data and the user’s speciﬁed

requirements to the Prediction Algorithms via the Con-

nector. The Compiler Selector invokes the Translator

if required, and afterward, the SDK Services contain-

ing the selected compilers with the quantum comput-

ers to be considered for compilation. The Prioritizer

coordinates the data collection and invocation of Pri-

oritization Methods to prioritize compiled circuits and

is extended to enable the user to specify the ratio for

weighted Borda count to combine pre-deﬁned needs,

as explained in Sect. 3.6. The selected lists of compiler

and quantum computer combinations and the metric

values of the input circuit are stored in repositories.

The user initiates the analysis and selection pro-

cess by selecting the input circuit and deﬁning their

requirements in the UI. The user selects between short

waiting times and precise execution results and deﬁnes

the ratio if both must be considered. Furthermore, they

choose the maximum number of returning compilation

results and, in the case of precise execution results, the

Prediction Algorithm. The Pre-Selector calls an SDK

Service that supports the programming language of the

input circuit over the Connector to analyze the input

circuit based on the deﬁned metrics. Additionally, the

Pre-Selector invokes QProv to retrieve actual metric

values of available quantum computers. The compo-

nent also collects metric values of prior input circuits

and related quantum computers, corresponding his-

togram intersection values, and used compilers. The

data retrieved and the constraints set by the user are

sent to the Predict & Prio Service via the Connector.

If the user desires short waiting times, the num-

ber of available quantum computers is multiplied by

the number of compilers, as described in Sect. 3.2.

The list is sorted based on the actual queue length

and shortened by the user’s threshold. If precise ex-

ecution results are required, the selected Prediction

Algorithm is invoked to predict the precision of future

execution results for the different quantum computer

and compiler combinations based on the prior data.

The Prediction Algorithm returns a list of all combi-

nations sorted by the estimated histogram intersection

values, which is then shortened. If short waiting times

and precise execution results are desired, both lists

are calculated separately. Weighted Borda count is ap-

plied as described in Sect. 3, and the combined list

is shortened. The resulting list is returned to the Pre-

Selector and stored in a repository. The Pre-Selector

invokes the Compiler Selector that invokes the Trans-

lator if one of the selected compilers requires another

programming language. Afterward, the Compiler Se-

lector sends the circuits to be compiled and the name

of the target quantum computers to the SDK Services

of the selected compilers. The QPU Selector of the

NISQ Analyzer examines the executability of the re-

turned compilation results. The user can prioritize the

executable compilation results via the Prioritization

Methods described by Salm et al. (2022b). Finally,

the calculated ranking is shown to the user. The user

How to Select Quantum Compilers and Quantum Computers Before Compilation

177

selects which compilation results should be executed

with the Executors of the related SDK Services on the

target quantum computer in parallel with the simulator.

With the extensibility of our plug-in-based system, fur-

ther Prediction Algorithms, programming languages,

metrics, and SDK Services can be added.

4.2 Prototype

The NISQ Analyzer and QProv are implemented in

Java using the framework Spring Boot. The UIs are

implemented in TypeScript with Angular. The SDK

Services, the Translator, and the Predict & Prio Ser-

vice are implemented in Python using Flask. Imple-

mentation details of existing components can be read

in previous work (Salm et al., 2022b,a, 2021, 2020a).

The prototypical implementation of our approach is

available open-source (University of Stuttgart, 2023b).

To support prediction algorithms, we use the

Python library scikit-learn

, which offers various ML

algorithms (Pedregosa et al., 2011). We tested all ML

algorithm implementations for regression of scikit-

learn available when the paper was written. The list

of all considered ML algorithm implementations and

applied settings can be viewed online (University of

Stuttgart, 2023c). We integrated the best performing

implementations from Sect. 5 which are different vari-

ants of the ML algorithms explained in Sect. 2: Our

prototype supports TheilSenRegressor (TSR) as a vari-

ant of multiple linear regression. We offer KNeigh-

borsRegressor (KNNR) as KNN regression. We sup-

port NuSVR as an implementation of SVR. Addition-

ally, the prototype offers ExtraTreesRegressor (ETR),

GradientBoostingRegressor (GBR), RandomForestRe-

gressor (RFR), and HistGradientBoostingRegressor

(HGBR), which are variants that combine multiple

decision trees. We implemented DecisionTreeRegres-

sor (DTR) for simple decision trees. Thereby, we con-

sidered every implementation stand-alone, with Ad-

aBoostRegressor (ABR) (Freund and Schapire, 1997),

and BaggingRegressor (BR) (Breiman, 1996). ABR

is a meta-estimator that applies the given regression

algorithm several times on the data set and slightly

adjusts the settings based on the latest estimation (Fre-

und and Schapire, 1997). Also, BR is a meta-estimator

whereby the regression algorithm to be considered is

applied several times on random subsets of the data,

and the outcomes are combined to form a single pre-

diction (Breiman, 1996). For the one-hot encoding of

the compilers, described in Sect. 2, we support the

OneHotEncoder implementation of scikit-learn.

https://scikit-learn.org

5 CASE STUDY

This section summarizes the case study of the approach

from Sect. 3. We compare the supported ML algorithm

implementations from Sect. 4.2 regarding their perfor-

mance of predicting histogram intersection values for

different quantum computer and compiler combina-

tions. Then, we analyze the quantum computer and

input circuits metrics and the compilers to investigate

their inﬂuence on the precision of execution results, an-

swering RQ2. Furthermore, we examine the precision

of the implementations and investigate the runtime of

the pre-selection, compilation, and analysis process.

An example of a predicted ranking of quantum com-

puter and compiler combinations regarding precise

execution results and short waiting times with a ra-

tio of 70:30 using weighted Borda count and ETR is

shown online (University of Stuttgart, 2023a).

The basis of our evaluation is the data set created

by Salm et al. (2022b). We compiled 52 input circuits

with the t

ket

⟩

compiler (Sivarajah et al., 2020) and

the Qiskit Transpiler (Aleksandrowicz et al., 2019) us-

ing the highest circuit optimization level (Salm et al.,

2022b). We considered the free accessible ibmq_lima,

ibmq_quito, ibmq_belem, and ibmq_bogota as target 5-

qubit quantum computers of the cloud provider IBMQ

and the ibmq_qasm_simulator to compute the his-

togram intersection values. The circuit set contains

three algorithmic circuits from Salm et al. (2022a), and

generated randomized Clifford gate circuits, where the

non-erroneous results are equal to the initial states,

such that a simulator is not required for histogram in-

tersection (Magesan et al., 2012; Salm et al., 2022b).

The randomized circuits have widths between three

and ﬁve qubits and depths between 11 and 355 single-

and two-qubit gates (Salm et al., 2022b). The data set

can be seen online (University of Stuttgart, 2023a). It

contains 229 samples, i.e., compiled circuits that were

successfully executed, and 16 features, listed in Fig. 4.

5.1 Performance of ML Algorithms

To evaluate the performance of the considered ML

algorithm implementations from Sect. 4.2, we use the

well-known

-fold cross-validation and split the data

set randomly into ﬁve folds, i.e.,

= 5, of similar

size (James et al., 2021). We control the splitting such

that compilation and execution results of the same

input circuit are part of the same fold to simulate the

handling of circuits that haven’t been considered yet;

thus, a more realistic scenario. The ﬁrst fold is the test

set, whereas the

k −

1 other folds build the training

set. Then, the often-used mean error is calculated due

to its easy interpretability (Willmott and Matsuura,

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

178

Figure 3: Mean error of the 20 best supported ML algorithm implementations.

2005; Yildiz et al., 2017). Each fold is iteratively the

ﬁrst fold. The mean error of all iterations is averaged.

This procedure is repeated ten times and the training

is repeated 50 times for each implementation. The

standard error of the mean (SEM) is determined by

calculating the variance of the 50 results divided by

the root of 50 (Altman and Bland, 2005).

Fig. 3 presents the mean error over the 50 repeti-

tions for the 20 best implementations based on our test

and training data setup. The error bar represents the

SEM. The performance and the execution times of all

implementations can be viewed online (University of

Stuttgart, 2023a). A slight decrease in the implemen-

tations’ performances regarding the test data can be

seen. ETR and ETR in combination with ABR and BR

deliver the smallest test errors on average, followed

by GBR, RFR, and DTR. Their predicted histogram

intersection values on the test data are on average be-

tween 0.04 and 0.05 above or below the actual values.

Thus, the decision tree variants deliver the best his-

togram intersection value estimations. NuSVR with

BR is in the eleventh place in the middle, followed

by its stand-alone variant. KNNR with BR is in the

ﬁfteenth place with a mean error over 0.05. Multiple

linear regression implemented with TSR seems to be

one of the worst-performing ML algorithms in our case

study regarding the test error. Nevertheless, especially

in the ﬁrst places of Fig. 3, the mean training error is

by far smaller than the related test error, also known as

overﬁtting (James et al., 2021). Overﬁtting means that

the ML algorithm implementations in the ﬁrst place

are less ﬂexible and learn patterns that do not occur in

the test data compared to the implementations in the

second half of the ranking, where the training error is

much higher. The SEM seem to be in a similar range

in Fig. 3 compared over the different implementations.

5.2 Inﬂuence of Metrics

To investigate the inﬂuence of the individual metrics,

we apply the permutation feature importance method

of scikit-learn (Breiman, 2001). We also consider the

one-hot encoded compilers to examine their impact

on the predictions. Thereby, an ML algorithm imple-

mentation learns on a data set where for an individual

feature, i.e., our metrics and compilers, its value is

replaced randomly by another given value of this fea-

ture in the data set. The method dissolves the feature’s

dependency on the response, and the estimation’s de-

terioration represents the feature’s inﬂuence. The pro-

cess is executed ten times for each feature. Then, we

repeat the overall procedure ten times and calculate

the average distance to the non-disturbed response.

Fig. 4 presents the individual importance’s dis-

tribution and mean of all features calculated with

the 20 best-performing ML algorithm implementa-

tions of Sect. 5.1. Some of the tested implementations

of Sect. 4.2 failed with the application of feature impor-

tance and returned invalid results. The list of results

of all implementations is shown online (University

of Stuttgart, 2023a). It seems that the t

ket

⟩

compiler

has, in general, more inﬂuence on predicting precise

execution results than the Qiskit Transpiler. The cir-

cuit metrics width, depth, and multi-qubit gate depth

inﬂuence the prediction models similarly. Also, the

comparatively more important total number of opera-

tions and the number of single-qubit gates are similar

in their inﬂuence. Whereby the total number of opera-

tions can slightly have higher importance. The number

of measurement operations follows with a difference

of 0.1 less mean importance. The most inﬂuencing

metric in Fig. 4 seems to be the number of multi-qubit

gates, whose importance is also stated by other work

How to Select Quantum Compilers and Quantum Computers Before Compilation

179

Figure 4: Feature importance measured by the 20 best-performing ML algorithm implementations.

because of their high error rates (Sivarajah et al., 2020;

Salm et al., 2022b). The inﬂuence of the quantum com-

puter metrics is relatively low, with values smaller than

0.05, compared to the metrics for non-compiled input

circuits. The single-qubit gate time, thereby, has the

smallest importance equal to 0.

5.3 Precision of Pre-Selection

We examine the precision of the best-performing im-

plementations of Sect. 5.1 by step-wise decreasing the

threshold of the maximum number of compiler and

quantum computer combinations to be returned, as de-

scribed in Sect. 3. Thereby, we analyze if the combina-

tion with the most precise real histogram intersection

value is in the returned set. As presented in Sect. 5.1,

we apply ten times 5-fold cross-validation. Fig. 5

shows the probability of returning the best combination

dependent on the percentage of removed combinations

using the ﬁve best-performing implementations. The

precision of the 20 best-performing implementations

can be found online (University of Stuttgart, 2023a).

By removing 50% of all possible combinations within

the Compiler & QPU Pre-Selection phase (Sect. 3.2),

the best combination is kept with a probability of over

80%. Removing 90% of all combinations keeps the

best combination with over 50% probability. The dif-

ferent variants of ETR show a higher precision com-

pared to BR(GBR) and GBR.

5.4 Runtime Analysis

We investigate how much the pre-selection approach

reduces the runtime of our framework with the re-

quirement of precise executions applying the best-

performing implementation ABR(ETR). Thus, we

measure the overall runtime of the phases Circuit Anal-

Figure 5: Precision of the ﬁve best-performing ML algorithm

implementations for different thresholds.

ysis, Compiler & QPU Pre-Selection, Compilation,

and Compilation Result Analysis, described in Sect. 3.

Based on the precision shown in Fig. 5, we set thresh-

olds such that 0%, 50%, 70%, and 90% of all possible

compiler and quantum computer combinations are re-

moved for three different circuits. As a ﬁrst attempt,

we considered an algorithmic implementation with

three qubits (Gr3) and a depth of 14 and two random-

ized circuits with four (RC4) and ﬁve (RC5) qubits

and depths of 85 and 77. We used the t

ket

⟩

compiler

and the Qiskit Transpiler with six quantum computers

of IBMQ, resulting in 12 combinations in addition to

one compiler and simulator combination. All circuit

and quantum computer metric values can be seen on-

line (University of Stuttgart, 2023a). We repeat the

process for each circuit and threshold combination ten

times and calculate the median, as shown in Table 1.

The framework was executed on a MacBook Pro

running Ventura 13.1 with a 2,4 GHz Quad-Core Intel

Core i5 processor and 16 GB of RAM.

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

180

Table 1: Median runtimes of our approach removing various

percentages of compiler-QPU-combinations (in seconds).

Circuit 0% 50% 70% 90%

Gr3 84.34 51.72 42.01 31.56

RC4 108.80 63.05 51.49 39.32

RC5 109.81 65.65 54.39 42.88

Table 1 shows that setting the threshold such that

50% of all possible combinations are removed during

pre-selection reduces the median runtime by around

40%. Removing 70% compared to 50% reduces the

runtime by an additional 18%. Lowering the full set

by 90% such that one compiler and quantum computer

as well as one simulator combination remains, reduces

the overall runtime by around 62%. Compiling circuits

with higher depths seems to require more runtime.

6 DISCUSSION

Our case study in Sect. 5 only covers 5-qubit quan-

tum computers and, besides randomized circuits, only

a few algorithmic circuits which are closer to real-

world applications (Salm et al., 2022b). The ﬁrst at-

tempt of analyzing the runtime reduction with our pre-

selection approach does not include the Translation

phase from Sect. 3.3. Nevertheless, it shows that the

extension reduces the computation time of our frame-

work by up to 62% and we want to examine the run-

time more extensive in the future. The pre-selection of

quantum computer and compiler combinations is only

possible if histogram intersection values of prior input

circuits are available. However, the ML algorithms can

learn on the data of various input circuits and are not

dependent on past results of the same circuit. Translat-

ing a circuit can change its size because gates that are

not supported by the target compiler and SDK must

be replaced by subroutines of supported gates, increas-

ing the total number (Leymann and Barzen, 2020).

The translated circuit could cause more errors and less

precise execution results. An additional selection step

could be added after the translation phase in Sect. 3.3.

However, another selection could also increase the risk

of sorting out quantum computer and compiler combi-

nations that may have led to precise execution results.

No monetary metrics are considered, but further met-

rics can be supported by our framework.

7 RELATED WORK

Selecting suitable resources for a given use case is

a common problem in various areas, such as cloud

computing. For example, Sáez et al. (2014) and Sáez

et al. (2016) propose approaches of a decision support

system guiding the user to distribute their applications

to multiple clouds. Their target is to choose and con-

ﬁgure cloud services based on changing workloads

and requirements. Peddi (2016) present a survey about

resource allocation methods for the cloud. The study

suggests ML to predict required resources based on

given prior data. Islam et al. (2012) propose a pre-

diction framework to enable the automated scaling

of resources regarding future workload using linear

regression and error correction neural networks. The

work of Verma et al. (2016) presents a framework

that predicts and allocates resources for multi-tenant

systems in the cloud using several ML algorithms.

However, the presented approaches do not consider

resource prediction in the ﬁeld of quantum computing.

Several approaches exist that compare the perfor-

mance of quantum compilers on different quantum

computers (Sivarajah et al., 2020; Amy and Gheorghiu,

2020; Mills et al., 2021). Kharkov et al. (2022) present

a framework to enable the automated benchmarking

of various compilers. The work of Proctor et al. (2022)

presents benchmarks to enable predicting whether a

circuit is executable on a certain quantum computer

based on collected error rates. However, none of these

works propose the automated selection of compilers

and quantum computers based on prior data and a

given input circuit before the compilation. Quetschlich

et al. (2022) present a framework that automatically

selects the best combination of quantum technologies,

quantum computers, compilers, and compiler settings

based on a given input circuit using ML algorithms.

They evaluate the execution result precision by consid-

ering the gate ﬁdelity and measurement ﬁdelity of the

available gates and qubits. Nevertheless, they do not

support the automated collection of up-to-date quan-

tum computer data (Weder et al., 2021) and do not

provide automated translation, SDK handling, and ex-

ecution for the input circuit. They also do not enable

the user to specify their own requirements and, e.g.,

besides precise execution results, support considering

short waiting times to a certain extent.

8 CONCLUSION

We presented an extension of our approach that auto-

matically selects quantum computers and compilers

for a given circuit before the translation and compila-

tion, supporting resource-saving and scalability. The

user can choose short waiting times until execution,

precise future execution results, or deﬁne a ratio con-

sidering a combination of both as a selection objective.

How to Select Quantum Compilers and Quantum Computers Before Compilation

181

To answer RQ1, we use ML to predict the precision of

future execution results based on executions of other

input circuits in the past. We reported a case study that

compared the prediction performance and precision

of various ML algorithm implementations. To answer

RQ2, we examined the inﬂuence on the execution re-

sults’ precision in dependence to the compilers and the

metrics for quantum computers and input circuits, iden-

tiﬁed by Salm et al. (2022a). The case study presented

that, especially, the number of multi-qubit gates has

strong inﬂuence, even regarding non-compiled circuits.

We showed a ﬁrst attempt to analyze the runtime reduc-

tion of our framework with our pre-selection extension

and measured a time saving of up to 62%.

In the future, we want to expand our sample data

by considering further quantum computers and various

input circuits. We plan to extend the runtime analysis

of our framework by including the translation process

and considering additional quantum circuits. Further-

more, we plan to support additional SDK Services

and examine further metrics to estimate the precision

of executions on today’s NISQ computers. We also

want to enable an estimation of monetary aspects to

further support the user in selecting compiled circuits

and quantum computers based on their needs.

ACKNOWLEDGEMENTS

This work was partially funded by the BMWK project

PlanQK(01MK20005N).

REFERENCES

Aleksandrowicz, G. et al. (2019). Qiskit: An Open-source

Framework for Quantum Computing.

Altman, D. G. and Bland, J. M. (2005). Standard deviations

and standard errors. Bmj, 331(7521):903.

Amy, M. and Gheorghiu, V. (2020). staq—a full-stack quan-

tum processing toolkit. Quantum Science and Technol-

ogy, 5(3):034016.

Arute, F. et al. (2019). Quantum supremacy using a

programmable superconducting processor. Nature,

574(7779):505–510.

Awad, M. and Khanna, R. (2015). Support Vector Regression,

pages 67–80. Apress, Berkeley, CA.

Bova, F., Goldfarb, A., and Melko, R. G. (2021). Commer-

cial applications of quantum computing. EPJ quantum

technology, 8(1):2.

Breiman, L. (1996). Bagging predictors. Machine Learning,

24(2):123–140.

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

Buluta, I., Ashhab, S., and Nori, F. (2011). Natural and

artiﬁcial atoms for quantum computation. Reports on

Progress in Physics, 74(10):104401.

B ˛aczkiewicz, A., Kizielewicz, B., Shekhovtsov, A., W ˛atrób-

ski, J., and Sałabun, W. (2021). Methodical Aspects

of MCDM Based E-Commerce Recommender Sys-

tem. Journal of Theoretical and Applied Electronic

Commerce Research, 16(6):2192–2229.

Cerda, P., Varoquaux, G., and Kégl, B. (2018). Similarity En-

coding for Learning with Dirty Categorical Variables.

Mach. Learn., 107(8–10):1477–1494.

De’ath, G. and Fabricius, K. E. (2000). Classiﬁcation and

regression trees: A powerful yet simple technique for

ecological data analysis. Ecology, 81(11):3178–3192.

Freund, Y. and Schapire, R. E. (1997). A Decision-Theoretic

Generalization of On-Line Learning and an Applica-

tion to Boosting. Journal of Computer and System

Sciences, 55(1):119–139.

Gill, S. S. et al. (2022). Quantum computing: A taxon-

omy, systematic review and future directions. Software:

Practice and Experience, 52(1):66–114.

Islam, S., Keung, J., Lee, K., and Liu, A. (2012). Empirical

prediction models for adaptive resource provisioning

in the cloud. Future Generation Computer Systems,

28(1):155–162.

James, G., Witten, D., Hastie, T., and Tibshirani, R. (2021).

Linear Regression, pages 59–128. Springer US, New

York, NY.

Kharkov, Y., Ivanova, A., Mikhantiev, E., and Kotelnikov, A.

(2022). Arline Benchmarks: Automated Benchmarking

Platform for Quantum Compilers.

LaRose, R. (2019). Overview and Comparison of Gate Level

Quantum Software Platforms. Quantum, 3:130.

Leymann, F. and Barzen, J. (2020). The bitter truth about

gate-based quantum algorithms in the NISQ era. Quan-

tum Science and Technology, 5(4):1–28.

Leymann, F., Barzen, J., Falkenthal, M., Vietz, D., Weder,

B., and Wild, K. (2020). Quantum in the Cloud:

Application Potentials and Research Opportunities.

In Proceedings of the 10

International Conference

on Cloud Computing and Services Science (CLOSER

2020), pages 9–24. SciTePress.

Magesan, E. et al. (2012). Efﬁcient measurement of quantum

gate error by interleaved randomized benchmarking.

Phys. Rev. Lett., 109:080505.

Mills, D., Sivarajah, S., Scholten, T. L., and Duncan, R.

(2021). Application-motivated, holistic benchmarking

of a full quantum computing stack.

National Academies of Sciences, Engineering, and Medicine

(2019). Quantum Computing: Progress and Prospects.

The National Academies Press.

Nielsen, M. A. and Chuang, I. L. (2011). Quantum Computa-

tion and Quantum Information. Cambridge University

Press, 10th edition.

Peddi, P. (2016). Comparative study on cloud optimized

resource and prediction using machine learning algo-

rithm. ISSN: 2455, 6300:88–94.

Pedregosa, F. et al. (2011). Scikit-learn: Machine Learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

182

Preskill, J. (2018). Quantum Computing in the NISQ era

and beyond. Quantum, 2:79.

Proctor, T., Rudinger, K., Young, K., Nielsen, E., and Blume-

Kohout, R. (2022). Measuring the capabilities of quan-

tum computers. Nature Physics, 18(1):75–79.

Quetschlich, N., Burgholzer, L., and Wille, R. (2022). Pre-

dicting Good Quantum Circuit Compilation Options.

Russell, N. (2007). Complexity of control of Borda count

elections.

Sáez, S. G., Andrikopoulos, V., and Leymann, F. (2016).

Consolidation of Performance and Workload Models

in Evolving Cloud Application Topologies. In Proceed-

ings of the 6th International Conference on Cloud Com-

puting and Service Science (CLOSER 2016), pages

160–169, Rome, Italy. SciTePress.

Salm, M., Barzen, J., Breitenbücher, U., Leymann, F., Weder,

B., and Wild, K. (2020a). The NISQ Analyzer: Au-

tomating the Selection of Quantum Computers for

Quantum Algorithms. In Proceedings of the 14th Sym-

posium and Summer School on Service-Oriented Com-

puting (SummerSOC 2020), pages 66–85. Springer In-

ternational Publishing.

Salm, M., Barzen, J., Leymann, F., and Weder, B. (2020b).

About a Criterion of Successfully Executing a Circuit

in the NISQ Era: What

wd ≪

/ε

eff

Really Means. In

Proceedings of the 1st ACM SIGSOFT International

Workshop on Architectures and Paradigms for Engi-

neering Quantum Software (APEQS 2020), pages 10–

13. ACM.

Salm, M., Barzen, J., Leymann, F., and Weder, B. (2022a).

Prioritization of Compiled Quantum Circuits for Differ-

ent Quantum Computers. In Proceedings of the 2022

IEEE International Conference on Software Analysis,

Evolution and Reengineering (SANER 2022), pages

1258–1265. IEEE.

Salm, M., Barzen, J., Leymann, F., Weder, B., and Wild,

K. (2021). Automating the Comparison of Quantum

Compilers for Quantum Circuits. In Proceedings of

the 15

Symposium and Summer School on Service-

Oriented Computing (SummerSOC 2021), pages 64–80.

Springer International Publishing.

Salm, M., Barzen, J., Leymann, F., and Wundrack, P. (2022b).

Optimizing the Prioritization of Compiled Quantum

Circuits by Machine Learning Approaches. In Pro-

ceedings of the 16

Symposium and Summer School

on Service-Oriented Computing (SummerSOC 2022),

pages 161–181. Springer.

Schuld, M., Sinayskiy, I., and Petruccione, F. (2016). Predic-

tion by linear regression on a quantum computer. Phys.

Rev. A, 94:022342.

Siraichi, M. Y., Santos, V. F. d., Collange, S., and Quin-

tão Pereira, F. M. (2018). Qubit Allocation. In CGO

2018 - International Symposium on Code Generation

and Optimization, pages 1–12.

Sivarajah, S., Dilkes, S., Cowtan, A., Simmons, W., Edging-

ton, A., and Duncan, R. (2020). t

ket

⟩

: A retargetable

compiler for NISQ devices. Quantum Science and

Technology, 6.

Swain, M. J. and Ballard, D. H. (1991). Color indexing.

International Journal of Computer Vision, 7(1):11–32.

Sáez, S. G., Andrikopoulos, V., Leymann, F., and Strauch,

S. (2014). Towards dynamic application distribution

support for performance optimization in the cloud. In

2014 IEEE 7th International Conference on Cloud

Computing, pages 248–255.

University of Stuttgart (2023a). Case Study.

https://github.com/UST-QuAntiL/nisq-analyzer-

content/tree/paper/pre-selection/pre-selection/Case-

Study.

University of Stuttgart (2023b). Content Reposi-

tory. https://github.com/UST-QuAntiL/nisq-analyzer-

content/tree/paper/pre-selection/pre-selection.

University of Stuttgart (2023c). ML Algorithm Imple-

mentations. https://github.com/UST-QuAntiL/nisq-

analyzer-content/tree/paper/pre-selection/pre-

selection/Prediction-Algorithms.

Vapnik, V. N. (1995). The Nature of Statistical Learning

Theory. Springer-Verlag, Berlin, Heidelberg.

Verma, M., Gangadharan, G. R., Narendra, N. C., Vadla-

mani, R., Inamdar, V., Ramachandran, L., Calheiros,

R. N., and Buyya, R. (2016). Dynamic resource de-

mand prediction and allocation in multi-tenant service

clouds. Concurrency and Computation: Practice and

Experience, 28(17):4429–4442.

Vietz, D., Barzen, J., Leymann, F., and Wild, K. (2021).

On Decision Support for Quantum Application De-

velopers: Categorization, Comparison, and Analysis

of Existing Technologies. In Computational Science

– ICCS 2021, pages 127–141. Springer International

Publishing.

Wang, J.-J., Jing, Y.-Y., Zhang, C.-F., and Zhao, J.-H. (2009).

Review on multi-criteria decision analysis aid in sus-

tainable energy decision-making. Renewable and Sus-

tainable Energy Reviews, 13(9):2263–2278.

Weder, B., Barzen, J., Leymann, F., Salm, M., and Wild,

K. (2021). QProv: A provenance system for quantum

computing. IET QuantumCommunication, 2(4):171–

181.

Willmott, C. J. and Matsuura, K. (2005). Advantages of the

mean absolute error (MAE) over the root mean square

error (RMSE) in assessing average model performance.

Climate research, 30(1):79–82.

Yildiz, B., Bilbao, J., and Sproul, A. (2017). A review and

analysis of regression and machine learning models

on commercial building electricity load forecasting.

Renewable and Sustainable Energy Reviews, 73:1104–

1122.

Zhong, H.-S. et al. (2020). Quantum computational advan-

tage using photons. Science.

How to Select Quantum Compilers and Quantum Computers Before Compilation

183