Supervised Learning for Untangling Braids

Alexei Lisitsa

1 a

, Mateo Salles

and Alexei Vernitski

2 b

University of Liverpool, U.K.

University of Essex, U.K.

Keywords:

Deep Learning, Supervised Learning, Behavioral Cloning, Braid.

Abstract:

Untangling a braid is a typical multi-step process, and reinforcement learning can be used to train an agent to

untangle braids. Here we present another approach. Starting from the untangled braid, we produce a dataset

of braids using breadth-ﬁrst search and then apply behavioral cloning to train an agent on the output of this

search. As a result, the (inverses of) steps predicted by the agent turn out to be an unexpectedly good method

of untangling braids, including those braids which did not feature in the dataset.

1 INTRODUCTION

Braids are mathematical objects which are studied us-

ing knot theory and group theory. For us in our study,

braids are a type of mathematical objects to which

machine learning can be usefully applied. See more

on the problem of untangling braids in Section 3. In

our earlier research we attempted to apply reinforce-

ment learning to the problem of untangling braids,

with limited success. In this study we develop and

successfully apply a new approach which is inspired

by behavioral cloning and includes supervised learn-

ing as one of its parts, see Section 2 for more details.

The contribution of the study is two-fold, combin-

ing a new insight in the problems related to braids, on

the one hand, and a new machine learning technique

which can be used in place of reinforcement learning,

on the other hand.

2 GENERAL IDEA

Consider a network having a certain regular structure

(for example, a grid), like the one in Figure 1.

We want to train an agent to ﬁnd a path, starting

from an arbitrary node in this network, to the node

O. There are many approaches which can be used,

including several ﬂavours of reinforcement learning

(Sutton and Barto, 2018). However, in this study we

https://orcid.org/0000-0002-3820-643X

https://orcid.org/0000-0003-0179-9099

use supervised learning, namely, a version of behav-

ioral cloning (Ho and Ermon, 2016).

D E

Figure 1: A sample network to apply breadth ﬁrst search to.

D E

Figure 2: Breadth ﬁrst search has been applied.

Starting from node O, we perform a breadth ﬁrst

search of a given depth. As a result of this search,

we obtain a tree within the network, which stores, for

each node in the tree, one of possible shortest ways

of reaching this node from O. Figure 2 shows such a

tree, with depth 2, in the network shown in Figure 1.

Then we train a neural network to predict, for a given

node picked from the tree, what was the last move

between two nodes in the tree that has reached this

node. For example, for node D in Figure 2 the correct

answer would be ‘reach it by moving from A to D’. To

be more precise, note that the network might contain a

large number of nodes, but only a very small number

of different kinds of moves; for example, in a grid the

moves are ‘move up’, ‘move right’, ‘move down’, and

784

Lisitsa, A., Salles, M. and Vernitski, A.

Supervised Learning for Untangling Braids.

DOI: 10.5220/0011775900003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 784-789

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

‘move left’. Thus, for node D in Figure 2 the correct

answer would be ‘reach it by moving down’.

Below, we will refer to the trained neural network

predicting the last step in the tree as Lara (for ‘last’).

After we have trained Lara, we use another piece of

code to ﬁnd a path from a given node to O; we call

this code Una (for ’untangle’). Starting from a given

node, Una asks Lara how this node is classiﬁed, and

then performs the opposite move; then the same step

is repeated until O is reached. For example, if Una

starts at node D, Lara classiﬁes this node as ‘move

down’, thus, Una applied the opposite move, ‘move

up’, reaching node A, then asks Lara again, etc., until

O is reached.

Lara

reverse

state action action

Figure 3: Diagram showing how Una works. A trained clas-

siﬁer Lara is applied to a state to produce an action; then the

action is reversed.

Note that the tree does not include all nodes in the

network, for example, node E in Figure 2 is not in the

tree. Lara is not trained on the nodes which are not in

the tree. However, due to the regular structure of the

network, we can hope that Lara will be able to gen-

eralize to these nodes and produce a reasonable rec-

ommendation for Una. For example, for node E one

can hope that Lara will conjecture that this node can

be reached from above or from the left, thus directing

Una, correctly, up or to the left.

In this paper we apply this idea to untangling

braids. However, before we delve into braid theory,

let us explain how this idea could potentially work on

another, more familiar example. Suppose we want to

train an agent to solve the Rubik’s cube. Visualise

a network in which nodes are all possible positions

of the Rubik’s cube (there are about 10

of them),

and in which two nodes are connected with an edge

if the nodes can be produced from one another by

one move (that is, one face turn). The network has

a regular structure, with each node connected to its

neighbors by a small number of possible moves. De-

note the solved position of the Rubik’s cube by O.

As described above, we can perform a breadth ﬁrst

search in the network starting from O. As a rough

estimation, conducting this breadth ﬁrst search up to

depth d reaches 10

nodes. It is known that one needs

20 moves (or 26 moves, depending on the exact def-

inition of moves (Kunkle and Cooperman, 2007)) to

reach every node from O, and it is not feasible to build

a tree containing 10

nodes. Realistically, a tree that

one can build would be much smaller, for example, a

tree can contain about 10

nodes. Thus, it is impor-

tant that Lara can generalize well from this relatively

small tree to the unfathomably large network.

3 BRAIDS

Braids are mathematical objects from low-

dimensional topology or, to be more precise,

knot theory (that is, the study of the relative position

of curves in the space). A braid on n strands consists

of n ropes whose left-hand ends are ﬁxed one under

another and whose right-hand ends are ﬁxed one

under another; you can imagine that the braid is laid

out on a table, and the ends of the ropes are attached

to the table with nails. Figures 4, 5 show examples

of braids on 3 strands with 10 crossings. Braids are

important because, on the one hand, they are useful

building blocks of knots and other constructions of

low-dimensional topology and, on the other hand,

have a simple structure and can be conveniently

studied using mathematics and, as in this study,

experimented with using computers.

The braids in Figures 4, 5 can be untangled, that is,

all crossings can be removed by moving certain parts

of strands up or down, as needed (without touching

the ends of the ropes); after the braid is untangled, the

braid diagram will look as in Figure 6, which shows

what we will call the canonical trivial braid. Not ev-

ery braid can be untangled. Those braids that can

be untangled are called trivial braids. The task that

we explore in this research is untangling braids using

ideas from Section 2.

When one studies braids (or knots) and how to un-

tangle them, the untangling process is split into el-

ementary local changes, affecting 2 or 3 consecutive

crossings, called Reidemeister moves (Kassel and Tu-

raev, 2008). Somewhat confusingly, the moves for

untangling braids are called the second Reidemeister

move and the third Reidemeister move; there exists a

move called the ﬁrst Reidemeister move, but it is used

only with knots and not with braids (Lickorish, 2012).

Please see all forms of the second Reidemeister move

in Figures 7, 8. The meaning of each of these ﬁgures

is that a braid fragment shown on the left can be re-

placed by a braid fragment shown on the right, or vice

versa.

All forms of the third Reidemeister move are

shown in Figures 9, 10, 11, 12, 13, 14.

As you can see, the second Reidemeister move,

when applied to one of directions, removes two cross-

ings from a braid; thus, if our aim is to untangle

the braid, it seems like a good move to use. How-

ever, not every Reidemeister move removes cross-

ings from a braid; one can say that some Reidemeis-

ter moves (including all versions of the third Reide-

Supervised Learning for Untangling Braids

785

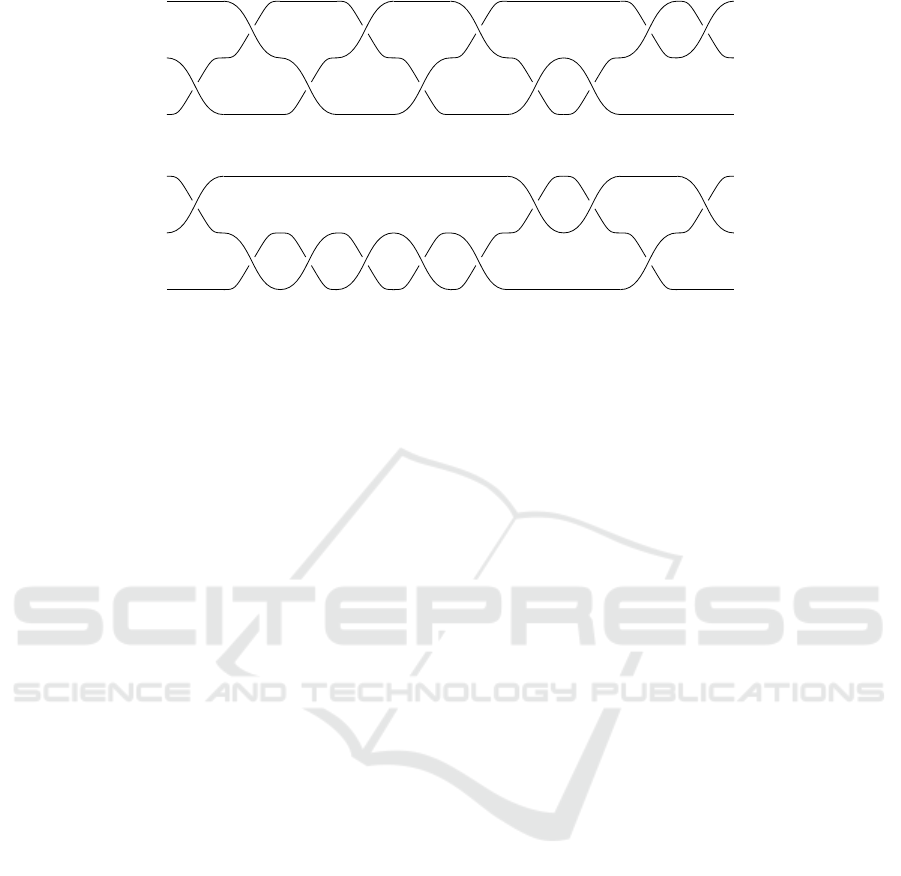
Figure 4: An example of a trivial braid which our agent successfully untangles.

Figure 5: An example of a trivial braid which our agent cannot untangle.

meister move) only prepare groundwork for remov-

ing crossings. Thus, the challenge for artiﬁcial intelli-

gence is to learn which Reidemeister moves it should

use to untangle a braid, even though initially it might

be not clear how these moves contribute to untangling

the braid.

Here is how we encode braids in the computer.

Considering a braid from left to right, we record

a clockwise (or anti-clockwise) crossing of strands

in positions i and i + 1 (counting from the bottom)

as the number i (or −i). Thus, for example, the

braid in Figure 5 is encoded as the list of numbers

−2, 1, −1, −1, 1, 1, 2, −2, −1, 2. We were prepared

to transform this encoding into one-hot encoding, if

needed, but so far, we are reasonably successful with

this simple encoding. This list of numbers is fed into

a neural network when Lara is trained. As to Reide-

meister moves, each of them is re-interpreted as an in-

struction stating that a certain two-digit or three-digit

fragment within the braid can be replaced by another

fragment of the same length. For example, the Rei-

demeister move in Figure 7 states that 0 0 can be re-

placed by 1 − 1 (or 2 − 2, etc., depending on which

strands the move is applied to) or vice versa.

For our experiments, we ﬁx the length of the braid,

as we did in our previous research (Khan et al., 2021).

If there is no intersection of strands in a certain part

of a braid, this part of the braid is denoted by 0. Thus,

for example, in the context of braids with up to 10

crossings, the canonical trivial braid (shown in Figure

6) is encoded by the list of 10 0s. Because of this

encoding, we need to add one more kind of moves in

addition to Reidemeister moves, namely, shifting zero

entries in the braid to the left or to the right, as needed;

that is, the fragment i 0 in the braid can be replaced by

0 i or vice versa.

Not every type of Reidemeister move can be ap-

plied at every position in a given braid; for example,

the Reidemeister move in Figure 7 cannot be applied

to the ﬁrst and the second crossing (counting from the

left) of the braid in Figure 5, but can be applied to

the second and the third crossing of this braid. When

Lara predicts the last move, it predicts a pair, consist-

ing of the type of the move and the position in the

braid where it was applied. Sometimes Lara is wrong

in the sense that this move could not have been ap-

plied at this position in the braid. In this sense, below,

when we discuss how Una should interpret Lara’s pre-

dictions, we discuss how to interpret valid and invalid

moves.

4 MODEL STRUCTURE

As we said in Section 2, our code consists of two main

parts, Lara and Una. The ﬁrst one, Lara, is an Multi-

Layered Perceptron (MLP) network that predicts the

last move that was made to obtain a given braid. The

second one, Una, is an algorithm that attempts to un-

tangle a given braid by executing a series of moves.

4.1 LARA

This model is used to predict the last move made to a

certain braid. The data generated for Lara comes from

a breath ﬁrst search tree, as in Figure 2, where there

is only one path from O to any other node. In this

sense, Lara is a single-label multi-class model. The

conﬁguration of this MLP is given by:

• Input layer that receives the array of an encoded

braid.

• Three hidden layers of size 128, 64 and 32, re-

spectively. Each one with ReLU as activation

function.

• Output layer of the the encoded action array, of

length (strands ∗ 2 + 4) ∗ length. with a softmax

activation function.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

786

Figure 6: The canonical trivial braid contains no crossings.

Figure 7: Second Reidemeister move (form 1).

Figure 8: Second Reidemeister move (form 2).

Figure 9: Third Reidemeister move (form 1).

Figure 10: Third Reidemeister move (form 2).

Figure 11: Third Reidemeister move (form 3).

Figure 12: Third Reidemeister move (form 4).

Figure 13: Third Reidemeister move (form 5).

Figure 14: Third Reidemeister move (form 6).

We could have trained Lara on all nodes of the

tree; however, we not only train Lara, but also test its

accuracy on a test set. The training and test sets come

from the tree dataset, being randomly chosen 80% and

20% of the nodes, respectively. As you can see in

Table 1, the performance of Lara is very promising,

maintaining overall accuracy above 99%.

After Lara has been trained, the predictions of

Lara need to be sequenced and inverted to use them

to untangle braid, as described below.

4.2 UNA

The purpose of this code is untangling a given braid

by executing a series of moves, namely, the inverses

of the moves produced by Lara. In order to test our

Lara/Una architecture, We wrote several versions of

Una, depending on how much they trust Lara’s output

and how they interpret it:

• Random (U NA

): Una performs a randomly cho-

sen valid move without consulting Lara.

• Valid or random (UNA

): Una executes the rec-

ommended move from Lara if the recommended

move is valid; otherwise, Una performs a ran-

domly chosen valid move (like UNA

• Best valid move (UNA

): Una executes, out of all

valid moves available, the one that is ranked most

highly by Lara.

• Tree only (UNA

): Una executes the recom-

mended action from Lara (like UNA

) if the cur-

rently considered braid belongs to the tree on

which Lara was trained. If the braid does not

belong to the tree, Una executes a random valid

move (like UNA

Every version works until it reaches one of two

situations. The ﬁrst one is when the braid is com-

pletely untangled; then it is a success. The second

Supervised Learning for Untangling Braids

787

one is when the current braid has already been vis-

ited; then it is a failure

5 EXPERIMENTS

To test the different versions of Una, we used a dataset

of randomly generated braids that do not necessarily

belong to the tree of braids created to train Lara. (To

be more precise, the randomly generated braids in the

test set are unlikely to be in the tree because we only

include braids without 0s, in other words, braids with

the maximal number of crossings, in the test set.) In

Table 1, we show the size of the braids used in the

experiments (the length and the number of strands),

the size of the tree used to train Lara (the depth and the

number of nodes), the total number of trivial braids in

the network containing the tree, Lara’s accuracy (on

the test set separated within the tree), and the success

rate of different implementations of Una.

The training set of Lara is represented in the Tree

size column. For length 8, this training set goes from

11% to 61% of the all braids. The test set of Una is

represented in the Test size column, and for length 8

it is 21% of all braids. For length 10, Lara’s training

set goes from 2% to 30%, with a test set of Una of

around 5% of all braids. Finally, with length 12 the

training set of Lara goes from 0.2% to 3.2% with the

test set of Una of 0.6% of all braids.

This data enables us to answer two research ques-

tions which we asked ourselves. Do Lara and Una,

between the two of them, learn something useful

about untangling braids? The answer is yes, because

the performance of the version of Una making random

moves, UNA

, is much lower than the performance of

all other versions of Una, which beneﬁt from learning.

Can Lara, after having been trained on a tree, gener-

alize this knowledge usefully to the braids it has not

been trained on? The answer is yes, because the per-

formance of the versions of Una that use Lara’s advice

outside the tree, UNA

and UNA

, are noticeably bet-

ter than the performance of the version of Una that

does not use Lara’s advice outside the tree, UNA

The performance of these models is calculated

with an accuracy ratio of the successfully untangled

braids over the total braids tested. For example, with

length 8 and depth 7, UNA

is able to untangle 74%

of the testing set braids.

We could have expanded our experiments to allowing

Una to visit the same node repeatedly and choose a different

random action each time it happens. However, these non-

deterministic approaches are of little interest to us, because

our main aim is to test how much Lara’s advice helps Una

in untangling the braid.

Although our experiment results make us sufﬁ-

ciently conﬁdent to formulate the general conclusions

stated in the previous paragraph, we can report that

speciﬁc numbers are noisy and depend on the ran-

domness in the training of Lara. For braids of length

8, we ran each experiment (including training Lara)

several times, and results are different; please see Ta-

ble 2 showing how the performance of Una changes

depending on Lara. The ﬁrst 4 rows in Table 2 are the

numbers from Table 1, and the next 4 rows are the

same experiments, but repeated with newly trained

Lara’s neural networks. The bottom 4 rows in Table

2 are the same experiments again, with longer trained

Lara’s neural networks.

From the mathematical point of view, we know

that only at the distance of 6 moves from O the third

Reidemeister move can be ﬁrst applied. For instance,

for length 10, the 24, 191 braids in the tree of depth 5

do not include any braids that require the third Reide-

meister move to be untangled, so Lara trained on this

dataset has never encountered any version of the third

Reidemester move applied. Accordingly, we can see,

for example, that for length 10 there is a clear im-

provement between depth 5 and 6, with the success

rate of both UNA

and UNA

improving almost two

times.

6 RELATED WORK

A Reinforcement Learning approach was attempted

for the same problem in previous research that we de-

veloped. Using Policy Gradient with a MLP we gave

a negative reward for every step the agent made in

order to encourage time efﬁciency. A comparative re-

sult is the RL approach obtained an accuracy of 22%

for untangling braids of 3 strands and 12 crossings.

In this sense, this Supervised Learning approach im-

proves that accuracy to 27% with UNA

, for example.

Multiple- and single-agent reinforcement learning

was applied to untangling braids in our earlier work

(Khan et al., 2021; Khan et al., 2022). The method

proposed in this paper demonstrates better perfor-

mance of untangling on comparable sizes of braids.

A closely related problem (with a slightly ex-

tended list of Reidemeister moves) is untangling

knots presented as closed braids. A range of single-

agent reinforcement learning methods was used in

(Gukov et al., 2021) to solve that problem. The

best accuracy (about 85% of braids untangled) was

reported for the trust region policy optimization

(TRPO) method. Although that is a not the same un-

tangling problem as the one we consider in this paper,

it is encouraging to see that this accuracy is compara-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

788

Table 1: Results of Una versions using different depths to train Lara. All experiments are with braids with 3 strands.

Length Depth Tree size Total braids Test size LARA UNA

UNA

8 3 1,271 11,317 2,400 99.30% 16% 52% 18% 30%

8 5 3,919 11,317 2,400 99.48% 16% 46% 59% 43%

8 6 5,639 11,317 2,400 97.36% 16% 64% 80% 62%

8 7 6,963 11,317 2,400 99.44% 16% 74% 64% 57%

10 3 3,455 191,645 10,000 99.12% 6% 32% 16% 18%

10 5 24,191 191,645 10,000 99.92% 6% 26% 33% 14%

10 6 38,759 191,645 10,000 99.85% 6% 51% 65% 36%

10 7 57,947 191,645 10,000 99.63% 6% 60% 54% 35%

12 3 7,367 3,427,517 20,000 99.52% 2% 18% 11% 8%

12 5 112,559 3,427,517 20,000 99.07% 2% 20% 27% 10%

Table 2: Experiments run two times with different NNs.

Depth U NA

UNA

3 16% 52% 18% 30%

5 16% 46% 59% 43%

6 16% 64% 80% 62%

7 16% 74% 64% 57%

3 16% 53% 27% 40%

5 16% 61% 77% 56%

6 16% 58% 72% 51%

7 15% 41% 37% 32%

3 16% 53% 27% 40%

5 16% 65% 77% 56%

6 15% 70% 85% 63%

7 15% 81% 81% 69%

ble with the best results we have achieved in our ex-

periments, with arguably a simpler off-line learning

approach.

7 CONCLUSION

We demonstrate that although Lara is only trained on

a small tree inside the network (that is, the network

of braids connected by actions), using Lara’s advice

when performing actions considerably increases the

probability of reaching the canonical trivial braid (that

is, untangling the braid).

As described in the end of Section 2, this approach

can be applied to other problems, too, in place of re-

inforcement learning.

In the future, we will extend our approach to

untangling knots presented as closed braids, as in

(Gukov et al., 2021); one speciﬁc challenging exam-

ple to tackle is the one presented in (Morton, 1983).

In addition to this, we want to untangle knots pre-

sented in a different form, called the plat represen-

tation of knots (Birman, 1976).

ACKNOWLEDGEMENTS

The work was supported by the Leverhulme Trust Re-

search Project Grant RPG-2019-313.

REFERENCES

Birman, J. S. (1976). On the stable equivalence of plat rep-

resentations of knots and links. Canadian Journal of

Mathematics, 28(2):264–290.

Gukov, S., Halverson, J., Ruehle, F., and Sułkowski, P.

(2021). Learning to unknot. Machine Learning: Sci-

ence and Technology, 2(2):025035.

Ho, J. and Ermon, S. (2016). Generative adversarial imi-

tation learning. Advances in neural information pro-

cessing systems, 29.

Kassel, C. and Turaev, V. (2008). Braid groups, volume

247. Springer Science & Business Media.

Khan, A., Vernitski, A., and Lisitsa, A. (2021). Untan-

gling braids with multi-agent Q-learning. In 23rd In-

ternational Symposium on Symbolic and Numeric Al-

gorithms for Scientiﬁc Computing (SYNASC), pages

135–139.

Khan, A., Vernitski, A., and Lisitsa, A. (2022). Rein-

forcement learning algorithms for the untangling of

braids. In Bart

ak, R., Keshtkar, F., and Franklin,

M., editors, Proceedings of the Thirty-Fifth Interna-

tional Florida Artiﬁcial Intelligence Research Society

Conference, FLAIRS 2022, Hutchinson Island, Jensen

Beach, Florida, USA, May 15-18, 2022.

Kunkle, D. and Cooperman, G. (2007). Twenty-six moves

sufﬁce for rubik’s cube. In Proceedings of the 2007

international symposium on Symbolic and algebraic

computation, pages 235–242.

Lickorish, W. R. (2012). An introduction to knot theory,

volume 175. Springer Science & Business Media.

Morton, H. R. (1983). An irreducible 4-string braid with un-

knotted closure. In Mathematical Proceedings of the

Cambridge Philosophical Society, volume 93, pages

259–261. Cambridge University Press.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-

ing: An introduction. MIT press.

Supervised Learning for Untangling Braids

789