A Game Theoretic Approach to Attack Graphs
Davide Catta
1
, Antonio Di Stasio
2
, Jean Leneutre
1
, Vadim Malvone
1
and Aniello Murano
3
1
T
´
el
´
ecom-Paris, Paris, France
2
Sapienza University of Rome, Rome, Italy
3
University of Naples Federico II, Naples, Italy
Keywords:
Attack Graphs, Game Theory, Automata Theoretic Approach.
Abstract:
An attack graph is a succinct representation of all the paths in an open system that allow an attacker to enter a
forbidden state (e.g., a resource), besides any attempt of the system to prevent it. Checking system vulnerabil-
ity amounts to verifying whether such paths exist. In this paper we reason about attack graphs by means of a
game-theoretic approach. Precisely, we introduce a suitable game model to represent the interaction between
the system and the attacker and an automata-based solution to show the absence of vulnerability.
1 INTRODUCTION
The inherent complexity of modern systems came
with a cost: as they became more complex, it also
becomes harder and harder to assure their security.
When dealing with security, one should be true to the
motto “Better safe than sorry”. This is because the
cost of repairing a system flaw during maintenance
is at least two order of magnitude higher, compared
to a fixing at an early design. As a consequence, in
order to develop a secure system, one should come
up with tools able to detect vulnerability and un-
expected behaviors at a very early stage of its life-
cycles (Clarke et al., 1999). To check systems relia-
bility a story of success is the use of formal methods
techniques (Clarke et al., 1999). They allow check-
ing whether a system is correct by formally checking
whether a mathematical model of it meets a formal
representation of its desired behaviour.
Recently, classic approaches such as model check-
ing and automata-theoretic techniques, originally de-
veloped for monolithic systems (Clarke and Emerson,
1981; Kupferman et al., 2000), have been meaning-
fully extended to handle open and multi-agent sys-
tems (Kupferman et al., 2001; Alur et al., 2002; Lo-
muscio et al., 2009; Mogavero et al., 2014; Jamroga
and Murano, 2015). These are systems that encap-
sulate the behaviour of two or more rational agents
interacting among them in a cooperative or adver-
sarial way, aiming at a designed goal (Jennings and
Wooldridge, 1998).
In system security checking, a malicious attack
can be seen as an attempt of an attacker to gain an
unauthorized resource access or compromise the sys-
tem integrity. In this setting, attack graph (Lippmann
and Ingols, 2005) is one of the most prominent at-
tack model developed and receiving much attention
in recent years. This encompasses a graph where each
state represents an attacker at a specified network lo-
cation and edges represent state transitions, i.e., at-
tack actions by the attacker. Then, it is a system duty
to prevent unauthorized accesses from the attacker in
each state of the graph.
In this paper, we reason about attack graphs by
introducing game models and an automata-based so-
lution to evaluate system reliability. We first set a
two-player turn-based reachability game between the
(system) defender and the (external and potential) at-
tacker, where in turn the latter moves along adjacent
states (w.r.t. the attack graph under exam) and the for-
mer inhibits some attacks by taking countermeasures.
We show how simple attack graphs can be reduced
to such game-model. We then build a finite tree au-
tomaton that accepts all the walking trees that allow
the attacker to reach the designated states, no matter
how the defender behaves. By checking the empti-
ness of the automaton, we show the robustness of the
system (i.e., the absence of bad paths in the attack
graph). Notably, the construction of the automaton
and its emptiness check can be performed in linear
time.
Outline. In section 2, we present related works.
In section 3 we formally introduce attack graphs and
two-player turn-based games, show a reduction from
Catta, D., Di Stasio, A., Leneutre, J., Malvone, V. and Murano, A.
A Game Theoretic Approach to Attack Graphs.
DOI: 10.5220/0011776900003393
In Proceedings of the 15th International Conference on Agents and Artificial Intelligence (ICAART 2023) - Volume 1, pages 347-354
ISBN: 978-989-758-623-1; ISSN: 2184-433X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
347

the former to the latter. Furthermore, we show how
to represent attacker’s strategies via trees and a tree
automaton accepting all such trees, where the latter
is used to prove whether an attacker has a winning
strategy. Finally, section 4 concludes the paper and
presents some future directions.
2 RELATED WORK
Several existing works have proposed different game-
theoretic solutions for finding an optimal defense pol-
icy based on attack graphs. Most of these approaches
do not use formal verification to analyze the game,
but rather try to solve them using analytic and opti-
mization techniques. The works in (Durkota et al.,
2015a; Durkota et al., 2015b) study the problem of
hardening the security of a network by deploying hon-
eypots to the network to deceive the attacker. They
model the problem as a Stackelberg security game in
which the attack scenario is represented using attack
graphs. The authors in (Nguyen et al., 2017) tackle
the problem of allocating limited security counter-
measures to harden security based on attack scenar-
ios modeled by Bayesian attack graphs using partially
observable stochastic games. They provide heuristic
strategies for players and employ a simulation-based
methodology to evaluate them. The work in (Zhang
and Malacaria, 2021) proposes an approach to se-
lect an optimal corrective security portfolio given a
probabilistic attack graph. They define a Bayesian
Stackelberg game that they solve by converting it into
Mixed-Integer Conic Programming (MICP) optimiza-
tion problem.
The work in (Bursztein and Goubault-Larrecq,
2007) shares some ideas with our approach. However,
they use a timed-logic framework and timed games
to express and evaluate network security properties,
which result in an EXPTIME-complete procedure.
Besides the problem of attack graph generation, a
large body of works on attack graphs proposes meth-
ods to analyze them, as surveyed in (Zeng et al.,
2019). These methods can be roughly divided into
two groups: the risk assessment methods aiming at
predicting the attacker’s behavior and the risk treat-
ment methods aiming at deploying new security coun-
termeasures. The second type of methods targets a
security hardening of the system by adopting an opti-
mal security policy to improve security. Since repair-
ing all vulnerabilities may be infeasible, these meth-
ods propose to remove some appropriate vulnerabili-
ties (or deploy new security countermeasures) to min-
imize the impact of attack under a given defense cost
threshold. However, most of these works consider a
static view corresponding to a prevention approach.
A more dynamic view or reaction approach is needed
when facing attack: given an action of the attacker,
which countermeasure the defender must deploy in
priority to minimize the risk on the system. Resource
consumption in games is a well established area of
research.
The practical study on attack graphs mainly refers
to “non model-based” approaches, with few excep-
tions. (Al Ghazo et al., 2020) introduces A2g2v, a
model checker that generates attack graphs and de-
tects an attack sequence by means of a counterex-
ample. (Ritchey and Ammann, 2000) introduces a
model checker for vulnerability analysis via attack
graphs; it uses the verification tool SMV (McMil-
lan, 1993), so it can only show one attack (coun-
terexample) at the time. Differently, (Jha et al., 2002)
uses a modified version of the tool NuSMV (Cimatti
et al., 1999) to represents all possible attacks. (Ou
et al., 2006) introduces MulVAL, an attack graph
generation and network security-analyzer tool based
on logical programming; it reduces the bottleneck of
the state-explosion problem by making use explic-
itly of the logical dependencies between attack goals
and configuration information. Most of the exist-
ing attack-graph tools are brute-force forward-search
based, which is a huge limitation in practice. Con-
versely, our automata-based approach allows check-
ing convoluted security properties, including liveness
and regular behaviors (Vardi, 2011), useful to specify
service guarantees against real malicious activity.
3 ATTACK GRAPHS
The term attack graph has been first introduced by
Phillips and Swiler (Phillips and Swiler, 1998). The
general idea is to represent the possible attack paths in
a system as a graph. This graph is generated given a
description of the system architecture (topology, con-
figurations of components, etc.) together with the list
of existing vulnerabilities, the attacker’s profile (his
capability, passwords knowledge, privileges, etc.) and
attack templates (attacker’s atomic action, including
preconditions and postconditions). An attack path in
the graph corresponds to a sequence of atomic at-
tacks. Several works have developed this approach,
see e.g., (Sheyner et al., 2002; Ammann et al., 2002;
Noel et al., 2003; Ou et al., 2006; Ingols et al., 2006),
and (Kaynar, 2016) for a survey.
There is no standardized definition of an attack
graph: each of the previously cited works introduced
its own attack graph model with its specificity, in par-
ticular regarding the semantics of nodes and edges
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
348

Figure 1: An illustrating LAN architecture example.
Table 1: Atomic attacks and countermeasures over the LAN depicted in Figure 1.
Attack Location Precondition Postcondition Counter
measure
att
1
Web Server web server : root
att
2
Server web server : root server : root c
2
att
3
Workstation web server : root password : 1234
att
4
Database A server : root databaseA : root c
4
att
5
Database B server : root∧ databaseB : root c
5
password : 1234
(some works even use hypergraphs and not graphs to
have a more concise representation of attack paths).
However, all introduced models can be mapped into
a canonical attack graph as introduced in (Heberlein
et al., 2012). It is a labelled oriented graph, where:
• each node represents both the state of the system
(including existing vulnerabilities) and the state of
the attacker including constants (attacker skills, fi-
nancial resources, etc.) and variables (knowledge
of the network topology, privilege level, obtained
credentials, etc.);
• each edge represents an action of the attacker (a
scan of the network, the execution of an exploit
based on a given vulnerability, access to a device,
etc.) that changes the state of the network or the
states of the attacker; an edge is labelled with the
name of the action (several edges of the attack
graph may have the same label).
We will consider in the rest of the paper monotonic
attack graphs, i.e., acyclic graphs. Furthermore, an
attack graph is said complete whenever the following
condition holds: for every state q and for every atomic
attack att, if the preconditions of the atomic attack
hold in q, then there is an out coming edge from q
labelled with att.
We now give an example of an attack graph that
corresponds to the architecture of the illustrating sce-
nario depicted in Figure 1. Precisely, we consider
an enterprise local area network (LAN) featuring a
Server, a Workstation, and two databases Database
A and Database B. The LAN also provides a Web
Server. Accesses via Internet to the LAN are con-
trolled by a firewall.
Table 1 gathers all possible atomic attacks an at-
tacker can perform over the LAN. For instance, att
2
specifies that an attacker can exploit a vulnerability
related to the Server: as a precondition the attacker
needs to have root access to the Web Server and, as a
postcondition, he will obtain root access to the Server.
An attack graph built from this set of atomic at-
tacks and collecting possible attack paths is depicted
in Figure 2. The attacker’s initial state is a node in
the attack graph. Let us suppose that the attacker is
in state v
1
and wants to reach state v
4
. To get to this
target, he can perform the sequences of atomic attacks
att
2
,att
4
or att
3
,att
2
,att
4
.
From the defender side, we consider that she is
able to dynamically deploy a predefined set of coun-
termeasures: for instance by reconfiguring the fire-
wall filtering rules, or patching some vulnerabilities,
that is by removing one or several preconditions of an
atomic attack. A given countermeasure c will prevent
the attacker from longing a given attack att: deploy-
ing c is equivalent to removing all the edges in the
attack graph labelled with att. In real situations, due
to budget limitation or technical constraints, the set of
available countermeasures may not cover all atomic
attacks. In our previous example, as reported in the
last column of Table 1, we suppose that the defender
has at her disposal a countermeasure c
2
for attack att
2
,
c
4
for attack att
4
, and c
5
for attack att
5
, but no one for
the attacks att
1
and att
3
.
Along the paper we address attack graphs in the
context of attack/response scenarios. We assume that:
A Game Theoretic Approach to Attack Graphs
349

web server:root
v
1
v
0
web server:root
server:root
v
2
webserver:root
server:root
database A:root
v
4
webserver:root
password:123
v
3
webserver:root
password:1234
server:root
v
5
webserver:root
password:1234
server:root
database B:root
v
6
att
1
att
2
att
3
att
4
att
2
att
5
att
4
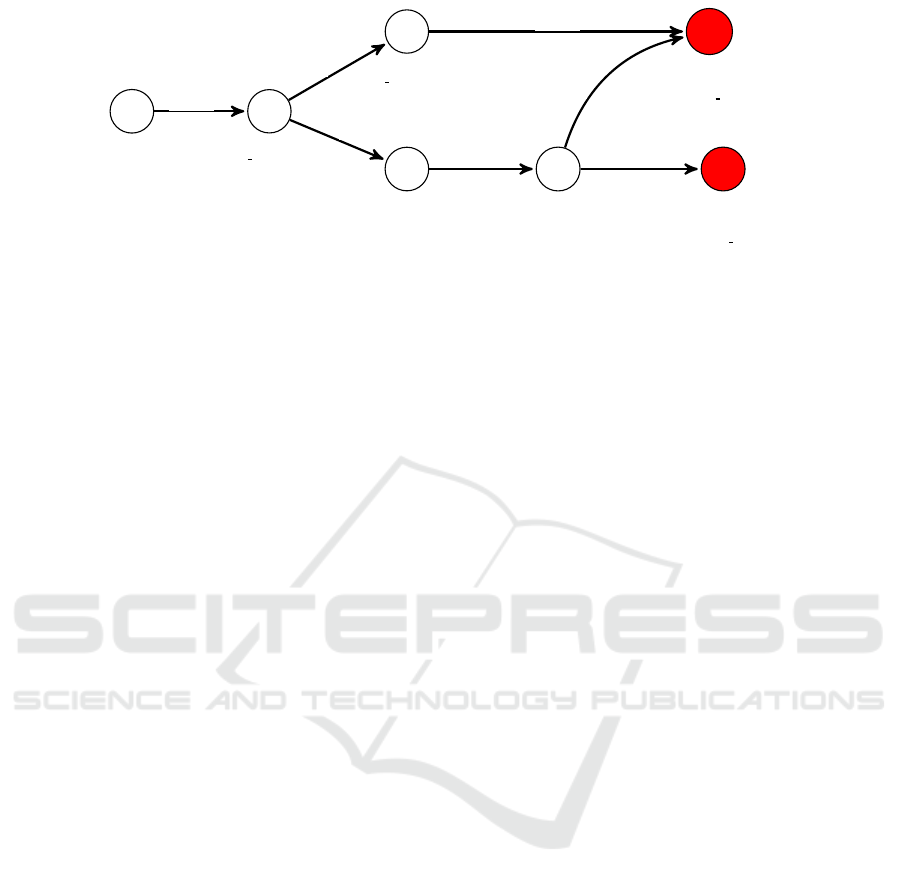
Figure 2: Example of attack graph.
1. the defender always knows the attack graph state
reached by the attacker, i.e. the defender can de-
tect an atomic attack launched by the attacker (us-
ing security supervision tools like the Intrusion
Detection System).
2. At every moment, the attacker is in a unique state
of the attack graph.
3. When the attacker launches an attack (if the pre-
conditions are satisfied and the corresponding
edge has not been removed by the defender),
then the attack always succeeds (i.e. the attacker
reaches the next state).
4. When the defender detects the attacker’s state, she
can react by deploying a unique countermeasure,
whose effect is to remove all edges in the attack
graph labelled with such a countermeasure.
5. When the defender deploys a new countermea-
sure, the attacker has the knowledge of its effect
(i.e., the attacker knows which edges have been
removed from the attack graph).
In the LAN example, a possible attacker-defender
interaction is the following: the attacker starts in state
v
0
, performs attack att
1
and reaches state v
1
; then, the
defender deploys countermeasure c
2
, so the attacker
cannot perform attack att
2
from v
1
; then, the attacker
performs attack att
3
from v
1
and reaches state v
3
; fi-
nally, since the defender deploys countermeasure c
2
,
the attacker is stopped in v
3
.
3.1 From Attack Graphs to Two-Player
Games
We now give a formal definition of attack graph and
two-player game. Then we show a model reduction
among them.
Definition 1. An attack graph is a tuple M =
hV,v
0
,E, L, Tri, where:
• V is a set of states;
• v
0
is an element of V (the initial state);
• E ⊆ V × V is a set of edges;
• L : E → N is a function that labels the elements of
E;
• Tr ⊆ V is a set of target states.
We formalize a two-player turn-based game as fol-
lows.
Definition 2. A turn-based two-player game (2TG,
for short) is a tuple G = hS,s
0
,R , Wi where:
• S = S
1
∪ S
2
is the set of states. S
1
and S
2
are two
disjoint sets of states corresponding to Player 1
and Player 2 states;
• s
0
is a member of S
1
(the initial state);
• R = R
1
∪R
2
is the transition relation, where R
1
⊆
S
1
× S
2
and R
2
⊆ S
2
× S
1
,
• W ⊆ S
2
is the set of states that are winning for
Player 1.
The size of a game G is the cardinality of S. Given
a game G, each player moves a token along the states
via the relation R , starting from the initial state, with
Player 1 moving first. If the token is in a Player 1’s
(resp., Player 2’s) state, then he can move in a sub-
set of states that belongs to Player 2 (resp., Player
1). A play ρ = ρ
0
,. .., ρ
n
over G is a finite, non-
empty, sequence of states in S such that ρ
0
= s
0
and
(ρ
i
,ρ
i+1
) ∈ R , for i ∈ {0,.. .,n − 1}. We use ρ and
π to denote plays. A play ρ = ρ
0
,. .., ρ
n
is won by
Player 1 iff ρ
n
∈ W .
A strategy for a game G is usually defined as a
function. A function that specifies, at each moment of
the game, which move a player must play according
to the moves previously played (the history of the
game). A strategy is winning when the player, who
is following the strategy, wins, whatever the strategy
of the opponent is. We choose another equivalent
definition, motivated by our approach to solve games.
We see a strategy as a tree in which each node is a
state of the game, each path from the root of the tree
to a given node is a play over the game, each play
ending in one of Player 2’s (the opponent) states s, has
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
350

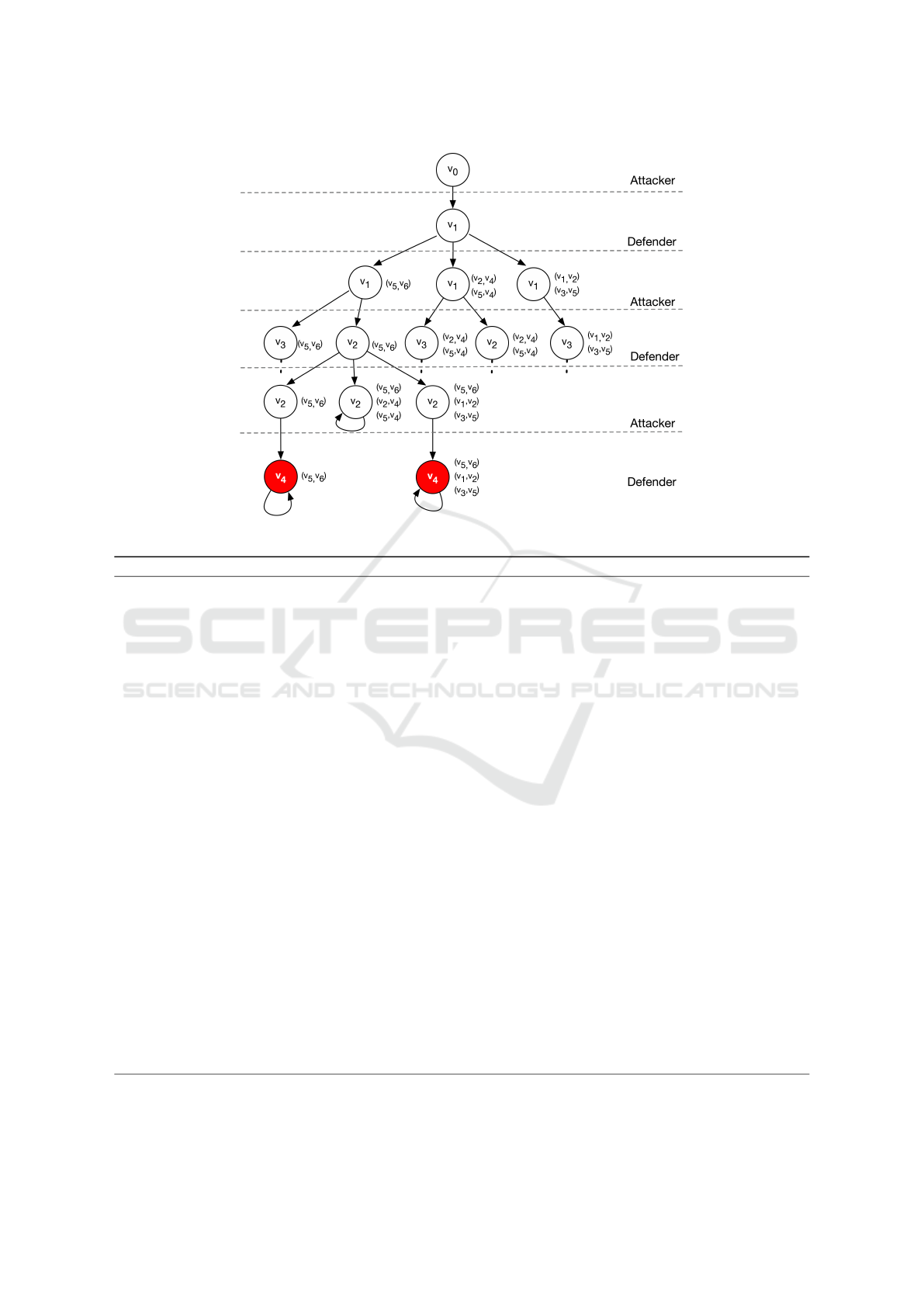
Figure 3: Part of the 2TG generated from the AT in Figure 2.
Algorithm 1: From Attack Graph to Two-Player Game.
1: procedure REDUCETOGAME(M , Act
d
)
2: token = 1  Set the turn
3: rm
v
0
= nil
4: S
1
= {(v
0
,rm
v
0
)}
5: queue = [(v
0
,rm
v
0
)]
6: while queue 6=
/
0 do
7: for i = 1 to size(queue) do
8: (v,rm
v
) = dequeue(queue)
9: if token = 1 then
10: for v
0
∈ Π
2
(E(v) \ rm
v
) do  chose a reachable state
11: enqueue(queue,(v
0
,rm
v
))
12: S
2
= S
2
∪ {(v
0
,rm
v
)}  update Player 2 states
13: R
1
= R
1
∪ {((v, rm
v
),(v
0
,rm
v
))}
14: if Π
2
(E(v) \ rm
v
) =
/
0 then
15: R
1
= R
1
∪ {((v, rm
v
),(v,rm
v
))}  Update Player 1 transitions
16: token = 2
17: else
18: for a ∈ Act
d
do
19: rm
0
v
= UPDATE(a, M )  Update the list of removed arcs
20: enqueue(queue,(v,(rm
v
∪ rm
0
v
)))
21: S
1
= S
1
∪ {(v, (rm
v
∪ rm
0
v
))}  Update Player 1 states
22: R
2
= R
2
∪ ((v, rm
v
),(v,(rm
v
∪ rm
0
v
))  Update Player 2 transitions
23: if v ∈ Tr then
24: W = W ∪ {(v , (rm
v
∪ rm
0
v
))}  Update the list of winning states
25: token = 1
26: procedure UPDATE(a,M )
27: temp =
/
0
28: for e ∈ E do
29: if L(e) = a then
30: temp = temp ∪ {e}
31: return (temp)
A Game Theoretic Approach to Attack Graphs
351

as many children as there are available R
2
-reachable
state from s and each play ending in one of Player 1’s
(the proponent) state has at most one child. Recall
that a tree is a (finite or infinite) connected directed
graph, with one node designated as the root, in which
every non-root node as a unique parent, and the root
has no parent (s is the parent of t, and t is the child of
s if there is an edge from s to t). A path P = x
0
,x
1
,. ..
is a (finite or infinite) sequence of nodes such that x
i
is the parent of x
i+1
for all i ≥ 0. A branch is a path
that is maximal and whose first node is the root of the
tree.
Definition 3. An attacker strategy σ for a game G =
hS,s
0
,R , Wi is a finite tree whose root is s
0
, whose
branches are plays over G and that satisfy the follow-
ing properties:
1. For each node s of σ: if s ∈ S
1
then s has at most
one child;
2. For each node s of σ: if s ∈ S
2
and s /∈ W then s
has as many child as there are nodes s
0
such that
(s,s
0
) ∈ R
2
.
An attacker strategy σ is winning whenever each
leaf of the strategy belongs to W .
Let M = hV,v
0
,E, L, Tri be an attack graph, we
denote by Act
d
the set of actions of the defender in
M . If v ∈ V we define E(v) = {(v,v
0
) ∈ E}. If e =
(v,v
0
) ∈ E , π
i
(e) for i ∈ {1,2} denote the i-projection
of e. If E
0
⊆ E is a set of edges Π
i
(E
0
) = {v ∈ V | v =
π
i
(e) for e ∈ E
0
}. We let nil denote the empty list.
Now, we have all the ingredients to present our
reduction. In Algorithm 1 we devise a procedure to
reduce an attack graph M to a two-player turn-based
game G in which the attacker is represented by Player
1 and the defender by Player 2. The algorithm pro-
ceeds as follows. For every state of G the proce-
dure keeps track of the edges disabled by the defender
along the path from the initial state to the current one.
In detail, we initialize a token that determines the turn
(line 2), a list to handle the edges disabled by the de-
fender in the initial state (line 3), the set of states in
G (line 4), and a queue to keep track of the states that
have not yet been explored (line 5). Then, there is a
loop (lines 6-25) that is divided in two different part
w.r.t. the token value. If token = 1, i.e., it is the turn
of the attacker, then given the state (v,rm
v
) from the
queue (line 8), for each state v
0
in accordance with
the adjacent states of v that are not disabled by the
defender, we add a new state in S
2
, a new transition,
and add it in the queue (lines 9-15). Otherwise, if it is
the defender’s turn, we analyze each possible action
for the defender (defined with the set Act
d
) and create
a new state in S
1
, the correspondent transition, add it
in the queue, and check whether it is a final state in
the attack graph (lines 18-24). In this second case, we
use an auxiliary procedure called UPDATE, to update
the list rm
v
0
(line 19) by adding edges in accordance
with the action a of the defender (lines 28-30).
Note that, for every state v, we associate a list of
removed edges rm
v
to memorize the actions selected
by the defender along the current computation from
the initial state. To conclude, since the attack graph is
monotonic, i.e. it is acyclic, it is easy to see that the
algorithm terminates.
Figure 3 shows an application of Algorithm 1 for
the attack graph depicted in Figure 2 by considering
Act
d
= {c
2
,c
4
,c
5
} and initial state for the attacker v
0
.
3.2 Automata-Based Approach for
Solving 2TG
We now present a top-down automata-theoretic ap-
proach to solve our game. According to definition 3,
a strategy for the attacker is a tree that takes for each
node corresponding to a state s in the game, one suc-
cessor if s belongs to the attacker, or all successors,
otherwise. If a strategy is winning, all the leaves of
this tree are target states of G, then surely the attacker
has a winning strategy over the game.
Now, we define the automaton that accepts all the
trees that are winning strategies for the attacker.
Definition 4. A nondeterministic tree automaton
(NTA, for short) is a tuple A = hQ,Σ, q
0
,δ, Fi, where:
Q is a set of states, q
0
∈ Q is an initial state, δ :
Q × Σ → 2
Q
is a transition function mapping pairs
of states and symbols to a set of tuples of states, and
F ⊆ Q is a set of the accepting states.
A NTA A recognizes trees and works as follows.
For a node tree labelled by a and A being in a state
q, it sends different copies of itself to successors in
accordance with δ. By L(A) we denote the set of trees
accepted by A. The automaton is not empty if L(A) 6=
/
0. We now give the main result of this section.
Theorem 1. Given a 2TG G it is possible to decide
in linear time w.r.t the size of G whether the attacker
has a winning strategy over G.
Proof. We build a NTA A that accepts all the winning
strategies for the attacker over G. We briefly describe
the automaton. The set of states Q is the set of states S
of the game. We use the alphabet Σ = S. For the initial
state, we set q
0
= s
0
. For the transitions, starting from
a state q = s, we have the following cases:
δ(q,a) =





(s
0
1
) ∨ ·· · ∨ (s
0
n
) if s ∈ S
1
and q = a
(s
0
1
,. .., s
0
n
) if s ∈ S
2
and q = a
/
0 otherwise
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
352

where s
0
i
∈ S and (s,s
0
i
) ∈ R , for all 1 ≤ i ≤ n. Note
that, n = |{s
0
∈ S | (s,s
0
) ∈ R }|. Finally, the set of ac-
cepting states is equal to W . The size of the automaton
is linear in the size of the game, and from (Thomas,
1990) we know that checking the emptiness of a NTA
can be done in linear time. So, the desired complexity
result follows.
4 CONCLUSION
In this paper, we restated the attack graph frame-
work by means of a two-player turn-based game, de-
fender vs attacker: the defender deactivates resource
accesses while the attacker chooses adjacent states
along which to move. We provided an automata so-
lution to the game, which amounts to show that the
defender can always prevent the attacker to enter for-
bidden states. Since the automata solution requires
linear-time, we justify the introduction of an ad-hoc
game model instead of using more expensive exist-
ing frameworks (L
¨
oding and Rohde, 2003; Kupfer-
man et al., 2001; Alur et al., 2002).
We plan to continue the work in a number of di-
rections. First, we want to extend our procedure to
attack graphs with cycles. Second, we aim to add
weights that represent the resources available for the
attacker and the defender. Furthermore, we want to
investigate more complex situations, involving multi-
ple attackers. In this setting, we also plan to exploit
resilient solutions with the aim of reducing a damage
when an attack cannot be stopped.
Finally, we can consider to study formal logics to
gain expressive power to define the attackers’ objec-
tives and check more intricate solution concepts. On
this respect, an approach to Sabotage Logic (van Ben-
them, 2005) is proposed in (Catta et al., 2022). Fol-
lowing this line, we can study logics for the strategic
reasoning such as ATL (Alur et al., 2002) and Strategy
Logic (Mogavero et al., 2014) to capture the features
on attackers vs. defenders games. Furthermore, in
this context, we can also study if an attacker has some
backup strategies to achieve his objectives by follow-
ing the line on graded modalities as done in (Faella
et al., 2010; Aminof et al., 2018). However, the more
realistic setting for games is with imperfect informa-
tion, but unfortunately, the model checking problem
with imperfect information for strategic logics is un-
decidable in general (Dima and Tiplea, 2011). Given
the relevance of this setting, even partial solutions to
the problem can be useful, such as abstractions either
on the information (Belardinelli et al., 2019; Belar-
dinelli and Malvone, 2019) or on the strategies (Be-
lardinelli et al., 2022) or on the formulas (Ferrano
and Malvone, 2022). In conclusion, we can embed
the mentioned techniques to provide a more powerful
framework.
To the best of our knowledge, this is the first
work providing a game-theoretic approach with an
automata solution to attack graphs. We hope that this
will serve as a fertilization for new solutions to chal-
lenging question in attack graphs.
REFERENCES
Al Ghazo, A. T., Ibrahim, M., Ren, H., and Kumar, R.
(2020). A2g2v: Automatic attack graph generation
and visualization and its applications to computer and
scada networks. IEEE TSMCS, 50(10):3488–3498.
Alur, R., Henzinger, T., and Kupferman, O. (2002).
Alternating-Time Temporal Logic. JACM, 49(5):672–
713.
B. Aminof, V. Malvone, A. Murano, and S. Rubin (2018).
Graded modalities in strategy logic. Inf. Comput.,
261:634–649.
Ammann, P., Wijesekera, D., and Kaushik, S. (2002). Scal-
able, graph-based network vulnerability analysis. In
CCS 2002, page 217–224.
F. Belardinelli, A. Lomuscio, and V. Malvone (2019). An
abstraction-based method for verifying strategic prop-
erties in multi-agent systems with imperfect informa-
tion. In AAAI 2019, pages 6030–6037.
F. Belardinelli, A. Lomuscio, V. Malvone, and E. Yu (2022).
Approximating perfect recall when model checking
strategic abilities: Theory and applications. J. Artif.
Intell. Res., 73:897–932.
F. Belardinelli and V. Malvone (2020). A three-valued ap-
proach to strategic abilities under imperfect informa-
tion. In KR 2020, pages 89–98.
Bursztein, E. and Goubault-Larrecq, J. (2007). A logical
framework for evaluating network resilience against
faults and attacks. In ASIAN 2007, pages 212–227.
D. Catta, J. Leneutre, and V. Malvone (2022). Subset sabo-
tage games & attack graphs. In WOA, pages 209–218.
Cimatti, A., Clarke, E., Giunchiglia, F., and Roveri, M.
(1999). Nusmv: A new symbolic model verifier. In
CAV 2009, pages 495–499.
Clarke, E. and Emerson, E. (1981). Design and Synthesis
of Synchronization Skeletons Using Branching-Time
Temporal Logic. In LP 1981, pages 52–71.
Clarke, E. M., Grumberg, O., and Peled, D. A. (1999).
Model Checking. The MIT Press, Massachusetts.
C. Dima and F. Tiplea (2011). Model-checking ATL under
imperfect information and perfect recall semantics is
undecidable. CoRR, abs/1102.4225, 2011.
Durkota, K., Lis
´
y, V., Bosansk
´
y, B., and Kiekintveld,
C. (2015a). Approximate solutions for attack graph
games with imperfect information. In GameSec 2015,
pages 228–249.
A Game Theoretic Approach to Attack Graphs
353

Durkota, K., Lisy, V., Bo
ˇ
sansky, B., and Kiekintveld, C.
(2015b). Optimal network security hardening using
attack graph games. In IJCAI 2015, pages 526–532.
M. Faella, M. Napoli, and M. Parente (2010). Graded
alternating-time temporal logic. Fundam. Informati-
cae, 105(1-2):189–210, 2010.
A. Ferrando and V. Malvone (2022). Towards the combi-
nation of model checking and runtime verification on
multi-agent systems. In PAAMS 2022, pages 140–
152.
Heberlein, T., Bishop, M., Ceesay, E., Danforth, M.,
Senthilkumar, C., and Stallard, T. (2012). A taxon-
omy for comparing attack-graph approaches. [Online]
http://netsq. com/Documents/AttackGraphPaper. pdf.
Homer, J., Zhang, S., Ou, X., Schmidt, D., Du, Y., Ra-
jagopalan, S. R., and Singhal, A. (2013). Aggregat-
ing vulnerability metrics in enterprise networks using
attack graphs. J. Comput. Secur., 21(4):561–597.
Ingols, K., Lippmann, R., and Piwowarski, K. (2006). Prac-
tical attack graph generation for network defense. In
ACSAC 2006, pages 121–130.
Jamroga, W. and Murano, A. (2015). Module checking of
strategic ability. In AAMAS 2015, pages 227–235.
Jennings, N. R. and Wooldridge, M. (1998). Application of
intelligent agents. In Agent Technology: Foundations,
Applications, and Markets. Springer-Verlag.
Jha, S., Sheyner, O., and Wing, J. (2002). Two formal anal-
yses of attack graphs. In CSFW-15, pages 49–63.
Kaynar, K. (2016). A taxonomy for attack graph generation
and usage in network security. J. Inf. Secur. Appl.,
29(C):27–56.
Kupferman, O., Vardi, M., and Wolper, P. (2000). An Au-
tomata Theoretic Approach to Branching-Time Mod-
elChecking. Journal of the ACM, 47(2):312–360.
Kupferman, O., Vardi, M., and Wolper, P. (2001).
Module Checking. Information and Computation,
164(2):322–344.
Lippmann, R. P. and Ingols, K. W. (2005). An annotated
review of past papers on attack graphs.
L
¨
oding, C. and Rohde, P. (2003). Solving the sabotage
game is pspace-hard. In MFCS 2003, pages 531–540.
Lomuscio, A., Qu, H., and Raimondi, F. (2009). MCMAS:
A model checker for the verification of multi-agent
systems. In CAV 2009, pages 682–688.
McMillan, K. L. (1993). Symbolic model checking. In
Symbolic Model Checking, pages 25–60.
Mogavero, F., Murano, A., Perelli, G., and Vardi, M. Y.
(2014). Reasoning about strategies: On the model-
checking problem. ACM Transactions in Computa-
tional Logic, 15(4):34:1–34:47.
Nguyen, T. H., Wright, M., Wellman, M. P., and Baveja,
S. (2017). Multi-stage attack graph security games:
Heuristic strategies, with empirical game-theoretic
analysis. MTD 2017, pages 87–97.
Noel, S., Jajodia, S., O’Berry, B., and Jacobs, M. (2003).
Efficient minimum-cost network hardening via exploit
dependency graphs. In ACSAC 2003, page 86.
Ou, X., Boyer, W. F., and McQueen, M. A. (2006). A
scalable approach to attack graph generation. In CCS
2006, pages 336–345.
Phillips, C. and Swiler, L. P. (1998). A graph-based system
for network-vulnerability analysis. In NSPW 1998,
pages 71–79.
Ritchey, R. W. and Ammann, P. (2000). Using model check-
ing to analyze network vulnerabilities. In S&P 2000,
pages 156–165.
Sheyner, O., Haines, J., Jha, S., Lippmann, R., and Wing, J.
(2002). Automated generation and analysis of attack
graphs. pages 273– 284.
Thomas, W. (1990). Automata on Infinite Objects. In Hand-
book of Theoretical Computer Science (vol. B), pages
133–191. MIT Press.
J. van Benthem (2005). An Essay on Sabotage and Obstruc-
tion. In MMR, pages 268–276.
Vardi, M. Y. (2011). The rise and fall of LTL. In Gandalf,
54.
Zeng, J., Wu, S., Chen, Y., Zeng, R., Wu, C., and Caballero-
Gil, P. (2019). Survey of attack graph analysis meth-
ods from the perspective of data and knowledge pro-
cessing. SCN.
Zhang, Y. and Malacaria, P. (2021). Bayesian stackel-
berg games for cyber-security decision support. Decis.
Support Syst., 148:113599.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
354