Multi-Objective Task Assignment Solution for Parked Vehicular

Computing

Jia He Sun, Salimur Choudhury and Kai Salomaa

School of Computing, Queen’s University, 99 University Ave, Kingston, Canada

Keywords:

Task Assignment, Smart Vehicles, Heuristics, Stable Matching, Multi-Access Edge Computing.

Abstract:

With signiﬁcant advances in recent technology, computational power must meet new demands. As a result,

Multi-access Edge Computing (MEC) is a new networking paradigm that has received a surge in interest from

both academia and industry. MEC aims to push powerful computing and storage capabilities from remote

cloud servers to up-close edge servers. Vehicular Edge Computing (VEC), a subﬁeld of MEC, has been intro-

duced to speciﬁcally increase the computing capacity of vehicular networks, an essential component for the

development of Intelligent Transportation Systems (ITS). A problem in the current development of VEC is the

high cost of installing enough edge servers to compute all ofﬂoaded tasks at peak hours. However, we have

observed that parked vehicles (PVs) are a rich reserve of underutilized computing resources, and their incor-

poration into the VEC network could lead to a solution to the aforementioned problem. This paper proposes

a task ofﬂoading system with an assumed parking time estimation mechanism. Then, a novel formulation of

the task ofﬂoading problem is presented that minimizes both task delay and wireless channel load. Finally, a

matching based heuristic is proposed and evaluated at various conﬁgurations of the VEC environment.

1 INTRODUCTION

Cloud computing is at the forefront of computing

paradigms by centralizing main computing and stor-

age capabilities in a remote location that is accessible

to all (Raza et al., 2019). However, with the vision

of the Internet of Things (IoT), we have realized that

the remote network system is simply not enough to

satisfy the intensive computational needs of the fu-

ture that we envision (Guo et al., 2018) (Mao et al.,

2017). Thus, MEC has been pushed forward as a

replacement system since it provides high computa-

tional power closer to users, thereby reducing latency

(Wang et al., 2017) (Wang et al., 2016). This is es-

pecially important in vehicles as the vehicular envi-

ronment requires incredibly low latency due to its dy-

namic nature (De Souza et al., 2020). Furthermore,

since it is ﬁnancially infeasible to mass install ex-

pensive computing hardware into every vehicle, edge

computing has become the foremost solution in ve-

hicular networks (Liu et al., 2021).

Vehicular Edge Computing (VEC) aims to use

roadside edge servers to augment the computing ca-

pacity of vehicular environments (Meneguette et al.,

2021). Under this framework, smart vehicles can reli-

ably ofﬂoad their computational tasks, alleviating the

heavy burden placed on the vehicles’ internal hard-

ware (Qiao et al., 2018) (Du et al., 2018). There are

three layers included in this model: the Cloud layer

(cloud computing servers), the MEC layer (RSU or

roadside units), and the User layer (vehicle devices).

The key advantages of VEC over Vehicular Cloud

Computing (VCC) are: low latency, mobility support,

real-time communication, heterogeneous device sup-

port, and lower cost of development. Although it is

not without drawbacks: limited capacity and lower

computing capability (Raza et al., 2019).

A current problem in VEC is the high cost of

installing enough edge servers to compute all of-

ﬂoaded tasks at peak hours (Raza et al., 2019). How-

ever, researchers have observed that parked vehicles

(PVs) are a rich reserve of underutilized computing

resources (Arif et al., 2012). Thus, their incorpora-

tion into the VEC network could lead to a solution to

the aforementioned problem. Research in this area is

called Parked Vehicular Computing (PVC).

However, there exist some challenges that should

be addressed to facilitate PVC. Firstly, scheduling

computational tasks on participating PVs poses an in-

teresting challenge (Zhang et al., 2019). PVs have

an inherent problem in that they may leave unexpect-

edly, perhaps in the middle of a task, which results

Sun, J., Choudhury, S. and Salomaa, K.

Multi-Objective Task Assignment Solution for Parked Vehicular Computing.

DOI: 10.5220/0011783100003396

In Proceedings of the 12th International Conference on Operations Research and Enterprise Systems (ICORES 2023), pages 193-202

ISBN: 978-989-758-627-9; ISSN: 2184-4372

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

193

in the system having to ofﬂoad the interrupted task

elsewhere, delaying it further. Secondly, the VEC

network mainly communicates over wireless channels

and the overuse of such channels would cause an over-

load, thereby decreasing the quality of existing com-

munications (Whaiduzzaman et al., 2014). There are

also security and privacy challenges, but these lie out-

side the scope of this paper (Ma et al., 2018) (Wei

et al., 2018) (Kang et al., 2017) (Huang et al., 2011).

Huang et al. (Huang et al., 2018) designed an

interactive protocol with basic request and response

operations for service provision in PVC. Then, they

solve the resource scheduling optimization problem

using a Stackelberg game approach. Ge et al. (Ge

et al., 2020) proposed an efﬁcient SEA algorithm to

solve the vehicle selection and task assignment prob-

lem regarding service migration, namely, the transfer

of tasks between base stations.

Wang et al. (Wang et al., 2019) implemented a

system-level simulator of LTE Sidelink C-V2X Com-

munication for 5G. This simulation showed that the

volume of data severely increased as the number of

users in the network increased. The packet reception

ratio (PRR) also drastically decreased as the network

size grew, reaching as low as 80.36% in a 1,920 user

setting. As VEC is expected to be implemented on

scales much larger than that, it is essential to maintain

the quality of communication in these settings.

However, there are currently very few works that

address the potential issues of large-scale implemen-

tation, speciﬁcally in terms of wireless communica-

tions. The current paradigm for wireless communi-

cation in vehicular networks is C-V2X, which has

strict requirements on Quality of Service (QoS) such

as high reliability and low latency (Lianghai et al.,

2018). Therefore, it is necessary for VEC networks to

not only provide reliable high-speed service but also

to maintain the quality of the communication chan-

nels used.

In this paper, we propose a many-to-one stable

matching algorithm to assign tasks to vehicles in such

a way that not only minimizes task delay but also

maintains the quality of the wireless communication

channels. Stable matching is chosen since we are fac-

ing a multi-objective problem. Stable matching al-

lows both the set of vehicles and the set of tasks to

have preference rankings over the other set which can

accurately represent both objectives of the problem.

The main contributions of this paper are summa-

rized as follows:

• To reﬂect the multifaceted problem of task assign-

ment within a VEC environment, we propose a

novel formulation that includes a weighted multi-

objective that aims to minimize both task delay

and wireless channel load. We then prove the NP-

completeness of the problem.

• We propose a many-to-one stable matching based

heuristic to efﬁciently assign tasks to vehicles.

• We evaluate and conﬁrm the performance of the

proposed heuristic through various simulations.

The work done in this paper is included as part of Jia

He Sun’s master thesis with Queen’s University (Sun,

2022).

2 SYSTEM MODEL

We consider one cell which has one BS, M users, and

N PVs with available computing resources. During

high usage hours, the BS will be overloaded and un-

able to complete all of the tasks ofﬂoaded to it by

the users. Then, it will have to ofﬂoad K tasks to

nearby PVs. The time-slot model is adopted where

the set of tasks and PVs remain ﬁxed within each time

slot while varying across different slots. Therefore, in

each time slot we have deﬁned the following variables

(it is assumed that this information will be available to

the scheduling system):

• N = number of vehicles

• K = number of tasks

• p

= computational power offered by vehicle i

• t

= parking time estimation of vehicle i (the as-

sumption of having knowledge of this variable

will be discussed)

• w

= computational power required for task j

• l

= task completion speed of task j if assigned to

vehicle i

To summarize the system model, the task assignment

problem can be described as assigning K tasks to N

vehicles where each task is assigned to only one ve-

hicle, each vehicle can be assigned multiple tasks but

cannot exceed their computational capacity, assigned

tasks’ computation time should not exceed their vehi-

cle’s estimated parking time.

2.1 Problem Formulation

Now, we will formulate the task assignment problem

as a weighted multi-objective ILP.

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

194

minimize

x, y

∑

j=1

∑

i=1

+ β

∑

i=1

(1a)

subject to

∑

i=1

= 1, j = 1, . . . , K, (1b)

∑

j=1

≤ p

,i = 1, . . . , N, (1c)

∑

j=1

≤ t

, i = 1, . . . , N, (1d)

∈ {0, 1} i = 1, . . . , N, (1e)

∈ {0, 1} j = 1, . . . , K, i = . . . , N (1f)

2.1.1 Variables

The two variables in the formulated ILP are:

• x

= 1 if task j is assigned to vehicle i and 0 oth-

erwise

• y

= 1 if vehicle i is assigned at least one task and

0 otherwise

2.1.2 Constraints

The constraints can be summarized as follows:

• (2b): each task is assigned to only one vehicle.

• (2c): the assigned tasks cannot go over vehicle’s

max load.

• (2d): the task for each vehicle must be able to ﬁn-

ish before the vehicle leaves.

• (2e): y

= 1 if vehicle i is assigned a task and 0

otherwise (integrality constraint).

• (2f): x

= 1 if task j is assigned to vehicle i and 0

otherwise (integrality constraint).

2.1.3 Objective

Firstly, α and β are constant objective weights. Their

values decide which which objective should be priori-

tized. The ﬁrst objective is to minimize the task com-

pletion time which is crucial in a VEC task assign-

ment environment. The task completion time consists

of two parts: computation time, and transmission time

(both ways). For a particular task, its computation

time, l

comp

, depends on the vehicle it is assigned to,

so l

comp

is the amount of time it takes vehicle i to com-

pute task j. For the transmission time of a task, l

trans

it depends on the transmission power of the BS. Then,

total task completion speed is the computation time

plus the transmission time as shown in Equation 2.

= l

comp

+ l

trans

(2)

The second objective is the number of vehicles

used for task assignment. This is because the deploy-

ment of tasks and any other form of information be-

tween the VEC base station and the parked vehicles

will be done through wireless channels which are lim-

ited in size. To maintain the quality of communication

on these wireless channels, especially in highly popu-

lated metropolitan areas, the number of vehicles used

is also minimized.

Theorem 1. (NP-Complete) The formulated ILP is

NP-Complete.

Proof. Consider the corresponding decision ver-

sion of this problem. That is, given M, is there a task

assignment that is within the deﬁned constraints that

has an objective value ≤ M? Certiﬁcate: A certiﬁ-

cate would be an assignment of tasks to the vehicles

denoted by the (K, N) matrix x where x

= 1 if task

j is assigned to vehicle i and 0 otherwise. To ver-

ify this certiﬁcate, we would need to check that the

assignment satisﬁes each constraint and calculate the

objective value, that is:

1. First obtain vector y from x where y

= 1 if vehicle

i has a task and 0 otherwise

2. Verify each task is assigned to only 1 vehicle

3. Verify assigned tasks do not go over vehicle’s max

load

4. Verify the assigned tasks ﬁnish before the vehicle

has to leave

This would take O(NK) time, which means verifying

a solution is polynomial. We will now show that bin

packing reduces to the formulated ILP (Cook et al.,

1995). First set the objective weights α = 0 and β = 1.

Then, set all p

= B, where B can be any constant.

Then set all l

and t

= 0. Then the optimization prob-

lem becomes:

minimize

x, y

∑

i=1

(3a)

subject to

∑

i=1

= 1, j = 1, . . . , K, (3b)

∑

j=1

≤ By

,i = 1, . . . , N, (3c)

∈ {0, 1} i = 1, . . . , N, (3d)

∈ {0, 1} j = 1, . . . , K, i = . . . , N (3e)

Notice that this is an exact formulation of the bin

packing problem where w

is the size of item j and

Multi-Objective Task Assignment Solution for Parked Vehicular Computing

195

B is the capacity of each bin. The decision bin pack-

ing problem is known to be NP-complete. Thus, the

decision version of our optimization problem is NP-

complete. Therefore, our optimization problem is

NP-complete.

3 PROPOSED SOLUTION

The heuristic proposed is a stable matching based

algorithm. The algorithm it is based on has sev-

eral names including: “Extended Gale-Shapley al-

gorithm”, “the Capacitated Gale-Shapley algorithm”,

“the Roth-Shapley algorithm”, and “the deferred ac-

ceptance algorithm”. Following, it will be referred

to as the RS algorithm (Roth, 2008). The proposed

heuristic is a version of the RS algorithm that is modi-

ﬁed to ﬁt the dynamic nature of the PVC environment.

The assignment of tasks to vehicles can be described

as a many-to-one matching.

Deﬁnition 1 (Matching). A matching A is a mapping

from the set of tasks T to the set of vehicles V , T → V ,

which satisﬁes all of the following:

• for any task j ∈ T , |A( j)| ≤ 1

• for any task j ∈ T , and any vehicle i ∈ V , A( j) = i

if and only if j ∈ A(i)

The proposed algorithm requires both sets V and T to

have preference rankings over each other. That is, for

all i ∈ V , i must have a preference ranking including

all j ∈ T and vice versa.

Deﬁnition 2 (Preference Ranking). For any vehicle

i ∈ V , its preference ranking is a list L including all

tasks in T . If task j ∈ T comes before task j

∈ T in

L, we say that vehicle i prefers task j to task j

. For

tasks in T , their preference rankings are deﬁned vice

versa.

How these rankings are to be computed are dis-

cussed later in this section. Next, we will deﬁne a

stable matching, but ﬁrst we will deﬁne two types of

blocking pairs.

Deﬁnition 3 (Type 1 Blocking Pair). Given a match-

ing A, ( j, i) ∈ (T,V ) forms a type 1 blocking pair if

all of the following conditions hold:

• task j prefers vehicle i over A( j)

• there exists task k with vehicle i ∈ A(k) such that

vehicle i prefers task j to task k and the removal of

task k allows the assignment of task k onto vehicle

The existence of a type 1 blocking pair ( j, i) ∈ (T,V )

in a given matching A is unstable since it means that

task j can be assigned to a more preferred vehicle and

vehicle i can be assigned a more preferred task at the

cost of a less preferred task. Apart from the type 1

blocking pair, there is also the type 2 blocking pair.

Deﬁnition 4 (Type 2 Blocking Pair). Given a match-

ing A, ( j, i) ∈ (T,V ) forms a type 2 blocking pair if

all of the following conditions hold:

• task j prefers vehicle i over A( j)

• vehicle i has enough resources to be assigned task

The existence of a type 2 blocking pair ( j, i) ∈ (T,V )

in a given matching A is unstable since vehicle i is

wasteful by not making full use of its resources.

Deﬁnition 5 (Stable Matching). Given a matching A,

A is a stable matching if and only if there are no type

1 or type 2 blocking pairs.

3.1 Algorithm Design

A key characteristic of the RS algorithm is the pref-

erence ranking made by both parties. Since the pref-

erence ranking by either party is made independent

of the other, they can be made to represent different

objectives which is a desired trait in multi-objective

problems such as the one discussed in this paper. The

crux of the RS algorithm is how the preference rank-

ings are formulated. For the algorithm to be effective,

the preference rankings must be a good reﬂection of

the optimization objectives.

• Preference ranking for tasks: prefer vehicles with

the most tasks, tie breaks between vehicles by

which vehicle completes said task faster. Task

j prefers vehicle n over vehicle k if

∑

i=1

∑

i=1

• Preference ranking for vehicles: prefer tasks that

complete the fastest on said vehicle. Vehicle i

prefers task a over task b if l

< l

The preference ranking for tasks aims to primarily

minimize the number of vehicles used which de-

creases the load on the wireless channels. The prefer-

ence ranking for vehicles aims to primarily minimize

the task completion speed. Together, these two pref-

erence mechanics accurately represent the two objec-

tives of the ILP formulated in the previous section.

Consider another matching algorithm, bipartite

matching, where the optimization objective is repre-

sented only by edge weights. It is extremely difﬁcult

to formulate an accurate representation of both objec-

tives when conﬁned to a single form. In our case, it is

especially difﬁcult to represent the second objective,

number of vehicles used, in such a way since it means

we are minimizing the number of nodes covered in a

bipartite matching. Hence, we can easily observe the

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

196

motivation behind designing a heuristic based on the

RS algorithm.

The proposed algorithm based on the RS algo-

rithm is deployed to produce a stable matching. The

proposed algorithm runs as follows: (The pseudocode

is given in Algorithm 1):

1. Put all tasks into a list called unmatched. Go to 2.

2. Update preference rankings for vehicles. Go to 3.

3. Update preference ranking for tasks. Take any

task in unmatched, j, and go to 4. If none, end

algorithm.

4. Consider task j’s most preferred vehicle, i. Go to

5. If task j has no preferred vehicle remaining,

remove task j from unmatched list and go to 3.

5. If vehicle i can accommodate task j (has enough

computational power and time). Match task j to

vehicle i and go to 3. If vehicle i does not have

enough time remaining, remove vehicle i from

task j’s preferences and go to 4. If vehicle i does

not have enough computational power, go to 6.

6. Consider all vehicle i’s currently matched tasks.

Then of these tasks, consider the set of tasks that

vehicle i prefers less than task j, call it U. Iter-

ate through U from least preferred to most pre-

ferred. If unmatching task k allows vehicle i to

have enough resources to be assigned task j, then

unmatch task k and match task j. Then remove ve-

hicle i from task k’s preference ranking and go to

3. If not, then remove vehicle i from task j’s pref-

erence and consider task j’s next most preferred

vehicle and go to 5.

3.2 Algorithm Analysis

First, we will analyze the output of the algorithm.

Lemma 2 (No Type 1 Blocking Pairs). The proposed

algorithm produces a matching A that has no type 1

blocking pairs.

Proof. Suppose for contradiction that produced

matching A has type 1 blocking pair ( j, i) ∈ (T,V ).

Then, consider the point in the algorithm at which

task j was assigned to vehicle l = A( j). Since task

j prefers vehicle i over vehicle l, that is

∑

i=1

∑

i=1

, vehicle i must have been considered before

vehicle l. Then, vehicle i must have rejected task j at

this point which means for all tasks k with A(k) = i

either of the following is true: no tasks who is as-

signed to vehicle i is less preferred than task j, or

+ w

< w

. Then vehicle i would have been re-

moved from task j’s preferences. This contradicts the

assumption that task j prefers vehicle l over vehicle

i. Therefore, the matching A cannot have a type 1

blocking pair ( j, i) ∈ (T,V ).

Algorithm 1: Pseudocode of the proposed RS Based

Heuristic.

Require: preference ranking for both vehicles and

tasks

1: while there are unmatched tasks do

2: for any unmatched task j do

3: update preference ranking of each task

4: i ⇐ task j’s most preferred vehicle

5: if p

≥ w

then

6: assign task j to vehicle i

7: break

8: end if

9: if l

> t

then

10: remove vehicle i from task j’s prefer-

ences

11: break

12: end if

13: if p

> w

then

14: U ⇐ tasks currently matched to vehi-

cle i that is less preferred

15: than task j in order from least pre-

ferred to most preferred

16: for task k ∈ U do

17: if unmatching task k allows as-

signment of task j then

18: unmatch task k and assign task

j to vehicle i

19: remove vehicle i from task k’s

preference ranking

20: break

21: end if

22: end for

23: remove vehicle i from task j’s prefer-

ence ranking

24: end if

25: end for

26: end while

Lemma 3 (No Type 2 Blocking Pairs). The proposed

algorithm produces a matching A that has no type 2

blocking pairs.

Proof. Suppose for contradiction that produced

matching A has type 2 blocking pair ( j, i) ∈ (T,V ).

Then, consider the point in the algorithm at which

task j was assigned to vehicle l = A( j). Since task

j prefers vehicle i over vehicle l, that is

∑

i=1

∑

i=1

, vehicle i must have been considered before

vehicle l. Then, it must be that vehicle i rejected task

j which means p

< c

or t

< l

. Then vehicle i would

have been removed from task j’s preferences which is

a contradiction to the assumption of the existence of

Multi-Objective Task Assignment Solution for Parked Vehicular Computing

197

Table 1: Experiment Variables.

Variables Experiment Settings

random between 20-25

random between 15-30

random between 4-5

random between 1-20

type 2 blocking pair ( j, i).

Theorem 4 (Stable Matching). The proposed algo-

rithm produces a stable matching A.

Proof. According to Lemma 1 and Lemma 2, there

are type 1 or type 2 blocking pairs in the produced

matching A. Therefore, the produced matching is sta-

ble.

Now, we will analyze the termination condition

and the complexity of the proposed algorithm.

Theorem 5 (Termination). The proposed algorithm

terminates after at most NK iterations.

Proof. First, notice that in each iteration of the al-

gorithm, a task is either matched to a vehicle (may be

after the unmatching of another task) or is removed

from the algorithm. That is to say, the number of

unmatched tasks never decreases in any iteration of

the algorithm. Then, for an inﬁnite loop to exist,

there must be an inﬁnite number of times where a

task is unmatched from a vehicle. However, when-

ever a task is unmatched from a vehicle, it is removed

from the vehicle’s preference ranking. That is, the

removed task will never be assigned to the vehicle it

was once unmatched with. Therefore, there can be at

most NK number of unmatchings and thus, an inﬁnite

loop is impossible and the algorithm is guaranteed to

terminate. Furthermore, for any given iteration, for

unmatchings to occur, some task must have been as-

signed to some vehicle. There can be at most NK

number of such assignments since each task can be

assigned to each vehicle at most once. Therefore, the

algorithm will take NK iterations to terminate in the

worst case.

4 EXPERIMENTAL RESULTS

There are two baseline algorithms that are used for

evaluation. The ﬁrst is a randomized algorithm that

randomly assigns a vehicle as the “current” vehicle.

Then, it will iterate through the tasks in an arbitrary

order, assigning each task onto the “current” vehicle.

If a task cannot ﬁt onto the “current” vehicle, the sys-

tem will choose another random vehicle as the “cur-

rent” vehicle. It will be referred to as the next ﬁt algo-

rithm. The second baseline algorithm is the standard

greedy algorithm that organizes tasks from largest to

smallest, then orders the vehicles from most to least

computational power offered. Then, the system will

iterate through the tasks in order and, for each task, it

will iterate through the vehicles in order until a vehi-

cle is found able to take on the task. This algorithm

is based on a greedy algorithm for the bin packing

problem (the formulated problem is similar to the bin

packing problem as shown by the NP-complete proof

in Section 2). The complexity of these algorithms are

O(K + N) and O(KN) respectively. Other algorithms

are not chosen as there are no other works that evalu-

ate the two objectives at the same time.

Figure 1: Average Experimental Loss with 50 Vehicles.

4.1 Approximation Loss

To evaluate how well the RS based heuristic performs,

we will test its objective value against that of the op-

timal to ﬁnd the approximation loss. However, due to

the high computational demands of computing the op-

timal solution of an ILP at large scales, this evaluation

had at most 50 vehicles. The objective weights will

be 1 and 10. This evaluation will be done at three dif-

ferent vehicles to task ratios to emulate how busy the

environment is. The three ratios are: 1:1 (abundance

of computational resources compared to tasks); 1:2

(moderate amount of computational resources com-

pared to tasks); and 1:3 (scarcity of computational re-

sources compared to tasks).

The variables for the experiments are once again

randomized as indicated in Table 1 To minimize the

effect of the randomized variables, each instance of

the experiment was ran 20 times and the averaged

results of the approximation loss experiment are dis-

played in Fig. 1. The y-axis represents how far from

the optimum the results are. For example, the match-

ing algorithm (1:1) gives a solution that is 1.7 times

the optimum. Evident in these results, the matching

algorithm performs signiﬁcantly better than the other

two algorithms, especially in settings with more tasks.

Comparing different task to vehicle ratios, more tasks

correlate to worse performance. This is to be expected

as it is much more difﬁcult to assign tasks optimally

when computational resources are more limited.

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

198

Figure 2: Objective Weights α = 1, β = 10, Delay Objective.

Figure 3: Objective Weights α = 1, β = 10, Number of Vehicles Used Objective.

4.2 Large Scale Experimentation

To examine the performance of the RS based heuristic

at a large scale, several experiments on various set-

tings were performed and evaluated against the two

baseline algorithms. The same three different vehicle

to task ratios were tested (1:1, 1:2, 1:3).

Two different pairs of objectives weights were

tested. These different objective weights are designed

to emulate different valuations of the objectives (the

ﬁrst number is the weight of the delay objective α and

the second number is the weight of the “number of

vehicles used” objective β): (1, 10) - for situations

where we mostly care about delay and not about the

number of vehicles used, and (1, 100) - for situations

where we mostly care about the number of vehicles

used.

Each experiment will be run on a scale from 50 ve-

hicles to 500 vehicles at intervals of 50 using all three

algorithms. The two different objectives are evaluated

separately. The variables for the experiments are once

again randomized as indicated in Table 1. To mini-

mize the effect of the randomized variables, the exper-

iment was performed 20 times. The CV was at most

0.15, indicating very low variance in the data sample.

Furthermore, any particular data point was at most

31% away from the mean. Therefore, it is reasonable

to conclude that the randomness of the initialized vari-

ables has little impact on the result of the experiments.

The experimental results for objective weights (1, 10)

Multi-Objective Task Assignment Solution for Parked Vehicular Computing

199

Figure 4: Objective Weights α = 1, β = 100, Delay Objective.

Figure 5: Objective Weights α = 1, β = 100, Number of Vehicles Used Objective.

are displayed in Fig. 2 and Fig. 3. In this case, where

the delay objective dominates the number of vehicles

used objective, the RS based matching algorithm per-

forms signiﬁcantly better in terms of delay while per-

forming similarly to the other two algorithms in terms

of the number of vehicles used.

In the second case, where the number of vehicles

used objective has weight 100, the simulation results

are displayed in Fig. 4 and Fig. 5. Again, the proposed

RS based algorithm outperforms the other two algo-

rithms by a large margin while performing similarly

in terms of the other objective.

Another simulation is performed where the vehi-

cle to task ratio is 1:5 to replicate an extremely busy

environment where most vehicles need to be used.

Fig. 6 displays the results of this simulation. We can

see that, on average, the proposed RS based algo-

rithm performs slightly better than the two baseline

algorithms. In this type of setting, where most avail-

able vehicles need to be used, assigning the right tasks

to the right vehicles becomes increasingly important.

Therefore, the RS based algorithm’s performance in

the number of vehicles used objective is slightly bet-

ter than the other two baseline algorithms while still

performing signiﬁcantly better in the delay objective.

5 CONCLUSION

This paper proposes a formulation of the task assign-

ment problem in the PVC environment as a weighted

multi-objective optimization problem that aims to

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

200

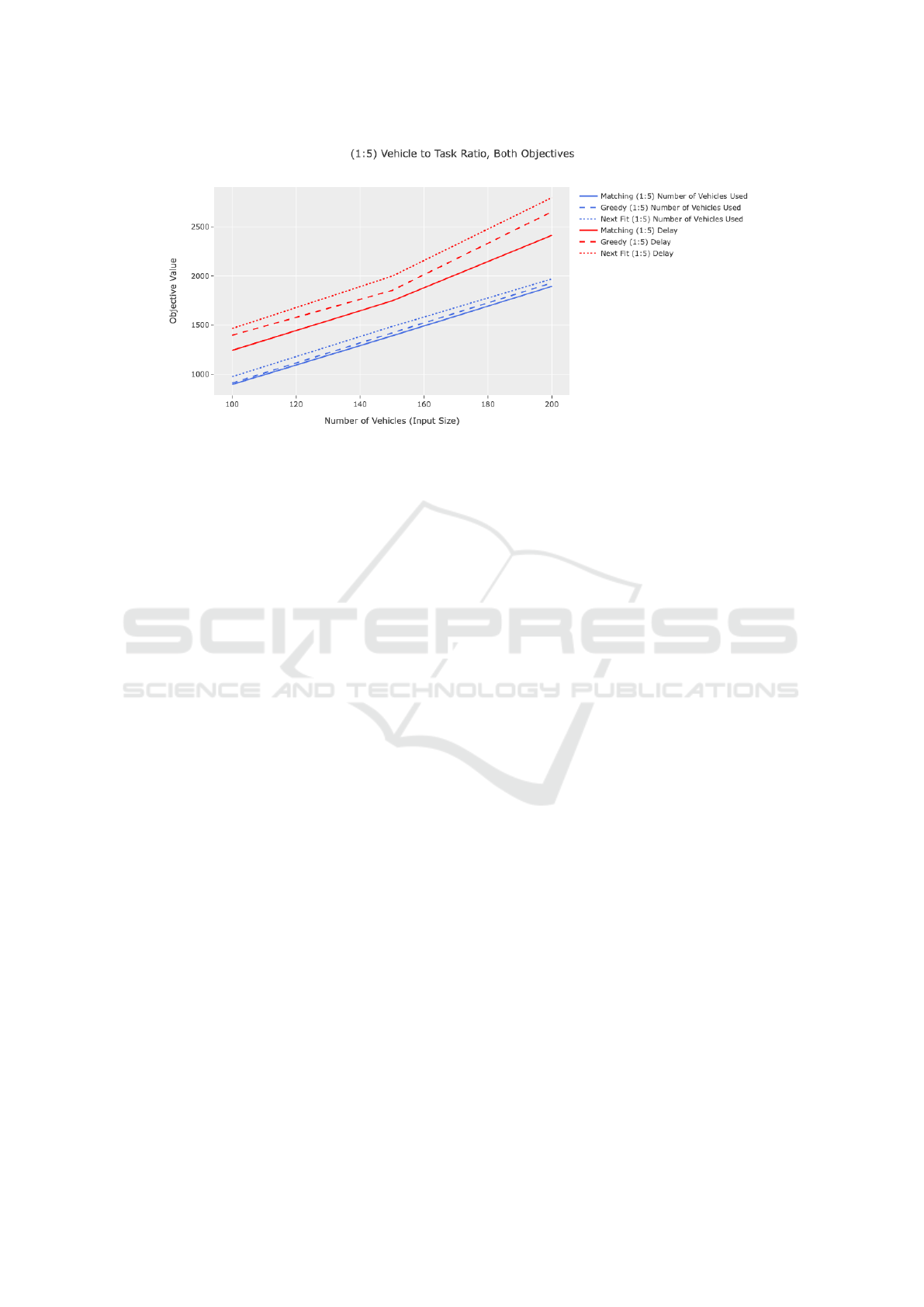
Figure 6: Objective Weights α = 1, β = 10, Both Objectives.

minimize both task delay and wireless channel load.

Then, a heuristic based on the RS algorithm is pro-

posed and evaluated against two other baseline algo-

rithms on various simulation settings on a scale of up

to 500 vehicles and 1,500 tasks.

The formulation of the optimization problem is a

key area. Currently, only the total task completion

speed is measured in terms of delay as it is the sim-

plest measure of delay. However, practically speak-

ing, there may be deadlines imposed on certain tasks.

Then, a deadline constraint would have to be added.

We could also incorporate deadlines and ignore how

fast the tasks are done as long as they are done before

their deadline. Furthermore, the transmission delay

is part of the total delay objective in the formulation.

However, that is related to the state of the wireless

channels, which is related to the number of vehicles

in use. So, perhaps the objective function could have

the transmission delay be dependent on the number of

vehicles used.

Secondly, only a general formulation of an incen-

tive mechanism is proposed in this paper. Future work

could include a formal formulation of such a mecha-

nism and evaluating the ability of the incentive mech-

anism to provide accurate remaining parking time es-

timates through various simulations. This should then

be compared against the effectiveness of remaining

parking time estimation via statistical modeling. An-

other extension would be designing a hybrid solution

using both statistical analysis and incentivized user

submissions.

ACKNOWLEDGMENT

We thank Dr. Sameh Sorour for his help in developing

the system model presented in this paper.

REFERENCES

Arif, S., Olariu, S., Wang, J., Yan, G., Yang, W., and

Khalil, I. (2012). Datacenter at the airport: Rea-

soning about time-dependent parking lot occupancy.

IEEE Transactions on Parallel and Distributed Sys-

tems, 23(11):2067–2080.

Cook, W., Lov

asz, L., Seymour, P. D., et al. (1995). Combi-

natorial optimization: papers from the DIMACS Spe-

cial Year, volume 20. American Mathematical Soc.

De Souza, A. B., Rego, P. A., Carneiro, T., Rodrigues,

J. D. C., Reboucas Filho, P. P., De Souza, J. N.,

Chamola, V., De Albuquerque, V. H. C., and Sikdar,

B. (2020). Computation ofﬂoading for vehicular envi-

ronments: A survey. IEEE Access, 8:198214–198243.

Du, J., Yu, F. R., Chu, X., Feng, J., and Lu, G. (2018).

Computation ofﬂoading and resource allocation in ve-

hicular networks based on dual-side cost minimiza-

tion. IEEE Transactions on Vehicular Technology,

68(2):1079–1092.

Ge, S., Cheng, M., He, X., and Zhou, X. (2020). A

two-stage service migration algorithm in parked ve-

hicle edge computing for internet of things. Sensors,

20(10):2786.

Guo, H., Liu, J., Zhang, J., Sun, W., and Kato, N.

(2018). Mobile-edge computation ofﬂoading for ultra-

dense iot networks. IEEE Internet of Things Journal,

5(6):4977–4988.

Huang, D., Misra, S., Verma, M., and Xue, G. (2011).

Pacp: An efﬁcient pseudonymous authentication-

based conditional privacy protocol for vanets. IEEE

Multi-Objective Task Assignment Solution for Parked Vehicular Computing

201

Transactions on Intelligent Transportation Systems,

12(3):736–746.

Huang, X., Yu, R., Liu, J., and Shu, L. (2018). Parked

vehicle edge computing: Exploiting opportunistic re-

sources for distributed mobile applications. IEEE Ac-

cess, 6:66649–66663.

Kang, J., Yu, R., Huang, X., and Zhang, Y. (2017). Privacy-

preserved pseudonym scheme for fog computing sup-

ported internet of vehicles. IEEE Transactions on In-

telligent Transportation Systems, 19(8):2627–2637.

Lianghai, J., Weinand, A., Han, B., and Schotten, H. D.

(2018). Multi-rats support to improve v2x communi-

cation. In 2018 IEEE wireless communications and

networking conference (WCNC), pages 1–6. IEEE.

Liu, L., Chen, C., Pei, Q., Maharjan, S., and Zhang,

Y. (2021). Vehicular edge computing and network-

ing: A survey. Mobile networks and applications,

26(3):1145–1168.

Ma, L., Liu, X., Pei, Q., and Xiang, Y. (2018). Privacy-

preserving reputation management for edge comput-

ing enhanced mobile crowdsensing. IEEE Transac-

tions on Services Computing, 12(5):786–799.

Mao, Y., You, C., Zhang, J., Huang, K., and Letaief, K. B.

(2017). A survey on mobile edge computing: The

communication perspective. IEEE communications

surveys & tutorials, 19(4):2322–2358.

Meneguette, R., De Grande, R., Ueyama, J., Filho, G.

P. R., and Madeira, E. (2021). Vehicular edge com-

puting: Architecture, resource management, security,

and challenges. ACM Computing Surveys (CSUR),

55(1):1–46.

Qiao, G., Leng, S., Zhang, K., and He, Y. (2018). Col-

laborative task ofﬂoading in vehicular edge multi-

access networks. IEEE Communications Magazine,

56(8):48–54.

Raza, S., Wang, S., Ahmed, M., and Anwar, M. R. (2019).

A survey on vehicular edge computing: architec-

ture, applications, technical issues, and future direc-

tions. Wireless Communications and Mobile Comput-

ing, 2019.

Roth, A. E. (2008). Deferred acceptance algorithms: His-

tory, theory, practice, and open questions. interna-

tional Journal of game Theory, 36(3):537–569.

Sun, J. H. (2022). Scheduling Problems in Next Generation

Computing Networks. PhD thesis.

Wang, D., Sattiraju, R. R., Weinand, A., and Schotten, H. D.

(2019). System-level simulator of lte sidelink c-v2x

communication for 5g. In Mobile Communication-

Technologies and Applications; 24. ITG-Symposium,

pages 1–5. VDE.

Wang, S., Zhang, X., Zhang, Y., Wang, L., Yang, J., and

Wang, W. (2017). A survey on mobile edge networks:

Convergence of computing, caching and communica-

tions. Ieee Access, 5:6757–6779.

Wang, Y., Sheng, M., Wang, X., Wang, L., and Li, J. (2016).

Mobile-edge computing: Partial computation ofﬂoad-

ing using dynamic voltage scaling. IEEE Transactions

on Communications, 64(10):4268–4282.

Wei, J., Wang, X., Li, N., Yang, G., and Mu, Y. (2018).

A privacy-preserving fog computing framework for

vehicular crowdsensing networks. IEEE Access,

6:43776–43784.

Whaiduzzaman, M., Sookhak, M., Gani, A., and Buyya, R.

(2014). A survey on vehicular cloud computing. Jour-

nal of Network and Computer applications, 40:325–

344.

Zhang, K., Mao, Y., Leng, S., Maharjan, S., Vinel, A., and

Zhang, Y. (2019). Contract-theoretic approach for

delay constrained ofﬂoading in vehicular edge com-

puting networks. Mobile Networks and Applications,

24(3):1003–1014.

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

202