Decision-Making in Hearthstone Based on Evolutionary Algorithm

Eiji Sakurai and Koji Hasebe

Department of Computer Science, University of Tsukuba, Japan

Keywords:

Game AI, Hearthstone, Decision-Making, Rolling Horizon Evolutionary Algorithm.

Abstract:

Hearthstone is a two-player turn-based collectible card game with hidden information and randomness. Gen-

erally, the search space for actions of this game grows exponentially because the players must perform a series

of actions by selecting each action from many options in each turn. When playing such a game, it is often

difﬁcult to use a game tree search technique to ﬁnd the optimal sequence of actions up until the end of a turn.

To solve this problem, we propose a method to determine a series of actions in Hearthstone based on an evolu-

tionary algorithm called the rolling horizon evolutionary algorithm (RHEA). To apply RHEA to this game, we

modify the genetic operators and add techniques for selecting actions based on previous search results and for

ﬁltering (pruning) some of the action options. To evaluate the effectiveness of these improvements, we imple-

mented an agent based on the proposed method and played it against an agent based on the original RHEA for

several decks. The result showed a maximum winning rate of over 97.5%. Further, our agent played against

the top-performing agents in previous competitions and outperformed most of them.

1 INTRODUCTION

With the rapid advance in artiﬁcial intelligence tech-

nologies, many studies have been made on the devel-

opment of agents playing games. In particular, many

researchers have paid attention to games with hidden

information and randomness, such as poker, mahjong,

and collectible card games.

Hearthstone (Blizzard Entertainment, nd) is a col-

lectible card game classiﬁed into a two-player turn-

based imperfect information game. In this game, each

player composes a bunch (called a deck) of 30 cards

of more than 1,000 different types of cards and plays

with them. The game progresses while alternating

turns between two players, and the player who uses

the deck on hand in their turn and eventually reduces

the opponent’s health to 0 wins.

Typically, in collectible card games, the search

space grows exponentially because players select a

sequence of actions from numerous options at each

turn. Many previous studies, such as (Zhang and

Buro, 2017;

Swiechowski et al., 2018; Choe and Kim,

2019), have used tree search techniques for collectible

card games. However, ﬁnding the optimal sequence

of actions to take to the end of the turn using a tree

search within time constraints is often difﬁcult.

To solve this problem, in this study, we pro-

pose a method for determining a sequence of ac-

tions in Hearthstone based on the evolutionary al-

gorithm called the rolling horizon evolutionary algo-

rithm (RHEA) (Perez et al., 2013). In RHEA, each

individual has a sequence of genes that represents a

series of behaviors in a certain interval. Furthermore,

each individual is given a ﬁtness value obtained by

evaluating the state reached through its series of ac-

tions. From a set of individuals, those with high ﬁt-

ness are selected, and a new generation is generated

by crossover and mutation. The optimal sequence of

actions is eventually determined by repeating this pro-

cess.

Despite being a versatile genetic algorithm, apply-

ing the RHEA directly to decision-making in Hearth-

stone is difﬁcult. Therefore, our proposed method has

the following three improvements. The ﬁrst improve-

ment is to modify the genetic operators to account for

subsequent actions. The second improvement is to

use a tree structure based on the study of Perez et al.

(Perez Liebana et al., 2015) to store and reuse statis-

tical information obtained from previously generated

individuals. Finally, the third improvement is to ﬁl-

ter action options (i.e., pruning) so that the series of

actions in a turn is consistent.

In this study, we evaluated the effectiveness of

these improvements by playing game against an agent

based on the original RHEA. The result showed that

the maximum winning rate of the proposed method

Sakurai, E. and Hasebe, K.

Decision-Making in Hearthstone Based on Evolutionary Algorithm.

DOI: 10.5220/0011783900003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 845-852

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

845

was 97.5% when using a deck called MidrangeJade-

Shaman.

Furthermore, to evaluate the performance of our

proposed method, we played our agent against sev-

eral agents that achieved high performance in the

past Hearthstone AI Competitions (Dockhorn and

Mostaghim, 2019). According to the results, our

agent outperformed most of them for several decks.

The remainder of this paper is organized as fol-

lows. Section 2 explains the related work. In Sec-

tion 3, we provide an overview of the background of

this study. Section 4 describes our proposed method

for determining the optimal sequence of actions in

Hearthstone based on RHEA. In Section 5, we present

the results of the evaluation by experiments. Finally,

Section 6 concludes the paper and presents future

work.

2 RELATED WORK

In research on decision-making in Hearthstone, many

attempts based on Monte Carlo Tree Search (MCTS)

(Browne et al., 2012) have been proposed. Choe et

al.’s study (Choe and Kim, 2019) suppressed the ex-

pansion of search trees by abstraction and sampling.

Some studies (Zhang and Buro, 2017;

Swiechowski

et al., 2018; Wang and Moh, 2019) have improved

the accuracy of state evaluation by combining neural

networks. A study (Dockhorn et al., 2018) presented

a method for estimating the opponent’s hand based

on the cards used by the opponent immediately be-

fore. Furthermore, a study (Dockhorn et al., 2018)

extended the method of (Bursztein, 2016) to improve

MCTS by estimating the opponent’s deck.

Furthermore, studies have been conducted on the

application of the RHEA to game-solving. In particu-

lar, there were many attempts at utilizing past search

information in research (Perez Liebana et al., 2015;

Gaina et al., 2017) that applied the RHEA to a frame-

work called general video game AI (GVGAI). GV-

GAI is a framework for handling relatively simple

games, such as Space Invaders and puzzle games.

A study (Justesen et al., 2016) proposed a method

called online evolutionary planning (OEP) to apply

RHEA to a turn-based strategy game, which deter-

mined a series of actions based on an action plan

rather than a single action decision. In a study

(Dockhorn et al., 2021) that applied the RHEA to a

real-time strategy game, the RHEA was not used to

search the action space but to search the script space,

where actions were abstracted. In each of (Justesen

et al., 2016) and (Dockhorn et al., 2021), experiments

showed that the RHEA-based agents were superior to

MCTS in several cases.

Generally, for collectible card games with many

options, it is often difﬁcult for the MCTS to ﬁnd the

optimal series of actions until the end of a turn within

a time limit. On the other hand, RHEA is expected to

perform decision-making for actions considering the

goal of the turn because it searches based on the state

evaluation after executing a series of actions.

3 BACKGROUND

This section outlines the rules of Hearthstone (in Sec-

tion 3.1) and RHEA (in Section 3.2), which are pre-

requisites for this study.

3.1 Rules of Hearthstone

A match in Hearthstone consists of two phases,

namely, deck-building and battle, as described below.

3.1.1 Deck-Building Phase

A player selects 30 cards from among the cards that

can be used by the selected hero and bundles them

together to complete the deck.

The cards used in Hearthstone are classiﬁed into

the following three types.

Minion: This can be summoned to the battleﬁeld by

playing from hand. A minion consists of health

and attack, and they are removed when the health

of a minion on the battleﬁeld reaches 0.

Spell: Players can use the effect of a card by playing

it from their hand.

Weapon: This can be equipped on heroes. A

hero equipped with a weapon acquires the attack

power.

Each card has a cost, and when a card is used, a player

needs to pay the card’s cost from the resource called

mana crystal.

3.1.2 Battle Phase

A hero’s health is set to 30 at the start of a battle,

and the ﬁrst player draws cards from their deck to

make a hand of three cards. The second player draws

one more card from their deck and add a special card

called a coin, to make their hand ﬁve cards. After

that, each player aims to reduce the opponent’s hero’s

health to 0 while taking turns. Here, we note that,

for each player, the state of the game is only partially

visible, and some information is hidden.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

846

The player who takes the ﬁrst turn adds one card

from the shufﬂed deck to the hand. At this time, the

upper limit of mana crystal is increased by 1. Mana

crystal increases up to its capacity of 10 as the turn

progresses. Then, the player can perform multiple ac-

tions, such as paying mana crystal to play cards or

attacking minions if they are on the battleﬁeld.

3.2 Rolling Horizon Evolutionary

Algorithm (RHEA)

RHEA (Perez et al., 2013) is a type of evolutionary al-

gorithm for decision-making that replaces tree search

in games with real-time state transitions. Each indi-

vidual comprises a sequence of genes and a ﬁtness

value. The former represents a series of actions, while

the latter indicates the evaluation of the state obtained

when performing a series of actions. Similar to other

genetic algorithms, RHEA searches for the optimal

sequence of actions by repeatedly changing genera-

tions through genetic manipulations.

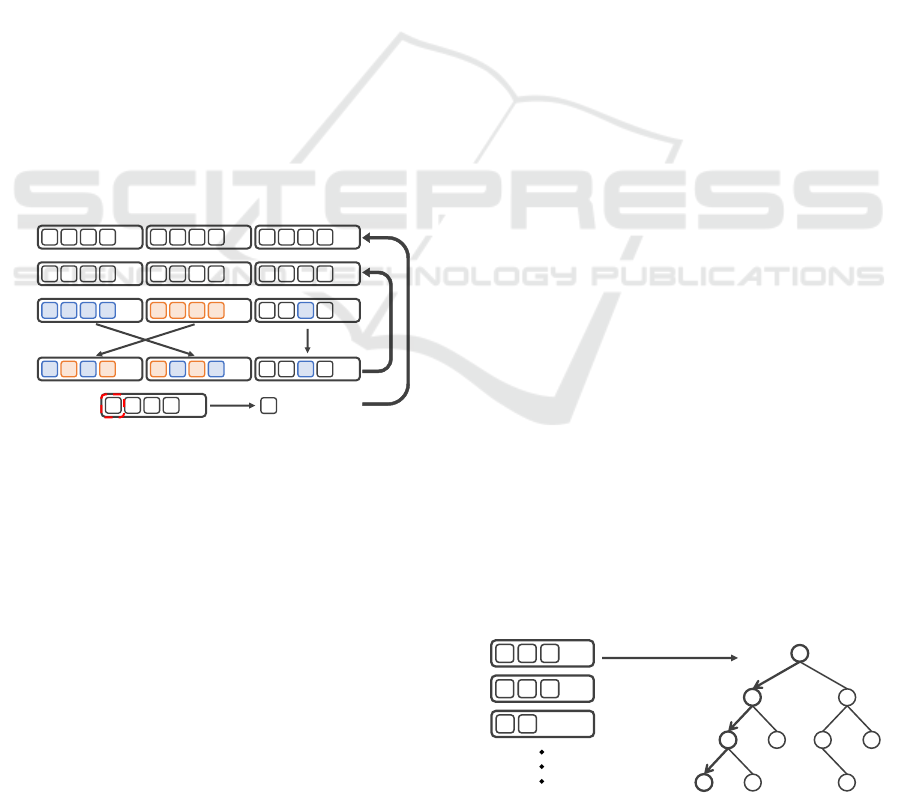
Figure 1 shows the optimization procedure by

RHEA. Here, the numbers in the ﬁgure correspond to

the step numbers in the following description. Also,

each alphabet surrounded by a square represents an

individual action, and a mass consisting of them rep-

resents a sequence of actions.

A B C D

0.6

E F G H

I J K L

E F G H

0.8

I J K L

0.7

M N O P

0.9

E F G H

0.8

I J K L

0.7

M F O H

0.7

E N G P

0.6

I J C L

0.8

Crossover

Mutation

Q R S T

1.0

Best individual

Execution

Figure 1: Steps for action decision based on RHEA.

1. Perform a series of actions at random, generate

multiple individuals, and form an initial popula-

tion.

2. Evaluate each individual. The ﬁtness of an indi-

vidual is the evaluation value of the state after per-

forming a series of actions.

3. Select individuals with high ﬁtness through tour-

nament or elitism selection.

4. Generate new individuals from selected individ-

uals through genetic operators. In a crossover,

the behavior of two individuals is randomly ex-

changed through a uniform crossover. In muta-

tion, the mutation point is determined at random,

and actions are randomly selected. This generates

an individual with a new set of behaviors.

5. Evaluate the generated new individuals.

6. Repeat Steps 2-5 until the time limit is reached.

7. The ﬁrst action of the individual with the highest

ﬁtness value is selected when determining an ac-

tion.

8. Transition to the next state and search for the sec-

ond action, which is the next action from Step 1.

As shown above, RHEA searches solely on the evalu-

ation value of the state after executing a series of ac-

tions, thereby allows for action decisions to be made

in anticipation of the ﬁnal state of the turn.

4 DECISION-MAKING WITH

RHEA

Our method for decision-making in Hearthstone is

based on the idea of RHEA. A more speciﬁc search

procedure is as follows. First, an initial population is

generated. Second, crossover and mutation are per-

formed for each individual contained in the popula-

tion. At this time, a statistical tree constructed on the

basis of the ﬁtness possessed by the generated indi-

viduals is used. In the initialization and mutation, op-

tions are pruned by a ﬁlter that encourages consistent

action decisions. The game transitions to the next step

by selecting and executing the ﬁrst action of the best

individual in the last generation when deciding on an

action. Then, the initial population is generated again

to search for the next action, and new individuals are

generated through genetic operators. The above pro-

cedure is repeated until the end of turn.

A more detailed description is provided below.

Section 4.1 ﬁrst explains the statistical tree. Section

4.2 describes the new genetic operators. Section 4.3

describes how to evaluate the ﬁtness of each individ-

ual. Finally, Section 4.4 describes ﬁltering for action

selection.

4.1 Statistical Tree

A C H

0.7

B E I

0.8

A D

0.3

Store the fitness

+0.7

A B

C D E F

G H I

+0.7

Population

Search tree

Figure 2: Store the ﬁtness in a statistical tree.

Decision-Making in Hearthstone Based on Evolutionary Algorithm

847

In the proposed method, to reuse the information ob-

tained by searching during evolution, the information

is stored in a tree structure using the techniques of

(Perez Liebana et al., 2015) and (Gaina et al., 2017).

Figure 2 shows how the ﬁtness value of individuals

is stored in a statistical tree. Here, the value stored

in each node is a pair of the evaluation value and the

number of visits at a node. Because this search tree

does not store the state of the game, nodes are deter-

mined only by actions. Therefore, the expansion of

the search tree can be suppressed, even if an action

or state transition, including randomness, occurs. In

addition, this statistical tree can construct another tree

whose root is the node that can be reached by that ac-

tion when a certain action is determined and executed.

In the proposed method, the Upper Conﬁdence

Bound (UCB) (Kocsis and Szepesv

ari, 2006), deﬁned

by the following equation, is used for crossover and

mutation.

∗

= arg max

{

V (s, a)

N(s, a)

√

lnN(s)

N(s, a)

}

. (1)

Here, s represents the current node, N(s) represents

the number of visits to the current node, V (s, a) de-

notes the cumulative evaluation value of the next

nodes reached by action a, N(s, a) represents the num-

ber of visits to the next node that selected the action

a, and C denotes the search coefﬁcient. It is possible

to prioritize and search for promising actions while

maintaining a balance between exploration and ex-

ploitation, because this formula selects actions with

high evaluation values and actions with low visit

counts.

4.2 Genetic Operators

4.2.1 Selection

! " #

!"#

$ % &

!"$

! '

!"%

&'(()*+,-)*)(.+/0*

$ (

!"1

23/+/45,4)3)6+/0*

70'(*.5)*+,4)3)6+/0*

8)9+,-)*)(.+/0*

! " #

!"#

! '

!"%

Figure 3: Tournament selection and elitism selection.

Tournament selection and elitism selection are com-

bined to generate a population to choose for the next

generation. Figure 3 shows the selection of individu-

als by tournament and elitism selection. Tournament

selection is a selection method that randomly selects n

individuals from the population of the current genera-

tion and chooses the individuals with the highest eval-

uation value among the selected individuals. Mean-

while, elitism selection is a selection method that se-

lects and retains n individuals with high evaluation

values from the population. Tournament selection

may lead to a more diverse selection of individuals

than elitism selection, which simply selects only indi-

viduals with high evaluation values, but may omit the

best individuals of the current generation. Therefore,

it is supplemented by elitism selection, which selects

individuals with high ﬁtness values.

4.2.2 Crossover

A B C D E F G E

Parents

UCB or random

selection

Repeat

Children

B F

Evaluation

0.8

0.6

Population

A C H

0.7

B E I

0.8

A D

0.3

Figure 4: Crossover based on the search information.

Figure 4 shows an example of individual generation

by crossover. The procedure for crossover is shown

below, where the numbers in the ﬁgure correspond to

the numbers in the following description:

1. Sequentially select one individual from the popu-

lation of the current generation and select another

randomly.

2. Select one individual with a probability of 50%,

and select the feasible action using the UCB. At

this time, if an executable action does not exist

in the search tree, that action is selected with a

certain probability. Thereafter, one individual is

selected again with a probability of 50%, and the

action is selected in the same manner. Repeat this

operation until the end of the turn to generate a

series of actions.

3. The evaluation value of the state after executing a

new series of actions is the ﬁtness of the individ-

ual.

Our method probabilistically select a parent to in-

herit the behavior and generate a new individual by

inheriting good behavior from the parent’s series of

behaviors by random selection or selection based on

the UCB. Thus, it is possible to generate a series of

actions that tend to be highly evaluated without gen-

erating unfeasible actions.

Either random selection or selection based on the

UCB is performed by γ

N(s)

when inheriting the par-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

848

ent’s behavior. Here, γ (0 ≤ γ 5 1) represents the at-

tenuation rate, and N(s) represents the number of vis-

its to the current node s that can be reached by actions

thus far. According to this value, if the search infor-

mation is sufﬁcient, the search is performed by selec-

tion based on the UCB with a high probability; oth-

erwise, the search is performed by random selection.

Random selection is also performed when search in-

formation about the current node does not exist.

4.2.3 Mutation

! " # $ %

! " &' %

(

!"#$%&$&'()%*$+,-,./0%(

! " &' %

( 123 45'-6'/0%(

7'()%*$+,-,./0%($%8$*6/'/,)$9%0(/

:%96-'/0%(

! " # $%&

' ( )

$%*

! +

$%,

Figure 5: Mutation based on search information.

Figure 5 shows an example of generating an individ-

ual by mutation. The mutation procedures are shown

below, where the numbers in the ﬁgure correspond to

those in the following description:

1. Select one individual from the population of the

current generation.

2. Randomly determine mutation points.

3. For each subsequent action, choose an action ei-

ther randomly with a rate γ

N(s)

or based on the

UCB. Repeat this until the end of the turn to gen-

erate a series of actions.

4. The evaluation value of the state after executing a

new series of actions is the ﬁtness of the individ-

ual.

Therefore, in our method, after randomly deter-

mining the mutation point, all subsequent behaviors

are mutated. For each behavioral mutation, two mu-

tations are used: random mutation and mutation based

on search information. The former selects randomly

from the current viable options, whereas the latter

selects the action using UCB. Similar to crossover,

in mutation, the selection method is determined by

N(s)

, and as the number of visits to nodes that can

be reached by actions increases, the ratio of random

mutations decreases, and the ratio of mutations based

on search information increases.

4.3 Evaluation of Individuals

Evaluating the state after executing a series of actions

is necessary to evaluate an individual. Our method

uses random playouts often used in MCTS. In addi-

tion, to determine the opponent’s deck and hand for

the simulation of the opponent’s actions, our method

randomly determines the cards included in the oppo-

nent’s deck from the observable information of the

opponent’s hero class. Furthermore, the opponent’s

hand is determined by taking it out from the generated

deck so that it matches the actual number of cards in

the hand.

In addition, our method abstracts card location

and other information, and keeps the abstracted state

and evaluation values. Therefore, evaluation can be

done without playouts.

4.4 Filtering for Consistent Action

Selection

In Hearthstone, consistent action decisions are re-

quired to execute a series of actions in one turn.

Therefore, eliminating unnecessary options from the

immediately preceding action and the current state

would allow for consistent action selection.

In the proposed method, a ﬁlter is used when ini-

tialization and during mutation, and a ﬁlter is ran-

domly applied from ﬁve ﬁlters other than the turn end

when selecting actions. Moreover, the same ﬁlter is

applied to subsequent action selections until the ﬁlter

becomes inapplicable. Here, a ﬁlter cannot be applied

if all options are blocked, in which case another ﬁlter

is applied. If there is no applicable ﬁlter, a ﬁlter other

than the turn end is applied only for one action, and

in subsequent action selections, it is once more ran-

domly applied from among the ﬁve types of ﬁlters.

Direct Attack: This ﬁlter keeps the action of attack-

ing the opponent’s hero.

Destroy Minion: This ﬁlter keeps actions that dam-

age destructible minions. Here, a certain minion is

destructible if the health of the minion is less than

or equal to the total attack value of its minion.

Deploy Minion: This ﬁlter keeps the action of sum-

moning minions. In addition, this ﬁlter keep spells

and hero powers that summon effect.

Protection: This ﬁlter keeps the summoning of min-

ions with taunts and actions that block opponent

attacks to mitigate health loss.

Keep Hand: This ﬁlter calculates the average cost of

the cards in player’s hand and keeps actions that

play card below that value.

Decision-Making in Hearthstone Based on Evolutionary Algorithm

849

Except Turn End: This ﬁlter is applied when none

of the above ﬁve ﬁlters is left with any options

left. This ﬁlter keeps the action except for the end

of the turn.

5 EXPERIMENTS

To evaluate the effectiveness of the proposed method,

we conducted the following two experiments. First,

to evaluate the effectiveness of the improvements

explained in the previous section, we performed

matches against an agent based on the original RHEA

(called Vanilla RHEA) and measured the winning

rate Second, we measured the winning rate of our

agent against conventional agents submitted in past

Hearthstone AI Competitions to demonstrate the per-

formance of our method.

5.1 Experimental Settings

As the environment of the experiments, we used Sab-

berStone (Dockhorn and Mostaghim, 2019), which

was used in Hearthstone AI Competitions. In our ex-

periments, there is no re-drawing of cards, and the

time limit per turn is set to 30 s to conform to the

rules of the competition. The turn end is forcibly se-

lected if the time limit is exceeded when deciding on

an action. Furthermore, the match may be prolonged

depending on the deck and will be treated as a draw

if it exceeds 25 turns. In the experiments, three decks

were used: MidrangeJadeShaman, AggroPirateWar-

rior, and CubeWarlock, which are deﬁned in a website

(Hearthstone Top Decks, nd).

In addition, during action search, our method as-

sumed a population size of 50 with a tournament size

of 2 and an elite size of 1. During state evaluation,

our method generates 20 game states, and performs

20 random playouts for each state.

5.2 Opponent Agents

The opponents used in the experiments were as fol-

lows. Here, except for vanilla RHEA and MCTS, the

agents who have excelled in previous Hearthstone AI

Competitions.

Vanilla RHEA: This is an agent developed for com-

parative experiments to evaluate the effectiveness

of our improvements. This agent is based on the

original RHEA algorithm, which searches by ge-

netic operators based on point mutation and uni-

form crossover.

Vanilla MCTS: This is a general MCTS-based agent

implemented for comparison of the search aspect

with the proposed method.

DynamicLookAhead (DLA): This agent uses sim-

ple evaluation function to evaluate the state, and

searches actions through depth-ﬁrst search with a

dynamically limited depth.

AlvaroAgent: This agent searches for actions itera-

tively based on the UCB using the optimized eval-

uation functions.

Monte Carlo graph search (MCGS): It is possible

to search for actions even after the end of the turn

by suppressing the expansion of the search tree

used in the MCTS by abstracting, sampling, and

pruning the state and assuming that the opponent’s

actions are random.

TycheAgent: This agent uses a random search, and

only the ﬁrst action with a high evaluation value

is selected after a certain number of iterations. It

uses a complex evaluation function for the state

evaluation.

5.3 Search Performance Evaluation

5.3.1 Impact of Genetic Operators and

Statistical Tree on Performance

We measured the winning rate against Vanilla RHEA

to evaluate the effectiveness of the proposed genetic

manipulation and the statistical trees. The results are

shown in Figure 6. Here, the genetic manipulation

rate is set to 50% in both cases, and the ﬁlter described

in Section 4.4 is not used. Combinations of methods

and settings that constitute each method are expressed

using the following abbreviations.

•

VC: uniform crossover.

• VM: point mutation.

• PC: crossover by the proposed method (see Sec-

tion 4.2.2).

• PM: mutation by the proposed method (see Sec-

tion 4.2.3).

• γ : ratio of random selection (see Section 4.2.2).

In Figure 6, the vertical axis presents the list of

agents, each of which represents a possible com-

bination of the components, whereas the horizontal

axis indicates the winning rate against Vanilla RHEA.

Here, the orange, green, and gray graphs show the

winning rates when using the decks called Midrange-

JadeShaman, AggroPirateWarrior, and CubeWarlock,

respectively.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

850

Figure 6: Match results against Vanilla RHEA.

The results show that there was no signiﬁcant dif-

ference between the proposed method and Vanilla

RHEA when search information was not used (i.e.,

γ = 1.0). However, it was observed that the win-

ning rate of the proposed method was signiﬁcantly

improved compared with Vanilla RHEA when search

information was used (i.e., γ ̸= 1.0). In particular,

the winning rate of the agent with PC, PM, and γ =

0.0 when using MidrangeJadeShaman improved to a

maximum of 97.5%. This was because the selection

based on the UCB during genetic manipulation could

generate many highly rated individuals with a promis-

ing set of behaviors. As a result, the proposed method

can search for promising series of action in the next

generation.

5.3.2 Impact of Genetic Operators’ Rate and

Filters on Performance

We also conducted experiments to measure changes

in the performance by varying the ratio of mutations

and crossovers and by using a ﬁlter. We used an agent

that applied the proposed crossover (PC) and muta-

tion (PM) to genetic operators based on the experi-

mental results presented in Section 5.3.1. Here, the

ratio of random selection ( γ ) was set to 0.0. The re-

sults are presented in Figure 7.

In this ﬁgure, the vertical axis presents the list of

agents with different genetic manipulation rates and

the presence or absence of ﬁltering, whereas the hori-

zontal axis represents the winning rate. The colors of

the graph are the same as in Figure 6.

Figure 7: Winning rates against agents with PC, PM, γ =

0.0.

This result shows that using the ﬁlter improved

the winning rate when using CubeWarlock to a max-

imum of 78.5% and MidrangeJadeShaman to a max-

imum of 65.5%. This was because CubeWarlock and

MidrangeJadeShaman tended to have more action op-

tions than AggroPirateWarrior, and the search per-

formance was improved by ﬁltering out inconsistent

choices. On the other hand, it was possible to search

sufﬁciently without using a ﬁlter when using Ag-

groPirateWarrior, which did not have many choices,

so the change in the winning rate was small.

5.4 Performance Comparison with

Conventional Methods

To demonstrate the performance of our method, we

performed matches between an agent based on the

proposed method and agents that achieved remark-

able results in past Hearthstone AI Competitions. Fig-

ure 8 shows the winning rate of our agent against

those agents. In this experiment, only decks called

MidrangeJadeShaman and AggroPirateWarrior were

used. Some other decks have been implemented, but

they were not used because of a lack of cards. Here,

as the difference in performance is expected to in-

crease depending on the state evaluation method, we

used the state evaluation function implemented in Al-

varoAgent for game state evaluation.

Figure 8: Winning rates of the proposed method against ex-

isting agents.

In Figure 8, the vertical axis presents the list of

the opponents, while the horizontal axis represents

Decision-Making in Hearthstone Based on Evolutionary Algorithm

851

the winning rate of the proposed method. This ﬁgure

demonstrates that the proposed method is as strong

as or stronger than almost all other agents, regard-

less of which deck is used. In particular, the pro-

posed method outperforms AlvaroAgent, which has

the same state evaluation function, by an average of

53%, suggesting that the proposed method is equally

or even better than AlvaroAgent at searching for ac-

tions. On the other hand, when using AggroPirate-

Warrior, the win rate was 40% against MCGS. This

is most likely because MCGS has an ingenious way

of pruning options even when conducting playouts,

which was more powerful than the state evaluation

function for the relatively simple deck of AggroPi-

rateWarrior, which was able to correctly evaluate the

state of the game.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we proposed a method for decision-

making for actions in Hearthstone based on the

RHEA. To apply the RHEA to Hearthstone, we im-

proved the original algorithm by introducing tech-

niques of genetic manipulation, utilizing past search

information, and ﬁltering action options.

We implemented agents based on the proposed

method and the original RHEA to evaluate the ef-

fectiveness of the proposed method. The results

showed that the winning rate for each improvement

was higher than that without the improvement. Fur-

thermore, our agent played against the top-performing

agents in past Hearthstone AI Competitions and out-

performed most of them.

In future work, we would like to investigate the

performance improvement by parameter tuning be-

cause the proposed method has various hyperparame-

ters. We are also interested in improving search efﬁ-

ciency. Speciﬁcally, we shall attempt to take over bet-

ter individuals found during the previous search steps

instead of generating the initial group only at random.

REFERENCES

Blizzard Entertainment (n.d.). Hearthstone ofﬁcial web-

site. Retrieved November 24, 2022, from https://

playhearthstone.com.

Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M.,

Cowling, P. I., Rohlfshagen, P., Tavener, S., Perez,

D., Samothrakis, S., and Colton, S. (2012). A survey

of monte carlo tree search methods. IEEE Transac-

tions on Computational Intelligence and AI in games,

4(1):1–43.

Bursztein, E. (2016). I am a legend: Hacking hearth-

stone using statistical learning methods. In 2016 IEEE

conference on computational intelligence and games

(CIG), pages 1–8. IEEE.

Choe, J. S. B. and Kim, J.-K. (2019). Enhancing monte

carlo tree search for playing hearthstone. In 2019

IEEE Conference on Games (CoG), pages 1–7. IEEE.

Dockhorn, A., Frick, M., Akkaya,

U., and Kruse, R.

(2018). Predicting opponent moves for improving

hearthstone ai. In International Conference on Infor-

mation Processing and Management of Uncertainty in

Knowledge-Based Systems, pages 621–632. Springer.

Dockhorn, A., Hurtado-Grueso, J., Jeurissen, D., Xu, L.,

and Perez-Liebana, D. (2021). Portfolio search and

optimization for general strategy game-playing. In

2021 IEEE Congress on Evolutionary Computation

(CEC), pages 2085–2092. IEEE.

Dockhorn, A. and Mostaghim, S. (2019). Introduc-

ing the hearthstone-ai competition. arXiv preprint

arXiv:1906.04238.

Gaina, R. D., Lucas, S. M., and Perez-Liebana, D. (2017).

Rolling horizon evolution enhancements in general

video game playing. In 2017 IEEE Conference on

Computational Intelligence and Games (CIG), pages

88–95. IEEE.

Hearthstone Top Decks (n.d.). Retrieved November 24,

2022, from https://www.hearthstonetopdecks.com/.

Justesen, N., Mahlmann, T., and Togelius, J. (2016). Online

evolution for multi-action adversarial games. In Euro-

pean Conference on the Applications of Evolutionary

Computation, pages 590–603. Springer.

Kocsis, L. and Szepesv

ari, C. (2006). Bandit based monte-

carlo planning. In European conference on machine

learning, pages 282–293. Springer.

Perez, D., Samothrakis, S., Lucas, S., and Rohlfshagen, P.

(2013). Rolling horizon evolution versus tree search

for navigation in single-player real-time games. In

Proceedings of the 15th annual conference on Genetic

and evolutionary computation, pages 351–358.

Perez Liebana, D., Dieskau, J., Hunermund, M.,

Mostaghim, S., and Lucas, S. (2015). Open loop

search for general video game playing. In Proceed-

ings of the 2015 Annual Conference on Genetic and

Evolutionary Computation, pages 337–344.

Swiechowski, M., Tajmajer, T., and Janusz, A. (2018). Im-

proving hearthstone ai by combining mcts and su-

pervised learning algorithms. In 2018 IEEE Con-

ference on Computational Intelligence and Games

(CIG), pages 1–8. IEEE.

Wang, D. and Moh, T.-S. (2019). Hearthstone ai: Oops to

well played. In Proceedings of the 2019 ACM South-

east Conference, pages 149–154.

Zhang, S. and Buro, M. (2017). Improving hearthstone ai

by learning high-level rollout policies and bucketing

chance node events. In 2017 IEEE Conference on

Computational Intelligence and Games (CIG), pages

309–316. IEEE.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

852