Automated Agent Migration over Distributed Data Structures

Vishnu Mohan

, Anirudh Potturi

and Munehiro Fukuda

Division of Computing and Software Systems, University of Washington Bothell, U.S.A.

Keywords:

ABM, Agent Migration, Data Structures, Data Analysis, Parallel Computing.

Abstract:

In contrast to conventional data streaming, we take an agent-based approach where a large number of reactive

agents collaboratively analyze attributes or shapes of distributed data structures that are mapped over a cluster

system. Our approach beneﬁts distributed graph database and GIS as agents are dispatched to data of interest

and navigate over nearby structured data for further exploration and exploitation. The successful key to this

approach is how to code agent propagation, forking, and ﬂocking over data structures. We automated such

agent migration in our MASS (multi-agent spatial simulation) library and wrote four benchmark programs

with these migration functions. The benchmarks include breadth-ﬁrst search, triangle counting, range search,

and closet pair of points in space. This paper demonstrates improvements of parallel performance with the

automated migration and presents our programmability comparison with Repast Simphony.

1 INTRODUCTION

Conventional big-data computing takes so-called

data-streaming approach that keeps pipelining

datasets to distributed data-analyzing libraries such

as MapReduce and Spark. While such datasets

are described in a structured ﬁle format, (e.g.,

CSV, XML, or JSon), they pass through distributed

memory as text data rather than form distributed

data structures (including graphs or geometric data

space). Therefore, data streaming has challenges in

repetitive data retrievals from and data analysis using

distributed graph database or GIS although it is still

used to feed initial data to these databases.

In contrast, we apply agent-based modeling

(ABM) to analyses of distributed data struc-

tures (Fukuda et al., 2020). Our approach constructs

graphs or arrays over a cluster system, dispatches a

large number of reactive agents to the datasets, and

have the agents compute data attributes or shapes.

Applying ABM to data science has been used in bio-

inspired optimization algorithms such as ant colony

optimization (ACO) (Blum, 2005). However, they

generally populate only tens of agents over a plain

dataset. Our work is differentiated in handling mil-

lions of agents over a distributed data structure.

To verify the efﬁciency of our agent-based data

https://orcid.org/0000-0002-1224-2950

https://orcid.org/0000-0002-9270-9628

https://orcid.org/0000-0001-7285-2569

analysis, we previously implemented benchmark pro-

grams with our MASS (multi-agent spatial simula-

tion) library (Fukuda et al., 2020). These include

breadth ﬁrst search, triangle counting, ACO, particle

swarm optimization, K-means, and K-nearest neigh-

bors. These benchmark programs revealed that our

approach and MASS library need two improvements

towards the practicalization (Gordon et al., 2019):

spatial description and agent migration support. As

we have addressed agent-navigable graph structures

including their construction (Gilroy et al., 2020),

pipelined computation (Hong and Fukuda, 2022), and

visualization (Blashaw and Fukuda, 2022), this paper

focuses on agent migration.

Agent migration we consider includes propaga-

tion, forking, and ﬂocking over a graph and a 2D con-

tiguous space, both mapped to a cluster system. Hav-

ing reviewed the above applications, we formulated

common patterns of agent migration and automated

them as migration functions. Using the new auto-

mated migration, we then reimplemented breadth-ﬁrst

search, triangle counting, range search, and closet pair

of points for our veriﬁcation purposes.

This paper presents the following three endeavors

of agent migration: (1) an implementation of new mi-

gration functions and platforms to support these func-

tions, (2) performance improvements in agent-based

graph and geometric computation, and (3) simpliﬁ-

cation of MASS agent code as well as programma-

bility comparison between MASS and Repast Sim-

Mohan, V., Potturi, A. and Fukuda, M.

Automated Agent Migration over Distributed Data Structures.

DOI: 10.5220/0011784500003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 1, pages 363-371

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

363

phony (North et al., 2007). The rest of this paper

is organized as follows: Section 2 considers con-

ventional ABM systems’ agent migration over dis-

tributed datasets and clariﬁes their challenges; Sec-

tion 3 designs and implements automated agent mi-

gration in MASS; Section 4 demonstrates improve-

ments of migration performance and programmabil-

ity, using graph and geometric benchmark programs;

and Section 5 concludes our discussions.

2 RELATED WORK

When applying ABM concepts to analysis of dis-

tributed data structures, we need to consider execution

performance and programmability for parallelization.

The former has been supported by MPI-based ABM

simulators represented by FLAME (Holcombe et al.,

2006) and RepastHPC (Collier and North, 2013).

Since their utmost goal is ABM parallel performance,

their C/C++ coding frameworks do not best support

programmability nor data visualization. However,

most interests of data scientists are quick coding and

easy visualization, for which they prefer interpretive

or script languages, (e.g., Java and Python). From this

viewpoint, we assume what if these scientists would

use NetLogo (NetLogo Models, 1999) or Repast Sim-

phony (North et al., 2007) as interpretive ABM sys-

tems when conducting their data analysis. Based on

our assumption, we focus on their descriptive features

for having agents migrate over data structures and an-

alyze their attributes.

NetLogo (NetLogo Models, 1999) supports agent

migration in a 2D continuous space and provides

agents with pre-deﬁned behaviors that can be utilized

by the model designers. It includes migration func-

tions such as FORWARD, BACKWARD, RIGHT,

LEFT, HATCH, DIE, JUMP and MOVE-TO. FOR-

WARD/BACKWARD enables agents to move for-

ward and backward from their current position in the

environment. RIGHT/LEFT enables agents to change

the direction of movement. DIE removes agents from

the environment. HATCH spawns new agents that in-

herit properties from their parent agent. MOVE-TO

moves agents to a given coordinate.

Repast Simphony (North et al., 2007) is another

ABM system that provides pre-deﬁned agent migra-

tion and behavior. This includes moveByDisplace-

ment, moveByVector, moveTo, VNContains, and

MooreContains. MoveByDisplacement moves agents

from their current location by a speciﬁed distance.

MoveByVector moves agents by a given distance

along a speciﬁed angle. MoveTo moves agents from

their current location to a new location. VNContains

determines whether or not a particular agent is in the

von Neumann neighborhood of a particular source.

MooreContains determines whether or not a particu-

lar agent is in the Moore neighborhood of a particular

source.

MASS has three versions, each in Java, C++, and

CUDA. For data sciences, we use MASS Java. The

library distinguishes two classes: Places and Agents.

The former constructs a multi-dimensional array over

a cluster system, whereas the latter populates and

walks agents over the array. For graph computing,

users can instantiate GraphPlaces that incrementally

constructs a distributed graph where agents move

along its edges. The library supports basic agent-

navigation and life-cycle-management functions: mi-

grate() to move agents to a speciﬁed place index;

spawn() to create new agents as inheriting their parent

properties; and kill() to terminate the calling agents.

All Places and Agents computation is performed in

parallel through their callAll() from the main() func-

tion. In addition, Places facilitates inter-place com-

munication with exchangeAll(), whereas Agents com-

mits all agent creation, termination, and migration at

once with manageAll().

All these ABM libraries deﬁne basic agent migra-

tion methods. However, they do not provide functions

that automate agent propagation and migration over

a graph or a 2D space. Users have to build custom

agent migration functions that would use these basic

migrations, which requires their signiﬁcant program-

ming capabilities to successfully perform data analy-

sis. Inability to automate agent navigational functions

gives a big burden to data scientists who hopes to con-

duct big-data computing with ABM. Knowledge of

these limitations motivated us to upgrade MASS Java

for supporting intelligent agent migration and propa-

gation out of the box.

3 ABSTRACTION OF AGENT

MIGRATION

This section ﬁrst looks at several applications in graph

computing and computational geometry to ﬁnd com-

mon patterns of agent migration. Thereafter, we will

explain their implementation and our infrastructural

supports for automated migration.

3.1 Application-Based Agent Migration

We consider the following ﬁve categories of appli-

cations: (1) breadth-ﬁrst search (BFS); (2) trian-

gle counting and connected components; (3) range

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

364

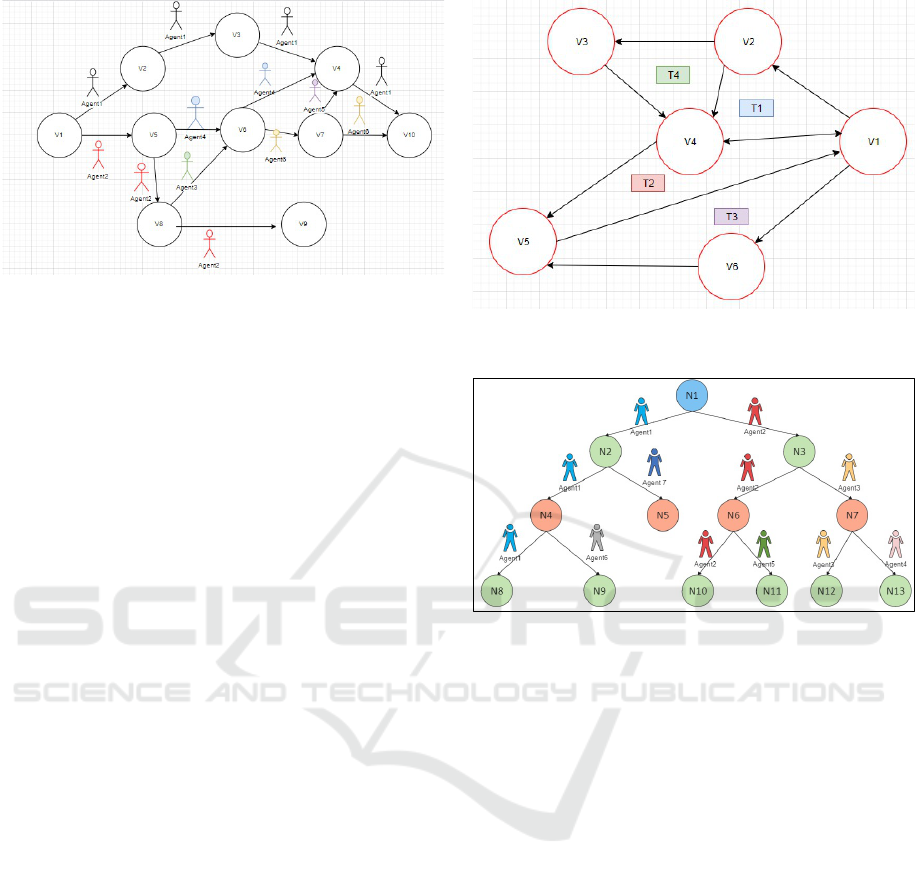
Figure 1: Agent propagation over a graph in BFS.

search; (4) the closet pair of points (CPP), Voronoi di-

agram construction, and K-nearest neighbors (KNN);

and (5) Dijkstra’ algorithms and ant colony optimiza-

tion (ACO).

3.1.1 BFS

This graph algorithm disseminates agents over a

graph until all vertices have been visited. Upon visit-

ing a next vertex, an agent needs to check if the cur-

rent vertex has been visited by another agent. If not, it

propagates its child agents to each of all neighboring

vertices except where it came from. To mitigate agent

creation and termination overheads, a parent agent it-

self should choose one of the next vertices to visit as

shown in Figure 1. We implement this feature in the

migratePropagate() function.

3.1.2 Triangle Counting and Connected

Components

To count the number of triangles in a graph, agents

walk on consecutively connected edges three times.

Those who come back to their original vertex can

report that they have successfully traveled around

a triangle. To avoid double-counting the same tri-

angle, agents are supposed to choose a next vertex

with a lower ID than the current vertex for the ﬁrst

two walks (see Figure 2). This is a special form

of migratePropagate() which we name migrateProp-

agateDownStream(). For their third walk, agents

must fetch an edge that leads back to their birth-

place. We implement this migration in migrateOrig-

inalSource(). Connected components have an agent

start its walk from each vertex with migrationProp-

agateDownStream(). As far as an agent successfully

migrates to a next vertex, it concurs this vertex with

the original vertex ID it is carrying from where it got

started. This eventually colors all connected vertices

with the largest vertex ID among them.

Figure 2: Edge traverses down to graph vertices with a

lower ID in triangle counting.

Figure 3: K-D tree traverse.

3.1.3 Range Search

Given a set of data points in a 2D space, range search

ﬁrst creates a k-d tree that recursively halves a space

along the x- and y-axes in turn so that left and right or

upper and lower spaces have the same number of data

points. To search for data points in a range of inter-

est, agents traverse from the tree root down to nodes

whose coverage is overlapped with the given range.

This computation involves a dynamic tree construc-

tion and agent propagation from the tree root. We

implement such agent propagation in migratePropa-

gateTree() that allows an agent to migrate along left,

right, or both links from the current tree node. As il-

lustrated in Figure 3, a parent agent must choose one

of tree links, which saves the number of agents to be

spawned.

3.1.4 CPP, Voronoi Diagram, and KNN

These applications simulate a ripple propagation from

each data point, which can be mimicked by repeti-

tively cloning agents from their current coordinates

to von Neumann or Moore neighborhood in turn, as

shown in Figure 4. The very ﬁrst agent that encoun-

ters another data point ﬁnds the closet pair of points.

Automated Agent Migration over Distributed Data Structures

365

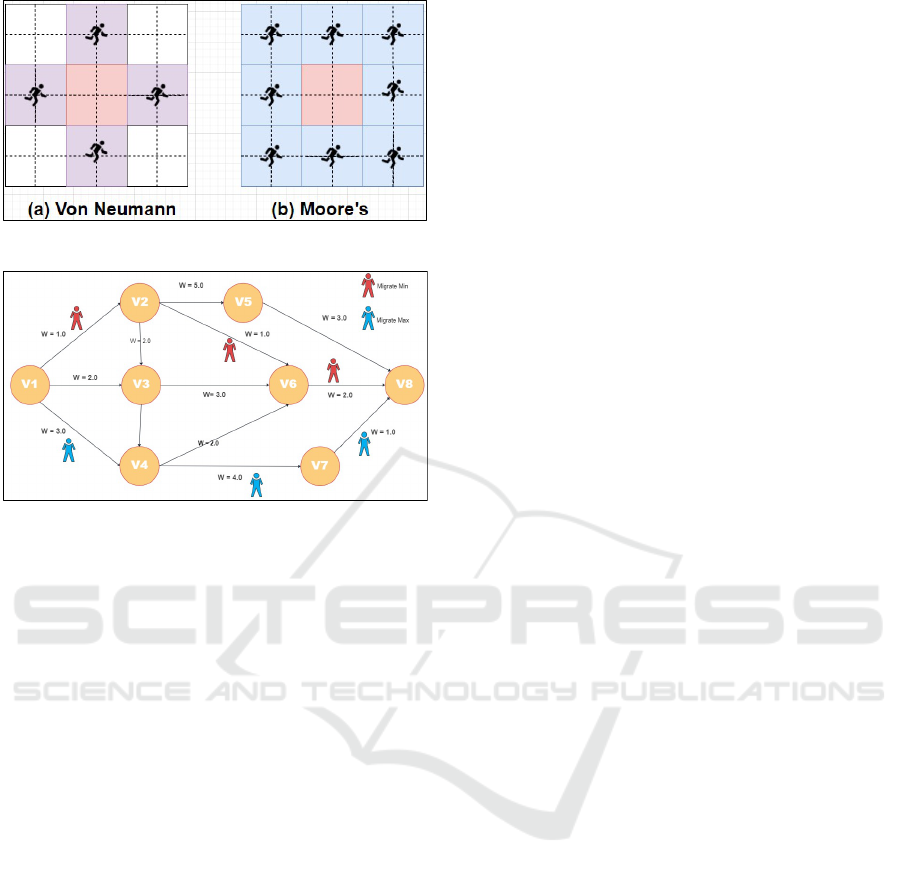
Figure 4: Ripple propagation over a 2D space.

Figure 5: Ants following the max amount of pheromone in

ACO.

Agent collision draws a bisector line between a pair

of two data points, which is considered as a Voronoi

edge. KNN simulates only one ripple propagation

from a test sample until the ripple covers N data points

in the same group.

3.1.5 Dijkstra’s Algorithm and ACO

Agents need to move along an edge whose weight

is either minimum or maximum among all edges

emanating from the current vertex. Dijkstra’s algo-

rithm chooses the shortest edge, while ACO choose

the edge with the largest amount of pheromone (see

Figure 5). In particular, an ant in ACO needs

to also choose a random edge for exploring new

routes. We implement these semantically directional

migrations in migrateMin(), migrateMax(), and mi-

grateRandom() respectively.

3.2 Mechanisms for Supporting

Abstraction

To support the new migration functions we formu-

lated in Section 3.1, we ﬁrst modiﬁed the MASS li-

brary’s agent and place management mechanisms, as

described below.

3.2.1 Agent Management

Derived from the Agent base class, SmartAgent im-

plements not only all the new migration functions

but also makes accessible additional properties: track,

prev, and next, each representing a chronological ID

list of places an agent navigated through so far, the ID

of the previous place it visited, and that of the next

place it will move to.

The new agent life-cycle management enhances

agent migration with a merger of spawn() and

migrate() functions. In contrast to the origi-

nal MASS library that needs two invocations of

Agents.callAll()/Agents.manageAll() pair, the ﬁrst to

commit spawn() and the second to commit migrate(),

the new spawn() function can dispatch child agents

to new destinations instantly in one invocation of

callAll() and manageAll(). This halves thread control

and inter-cluster communication overheads as each

call handles agent with multi-threading and involves

a cluster-wide barrier synchronization.

3.2.2 Spatial Management

SmartPlace is a subclass of the Place base class for

providing a user application with additional spatial

properties such as a list of neighboring places and

their logical distances. These properties are used in

the logic to implement Agent.migratePropagate() that

clones a calling agent to all neighboring vertices.

Instead of mimicking a binary or k-d tree with

GraphPlaces at a user level, we implement Binary-

TreePlaces, each including left and right branch ref-

erences to its child places. This new class eases our

Agent.migratePropagateTree() implementation. Fur-

thermore, it allows main() to add a new leaf to a given

tree node without any user-level agent deployment

that needs to manually perform this leaf addition.

3.3 An Implementation of Migration

Functions

Given the new mechanisms to support agent migra-

tion, below we explain each migration function.

1. migratePropagate(): has a calling agent declare

its migration to the ﬁrst neighbor that is not the

previous vertex (lines 9-16 in Listing 1). IDs of all

the other neighbors are packetized in an argument

list (lines 17-22). It is passed to spawn() (line 23)

that creates the same number of child agents and

dispatches each to a different vertex.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

366

Listing 1: Propagating to unvisited neighboring vertices.

1 public void migratePropagate( int time ) {

2 int[] nbrs = getPlace( ).getNeighbors( );

3 if ( getPlace( ).footprint || nbrs.length == 0 ) {

4 kill( ); // already visited or no more edges to

traverse

5 return;

6 }

7 getPlace( ).footprint = true;

8 int prev = −1; int next = −1;

9 if ( nbrs.length == 1 ) {

10 next = nbrs[0];

11 } else { // ﬁnd the ﬁrst neighbor, (i.e., next) to visit

12 for ( int i = 1; i < track.length; i++ )

13 if ( track[i] == −1 ) prev = track[i − 1];

14 next = ( nbrs[0] != prev ) ? nbrs[0] : nbrs[1];

15 }

16 migrate( next ); // the parent agent migrates to

17 int[] dests = new int[nbrs.length − 1]

18 for ( int i = 1; i < nbrs.length; i++ ) {

19 if ( nbrs[i] == prev || nbrs[i] == next )

20 continue;

21 dests[j++] = nbrs[i] // each child gets a different

dest.

22 }

23 spawn( dests.length, dest ); // children dispatched

24 }

Listing 2: Migrating to the source vertex.

1 public void migrateOriginalSource( ) {

2 int[] neighbors = getPlace( ).getNeighbors( );

3 boolean found = false;

4 for ( int i = 0; i < neighbors.length; i++ ) {

5 if ( neighbors[i] == track[0] ) {

6 migrate( neighbors[i]] ); // found the source

7 break;

8 } }

9 if ( !found ) kill( ); // no way to go back to the

source

10 }

2. migratePropagateDownStream(): needs to add

“nbrs[i] > getPlace( ).ID” to line 19’s if state-

ment in Listing 1.

3. migrateOriginalSource(): scans all the neighbor-

ing vertices and identiﬁes the one whose ID is this

agent’s track[0] where it needs to go back (lines

4-6 in Listing 2).

4. migratePropagateTree(): checks which of left,

right, or both paths a calling agent needs to go

(lines 9, 11, and 15 in listing 3). If the desired

path exists, the agent can migrate along it (lines

13 and 17). If necessary, the calling agent forks a

child to the right direction while taking left as its

own direction (line 10).

5. migratePropagateRipple(): receives the current

time to decide which of von Neumann or Moore

neighborhood a calling agent should take for its

2D propagation. As shown in listing 4, if time

is even, the agent propagates its copies to north,

Listing 3: Migrating down to child tree nodes.

1 public void migratePropagateTree( int path ) {

2 if ( getPlace( ).footprint ) {

3 kill( );

4 return;

5 }

6 getPlace( ).footprint = true;

7 int left = getPlace( ).left; int right = getPlace( ).

right;

8 switch( path ) {

9 case BothBranch: // go left and dispatch a child

right

10 if ( left != −1 && right != −1 ) spawn( 1,

right );

11 case LeftBranch:

12 if ( left != −1 )

13 migrate( left );

14 return;

15 case RightBranch:

16 if ( right != −1 )

17 migrate( right );

18 return;

19 }

20 kill( ) // no way to go

21 }

Listing 4: Propagating over 2D.

1 public void migratePropagateRipple( int time ) {

2 if ( getPlace( ).footprint ) {

3 kill( );

4 return;

5 }

6 getPlace( ).footprint = true;

7 int nAgs = ( time % 2 == 0 ) ? 4 : 8; // #neighbors

8 Vector<int[]> nbrs = new Vector<int[]>( nAgs

);

9 int[] cur = getPlace( ).coordinates;

10 // N, E, S, and W propagations

11 nbrs.get(0)[0] = cur[0]; nbrs.get(0)[1] = cur[1]+1;

12 nbrs.get(1)[0] = cur[0]+1; nbrs.get(1)[1] = cur[1];

13 nbrs.get(2)[0] = cur[0]; nbrs.get(2)[1] = cur[1]−1;

14 nbrs.get(3)[0] = cur[0]−1; nbrs.get(3)[1] = cur[1];

15 if ( nAgs == 8 ) { // #agents == 8 in Moore’s

16 // NE, SE, SW, and NW propagations

17 nbrs.get(4)[0] = cur[0]+1; nbrs.get(4)[1] = cur

[1]+1;

18 nbrs.get(5)[0] = cur[0]+1; nbrs.get(5)[1] = cur

[1]−1;

19 nbrs.get(6)[0] = cur[0]−1; nbrs.get(6)[1] = cur

[1]−1;

20 nbrs.get(7)[0] = cur[0]−1; nbrs.get(7)[1] = cur

[1]+1;

21 }

22 spawn( nAgs, nbrs ); // propagate ripples to

neighbors

23 kill( ); // no more ripple at the current coordinates

24 }

east, south, and west only (lines 11-14). Other-

wise, it also clones itself to northeast, southeast,

southwest, and northwest (lines 17-20). The call-

ing agent then gets terminated (line 23).

6. migrateMax(): chooses the one with the maxi-

mum weight among all edges emanating from the

current vertex. Listing 5 shows no special tech-

niques but can save lines of user-level code.

Automated Agent Migration over Distributed Data Structures

367

Listing 5: Migrating along the max-weighted edge.

1 public void migrateMax( ) {

2 int[] neighbors = getPlace( ).getNeighbors( );

3 int[] weights = getPlace( ).getWeights( );

4 int weight = Integer.MIN VALUE;

5 int maxIndex = 0;

6 for ( int i = 0; i < weights.length; i++ ) {

7 if ( weight < weights[i] ) {

8 weight = weights[i];

9 maxIndex = i;

10 } }

11 migrate( neighbors[maxIndex] );

12 }

Table 1: Benchmark programs and test parameters.

Methods Applications

Test

Parameters

MigratePropagate BFS

Graphs with

100, 500, 1K,

and 2K

vertices

MigratePropagateDownStream

Triangle Counting

Graphs with

1K, 3K, 10K

MigrateOriginalSource vertices

MigratePropagateTree

(BothBranch)

Range Search

Trees with

100, 100K,

MigratePropagateTree

(LeftBranch)

and 200K

vertices

MigratePropagateTree

(RightBranch)

MigratePropagateRipple CPP

2D continuous

space with 64,

100, 100K,

and 200K data

points

4 EVALUATION

Our performance and programmability evaluation

used four benchmark programs: BFS, triangle count-

ing, range search, and CPP. The ﬁrst two programs

are graph computing, whereas the last two are catego-

rized in computational geometry.

For the performance evaluation, we coded these

four benchmark programs with MASS Java in two

version: one without using the automated migration

functions and the other using these functions. (In the

following discussions, we distinguish them as legacy

MASS and new MASS, respectively.) Then, we ran

them on a cluster of four Linux machines, each with

a Xeon Gold 6130 @ 2.10GHz processor and 16GB

memory. The measurements were repeated ﬁve times

for each of spatial parameters as listed in Table 1.

For the programmability evaluation, we ﬁrst com-

pared legacy and new MASS versions to demonstrate

substantial improvements when using the automated

Figure 6: Performance of breadth ﬁrst search.

migration. We then coded the same benchmark pro-

grams with Repast Simphony, which allowed us to

compare MASS and Repast Simphony in their pro-

grammability.

4.1 Execution Performance

Figures 6 through to 10 demonstrate how the new

MASS version brings performance impacts onto BFS,

triangle counting, k-d tree construction followed by

range search, and CPP. Below we analyze parallel per-

formance of each benchmark program.

4.1.1 BFS

As shown in Figure 6, the execution time for mi-

gratePropagate() is lower than that taken by the

legacy migration. Their performance difference di-

verges as the number of vertices in a graph gets in-

creased. The performance improvement is primarily

due to the usage of the new manageAll() that spawns

and moves child agents as a part of a single execution.

The more graph vertices there are, the more agents

need to be spawned for migration, which is efﬁciently

supported by the new manageAll().

4.1.2 Triangle Counting

Figure 7 demonstrates the performance improvements

by migratePropagateDownStream() and migrateO-

riginalSource(). Since these two automated functions

are rather restrictive to spawning agents than explo-

sive migratePropagate(), they did not reduce execu-

tion time so drastically.

4.1.3 K-D Tree Construction and Range Search

The legacy MASS is not scalable enough to construct

a k-d tree covering 100K or more data points. On the

other hand, as mentioned in Section 3.2.2, the new

MASS increased the tree construction scalability so

as to handle beyond 100K data points. Figure 8 shows

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

368

Figure 7: Performance of triangle counting.

Figure 8: Performance of k-d tree construction.

almost a linear increase of tree-construction time

with the new MASS version. Using migratePropa-

gateTree(), the new MASS clearly demonstrates the

O(nlog n) performance of range search from 100 to

200K data points (see Figure 9).

4.1.4 CPP

Figure 10 compares the legacy and new MASS ver-

sions for their CPP execution performance. Both ver-

sions show little difference in their execution time.

This is because a ripple propagation does not in-

Figure 9: Performance of range search.

Figure 10: Performance of closets pair of points.

crease agent population so drastically as observed in

BFS. Furthermore, the more data points there are, the

higher the chances an agent encounters the nearest

data point within less simulation cycles.

In summary, the automated agent migration

mainly improves the execution performance and spa-

tial scalability of graph propagation and tree traverse

by agents.

4.2 Programmability Evaluation

Tables 2, 3, and 4 respectively compare the pro-

grammability between legacy and new MASS ver-

sions, between new MASS and Repast Simphony, and

across ABM libraries.

4.2.1 Improvements Within MASS

We counted each benchmark program’s lines of code

(LoC) by removing all blanks and comments from the

source code. Then, we measured how much reduction

was made for each benchmark program from legacy

to new MASS versions. Table 2 shows that BFS and

triangle counting achieved the highest percentage of

lines removed (83% and 60% respectively) while CPP

had the lowest reduction, (i.e., 22%). This is be-

cause migratePropagate(), migratePropagateDown-

Stream(), and migrateOriginalSource() were able to

fully abstract the agent navigation and propagation

from BFS and triangle-counting logic.

While CPP utilized the SpaceAgent class that au-

tomated propagation to the von Neumann or Moore

neighborhood, it still needed user-level logic to re-

move redundant agents that were duplicated from the

previous ripple propagation. For instance, agents dis-

patched from west to east and from south to north may

collide each other at the same coordinates, in which

case one of them must be removed. At present, these

redundancy check and agent removal operations are

not supported by the new migration functions.

Automated Agent Migration over Distributed Data Structures

369

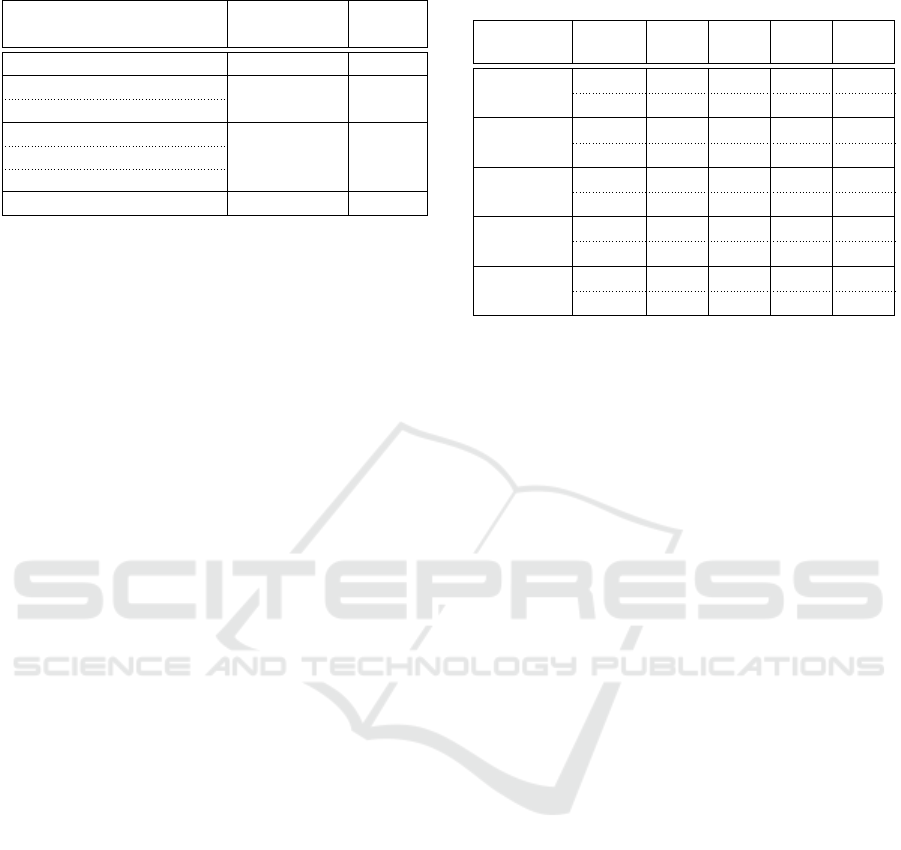
Table 2: LoC reduction with automated agent migration.

Methods Applications LoC

Reduction

MigratePropagate BFS 83%

MigratePropagateDownStream

Triangle Counting 60%

MigrateOriginalSource

MigratePropagateTree (BothBranch)

Range Search 44%

MigratePropagateTree (LeftBranch)

MigratePropagateTree (RightBranch)

MigratePropagateRipple CPP 22%

4.2.2 MASS vs Repast Simphony

New MASS no longer requires benchmark programs

to write ﬁne-grain instructions to support automatic

agent migration, tree traversal, and 2D propagation.

Instead, they are built upon these new features. On the

other hand, for Repast Simphony, we had to develop

the AgentManager class from scratch as it was essen-

tial to all its benchmark programs but was not read-

ily available. As the name suggests, AgentManager

is responsible for basic agent-management operations

including agent creation, termination, and migration

control. Implementing the same auto-navigation as

MASS Java in Repast Simphony for each benchmark

program requires slight modiﬁcations to this base

code.

To evaluate the programmability of these applica-

tions, LoC is a measure used to identify how much

programming must be done to implement an applica-

tion. Cyclomatic complexity is another metric used to

determine the complexity of a program based on the

number of logical paths in it. The LoC and Cyclo-

matic complexity are good metrics to explain better

how much complex code one needs to develop for an

application. Agent LoC represents LoC used to deﬁne

the patterns of agent behavior and their tasks. Space

LoC is code used to deﬁne the space within which the

problem is distributed and built on.

As detailed in Table 3, the overall LoC in Repast

is higher than MASS, (i.e., 1545 versus 1056 in total)

because of the need for code deﬁning the structural

elements. Agent LoC is higher in Repast, (i.e., 553

versus 274) because of the mandatory use of Agent-

Manager, much of which contributed to the Agent

LoC. An agent reacts to a change in its environment.

Hence, Space LoC is higher, too in Repast, (i.e.,

378 versus 186) because this section is used to de-

velop the space and acts as a point of invocation of

method calls to AgentManager. This process is sim-

ple yet seeks ﬁne-grained instructions, as mentioned

above. By choice of design, CPP in MASS used an

additional class, taking advantage of the strengths of

object-oriented programming in storing the CPP re-

Table 3: Quantitative Programmability Comparison be-

tween MASS and Repast Simphony.

Measures

Libraries BFS

Tri

Count

Range

CPP

LoC

MASS 79 175 400 362

Repast 432 260 539 314

Cyclomatic

MASS 2.25 3.875 3.944 3.1

complexity

Repast 1.785 2.45 2.6 2.31

Agent LoC

MASS 17 40 122 95

(A)

Repast 229 76 139 109

Space LoC

MASS 19 37 120 10

(S)

Repast 111 94 130 43

Model Mgmt

MASS 43 98 158 257

LoC - (A + S)

Repast 92 90 270 162

sults; unlike in Repast, a simple array of points was

used. Repast’s CPP saw reduced code (i.e., 314 ver-

sus 362) because of the simpliﬁed approach to record-

ing the results. The Cyclomatic complexity in MASS

is increased through iterations and conditionals. It

ranges from 2.25 to 3.944 as compared to Repast’s

Cyclomatic complexity in 1.785 through to 2.6. The

decision-making process contributes to this by call-

ing the appropriate agent migration methods followed

by other utility methods. The repeated use of condi-

tionals can be closely associated with MASS’ object-

oriented approach and switch statements in calling ap-

propriate base methods. Lastly, in BFS with Repast,

the modiﬁed AgentManager increased Agent LoC.

Space LoC was majorly increased because, unlike

other implementations, the generation of vertices and

their neighbors was in-built into the application.

4.2.3 Availability of Automated Agent Migration

Across Products

We also compared the availability of automated agent

migration methods with Netlogo and Repast Sim-

phony. As summarized in Table 4, with the introduc-

tion of the new automated agent navigation, MASS

now has the greatest number of advanced agent mi-

gration methods. Repast Simphony supports cer-

tain agent navigational methods such as Shortestpath,

MoveAgentByDisplacement and MoveAgentbyVec-

tor that are currently not supported in MASS. How-

ever, SmartAgent in MASS can be easily extended to

incorporate these agent navigational patterns.

Based on our evaluation in this section, we can

conclude that the new automated agent migration

along with the improvements in the agent/spatial

management has brought signiﬁcant performance im-

provements to MASS while executing the benchmark

programs. The new automated agent migration has

also made MASS easier to use and has improved

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

370

Table 4: Availability of automated agent migration across

products.

Methods

NetLogo Repast MASS

MigratePropagate

No Yes

Yes

MigratePropagateDownStream

No No Yes

MigrateOriginalSource

No No Yes

MigratePropagateTree

No Yes Yes

MigratePropagateRipple

Yes

(Yes)

Yes

MigrateMin

No No Yes

MigrateMax

No No Yes

MigrateRandom

No No Yes

ShortestPath

No Yes No

MoveAgentByDisplacement

No Yes No

MoveAgentByVector

No Yes No

Repast Simphony can perform breadth ﬁrst search.

NetLogo supports Voronoi diagram and K-Nearest Neighbor.

Repast Simphony can check if an agent is present in the von Neumann or

Moore neighborhood.

the programmability when compared to Repast Sim-

phony and Netlogo.

5 CONCLUSIONS

Focusing on agent-based graph computing and com-

putational geometry, we found common agent mi-

gration patterns from several benchmark programs

and formulated them as high-level migration func-

tions. Using these migration functions, we re-coded

the same MASS benchmark programs. Our perfor-

mance and programmability measurements demon-

strated that the automated agent migration not only

accelerated the execution but also improved the pro-

grammability as compared to Repast Simphony.

To further extend the work we have completed, we

see the following three opportunities. The ﬁrst plan

intends to introduce additional agent navigation func-

tions including:

• PropagateRippleWithBouncing: to support the

calculation of Euclidean shortest path between

two points over contiguous space by propagating

a ripple from the source point and bouncing off

opaque obstacles until the ripple detects the desti-

nation point.

• MigrateLowestCoordinatePoint and MigrateUn-

boundedRegion: to construct a convex hull by

moving an agent to the starting coordinate point

and thereafter by walking the agent to the Voronoi

site present in the unbounded Voronoi region.

• MoveAgentByDisplacement and MoveAgent-

ByVector: to move an agent from its current

location by a given distance over a continuous

space or to move an agent by the distance along a

speciﬁed angle.

Our second plan is to evaluate MigrateMin,

MigrateMax, and MigrateRandom with additional

benchmark programs such as Dijkstra’s algorithm. Fi-

nally, our third plan is re-implementations of more

benchmark programs including Voronoi diagram and

convex hulls in MASS, using the automated agent

navigation methods.

REFERENCES

Blashaw, D. and Fukuda, M. (2022). An Interactive En-

vironment to Support Agent-based Graph Program-

ming. In Proc. of the 14th International Conference

on Agents and Artiﬁcial Intelligence - Volume 1, pages

148–155.

Blum, C. (2005). Ant colony optimization: introduction and

recent trends. Physics of Life Reviews, 2(4):353–373.

Collier, N. and North, M. (2013). Parallel agent-based sim-

ulation with Repast for High Performance Computing.

Simulation, 89(10):1215–1235.

Fukuda, M., Gordon, C., Mert, U., and Sell, M. (2020).

Agent-Based Computational Framework for Dis-

tributed Analysis. IEEE Computer, 53(3):16–25.

Gilroy, J., Paronyan, S., Acoltz, J., and Fukuda, M. (2020).

Agent-Navigable Dynamic Graph Construction and

Visualization over Distributed Memory. In 7th Int’l

Workshop on BigGraphs’20, pages 2957–2966. IEEE.

Gordon, C., Mert, U., Sell, M., and Fukuda, M. (2019).

Implementation techniques to parallelize agent-based

graph analysis. In Int’l Workshops of PAAMS 2019,

Highlights of Practical Applications of Survivable

Agents and Multi-Agent Systems, pages 3–14, Avila,

Spain.

Holcombe, M., Coakley, S., and Smallwood, R. (2006).

A General Framework for Agent-based Modelling of

Complex Systems. In European Conference on Com-

plex Systems 2006 - ECCS’06, pages 83–88, Oxford,

UK.

Hong, Y. and Fukuda, M. (2022). Pipelining Graph Con-

struction and Agent-based Computation over Dis-

tributed Memory. In 9th Int’l Workshop on Big-

Graphs’22, page to appear. IEEE.

NetLogo Models (1999). Accessed on:

November 20, 2022. [Online]. Available:

https://ccl.northwestern.edu/netlogo/models/.

North, M. J., Tatara, E., Collier, N., and Ozik, J. (2007).

Visual Agent-based Model Development with Repast

Simphony. In Agent 2007 Conference on Complex In-

teraction and Social Emergence, Chicago, IL.

Automated Agent Migration over Distributed Data Structures

371