On the Use of Multiple Approximations in the Linear Cryptanalysis of

Baby Rijndael

Josef Koke

s and R

obert L

orencz

Department of Information Security, Faculty of Information Technology,

Czech Technical University in Prague, Thakurova 9, Praha 6, Czech Republic

Keywords:

AES, Rijndael, Baby-Rijndael, Linear Cryptanalysis, Key Recovery.

Abstract:

In this paper, we follow up on our previous research on the resistance of Baby Rijndael, a reduced AES variant,

to linear cryptanalysis. We address the issue of relatively low accuracy of the recovery of the encryption key

by exploiting multiple linear approximations at once to deduce the correct bit of the key. We try several

different methods with varying degree of success, with the ﬁnal technique increasing the average accuracy of

the recovery of the bit of the key to over 82 % in the best case. However, even that technique is not capable of

breaking the cipher with less effort than the brute force.

1 INTRODUCTION

The Rijndael cipher, designed in 1998 by Vincent Ri-

jmen and Joan Daemen (Daemen and Rijmen, 1999),

is the most commonly used symmetric block cipher

in the world, thanks to its status as the winner of the

Advanced Encryption Standard (NIST, 2001) (AES)

public competition conducted by the National In-

stitute of Standards and Technology between 1997

and 2001. It is freely available to everyone, se-

cure, fast, easy to implement on many platforms (Fis-

cher and Drutarovsk

y, 2001)(Satoh et al., 2001), and

as such commonly found in many different appli-

cations, both hardware and software. AES is sup-

ported by modern CPUs (Gueron, 2010) as well as

modern operating systems (Microsoft Corporation,

2018)(Google Corporation, 2021) and it is an inte-

gral part of many security-related standards and pro-

tocols, including such commonly used protocols as

the SSL/TLS (where it is one of the very few re-

maining block encryption algorithms, as per the cur-

rent TLS version 1.3) (Rescorla, 2018), SSH (Bellare

et al., 2006) or WPA.

From the very beginning, Rijndael was designed

with security in mind (Daemen and Rijmen, 1999).

In particular, NIST’s proposals required that an AES

candidate must be resistant to all currently-known

cryptanalytic techniques, including algebraic crypt-

analysis (Bard, 2009), linear cryptanalysis (Mat-

sui, 1993) and differential cryptanalysis (Biham and

Shamir, 1991), and Rijndael does indeed address

this requirement in its design (Daemen and Rijmen,

2002). In practical terms, however, this fact is dif-

ﬁcult to actually verify due to the effort needed for

such a veriﬁcation: The cipher is designed to with-

stand brute force attacks on its security and that nec-

essarily affects also attempts of cryptanalysts to verify

the security claims.

In our past research, we tried to work around this

limitation by exploiting the highly adjustable nature

of Rijndael to choose a suitable reduced-size model of

the cipher (Cid et al., 2005)(Bergman, 2005) and then

perform linear cryptanalysis on this model (Koke

2013). The expectation here is that either an attack

would be successful and then we can explore the

properties that made it possible, hopefully extending

it to full AES, or that an attack would fail, which

would tend to indicate that a similar attack on the

more complex but conceptually similar AES would

be even more likely to fail. While our past studies

(Koke

s and L

orencz, 2015) were not able to actually

break even the tiny Baby Rijndael (Bergman, 2005),

they did reveal some interesting phenomena in respect

to the cipher and its linear cryptanalysis, worth further

study.

This paper represents a continuation of these ef-

forts.

174

Kokeš, J. and Lórencz, R.

On the Use of Multiple Approximations in the Linear Cryptanalysis of Baby Rijndael.

DOI: 10.5220/0011785400003405

In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 174-179

ISBN: 978-989-758-624-8; ISSN: 2184-4356

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 STATE OF THE ART

The Rijndael cipher was designed to be highly conﬁg-

urable (Daemen and Rijmen, 2002), able to adapt to

many different security needs. AES is by far the most

common conﬁguration of Rijndael, but many others

with presumably the same security properties are pos-

sible due to the fact that the cipher’s design strictly

follows the following process:

1. Deﬁne properties required for security.

2. Propose options of achieving these properties.

3. If multiple options are available, choose the

clearly more secure ones.

4. If multiple options are available, choose those that

are more efﬁcient to implement on the target plat-

forms.

5. If multiple options are available, choose the “sim-

plest” one.

This has led to a development of many other variants

of Rijndael by varying the core conﬁguration param-

eters such as the number of rounds or the dimensions

of the cipher’s state (Cid et al., 2005) and then ana-

lyzed as to their security properties (Solil, 2016). One

particularly interesing variant is the Baby Rijndael.

Baby Rijndael is a block cipher proposed by Cliff

Bergman (Bergman, 2005) as an educational block ci-

pher. It is modeled after Rijndael (AES), but with

reduced key- and block-space: it uses 16-bit blocks

and 16-bit keys. Its design, however, follows the de-

sign of the full Rijndael, respecting the requirements,

implementations and design decisions set by Daemen

and Rijmen in the Rijndael proposal (Daemen and Ri-

jmen, 1999) and further explained in the cipher docu-

mentation (Daemen and Rijmen, 2002). The cipher’s

properties in regards to the differential cryptanalysis

were studied by Wrolstad (Wrolstad, 2009), Tomanek

(Tomanek, 2017) and Poljak (Poljak, 2017).

In our research, we ﬁrst performed some prelimi-

nary analyses of the cipher (Koke

s, 2013) in regards

to its suitability as a model for AES and to its vulner-

ability to basic linear cryptanalysis, and when these

properties were found satisfactory, we extended the

research to perform an exhaustive study (Koke

s and

orencz, 2015). At the core of our approach was the

intention to exploit the small scale of the cipher to try

out all possible combinations of inputs to verify that

the cipher performs reasonably well in all cases, i.e.

that it is not vulnerable to a class of weaker keys or

easier-to-break plain-texts.

Among the key results of this research (Koke

s and

orencz, 2015) was the discovery that the cipher can

be expressed with a great number of alternative lin-

ear approximations, all sharing the same high linear

probability bias but exhibiting a signiﬁcant difference

in their ability to ﬁnd the correct encryption key when

averaged over all possible keys (see table 1).

Furthermore, when we focused at the apparently

most successful set of linear approximations with the

second and fourth active S-box, we found that there

was a great variance in each approximation’s ability

success rates, with the “best” approximations putting

the correct key at position around 40 on average and

the “worst” ﬁnding the correct key at position about

57 on average (see table 2).

It should be noted that these positions are not

very good considering the large number of required

plaintext-ciphertext samples for each key, the fact that

even the best approximations performed very poorly

with some keys and that the top candidate key was

only correct in 4.632 bits (out of 8) on average over

all approximations and all keys, with the best approxi-

mation only recovering 4.895 bits of a key on average.

To put this into a context, random guessing would ﬁnd

the correct key in position 128 on average and one

random guess would successfully recover 4 bits of the

key.

To increase the probability of a successful break,

we decided to shift our focus to guessing just individ-

ual bits — that is, to use linear cryptanalysis as usual,

but instead of trying to break the key as a whole, only

recover one bit at a time. Unfortunately, even though

this approach did increase the probability of a suc-

cessful guess to a little more than 70 % in case of the

best approximations (see table 3), that is still far too

unreliable to be used.

3 USING MULTIPLE

APPROXIMATIONS TO

IMPROVE THE SUCCESS RATE

Our current research was focused on trying to im-

prove the technique to increase the probability of a

successful recovery of the key, disregarding all other

factors such as the performance. In particular, we

considered the possibility of using multiple linear ap-

proximations on the same sample set — as Kaliski

and Robshaw suggest (Kaliski and Robshaw, 1994),

we can use multiple approximations to generate a

new statistic for our set of candidate keys, one which

would reduce variance of the result and thus decrease

the size of the required sample set.

We adapted the idea to the concept of Baby Rijn-

dael and the recovery of individual key bits. We used

a simple algorithm 1 for estimating the value of a bit

using majority voting and then used it to try to recover

On the Use of Multiple Approximations in the Linear Cryptanalysis of Baby Rijndael

175

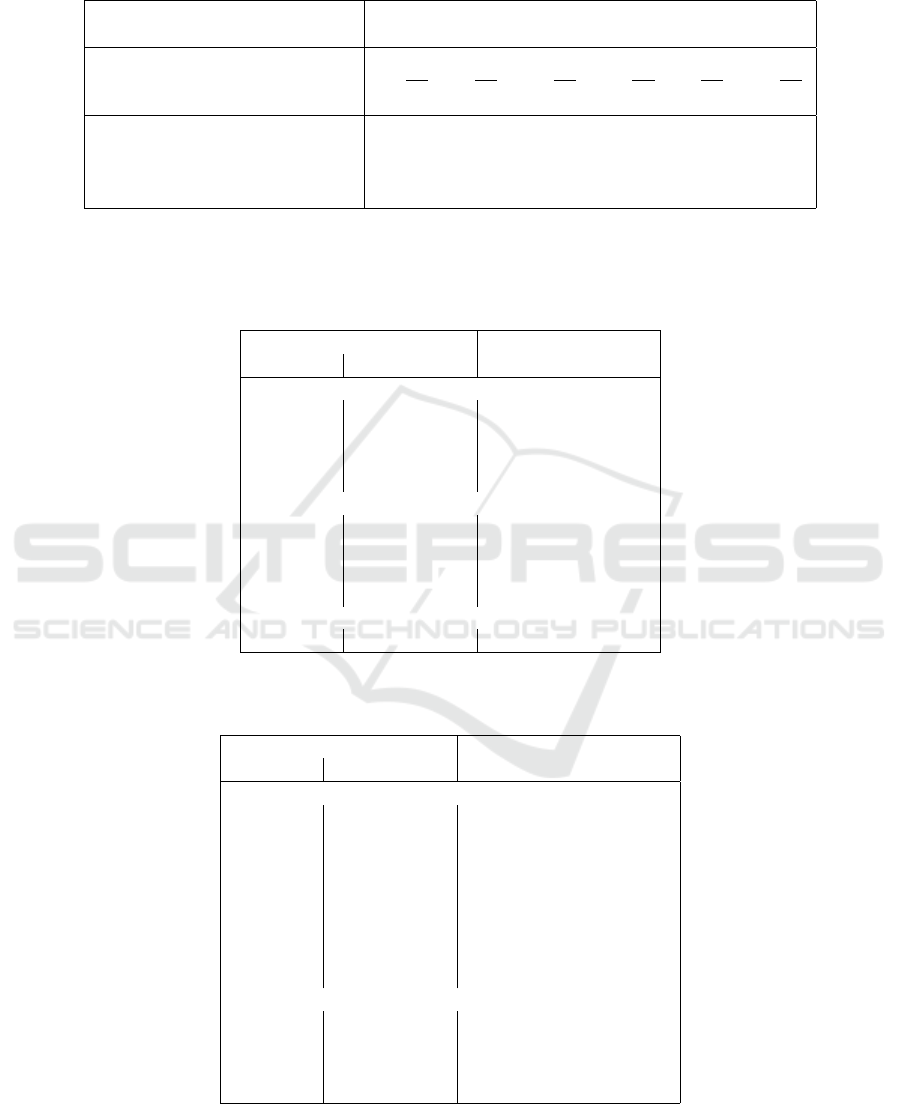
Table 1: Success rate of Baby Rijndael’s linear approximations. The lower the average rank, the better can Algorithm 2

recover the correct key. The value of one-half of the number of candidate keys is the worst case, the linear approximations

can’t determine the correct key better than a random guess.

Active SubBytes

0011 0101 0110 1001 1010 1100

Optimal approximation’s

probability bias ±

256

Nr. of opt. approximations 3840 48 48 48 48 3840

Nr. of candidate keys 256 256 256 256 256 256

Average rank of the correct key 114.75 49.58 111.91 111.90 49.58 114.72

Median rank of the correct key 114.91 49.85 111.77 111.65 49.88 115.08

Std. deviation of the correct key 2.89 6.03 2.23 2.32 6.03 2.77

Table 2: Success rate of Baby Rijndael’s linear approximations of the “0101” class. The lower the average rank, the better

can Algorithm 2 recover the correct key. “Inner state” represents the bits at the beginning of the last round, after performing

the ShiftRows transformation. The active bits are counted from the right, that is, the left-most bit is number 15, the right-most

bit is number 0.

Active bits Average Std. dev.

Plaintext Inner state rank of rank

Best approximations

0, 2, 3 1, 2, 9, 10, 11 40.27 46.72

12, 14, 15 1, 2, 9, 10, 11 40.37 46.82

8, 10, 11 1, 2, 3, 9, 10 40.38 46.84

4, 6, 7 1, 2, 3, 9, 10 40.43 46.85

Worst approximations

4, 6, 7 0, 1, 8, 11 57.20 69.50

4, 6 0, 3, 9, 11 57.20 70.50

12, 14, 15 0, 3, 8, 9 57.25 69.55

0, 2, 3 0, 3, 8, 9 57.40 69.65

Average over all 48 approximations

49.58 61.04

Table 3: The probability of recovery of individual bits of the key, when calculated as the probability that the given bit in a

recovered last-round key is correct across all possible keys.

Active bits Recovered Probability

Plaintext Inner state bit of recovery

Best approximations

0, 2 1, 3, 8, 11 3 0.703

8, 10 0, 3, 9, 11 11 0.701

4 0, 1, 8, 11 3 0.683

12 0, 3, 8, 9 11 0.682

0 0, 3, 8, 9 11 0.682

8 0, 1, 8, 11 3 0.679

12, 14, 15 0, 3, 8, 9 11 0.677

10, 11 1, 2, 3, 9, 10 0 0.676

Worst approximations

12, 14, 15 1, 2, 9, 10, 11 11 0.511

4, 6, 7 1, 2, 3, 9, 10 3 0.510

8, 10 1, 2, 11 11 0.493

0, 2 3, 9, 10 3 0.491

every bit position available in the key mask individu-

ally as per algorithm 2.

We performed the test for bits 0, 3, 8 and 11,

which were shown to be the most easily recoverable

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

176

Algorithm 1: Calculate average bit value.

1: function CALCBIT(BitSum, BitCount)

2: if 2 · BitSum > BitCount then

3: return 1

4: else if 2 · BitSum < BitCount then

5: return 0

6: else

7: Raise an error

8: end if

9: end function

Algorithm 2: One key bit recovery using multiple linear

approximations.

1: function ONEKEYBITRECOV-

ERY(Approximations, MasterKey, BitPosition)

2: Samples ← GENERATESAMPLES(MasterKey)

3: LastRoundKey ←

KEYEXPANSION(MasterKey, NumberO f Rounds − 1)

4: BitSum ← 0

5: BitCount ← 0

6: for all Approximation inApproximations do

7: ApproxBitSum ← 0

8: ApproxBitCount ← 0

9: RankedCandidates ←

RANKCANDIDATEKEYS(

Approximation.PlainTextMask,

Approximation.InnerStateMask, Samples)

10: for all CandidateKeyin RankedCandidates do

11: if CandidateKey.Rank = 0 then

12: if GETBITVALUE(

CandidateKey.Key, BitPosition)

= GETBITVALUE(LastRoundKey, BitPosition) then

13: ApproxBitSum ← ApproxBitSum +

14: end if

15: ApproxBitCount ← ApproxBitCount +

16: end if

17: end for

18: BitSum ← BitSum +

CALCBIT(ApproxBitSum, ApproxBitCount)

19: BitCount ← BitCount + 1

20: end for

21: return CALCBIT(BitSum, BitCount)

22: end function

key bits in our previous tests. Five best approxima-

tions were used for each bit and an average success

rate was measured over all existing master keys. The

results are stored in Recovery of bit ??.log ﬁles.

The summary results for all algorithms are shown in

table 4.

This approach, unfortunately, leads to a large

number of indeterminate results in cases where the

correct and incorrect results are evenly matched. To

improve that, a modiﬁcation was made which would

work with “fuzzy” (indeterminate) bits, hoping that

the remaining approximations would overcome these

matched opposites. The bit-calculating algorithm is

shown in algorithm 3, the key recovery in algorithm 4

with the UseWeight argument set to False. The sum-

mary results for all algorithms are shown in table 4.

Algorithm 3: Calculate fuzzy average bit value.

1: function CALCFUZZYBIT(BitSum, BitCount)

2: if 2 · BitSum > BitCount then

3: return 1

4: else if 2 · BitSum < BitCount then

5: return 0

6: else

7: return 0.5

8: end if

9: end function

Algorithm 4: One key bit recovery with fuzzy bits.

1: function ONEKEYBITRECOVERYFUZZY(

Approximations, MasterKey, BitPosition,

UseWeight)

2: Samples ← GENERATESAMPLES(MasterKey)

3: LastRoundKey ←

KEYEXPANSION(MasterKey, NumberO f Rounds − 1)

4: BitSum ← 0

5: BitCount ← 0

6: for all Approximation in Approximations do

7: ApproxBitSum ← 0

8: ApproxBitCount ← 0

9: if UseWeight then

10: ApproxWeight ← Approximation.Weight

11: else

12: ApproxWeight ← 1

13: end if

14: RankedCandidates ←

RANKCANDIDATEKEYS(

Approximation.PlainTextMask,

Approximation.InnerStateMask, Samples)

15: for all CandidateKeyin RankedCandidates do

16: if CandidateKey.Rank = 0 then

17: if GETBITVALUE(

CandidateKey.Key, BitPosition)

= GETBITVALUE(LastRoundKey, BitPosition) then

18: ApproxBitSum ← ApproxBitSum +

ApproxWeight

19: end if

20: ApproxBitCount ← ApproxBitCount +

ApproxWeight

21: end if

22: end for

23: BitSum ← BitSum + ApproxWeight

· CALCFUZZYBIT(ApproxBitSum,

ApproxBitCount)

24: BitCount ← BitCount + ApproxWeight

25: end for

26: return CALCFUZZYBIT(BitSum, BitCount)

27: end function

On the Use of Multiple Approximations in the Linear Cryptanalysis of Baby Rijndael

177

Table 4: The probability of a successful recovery of a bit of the encryption key using a speciﬁed algorithm. The probability is

calculated as an average number of correct occurrences of the bit over all possible keys, using all possible plaintext-ciphertext

samples for that key.

Algorithm Bit 0 Bit 3 Bit 8 Bit 11

Success Failure Success Failure Success Failure Success Failure

Simple recovery

Algorithm 2 74.57 18.82 77.18 16.64 74.86 18.83 77.43 16.34

Non-weighted recovery

Algorithm 4 with U seWeights = False 78.59 19.57 81.19 17.20 78.86 19.32 81.33 16.98

Non-weighted recovery

Algorithm 4 with U seWeights = True 79.47 20.53 82.01 17.99 79.85 20.15 82.19 17.81

This approach led to a marked decrease in the in-

determinate cases, but still some remained, as can be

seen in the NonWeightedRecovery of bit ??.log

ﬁles. A further modiﬁcation introduced a weight for

each linear approximation, where the weight is given

as the probability that the approximation would cor-

rectly calculate the bit over all possible keys. The al-

gorithm is shown in algorithm 4 with the UseWeight

argument set to True.

This algorithm completely removes the indeter-

minate bits, as seen in the WeightedRecovery

of-

bit ??.log ﬁles. However, the overall efﬁciency is

not signiﬁcantly improved — the indeterminate bits

simply split into the “correct” and “incorrect” groups

without any apparent reason for either category. The

summary results for all algorithms are shown in table

4 DISCUSSION AND

CONCLUSION

An interesting aspect of the optimal linear approxi-

mations is their varying ability to recover the master

key. We can divide the approximations into several

classes, and through exhaustive testing of all possible

keys we showed that approximations from some of

these classes are, on average, signiﬁcantly more suc-

cessful than approximations from other classes. This

suggests that, when we consider linear cryptanalysis,

we need to pay attention not only to the probability

bias, but also the choice among several possible ap-

proximations. We don’t as yet know why the classes

“0101” and “1010” are so much better than the others,

but we intend to ﬁnd out.

Even within a class of approximations, the vari-

ations in key recovery abilities are quite surprising.

We would deﬁnitely like to precisely measure, what

makes the “good” approximations different from the

“bad” ones. If we could discover some metric which

would let us choose the best approximation in ad-

vance, without having to perform intensive calcula-

tions, it would certainly be a useful result in its own.

It came as a distinct surprise to us that individual

key bits show quite a large difference in their ability

of being successfully recovered. We weren’t able to

formulate the reasons behind this behavior so far, but

this is also one of our research targets. We are par-

ticularly eager to continue our research in this area,

because we would like to explore our idea of using

information revealed by one cryptanalytic technique

(e.g. linear cryptanalysis in this case) to enhance the

power of another technique (e.g. algebraic cryptanal-

ysis) — and then inject the results back to the original

technique. It seems possible to achieve synergistic ef-

fects here.

The ultimate goal, of course, isn’t cryptanalysis

of Baby Rijndael, however interesting it may be. We

hope, though, that the principles we discover will

eventually allow us to attack even the full Rijndael

itself — or, failing that, at least give us some idea of

which approaches do have a hope of succeeding and

which do not.

It needs to be stressed that while our approach

did reveal some interesting information, it was not

successful in actually breaking the cipher — specif-

ically, it couldn’t recover the key with a lesser ef-

fort than brute force trial of all keys would. Quite

the opposite, in fact — in order to achieve a reason-

able level of success even in the best circumstances,

we had to much perform more work than if we sim-

ply tried out all keys, which would additionally use

simpler operations (i.e. the exponential complexity

would use a lower base), much less memory, only

need one plaintext-ciphertext sample and in addition

to all that it would be assured success after trying all

the combinations, something the key recovery using

linear cryptanalysis could not do. That, however, is

not a bad thing — it convincingly demonstrates that

Baby Rijndael is indeed resistant to linear cryptanaly-

sis even when conditions are extremely skewed in its

disfavor. We can expect even more resistance with the

standard Rijndael which does not contain these addi-

tional weaknesses.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

178

ACKNOWLEDGEMENTS

The authors acknowledge the support

of the OP VVV MEYS funded project

CZ.02.1.01/0.0/0.0/16 019/000 0765 “Research

Center for Informatics”.

REFERENCES

Bard, G. (2009). Algebraic Cryptanalysis. Springer US, 1st

edition.

Bellare, M., Kohno, T., and Namempre, C. (2006). The

secure shell (ssh) transport layer encryption modes.

Bergman, C. (2005). A description of baby rijndael. Tech-

nical report, Iowa State University.

Biham, E. and Shamir, A. (1991). Differential cryptanalysis

of des-like cryptosystems. Journal of CRYPTOLOGY,

4(1):3–72.

Cid, C., Murphy, S., and Robshaw, M. (2005). Small scale

variants of the aes. In Fast Software Encryption, pages

145–162. Springer Berlin Heidelberg.

Daemen, J. and Rijmen, V. (1999). Aes proposal: Rijndael.

Daemen, J. and Rijmen, V. (2002). The design of Rijndael:

AES – the Advanced Encryption Standard. Springer-

Verlag, Berlin, Heidelberg, 1st edition.

Fischer, V. and Drutarovsk

y, M. (2001). Two methods of ri-

jndael implementation in reconﬁgurable hardware. In

International Workshop on Cryptographic Hardware

and Embedded Systems, pages 77–92. Springer.

Google Corporation (2021). Android Developers: Cryptog-

raphy. Google Corporation.

Gueron, S. (2010). Intel Advanced Encryption Standard

(AES) New Instructions Set. Technical report, Intel

Corporation.

Kaliski, B. S. and Robshaw, M. J. (1994). Linear crypt-

analysis using multiple approximations. In Annual

International Cryptology Conference, pages 26–39.

Springer.

Koke

s, J. (2013). Cryptanalysis of baby rijndael.

Koke

s, J. and L

orencz, R. (2015). Linear cryptanalysis

of baby rijndael. In The Fourth International Con-

ference on e-Technologies and Networks for Develop-

ment (ICeND2015), pages 28–33. Lodz University of

Technology.

Matsui, M. (1993). Linear cryptanalysis method for des ci-

pher. In Workshop on the Theory and Application of of

Cryptographic Techniques, pages 386–397. Springer.

Microsoft Corporation (2018). Microsoft AES Crypto-

graphic Provider. Microsoft Corporation.

NIST (2001). Announcing the ADVANCED ENCRYP-

TION STANDARD (AES). Technical report, National

Institute of Standards and Technology (NIST).

Poljak, P. (2017). The impossible differential cryptanalysis.

Rescorla, E. (2018). The transport layer security (tls) pro-

tocol version 1.3.

Satoh, A., Morioka, S., Takano, K., and Munetoh, S. (2001).

A compact rijndael hardware architecture with s-box

optimization. In International Conference on the The-

ory and Application of Cryptology and Information

Security, pages 239–254. Springer.

Solil, L. (2016). Redukovan

e modely

sifry rijndael.

Tomanek, J. (2017). Diferenci

aln

ı kryptoanal

yza

sifry baby

rijndael.

Wrolstad, J. (2009). A differential cryptanalysis of baby

rijndael.

On the Use of Multiple Approximations in the Linear Cryptanalysis of Baby Rijndael

179