Improving Unlinkability in C-ITS: A Methodology For Optimal
Obfuscation
Yevhen Zolotavkin
1 a
, Yurii Baryshev
2 b
, Vitalii Lukichov
2 c
, Jannik M
¨
ahn
1 d
and Stefan K
¨
opsell
1 e
1
Barkhausen Institut gGmbH, W
¨
urzburger Straße 46, Dresden, Germany
2
Department of Information Protection, Vinnytsia National Technical University,
Khmelnytske Shosse 95, Vinnytsia, Ukraine
Keywords:
Privacy, V2X, Unlinkability, Hidden Markov Model, Cybersecurity, Entropy, Obfuscation.
Abstract:
In this paper, we develop a new methodology to provide high assurance about privacy in Cooperative Intelli-
gent Transport Systems (C-ITS). Our focus lies on vehicle-to-everything (V2X) communications enabled by
Cooperative Awareness Basic Service. Our research motivation is developed based on the analysis of unlink-
ability provision methods indicating a lack of such methods. To address this, we propose a Hidden Markov
Model (HMM) to express unlinkability for the situation where two vehicles are communicating with a Road-
side Unit (RSU) using Cooperative Awareness Messages (CAMs). Our HMM has labeled states specifying
distinct origins of the CAMs observable by a passive attacker. We then establish that high assurance about the
degree of uncertainty (e.g., entropy) about labeled states can be obtained for the attacker under the assump-
tion that he knows actual positions of the vehicles (e.g., hidden states in HMM). We further demonstrate how
unlinkability can be increased in C-ITS: we propose a joint probability distribution that both drivers must use
to obfuscate their actual data jointly. This obfuscated data is then encapsulated in their CAMs. Finally, our
findings are incorporated into an obfuscation algorithm whose complexity is linear in the number of discrete
time steps in the HMM.
1 INTRODUCTION
Due to the intense development of transport systems
over the recent decades, different modes of cooper-
ative intelligence have been incorporated into their
functionalities. Intelligent transport systems (ITS)
are transport systems in which advanced information,
communication, sensor and control technologies, in-
cluding the Internet, are applied to increase safety,
sustainability, efficiency, and comfort. Cooperative
Intelligent Transport Systems (C-ITS) are a group of
ITS technologies where service provision is enabled
by, or enhanced by, the usage of ‘live’, present situa-
tion related, dynamic data/information from other en-
tities of similar functionality, and/or between different
elements of the transport network, including vehicles
and infrastructure (ISO/TC 204, 2015).
a
https://orcid.org/0000-0002-1875-122X
b
https://orcid.org/0000-0001-8324-8869
c
https://orcid.org/0000-0002-3423-5436
d
https://orcid.org/0000-0003-0870-7193
e
https://orcid.org/0000-0002-0466-562X
Technology allowing a vehicle to exchange ad-
ditional information with infrastructure, other vehi-
cles and other stakeholders in the context of C-ITS
is called vehicle-to-everything (V2X). Multiple ad-
vances in modern C-ITS applications, such as col-
laborative forward collision warning and emergency
electronic brake lights, are impossible without V2X.
These advances, however, come at a cost: C-ITS ap-
plications rely on vehicles broadcasting signals to in-
dicate their location, signals which are intended to be
received and processed by a range of other devices.
For example, vehicles may cooperatively broadcast
(with the frequency of 1-10 Hz) geo-spatial informa-
tion to nearby peers using short Cooperative Aware-
ness Messages (CAMs). Hence, V2X raises essen-
tial privacy questions: i) to what degree can specific
vehicles be located and tracked based on such infor-
mation? ii) what are the techniques able to improve
privacy of V2X? To answer these questions, we use
the concept of unlinkability to reason about privacy.
Zolotavkin, Y., Baryshev, Y., Lukichov, V., Mähn, J. and Köpsell, S.
Improving Unlinkability in C-ITS: A Methodology For Optimal Obfuscation.
DOI: 10.5220/0011786900003405
In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 677-685
ISBN: 978-989-758-624-8; ISSN: 2184-4356
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
677

1.1 Research Motivation
Even though the problems of privacy in C-ITS were
acknowledged in several relevant documents (hav-
ing normative and informative character), satisfac-
tory answers have yet to be provided to the privacy
questions mentioned above. For example, the doc-
ument (ISO/TC 204, 2018) recognizes the impor-
tance of unlinking private data from traceable ad-
dress elements and identifiers in wireless messages
sent by an ITS station unit (ITS-SU). However, rel-
evant considerations in this document do not go be-
yond suggesting that “such unlinking can be done
by means of pseudonyms”: the sufficiency of these
and many similar suggestions remain unaddressed. In
contrast, limitations of pseudonym changes in CAMs
have been recognized by academic authors (Wieder-
sheim et al., 2010; Karim Emara, 2013; Escher et al.,
2021). In particular, vehicle tracking becomes pos-
sible due to CAM content being signed but not en-
crypted: this is demanded by the relevant standards
in C-ITS (WG1, 2019). This is because full encryp-
tion of CAMs may impede C-ITS functionalities that
are critical for safety. Nonetheless, recognition of
privacy-affecting issues in C-ITS has yet to result in a
solution where the degree of privacy is correctly mea-
sured, and privacy limitations are eliminated. In this
paper, a methodology to address these challenges is
developed: we provide an assurance for the procedure
estimating the lower bound of unlinkability for CAMs
and an algorithm maximizing this criterion under the
overall constraint of location precision degradation.
1.2 Our Contribution
The unique contribution is due to combination of the
study objective (guided by the criterion of unlinkabil-
ity), robust assumptions, and the optimal obfuscation
technique developed in the paper.
• First, the aim of this study is to protect C-ITS
from the threat of linking: this is in contrast with
the numerous obfuscation approaches which aim
at impeding inferencing about the actual location
of ITS-SU (Andr
´
es et al., 2013; Bordenabe et al,
2014);
• Second, to obtain high confidence in the measured
unlinkability, we assume that an attacker has com-
plete knowledge about the system design, obfus-
cation algorithms, quality degradation (distortion)
constraints, has access to CAMs, stored states ve-
hicles’ geo-positions, and the true states charac-
terizing the geo-positions of the vehicles at any
moment in time;
• Third, we develop an optimal obfuscation algo-
rithm: for a given distortion constraint, it pro-
vides the highest level of uncertainty for the at-
tacker trying to link obfuscated CAMs with their
sources.
The rest of this paper is structured as follows. In
section 2, we set the grounds for the study and pro-
vide basic definitions. It is followed by section 3,
where we propose Hidden Markov Model (HMM),
used to study unlinkability. In section 4, we formal-
ize assumptions, define unlinkability through entropy
and optimize joint obfuscation producing observable
states in HMM. Next, section 5 describes a compact
and efficient algorithm calculating the unlinkability
in C-ITS and implementing previous findings to im-
prove privacy. Finally, we conclude
1
the paper in sec-
tion 6.
2 PRELIMINARIES
To justify subsequent modelling steps better, we intro-
duce contextual information supporting our aim, set-
tings and privacy assumptions.
2.1 Aim of the Study
To specify the aim, we analyze relevant cybersecu-
rity requirements. Here, we use some of the clas-
sical definitions for privacy in complex systems to
specify our aim with greater precision. Privacy re-
quirements for C-ITS are often derived from ISO/IEC
15408-2. For example, (WG5, 2021) suggests that
the combination of pseudonymity and unlinkability
offers the appropriate sender privacy protection for
basic ITS safety messages (such as CAM). In sim-
ple terms, pseudonymity requires that the identity of a
user is never revealed or inferred. However, one of the
major complications in dealing with pseudonymity is
the following: an attacker may learn the user’s iden-
tity composition based on multiple sessions, events,
or traces. Unlinkability is the assurance about the
ability to resist learning such a composition (ISO/IEC
JTC 1/SC 27, 2022):
Definition 1 (Unlinkability of Operations). Re-
quires that users and/or subjects are unable to deter-
mine whether the same user caused certain specific
operations in the system, or whether operations are
related in some other manner.
In the context of V2X communication in C-ITS
with many users, the cryptographically signed mes-
1
For an in-depth discussion, see the full version of the
paper (Zolotavkin et al., n.d.)
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
678

sages broadcasted by the ITS-SUs (controlled by
these users) should have the property of definition 1
(WG5, 2021; Hicks eta al., 2020). Nonetheless,
such interpretation has certain disadvantages, major
of which is inflexibility. Indeed, ‘...unable to deter-
mine...’ statement can either be false or true, meaning
that the unlinkability of the whole C-ITS (with many
vehicles and observable during many hours) is ex-
pressed using a binary value. This issue has been rec-
ognized by practitioners and researchers alike, which
is reflected in comments and best practice recommen-
dations to ITS engineers and managers. For example,
(ISO/TC 22/SC 32, 2021) contains the table ‘Exam-
ple privacy impact rating criteria’: it includes Impact
rating Criteria interpreting the meaning for the sever-
ity degrees (e.g., Negligible, Moderate, Major, Se-
vere) for privacy impact rating indicator. Importantly
enough, interpretations in this table evolve around
two aspects: a) the level of sensitivity of the informa-
tion about road user; b) how easily it can be linked to
a PII (Personally Identifiable Information) principal.
Such emphasis on the easiness of linking motivates us
to modify definition 1 in the following manner:
Definition 2 (Unlinkability of Operations*). Is the
degree of inability to determine (by users and/or sub-
jects) whether the same user caused certain specific
operations in the system, or whether operations are
related in some other manner.
To provide convenience in comparing unlinkabil-
ity in C-ITS under different conditions, we use Shan-
non entropy: it is an integral criterion of uncertainty
in a system that fully captures the ‘...degree of inabil-
ity to determine...’ (Wagner and Eckhoff, 2018).
Henceforth, the main aim of our paper is to de-
velop a methodology providing high level of assur-
ance that entropy for CAMs’ origins is high in C-ITS.
2.2 Settings for the Study
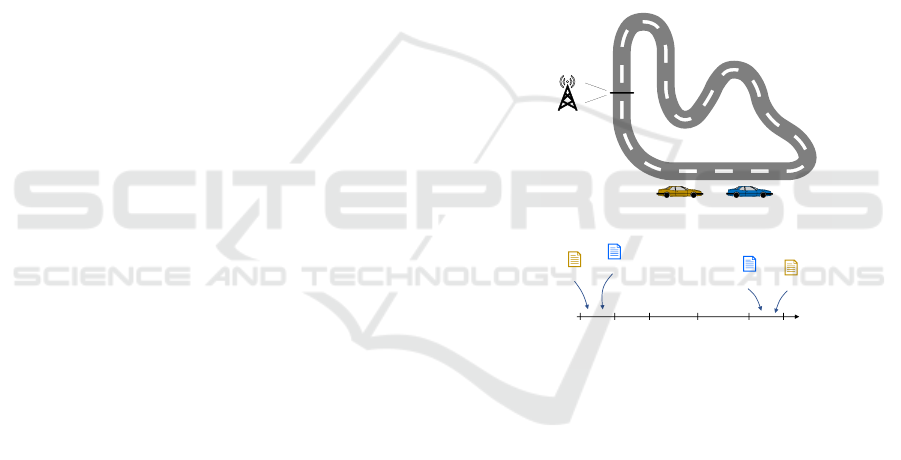
In fig. 1, we introduce a general setup for our study. In
fig. 1(a), two vehicles (ITS-SUs) are driven by Alice
and Bob, respectively. Both ITS-SUs transmit CAMs
with the same frequency, and the roadside unit (RSU)
receives them without losses. The role of the attacker
is played by the RSU, who tries to separate CAMs of
Alice from CAMs of Bob: this allows the attacker to
link CAMs belonging to the same entity. Although
CAMs are signed, in our study we assume that a sig-
nature scheme providing unlinkability is used. There-
fore, the separation is done based on the content of
the CAMs (since the are transmitted unencrpyted) and
the order of arrival of CAMs within each time in-
terval – see fig. 1(b). We consider the ordering of
CAMs’ arrivals to be non-uniform in general: for ex-
ample, in one extreme case, the CAM from Alice ar-
rives first, and Bob’s CAM arrives second at any time
interval i. If an attacker knows about such a unique
property, he can link CAMs without considering their
payload. However, these cases are unlikely, meaning
that an attacker should also be able to infer the source
(e.g., ‘from Alice’ or ‘from Bob’) of a CAM based
on its content. The requirements for the content of
CAMs can be found in (WG1, 2019). In particular,
we consider that geo-position, velocity and acceler-
ation are essential. On the one hand, these parame-
ters are mandatory for the HighFrequency container
in CAM. On the other hand, numerous techniques
using these parameters have been developed for the
domain of Multiple-Target Tracking (MTT): corre-
sponding estimators can be of great use for reason-
ing about privacy in C-ITS (Blackman, 1986; Karim
Emara, 2013).
BobAlice
RSU
… …
CAM(A)
CAM(B)
𝑡
0 1 2 𝑖 𝑁 − 2 𝑁 − 1
CAM(A)
CAM(B)
𝑎)
𝑏)
Figure 1: Setting for our study of unlinkability of CAMs.
In this study, CAMs’ content unlinkability is the
core of our attention. We exclude from further con-
sideration the following CAM payload: 1) crypto-
graphically produced proofs of authenticity (e.g., sig-
natures); 2) categorical data (e.g., vehicle role). These
exclusions are due to substantial attention to issue ‘1)’
among the members of the cryptographic community.
For example, pseudonym unlinking solutions were
proposed in (Camenisch et al., 2020; Hicks eta al.,
2020). Nevertheless, there is a need to complement
these efforts by our study: the absence of encryption
(due to safety reasons) in CAMs makes pseudonym
unlinking necessary but not sufficient for CAMs’ un-
linkability. This is because other data, such as geo-
graphic positions, in CAMs may be used for linking.
Issue ‘2)’ can be omitted since categorical data is a
part of basicVehicleContainerLowFrequency and
is OPTIONAL in CAMs (WG1, 2019). We also exclude
Improving Unlinkability in C-ITS: A Methodology For Optimal Obfuscation
679

VehicleLength and VehicleWidth (compulsory for
the HighFrequency container), which otherwise are
likely to be of great use in discriminating different ve-
hicles (Escher et al., 2021). For such an exclusion we
find justification in (WG1, 2018) which allows usage
of the codes 1023 and 62 for the length and width,
respectively, if the corresponding information is un-
available.
Because of the details described above, we will
model CAM as a vector in R
z
where z ≥ 1. Such a
step is beneficial: we can apply commonly used dis-
tortion measures such as, for example, Squared Error
(SE). This is a clear and straightforward way to re-
fer to the quality degradation of essential location ser-
vices (Shokri et al., 2016). We, nevertheless, refrain
from further discussions about the chosen distortion
measure in this paper.
2.3 Privacy Assumptions and Threats
Here we provide a high-level intuition for the system
and the threat of linkability, while the details will be
introduced in the subsequent sections. Alice and Bob
coordinate their efforts. They distribute the total al-
lowed distortion among N −1 time steps: as a result,
they know the distortion limit for every time step i.
At the beginning of every time interval i, Alice and
Bob know the true measurements (including position,
speed, acceleration, etc.) of each other. To obfus-
cate data in their CAMs they randomly agree on the
order of their arrival at RSU at every i. For every
i they define a joint distribution according to which
they change (obfuscate) their actual measurements: in
expectation, they remain within the distortion limits.
An attacker who fully controls RSU statistically
infers the source of every pair of CAMs which he ob-
serves during time i: this statistical inference is used
to calculate entropy and aligns with definition 2. For
this, the attacker refers to the joint distribution used by
Alice and Bob during the obfuscation. He also knows
other information, such as the original geo-positions
of the players at every i, and the probabilities for the
order of CAMs’ arrivals. The resulting unlinkability
in the system depends on: i) statistics for the order
of arrival of CAMs from the players; ii) the level of
allowed distortion; iii) how far apart actual measure-
ments of Alice and Bob are at every i.
3 MATHEMATICAL MODEL
We explain our mathematical model in the follow-
ing sections. To easy the reading, table 1 contains
an overview about our notations.
Table 1: Notations.
Notation Description
ITS Intelligent Transport Systems
C-ITS Cooperative Intelligent Transport Systems
ITS-SU ITS Station Unit (including installed in vehicles)
V2X Vehicle-to-Everything
CAM Cooperative Awareness Message
RSU Roadside Unit
HMM Hidden Markov Model
D
u
Set of user-related data
D
s
Set of information system-related data
U Set of information system’s users
P Set of data processing procedures at the information system
P Set of players including Alice and Bob
x
A
k
, 1 ≤k ≤ µ A hidden state for Alice
X
A
= {x
A
k
} Set of hidden states for Alice
x
B
j
, 1 ≤ j ≤ ω A hidden state for Bob
X
B
= {x
B
j
} Set of hidden states for Bob
X
(A,B)
Set of joint hidden states for

Alice, Bob

X
(B,A)
Set of joint hidden states for

Bob, Alice

R Index (label) for rose nodes
X
R
= X
(A,B)
Set of all rose nodes
B Index (label) for blue nodes
X
B
= X
(B,A)
Set of all blue nodes
L = {R ,B} Set of labels encoding
|
P
|
! combinations
Y Set of joint observable states for Alice and Bob
i ∈{1, 2,..., N −1} Time-step in discrete HMM
X
A
i
Variable on X
A
at i
X
B
i
Variable on X
B
at i
X
i
Variable for joint hidden state on step i
ℓ
i
Variable on L at i
Y
i
Variable on Y on step i
Pr(X
i+1
| X
i
) Probability of transition between hidden states
Pr(Y
i
| X
i
) Conditional probability for observable states
ϕ Order mixing (label permuting) probability
ρ
i
Distribution over hidden states on step i
ρ
i+1
|ρ
i
Conditional distribution over hidden states on step i+ 1
3.1 Markov Model for Unlinkability
To study unlinkability in V2X we use Hidden Markov
Model which graphical representation is given on
fig. 2. The following sets are needed to de-
scribe the model. The set of all players is P =
{
Alice, Bob,...
}
. For each player, there exists a set
of hidden states for his vehicle, e.g., for Alice there
is X
A
=

x
A
1
,x
A
2
,...,x
A
k
,...,x
A
µ

and for Bob there is
X
B
=
n
x
B
1
,x
B
2
,...,x
B
j
,...,x
B
ω
o
. Each state, for example,
x
A
1
can be a vector including specific position, veloc-
ity, acceleration and other characteristics applicable to
Alice’s vehicle at certain time. Throughout the paper
we assume that X
A
∩X
B
is in general non-empty.
The system of |P| players is characterized by hid-
den and observable joint states. Transition happens
between hidden states X
i
and X
i+1
when time step i
proceeds to i + 1, where joint state X
i
=

X
A
i
,X
B
i

is
the composition (concatenation) of variables X
A
i
∈X
A
and X
B
i
∈ X
B
. As such, ∀k, j(x
A
k
,x
B
j
) ∈ X
(A,B)
, where
|X
(A,B)
| = |X
A
|×|X
B
| (for simplicity of representa-
tion we further assume |P| = 2, |X
A
| = µ = 2, |X
B
| =
ω = 2).
Possible transitions from X
i
to X
i+1
are denoted
using indices 1 −16 (see fig. 2): these transitions
are governed by corresponding probabilities. For ex-
ample, the transition from X
i
=

X
A
i
= x
A
1
,X
B
i
= x
B
1

to X
i+1
=

X
A
i+1
= x
A
2
,X
B
i+1
= x
B
2

is denoted by
index 4. The probability of such a transition
is Pr

X
A
i+1
= x
A
2
,X
B
i+1
= x
B
2
| X
A
i
= x
A
1
,X
B
i
= x
B
1

. In
practice, these probabilities can be obtained based on
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
680

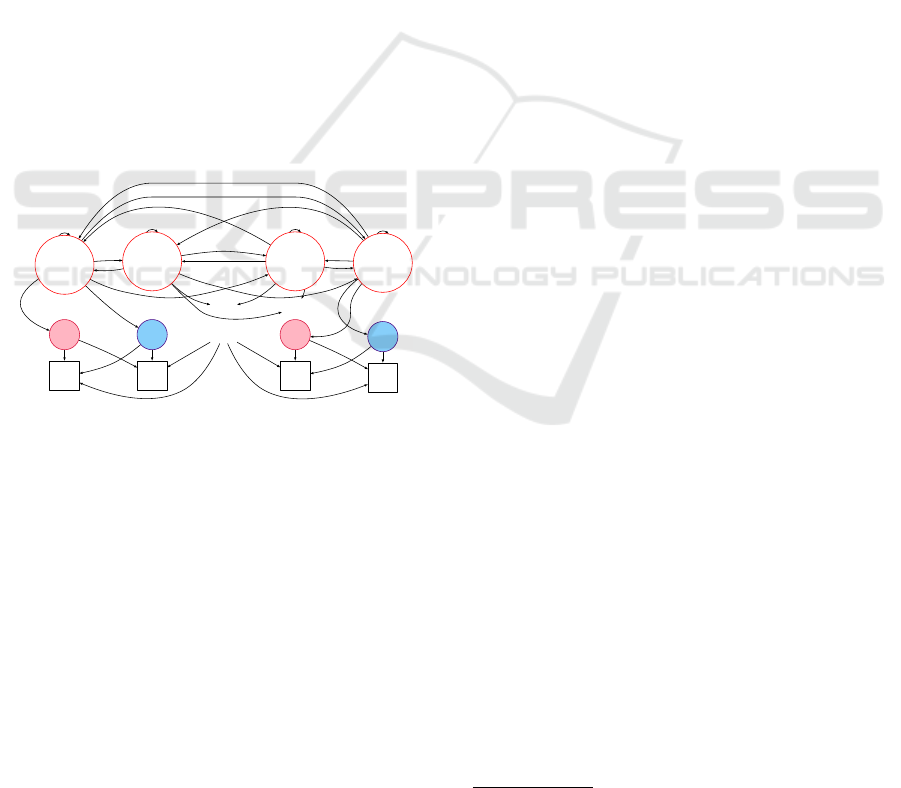
the well-studied physical models for vehicles (Black-
man, 1986).
For each X
i
of the hidden joint states there are
|P|! possible permutations for its concatenated com-
ponents originating from the users. These permu-
tations are the major cause of uncertainty when an
attacker attempts to label combined CAMs of Alice
and Bob. In practice, this is caused by the unpre-
dictable arrangement of CAMs within each scan (or
session) i. Hence, a permutation should be selected
by randomly following one of the possible transi-
tions. For example, while the system is in a joint
state

X
A
i
= x
A
1
,X
B
i
= x
B
1

permutation

x
A
1
,x
B
1

(rose
colored node) should be considered if transition with
index 17 takes place, and

x
B
1
,x
A
1

(blue coloured
node) should be considered if transition 18 happens
(see fig. 2). We will use notations X
i,R
and X
i,B
for
rose and blue nodes, respectively, where X
i,R
∈ X
R
,
X
i,B
∈ X
B
, and X
R
= X
(A,B)
, X
B
= X
(B,A)
. Fur-
ther in the text, we will refer to the states repre-
sented by the coloured nodes as ‘labelled states’. For
the sake of simplicity and without loss of generality,
for all realizations of hidden states X
i
, we consider
Pr

X
i,R
|X
i

= ϕ ≤ 0.5, and Pr

X
i,B
|X
i

= 1 −ϕ.
1
2
3
4
17
18
6
5
7
8
10
11
9
12
14
15
16
13
19
20
21
23
22
24 25
27
26
28

X
A
= x
A
1
, X
B
= x
B
1


x
A
1
, x
B
1

(ˆy
1
, ˇy
1
)

X
A
= x
A
1
, X
B
= x
B
2


x
B
1
, x
A
1

(ˇy
1
, ˆy
1
)
...
...

X
A
= x
A
2
, X
B
= x
B
1


x
A
2
, x
B
2

(ˆy
2
, ˇy
2
)
...

X
A
= x
A
2
, X
B
= x
B
2


x
B
2
, x
A
2

(ˇy
2
, ˆy
2
)
Figure 2: Hidden Markov Model for 2 players sending
CAMs.
To denote the totality of hidden permuted joint
states we use set X
{R ,B}
= X
R
∪ X
B
, where
|X
R
| ≤ |X
{R ,B}
| ≤ 2|X
R
|. For every X
i,R
and
X
i,B
there are transitions to observable joint states
Y
i
∈Y, Y =

( ˆy
1
, ˇy
1
),( ˇy
1
, ˆy
1
),...,( ˆy
q
, ˇy
q
),( ˇy
q
, ˆy
q
) , ...,
( ˆy
ξ
, ˇy
ξ
),( ˇy
ξ
, ˆy
ξ
)

. Some of these transitions to observ-
able states are denoted with indices 21 −28 on fig. 2.
Until proven otherwise, the cardinality of Y is consid-
ered independent on |X
{R ,B}
|.
Measuring uncertainty about label ℓ ∈ L, L =
{R ,B}, is of our main interest: this is done based
on observable states.
4 MODEL PROPERTIES
To formally express unlinkability following
definition 2 we will use conditional entropy
H (ℓ
1
,ℓ
2
,...|Y
1
,Y
2
,...) for the sequence of la-
bels ℓ
1
,ℓ
2
,...,ℓ
N−1
given that an attacker observes
Y
1
,Y
2
,...,Y
N−1
(Wagner and Eckhoff, 2018).
4.1 General Expression for
Unlinkability
For the described HMM, probability of any hidden
state at any time step can be specified using multivari-
ate discrete distribution ρ
ρ
ρ : X
(A,B)
×{0,1, ...,N −1}→
[0,1]
N
|
X
(A,B)
|
. We will further use ρ
i
slices of ρ
ρ
ρ such
that ρ
ρ
ρ =
N−1
S
i=0
ρ
i
, where each slice represents a distri-
bution over hidden states at step i. Slice ρ
0
defines
distribution over the hidden states before the start of
the system. Because HMM has been previously de-
fined (see fig. 2) using transitional probabilities that
remain unchanged for all time steps, each slice can
be fully determined in a conditioned sequential man-
ner: ρ
i+1
|ρ
i
means that ρ
i+1
is trivially derived if ρ
i
is given.
Since an attacker observes Y
1
,Y
2
,...,Y
N−1
and
knows ρ
ρ
ρ analysis of H (ℓ
1
,ℓ
2
,... | Y
1
,Y
2
,...,ρ
ρ
ρ) is cen-
tral to our reasoning about unlinkability. We state the
following.
Lemma 1. Unlinkability in V2X system (as per
fig. 2) is expressed as:
2
H

ℓ
1
,ℓ
2
,...


Y
1
,Y
2
,...,ρ
ρ
ρ

=
N−2
∑
i=0
H

ℓ
i+1


Y
i+1
,{ρ
i+1
|ρ
i
}

.
(1)
4.2 Worst-Case Unlinkability
We aim to obtain a computationally feasible estima-
tion of unlinkability. Direct utilization of the re-
sults of lemma 1 presupposes computing {ρ
i+1
|ρ
i
}
which has several disadvantages: a) transition prob-
abilities for hidden states need to be specified (which
usually requires studying physical models of move-
ment for the users); b) total computational com-
plexity for defining distributions over the hidden
states is therefore O(Nµ
2
ω
2
). To avoid these
complications, we develop our unlinkability assur-
ance based on a rational lower bound H
r
for
H

ℓ
1
,ℓ
2
,...


Y
1
,Y
2
,...,ρ
ρ
ρ

. The concept of the ratio-
nal lower bound is explained through the following
assumptions (Sniedovich, 2016).
2
For proof, see the full version of the paper (Zolotavkin
et al., n.d.)
Improving Unlinkability in C-ITS: A Methodology For Optimal Obfuscation
681

Assumption 1 (Worst-Case Unlinkability). Re-
quires that an attacker knows sets for the hidden, la-
belled and observable states. He knows all the tran-
sitions and the order mixing probability ϕ. For each
observable state at time i he then defines the worst
possible hidden state(s) which does not contradict his
knowledge.
We nevertheless stress that despite assumption 1
might be viewed as excessive, the attacker does not
know the labelled state ℓ
i
(and can not force its selec-
tion) at time i.
Assumption 2 (Rational Lower Bound H
r
). Re-
quires that users are rational and maximize worst-case
unlinkability: observable states are obtained through
rational obfuscation of the worst labelled states con-
sidered by the attacker.
There are several aspects affecting the task of cal-
culating such H
r
: 1) probabilities for transitions be-
tween hidden states (e.g., the probabilities defining
ρ
ρ
ρ); 2) probabilities for transitions from the hidden
states to the labelled states (e.g., ϕ, 1 −ϕ), and from
the labelled states to the observable states. Further, we
consider a situation where the worst case ρ
ρ
ρ (minimiz-
ing entropy) is defined for 1) while the most optimal
probabilities (maximizing entropy) are then specified
for 2) under constraint
˜
D on the total distortion over
N −1 steps.
We use the results of lemma 1 to require the fol-
lowing:
H
r
= min
ρ
ρ
ρ
h
H

ℓ
1
,ℓ
2
,...


Y
1
,Y
2
,...,ρ
ρ
ρ

i
=
N−2
∑
i=0
min
{ρ
i+1
|ρ
i
}
h
H

ℓ
i+1


Y
i+1
,{ρ
i+1
|ρ
i
}

i
.
(2)
To obfuscate hidden states in the way maximizing
H
r
we need to determine properties of
ρ
min,i+1
= arg min
{ρ
i+1
|ρ
i
}
h
H

ℓ
i+1


Y
i+1
,{ρ
i+1
|ρ
i
}

i
. (3)
Probabilities Pr

ℓ
i+1
= R ,Y
i+1


{ρ
i+1
|ρ
i
}

,
Pr

ℓ
i+1
= B,Y
i+1


{ρ
i+1
|ρ
i
}

will be used in our
further derivations. To simplify notations we
will use Pr (ℓ
i+1
= R ,Y
i+1
), Pr (ℓ
i+1
= B,Y
i+1
),
respectively. The probabilities are defined as:
Pr(ℓ
i+1
= R , Y
i+1
) =
∑
X
i+1,R
∈X
R
Pr

Y
i+1
| X
i+1,R

Pr

X
i+1,R

=
∑
X
i+1,R
∈X
R
Pr

Y
i+1
| X
i+1,R

ϕPr(X
i+1
) ,
(4)
Pr(ℓ
i+1
= B,Y
i+1
) =
∑
X
i+1,B
∈X
B
Pr

Y
i+1
| X
i+1,B

Pr

X
i+1,B

=
∑
X
i+1,B
∈X
B
Pr

Y
i+1
| X
i+1,B

(1 −ϕ)Pr (X
i+1
) .
(5)
We then point out that
Pr(ℓ
i+1
= R | Y
i+1
) =
Pr(ℓ
i+1
= R ,Y
i+1
)
Pr(Y
i+1
)
, (6)
Pr(ℓ
i+1
= B | Y
i+1
) =
Pr(ℓ
i+1
= B,Y
i+1
)
Pr(Y
i+1
)
, (7)
where
Pr(Y
i+1
) = Pr (ℓ
i+1
= R , Y
i+1
) + Pr (ℓ
i+1
= B,Y
i+1
) . (8)
The following result establishes an important
property of ρ
min,i+1
.
Lemma 2. For all i ∈ [1,N −1] distribution ρ
min,i
is
degenerate.
3
Based on the result of lemma 2, for every Y
i
there
is one and only worst-case hidden state
˜
X
i
(because
Pr

˜
X
i
| ρ
min,i

= 1). It implies the following:
Corollary 1. Design of HMM where for every state
(realization) in Y there is one and only transition from
X
(A,B)
explicitly satisfies assumption 1.
Therefore, we will further adhere to such design
principle and use
˜
X
i
to denote hidden states. Next,
we will elaborate on: a) what is the optimal number
of different observable states Y
i
for every
˜
X
i
? b) how
should we define optimal observable states? c) what
are the probabilities of transition (from the labelled
states to the observable states)?
4.3 Requirements for the Observable
States
Here we provide our analysis from the standpoints of
the system that obfuscates hidden states (e.g., the sys-
tem produces observable states) on behalf of Alice and
Bob, and hence
˜
X
i
is assumed to be known. The pos-
sibilities of transitions
˜
X
i,R
→ Y
i
and
˜
X
i,B
→ Y
i
im-
ply that a non-zero distortion E [D
i
] takes place:
E [D
i
] =
∑
y
(i)
j
∈Y
(i)
D
i, j
Pr

Y
i
= y
(i)
j
|
˜
X
i

, (9)
where
D
i, j
= Pr

ℓ
i
= R | Y
i
= y
(i)
j

d

˜
X
i,R
,y
(i)
j

+
Pr

ℓ
i
= B | Y
i
= y
(i)
j

d

˜
X
i,B
,y
(i)
j

.
(10)
Here Y
(i)
is the set of all observable states to which
transitions exist from the realizations of
˜
X
i,R
and
˜
X
i,B
at time i; y
(i)
j
is an element in Y
(i)
; d (·,·) is some
distortion measure (e.g., SE).
The optimization effort is two-fold: i) how shall
we obtain observable states Y
(i)
in a way that H
r,i
3
For proof, see the full version of the paper (Zolotavkin
et al., n.d.)
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
682

is maximized under constraint
˜
D
i
≥ E [D
i
]? ii) how
shall we define
˜
D
i
for every time step i such that
H
r
is maximized and the total distortion constraint
˜
D ≥
∑
i
E [D
i
] is satisfied? We start with answering
question i), which will assist us in answering question
ii).
For the obfuscation, we utilize the following
principles: every element y
(i)
j
in Y
(i)
can be fully
specified by the realizations of
˜
X
i,R
,
˜
X
i,B
, and pa-
rameter λ
j
. Probabilities Pr

ℓ
i
= R | Y
i
= y
(i)
j

,
Pr

ℓ
i
= B | Y
i
= y
(i)
j

then affect H
r,i, j
. All these pa-
rameters affect D
i, j
. The diagram explaining relations
between all the mentioned parameters is provided on
fig. 3. In this example, labelled states are
˜
X
i,R
=

x
A
,x
B

,
˜
X
i,B
=

x
B
,x
A

; set Y
(i)
contains only two
elements y
(i)
1
=

ˆy
(i)
, ˇy
(i)

and y
(i)
2
=

ˇy
(i)
, ˆy
(i)

. For
example, to specify y
(i)
1
we only need λ
1
in addi-
tion to the labelled states (∆ is the distance between
them). To obtain y
(i)
2
we should apply a similar pro-
cedure where λ
2
is known (in our particular example
λ
2
= 1 −λ
1
). Probability Pr

ℓ
i
= R | Y
i
= y
(i)
1

is
denoted as p
1
: its value affects attacker’s uncertainty
H
r,i, j
as well as the distortion D
i, j
.
Figure 3: Scheme for obfuscation principle.
To maximize H
r,i
under
˜
D
i
≥ E [D
i
] we consider
realizations of Y
i
and optimal adjustment of λ: such
adjustment then allows us to increase p
1
and 1 −p
2
.
We note that Y
i
shall belong to a line segment (in
a multidimensional space) connecting
˜
X
i,R
and
˜
X
i,B
.
This property is trivial (goes without proof) and can
be best understood if triangle △
˜
X
i,R
Y
i
˜
X
i,B
is consid-
ered. As a result:
∀Y
i

Y
i
∈ Y
(i)
=⇒

∃λ ∈ [0,1]

∧

⃗
Y
i
=
−−→
˜
X
i,R
+ λ
−−−−−→
˜
X
i,R
˜
X
i,B


. (11)
We then establish the following:
Lemma 3. To minimize D
i, j
it is required that λ
j
=
1 −Pr

ℓ
i
= R | Y
i
= y
(i)
j

.
4
4
For proof, see the full version of the paper (Zolotavkin
et al., n.d.)
Corollary 2. Minimal distortion is D
i, j
= ∆
2
i
p
j
(1 −
p
j
) ≤
∆
2
i
4
, where p
j
= Pr

ℓ
i
= R | Y
i
= y
(i)
j

, ∆
2
i
=
d

˜
X
i,R
,
˜
X
i,B

.
Corollary 3. For every i, the highest lower bound
(maxmin entropy) is:
4
H
r,i
= −ν
i
log
2
ν
i
−(1 −ν
i
)log
2
(1 −ν
i
) , (12)
where ν
i
= min

ϕ,
∆
i
−
√
∆
2
i
−4E[D
i
]
2∆
i

.
There are several important takeaways from the
proof of corollary 3. First, for every hidden state
˜
X
i
there are two observable states that are obtained ac-
cording to eq. (11) where λ
(i)
1
= 1 −ν
i
is used to de-
fine realisation y
(i)
1
, and λ
(i)
2
= 1 −λ
(i)
1
is used for y
(i)
2
.
Second, maximum allowed distortion should be used
at step i meaning that E [D
i
] =
˜
D
i
. Third, probabili-
ties for transitions from labelled states to observable
states are
Pr

Y
i
= y
(i)
1
| ℓ
i
= R

=
1−ν
i
ϕ
ϕ+ν
i
−1
2ν
i
−1
;
Pr

Y
i
= y
(i)
2
| ℓ
i
= R

= 1 −Pr

Y
i
= y
(i)
1
| ℓ
i
= R

;
Pr

Y
i
= y
(i)
1
| ℓ
i
= B

=
ν
i
1−ϕ
ϕ+ν
i
−1
2ν
i
−1
;
Pr

Y
i
= y
(i)
2
| ℓ
i
= B

= 1 −Pr

Y
i
= y
(i)
1
| ℓ
i
= B

.
(13)
4.4 Optimal Obfuscation for N −1 Time
Steps
For every i we now define
˜
D
i
such that H
r
=
∑
i
H
r,i
is
maximized under the total distortion constraint
˜
D ≥
∑
i
˜
D
i
. For this reason, we obtain optimal observ-
able states and corresponding transition probabilities
(from the labelled states) for all the time steps. From
the proof of the corollary 3 we use that
∂
∂
˜
D
i
H
r,i
≥0 and
∂
2
∂
˜
D
2
i
H
r,i
≤ 0. To maximize H
r
we therefore require





∀i
∂
∂
˜
D
i
H
r,i
=
1
∆
2
i
√
1−κ
i
log

1+
√
1−κ
i
1−
√
1−κ
i

= C ;
˜
D =
N−1
∑
i=1
˜
D
i
=
1
4
N−1
∑
i=1
κ
i
∆
2
i
,
(14)
where C is some constant, κ
i
=
4
˜
D
i
∆
2
i
. We then
solve the system eq. (14) for all κ
i
, i ∈ [1,N −
1], and according to corollary 3 obtain ν
i
=
min

ϕ, 0.5 −
√
0.25 −0.25κ
i

.
5 OBFUSCATION ALGORITHM
Here we represent our aforementioned findings in the
form of obfuscation algorithm (see algorithm 1). It is
practical and can be implemented in real settings: its
Improving Unlinkability in C-ITS: A Methodology For Optimal Obfuscation
683

complexity (excluding the complexity of solve pro-
cedure) is only O(N). For input, the algorithm ac-
cepts arrays (of size N) X
A
, X
B
, and scalars
˜
D, ϕ. El-
ements of these arrays are scalar/vector realizations
for X
A
i
and X
B
i
characterizing geo-positions of Alice
and Bob, respectively, at time i. In practice, these ar-
rays may contain extrapolations based on historical
data and repetitive patterns. For example, Alice and
Bob may commute to work using the same routes and
roughly at the same time every day. Procedure solve
provides a solution to eq. (14): array κ
κ
κ contains ele-
ments κ
i
needed to define realizations for obfuscated
state Y
i
. It is also needed to calculate the unlink-
ability criterion (entropy) H
r,i
dependent on the ob-
fuscation process. Procedure send RSU encapsulates
data obfuscated at time i in accordance with one of the
V2X communication formats and sends it to the near-
est RSU. The output of the algorithm is, therefore, an
array Y containing all the obfuscated records and the
indicator of the total unlinkability in the system over
N −1 steps, H
r
.
Algorithm 1: Obfuscation algorithm.
input : X
A
, X
B
,
˜
D, ϕ ;
output: Y, H
r
;
begin
H
r
← 0, Y ← ∅, κ
κ
κ ← solve

˜
D,X
A
,X
B

;
for i ← 1 to N −1 do
ν
i
← min

ϕ, 0.5 −
√
0.25 −0.25κ
i

,
α ← (ϕ + ν
i
−1)/(2ν
i
−1),
H
r,i
← −ν
i
log(ν
i
) −(1 −ν
i
)log(1 −ν
i
),
H
r
← H
r
+ H
r,i
, P
1,R
← (1 −ν
i
)α/ϕ,
P
1,B
← ν
i
α/(1 −ϕ), r
1
← UniRand

[0,1]

,
r
2
← UniRand

[0,1]

,
Λ
R
← 0.5 + (0.5 −ν
i
) sign
±

P
1,R
−r
2

,
Λ
B
← 0.5 + (0.5 −ν
i
) sign
±

P
1,B
−r
2

;
if r
1
≤ ϕ then ˆy
(i)
← X
A
i
+ Λ
R

X
B
i
−X
A
i

,
ˇy
(i)
← X
B
i
+ Λ
R

X
A
i
−X
B
i

, Y
i
= concat( ˆy
(i)
, ˇy
(i)
);
else ˆy
(i)
← X
A
i
+ Λ
B

X
B
i
−X
A
i

,
ˇy
(i)
← X
B
i
+ Λ
B

X
A
i
−X
B
i

, Y
i
= concat( ˇy
(i)
, ˆy
(i)
);
send RSU(Y
i
), Y = concat(Y,Y
i
) ;
6 CONCLUSIONS
5
In this paper, our research motivation aligns with
other authors from the domain of C-ITS privacy pro-
tection: unlinkability of CAMs is an issue that needs
to be addressed (Karim Emara, 2013; Escher et al.,
2021). Our approach, however, differs in how we ad-
dress our main aim (see section 2.1).
First, we use the classical definition of unlinka-
bility. Despite being an apparent requirement based
5
For an in-depth discussion, see the full version of the
paper (Zolotavkin et al., n.d.)
on standards and regulations, in many works, unlink-
ability is substituted by less demanding requirements
such as geo-indistinguishability (Andr
´
es et al., 2013;
Bordenabe et al, 2014). We address unlinkability by
adapting HMM to enable Bayesian inference about
the labeled joint states (see fig. 2) in a system with
two players, Alice and Bob. Based on such inference,
we then calculate uncertainty about the labels: we use
Shannon entropy to measure unlinkability.
Second, we assume a strong attacker who fully
controls RSU and knows actual characteristics (e.g.,
positions, velocities, etc.) of the vehicles of Alice
and Bob at any moment. The main benefit of such
a worst-case assumption is that we obtain high confi-
dence about the lower bound for the unlinkability of
CAMs in C-ITS.
Third, we improve CAMs’ unlinkability by de-
veloping the optimal joint obfuscation technique: we
maximize the total entropy over N − 1 time steps
under the constraint on the distortion introduced to
CAMs by Alice and Bob. This is complemented by
an obfuscation algorithm whose complexity is only
O(N) (see algorithm 1).
Some of the application details of our findings are
yet to be developed. For example, this may include
the development of a secure and privacy-preserving
protocol for joint obfuscation that is based on the
proposed algorithm. Further developments will also
focus on scaling the proposed obfuscation algorithm
and conducting experiments, including simulations of
different traffic situations.
ACKNOWLEDGMENT
This research is co-financed by public funding of the
state of Saxony, Germany.
REFERENCES
Andr
´
es, M. E., Bordenabe, N. E., Chatzikokolakis, K., &
Palamidessi, C. (2013). Geoindistinguishability: Dif-
ferential privacy for location-based systems. Proceed-
ings of the 2013 ACM SIGSAC Conference on Com-
puter & Communications Security, 901–914.
Blackman, S. S. (1986, January 1). Multiple-target tracking
with radar applications.
Bordenabe, N. E., Chatzikokolakis, K., & Palamidessi, C.
(2014). Optimal Geo-Indistinguishable Mechanisms
for Location Privacy. Proceedings of the 2014 ACM
SIGSAC Conference on Computer and Communica-
tions Security, 251–262.
Camenisch, J., Drijvers, M., Lehmann, A., Neven, G., &
Towa, P. (2020). Zone Encryption with Anonymous
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
684

Authentication for V2V Communication. 2020 IEEE
European Symposium on Security and Privacy (Eu-
roS&P), 405–424.
Escher, S., Sontowski, M., Berling, K., K
¨
opsell, S., &
Strufe, T. (2021). How well can your car be tracked:
Analysis of the European C-ITS pseudonym scheme.
2021 IEEE 93rd Vehicular Technology Conference
(VTC2021-Spring), 1–6.
Hicks, C., & Garcia, F. D. (2020). A Vehicular DAA
Scheme for Unlinkable ECDSA Pseudonyms in V2X.
2020 IEEE European Symposium on Security and Pri-
vacy (EuroS& P), 460–473.
ISO/IEC JTC 1/SC 27. (2022). Evaluation criteria for
IT security — Part 2: Security functional compo-
nents (International Standard No. ISO/IEC 15408-
2:2022(E)). International Organization for Standard-
ization. Geneva, CH.
ISO/TC 204. (2015). Cooperative ITS — Part 7: Privacy
aspects (Technical Report (TR) No. ISO/TR 17427-
7:2015(E)). International Organization for Standard-
ization. Geneva, CH.
ISO/TC 204. (2018). ITS station management — Part
1: Local management (International Standard No.
ISO 24102-1:2018(E)). International Organization for
Standardization. Geneva, CH.
ISO/TC 22/SC 32. (2021). Cybersecurity engineering (In-
ternational Standard No. ISO/SAE 21434:2021). In-
ternational Organization for Standardization. Geneva,
CH.
Karim Emara, W. W. (2013). Beacon-based Vehicle Track-
ing in Vehicular Ad-hoc Networks (Technical Report).
TUM. Munich, Germany.
Shokri, R., Theodorakopoulos, G., & Troncoso, C. (2016).
Privacy Games Along Location Traces: A Game-
Theoretic Framework for Optimizing Location Pri-
vacy. ACM Transactions on Privacy and Security,
19(4), 11:1–11:31.
Sniedovich, M. (2016). Wald’s mighty maximin: A tutorial.
International Transactions in Operational Research,
23(4), 625–653.
Wagner, I., & Eckhoff, D. (2018). Technical privacy met-
rics: A systematic survey. ACM Computing Surveys
(CSUR), 51(3), 1–38–1–38.
WG1, I. (2018). Intelligent Transport Systems (ITS); Users
and applications requirements; Part 2: Applications
and facilities layer common data dictionary (Techni-
cal Specification No. ETSI TS 102 894-2). European
Telecommunications Standards Institute. Sophia An-
tipolis, France.
WG1, I. (2019). Intelligent Transport Systems (ITS); Ve-
hicular Communications; Basic Set of Applications;
Part 2: Specification of Cooperative Awareness Ba-
sic Service (European Standard No. DS/ETSI EN 302
637-2). European Telecommunications Standards In-
stitute. Sophia Antipolis, France.
WG5, I. (2021). Intelligent Transport Systems (ITS); Se-
curity; Trust and Privacy Management; Release 2
(Technical Specification No. TS 102 941). European
Telecommunications Standards Institute. Sophia An-
tipolis, France.
Wiedersheim, B., Ma, Z., Kargl, F., & Papadimitratos, P.
(2010). Privacy in inter-vehicular networks: Why sim-
ple pseudonym change is not enough. 2010 Seventh
International Conference on Wireless On-demand
Network Systems and Services (WONS), 176–183.
Zolotavkin, Y., Baryshev, Y., Lukichov, V., M
¨
ahn, J., &
K
¨
opsell, S. (n.d.). Improving unlinkability in C-ITS.
doi.org/10.6084/m9.figshare.21830418
Improving Unlinkability in C-ITS: A Methodology For Optimal Obfuscation
685