Coupled Assignment Strategy of Agents in Many Targets Environment

Azizkhon Afzalov

, Ahmad Lotﬁ

and Jun He

Department of Computer Science, Nottingham Trent University, Clifton Campus, Nottingham, NG11 8NS, U.K.

Keywords:

Path Finding, Multi-Agent, Moving Multiple Targets, Assignment Strategy, Heuristic Search Algorithm.

Abstract:

There are multi-agent algorithms that provide solutions with the shortest path without considering other pur-

suing agents. However, less attention has been paid to computing an assignment strategy for the pursuers that

assign targets before the move action. Besides, the pathﬁnding problem for multiple agents becomes even

more challenging if the goal destinations change over time. The path-planning problem for multiple pursuing

agents requires more efﬁcient assignment strategy algorithms. Therefore, this study considers existing and the

most recent solutions and conducts experiments in a dynamic environment where multiple pursuing agents are

outnumbered and required to capture the moving targets for a successful outcome. The existing cost function

strategies, such as sum-of-costs and makes, are compared and analysed to the recent twin cost, cover cost

and weighted cost assignment strategies. The results indicate that the recent criterion, the cover cost algo-

rithm, shows the optimal outcomes in terms of pathﬁnding cost and runtime. Statistical analyses have also

demonstrated the signiﬁcance of the ﬁndings.

1 INTRODUCTION

Finding a path and navigating the pursuing agent from

its starting position to a target position while avoid-

ing obstacles is an important problem in Artiﬁcial In-

telligence (AI) (Standley and Korf, 2011; Vermette,

2011). In the presence of a single pursuer in the

environment, the A* algorithm (Hart et al., 1968)

can be an effective solution. The environment be-

comes dynamic with multiple pursuing agents while

each pursuer is given a target position to reach, as-

suming it is static. However, relaxing the assump-

tion and repositioning the targets’ positions make the

multi-agent pathﬁnding problem more complicated

(

Unde

ger, 2007). While the problem is becoming

increasingly important, issues with coordination, tar-

get assignment, communication, obstacle or collision

avoidance, outsmarting targets while reaching with

fewer time steps and moving quicker in a limited time

need to be considered (Standley, 2010; Wagner and

Choset, 2015). Therefore, it is necessary to ﬁnd a so-

lution for multiple pursuing agents that successfully

catch moving targets.

In recent years, attention has increased to

pathﬁnding problems in multi-agent systems, mainly

https://orcid.org/0000-0002-1456-542X

https://orcid.org/0000-0002-5139-6565

https://orcid.org/0000-0002-5616-4691

due to the expansion in computer video games (Lu-

cas, 2008; Johnson and Wiles, 2001; Yannakakis and

Togelius, 2015), robotics (Russell and Norvig, 2021;

Kloder and Hutchinson, 2006; Berg et al., 2009), and

warehouse management (Li et al., 2020; Ma et al.,

2016). In pursuing games, such as cop and robber,

prey and hunter, and military simulated applications,

both side players can move and change their posi-

tions, and this makes it difﬁcult to search and plan

paths and navigate towards the targets while avoiding

obstacles. The challenge increases when the targets

are not stationary and their number increments. The

moving targets can evade capture while time permits

if the pursuers do not have a winning strategy (Mold-

enhauer and Sturtevant, 2009). Well-deﬁned assign-

ment strategies aim to help efﬁcient planning, reduce

computation time, increase the success of the task,

and affect the total performance of catching all mov-

ing targets. Thus, an assignment strategy is important,

and a good assignment strategy is essential for the de-

sired outcome.

Multiple pursuers can beneﬁt from two stages,

which are coupled and decoupled pathﬁnding algo-

rithms. The coupled approach focuses on planning

and distributing tasks to all pursuers as a single task,

whereas the decoupled approach concentrates on ﬁnd-

ing a path individually. The assignment strategy al-

gorithm computes all possible combinations (pursuer-

372

Afzalov, A., Lotﬁ, A. and He, J.

Coupled Assignment Strategy of Agents in Many Targets Environment.

DOI: 10.5220/0011787100003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 1, pages 372-379

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Figure 1: First, coupled approach assigns pursuers to the

targets and then in decoupled approach the pursuers chase

their targets.

to-target route) for all pursuers in the coupled stage.

This coupled approach produces optimal solutions

(Chouhan and Niyogi, 2017), however, the computa-

tion increases exponentially with the number of pur-

suers. Once the targets are assigned, in the decoupled

stage, all pursuers search their path independently and

navigate towards the moving targets using the heuris-

tic search algorithm. The decoupled approach is fast

but occasionally fails in ﬁnding a complete solution

because of conﬂicts that can arise afterwards, where

pursuers let other pursuers pass (Sharon et al., 2011;

Standley and Korf, 2011; Ryan, 2006). Moreover, its

usage is practical and robust, if one pursuer fails, that

does not affect the entire team’s success (Tovey et al.,

2005). Figure 1 illustrates both approaches.

In this paper, the existing assignment strategies,

such as sum-of-costs and makespan criteria (Atzmon

et al., 2020) and twin-cost, cover-cost and weighted-

cost criteria (Afzalov et al., 2021a), are evaluated to

ﬁnd the optimal criterion in a new multiple Pursuing

Agents and multiple Moving Targets (PAMT) prob-

lem set. A preliminary version of this study was pub-

lished in a conference paper (Afzalov et al., 2021a).

However, the previous study was limited in experi-

mentation, it did not compare all ﬁve criteria together,

nor the runtime and only covered a condition where

agents ≥ targets. The heuristic function is Manhattan

distance in contrast to the previous diagonal moves.

Therefore, in this study, the main contribution is to

evaluate the existing methods through the conduct

of experiments that extend the work signiﬁcantly, by

providing:

• A description of the assignment strategy criteria.

• A comprehensive set of experiments to evaluate

pathﬁnding cost, computation time to assign tar-

gets as well as a runtime for pursuing agents.

• A variety of pursuer-to-target combinations,

where targets outnumber pursuers and increased

in each test run (pursuers < targets).

• Benchmark environments from the Baldur’s Gate

video game.

• Statistical analysis using Friedman test.

In the remaining parts of this paper, related work

is discussed in Section 2. Section 4 explains existing

and recent assignment strategy algorithms. Section 5

evaluates the algorithms empirically and provides the

results of statistical tests. Section 6 concludes with

areas that are left for future work.

2 RELATED WORK

Moving Target Search (MTS) (Ishida and Korf, 1991)

is a problem of a single agent chasing a single mov-

ing target with full knowledge of the environment

and position of the target. This problem has been

extended to multiple agents and targets (MAT) (Xie

et al., 2017) where pursuing agents such as police ve-

hicles chase suspects. This method computes a se-

ries of autonomous agent-to-target searches with a

given assignment strategy. An effective solution to

this problem is challenging, computationally expen-

sive and known to be NP-hard (Li et al., 2020; Shi

et al., 2021; Fomin et al., 2008).

There are many formulations of this problem, and

Multirobot Path Planning on graphs (MPP) (Yu and

LaValle, 2016) is one of them, where robots move

from one vertex to an adjacent vertex at a one-time

step. To avoid a collision of robots’ moves, the MPP

allows synchronous rotation for all robots in contrast

to only a single robot move, and the global objec-

tive is to reduce time in the completion of tasks. A

similar problem is Multi-Agent PathFinding (MAPF)

(Sharon et al., 2011) which deals with multiple static

destinations or Multi-Agent Meeting (MAM) (Atz-

mon et al., 2020), which gathers multiple agents at

the chosen meeting point among all possible destina-

tions.

Finding an optimal algorithm for a given envi-

ronment is a difﬁcult task while ﬁnding an opti-

mal algorithm for all environments is impossible in

principle (Maple et al., 2014). For instance, the

Multi-Directional Meet in the Middle (MM*) (Atz-

mon et al., 2020) algorithm promises an optimal path

for MAM problems with a unique priority function

for Sum-Of-Costs (SOC) and the maximum distance

cost (makespan). The distance towards the meeting

position is minimised using these two different costs,

ﬁrstly SOC and secondly makespan. The algorithm

uses the best-ﬁrst search method when ﬁnding the

middle meeting point for several starting locations.

Several agents can be tasked to ﬁnd a collision-

free path to the static goal positions in multi-agent

pickup and delivery problems. Agents are allowed to

move from starting position to the pickup location,

Coupled Assignment Strategy of Agents in Many Targets Environment

373

wait and then continue to the ﬁnal location. A task

to pick up from a location and deliver to a goal des-

tination is a speciﬁc multi-goal MAPF problem that

is referred to as a Multi-Agent Pickup and Delivery

(MAPD) (Ma et al., 2017) problem. This process re-

quires multiple paths and involves planning for mul-

tiple agents. The Multi-Label A* (MLA*) (Grenouil-

leau et al., 2019) algorithm is able to provide a so-

lution by computing multiple paths by using the A*

algorithm.

Conﬂict Based Search (CBS) (Sharon et al.,

2012b) is the algorithm for MAPF problems that

promises optimal solutions at the expense of com-

putation by using a coupled approach, however, all

pathﬁnding searches are single-agent which is simi-

lar to the decoupled approach (Sharon et al., 2013).

CBS uses both high-level and low-level searches. At

the high level, the search is structured to use the best-

ﬁrst search, and the arising conﬂicts need to be re-

solved for pairs of agents. The CBS algorithm uses

a Constraint Tree (CT), with each node having con-

straints on time and location. At the low level, the A*

based search is run only for the single agent, while

disregarding the other agents, to ﬁnd the optimal path

under a set of constraints that are established at the

high-level search.

CBS solves MAPF problems optimally, however,

the worst-case performance needs to be reduced and

therefore, CBS has been generalised into a new al-

gorithm called Meta-Agent CBS (MA-CBS) (Sharon

et al., 2012a). This approach has been generalised to

merge the conﬂicting agents into one compound as

a meta-agent if the predeﬁned conﬂict bound is met,

which then is processed to ﬁnd a path at the lower

level.

The combined Target-Assignment and Path-

Finding (TAPF) (Ma and Koenig, 2016) problem is

a different kind of MAPF problem. The number of

agents is equal to the number of targets, and the agents

are aimed ﬁrst to assign all targets and then plan their

path with no collision by minimising the makespan in

the known environments. The agents are split into

teams and each team is given the same number of

targets to match the number of agents in the team.

It is allowed for each agent within its team to swap

the assigned targets but the agents from the differ-

ent teams are not allowed to swap the targets with

other teams. The solution for this problem is ad-

dressed with a Conﬂict-Based Min-Cost-Flow (CBM)

(Ma and Koenig, 2016) algorithm that solves TAPF

instances using anonymous (swappable target assign-

ments) and non-anonymous (pre-determined target

assignments) multi-agent pathﬁnding algorithms.

3 PROBLEM DEFINITION

In the PAMT problem, an undirected and unweighted

graph G = (V,E) is given with a set of n pursuing

agents P = {p

,...,p

}. Each pursuer p

∈ P starts

at a vertex s

∈ V and navigates to the target vertex t

∈ V. Time is discretised into time steps and each pur-

suer p

can occupy exactly one vertex. At each time

step, the pursuer can either move to an adjacent avail-

able vertex or wait in its current vertex, where each

action is assigned with a cost of one. The goal of the

PAMT problem is to ﬁnd a sequence of actions (move

or wait) for each pursuer p

with a set of path routes R

= {r

,...,r

} where r

is a path route for the pursuer

from s

to t

. The solution results in moving all pur-

suers from their start vertices to the targets with the

optimal pathﬁnding cost, which is the minimum cost

of the last caught target.

4 FINDING OPTIMAL

ASSIGNMENT STRATEGIES

In the coupled stage, the pursuers coordinate using the

assignment strategy criterion to assign existing targets

in a deﬁned scenario. The given assignment strategy

then provides the optimum combination to enable the

pursuers to achieve their goal of catching targets the

most cost-effectively. The research has been taken

to ﬁnd an optimal combination of assignments and

common cost functions that have been used are the

summation of distances or the maximum time step

(makespan). This section introduces existing assign-

ment strategy criteria that are used in assigning targets

to the pursuing agents and the following provides a

brief description of each algorithm.

4.1 Sum-of-Cost

The total cost of all distances is used in this criterion

(Atzmon et al., 2020). The distance is computed from

the current position of pursuers and not the future

positions. In Figure 2, a two-dimensional map with

black-shaded obstacles, there are two pursuing agents

, P

) and two targets (T

, T

). Each pursuing agent

has an admissible path towards the targets; therefore,

they have got a choice of which one of two targets

to follow. The SOC criterion chooses a combination

with the lowest distance in total. Table 1 displays the

distance cost for each pursuer towards the target. The

column SOC is the sum of two costs within the same

combination. Combination 1 is chosen as its total is

lower than that of combination 2. The cost

equation

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

374

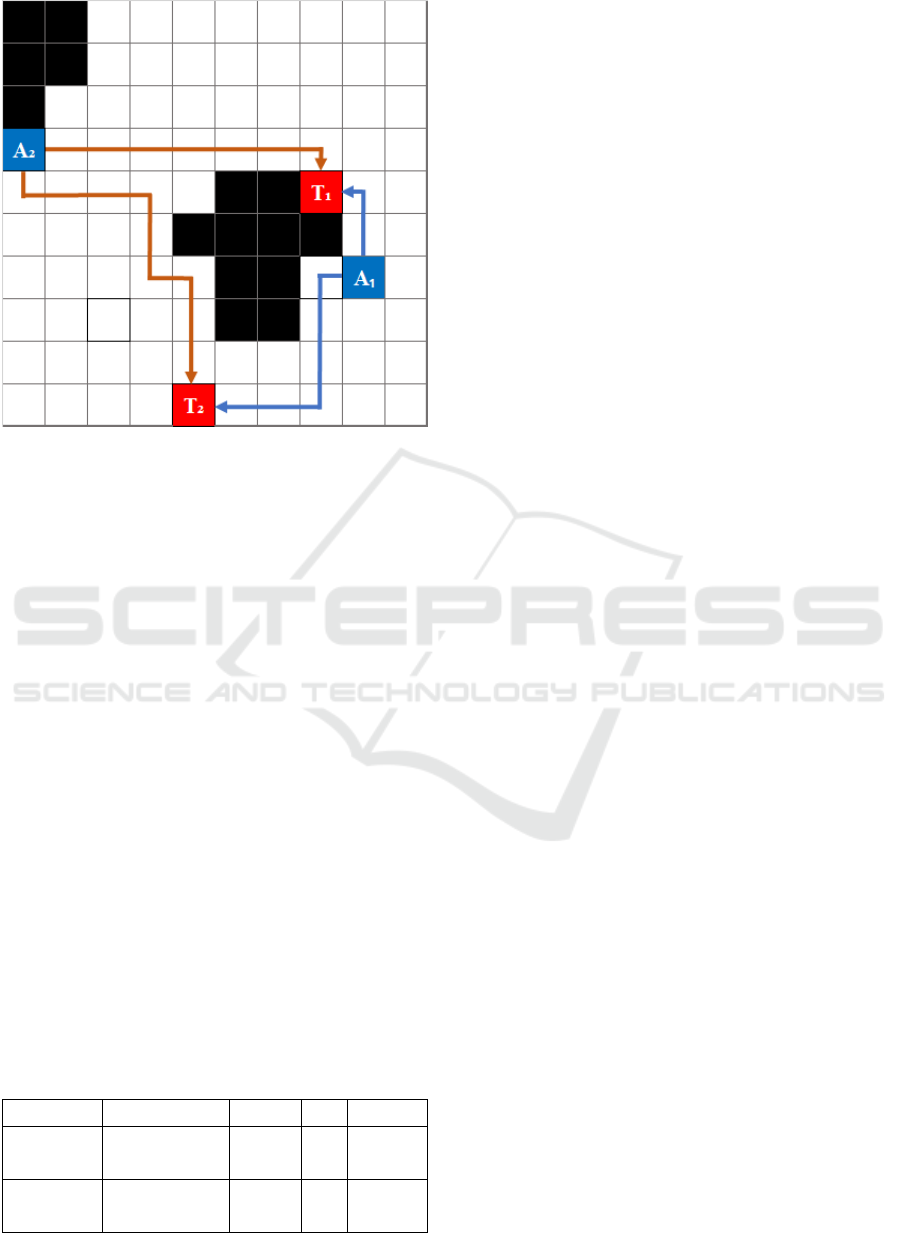
Figure 2: Demonstrating pursuers’ (P

and P

) possible di-

rections towards the targets (T

and T

) on a sample map.

Black shades are obstacles.

for SOC is:

cost

= (P

→ T

)

distance

+ (P

→ T

)

distance

(1)

4.2 Makespan

Makespan criterion uses the maximum distance cost

within the combination instead of its total (Xie et al.,

2017). Makespan has been named timesteps too, as

each move is equal to a single time step. Therefore, it

focuses on the maximum time spent to reach the cur-

rent position of the targets for all pursuers. This is

important in many situations, for example, hot food

delivery drivers might want to take their customers’

orders to their destinations such that the maximum

time is as low as possible. Table 1 additionally dis-

plays this criterion in the column named makespan.

Combination 2 has the lowest value for the makespan

criterion. The cost

equation for makespan is:

cost

= max{(P

→ T

)

distance

, (P

→ T

)

distance

}

(2)

Table 1: The distance cost combinations for two agents to-

wards two targets as illustrated in Figure 2.

Combination Pursuer to Target Distance SOC makespan

→ T

13 10

→ T

15 8

→ T

4.3 Twin Cost

The twin cost (Afzalov et al., 2021a) criterion, just

like the previous SOC and makespan criteria, uses

the distance values to determine the best cost for its

new assignment approach. The product of SOC and

makespan in the column of Table 1 is the generated

value for each combination. In the situations, when

there is a tie-breaker needed, then the average of SOC

and makespan is taken. Two values are multiplied to-

gether for the twin cost criterion equation:

cost

= SOC × makespan (3)

4.4 Weighted Cost

This weighted cost (Afzalov et al., 2021a) crite-

rion relevant to the problems where both SOC and

makespan costs needed to be considered together.

When all distances are computed and their combi-

nation values are obtained for each pursuer, then the

results in Table 1 for SOC and makespan will allo-

cate a speciﬁc weight value according to the given

weighted-cost criterion.

For instance, a delivery driver with a scheduled

plan drives fast to get to the goal destination quickly,

which is the makespan criterion, however, at the same

time, the driver needs to consider shorter routes to get

there, the SOC criterion. If the weight value of 0.2%

is given for SOC and 0.8% for makespan, then with

equation 4 the result for combination 1 is 10.6 and

for combination 2 is 9.4. Therefore, the lowest value,

which is combination 2 is the choice of route plan for

the delivery driver.

cost

= (SOC × m)+ (makespan × n) (4)

4.5 Cover Cost

The above-mentioned criteria use a distance to com-

pute the best assignment strategy for the multiple

agents. The cover cost (Afzalov et al., 2021a) cri-

terion proposes a different approach which is not to

use the cost of distances, but instead, while idle be-

fore the action starts, it expands and marks each state

on the map as covered for each pursuer. The expan-

sion is similar to the cells in the breadth-ﬁrst search

algorithm. These covered states are divided by the

number of empty states and the percentage is the re-

sult for each pursuer. Depending on the number of

pursuers present on the map, the mean is taken for

each combination. In contrast to the previous crite-

ria, not the lowest percentage value, but instead, the

highest percentage value is optimal.

Coupled Assignment Strategy of Agents in Many Targets Environment

375

Figure 3: Grid-based AR0509SR map from Baldur’s Gate

video game with black obstacles and narrow passages.

4.6 Pursuing Algorithm and Target

The pursuing agents use the Strategy Multiple Tar-

get A* (STMTA*) (Afzalov et al., 2021b) algorithm

which runs autonomous paths to the assigned targets.

STMTA* uses an assignment strategy algorithm in

the coupled stage, and once all targets are assigned

to the pursuers while they idle, then in the decoupled

stage, the pursuers move a step towards the targets. If

the target is re-positioned and moved to another state,

then STMTA* search for a new path to the already as-

signed target. If the assigned target is captured by the

pursuer, it can get re-assigned to another non-captured

target. Moreover, it is possible to navigate all pursuers

to the last target as this increases the capture.

It is worth mentioning that the targets use the Sim-

ple Flee (SF) (Isaza et al., 2008) algorithm which is

based on the A* algorithm that evades pursuers and

checks periodically if the path is still the best to es-

cape.

5 EMPIRICAL EVALUATIONS

This section presents the empirical results for the as-

signment strategies which are described in Section 4.

Initially, the setting for the experiments is described

and then follows the presentation of the performance

results. The pathﬁnding cost, the computation time

in assigning targets to the pursuers and the runtime to

reach the targets, are all measured for performance.

Finally, statistical tests are conducted for the signiﬁ-

cance of the results.

5.1 Experimental Setup

The experiments are adapted to a simulated gaming

environment and set to run on commercial game in-

Figure 4: Pathﬁnding cost mean for pursuing agents.

dustry maps, which are standardised benchmarked

maps from Baldur’s Gate video game (Stern et al.,

2019). The environments are grid-based 2-D rect-

angular with four-connected states. The selection

of these ﬁve maps is based on the size, existence

of obstacles and difﬁculty of navigation. A sample

AR0509SR map is illustrated in Figure 3. All play-

ers have equal speed and one action is performed at

each time step. However, it is possible to apply var-

ious moving costs and speeds. It can be imagined as

a scenario with cops (pursuing agents) and robbers

(targets), where cops need to unite their forces to suc-

cessfully catch robbers at a minimum cost or similar

to the multi-player computer video game Prey: Ty-

phon Hunter (Arkane Studios, 2018).

The initial scenario is conﬁgured with 2 pursuing

agents and 4 moving targets (2vs4). The number of

targets is increased by 2 in each scenario until reaches

10 targets. Similarly, three and four pursuing agents

are compared for their behaviour with similar target

settings. Each problem is deﬁned by the starting po-

sition for pursuers and targets that are randomly dis-

persed at pre-selected locations in the environment.

Each pursuer and target has knowledge of the loca-

tions of others. Time is discretised into time steps and

only orthogonal moves are allowed with a cost of one.

Each assignment strategy algorithm is tested un-

der the same conﬁgurations in the same environment.

Each setup was tested 20 times, totalling 30,000 in-

dividual test runs. The base of the implementation

(Isaza et al., 2008) was kindly provided by Alejandro

Isaza and it has been extended such that multiple tar-

gets and various pursuer-target assignment strategies

could be tested. The experiments are conducted on a

Linux machine on Intel® Core™ i7 at 2.2 GHz CPU

with 16 GB of RAM.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

376

Table 2: Ranking assignment strategies using Friedman statistical analysis test and displaying p-values for signiﬁcance.

Maps

Ranking Values

p-value

SOC

Make

span

Twin

cost

Cover

cost

Weighted

cost

AR0311SR 2 4 5 1 3 2.25E-03

AR0509SR 4 3 1 2 5 1.25E-02

AR0527SR 1 5 4 2 3 1.34E-06

AR0707SR 3 5 4 1 2 1.06E-07

AR0712SR 4 2 3 5 1 7.59E-01

Total

Ranking

2 3.5 5 1 3.5

5.2 Results

The performance of the assignment strategy algo-

rithms is evaluated, and the results are presented for

the pathﬁnding cost, the time it takes to assign targets,

and the runtime to reach the targets. Having different-

sized maps, the experiments are not limited to a ﬁxed

deadline, but it is adjusted to the size of the map and

runs out of time (timeout) at 10 times the height of

the map. The pathﬁnding cost is measured for the

number of time steps taken at capturing all targets for

successful runs or until timeout for unsuccessful runs.

The success is recorded when all targets are captured,

i.e., at least one pursuer occupies the same state as the

target. The runtime is measured in seconds. Mean

is taken for all measurements considering all pursuers

and conﬁgurations.

5.2.1 Pathﬁnding Cost

The pathﬁnding costs for assignment strategy algo-

rithms are measured and depicted in Figure 4. The

graph shows the mean for the pathﬁnding cost of ﬁve

maps for all pursuer-target combinations. Pre-deﬁned

weight parameters are used for the weighted cost al-

gorithm. For the experiments in this study, the ratio

of 50/50 is used for SOC and makespan.

The results in Figure 4 display that the cover cost

algorithm has the lowest number of steps on average

and while using the maximum coverage in assign-

ing targets produced the best performance. The twin

cost and weighted cost algorithms displayed similar

performance, while SOC performed slightly better.

Makespan has the highest number of steps in catching

all moving targets. These results are averaged across

all maps and conﬁguration settings, however, even if

it is occasionally, it is possible to see the twin cost

displaying better results than others. Obviously, the

pathﬁnding cost increased with the increase of targets

during the experiments, and this did not affect the suc-

cess of the algorithms, as none of them failed in cap-

Table 3: Runtime in seconds for pursuing agents over all

maps.

SOC

Make-

span

Twin

cost

Cover

cost

Weighted

cost

Average: 9.4448 9.4880 9.3927 9.1737 9.4895

turing the targets, thus the success rate is 100% across

all.

Although the cover cost algorithm produces better

results, statistical tests are conducted on the pathﬁnd-

ing costs to identify signiﬁcance. The data obtained

from the test runs are not normally distributed and

there are ﬁve algorithms to compare, therefore, the

Friedman test (Dem

sar, 2006) is used for statistical

analysis. First, the ranking is used in the Fried-

man test where each data set is ranked separately for

each algorithm and the algorithm with the best perfor-

mance is rank no. 1, as shown in Table 2. The ranking

is obtained for all algorithms per map and added up

accordingly. To obtain the overall ranking results, all

ranking values are added to get the total sum and the

ﬁnal total ranking as displayed at the bottom of Table

2. Second, the Friedman test uses these ranking re-

sults to obtain p-values. The 0.05 is used for the level

of signiﬁcance and the results are displayed in the

same table under p-value column. The evidence sug-

gests that the results display statistically strong signif-

icant differences and the results on AR0509SR show

little signiﬁcance. It is possible to conclude that the

cover cost algorithm displays signiﬁcantly better.

5.2.2 Runtime

The time spent on assignment strategy algorithms to

identify and assign targets to the pursuing agents is

evaluated in seconds. In each test run, the time is

measured until all pursuers are provided with the most

optimal conﬁguration set and assigned all existing tar-

gets on the map. Figure 5 illustrates the results for all

algorithms and their behaviour on the provided map.

Because the starting positions are ﬁxed on every test

Coupled Assignment Strategy of Agents in Many Targets Environment

377

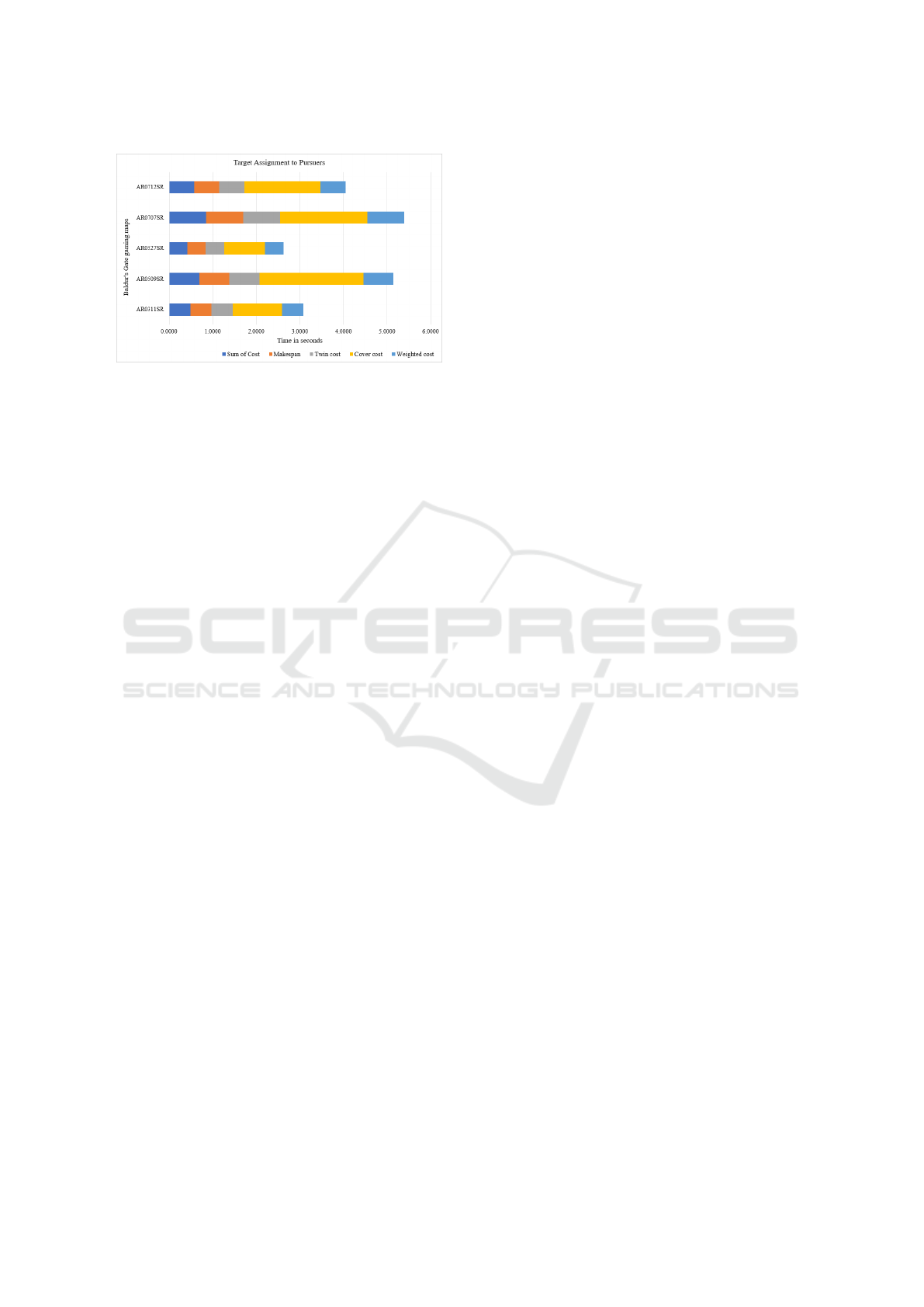
Figure 5: The time to assign targets before pursuers move.

run and the time to assign targets is measured exclud-

ing the navigation time, the average time to assign

targets has a very small difference among all but not

the cover cost. It is always expensive to compute all

non-blocked states and this is the feature of the cover

cost. Therefore, as expected, cover cost displays the

highest computation cost with 2.7% times slower. All

other algorithms display similar results and there is no

global algorithm whose approach displays the quick-

est assignment time.

The runtime measures once pursuers start the ac-

tion and navigate until the capture of all targets. This

action is recorded in seconds and the results are aver-

aged over all tests. It is possible that the pathﬁnding

cost is related to runtime. The shortest path produces

the quickest solution. Figure 4 shows that cover cost

has the lowest cost; similarly, this can be seen in Ta-

ble 3 for runtime. Despite the fact that the cover cost

takes longer during the assignment, it is faster in cap-

turing all targets.

6 CONCLUSION

In this study, assignment strategy algorithms are in-

vestigated and experimentally compared to analyse

the optimal criterion in assigning multiple targets

to multiple pursuing agents. As discussed in Sec-

tion 2, the existing cumulative cost such as SOC or

makespan is used to assign targets or goal destina-

tions. The new cost function approaches, twin cost,

cover cost and weighted cost, are empirically evalu-

ated with the existing criteria. The cover cost algo-

rithm can navigate the pursuing agents to the moving

targets cost-effectively and is statistically proven to be

signiﬁcant. At the same time, the cover cost is quicker

but performance in assigning targets to the pursuers is

lower due to the high-cost computation. Alongside

this, the weighted cost with a 50/50 parameter setting

has been the quickest with a very small difference to

assign available targets to the pursuers before the pur-

suers’ navigation towards moving targets starts.

Although the experiments are conducted for mov-

ing targets, it is possible to apply for stationary posi-

tioned targets that are similar to the warehouse exam-

ple. It is expected that the time to assign targets will

be similar, as it computes before any move action.

REFERENCES

Afzalov, A., He, J., Lotﬁ, A., and Aydin, M. E. (2021a).

Multi-agent path planning approach using assign-

ment strategy variations in pursuit of moving tar-

gets. In Agents and Multi-Agent Systems: Technolo-

gies and Applications 2021, pages 451–463, Singa-

pore. Springer.

Afzalov, A., Lotﬁ, A., and Aydin, M. E. (2021b). A strategic

search algorithm in multi-agent and multiple target en-

vironment. In RiTA 2020, pages 195–204, Singapore.

Springer.

Arkane Studios (2018). Prey: Typhon hunter. Microsoft

Windows.

Atzmon, D., Li, J., Felner, A., Nachmani, E., Shperberg,

S., Sturtevant, N., and Koenig, S. (2020). Multi-

directional heuristic search. In Proceedings of the

29th International Joint Conference on Artiﬁcial In-

telligence, IJCAI, pages 4062–4068.

Berg, J. V. D., Snoeyink, J., Lin, M., and Manocha, D.

(2009). Centralized path planning for multiple robots:

Optimal decoupling into sequential plans. In Trinkle,

J., Matsuoka, Y., and Castellanos, J. A., editors, Pro-

ceedings of Robotics: Science and Systems, volume 5,

page 137 – 144. MIT Press Journals, Seattle, USA.

Chouhan, S. S. and Niyogi, R. (2017). DiMPP: a complete

distributed algorithm for multi-agent path planning.

Journal of Experimental and Theoretical Artiﬁcial In-

telligence, 29(6):1129–1148.

Dem

sar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. The Journal of Machine learn-

ing research, 7:1–30.

Fomin, F. V., Golovach, P. A., and Kratochv

ıl, J. (2008).

On tractability of cops and robbers game. In Ausiello,

G., Karhum

aki, J., Mauri, G., and Ong, C. L., edi-

tors, Fifth IFIP International Conference On Theoret-

ical Computer Science - TCS 2008, volume 273, pages

171–185.

Grenouilleau, F., van Hoeve, W.-J., and Hooker, J. N.

(2019). A multi-label A* algorithm for multi-agent

pathﬁnding. In ICAPS 2019 - Proceedings of the 29th

International Conference on Automated Planning and

Scheduling, volume 29, pages 181–185.

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE Transactions on Systems Science and

Cybernetics, 4(2):100–107.

Isaza, A., Lu, J., Bulitko, V., and Greiner, R. (2008). A

cover-based approach to multi-agent moving target

pursuit. In Proceedings of the 4th Artiﬁcial Intelli-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

378

gence and Interactive Digital Entertainment Confer-

ence, AIIDE, page 54 – 59.

Ishida, T. and Korf, R. E. (1991). Moving target search.

In Proceedings of the 12th International Joint Confer-

ence on Artiﬁcial Intelligence, IJCAI, volume 1, pages

204–210.

Johnson, D. and Wiles, J. (2001). Computer games with in-

telligence. In Proceedings of the 10th IEEE Interna-

tional Conference on Fuzzy Systems, volume 3, pages

1355–1358.

Kloder, S. and Hutchinson, S. (2006). Path planning for

permutation-invariant multirobot formations. IEEE

Transactions on Robotics, 22:650–665.

Li, J., Gange, G., Harabor, D., Stuckey, P. J., Ma, H.,

and Koenig, S. (2020). New techniques for pairwise

symmetry breaking in multi-agent path ﬁnding. In

Proceedings of the 13th International Symposium on

Combinatorial Search, SoCS, volume 30, pages 193–

201.

Lucas, S. M. (2008). Computational intelligence and

games: Challenges and opportunities. International

Journal of Automation and Computing, 5(1):45–57.

Ma, H. and Koenig, S. (2016). Optimal target assignment

and path ﬁnding for teams of agents. In Proceedings

of the 15th International Conference on Autonomous

Agents and Multiagent Systems, AAMAS, page 1144 –

1152.

Ma, H., Koenig, S., Ayanian, N., Cohen, L., H

onig, W., Ku-

mar, T. K., Uras, T., Xu, H., Tovey, C., and Sharon,

G. (2016). Overview: Generalizations of multi-agent

path ﬁnding to real-world scenarios. In IJCAI-16

Workshop on Multi-Agent Path Finding.

Ma, H., Li, J., Kumar, T. K., and Koenig, S. (2017). Life-

long multi-agent path ﬁnding for online pickup and

delivery tasks. In Proceedings of the 16th Interna-

tional Conference on Autonomous Agents and Multia-

gent Systems, AAMAS, volume 2, pages 837–845.

Maple, C., Prakash, E., Huang, W., and Qureshi, A. N.

(2014). Taxonomy of optimisation techniques and ap-

plications. International Journal of Computer Appli-

cations in Technology, 49(3-4):251–262.

Moldenhauer, C. and Sturtevant, N. R. (2009). Optimal

solutions for moving target search. In Proceedings

of the 8th International Conference on Autonomous

Agents and Multiagent Systems, AAMAS, volume 2,

pages 1249–1250.

Russell, S. and Norvig, P. (2021). Artiﬁcial intelligence: A

modern approach (Global edition). Pearson Educa-

tion Limited, 4 edition.

Ryan, M. (2006). Multi-robot path-planning with sub-

graphs. In Proceedings of the 19th Australasian Con-

ference on Robotics and Automation, ACRA, pages 1–

Sharon, G., Stern, R., Felner, A., and Sturtevant, N. (2012a).

Meta-agent conﬂict-based search for optimal multi-

agent path ﬁnding. In Proceedings of the 5th Inter-

national Symposium on Combinatorial Search, SoCS,

page 97 – 104.

Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R.

(2012b). Conﬂict-based search for optimal multi-

agent path ﬁnding. In Proceedings of the 26th Na-

tional Conference on Artiﬁcial Intelligence, AAAI,

volume 1, page 563 – 569, Ontario, Canada. AAAI

Press.

Sharon, G., Stern, R., Goldenberg, M., and Felner, A.

(2011). The increasing cost tree search for optimal

multi-agent pathﬁnding. In Proceedings of the 22nd

International Joint Conference on Artiﬁcial Intelli-

gence, IJCAI, page 662 – 667.

Sharon, G., Stern, R., Goldenberg, M., and Felner, A.

(2013). The increasing cost tree search for opti-

mal multi-agent pathﬁnding. Artiﬁcial Intelligence,

195:470 – 495.

Shi, Y., Hu, B., and Huang, R. (2021). Task allocation

and path planning of many robots with motion uncer-

tainty in a warehouse environment. In 2021 IEEE In-

ternational Conference on Real-Time Computing and

Robotics, RCAR, page 776 – 781.

Standley, T. (2010). Finding optimal solutions to coopera-

tive pathﬁnding problems. In Proceedings of the 24th

National Conference on Artiﬁcial Intelligence, AAAI,

volume 1, page 173 – 178.

Standley, T. S. and Korf, R. E. (2011). Complete algorithms

for cooperative pathﬁnding problems. In Proceedings

of the 22nd International Joint Conference on Artiﬁ-

cial Intelligence, IJCAI, page 668 – 673.

Stern, R., Sturtevant, N. R., Felner, A., Koenig, S., Ma, H.,

Walker, T. T., Li, J., Atzmon, D., Cohen, L., Kumar,

T. K. S., Boyarski, E., and Bart

ak, R. (2019). Multi-

agent pathﬁnding: Deﬁnitions, variants, and bench-

marks. In Proceedings of the 12th International Sym-

posium on Combinatorial Search, SoCS, page 151 –

158.

Tovey, C., Lagoudakis, M. G., Jain, S., and Koenig, S.

(2005). The generation of bidding rules for auction-

based robot coordination. In Multi-Robot Systems.

From Swarms to Intelligent Automata - Proceedings

from the 2005 International Workshop on Multi-Robot

Systems, volume 3, page 3 – 14.

Unde

ger, C¸ . (2007). Single and multi agent real-time path

search in dynamic and partially observable environ-

ments. PhD thesis, Middle East Technical University,

C¸ ankaya, Ankara, Turkey.

Vermette, J. (2011). A survey of path-ﬁnding algorithms

employing automatic hierarchical abstraction. Jour-

nal of the Association for Computing Machinery,

377:383.

Wagner, G. and Choset, H. (2015). Subdimensional expan-

sion for multirobot path planning. Artiﬁcial Intelli-

gence, 219:1–24.

Xie, F., Botea, A., and Kishimoto, A. (2017). A scalable ap-

proach to chasing multiple moving targets with mul-

tiple agents. In Proceedings of the 26th International

Joint Conference on Artiﬁcial Intelligence, IJCAI, vol-

ume 0, page 4470 – 4476.

Yannakakis, G. N. and Togelius, J. (2015). A panorama

of artiﬁcial and computational intelligence in games.

IEEE Transactions on Computational Intelligence and

AI in Games, 7:317–335.

Yu, J. and LaValle, S. M. (2016). Optimal multirobot

path planning on graphs: Complete algorithms and

effective heuristics. IEEE Transactions on Robotics,

32(5):1163–1177.

Coupled Assignment Strategy of Agents in Many Targets Environment

379