Computational Study of Particle Separation Based on Inertial Effects in

Rectangular Serpentine Channels with Different Aspect Ratios

zbeta Bug

nov

1 a

and Ivan Cimr

1,2 b

Cell-in-ﬂuid Biomedical Modelling & Computations Group, Faculty of Management Science and Informatics,

University of

Zilina, Slovakia

Research Centre, University of

Zilina, Slovakia, Slovak Republic

Keywords:

Inertial Microﬂuidics, Rectangular Cross-Section, Particle Separation, Focusing Length.

Abstract:

Inertial effects in straight and curved microﬂuidic channels have great potential for separation of particles of

different sizes. the geometry of the channels inﬂuences the separation. In this work we consider a serpentine

channel with rectangular cross section of different sizes to explore the inﬂuence of aspect ratio on focusing

performance and particle separation possibilities. Particle trajectories of different sizes are studied by means

of a computational simulations. We show that low-aspect ratio offers more possibilities for separation in terms

of particle sizes as well as in terms of higher throughput.

1 INTRODUCTION

The inertial migration of particles in a ﬂow through

a cylindrical tube was ﬁrst observed by (Segr

e and

Silberberg, 1961). In their experiments, spherical

particles migrated to an annulus located about 0.6

times of tube radius between centerline and pipe

wall. Subsequently, many research studies were fo-

cused to understand the underlying physics of this

phenomenon through experimental studies, theoreti-

cal analyses and numerical simulations (McLaughlin,

1993; Chun and Ladd, 2006; Hood et al., 2015) and

the references therein.

After big leap in microﬂuidics in last decades,

where the size of patterned micro-channel is compa-

rable to that of the suspended particles (so that inertial

migration can be more obvious within a short channel

length), inertial effects have found their use in practi-

cal applications in medicine and biomedicine e.g. re-

covery of rare cells from blood (Tanaka et al., 2012),

separation of particles by deformability for instance

diseased red blood cells from healthy ones or search

for sepsis markers (Gossett et al., 2012).

Inertial microﬂuidics provide precise manipula-

tion with immersed particles or cells, simple structure

and high throughput. In contrast to active microﬂu-

idic manipulation technologies (Cetin and Li, 2011;

https://orcid.org/0000-0001-6772-2970

https://orcid.org/0000-0002-0389-7891

Forbes and Forry, 2012; Li et al., 2013) where exter-

nal force ﬁelds (electric, magnetic, acoustic) are sup-

plied to control the motion of target particles or cells,

inertial microﬂuidics is a passive manipulation tech-

nology, and it employs intrinsic hydrodynamic force

for manipulation. Therefore, the operation of inertial

microﬂuidics is very simple and robust, and the cost

of inertial microﬂuidic device is low.

Computational models provide effective way for

prototyping the correct geometries of the channels.

(Rasooli and C¸ etin, 2018) developed a Lagrangian

model using COMSOL Multiphysics to solve the con-

tinuous phase and simulate particle trajectories in a

spiral microchannel. (Jiang et al., 2016) explored

the particle focusing mechanisms of a symmetric ser-

pentine microchannel using model based on a lattice

Boltzmann method. (Ying and Lina, 2020) studied

special zig-zag shape of serpentine channel conclud-

ing several advantages of this type of channel com-

pared to squared or curved serpentines. Their results

indicate that the zigzag channel has the best focusing

effect at a high Reynolds number and that the serpen-

tine channel is second in terms of performance.

Contents of This Work

In this work we focus on studying how different as-

pect ratio of the channel cross section affects the even-

tual focusing positions of particles with two different

sizes. In (Ying and Lina, 2020) the authors consid-

284

Bugá

nová, A. and Cimrák, I.

Computational Study of Particle Separation Based on Inertial Effects in Rectangular Serpentine Channels with Different Aspect Ratios.

DOI: 10.5220/0011788200003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 3: BIOINFORMATICS, pages 284-291

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

ered the cross section with dimensions 80× 40µm. We

added two more cases to see whether more square-

like cross section or a cross section with lower as-

pect ratio will affect the stable positions. Therefore

we picked rectangular cross sections 60 × 52µm and

100 × 32µm, see Figure 7. All three cases have sim-

ilar area of around 3100µm

. This ensures that with

the same volumetric ﬂow we get similar maximal ve-

locities in the channels.

In Section 2 we brieﬂy provide theoretical aspects

of inertial focusing. In Section 3 we describe the

physical model and its numerical implementation to-

gether with several technical details about the experi-

mental setup. In Section 4 we provide computational

results and in the last section we discuss the results.

2 PRINCIPLES OF INERTIAL

FOCUSING

Particle focusing in straight channels about 60% away

from the tube centerline is caused by a balance of in-

ertial shear gradient lift forces pushing the particles

towards the wall and a wall repulsion forces caused

by an increased pressure between the particles and

the wall (Matas et al., 2009). Altering the channel

cross section or curving the channel into serpentine

or spiral geometries changes the number and location

of lateral equilibrium positions and can accelerate lat-

eral focusing of particles (Martel and Toner, 2014).

The forces responsible for such behaviour are three-

Figure 1: Competing inertial forces. Reprinted from (Mar-

tel and Toner, 2014) with permissions.

fold: the wall interaction lift forces, the shear gradient

lift forces and the secondary-ﬂow induced Dean drag

forces, see Figure 1. As the streamlines are diverted

toward the side of the particle away from the wall, the

ﬂuid accelerates, causing low pressure on the top and

higher pressure on the wall side of the particle, which

generates the wall interaction force, Figure 1 on the

left. The formula giving the magnitude of the wall

induced force is

= C

ρU

max

, (1)

where C

is a lift coefﬁcient dependent on particle

position and on Reynolds number (Di Carlo et al.,

2009), ρ is the ﬂuid density, U

max

is the maximal ﬂuid

velocity, a is the particle diameter, and D

is the hy-

draulic diameter of the channel.

A typical microﬂuidic velocity proﬁle is parabolic

and, thus, curved. A particle at a position in such

a ﬂow will experience velocities of different magni-

tudes on either side. The ﬂuid ﬂow around the parti-

cle must compensate for this difference and induces

a force on the particle directed toward the side of the

particle with a higher relative velocity (normally to-

ward the walls of a microﬂuidic channel or areas of

increasing shear), Figure 1 in the middle. This shear

induced lift force has magnitude

= C

ρU

max

, (2)

here C

is a shear coefﬁcient dependent on particle po-

sition and on Reynolds number (Di Carlo et al., 2009).

In curved channels, the centrifugal force gener-

ates a secondary ﬂow that is perpendicular to the main

ﬂow direction. Normally, this ﬂow is two orders mag-

nitude weaker than the main ﬂow, however it is suf-

ﬁcient to create the drag around the particles causing

transversal motion across the cross section, Figure 1

on the right. The formula for the evaluation of Dean

force takes the form

= 3πµaU

, (3)

where averaged Dean velocity can be approximated

by (Ookawara et al., 2004)

= 1.8 · 10

−4

1.63

. (4)

Here, De denotes Dean number given by

De = Re

ρU

max

, (5)

Re being the Reynolds number and R

the curvature

radius of the channel.

The interplay between the wall and shear induced

forces and the Dean force determines the cross sec-

tional trajectory of a particle. There are however nu-

merous assumptions for the validity of provided for-

mulas, such as straight channels for lift forces and

curved channels for Dean forces, which are not pos-

sible to be met simultaneously. Also, position de-

pendent coefﬁcients C

cause the evaluation of

the forces difﬁcult. Therefore the actual simulations

of the channel ﬂow with immersed particles are ex-

tremely useful for studying the stabilized positions af-

ter focusing.

Inertial microﬂuidics can be categorized accord-

ing to the shape of the channels: straight, spiral, ser-

pentine channels and so called contraction-expansion

array (CEA). Common feature of all these channels is

the branching the main channel at the end into several

output channels collecting particles of different sizes

or a particle-free ﬂuid, see Figure 2.

Computational Study of Particle Separation Based on Inertial Effects in Rectangular Serpentine Channels with Different Aspect Ratios

285

Figure 2: Typical shapes of channels used in inertial mi-

croﬂuidics (a) straight (b) spiral (c

) square serpentine (c

)

curved serpentine and (d) CEA channels. Large black cir-

cles represent inﬂow of the suspension and several smaller

circles represent outﬂow with separated particles.

Although we focus on serpentine channels, we

brieﬂy sum up the results concerning stabilized posi-

tions of particles in straight channels with rectangular

crossection. We need this, because as can be seen in

Figure 2 (c

) and in close detail in Figure 3, the ﬁrst

part of the channel is often straight and the particles

tend to focus before entering the serpentine part. This

must be taken into account when seeding the particles

or cells at the inﬂow of the serpentine channel in the

simulation.

Figure 3: Focusing of particles before entering the serpen-

tine part of the channel. Blue particles are in the upper part

and the green particles in the lower part of the channel. Sec-

tor A - particles are distributed across the whole cross sec-

tion coming from the inlet. Sector B - particles are being

focused. Sector C - before entering the serpentines, the par-

ticles are focused in two (or four) positions.

The thorough numerical analysis conﬁrmed by

comparison with experimental results has been pro-

vided by (Mashhadian and Shamloo, 2019). The au-

thors show a detailed analysis of stabilized positions

of particles various sizes in straight rectangular chan-

nels depending on the channel Reynolds number and

the channel aspect ratio. They show (see Figure 4)

different stabilized positions in a rectangular cross

section: center of short walls (red), center of long

walls (yellow) and two other positions near long wall

(green). Therefore we are able to derive stable posi-

tions at the entrance of our serpentine channels. This

is done later in Section 3.4.

We must emphasize that straight channels are not

suitable for separating particles of different sizes due

to the similarity of focused positions for particles of

different sizes.

Figure 4: Different stabilized positions in a rectangular

cross-section. Reprinted from (Mashhadian and Shamloo,

2019) with permissions.

3 MODEL AND

COMPUTATIONAL SETUP

3.1 Numerical Model

We use well-established computational model of ﬂuid

and the immersed particles or cells. Here, the liquid

is calculated with the lattice-Boltzmann (LB) method

(Arnold et al., 2013). The cells are taken into ac-

count as immersed objects with fully 3D discretiza-

tion using tetrahedrons that cover whole inner space

inside the sphere. At the edges of the small tetrahe-

drons, fairly rigid springs are set so that the object

almost does not undergo any deformation during the

ﬂow. Detailed description of the underlying models

are available in (Jan

cigov

a et al., 2020; Jancigova and

Tothova, 2014; Bachrat

y et al., 2018). The valida-

tion and veriﬁcation of the computational models has

been provided in (Jan

cigov

a et al., 2020; Jan

cigov

2020; Tothova et al., 2015). For all simulations we

used tetrahedral meshes with edges of sizes approxi-

mately 0.4 µm.

3.2 Channel Geometry

Our aim is to simulate rectangular serpentine chan-

nels as depicted in Figure 2 (c

). In the ﬁgure, there

are only six S-shaped repeating sections displayed,

however in practise, there are more sections needed

to obtain desired focusing positions. Together with

long straight channels before and after serpentines,

the whole channel is too large to model at whole.

Therefore we will model only one repeating section

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

286

(between the dashed seeding and reseeding line in

Figure 5) enlarged by ﬂuid evolution sections before

and after, with periodical boundary conditions at the

inﬂow and outﬂow. This way we ensure that the ﬂuid

is fully evolved at the seeding and reseeding lines. Pe-

riodicity of the middle section allows to reseed the

cells back to the seeding line as soon as they reach

the reseeding line. Their relative position at the cross

section is preserved during the reseeding, as well as

their velocity.

Figure 5: Simulation box for the case of the cross section

with dimensions 80 × 40µm. One repeating S-shaped sec-

tions enlarged by two ﬂuid evolution sections.

After initial seeding of particles on the seeding

line in the channel at the beginning of the ﬂow, we

watched the positions of the origins of the particles

during the ﬂow. When the particles have arrived to the

reseeding line, we reseeded them back to the seeding

line with the new coordinates of the particle origins

and we have continued the watching of these origins

coordinates. With this kind of reseeding by repeating

the S-shaped section, as you can see on the picture

in Figure 5, we have done a simulation of periodical

ﬂow without real construction of the real microchan-

nel. As a result we get the trajectories (from the origin

coordinates during the ﬂow process). In Section 4 you

can see analyses.

Since we study three different cross sections, the

respective dimensions of the channels are different for

all three cases. The respective dimensions of channels

are depicted in Figure 6. Note that the lengths of the

channel along the axial center of the channel are pre-

served.

3.3 Geometry and Fluid Set-up

To create a speciﬁc geometry as a serpentine channel,

we need to deﬁne boundaries in the simulation box.

This is done using geometrical shapes of rhomboids

in the open-source scientiﬁc simulation package

ESPResSo with PyOIF module (Jan

cigov

a et al.,

2020).

To let the static ﬂuid at the beginning of the simu-

Figure 6: Dimensions of three different geometries in µm.

The darkest boundaries represent 100 × 32µm, the medium

dark represent 80 × 40µm and the brightest represent 60 ×

52µm cross section.

lation fully evolve, we simulate 500µs without the

particles. The uniform boundary conditions at inlet

and outlet deﬁne the average velocity in the channel

which is proportional to the volumetric ﬂow rate.

This can be done in PyOIF using a special velocity

boundary (visualized in Figure 5 by dashed rectan-

gles), with predeﬁned constant values of velocity

ﬁeld at the boundary points.

Speciﬁc values of the inlet conditions and the cor-

responding ﬂow rates are presented in Table 1.

Table 1: Fluid parameters in 80× 40µm rectangular channel.

Values in channels with other cross sections are similar.

Average Reynolds Volumetric

velocity number ﬂow

[µm/µs] [ - ] [mL/min]

0.18 19.2 0.035

0.35 37.3 0.062

0.45 48 0.086

0.6 64 0.115

We are interested in studying the ﬂows in phys-

ically relevant cases. We consider ﬂuid with density

and viscosity similar to physiological solutions or wa-

ter being 1000kg/m

and 10

−3

Pa.s. In inertial mi-

croﬂuidics, the relevant ranges for the Reynolds num-

ber are up to 100 (Ying and Lina, 2020). We consider

four different average velocities up to 0.6m/s in the

channel so that Reynolds number varies up to 64. For

maximal velocity for evaluation of Reynolds number

in (5) we take the double of the average velocity. With

cross sectional area of around 3100µm

it accounts for

the volumetric ﬂow rate being up to 0.115mL/min.

3.4 Particle Seeding

Since in various straight channels with a rectangular

cross-section the particles in the ﬂow settle in two sta-

ble positions over time, we also placed the particles in

the running ﬂow of the simulation in close neighbour-

hood of two concrete positions. We wanted the place-

Computational Study of Particle Separation Based on Inertial Effects in Rectangular Serpentine Channels with Different Aspect Ratios

287

ment randomly, so we used the normal distribution for

seeding particles around this two positions. As you

can see in Figure 7, we have three different geome-

tries with particles seeded at the beginning of every

simulation by normal distribution with same standard

deviation, which we chose around the two positions.

In order to assure the reproducibility of the experi-

ments we used the same random seeding for 5µm par-

ticles and 10µm particles.

Figure 7: Three different cross sections of rectangular chan-

nels with particle seeding. Centers of the particles (blue

dots) are depicted distributed by normal distribution around

stable positions of straight channels (red dots).

4 COMPUTATIONAL RESULTS

Our aim is to examine how the stable positions within

several cross-sections are dependent on geometric pa-

rameters of the channel. We compared three differ-

ent cross-sections in square wave channel and in each

cross section, we modiﬁed average ﬂuid velocity and

the size of the particles. The other parameters were

kept constant. In Table 2 we present values of the

parameters that were examined. Together we run 24

simulations.

Table 2: Overview of three varying parameters: size, veloc-

ity and cross section. Simulations have been performed for

all 24 combinations.

Particle size Average velocity Cross section

µm µm/µs µm × µm

5 0.18 60 × 52

10 0.35 80 × 40

0.45 100 × 32

0.6

4.1 Focusing Length

First we need to determine the focusing length of the

channel. We tracked the trajectories of the cells un-

til the particles reach stable region. Each of the 24

simulations was run such that at least 28 passes of the

particles through the repeating S-section occurred.

In Figure 8 we see four 100 × 32µm cases: 5 and

10µm particles each for two different Reynolds num-

bers. Horizontal axis shows the number of passes

through the repeating S-shaped section and vertical

axis shows the particle position along the width of

the channel ranging from 0 to 100µm in these cases.

We can clearly see when the particles start stabilize

and we can deﬁne the minimal focusing length. In

the ﬁgure we show trajectories for only two values of

Reynolds number, however, taking account of all four

values we arrive at the focusing length for cross sec-

tion 100 × 32µm to be 19 passes. Analogous we de-

duce 15 passes and 18 passes to be focusing lengths

for 60 × 52µm and 80 × 40µm, respectively.

After determining the focusing length, we further

work with positions of particles across the channel

width at the moment of passing this focusing length.

Figure 8: Trajectories of 5µm particles (top ﬁgures) and

10µm particles (bottom ﬁgures) in channel with 100× 32µm

cross section for Reynolds number 37.3 (ﬁgures on the left)

and 64 (ﬁgures on the right). Black vertical lines indicate

minimal focusing length. Horizontal axis gives number of

passes through the repeating S-section. Vertical axis gives

particle position across the width of the channel.

4.2 Particle Separation

The three different geometries achieve different fo-

cusing performance for small and large particles. All

three geometries have different focusing length but

this is not a limitation: Once we pick the desired ge-

ometry, the channel length will be adapted accord-

ingly. The particle focusing positions are either dis-

tinct and separated to more positions or focused along

the center of the channel width. In some cases we

could separate them, but in some cases they are fully

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

288

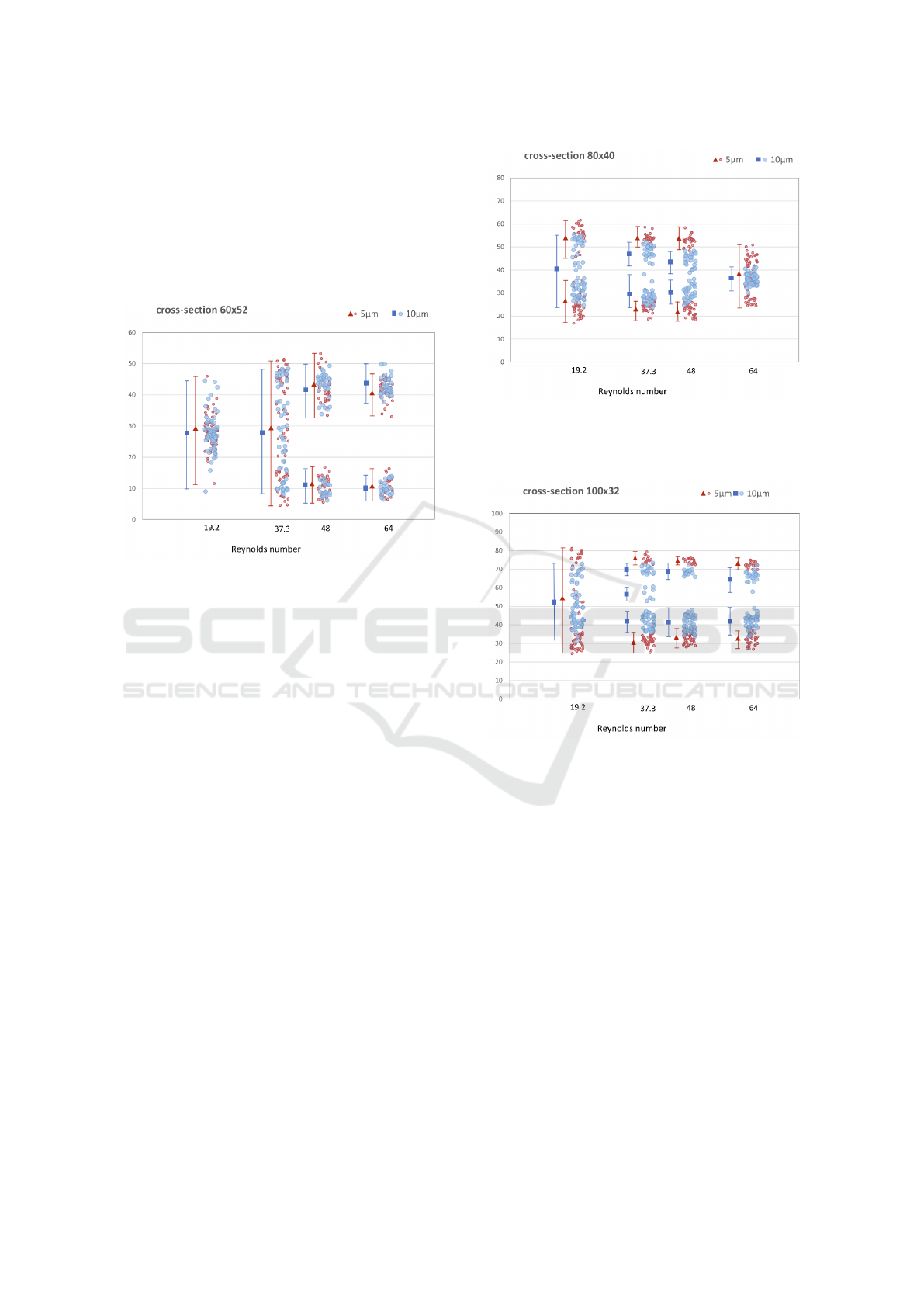
overlapping. The results are depicted in Figures 9 –

11.

For the case of 60 × 52 rectangular channel we

assigned the smallest focusing length. The particles

were focused already after 15 times of S-shaped sec-

tions repeating. However we get almost fully overlap-

ping distributions of 5µm and 10µm particles across

the channel width.

Figure 9: Particle focusing in 60 × 52µm cross section for

various Reynolds numbers. Focusing length was 15 passes

of the repeating S-section. Vertical axis gives particle posi-

tion in [µm] across the width of the channel.

In 80 × 40 rectangular channel we can stop the

simulations after 18 passes of S-shaped section. We

can observe the best focusing performance for the

Reynolds number between 32 and 50. The 5µm parti-

cles are separated in two positions across the channel

width. The 10µm particles are focused along the cen-

ter of the channel width, and the width of particle dis-

tribution gradually decreases to a single stable focus-

ing line with higher Reynolds number. At Reynolds

numbers 37.3 and 48 we can see in Figure 10 slightly

overlapping of focusing sections for 5µm and 10µm

particles which may result in non-perfect separation.

This contributes to the best possibility of separating

particles of two sizes. For the highest Reynolds num-

ber we can see overlapping of these two different par-

ticle sizes and it is not able to separate them.

For the case of 100 × 32 rectangular channel we

needed 19 passes of the S-shaped section to get the

best focusing of the particles. The 5µm particles have

the best particle separation possibility. The focusing

positions are fully distinct and we get the biggest gap

between them as you can see in Figure 11, more than

30µm with Reynolds numbers 37,3 and 48. In this

case, we have larger range of Reynolds numbers for

separation.

Figure 10: Particle focusing in 80 × 40µm cross section for

various Reynolds numbers. Focusing length was 18 passes

of the repeating S-section. Vertical axis gives particle posi-

tion in [µm] across the width of the channel.

Figure 11: Particle focusing in 100× 32µm cross section for

various Reynolds number. Focusing length was 19 passes of

the repeating S-section. Vertical axis gives particle position

in [µm] across the width of the channel.

5 DISCUSSION

First of all we have very good agreement with results

presented in (Ying and Lina, 2020) for the cross sec-

tion 80 × 40µm. This validates our computational ap-

proach.

To compare various cross sections, we can draw

several conclusions.

First observation is that the 60 × 52µm cross sec-

tion is not suitable for particle separation. Although

the particles focused after the shortest distance, the fo-

cused position of particles overlap for both analyzed

sizes.

As previous results from (Ying and Lina, 2020)

suggested, a good candidate for separation is the

Computational Study of Particle Separation Based on Inertial Effects in Rectangular Serpentine Channels with Different Aspect Ratios

289

channel with 80 × 40µm cross section. This was

conﬁrmed by our computations and indeed, with

Reynolds numbers 37 and 48 we get the possibility for

particle separation. In this cross section, with higher

Reynolds numbers we loose the possibility for sepa-

ration because particles of both sizes drift towards the

center of the channel. 10µm particles focus in nar-

rower strip (width 10µm) while 5µm particles focus

in wider strip (width 30µm). However, the two strips

completely overlap.

The results for cross section 100 × 32µm give

larger possibility for separation. Not only the offer

separation for Reynolds numbers 37 and 48 but also

at 64 we still have distinctive focusing position for

particles of different sizes. Again, with increasing

ﬂow velocity we see tendency of particles to focus

closer to the channel center, however this tendency is

much weaker than for 80× 40µm cross section and the

particles still leave a particle-free strip in the middle

of the channel.This results have two important conse-

quences:

• Higher throughput is possible due to large

Reynolds number and thus larger ﬂuid velocity.

• Separation of even large particles is possible.

Since 5µm and 10µm particles leave a particle-free

strip in the middle of the channel, it may be possi-

ble to separate a third size of particles that would

focus right in that strip.

This paper is expected to be instructive for opti-

mization of inertial microchannel structures and for

next bio-related studies and applications, for example

blood cell separation in medicine.

ACKNOWLEDGEMENTS

This publication has been produced with the support

of the Integrated Infrastructure Operational Program

for the project: Systemic Public Research Infrastruc-

ture - Biobank for Cancer and Rare diseases, ITMS:

313011AFG5, co-ﬁnanced by the European Regional

Development Fund.

REFERENCES

Arnold, A., Lenz, O., Kesselheim, S., Weeber, R., Fahren-

berger, F., Roehm, D., Ko

sovan, P., and Holm, C.

(2013). ESPResSo 3.1: Molecular dynamics soft-

ware for coarse-grained models. In Meshfree Methods

for Partial Differential Equations VI, Lecture notes in

computational science and engineering, pages 1–23.

Springer Berlin Heidelberg, Berlin, Heidelberg.

Bachrat

y, H., Bachrat

a, K., Chovanec, M., Kaj

anek, F.,

Smie

skov

a, M., and Slav

ık, M. (2018). Simulation

of blood ﬂow in microﬂuidic devices for analysing of

video from real experiments. In Bioinformatics and

Biomedical Engineering, Lecture notes in computer

science, pages 279–289. Springer International Pub-

lishing, Cham.

Cetin, B. and Li, D. (2011). Dielectrophoresis in microﬂu-

idics technology. Electrophoresis, 32(18):2410–2427.

Chun, B. and Ladd, A. J. C. (2006). Inertial migration of

neutrally buoyant particles in a square duct: An in-

vestigation of multiple equilibrium positions. Phys.

Fluids (1994), 18(3):031704.

Di Carlo, D., Edd, J. F., Humphry, K. J., Stone, H. A., and

Toner, M. (2009). Particle segregation and dynamics

in conﬁned ﬂows. Phys. Rev. Lett., 102(9):094503.

Forbes, T. P. and Forry, S. P. (2012). Microﬂuidic mag-

netophoretic separations of immunomagnetically la-

beled rare mammalian cells. Lab Chip, 12(8):1471–

1479.

Gossett, D. R., Tse, H. T. K., Lee, S. A., Ying, Y., Lindgren,

A. G., Yang, O. O., Rao, J., Clark, A. T., and Di Carlo,

D. (2012). Hydrodynamic stretching of single cells for

large population mechanical phenotyping. Proc. Natl.

Acad. Sci. U. S. A., 109(20):7630–7635.

Hood, K., Lee, S., and Roper, M. (2015). Inertial migration

of a rigid sphere in three-dimensional poiseuille ﬂow.

J. Fluid Mech., 765:452–479.

Jan

cigov

a, I. (2020). Computational modeling of blood

ﬂow with rare cell in a microbifurcation. In Lec-

ture Notes in Computational Vision and Biomechan-

ics, Lecture notes in computational vision and biome-

chanics, pages 518–525. Springer International Pub-

lishing, Cham.

Jan

cigov

a, I., Koval

ıkov

a, K., Bohinikov

a, A., and

Cimr

ak, I. (2020). Spring-network model of red blood

cell: From membrane mechanics to validation. Int. J.

Numer. Methods Fluids, 92(10):1368–1393.

Jancigova, I. and Tothova, R. (2014). Scalability of forces in

mesh-based models of elastic objects. In 2014 ELEK-

TRO. IEEE.

Jan

cigov

a, I., Koval

ıkov

a, K., Weeber, R., and Cimr

ak, I.

(2020). Pyoif: Computational tool for modelling of

multi-cell ﬂows in complex geometries. PLoS Com-

putational Biology, 16:e1008249.

Jiang, D., Tang, W., Xiang, N., and Ni, Z. (2016). Nu-

merical simulation of particle focusing in a symmetri-

cal serpentine microchannel. RSC Adv., 6(62):57647–

57657.

Li, S., Ding, X., Guo, F., Chen, Y., Lapsley, M. I., Lin, S.-

C. S., Wang, L., McCoy, J. P., Cameron, C. E., and

Huang, T. J. (2013). An on-chip, multichannel droplet

sorter using standing surface acoustic waves. Anal.

Chem., 85(11):5468–5474.

Martel, J. M. and Toner, M. (2014). Inertial focusing in

microﬂuidics. Annu. Rev. Biomed. Eng., 16(1):371–

396.

Mashhadian, A. and Shamloo, A. (2019). Inertial microﬂu-

idics: A method for fast prediction of focusing pattern

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

290

of particles in the cross section of the channel. Anal.

Chim. Acta, 1083:137–149.

Matas, J.-P., Morris, J. F., and Guazzelli,

E. (2009). Lateral

force on a rigid sphere in large-inertia laminar pipe

ﬂow. J. Fluid Mech., 621:59–67.

McLaughlin, J. B. (1993). The lift on a small sphere in

wall-bounded linear shear ﬂows. J. Fluid Mech., 246(-

1):249–265.

Ookawara, S., Higashi, R., Street, D., and Ogawa, K.

(2004). Feasibility study on concentration of slurry

and classiﬁcation of contained particles by microchan-

nel. Chem. Eng. J., 101(1-3):171–178.

Rasooli, R. and C¸ etin, B. (2018). Assessment of lagrangian

modeling of particle motion in a spiral microchan-

nel for inertial microﬂuidics. Micromachines (Basel),

9(9).

Segr

e, G. and Silberberg, A. (1961). Radial particle dis-

placements in poiseuille ﬂow of suspensions. Nature,

189(4760):209–210.

Tanaka, T., Ishikawa, T., Numayama-Tsuruta, K., Imai, Y.,

Ueno, H., Matsuki, N., and Yamaguchi, T. (2012).

Separation of cancer cells from a red blood cell sus-

pension using inertial force. Lab Chip, 12(21):4336–

4343.

Tothova, R., Jancigova, I., and Busik, M. (2015). Calibra-

tion of elastic coefﬁcients for spring-network model

of red blood cell. In 2015 International Conference

on Information and Digital Technologies. IEEE.

Ying, Y. and Lina, Y. (2020). Inertial focusing and separa-

tion of particles in similar curved channels. Scientiﬁc

reports, natureresearch, 391:123570.

Computational Study of Particle Separation Based on Inertial Effects in Rectangular Serpentine Channels with Different Aspect Ratios

291