Verifying Static Constraints on Models Using General Formal

Veriﬁcation Methods

Norbert Somogyi

and Gergely Mezei

Department of Automation and Applied Informatics, Faculty of Electrical Engineering and Informatics,

Budapest University of Technology and Economics, M

uegyetem rkp. 3., H-1111 Budapest, Hungary

Keywords:

Formal Veriﬁcation, UML, CTL, Kripke Structure, NuSMV, OCL.

Abstract:

Over the years, the ﬁeld of software modeling has gained signiﬁcant popularity. By capturing the static aspects

of the requirements of the software, model-driven engineering easens the development and maintenance of

software. However, additional constraints that the solution must conform to may be too complex to include in

the structure of the model itself. For this reason, external solutions are often used to describe static constraints

on models, the most prevalent approach being the Object Constraint Language (OCL) and its formal variants.

This paper proposes a general approach for verifying static constraints on software models by employing

different formal veriﬁcation methods than previous solutions. The approach deﬁnes a general Kripke Structure

(KS) that captures the static structure of the model. In the next step, the constraints that the model must

conform to are formalized using a ﬁrst-order branching-time logic, the Computational Tree Logic (CTL).

Finally, the NuSMV model checker tool is used to check whether the constraints formalized in CTL hold on

the formal Kripke Structure. To demonstrate the feasibility of the approach, the concepts are illustrated on a

running UML class diagram.

1 INTRODUCTION

The design and maintainability of complex industrial

software systems is a crucial part of the development

and operations process. Model-driven engineering

aims to alleviate this complexity by deﬁning domain

models that capture the most crucial aspects of the

speciﬁcation. The most widespread approach to mod-

eling the static structure of the system is OMG’s UML

class diagram (UML, 2017), but different approaches

also exist (MOF, 2005). Further restrictions on the

model are often necessary, namely, those that cannot

(or should not) be expressed in the structure of the

model itself. For example, considering UML class di-

agrams, these could be deﬁning rules for invariants

or adding extra constraints to what constitutes a valid

class diagram. For example:

• The value of a certain attribute of a certain class

must always be above 0.

• Interfaces cannot contain attributes.

• Attributes of primitive type cannot hold further at-

tributes. In fact, only classes are allowed to hold

attributes.

https://orcid.org/0000-0001-6908-7907

https://orcid.org/0000-0001-9464-7128

• Inheritance hierarchies must not contain cycles

and multiple inheritance is not allowed.

In this paper, we refer to such restrictions as

static constraints. One of the most prevalent solu-

tions for deﬁning static constraints on software mod-

els is the Object Constraint Language (OCL) (Cabot

and Gogolla, 2012) and its variants. OCL is an

OMG speciﬁcation for a (mostly) declarative, side-

effect free language to deﬁne additional restrictions

on UML class diagrams. Although OCL was de-

signed speciﬁcally with UML class diagrams in mind,

it is general enough to apply to any modeling lan-

guage, with slight modiﬁcations and tailoring to the

modeling notations.

Formal approaches inspired by OCL also

emerged. The most widespread and successful of

these is Alloy (Jackson, 2012), which provides a sim-

ple language for modeling a system and expressing

its properties. In the background, Alloy converts the

model and its properties to a boolean representation

and uses SAT solvers (S

orensson and Een, 2005; Ma-

hajan et al., 2004) to check whether the deﬁned model

conforms to the deﬁned properties. In this paper, we

propose an alternative, general approach for deﬁning

static constraints on software models. The proposed

approach uses different formal veriﬁcation methods,

Somogyi, N. and Mezei, G.

Verifying Static Constraints on Models Using General Formal Veriﬁcation Methods.

DOI: 10.5220/0011796500003402

In Proceedings of the 11th International Conference on Model-Based Software and Systems Engineering (MODELSWARD 2023), pages 85-93

ISBN: 978-989-758-633-0; ISSN: 2184-4348

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

speciﬁcally model checking, to verify whether the

static constraints hold on the software model. In the

ﬁrst step, the structure of the model is expressed

by a Kripke Structure. The static constraints that

the model must adhere to are then formalized using

the Computational Tree Logic (CTL). Finally, the

NuSMV (Cimatti et al., 2002a; Cimatti et al., 2002b)

model checker tool is reused to check whether the

formalized requirements hold on the formal model.

The approach becomes fully automatic after deﬁning

the mapping from the original model to the Kripke

Structure. The advantage of using formal methods

is that any and all violations are guaranteed to be

found. Thus, formal proof is provided that the static

constraints hold on the model.

The paper is structured as follows. In Section 2,

we present related work and compare them with our

approach. In Section 3, we describe the relevant

theoretical background of model checking, includ-

ing Kripke Structures and CTL. In Section 4, we

present the contribution of this paper. We also illus-

trate the proposed approach on a running example.

Finally, Section 5 concludes the paper, highlighting

main strengths and weaknesses of the approach and

discussing future work.

2 RELATED WORK

One of the most widespread solutions for enforc-

ing static constraints on models is OCL (Cabot and

Gogolla, 2012). OCL supports the expression of

many features, such as invariants, initialization ex-

pressions, or derived elements. It also features its own

typesystem. In their work, Cabot et al. (Cabot et al.,

2021) performed a SWOT ( Strengths-Weaknesses-

Opportunities-Threats) analysis on OCL. The authors

argue that the two main weaknesses of OCL are the

complexity of the language, and the lack of tool

ecosystem and reusable OCL libraries. As a conse-

quence, if a custom modeling language (for which an

OCL implementation does not already exist) intends

to use OCL, implementing an OCL interpreter is a

troublesome, relatively difﬁcult process (Vaziri and

Jackson, 2003).

In contrast, formal veriﬁcation approaches have

a well-developed ecosystem of tools and methods

available and a well-deﬁned focus for verifying con-

straints. Over the years, a number of such approaches

also emerged. HOL-OCL (Brucker and Wolff, 2008)

intends to deﬁne formal semantics for OCL by ”shal-

low embedding of OCL into the Higher-order Logic

(HOL) instance of the interactive theorem prover Is-

abelle.” This approach is designed speciﬁcally with

UML in mind, and does not (explicitly) support

other types of models. In their work, Nobakht et

al. (Nobakht and Truscan, 2013) extend static UML

+ OCL models with dynamic veriﬁcation. By trans-

forming static and dynamic aspects (class diagrams

and statecharts), the whole UML speciﬁcation is

adapted into the UPPAAL model checker (Behrmann

et al., 2004).

Other approaches focus on checking pre-deﬁned

properties on UML class diagrams. The goal in these

cases is not to replace OCL for deﬁning and checking

constraints on instances of models, but to verify static

properties on the existing UML + OCL model, includ-

ing consistency, executability, reachability, liveness

and satisﬁability. UMLtoCSP (Cabot et al., 2007) ap-

plies constraint programming to check the satisﬁabil-

ity of OCL constraints on a UML class diagram. Sim-

ilarly, (Shaikh et al., 2010) focuses on improving the

performance of OCL satisﬁability checking. In their

work, Przigoda et al. (Przigoda et al., 2016) propose

a formal approach for verifying the structure and be-

havior in UML/OCL models. The possible states of

the system, along with the OCL invariants are trans-

lated into a symbolic representation and SAT solvers

are used to execute veriﬁcation.

Alloy (Jackson, 2012) is one of the most success-

ful of formal veriﬁcation-based approaches. Alloy

was inspired by the weaknesses of OCL. It is impor-

tant to emphasize that Alloy is a general approach,

not limited to UML or OCL. It is usable to deﬁne any

static constraint on any model. It provides a language

for deﬁning models and uses SAT solvers to formal-

ize and check properties on the model. Similarly to

OCL, it provides its own typesystem, which is more

compact and easier to use. UML2Alloy (Anastasakis

et al., 2007) deﬁnes a transformation from UML class

diagrams extended with OCL expressions to Alloy

models. The goal of this approach is to reuse the for-

mal aspects of Alloy to analyse UML speciﬁcations.

The authors also note that deﬁning the transformation

from UML class to Alloy was ”challenging”.

When compared to non-formal OCL variants, our

approach has several advantages:

• It uses formal veriﬁcation methodologies and

tools that are well developed and widespread, pro-

viding automatic, formal proof of the correctness

of the model.

• Our approach is fully independent of the modeling

language that is being checked, making it easier to

integrate with custom modeling languages.

• Our approach focuses speciﬁcally on checking

static constraints only. On one hand, it becomes

easier to be used for this purpose. On the other

hand, its expressive power is signiﬁcantly less

MODELSWARD 2023 - 11th International Conference on Model-Based Software and Systems Engineering

than that of OCL. Our approach cannot express

other features of OCL, such as querying models.

Compared to formal approaches, previous solu-

tions focus mainly on extending UML + OCL with

formal semantics or checking the satisﬁability or con-

sistency of the models. Against these approaches, the

generality of our approach is the main beneﬁt.

When compared to Alloy, our approach works on

similar grounds but with different formal methods.

Moreover, it is more general, in the sense that it does

not depend tightly on the NuSMV tool. This means

that instead of using NuSMV and the various for-

mal methods it employs (SAT solvers, bounded model

checking etc.), it is possible to use an entirely differ-

ent model checker. In this sense, our approach is easy

to extend with different model checking techniques. It

would also be possible to support different tools, and

let the model designer choose between them. This

is not the case for Alloy, it is built speciﬁcally with

SAT solvers in mind. The only requirement in our

case is that the Joint Relational Model (Section 4.3)

should be expressed in the modeling language of the

model checker and a query language similar to CTL

has to be available to formulate the constraints. For

example, a viable alternative to NuSMV would be

Uppaal (Behrmann et al., 2004), with its modeling

language of extended timed automata and a query lan-

guage similar to CTL.

3 BACKGROUND

Formal veriﬁcation is a group of methodologies

aimed at formally proving the correctness of a spec-

iﬁed system. In our work, we propose to use model

checking to enforce constraints on models. One of the

most typically used and simplest formal models is the

Kripke Structure (Muller-olm et al., 1999) and one

of the most common and practical ways of formal-

izing requirements is the Computational Tree Logic

(CTL)(Muller-olm et al., 1999).

A Kripke Structure is a 4-tuple (S, I, R, L) over

a set of atomic propositions AP, where:

– AP = {P

, P

, ..., P

} set of atomic propositions

– S = {S

, S

, ..., S

} ﬁnite set of states

– I ⊆ S set of initial states

– R ⊆ S × S transition relation between states

– L : S 7→ 2

labeling of states with atomic propo-

sitions

Figure 1 illustrates a KS in a graphical represen-

tation. The model consists of 3 states: S

, S

and S

The initial state is S

, denoted by a double circle. S

is labeled with the atomic propositions P and Q, S

is labeled with P, and S

is labeled with Q and R. Fi-

nally, there exists a transition relation from S

to S

and S

, from S

to S

and from S

to S

. A path in a

KS is a possible series of states along transitions. For

example, in this case S

→ S

is a

possible path.

Figure 1: Graphical representation of a Kripke Structure

with 3 states and 4 transitions.

In CTL, requirements can be formalized using

logical formulae, all of which are presented in Ta-

ble 1. A CTL expression is always evaluated on a

speciﬁc state, beginning with the initial state.

Consider now the Kripke Structure depicted in

Figure 1 and the following CTL formula.

AG((Q ∧ P)) =⇒ ((EX¬Q)∨ (EF(P ∧ R))) (1)

The formula prescribes that on all states of all

paths in the Kripke Structure, if a state is labeled with

both Q and P, then there must exist a next state that

is not labeled with Q or there must exist a path on

which eventually a state is labeled with both P and R.

When evaluated over the example, this formula holds,

because S

is the only state for which the left side of

the implication holds, and the right side holds as well

because S

is a potential next state and it is not labeled

with Q.

4 FORMAL VERIFICATION OF

STATIC CONSTRAINTS

We propose the following approach for checking

static constraints on software models. Figure 2 shows

the steps of the process. Firstly, based on the software

model to be veriﬁed, a Joint Relational Model (JRM)

is created. This is a Kripke Structure that models the

structure of the original model to be checked, in the

form of relations between basic model elements. Sec-

ondly, the constraints that the model must conform

to have to be formalized using CTL. The JRM and

the CTL formulae are then forwarded as input to the

NuSMV model checker tool, which veriﬁes whether

the formalized requirements hold on the JRM, and

consequently, on the original model itself. For each

violated CTL formula, a counter example is gener-

ated.

Verifying Static Constraints on Models Using General Formal Veriﬁcation Methods

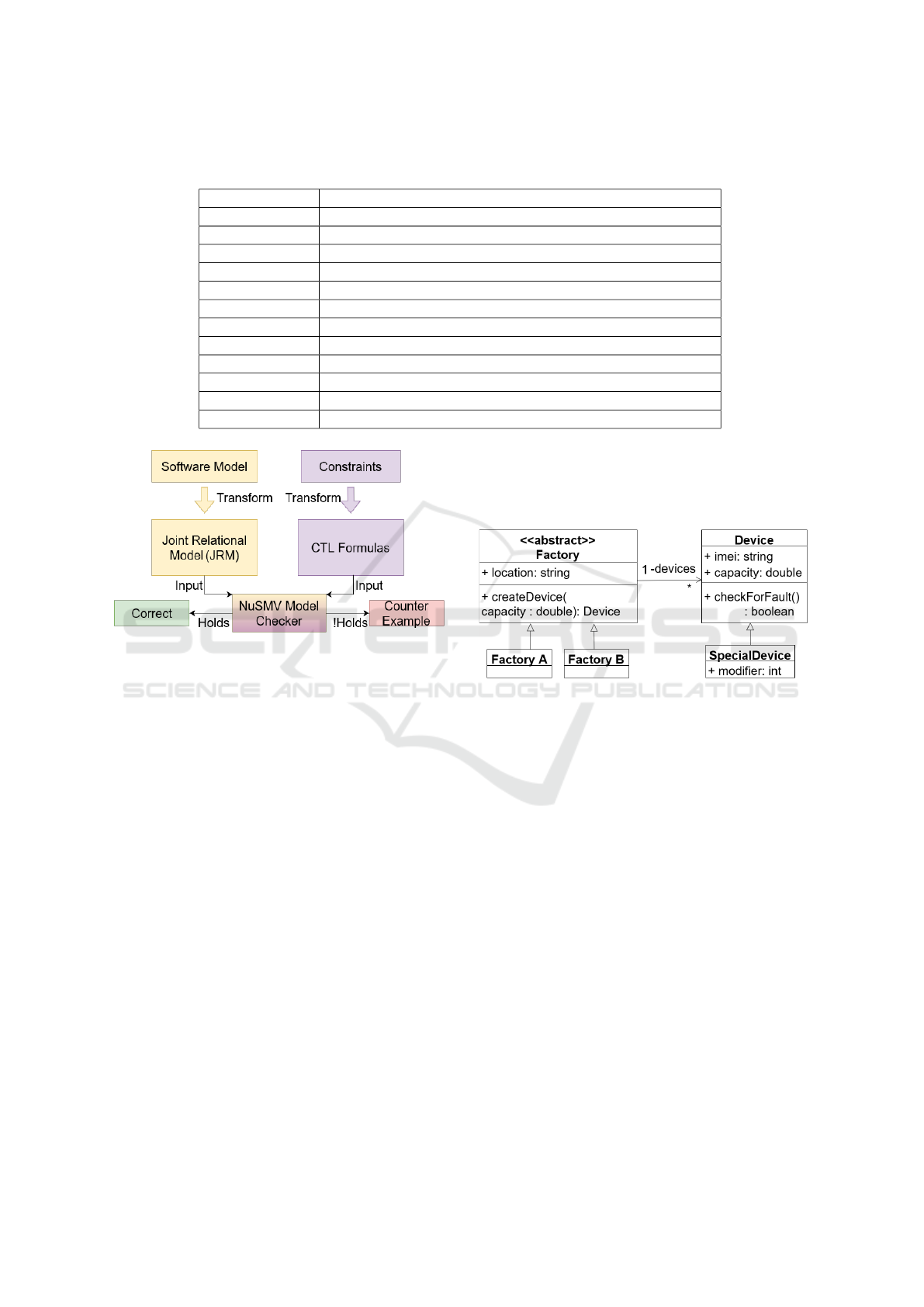
Table 1: CTL expressions and their semantics. α, β and φ are arbitrary CTL expressions, ∃ means the existential quantiﬁer, ∀

means the universal quantiﬁer.

CTL Expression Semantic

α ∧ β α ∧ β (logical and)

α ∨ β α ∨ β (logical or)

¬α not α (logical not)

α =⇒ β α implies beta (logical implication)

EX φ ∃ next state, where φ holds

EF φ ∃ path from the state, where φ holds eventually

EG φ ∃ path from the state, where φ holds on all states

AX φ ∀ next states, φ holds

AF φ ∀ paths from the state, φ holds eventually

AF φ ∀ paths from the state, φ holds on all states

E [α U β] ∃ path from the state, where α holds on all states until β holds

A [α U β] ∀ paths from the state, α holds on all states until β holds

Figure 2: The steps of the proposed approach for verifying

static constraints on software models.

Further along this section, we present our notions

of model elements and relations, Relational Models,

the JRM and the formalization of constraints as CTL

formulae.

4.1 Running Example - UML Class

Diagram

Throughout the rest of this section, an example UML

class diagram will be used to demonstrate the main

ideas of the veriﬁcation approach. The goal of this

example is not to deﬁne an exhaustive formalization

of UML class diagrams, but to provide a compact ex-

ample and thus to make the veriﬁcation concepts eas-

ier to understand. To keep things concise, the model

is deliberately minimalistic and contains only a few

elements.

The running example is described in Figure 3. The

diagram consists of ﬁve classes. The Factory class is

abstract, with two concrete subtypes: FactoryA and

FactoryB. A factory has an attribute of type string,

and a method which takes a double parameter and re-

turns an object of type Device. Factory also has an

association towards Device, intended for storing the

devices created in that factory. A device also has two

attributes with primitive types, as well as a method

that returns a boolean value. Device also has a sub-

type: SpecialDevice.

Figure 3: A UML class diagram example, to be used as a

running example further in this section.

4.2 Relational Formal Model

When deﬁning the formal model (in the form of a

Kripke Structure), our goal is to express the struc-

ture of the original model completely. This means

that all the elements of the original model are mapped

to elements in the KS. This way, when the various

model checker algorithms employed by NuSMV tra-

verse the state-space of the model and ﬁnd violations

of the constraints, the results can be mapped back

to show which element of the original model vio-

lates which constraints. To achieve this, we deﬁne

the notions of model element and relation. We de-

ﬁne a model element as the basic building block of the

software model. In object-oriented models, such as a

UML class diagram, this typically means classes, in-

terfaces, attributes and methods. A relation is a struc-

tural relationship between model elements that con-

nect them in the model. In a UML class diagram,

this would include all the relationships that classes or

interfaces can have with one-another, meaning asso-

MODELSWARD 2023 - 11th International Conference on Model-Based Software and Systems Engineering

ciation, composition, aggregation, dependency, inher-

itance and interface-realization, as well as holding of

attributes and methods. To avoid confusion of termi-

nologies between the Relational Models and the orig-

inal model that must conform to the static constraints,

we will refer to the latter as the source model.

The main idea behind Relational Models is to rep-

resent every model element of the source model as

a state in the Kripke Structure. Every such state is

then labeled with an identiﬁer that corresponds to the

model element that it represents. For example, if a

class in the source model is called “Factory”, then

in the Kripke Structure a state is created to represent

this class, labeled with the proposition “Factory”. At

this point, we assume that every model element has a

unique identiﬁer. If this is not the case, one only needs

to deﬁne an ordering on the model elements and iden-

tify them by their assigned position in the ordering.

Relations are captured in the form of transitions

in the Kripke Structure. If a relation exists between

modeling elements m

and m

, then a transition is de-

ﬁned in the formal model between their correspond-

ing states S

and S

. Since Kripke Structures have

limited ways to express information (only through la-

beled states and unlabeled transitions), a Relational

Model is only capable of expressing a single relation.

Thus, for each possible relation, a corresponding Re-

lational Model is created. At this point, let us gener-

alize the concept of a Relational Model.

We deﬁne a Relational Model over a set of model

elements M = {m

, m

, ..., m

} and Relation : M

7→

{0, 1} as a Kripke Structure, where:

– AP = {L|∃1 ≤ i ≤ k : m

[ID] = L}

– S = {IS, S

, S

, ..., S

}

– I = {IS}

– R = {(s, t) ∈ S|(s = IS ∧ ∃1 ≤ i ≤ k : ∄1 ≤ j ≤ k :

t = S

∧ Relation(m

, m

) ∨ (∃1 ≤ i, j ≤ k, i ̸= j :

= s ∧ S

= t ∧ Relation(m

, m

)}

– L(s ∈ S) = {L|∃1 ≤ i ≤ k : S

= s ∧ m

[ID] = L}

The set of possible atomic propositions contains

all the identiﬁers of the model elements. The set of

states includes a corresponding state for each model

element and an additional initial state. The transi-

tions from the initial state must be tailored to the spe-

ciﬁc source model. It should point to all other states

that are otherwise not reachable in the model. This

way, it becomes possible to actually traverse the full

model. A transition is deﬁned between the corre-

sponding states of two model elements m

and m

the relation between them holds from m

to m

. This is

denoted by the deﬁned Relation function, which maps

two model elements to 0, if the relation does not hold

from the ﬁrst argument to the second, and to 1 if it

holds. Finally, every state is labeled with the identi-

ﬁer of its corresponding model element.

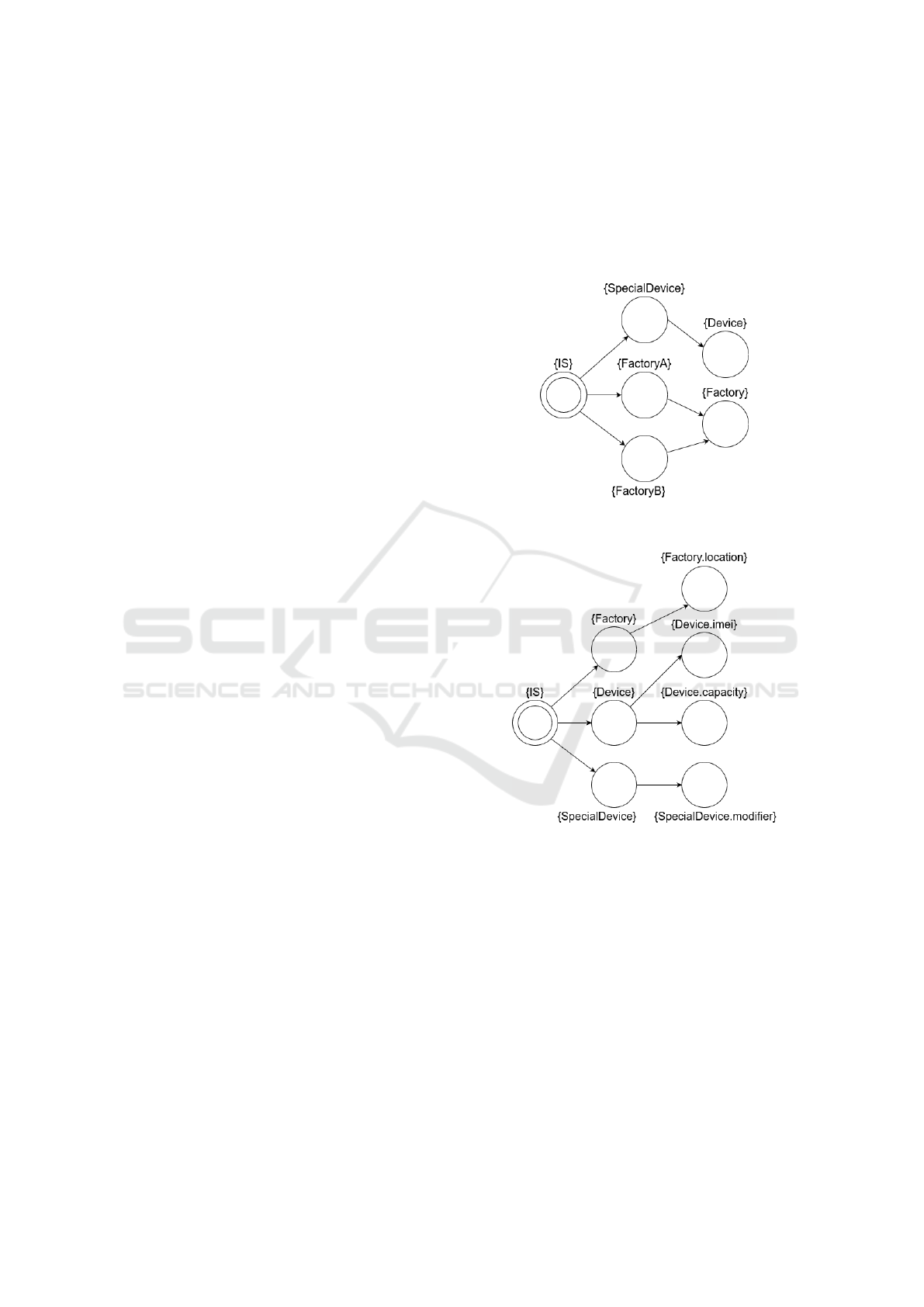
Considering the example depicted in Figure 3, for

each relation deﬁned on UML class diagrams, a Rela-

tional Model may be generated. For instance, Figure 4

shows the inheritance model and Figure 5 shows the

attribute model of the example.

Figure 4: The inheritance model of the UML class example.

The transitions denote an inheritance relation.

Figure 5: The attribute model of the UML class example.

The transitions denote an attribute relation.

For every model element that is either the source

or the target of the given relation in the class diagram,

a state is deﬁned labeled with the name of the model

element. Note that from now on, in examples, the

names of the states will be omitted, as they are of

no importance for the semantics of the formal model.

The states are denoted by circles, the initial state by

double circles, and the text next to a state means the

set of labels deﬁned on that state. In these models, a

transition means inheritance or holding of an attribute

between the participants, respectively. It should be

emphasized that, in practice, it is sufﬁcient to create

states only for those model elements that are actually

Verifying Static Constraints on Models Using General Formal Veriﬁcation Methods

connected to another element through the given rela-

tion. This way, the state-space of the model becomes

much more concise.

4.3 Joint Relational Model

In practice, the previously deﬁned Relational Models

may not be sufﬁcient as models can only capture one

relation at a time. Besides the redundant representa-

tion, the problem is that constraints may typically re-

fer to multiple relations at once, requiring more than

one relation to be present in the same model in or-

der to be evaluated successfully. Moreover, multiple

relations may also be used to infer additional infor-

mation based on the relations. For instance, in the

examples depicted in Figure 3 and Figure 4, the at-

tribute model is only capable of enumerating direct at-

tributes. If both the inheritance and the attribute hold-

ing relations were present in a single formal model,

derived attributes may be handled as well. A solu-

tion is needed that is capable of capturing any (ﬁnite)

number of relations in a single Kripke Structure. The

main reason why a Relational Model could not ex-

press more than one relation is that transitions cannot

be labeled.

The idea is to simulate the labeling of transitions

with additional states. For every relation that a model

element has towards another model element, an extra

relational state is deﬁned, labeled with the name of

the relation it represents. A transition is then added

from the source of the relation to the relational state,

and from the relational state to the target of the re-

lation. For example, if in a UML class-diagram the

class “FactoryA” inherits from the class “Factory”,

then: (i) A relational state is added, labeled with “In-

heritance”. (ii) A transition is deﬁned from the state

labeled with “FactoryA” to the new relational state la-

beled with “Inheritance”. (iii) A transition is deﬁned

from the relational state of “FactoryA” labeled with

“Inheritance” to the state labeled with “Factory”.

This way, relational states serve as pointers to the

target(s) of the relation. Note that relational states

cannot be merged between states but they can point

to any number of targets. For example, both the “Fac-

toryA” and “Factory” states will have their own, sep-

arate relational “Inheritance” states. But if multiple

inheritance would be possible, then only one “Inher-

itance” relational state would have to be deﬁned for

each of them, that points to all the parent classes.

This way, it is easy to capture n-ary relations between

model elements.

The atomic propositions of a JRM consist of the

union of all the propositions of the Relational Mod-

els, extended with the set of relations for labeling the

relational states. Similarly, the states of the Relational

Models are combined, along with adding the rela-

tional states. The initial state remains the same, but

the transitions going out from it may be different (de-

noted by R

). The goal here is to guarantee that the

entire state-space can be traversed. Thus, this must

be tailored speciﬁcally to the source model that is be-

ing formalized. If ﬁnding a relation that guarantees

this is not trivial or does not exist, then the transitions

from the initial state should point to all model ele-

ments that are not accessible from any relation at all

(leaves in the hierarchy). The rest of the transitions

are then deﬁned as mentioned before: from a state to

its relational states, and from the relational states to

the target(s) of the relation. Finally, the labeling of

states remains the same as before, with the addition

of labeling the relational states with the name of the

relation they represent.

Let us now generalize this notion. Let Relations

= {Rel

, Rel

,, ... Rel

} be the set of all possible rela-

tions between model elements and RelationalModels

= {KS

, KS

, . . . , KS

} be the set of the corresponding

Relational Models. KS

[] denotes a certain part of KS

(AP – atomic propositions, S – state set, etc.), Rel

[S]

denotes all of the relational states combined for the re-

lation Rel

. We deﬁne a Joint Relational Model over

a set of model elements M, set of relations Relations,

and set of Relational Models RelationalModels as a

Kripke Structure, where:

– AP = {KS

[AP] ∪ ... ∪ KS

[AP] ∪ Relations}

– S = KS

[S] ∪ ... ∪ KS

[S] ∪ Rel

[S] ∪ ... ∪ Rel

[S]

– I = {IS}

– R = R

∪ {(s, t)|∃1 ≤ i ≤ r : ∃(sKS, tKS) ∈

[R], sRel ∈ Rel

[S] : (s = sKS ∧t = sRel)∨(s =

sRel ∧t = tKS)}

– L(s ∈ S) = {L|∃1 ≤ i ≤ r : (s ∈ Rel

[S] ∧ L =

Rel

) ∨ (s ∈ KS

[S] ∧ L = KS

[L](s))}

Figure 6 demonstrates how the previously men-

tioned Relational Models can be combined into a

Joint Relational Model. Every model element (that

is the source or target of at least one relation) is rep-

resented as a state. The attribute and inheritance re-

lations are then modeled by states labeled with these

relations. For example, the attributes of the class De-

vice are reachable in the model by taking the transi-

tion from the state labeled with “Device” to the next

state labeled with “Attributes”, from which a tran-

sition points to each and every attribute that Device

holds (imei and capacity).

MODELSWARD 2023 - 11th International Conference on Model-Based Software and Systems Engineering

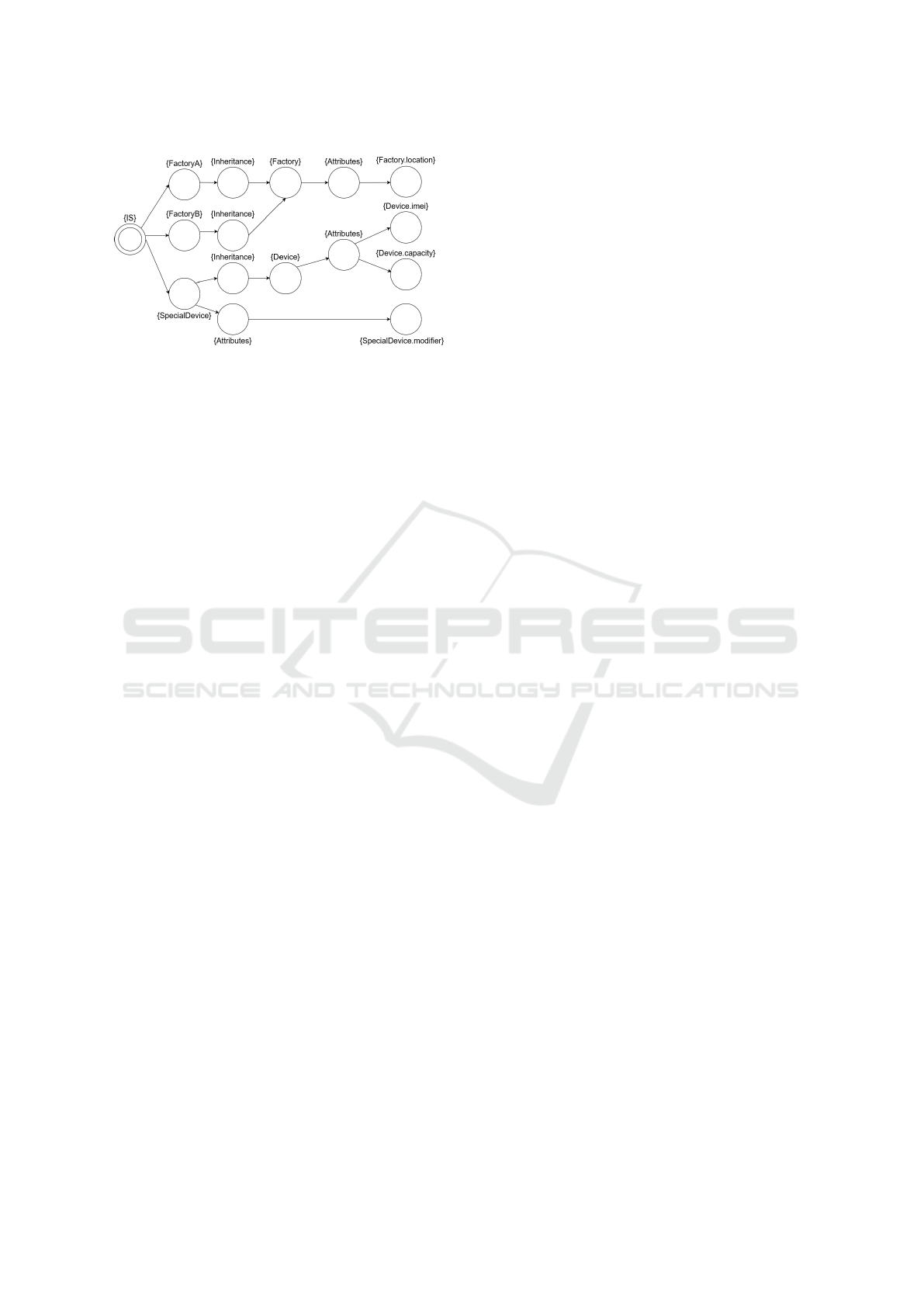
Figure 6: The Joint Relational Model of the UML class ex-

ample, joining the attribute and inheritance relations.

4.4 Formalizing Constraints in CTL

The static constraints to be veriﬁed are formalized

using the previously mentioned CTL. However, in a

JRM, two core difﬁculties arise. Firstly, most con-

straints should only be evaluated on states represent-

ing actual model elements, not on the relational states.

Secondly, since multiple relations are now present in

the formal model, navigating between them is nec-

essary. This means that it should be possible to

prescribe that when evaluating the constraint, only

paths through certain relations should be considered.

For example, consider a constraint on a UML class-

diagram that states that inheritance hierarchies should

be acyclic. When creating the CTL formula, it must

be speciﬁed that no state can reach back to itself

through paths containing only the inheritance relation,

cycles through other relations can be perfectly valid

(e.g. bi-directional associations).

Since this problem arises from the nature of

our approach, a general solution is needed. Let

Relations = {Rel

, Rel

, . . . , Rel

} and R = {Rel

, . . . ,

Rel

} ⊆ Relations a subset of relations. To solve both

problems, we can deﬁne an Exclude formula in the

following way:

Exclude(R) = ¬Rel

∧ ¬Rel

i+1

∧ ... ∧ ¬Rel

(2)

By negating all the given relations (which are

atomic propositions), this formula excludes all the re-

lations in some context. For example, the problem of

only evaluating constraints on states representing ac-

tual model elements can be solved like this:

AG(Exclude(R) =⇒ φ), (3)

where φ is the formula to be veriﬁed. By using an

implication and the Exclude formula, the given rela-

tions can be excluded from the paths. Considering the

running UML class example (Figure 3), suppose we

would like to formalize the following constraints: (i)

An attribute (of primitive type, class types would be

associations) cannot hold further attributes. (ii) Inher-

itance hierarchies must be acyclic. (iii) The value of

SpecialDevice.modiﬁer can never be 0.

Equation 4 prescribes that if a state is encountered

that is labeled with “Attributes”, then there must not

exist a next state, from which exists a second next

state which is also labeled with “Attributes”. Since

we begin from an “Attributes” state, this means that

any next state will correspond to an attribute that is

held by some model element. The second next state,

labeled with “Attributes”, would then imply that an at-

tribute holds another attribute, which is exactly what

was prohibited in the ﬁrst constraint.

AG(Attributes =⇒ ¬(EXEXAttributes)) (4)

For the second constraint, for every class in the

UML class diagram, a formula should be generated.

The only difference between the generated formulae

are the labels denoted by “Class”. The reason why is

the expressive power of CTL. We have so far found

it difﬁcult to express constraints that require “cross-

referring” some parts of the state-space. For example,

in the case of acyclic inheritance hierarchies, the con-

straint basically means that for every model element,

there must not exist a path that goes through only in-

heritance relations and leads back to itself. The part

that makes this troublesome is the “itself” part. It is

not difﬁcult to express that for a concrete label, that

label must not be found again. But we have so far not

found it possible to express this generally, in a single

formula.

Equations 5 and 6 describe that for every state that

corresponds to a class, there must not exist a next state

labeled with ”Inheritance”, from which exists a path

through the state-space that does not touch any rela-

tional state other than “Inheritance”, and takes control

back to the given class that we have begun with. This

is accomplished by using the previously deﬁned Ex-

clude function to ensure that on the right side of the

implication, only paths through “Inheritance” states

are considered. Note that the semantics of E [p U q]

(Table 1) are comfortably usable to express that some

states must (not) be reachable in the state-space. It

is even possible to specify conditions that must (not)

hold until the target state is (not) reached. This way,

in our approach, it is easy to express that a path must

exist between some model elements.

∀Class : AG(Class =⇒ ¬EX(I ∧ E[(φ)UClass]),

(5)

where I abbreviates Inheritance and φ denotes the

following:

φ = Exclude(Relations \ {Inheritance}) (6)

Verifying Static Constraints on Models Using General Formal Veriﬁcation Methods

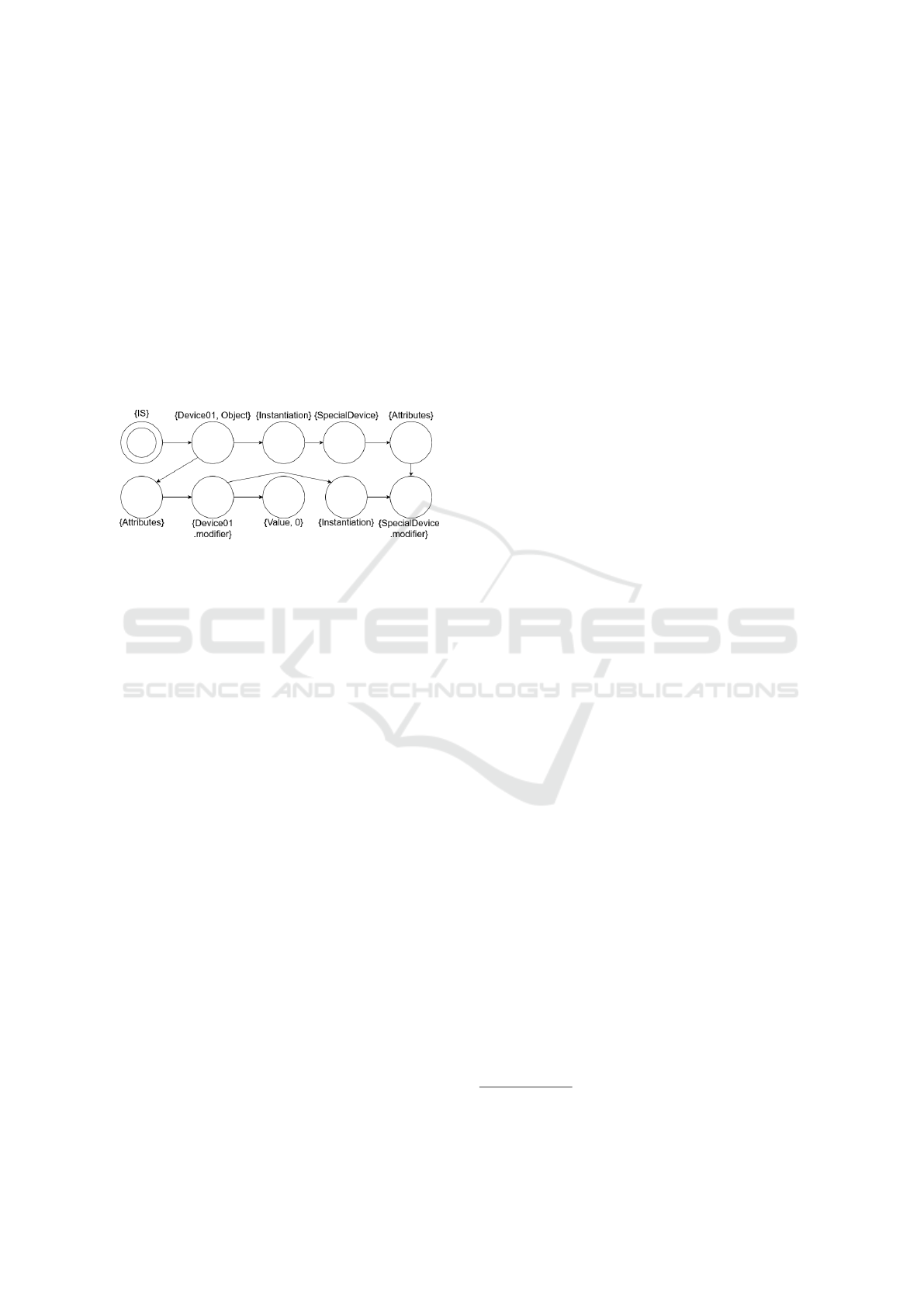
4.4.1 Handling Objects

So far, we have only formalized constraints that must

be true on the level of classes, objects were never con-

sidered. However, the third constraint states that the

value of a certain attribute can never be 0. Since the

attribute is not static, it will only gain a concrete value

when the class is instantiated. Objects can be han-

dled in the same way as classes. The idea is to simply

add the objects to the same JRM that also contains the

classes. In this case, let us extend the previous JRM

example (Figure 6) with an object. Figure 7 shows

the snippet that would be inserted additionally to the

original contents of the JRM.

Figure 7: Adding an object named Device01 to the JRM,

instantiating the class SpecialDevice. The rest of the JRM

would remain unchanged.

To handle objects, we deﬁne a new relation: In-

stantiation. We can then add an object named De-

vice01 that instantiates the class SpecialDevice. At

this point, the attributes of the parent class cannot be

reused, since for every object, its own attributes must

be available. For this reason, the attributes of De-

vice01 contain modiﬁer that instantiates the attribute

of the parent class. To express the value of this at-

tribute, another relation is deﬁned: Value. However,

unlike other relational states, values do not have to

point to a new state labeled with the value. Instead,

applying both the label Value and the concrete value,

in this case 0, on the same state is beneﬁcial. This

way, less states have to be used, keeping the state-

space smaller. It should also be noted that Value states

can be reused: if another attribute also had the value

of 0, then it would not be needed to add a new state.

With this formalism in mind, it is not difﬁcult

to formulate the third constraint. Equation 7 shows

the formula, where SD.m abbreviates SpecialDe-

vice.modiﬁer and I abbreviates Instantiation. The for-

mula describes that for every state that instantiates the

attribute SpecialDevice.modiﬁer, there must not exist

a next state that is labeled with both Value and 0.

AG((EX(I ∧ EXSD.m)) =⇒ ¬EX(Value ∧ 0)) (7)

Storing every value in the JRM as a relation might

cause problems in terms of performance if the number

of model elements is very high or if most of the model

elements hold some kind of value. For cases where

modeling the values is not feasible, there is another,

more straight-forward solution. NuSMV also offers

its own typesystem that supports most primitive types,

as well as basic set types and operations on them. It is

possible to deﬁne variables and store the values inside

them. Checking these values in CTL formulae is as

simple as referencing them by name and using basic

arithmetic operators on them. In our example, instead

of modeling the value relation in the JRM, we would

store the value of Device01.modiﬁer in a variable Val-

ueDevice01Modiﬁer, and check its non-nullity.

We have created a demo application

that demon-

strates the formalization and veriﬁcation of the run-

ning UML class diagram in practice.

5 CONCLUSIONS

In this work, we have proposed a general approach for

verifying static constraints on software models.

A formal Kripke Structure is created that captures

the static aspects of the original software model, the

constraints are formalized using CTL and a model

checker tool, NuSMV is used to verify whether

the formalized CTL expressions hold on the formal

model. The approach was presented through a run-

ning UML class diagram example.

The main strength of the proposed approach lies in

its formal aspect. Since a cutting-edge model checker

tool (NuSMV) is reused, the checking of models is

fully automatic, and formal proof is given that the

model satisﬁes the constraints. It is guaranteed to

ﬁnd any violations of the formalized constraints. If

no violations are found, the constraint is guaranteed

to hold. The approach is general and independent of

the modeling language of the source model. While

this is mostly true for OCL and its variants as well,

deﬁning a mapping between the source model and the

JRM is easier and takes less effort than implementing

an OCL interpreter for the given modeling language.

A consequence of the generality is that the approach

becomes independent of the concrete model checker

behind it. It currently uses NuSMV, but could easily

be extended to use a different model checker or sup-

port multiple options.

The main weakness of the approach is the expres-

sive power of CTL. Constraints that would require

cross-referencing parts of a CTL expression are dif-

ﬁcult to handle. This could be alleviated by deﬁn-

ing transformations on the formal Kripke Structure.

https://github.com/NorbertSomogyi/

FormalModelVeriﬁcationDemo

MODELSWARD 2023 - 11th International Conference on Model-Based Software and Systems Engineering

Temporarily manipulating the structure of the formal

model (such as adding new states and transitions, or

changing existing ones) may make it easier to nav-

igate the model and handle CTL expressions that

would otherwise prove difﬁcult. The second weak-

ness is that the approach is mainly designed to deal

with static constraints on the source model. It is not

capable of interpreting functions. Thus, it is not in-

tended to verify dynamic behavior. If that is required,

a static view of the dynamic behavior would be re-

quired, such as Abstract Syntax Trees (AST). Finally,

deﬁning CTL expressions requires proﬁciency in for-

mal veriﬁcation. For this reason, in the future, a Do-

main Speciﬁc Language (DSL) (Fowler, 2010) must

be created to hide the complexity of writing CTL ex-

pressions from the model designer.

In terms of future work, thoroughly evaluating

the expressive power of CTL on real-world models

and constraints is our main priority. Depending on

the results of the evaluation, an extension of CTL

or a whole new language might be needed. In the

ﬁrst case, by introducing model transformations on

Kripke Structures, constraints that are difﬁcult to ex-

press through CTL may become easier. In the sec-

ond case, along with the new language, signiﬁcant

enhancements to a model checker tool might be nec-

essary. The performance of the approach will also be

evaluated, making sure it is efﬁcient enough to be ap-

plicable in practice, even on larger models and a sig-

niﬁcant amount of constraints to be veriﬁed.

REFERENCES

Anastasakis, K., Bordbar, B., Georg, G., and Ray, I.

(2007). Uml2alloy: A challenging model transfor-

mation. In ACM/IEEE International Conference on

Model Driven Engineering Languages and Systems,

pages 436–450.

Behrmann, G., David, A., and Larsen, K. (2004). A tutorial

on uppaal. In International School on Formal Meth-

ods for the Design of Computer, Communication and

Software Systems, volume 3185, pages 200–236.

Brucker, A. and Wolff, B. (2008). Hol-ocl: A formal proof

environment for uml/ocl. pages 97–100.

Cabot, J., Calegari, D., Claris

o, R., Gogolla, M., Vallecillo,

A., and Willink, E. D. (2021). A swot analysis of the

object constraint language. pages 178–184.

Cabot, J., Claris

o, R., and Riera, D. (2007). Umltocsp: A

tool for the formal veriﬁcation of uml/ocl models us-

ing constraint programming. In Proceedings of the

Twenty-Second IEEE/ACM International Conference

on Automated Software Engineering, ASE ’07, page

547–548, New York, NY, USA. Association for Com-

puting Machinery.

Cabot, J. and Gogolla, M. (2012). Object constraint lan-

guage (ocl): A deﬁnitive guide. volume 7320, pages

58–90.

Cimatti, A., Clarke, E., Giunchiglia, E., Giunchiglia, F., Pi-

store, M., Roveri, M., Sebastiani, R., and Tacchella,

A. (2002a). Nusmv 2: An opensource tool for sym-

bolic model checking. 14th International Conference,

CAV, Copenhagen, Denmark.

Cimatti, A., Giunchiglia, E., Pistore, M., Roveri, M., Sebas-

tiani, R., and Tacchella, A. (2002b). Integrating bdd-

based and sat-based symbolic model checking. vol-

ume 2309.

Fowler, M. (2010). Domain Speciﬁc Languages. Addison-

Wesley Professional, 1st edition.

Jackson, D. (2012). Software Abstractions: Logic, Lan-

guage, and Analysis. The MIT Press.

Mahajan, Y., Fu, Z., and Malik, S. (2004). Zchaff2004: An

efﬁcient sat solver. volume 3542, pages 360–375.

MOF (2005). OMG: MetaObject Facility.

http://www.omg.org/mof/. Accessed:2022-11-24.

Muller-olm, M., Schmidt, D., and Steffen, B. (1999).

Model-checking: A tutorial introduction. volume

1694, pages 330–354.

Nobakht, M. and Truscan, D. (2013). Tool Support for

Transforming UML-Based Speciﬁcations to UPPAAL

Timed Automata. Turku Centre for Computer Sci-

ence (TUCS). TUCS Technical Report No 1087, June

2013.

Przigoda, N., Soeken, M., Wille, R., and Drechsler, R.

(2016). Verifying the structure and behavior in um-

l/ocl models using satisﬁability solvers. IET Cyber-

Physical Systems: Theory & Applications, 1.

Shaikh, A., Claris

o, R., Wiil, U. K., and Memon, N. (2010).

Veriﬁcation-driven slicing of uml/ocl models. In Pro-

ceedings of the IEEE/ACM International Conference

on Automated Software Engineering, ASE ’10, page

185–194, New York, NY, USA. Association for Com-

puting Machinery.

orensson, N. and Een, N. (2005). Minisat v1.13-a sat

solver with conﬂict-clause minimization. Interna-

tional Conference on Theory and Applications of Sat-

isﬁability Testing.

UML (2017). OMG: Uniﬁed Modeling Language.

https://www.omg.org/spec/UML/2.5.1/PDF/.

Accessed:2022-11-24.

Vaziri, A. and Jackson, D. (2003). Some shortcomings of

ocl, the object constraint language of uml.

Verifying Static Constraints on Models Using General Formal Veriﬁcation Methods