Studying Narrative Economics by Adding Continuous-Time Opinion

Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive

Financial Markets

Arwa Bokhari

and Dave Cliff

Department of Computer Science, University of Bristol, Bristol BS8 1UB, U.K.

Keywords:

Narrative Economics, Opinion Dynamics, Co-Evolutionary Systems, Adaptive Markets, Financial Markets,

Automated Trading, Agent-Based Computational Economics.

Abstract:

In 2017 Robert Shiller, a Nobel Laureate, introduced Narrative Economics, an approach to explaining aspects

of economies that are difﬁcult to comprehend when analyzed using conventional methods: in light of narratives

(i.e., stories) that participants in asset markets hear, believe, and tell each other, some observable economic

factors, such as price dynamics of otherwise valueless digital assets, can be explained largely within the

context of those narratives. As Shiller argues, it is best to explain and understand seemingly irrational and

hard-to-explain behaviors, such as investing in highly volatile cryptocurrency markets, in narrative terms:

people invest because they believe that it makes sense to do so, or have a heartfelt opinion about the prospects

of the asset, and they share these beliefs and opinions with themselves and others in the form of narratives.

In this paper, we address the question of how an agent-based modeling platform can be developed to be

used for studying narrative economics. To do this, we integrate two very recently published developments.

From the ﬁeld of agent-based models of ﬁnancial markets, we use the PRDE adaptive zero-intelligence trader

strategy introduced by Cliff (2022), and we extend it to integrate a continuous-time real-valued nonlinear

opinion dynamics model reported by Bizyaeva et al. (2022). In our integrated system, each trader holds an

opinion variable whose value can be altered by interaction with other agents, modeling the inﬂuence that

narratives have on an agent’s opinions, and which can also be altered by observation of events in the market.

Furthermore, the PRDE algorithm is modiﬁed to allow each trader’s trading behavior to smoothly alter as that

trader’s opinion dynamically varies. Results reported for the ﬁrst time here show that in our model there is

a tightly coupled circular interplay between opinions and prices: changes in the distribution of opinions can

affect subsequent price dynamics; and changes in price dynamics can affect the consequent distribution of

opinions. Thus this paper presents a ﬁrst demonstration of the reliability and effectiveness of our new agent-

based modeling platform for use in studying issues in narrative economics. Python source-code for our model

is being made freely available as open-source release on GitHub, to allow other researchers to replicate and

extend our work.

1 INTRODUCTION

The notion of narrative economics, introduced

and popularized by Nobel Prize winner Robert

Shiller (Shiller, 2017; Shiller, 2019), involves the

study of the spread and dynamics of “narratives”, i.e.

the stories (particularly those of human interest and

emotions) told and believed by market participants

about the nature of the market, and how these change

over time, to understand the dynamics of economic

and market systems. In particular, Shiller argues that

https://orcid.org/0000-0003-2987-4601

https://orcid.org/0000-0003-3822-9364

phenomena which are difﬁcult to explain in any other

way, as such cryptocurrency price ﬂuctuations, can

best be explained by reference to the narratives in play

among participants in the relevant markets.

In their 2021 prize-winning ICAART paper, Lo-

mas & Cliff (Lomas and Cliff, 2021), noted that a nar-

rative is simply an expression of an opinion, and used

this to forge an initial link between agent-based mod-

els of ﬁnancial markets, and the long-established ﬁeld

of research in the social sciences literature known as

Opinion Dynamics (OD). Research in OD aims to un-

derstand how individuals in a population can inﬂu-

ence others to change their opinions, and how they

Bokhari, A. and Cliff, D.

Studying Narrative Economics by Adding Continuous-Time Opinion Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive Financial Markets.

DOI: 10.5220/0011797000003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 2, pages 355-367

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

355

may change their own opinions, as a result of those in-

ﬂuences. Lomas & Cliff presented a novel approach

to integrating mathematically naive 20-year-old OD

models with agent-based computational economics.

In the Lomas & Cliff model, traders buy and sell as-

sets by submitting bid and/or ask orders to an auto-

mated central ﬁnancial exchange (such as a real-life

stock exchange or a cryptocurrency exchange web-

site), and showed how changes in the trader-agent’s

opinions could be reﬂected in the price dynamics of

the market. While notable for its novelty, Lomas

& Cliff’s work could be improved upon in two ma-

jor ways: ﬁrst, their method for integrating OD with

trader-agents has since been shown to have a vulnera-

bility that can result in the market collectively grind-

ing to an irreversible halt; and second they did not

discuss or explore any mechanisms by which mar-

ket events could alter the traders’ opinions – in their

model, causality was one-directional from opinions to

prices. In this paper, we present our model which

addresses both those issues and also relies on a less

mathematically naive OD model, which enables fur-

ther work in exploring the stability of the dynamics of

our model, as is discussed further later in this paper.

Although the OD literature is substantial, the vast

majority of it discusses models where agents hold ab-

stract opinions that are altered only by interactions

with other agents and which do not contain external

references to establish whether certain opinions are

true or false (for example, opinions may be held about

politics or religion, on which people hold strong per-

sonal views and ﬁrmly believe that their opinions are

correct, but for which there is no one objectively cor-

rect opinion). In contrast to much of the existing OD

literature, Lomas & Cliff’s work was notable because

the opinions of their trader-agents regarding the cur-

rent price of an asset could later prove to be true or

false. For example, a trader may believe that the price

of an asset would decrease in the near term, but in

fact it increases. Therefore, in agent-based models

of narrative economics traders need to be able to ad-

just their opinions based not only on local interactions

with other agents but also on uncertain future globally

observable outcomes that have not yet been resolved

or revealed: this is unusual in the ﬁeld of OD, with

almost no prior papers addressing this issue.

As with OD research, research in agent-based

modelling of economic and ﬁnancial systems has

been underway for several decades, and it is a sufﬁ-

ciently mature ﬁeld that it has its own name: Agent-

Based Computational Economics (ACE: see e.g.,

(Chen, 2018; Hommes and LeBaron, 2018)). In ACE

models, a simulated economic or ﬁnancial system

is created and populated with some number of au-

tonomous agents, where each agent follows some spe-

ciﬁc algorithm or strategy for interacting with other

agents in the system. It has been repeatedly demon-

strated that ACE models employing only minimally

simple trader strategies can be surprisingly informa-

tive, and these so-called zero intelligence (ZI) trading

strategies are now commonly used to illustrate and ex-

plore various economic and market phenomena. The

seminal paper in establishing markets populated by ZI

traders as worthwhile objects of study is (Gode and

Sunder, 1993); and for reviews of the impact and ef-

fectiveness of ZI studies in ACE, see (Farmer et al.,

2005; Ladley, 2012; Axtell and Farmer, 2022).

Very recently, (Cliff, 2022) proposed the

PRDE (Parameterized-Response zero-intelligence

with Differential Evolution) as an instance of

an efﬁciently adaptive ZI trading strategy, i.e. a

minimal-intelligence strategy that can usefully alter

its trading behavior to better ﬁt its immediate market

conditions, with the aim of maximizing its individual

proﬁtability at all times. Cliff’s PRDE is an extension

of his earlier PRZI (Parameterized-Response Zero-

Intelligence) trading strategy (Cliff, 2021) which

was introduced to address a problem identiﬁed in the

original Lomas & Cliff work: the modiﬁed ZI trading

strategies reported by Lomas & Cliff did integrate the

trader’s opinions into their trading behavior, but could

result in situations where the opinionated traders all

settled to a state in which no further transactions

could take place in the market, so the market ceased

to show any activity at all: for full details of this,

see the discussion in (Cliff, 2021). PRZI and then

PRDE were introduced as remedies to this problem

in Lomas & Cliff’s 2021 paper, but to the best of

our knowledge our paper here is the ﬁrst to integrate

PRDE with a leading-edge OD model.

While the Lomas & Cliff paper is deﬁnitely novel,

it is somewhat disappointing that the OD models

they explored adding to existing ZI trader strate-

gies were old, extremely simple, and mathematically

naive. Speciﬁcally, Lomas & Cliff explored the in-

tegration of three OD models to two ZI strategies.

The two ZI strategies were the Zero-Intelligence Con-

strained (ZIC) of (Gode and Sunder, 1993) and the

Near-Zero Intelligence (NZI) of (Duffy and

Unver,

2006): when Lomas & Cliff added OD models to

these two strategies, they named the extended strate-

gies OZIC and ONZI, respectively. The three OD

models were the Bounded Conﬁdence (BC) model of

(Hegselmann and Krause, 2002), the Relative Agree-

ment (RA) model described in (Deffuant et al., 2002;

Meadows and Cliff, 2012), and the Relative Disagree-

ment (RD) model of (Meadows and Cliff, 2013), the

most recent of which is over a decade old. All three

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

356

of BC, RA, and RD are simple abstract discrete-time

models where time advances according to t ← t + 1

with no clear links from the integer-valued t to contin-

uous real-world time – that is, in these simple old OD

models there is no use of differential equations with

stated time-constants, which would in principle allow

the whole arsenal of continuous-time dynamical sys-

tems modelling and analysis tools and techniques to

be deployed, such as Lyapunov stability analysis To

address this issue, in our paper here we switch away

from the simplistic discrete-time OD models used

by Lomas & Cliff, and use instead a contemporary

continuous-time nonlinear differential-equation based

OD model recently reported by Bizyaeva, Franci, &

Leonard (2022) which we refer to hereafter as the

BFL model.

The novel results in our paper concern the over-

all dynamics of the integration of the BFL OD model

with PRDE traders. For consistency with the nam-

ing convention introduced by Lomas & Cliff, we refer

to opinionated-PRDE traders as OPRDE, and then to

distinguish our use of BFL from any later attempts to

create opinionated PRDE traders using different OD

models, we refer to our model as OPRDE-BFL.

We show here that our ACE-style market simula-

tions populated by OPRDE-BFL traders can exhibit

situations in which changes in market opinion alter

subsequent price dynamics (as was demonstrated by

Lomas & Cliff with OZIC and ONZI) and also that

changes in prices can plausibly alter the subsequent

distribution of opinions in the population of traders

(as was not demonstrated by Lomas & Cliff).

In Section 2 we give further details of the back-

ground to our work, concentrating on explaining the

PRDE trader strategy and the BFL opinion dynam-

ics model. In Section 3 we illustrates how the BFL

model can be customized for PRDE integration. In

Section 3.3 we explain how BFL is integrated into

PRDE traders. In Section 4 we describe the details of

our experiments and discuss the results. In Section 5

we discuss future directions and the implications of

our ﬁndings.

2 BACKGROUND

2.1 Simulated Financial Markets

The study of simulation models of ﬁnancial markets

has been known for a long time as a means of ex-

ploring the ﬁne-grained dynamics of various form of

market. Such models very often require populating

a market mechanism with a number of trader-agents:

autonomous entities that work independently within

the framework of the particular market mechanism

being simulated. As per the market simulation litera-

ture reviewed here, usually each trader in the market

is assigned a role, either that of a buyer or a seller, and

there is a systematic way in which each buyer (seller)

is assigned an order to buy (sell) a certain quantity

of an arbitrary abstract commodity in which the mar-

ket trades, as well as a private (secret to the trader)

limit price, which is the maximum (minimum) unit-

price at which they can buy (sell) the item. The dif-

ference between the transaction price and the trader’s

limit price is the proﬁt (sometimes referred to as util-

ity or surplus). Over the 30 years or so that ACE has

been the topic of active development, a few speciﬁc

trader-agent algorithms are notable for their longevity

in the literature: SNPR (Rust et al., 1992); ZIC (Gode

and Sunder, 1993); ZIP (Cliff, 1997); GD (Gjerstad

and Dickhaut, 1998); MGD (Tesauro and Das, 2001);

GDX (Tesauro and Bredin, 2002); HBL (Gjerstad

et al., 2003); and AA(Vytelingum et al., 2008). The

seminal ZIC developed by Gode and Sunder (1993)

is highly stochastic however it shows surprisingly

human-like market dynamics. In a landmark paper by

IBM researchers (Das et al., 2001), GD and ZIP were

the ﬁrst to be demonstrated to consistently show supe-

rior performance to human traders (see also: (De Luca

and Cliff, 2011b; De Luca and Cliff, 2011a; De Luca

et al., 2011)), and the IBM result is widely cited as

initiating the rise of algorithmic trading in real-world

ﬁnancial markets. All of the these strategies, except

for SNPR and ZIC, use some form of machine learn-

ing (ML) or artiﬁcial intelligence (AI) to modify their

responses over time, better-adapting their trading be-

havior to the market conditions they ﬁnd themselves

in, and the details of these algorithms have often been

published in major AI/ML conferences and journals.

Recently (Cliff, 2021) proposed the PRZI trading

algorithm: PRZI traders are ﬁrmly in the ZI tradi-

tion but they each have a scalar real-valued strategy

parameter s ∈ [−1,+1] ∈ R which governs their re-

sponse to market events: when a PRZI trader has s = 0

its trading behavior is identical to the seminal ZIC of

(Gode and Sunder, 1993), but when s > 0 it becomes

more “urgent”, quoting prices that are more likely to

ﬁnd a counterparty and lead to a transaction, but for

which the expected proﬁtability of the transaction will

be reduced relative to the prices quoted when s = 0;

and similary when s < 0 the PRZI trader is more “re-

laxed” quoting prices that are more proﬁtable if they

do lead to a transaction, but less likely to lead to a

transaction than the prices quoted when s = 0.

At the extremes, when a PRZI trader i has s

−1.0 its trading strategy is equivalent to the max-

imally relaxed Shaver (abbreviated SHVR) strategy

Studying Narrative Economics by Adding Continuous-Time Opinion Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive

Financial Markets

357

proposed in (Cliff, 2012; Cliff, 2018); and when s

+1.0 it is acting as the maximally urgent Give-away

(GVWY) strategy, also described in (Cliff, 2012;

Cliff, 2018).

As thus deﬁned, an individual PRZI trader is non-

adaptive: it is assigned an s-value at creation, and

keeps that same s value for all of its lifetime. How-

ever, in subsequent work PRZI traders have been ex-

tended to adapt their s-values dynamically, as market

conditions change, attempting to always increase or

maintain their proﬁtability as market circumstances

alter. This allows populations of adaptive PRZI

traders to be used as a tool for simulation modelling of

contemporary real-world ﬁnancial markets, in which

all traders are simultaneously adapting their trading

strategies, each seeking to maximize their own prof-

itability, while burdened by the complexity and un-

certainty of adapting to a market environment where

every other trader is simultaneously adapting, contin-

uously adjusting its strategy in real-time.

The most recent and currently most efﬁcient adap-

tive PRZI trader was described in (Cliff, 2022): PRzi

with Differential Evolution (PRDE), which makes use

of Differential Evolution (DE: see e.g. (Storn and

Price, 1997; Bilal et al., 2020)) as its optimization

strategy. Each PRDE trader maintains a population

of size k ≥ 4 candidate s-values, and iterates over an

inﬁnite loop in which on each iteration it evaluates

each of the k candidates in turn, and then uses a basic

DE process to create a new candidate s-value, which

is also evaluated: if that new candidate is better than

one of the four in the original population, it replaces

that one; if not, it is discarded; and the loop iterates

again. Evaluation of any one candidate s-value in-

volves the PRDE trader operating in the market using

only that s-value for some period of time, and then

calculating the proﬁt-per-unit-time for that s-value as

its “ﬁtness” score in the DE process. For all our ex-

periments reported here, we used the Python PRDE

reference implementation published on Github as part

of the freely-available BSE platform for agent-based

modelling of contemporary ﬁnancial markets, avail-

able as (Cliff, 2012).

In all of our experiments reported here we used

BSE in its default conﬁguration, where it allows for

the deﬁnition of some number of buyer-agents N

and some number of seller-agents N

. Each buyer

(seller) is periodically issued with assignments to buy

(sell) a unit of the exchange’s tradeable asset at a price

no higher (lower) than that trader’s given private limit

price, and to ﬁnd a willing seller (buyer) as a trading

counte-party via interacting within a continuous dou-

ble auction (CDA) running on a centralised ﬁnancial

exchange that operates a Limit Order Book (LOB), by

submitting bid (ask) orders to the exchange. The CDA

is an auction mechanism in which any buyer can sub-

mit a bid order to the exchange at any time, and any

seller can submit a sell order at any time, and the ex-

change continuously runs a matching engine to pair

up buyers and sellers whose orders are compatible –

e.g. if a seller S1 quotes an ask of $100 for a unit of

the asset and a buyer B1 then quotes a bid price of

more than $100, the exchange matches B1 and S1 as

counter-parties to a transaction and S1 then sells to

B1 for $100, because that was the earlier-quoted of

the two prices. However, whenever a trader quotes

a price that cannot be matched with a counter-party,

that quote “rests” at the exchange and is entered on

the LOB; with the exchange publishing an updated

LOB to all market participants every time the LOB

changes. The published LOB shows a summary of

the array of all unmatched buyer orders resting at the

exchange (on the bid-side of the LOB) and all un-

matched seller orders (on the ask-side) of the LOB,

with the two sides of the LOB sorted in price-order

from best (highest bid, lowest ask) to worst (low-

est bid, highest ask). All major ﬁnancial exchanges

around the world for stocks/shares, currencies, com-

modities, and digital assets run LOB-based CDAs, so

in this respect BSE is an excellent model of real-world

exchanges. For further details of CDAs and LOBs,

see e.g. (Friedman and Rust, 1992; Gould et al., 2013;

Abergel et al., 2016). Limit prices on the trader’s as-

signments were drawn from a pair of supply and de-

mand curves that we speciﬁed, allowing us to control

the equilibrium price and quantity in each market ses-

sion.

3 OPRDE: OPINIONATED PRDE

In this section we describe our rationale for the spe-

ciﬁc set of changes we introduced to give Opinionated

PRDE (OPRDE) traders, which fully enable the study

of narrative economics via agent-based models.

3.1 Opinions About What?

First, we need to be speciﬁc about what our trader-

agents hold opinions about. In the ﬁrst instance, we

are working with agents whose opinions at time t con-

cern the qualitative shift in price P(t) of a tradeable

asset at a particular future point in time ω, denoted

by T

, relative to the price at some earlier point in

time T

when the opinion was ﬁrst formed. Each

trader i’s individual opinion at time t is a real number

(t) ∈ [−1.0, +1.0] ∈ R, which we interpret qualita-

tively as mapping onto one of two opinion-states such

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

358

that x

(t) ∈

{

−1,+1

}

; where x

(t) = +1 implies that

i’s opinion is that the price will signiﬁcantly rise; and

correspondingly that x

(t) = −1 implies that i’s opin-

ion is that the price will signiﬁcantly fall. Here the

notion of “signiﬁcant” rises or falls in price is deﬁned

in terms of whether the absolute percentage change in

price is above some threshold percentage ∆

; that is,

a price change is signiﬁcant if:



P(T

) − P(T

)

P(T

)



> ∆

This deﬁnition, with each trader i having its own indi-

vidual values for T

0,i

, T

ω,i

, and ∆

p,i

, allows the model

be able to capture situations in which different traders

form their opinions at different times (i.e., the T

0,i

val-

ues may vary with i), have differing time-horizons

over which they judge the rise/fall/unchanged nature

of any difference in price (i.e., the T

ω,i

values may

vary with i), and have different views of what counts

as a signiﬁcant change in price (i.e., the ∆

p,i

values

may vary with i, too). However, for simplicity, in the

experiments reported here we study only situations in

which all traders have the same values of these three

variables: that is, in our experiments here, all traders

form their opinions at the same time, when the mar-

ket session opens; all traders assess the price-change

at the same time, when the market session closes; and

all traders have the same deﬁnition of “signiﬁcant”,

here ∆

p,i

= 0.2,∀i. This means that our traders will

exhibit opinion dynamics both within any one mar-

ket session, and also across a sequence of successive

market sessions. In this paper we concentrate only

on the within-session dynamics, studying only a sin-

gle market session at a time. In later papers we will

explore opinion dynamics in our system when it runs

for continuous sequences of multiple successive mar-

ket sessions.

3.2 The BFL Nonlinear OD Model

Here we present our condensed summary of

(Bizyaeva et al., 2022): for full details, readers are

of course referred to the original paper.

Consider a network of N

= N

+ N

trading

agents each forming a scalar opinion x

,...,x

∈ R

about the price of a tradeable asset, and M ≥ 1 com-

munication sources (such as mass media), offering

static opinions c

,...,c

∈ R about the same asset.

Consider x

the real-valued opinion variable of trader

i, where negative values indicate a belief that prices

are about to decline, while positive values indicate an

increase, and the same is true for the value of the opin-

ions from the communication sources, for instance c

denotes the opinion from communication source k re-

garding the price of the asset. Let X = (x

,...,x

)

be the opinion state of the agent network, a special

case being the neutral state at the origin X = 0 which

would be the case if all agents held no ﬁrm opinion

about the directionality of any near-term price move-

ments. Agent i is unopinionated if its opinion state

is small, i.e.,

6 ϑ, for a ﬁxed threshold ϑ ' 0;

agent i is opinionated if

≥ ϑ. Agents can agree

and disagree: when two agents have the same qual-

itative opinion state (e.g., they both favor the same

option), they agree. When they have qualitatively dif-

ferent opinions, they disagree.

In the BFL model proposed by (Bizyaeva et al.,

2022), the opinions of agents are assumed to evolve

nonlinearly in continuous time, and we have tailored

the BFL model to best suit it to the ﬁnancial market

context in which we are using it. Our application con-

sists of the following parameters and property speci-

ﬁcations:

• Saturated Opinion Exchanges. Almost ev-

ery signaling network, whether natural or artiﬁcial,

exhibits saturated nonlinearities due to the limits of

action and sensing. In the case of an agent opinion

dynamics network, the saturation of interactions be-

tween agents efﬁciently bounds the attraction between

their opinions, thus, overcoming the paradox of linear

weighted average models. (Bizyaeva et al., 2022).

• Local Opinion. A trader’s local opinion is ob-

tained as a linear weighted sum of the opinions ex-

pressed by all the other traders in the network. The

weighted average is based on an adjacency matrix de-

noted here by A = [a

i j

] ∈ R

× R

. It is important

to note that there are two types of network interac-

tions: self-reinforcing interactions, weighted by a

;

and neighbour interactions, weighted by a

i j

, where

the sign of the adjacency weight determines the sign

of the network interaction, for all existing links be-

tween traders in the traders’ social network satisfying

i j

6= 0, with a

i j

weighing the extent to which agents

are inﬂuenced by their neighbors.

• Opinions From Communication Sources. The

impact of communication sources, such as the mass

media, on a trader’s opinion, is captured by a

weighted linear sum of the static opinions of these

sources. This sum is weighted by the weight matrix

B = [b

] ∈ R

× R

which identiﬁes to what extent

each trader can be inﬂuenced by a given communica-

tion source.

• Attention. It is important to note that traders’

attention or susceptibility to exchange opinions may

vary. In our model, each trader i’s attention param-

eter u

is linked to i’s proﬁt, meaning that when a

trader loses proﬁtability, its attention increases, oth-

erwise it remains the same; thus if the agent loses it

will be more alert to its neighbors and communication

Studying Narrative Economics by Adding Continuous-Time Opinion Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive

Financial Markets

359

sources. Let π

represents the trader’s proﬁt at time t

and π

t−1

is the trader’s proﬁt at a previous period t −1,

then the trader’s attention is updated as follows:

t+1



+ ξ π

− π

t−1

< 0

− π

t−1

≥ 0

(1)

where ξ is an incremental value that gets increased

as the market session approaches the end.

• Resistance. A trader’s resistance parameter d

represents its willingness to change its opinion.

• Inputs. Our agents have exogenous inputs: two

input parameters g

and e

are introduced for each

agent. The ﬁrst input parameter g

represents the col-

lective opinion of the market, as summarised by pub-

lic data shown on a central exchange’s LOB, such as

the market’s current mid-price or micro-price (both

of which are deﬁned below), which is analogous to

the global opinion in the work of (Guzelyte and Cliff,

2022). The second input parameter e

represents some

indication of the likelihood of a speciﬁc opinion prov-

ing to be true at its stated T

– what (Guzelyte and

Cliff, 2022) referred to as the “event opinion”. In

principle, supply and demand data can be used to pre-

dict whether prices are likely to rise or fall in the short

term. In the event that there is an excess of supply

relative to demand, the price of the asset will likely

fall; and vice versa. A simple way for ZI traders to

estimate supply/demand imbalance, as introduced in

(Church and Cliff, 2019), is by taking the difference

between the current market mid-price, denoted here

by p

(t) = (p

∗

bid

(t)+ q

∗

ask

(t))/2, and the current mar-

ket micro-price (as deﬁned by (Cartea et al., 2015)),

denoted here by p

(t), where

(t) =

∗

ask

(t)q

∗

bid

(t) + p

∗

bid

(t)q

∗

ask

(t)

∗

bid

(t) + q

∗

ask

(t)

(2)

in which p

∗

ask

(t) is the price of the best ask at time

t (i.e., the price at the top of the ask side of the ex-

change’s LOB); p

∗

bid

(t) is the price of the best bid

at time t (i.e. the price at the top of the bid side

of the LOB); q

∗

bid

(t) is the total quantity available at

∗

bid

(t); and q

∗

ask

(t) is the total quantity available at

∗

ask

(t). In the case of zero supply/demand imbal-

ance at the top of the LOB (i.e., Equation 2 reduces

to the equation for the market midprice, and there-

fore the difference between the two prices, denoted by

∆

(t) = p

(t) − p

(t) is zero). Accordingly, a posi-

tive imbalance (i.e. ∆

(t) >> 0) indicates that the

subsequent transaction prices are likely to increase,

and a negative imbalance (i.e. ∆

(t) << 0) indicates

that subsequent transaction prices are likely to fall.

As per (Bizyaeva et al., 2022), the networked

opinion dynamics ˙x

are then summarised as:

(3)

= −d

+ u

) + S

)) + (g

+ e

)

where s

∑

j=1

i j

and s

∑

k=1

The evolution of agent i’s opinion is determined

by four terms. These terms are the linear damp-

ing term, the saturated network interaction term,

the saturated communication sources inﬂuence term,

and the environmental signal term. S

: R → R

are bounded saturation functions satisfying S(0) =

0, S(0)

= 1, S(0)

= 0, S(0)

000

6= 0 with an odd sym-

metry S(−y) = −S(y); S

saturates the network in-

teractions, S

saturates the communication sources

inﬂuence; the damping coefﬁcient d

> 0 represents

a trader’s reluctance to form a strong belief since it

drives the values ˙x

to the neutral point, which im-

plies that higher d

indicates that the trader will be

more resistant to forming an opinion, however, the

parameter u

≥ 0 indicates how attentive agents are

to their social interactions, which affects the degree

to which their opinions are socially inﬂuenced. En-

vironment inputs e

and g

represent “opinions” (or,

more accurately, opinion-inﬂuencing factors) derived

from the environment, which are independent of the

other agents’ opinions.

3.3 Adding BFL to PRDE

In this study, we provide PRDE traders with a real-

valued opinion variable, which means that opinion-

ated PRDE buyers will behave differently from opin-

ionated PRDE sellers in the same market environ-

ment. For instance, when opinions indicate that prices

are on the rise, OPRDE buyers will respond with a

heightened sense of urgency as a hybrid of GVWY

and ZIC. As a result, they will quote prices based

on strategy values inﬂuenced by their opinions; con-

versely, OPRDE sellers will act more relaxed and

quote prices based on strategy values that are a hybrid

of ZIC and SHVR. On the other hand, when opinions

indicate that asset prices are falling, the same reason-

ing applies mutatis mutandis.

By this point, it should be obvious that we re-

quire some function that maps from trader i’s opin-

ion variable x

to its PRDE strategy s

, i.e. s

= F

Considering the simplest case, since both s

and x

∈

[−1,+1] ∈ R, it is possible for the mapping to be

the identity function, or its opposite, depending upon

whether i is a buyer or a seller. A buyer’s simplest

is identity function: F

(+1) = +1, F

(−1) = −1,

whereas a seller’s simplest F

is negative identity func-

tion: F

(+1) = −1, F

(−1) = +1. It should be noted,

however, that this fairly rapidly shifts the trader’s

strategy to the extremes (either SHVR or GVWY) as

|x|→ 1, therefore, this may not always be the most

effective approach: because at the extremes, buyers

usually lose. Consider, for example, a buyer play-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

360

ing SHVR. It will be moving away from it minimum

price to it limit price, which means it ends up quot-

ing high quote prices. In contrast, a seller playing

SHVR moves from it maximum price while still mak-

ing high quote prices, and generates more proﬁt as a

result. Additionally, when a buyer plays GVWY, it

loses since it limit price is it maximum price. At the

extremes, a buyer only has a chance of winning when

the seller plays GVWY. It is due to the fact that the

seller will maintain it limit price as it minimum price.

This results in the deal being in favor of the buyer,

even if the buyer is bidding higher than it limit price.

Furthermore, it is important to note that if the strate-

gies are always at -1, 0, and +1, the PRZI family of

traders will be unable to utilize the full potential of the

inﬁnite number of strategies that PRZI offers. Thus,

it is clear that we need a nonlinear mapping from an

opinion to a strategy that will not push the strategies

to the extreme edges

{

−1,+1

}

. In such a manner

that when prices fall, a buyer acts as a hybrid with

a high probability of quoting low prices; and when

prices rise, however, the seller acts as a hybrid, with

a high probability of quoting high prices. We have

found that the sine function usefully maps a trader’s

opinion to its strategy: it has the virtue of simplicity,

and the fact that it provides values for a strategy that

are close to those for the identity function. This is

necessary to determine the appropriate quote prices.

Nevertheless, when the sine function has a value of

+1 or 1, we clip it to keep it below those extreme val-

ues.

Recall that each PRDE trader maintains a pri-

vate local population of potential strategy-values, of

population-size k ≥ 4, which for trader i can be rep-

resented by s

i,1

i,2

,...,s

i,k

. Since PRDE traders use

just a single real scalar value to specify their bargain-

ing behavior, every individual in trader i’s local DE

population is just a single value. Consequently, the

conventional DE concept of crossover (i.e., selecting

alleles from two parents, one allele per dimension

of the genomes) is not applicable here: PRDE con-

structs a genome entirely by operating on the base

vector. In its current conﬁguration, PRDE applies

the basic “vanilla” DE/rand/1 where, after evaluat-

ing a particular strategy s

i,x

, three other s-values are

randomly selected from the population: s

i,a

i,b

, and

i,c

where x 6= a 6= b 6= c, and therefore a new candi-

date strategy s

i,y

is created s.t. s

i,y

= max(min(s

i,a

i,b

−s

i,c

,+1),−1) where F

represents the trader’s

differential weight coefﬁcient (in the experiments re-

ported here, F

= 0.8; ∀i), with the nested min and max

functions keeping the candidate strategy value within

the range [-1.0, +1.0]. In OPRDE we introduce the

trader’s opinion s

i,o

as a new candidate strategy. Then

the ﬁtness of s

i,y

and s

i,o

are evaluated and the best

strategy replaces s

i,x

, otherwise, it is discarded; and

then the next strategy s

i,x+1

is evaluated.

3.4 Implementation Details

The experiments reported in Secction 4 use BSE to

simulate a ﬁnancial market for a single abstract trade-

able commodity, where N

= N

= 30 and hence

= 60; and where each trader is running OPRDE

with k = 5. Throughout the process, buyers are given

a maximum purchase price of $140 per unit, while

sellers are restricted to a minimum sale price of $60

per unit. A schedule such as this provides what

economists refer to as perfect elasticity of supply and

demand, and it is widely used in experimental eco-

nomics research (such as (Smith, 1965)): this en-

sures that every seller can ﬁnd a buyer that could act

as a counterparty, and vice versa. In other words,

no traders would be given extra-marginal prices that

would limit their ability to ﬁnd counterparties. As a

result of a transaction between two traders, both their

cash assignments and their stock assignments are de-

pleted to render them inactive, and they each wait for

a random period of up to ﬁve seconds before they are

re-assigned fresh cash or stock, enabling them to re-

join the market as active traders once again.

BSE simulates continuous time using a discrete

time-slicing approach using a temporal step-size of

∆t = 1/N

, i.e. 0.0167sec for N

= 60, as a result,

each trader can interact with the market at least once

a second. Our experiments here simulate 300 days

of continuous round-the-clock 24 × 7 tradings: the

trading takes place on sub-second timescales, but the

co-evolutionary dynamics play out over much longer

periods. The proﬁt per second (PPS) of a strategy s

at time t is calculated by summing all proﬁts gen-

erated over the time period [t − ∆

,t] and dividing

that accumulated proﬁt by the evaluation period ∆

in our experiments here we use ∆

=7200sec (i.e., 2

hours); given there are k = 5 strategies, any one trader

takes 10 simulated hours to evaluate all its candi-

date strategies. As stated earlier, every transaction’s

proﬁt is determined by the difference between the

price agreed by the buyer and seller and their indi-

vidual limit prices: e.g., if a transaction takes place at

a price of $90, then the buyer’s proﬁt on the transac-

tion is $50 (denoted by π

) and the seller’s proﬁt is

$30 (denoted by π

) because in these experiments all

buyers had a limit price of $140, and all sellers had a

limit price of $60.

For the BFL opinion dynamics model, for the il-

lustrative outputs shown in this paper we used the

following parameter values: u

= 0.5; d

= 1,∀i =

Studying Narrative Economics by Adding Continuous-Time Opinion Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive

Financial Markets

361

1,...,N

; the adjacency matrix A = [a

i j

] = [1]∀i∀ j;

and for these preliminary experiments the communi-

cation sources are switched off: exploring the inter-

play between the agents’ opinions and the communi-

catins sources is something that we intend to explore

in depth in a later paper.

4 RESULTS

This section evaluates OPRDE as an extension of

PRDE by giving illustrative answers to the following

three questions: (1) How does the OD of OPRDE af-

fect market prices? (2) How can the distribution of

prices affect the opinions of traders? And ﬁnally (3)

How do markets populated wholly by OPRDE traders

compare to those populated only by PRDE traders?

4.1 Opinions Affecting Prices

Our ﬁrst evaluation question is addressed by exam-

ining the results from extreme opinion distributions,

such as those in which all traders hold extremely pos-

itive opinions, those in which all hold extremely neg-

ative opinions, and those in which the opinion distri-

bution shifts over time.

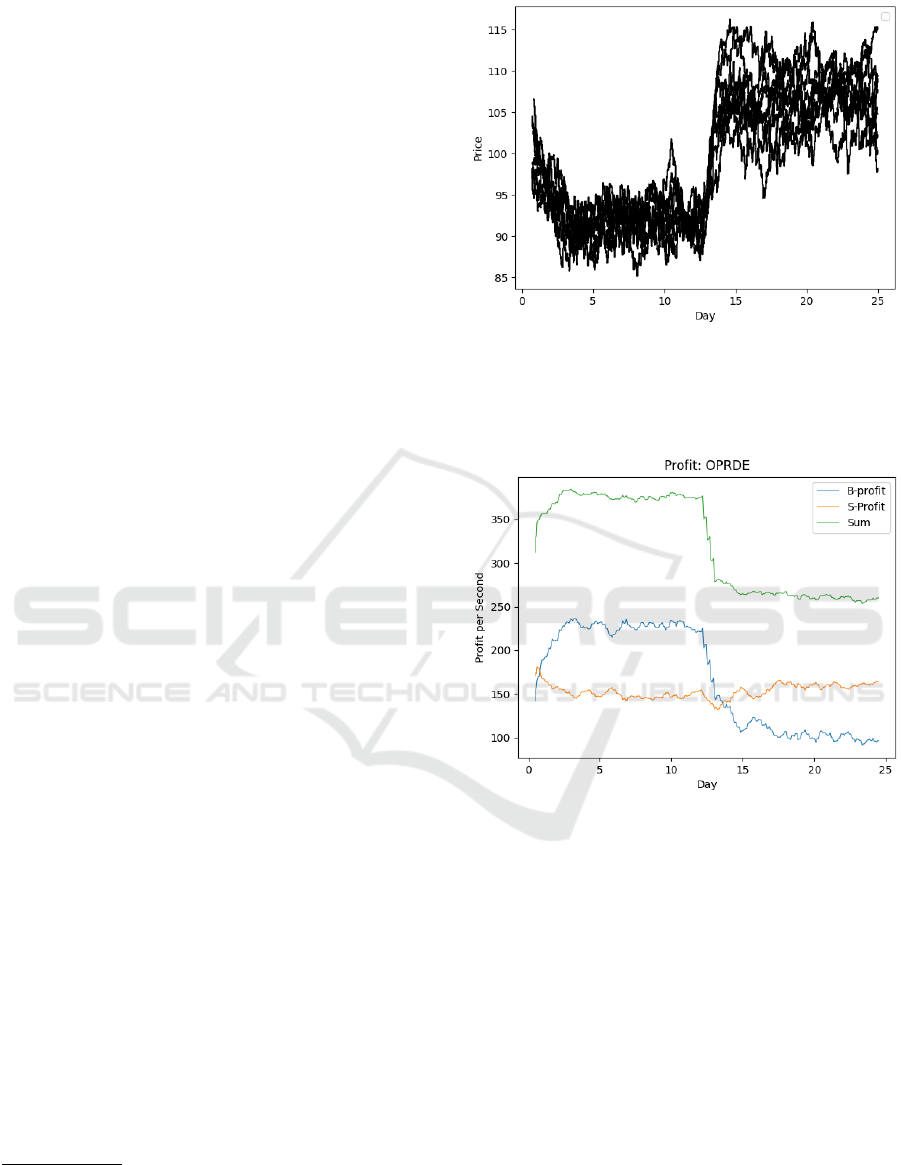
Figure 1 illustrates how market prices change

when traders’ exogenously imposed opinions start out

as negative for the ﬁrst half of the period , and then

shift to positive toward the end of the 25-day experi-

ment. In both phases, transaction prices were highly

correlated with opinions, demonstrating a causal link

between traders’ opinions and their price-quoting de-

cisions. Figure 2 then shows the corresponding

changes in traders’ proﬁt per second (PPS) values: in

the ﬁrst ﬁve days, with all traders holding negative

opinions, sellers trade urgently and hence enter into

transactions that yield less proﬁt for them while the

buyers trade with less urgency (i.e., are more relaxed)

and are able to hold out for more proﬁtable prices;

and in the second period of ﬁve days the fortunes of

the buyers and sellers reverse as the opinions do.

This causal effect of opinions on prices in our

opinionated-agent-based model of a ﬁnancial market

functionally replicates what was ﬁrst demonstrated by

(Lomas and Cliff, 2021). In the next section, we

demonstrate functionality in our system beyond what

was demonstrated by Lomas & Cliff: that is, causality

in the opposite direction, where changes in the distri-

For clarity, data from single experiments are presented

here; for data from additional experiments which demon-

strates that the results presented here are typical (rather than

cherry-picked special cases), see (Bokhari and Cliff, 2023).

Figure 1: Plot of transaction prices from 10 IID experiments

each involving all-OPRDE market over a 25-day period in

which opinions initially start out as extremely negative for

the ﬁrst half of the period, and are then positive for the re-

maining of the period. See text for further discussion.

Figure 2: Proﬁtability-per-second (PPS) plot for one of the

25-day experiments from Figure 1: the traces show aggre-

gate PPS for all buyers; aggregate PPS for all sellers; and

the sum of the two aggregates, i.e. total PPS extracted by the

whole population of traders. See text for further discussion.

bution of prices in the market go on to affect the dis-

tribution of opinions among the population of traders.

4.2 Prices Affecting Opinions

Among traders in ﬁnancial markets, the phrase market

impact is commonly used to refer to situations where

the price of an asset quoted by potential counter-

parties to a large trade (where “large” means a trad-

ing volume sufﬁciently large to shift the supply or de-

mand curve for that asset) moves in such a way that

the trader trying to execute the large trade gets a worse

price than was quoted on the exchange at the time

that trader issued the order; and crucially this shift in

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

362

price occurs before any transaction has actually taken

place. For example if a real-world stock-trader issues

a bid-quote to buy a single share of IBM, the price that

trader is quoted by potential sellers of IBM will be

very close to whatever the current best ask price is on

the exchange’s LOB for IBM; but if the trader instead

issues a bid-quote for one million IBM shares, this

sudden revelation of excess demand for IBM stock

means that potential sellers of IBM are all likely to

alter the prices they quote, shifting upward, to reﬂect

the rise in IBM’s share-price that the sellers anticipate

occurring as an immediate consequence of the newly

increased demand for that stock. Similarly, the arrival

of a large ask order will prompt potential buyers to

instantly revise their bid-prices down – and, in both

cases, the price change happens before any transac-

tion takes place.

In Section 3, we introduced ∆

(t) as a way of

measuring supply/demand imbalance at the top of the

LOB and so we add ∆

(t) to the opinion dynamics

model as the environment factor e

in Equation 3. In

consequence, OPRDE traders alter their behavior in

response to anticipated changes in price – that is, they

will be sensitive to market impact, because their opin-

ions will be affected by the distribution of prices (and

quantities) on the LOB. For example, when prices are

likely to rise, OPRDE buyers should feel an increased

sense of urgency and OPRDE sellers should feel a de-

creasing sense of urgency. In contrast, when prices

are likely to fall, OPRDE sellers should increase their

urgency, whereas OPRDE buyers should reduce their

urgency.

To test this, here we show results from one long-

term experiment in which the market is suddenly

ﬂooded with a large number of sell orders all priced

at $60 during the period from day 30 to day 60, af-

ter which the excess sell orders are abruptly removed:

this step-change in excess supply in the market causes

an imbalance at the top of the LOB, resulting in a

negative value of ∆

(t), which indicates an expected

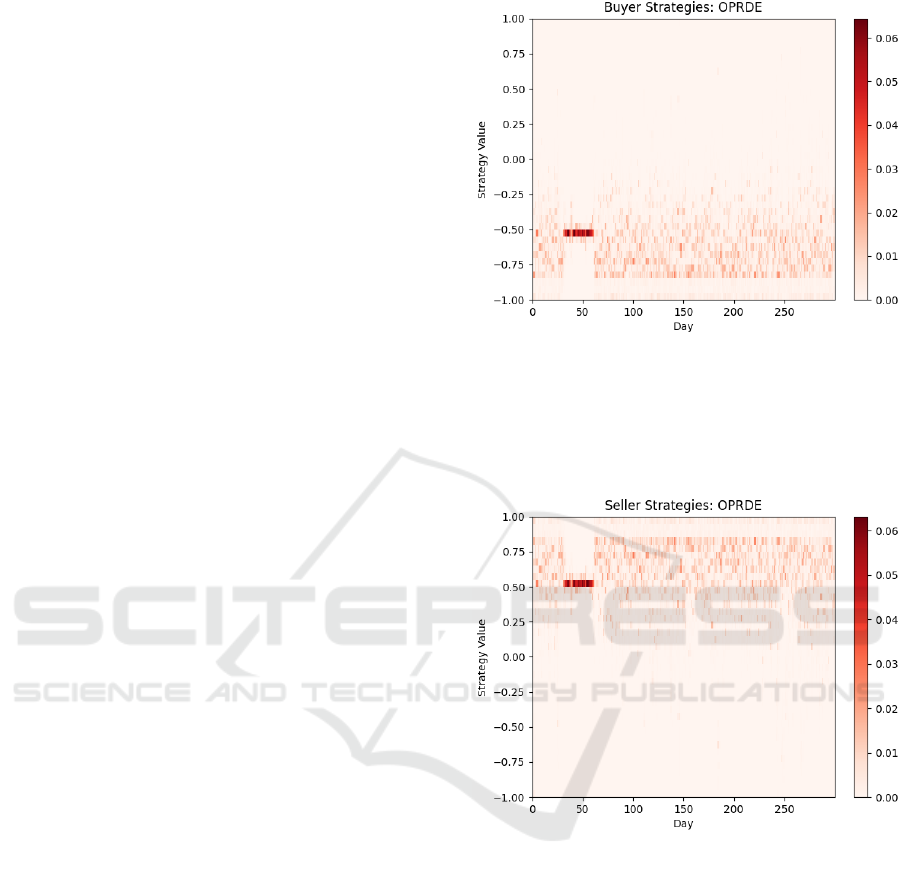
near-term decline in the asset price. Figure 3 shows

buyers’ strategies at this point clustering around −0.5,

which means buyers are being relaxed and acting as a

hybrid of ZIC and SHVR; on the other hand, Figure

4 shows sellers’ strategies over the same period clus-

tering around +0.5 i.e. acting urgently as a hybrid of

ZIC and GVWY. As can be seen from Figure 5, the

change in strategies is reﬂected in the quoted prices,

leading to a substantial decline in transaction prices

during the period of excess supply. The same effect

is shown in the PPS time series shown in Figure 6:

sellers have suffered signiﬁcant losses, while buyers

have made huge proﬁts during the period of excess

supply. This demonstrates that market dynamics have

Figure 3: Heat-map of individual strategy-values for the

population of 30 OPRDE buyers in a 300-day experiment

where severe excess supply is suddenly introduced to the

market on Day 30 and suddenly removed on Day 60. Hori-

zontal axis is day-number; vertical axis is strategy; shading

intensity shows proportion of traders in the population with

that strategy (darker shading signiﬁes more traders).

Figure 4: Heat-map of individual strategy-values for the

population of 30 OPRDE sellers in the experiment for the

same experiment as Figure 3.

an impact on opinion dynamics. Thus, we are able to

afﬁrmatively answer our second evaluation question.

A simpliﬁed version of OPRDE is presented here.

However, Equation 2 has the weakness of being sen-

sitive only to imbalances at the top of the LOB (the

measure is not sensitive to imbalances at deeper lev-

els of the LOB, thus being quite fragile). Multi-level

order ﬂow imbalance (MLOFI) is an alternative met-

ric that can be used to measure imbalance as proposed

by (Cont et al., 2021), which takes into account mul-

tiple levels of the LOB when determining LOB sup-

ply/demand imbalance.

Studying Narrative Economics by Adding Continuous-Time Opinion Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive

Financial Markets

363

Figure 5: Transaction prices plot for the same experiment

as Figure 3.

Figure 6: A proﬁtability plot of one 300-day experiment

populated exclusively with OPRDE traders (from the same

experiment as Figure 5).

4.3 OPRDE Compared to PRDE

To illustrate the co-evolutionary dynamics under the

BFL OD model at the level of individual traders’

strategies, Figure 9 and 10 and Figure 12 and 13 show

heatmaps illustrating the elite s-values of the 30 buy-

ers and sellers in 25-day experiment of a market pop-

ulated by PRDE and OPRDE, respectively, for which

the corresponding PPS is shown in Figure 8 and 11.

Both experiments assigned initial strategy values at

(t=0) randomly from a uniform distribution over the

range [−1.0,+1.0]. Upon visual inspection, it is clear

that OPRDE traders are moving in a more diverse

strategy space than PRDE traders.

Figure 11 illustrates a PPS plot for a typical ex-

periment on a market populated by OPRDE traders.

Although, the total proﬁt extracted (i.e. π

(t))) by

OPRDE traders is less than of PRDE traders Figure

8, it is clear that OPRDE sellers and buyers are both

Figure 7: Heatmap demonstrating the impact of introduced

excess supply on the distribution of opinions among traders

(from the same experiment as Figure 5): vertical axis is

opinion-value; darker shading signiﬁces more traders hav-

ing that opinion.

Figure 8: Plot of proﬁtability data from one 25-day experi-

ment in a market populated entirely by PRDE traders.

making proﬁts interchangeably and no side is con-

stantly getting ripped off as is the case with PRDE

traders, as PRDE buyers are constantly losing, which

may indicate that OPRDE traders are adapting faster

than PRDE traders since they are opinionated.

5 DISCUSSION & CONCLUSIONS

The purpose of this work is to provide a platform for

the experimental exploration of agent-based models

of narrative economics: this paper is the ﬁrst to report

on our model; and, having introduced the rationale

for the model and the details of its mechanisms, we

now expect to follow this with other papers that ex-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

364

Figure 9: Heatmap of PRDE buyers strategy distribution

from the same experiment as Figure 8.

Figure 10: Heatmap of PRDE sellers strategy distribution

from the same experiment as Figure 8.

Figure 11: Plot of proﬁtability data from one 25-day exper-

iment in a market populated entirely by OPRDE traders.

Figure 12: Heatmap of OPRDE buyers strategy distribution

from the same experiment as Figure 11.

Figure 13: Heatmap of OPRDE sellers strategy distribution

from the same experiment as Figure 11.

plore various aspects of the space of market systems

in which narrative and opinions can move prices, and

where prices can can alter opinions. Shiller argues,

in his seminal proposal for work on narrative eco-

nomics, that empirical research should be conducted

by gathering data on the stories that individuals tell

each other regarding economic matters, which inﬂu-

ence their perceptions of future economic events and

are themselves signiﬁcant factors in economic dy-

namics. The work we have described here offers an

alternative experimental approach that complements

that proposed by Shiller: experimentalists now have

access to agent-based simulations using our platform,

allowing them to gain a deeper understanding of how

opinions, expressions of those opinions, and subse-

quent economic outcomes interact dynamically. To

aid other researchers in replicating and extending our

results, we will make the source-code for our sys-

Studying Narrative Economics by Adding Continuous-Time Opinion Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive

Financial Markets

365

tem freely available as an open-source repository on

GitHub:

we look forward to seeing what uses other

people put our system to.

REFERENCES

Abergel, F., Anane, M., Chakraboti, A., Jedidi, A., and

Toke, I. (2016). Limit Order Books. Cambridge Uni-

versity Press.

Axtell, R. L. and Farmer, J. D. (2022). Agent-based mod-

eling in economics and ﬁnance: past, present, and fu-

ture. Journal of Economic Literature.

Bilal, Pant, M., Zaheer, H., Garcia-Hernandez, L., and

Abraham, A. (2020). Differential evolution: A review

of more than two decades of research. Engineering

Applications of Artiﬁcial Intelligence, 90:103479.

Bizyaeva, A., Franci, A., and Leonard, N. E. (2022).

Nonlinear opinion dynamics with tunable sensitivity.

IEEE Transactions on Automatic Control.

Bokhari, A. and Cliff, D. (2023). Studying narrative eco-

nomics by adding continuous-time opinion dynamics

to an agent-based model of co-evolutionary adaptive

ﬁnancial markets. SSRN, 4316574.

Cartea,

A., Jaimungal, S., and Penalva, J. (2015). Algorith-

mic and high-frequency trading. Cambridge Univer-

sity Press.

Chen, S. H. (2018). Agent-Based Computational Eco-

nomics. Routledge.

Church, G. and Cliff, D. (2019). A simulator for study-

ing automated block trading on a coupled dark/lit ﬁ-

nancial exchange with reputation tracking. In Proc.

EMSS2019, pages 284–293. CAL-TEK Srl.

Cliff, D. (1997). Minimal-intelligence agents for bargaining

behaviours in market-based environments. Technical

Report HPL-97-91, HP Labs Technical Report.

Cliff, D. (2012). Bristol Stock Exchange:

open-source ﬁnancial exchange simulator.

https://github.com/davecliff/BristolStockExchange.

Cliff, D. (2018). BSE: A minimal simulation of a limit-

order-book stock exchange. ArXiv:1809.06027.

Cliff, D. (2021). Parameterised-response zero-intelligence

traders. arXiv preprint arXiv:2103.11341.

Cliff, D. (2022). Metapopulation differential co-evolution

of trading strategies in a model ﬁnancial market. Proc.

IEEE SSCI Symposium on Differential Evolution.

Cont, R., Cucuringu, M., and Zhang, C. (2021). Price

impact of order ﬂow imbalance: Multi-level, cross-

sectional and forecasting. ArXiv:2112.13213.

Das, R., Hanson, J. E., Kephart, J. O., and Tesauro, G.

(2001). Agent-human interactions in the CDA. In

Proc. IJCAI2001, pages 1169–1178.

De Luca, M. and Cliff, D. (2011a). Agent-human interac-

tions in the CDA, redux. Proceedings ICAART-2011.

De Luca, M. and Cliff, D. (2011b). Human-agent auction

interactions: Adaptive-aggressive agents dominate. In

Proceedings IJCAI 2011.

https://github.com/NarrativeEconomics/OD

De Luca, M., Szostek, C., Cartlidge, J., and Cliff, D. (2011).

Studies of interaction between human traders and al-

gorithmic trading systems. Technical report, UK Gov-

ernment Ofﬁce for Science, London.

Deffuant, G., Neau, D., and Amblard, F. (2002). How

can extremism prevail? A study based on the rela-

tive agreement interaction model. Journal of Artiﬁcial

Societies and Social Simulation, 5(4):1.

Duffy, J. and

Unver, M. U. (2006). Asset Price Bubbles and

Crashes with Near-Zero-Intelligence Traders. Eco-

nomic Theory, 27:537–563.

Farmer, J. D., Patelli, P., and Zovko, I. (2005). The Predic-

tive Power of Zero Intelligence in Financial Markets.

PNAS, 102(6):2254–2259.

Friedman, D. and Rust, J., editors (1992). The Double Auc-

tion Market. Addison-Wesley.

Gjerstad, S. and Dickhaut, J. (1998). Price formation in

double auctions. Games & Econ. Behav., 22(1):1–29.

Gjerstad, S. et al. (2003). The impact of pace in double auc-

tion bargaining. University of Arizona, Department of

Economics Working Paper, pages 03–03.

Gode, D. K. and Sunder, S. (1993). Allocative efﬁciency

of markets with zero-intelligence traders: Market as a

partial substitute for individual rationality. Journal of

Political Economy, 101(1):119–137.

Gould, M., Porter., M., Williams, S., McDonald, M., Fenn,

D., and Howison, S. (2013). Limit order books. Quan-

titative Finance, 13(11):1709–1742.

Guzelyte, R. and Cliff, D. (2022). Narrative economics of

the racetrack: An agent-based model of opinion dy-

namics in in-play betting on a sports betting exchange.

In Rocha, A.-P., Steels, L., and van den Herik, J., edi-

tors, Proceedings ICAART2022, pages 225–236.

Hegselmann, G. and Krause, U. (2002). Opinion dynamics

and bounded conﬁdence: models, analysis and simu-

lation. J. Art. Societies & Social Simulation, 5(3):2.

Hommes, C. and LeBaron, B., editors (2018). Compu-

tational Economics: Heterogeneous Agent Modeling.

North-Holland.

Ladley, D. (2012). Zero Intelligence in Economics

and Finance. The Knowledge Engineering Review,

27(2):273–286.

Lomas, K. and Cliff, D. (2021). Exploring narrative eco-

nomics: An agent-based-modeling platform that inte-

grates automated traders with opinion dynamics. In

Proceedings ICAART2021.

Meadows, M. and Cliff, D. (2012). Reexamining the Rela-

tive Agreement Model of Opinion Dynamics. Journal

of Artiﬁcial Societies and Social Simulation, 15(4):4.

Meadows, M. and Cliff, D. (2013). The Relative Disagree-

ment Model of Opinion Dynamics: Where Do Ex-

tremists Come From? 7th International Workshop on

Self-Organizing Systems (IWSOS), pages 66–77.

Rust, J., Miller, J., and Palmer, R. (1992). Behavior of trad-

ing automata in a computerized double auction mar-

ket. In Friedman, D. and Rust, J., editors, The Double

Auction Market, pages 155–198. Addison-Wesley.

Shiller, R. (2017). Narrative economics. American eco-

nomic review, 107(4):967–1004.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

366

Shiller, R. (2019). Narrative Economics: How Stories Go

Viral & Drive Major Economic Events. Princeton.

Smith, V. L. (1965). Experimental auction markets and the

walrasian hypothesis. Journal of Political Economy,

73(4):387–393.

Storn, R. and Price, K. (1997). Differential evolution: A

simple and efﬁcient heuristic for global optimization

over continuous spaces. Journal of Global Optimiza-

tion, 11:341–359.

Tesauro, G. and Bredin, J. (2002). Sequential strategic bid-

ding in auctions using dynamic programming. In Pro-

ceedings AAMAS2002.

Tesauro, G. and Das, R. (2001). High-performance bidding

agents for the continuous double auction. In Proc. 3rd

ACM Conference on E-Commerce, pages 206–209.

Vytelingum, P., Cliff, D., and Jennings, N. R. (2008).

Strategic bidding in continuous double auctions. Arti-

ﬁcial Intelligence, 172(14):1700–1729.

Studying Narrative Economics by Adding Continuous-Time Opinion Dynamics to an Agent-Based Model of Co-Evolutionary Adaptive

Financial Markets

367