Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement
Learning
Yongshuai Liu and Xin Liu
Department of Compute Science, University of California, Davis, CA, U.S.A.
Keywords:
Uncertainty, Bayesian Modeling, Exploration, Deep Reinforcement Learning.
Abstract:
Uncertainty-based exploration in deep reinforcement learning (RL) and deep multi-agent reinforcement learn-
ing (MARL) plays a key role in improving sample efficiency and boosting total reward. Uncertainty-based
exploration methods often measure the uncertainty (variance) of the value function; However, existing ex-
ploration strategies either underestimate the uncertainty by only considering the local uncertainty of the next
immediate reward or estimate the uncertainty by propagating the uncertainty for all the remaining steps in an
episode. Neither approach can explicitly control the bias-variance trade-off of the value function. In this pa-
per, we propose Farsighter, an explicit multi-step uncertainty exploration framework. Specifically, Farsighter
considers the uncertainty of exact k future steps and it can adaptively adjust k. In practice, we learn Bayesian
posterior over Q-function in discrete cases and over action in continuous cases to approximate uncertainty in
each step and recursively deploy Thompson sampling on the learned posterior distribution with TD(k) update.
Our method can work on general tasks with high/low-dimensional states, discrete/continuous actions, and
sparse/dense rewards. Empirical evaluations show that Farsighter outperforms SOTA explorations on a wide
range of Atari games, robotic manipulation tasks, and general RL tasks.
1 INTRODUCTION
Deep reinforcement learning (DRL) and deep multi-
agent reinforcement learning (MARL) have shown
great performance in tasks such as robots (Yang and
Gu, 2004) and Atari games (Mnih et al., 2015), etc.
They are also promising methods for problems such
as biometrics (Lu and Liu, 2015; Lu et al., 2017; Qu
et al., 2015) and security (Liu et al., 2018). However,
sample inefficiency remains to be a significant barrier
to applying DRL and MARL in real-world applica-
tions (Liu and Liu, 2023b; Liu and Liu, 2021; Liu
et al., 2020a). One bottleneck is the exploration prob-
lem, which can be even more challenging in complex
environments with sparse rewards, noisy distractions,
long horizons, and nonstationary co-learners.
Recently, the uncertainty-based exploration strate-
gies (Yang et al., 2021; Liu and Liu, 2023a) are pro-
posed in DRL to tackle the above problems. Such
strategies estimate the uncertainty (variance) of Q
values via Bayesian posterior and incentivizes ac-
tions based on its uncertainty. Those approaches can
be directly extended to the multi-agent problem as
well (Zhu et al., 2020). However, the majority of ex-
isting approaches (Osband et al., 2016; Janz et al.,
2019) easily underestimate the uncertainty by only
considering the local uncertainty of next step’s im-
mediate reward, e.g., BDQN (Azizzadenesheli et al.,
2018), and thus remain inadequate. First, none of
them works very well on the tasks with sparse re-
wards, e.g., Skiing. Futhermore, these methods in-
troduce a new uncertainty vanishing issue (Ecoffet
et al., 2019): as an agent explores the environment
and becomes familiar with a local area after a num-
ber of steps, the uncertainty of the area diminishes,
thus the agent loses its exploration ability and may
get stuck in a local area. Because of those problems,
the agent usually cannot explore the environment
enough which causes the Q-value estimation to be bi-
ased. To address the problems, UBE (O’Donoghue
et al., 2018), OB2I (Bai et al., 2021), WQL (Metelli
et al., 2019) argue that, to achieve effective explo-
ration, it is necessary that the uncertainty about each
Q value, quantified by its variance, is equal to the un-
certainty about the next step’s immediate reward and
the next state’s Q value. Thus, the new family of algo-
rithms propagate the uncertainty in a long-term man-
ner: they accumulate uncertainties for all the remain-
ing steps in an episode. However, because the envi-
ronments usually contain thousands of steps, this ap-
380
Liu, Y. and Liu, X.
Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement Learning.
DOI: 10.5220/0011800600003393
In Proceedings of the 15th International Conference on Agents and Artificial Intelligence (ICAART 2023) - Volume 2, pages 380-391
ISBN: 978-989-758-623-1; ISSN: 2184-433X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

proach tends to have too large uncertainty (variance),
e.g., the OB2I estimation in Atari games. Both the
local uncertainty and uncertainty propagation meth-
ods lack the ability to explicitly adjust the number of
future uncertainty steps to be considered and thus it
is difficult to use them to explicitly control the bias-
variance(uncertainty) trade-off of the Q function.
To address this challenge, we propose Farsighter,
an explicit multi-step uncertainty exploration frame-
work in DRL, to balance the bias-variance of Q es-
timation. Farsighter considers the uncertainty for k
future steps, whose value can be explicitly adjusted to
balance the bias-variance trade-off of Q estimation.
Compared to the “one-step” local uncertainty meth-
ods, it is beneficial in cases with long-term sparse re-
wards. The agent learns the impact of the current ac-
tion on future k-step rewards even if no immediate re-
ward is given. Moreover, considering k-step future
uncertainties helps escape the local familiar areas,
thus alleviating the uncertainty vanishing issue. Com-
pared to the uncertainty propagation methods, Far-
sighter is capable to rightly estimate the uncertainty
with an suitable step value k, which is adjustable.
Specifically, Farsighter learns Bayesian poste-
rior over Q-function/action to approximate uncer-
tainty in both discrete and continuous action tasks.
For discrete action tasks, we deploy the value-based
DDQN (Van Hasselt et al., 2016) and use Bayesian
linear regression for the last layer of the Q-network to
approximate the Bayesian posterior over Q-function.
For continuous action tasks, we build on NAF (Gu
et al., 2016), and use the Bayesian Neural network
to approximate the Bayesian posterior over actions of
the Q-function. This allows us to directly incorporate
the uncertainty over the Q-function in each step. To
estimate the “k-step” uncertainty in practice without
exponential computational complexity, we formulate
the problem as a recursive Gaussian process and per-
form TD(k) update instead of TD(0), in which we re-
cursively deploy Thompson sampling on the learned
posterior distributions for k steps.
In summary, we make the following contributions:
• We propose Farsighter that allows explicit k-step
uncertainty exploration to balance the bias and
variance trade-off of Q values. Moreover, we also
develop an adaptive Farsighter to further improve
the exploration performance.
• We develop Farsighter implementations in both
discrete and continuous action tasks. It can also
apply on a wide range of RL tasks with high/low-
dimensional states and sparse/dense rewards.
• Empirical results show that Farsighter outper-
forms SOTA in high-dimensional Atari games and
continuous control robotic tasks.
2 RELATED WORK
Uncertainty-based methods usually model the uncer-
tainty of the Q function via the Bayesian posterior.
The agent is encouraged to explore the unknown en-
vironment with high uncertainty.
The majority of existing exploration approaches
consider the local uncertainty of next immediate
reward. RLSVI (Osband et al., 2016) performs
Bayesian regression in linear MDPs so that it can
sample the value function through Thompson Sam-
pling. BDQN (Azizzadenesheli et al., 2018) performs
Bayesian Linear Regression (BLR) in the last layer of
the Q-network. It approximately considers the last-
layer Q-network as a linear MDP problem. Successor
Uncertainty (Janz et al., 2019) approximates the pos-
terior through successor features which are linear to
the Q value of the corresponding state-action pairs.
The above methods only consider the local un-
certainty in next one-step. Nevertheless, some
other methods propagate the uncertainty with all
the remaining steps in an episode. For example,
UBE (O’Donoghue et al., 2018) proposes to learn
the uncertainty with Uncertainty Bellman Equation.
WQL (Metelli et al., 2019) approximates the para-
metric posterior distribution based on Wasserstein
barycenters. OB2I (Bai et al., 2021) performs back-
ward induction of bootstrapped-based uncertainty
to capture the long-term uncertainty in an whole
episode. Although those methods also propagate the
uncertainty in a multi-step manner, which can allevi-
ate the uncertainty vanishing issue as well, they usu-
ally have too large uncertainty in long-horizon cases
(e.g., Atari Games). Thus we propose Farsighter in
the next sections, which can explicitly balance the
bias-variance of the Q-estimation.
3 PRELIMINARIES
3.1 Markov Decision Process (MDP)
A MDP is represented by the tuple (S, A,R, P, γ) (Liu
et al., 2021a; Liu et al., 2021b; Liu et al., 2021c),
where S is the set of states; A is the set of actions; R
is the reward function; P is the transition probability
function and γ is the reward discount factor. The ob-
jective of an MDP is to learn a policy π to maximize
the discounted cumulative reward. Given a state s and
action a, the Q function is
Q(s, a) = E
τ∼π
[
∞
∑
t=0
γ
t
R(s
t
, a
t
, s
t+1
)|s
0
= s, a
0
= a].
Following the Bellman equation in MDPs, we
Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement Learning
381

have the Q-function
Q(s
t
, a
t
) = R
a
t
s
t
+
γ
∑
s
t+1
∈S
P
a
t
s
t
s
t+1
∑
a
t+1
∈A
π(a
t+1
|s
t+1
)Q(s
t+1
, a
t+1
).
(1)
3.2 Double Deep Q Networks (DDQN)
For discrete action tasks, we build our algorithm on
the value-based DDQN (Van Hasselt et al., 2016) ,
which is an extension of DQN (Mnih et al., 2015).
DDQN uses two identical neural network models.
One learns during the experience replay, just like
DQN, and the other one, called target network Q
target
,
is a copy of the last episode of the first model. The
core of DDQN is to learn the Q-function through
minimizing a surrogate to Bellman residual (An-
tos et al., 2008) using temporal difference (TD) up-
date (Tesauro et al., 1995).
Given a consecutive experience tuple (s, a, r, s
′
),
the target value is
y = r + γQ(s
′
, arg max
a
′
Q(s
′
, a
′
, θ), θ
target
). (2)
DDQN learns the Q function by approaching the
empirical estimates of the following regression loss:
L(Q, Q
target
) = E[(Q(s, a) −y)
2
]. (3)
Moreover, the parameters of the target network
Q
target
are updated frequently by copying the param-
eters of the learning network Q.
3.3 Normalized Advantage Function
(NAF)
Value-Based methods, like DDQN, suit problems
with discrete action spaces. NAF is designed for con-
tinuous action-space tasks. The idea behind NAF is to
let the maximization of the Q function be determined
during the Q-learning update. Specifically, instead of
having one output stream from the Q-network, NAF
has three streams. One stream estimates the value
function V(s|θ
V
) (parameterized by θ
V
), and another
estimates the Advantage A(s, a|θ
A
) (parameterized by
θ
A
), which is further parameterized as a quadratic
function based on action µ(s|θ
a
) (parameterized by
θ
a
) and matrix P. Combined together, we estimate
Q-Values as:
Q(s, a) = A(s, a|θ
A
) +V (s|θ
V
),
A(s, a|θ
A
) = −
1
2
(a −µ(s|θ
a
))
T
P(s|θ
P
)(a −µ(s|θ
a
)).
(4)
P(s|θ
P
) is a state-dependent, positive-definite
square matrix, which is parametrized by P(s|θ
P
) =
L(s|θ
P
)L(s|θ
P
)
T
. L is a lower-triangular matrix,
where the diagonal terms are exponentiated. Since
the Q-function is quadratic in action a, the action
that maximizes the Q-function is always given by
µ(s|θ
a
). NAF updates the parameter based on the rule
of DDQN (Eq. 3). The different between those two
methods is how to select action in each step.
4 FARSIGHTER: MULTI-STEP
EXPLORATION
In this section, we introduce Farsighter that performs
exploration by considering the uncertainty of the next
“k-step”. In Sec. 4.1, we formulate the multi-step un-
certainty estimation problem. In Sec. 4.2 and 4.3, we
present how to estimate uncertainty with discrete ac-
tions and continuous actions in each step. In Sec. 4.4,
we introduce how to perform multi-step exploration.
Last, in Sec. 4.5, we show how to adaptive choose the
number of k.
4.1 Problem Formulation
Assume the ground truth of a Q-value is Q
g
. we define
the Bayesian posterior of a Q-estimation as N (Q
e
, ε),
where Q
e
is the mean value and ε is the variance of
the Q-estimation. We call the distance of |Q
g
−Q
e
| as
the bias of the Q-estimation and ε is the uncertainty.
The uncertainty of Q-estimation ε follows
the uncertainty Bellman equation (Theorem 1 of
UBE (O’Donoghue et al., 2018)):
ε(s
t
, a
t
) = δ
a
t
s
t
+
γ
∑
s
t+1
∈S
P
a
t
s
t
s
t+1
∑
a
t+1
∈A
π(a
t+1
|s
t+1
)ε(s
t+1
, a
t+1
),
(5)
for all (s, a) and t = 1, ..., T , where ε
T +1
= 0 and
where we call δ
a
t
s
t
the local uncertainty at (s
t
, a
t
).
In “one-step” uncertainty estimation methods
(e.g., BDQN), the uncertainty of the Q estimation
only contains the local uncertainty, thus ε(s
t
, a
t
) =
δ
a
t
s
t
. Empirically, the local “one-step” uncertainty
is usually small and it is easy to be vanished,
which leads the agent cannot explore the environ-
ment enough. Not exploring enough results the Q-
estimation usually has high bias. On the other hand, in
uncertainty propagation methods (e.g., OB2I), which
propagate all the remaining uncertainty in an episode
(Eq. 5 can be unfolded to T steps), the variance ε is
usually very large. Hence, the Q estimation exhibits
high uncertainty and the agent can explore more in
the environment. In such cases, the Q-estimation is
usually less biased, however, large variance is at the
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
382

risk of too much unnecessary exploration and thus
slow down the learning convergence. Thus we need
a method that explicitly adjust the uncertainty explo-
ration steps k that balance the bias-variance trade-off.
The uncertainty we use in Farsighter is:
ε(s
t
, a
t
) = δ
a
t
s
t
+ ...+
γ
k
∑
s
t+k
∈S
P
a
k
s
t
s
t+k
∑
a
t+k
∈A
π(a
t+k
|s
t+k
)δ(s
t+k
, a
t+k
).
(6)
In Sec. 5.1, we empirically demonstrate the benefits
of Farsighter.
4.2 Estimating Bayesian Uncertainty
with Discrete Actions
For discrete action cases, we build our algorithm
on the DDQN and estimate the uncertainty of the
Q-function. DDQN architecture consists of a deep
neural network where the last layer is usually a lin-
ear MLP function of the state representation and ac-
tion. Thus, given any state s and action a, Q(s, a) =
φ
θ
(s)
T
ω
a
, where φ
θ
(s) ∈ R
d
parameterized by θ rep-
resents state s and ω
a
∈R
d
is the parameter of the last
linear MLP layer on action a.
To estimate the uncertainty, we build Farsighter
over DDQN with Bayesian framework. In the last
layer of Q-network Q(s, a), instead of using the lin-
ear MLP regression, Farsighter deploys the Gaussian
Bayesian linear regression (BLR) (Rasmussen, 2003),
which results in an approximated Bayesian posterior
on the ω
a
and consequently on the Q-function. The
Bayesian posterior ω
a
is modeled as Gaussian with
{
¯
ω
a
,Cov
a
}, where
¯
ω
a
is the posterior mean and Cov
a
is the posterior covariance. Moreover, we leverage the
re-parameterization trick to write
Q(s, a) = φ
θ
(s)
T
ω
a
= φ
θ
(s)
T
(
¯
ω
a
+
p
Cov
a
z), (7)
where z is a random variable z ∼ N (0, I). Through
BLR, the agent efficiently captures the uncertainty
over the Q estimates. In practice, the algorithm takes
as input φ
θ
(s) which has two output ‘heads’, one
which is attempting to learn the optimal Q-values as
normal DDQN, the other is attempting to learn the un-
certainty values of the Q estimation. In other words,
Q(s, a) = Q
θ
(s, a) + φ
θ
(s)
T
p
Cov
a
z, (8)
In the parameter updating process, the BLR-based Q-
function updates parameters θ and ω
a
separately. The
process is shown in the Algorithm 1.
Update θ: We fix the head ω
a
and update θ us-
ing the normal head following the standard DDQN
(Eq. 3).
Update
¯
ω
a
,Cov
a
: we update
¯
ω
a
and Cov
a
with
fixed φ
θ
(s). Given a dataset D = {s
i
, a
i
, y
i
}
D
i=1
, where
y
i
are target values, we construct |A| disjoint datasets
for each action, D = ∪
a∈A
D
a
, where D
a
is a set of tu-
ples (s
i
, a
i
, y
i
) with the action a
i
= a. Let us construct
a matrix Φ
a
∈ ℜ
d×D
a
, a concatenation of feature col-
umn vectors {φ(s
i
)}
D
a
i=1
, and y
a
∈ ℜ
D
a
, a concatena-
tion of target values in set D
a
. We then approximate
the posterior distribution of ω
a
as follows
¯
ω
a
=
1
σ
2
ε
Cov
a
Φ
a
y
a
, Cov
a
=

1
σ
2
ε
Φ
a
Φ
⊤
a
+
1
σ
2
I

−1
,
(9)
where I ∈ℜ
d
is an identity matrix. This is the deriva-
tion of the BLR, with zero mean prior and as σ and σ
2
ε
as the variance of prior and likelihood respectively.
4.3 Estimating Bayesian Uncertainty
with Continuous Actions
Value-Based methods, like DDQN, suit problems
with discrete action spaces. For continuous action
cases, we build our algorithm on the NAF and es-
timate the uncertainty on actions. NAF architecture
consists three output streams µ(s|θ
a
), L(s|θ
P
), and
V (s|θ
V
), as shown in Eq. 4. Usually, the three sub-
networks are functions of a shared state representation
network φ
θ
(s). Thus, we have µ(s|θ
a
) = µ(φ(s)|θ
a
),
where θ
a
is the parameter of layers taking state repre-
sentation φ(s) as input and output action a.
The Original NAF cannot estimate the uncer-
tainty for actions. Therefore, in our work, we
first propose to estimate the exploration uncertainty
for continuous actions using a Bayesian neural net-
work (BNN) (Kononenko, 1989) for the action sub-
network, µ(φ(s)|θ
va
). BNN treats the model weights
and output action as variables. Instead of finding a set
of optimal estimates, BNN fits the Bayesian posterior
distributions for them. Every weight in θ
va
is mod-
eled as a Gaussian distribution with a mean and vari-
ance. It directly learns the uncertainties of the actions
given a state representation φ(s). To get action, we
can sample one set of weights from the distribution.
In practice, our new architecture consists four out-
put streams, µ(s|θ
va
), µ(s|θ
a
), L(s|θ
P
), and V (s|θ
V
),
where µ(s|θ
va
) leans the BNN of actions. To update
the parameters, we update parameters of θ
a
, θ
V
, θ
P
, θ
and θ
va
separately.
Update θ
a
, θ
V
, θ
P
, θ: we update θ
a
, θ
V
, θ
P
, θ with
a fixed θ
va
and update them with the normal NAF.
Update θ
va
: to learn the posterior distribu-
tion µ(θ
va
|(φ(s), a)), we fix the parameters of
(θ
a
, θ
V
, θ
P
, θ) and update the parameters of θ
va
with
the Evidence Lower Bound(ELBO) loss (Kononenko,
1989). Specifically, we approximate the posterior
distribution µ(θ
va
|(φ(s), a)) with another distribution
Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement Learning
383

ˆµ(θ
va
), which is called a variational distribution. We
further minimize the KL divergence between them
D
KL
(ˆµ(θ
va
)||µ(θ
va
|(φ(s), a))). Based on the varia-
tional inference theory (Blei et al., 2017), we get the
ELBO loss:
D
KL
(ˆµ(θ
va
)||µ(θ
va
)) −E
θ
va
∼ˆµ
[logµ(a|s, θ
va
)] (10)
Note that we use BNN for continuous action tasks
and BLR for discrete ones. BNN has better perfor-
mance but at the cost of higher computation com-
plexity. Because the dimension of state representa-
tion is typically low for continuous action tasks, e.g.,
robotic manipulation tasks, we consider it computa-
tionally acceptable. In comparison, as discussed in
the appendix, BLR does not increase the computation
complexity compared to MLP. It is suitable when the
dimension of state representation is high, and thus we
choose it for discrete action tasks.
4.4 Exploration with Multi-Step
Uncertainty
In Sec. 4.2 and 4.3, we show how to estimate the
uncertainty. Each step is a Gaussian process with a
posterior on Q-function/actions. For example, in dis-
crete cases, the GP posterior applies on the ω
a
(Eq. 8)
and consequently on the Q-function. In each step,
we can sample an instance from the posterior. Since
each step has different GP posteriors based on differ-
ent states and actions, these nested expectations are
analytically intractable; we cannot directly calculate
the “k-step” uncertainty distribution. Moreover, the
number of instances in the recursive Gaussian process
grows exponentially in the horizon k. Therefore, con-
sidering all the possible roll-outs in k steps is com-
putationally difficult. To address it, we formulate the
“k-step” process as a recursive Gaussian process and
perform TD(k) update instead of TD(0). More specif-
ically, we recursively deploy Thompson sampling on
the learned posterior distributions for k steps to ap-
proximate the k-step uncertainty (Eq. 6), which means
the Q-function becomes
Q(s
t
, a
t
) =E
τ∼π
[R(s
t
, a
t
, s
t+1
) + γR(s
t+1
, a
t+1
, s
t+2
)
+ ... + γ
k
max
a
t+k
∈A
Q
∗
(s
t+k
, a
t+k
)|s
t
, a
t
]
For discrete action cases, we sample a random
variable z for Eq. 8 in each step and obtain a determin-
istic Q-function. Given the deterministic Q-function,
we can decide which action maximizes the Q values.
For continuous action cases, we sample a variance
ε from the BNN posterior µ(s|θ
va
) in each step and
then directly get action µ(s|θ
a
) + ε from the sampled
weights . After taking the action, we go to the next
Algorithm 1: Farsigher: Multi-step Exploration.
Initialize θ, θ
target
, k, Q-variance target
ˇ
ε, and
∀a,
¯
ω
a
,Cov
a
,
¯
ω
target
a
; Replay buffer RB = {}
1: for t=0, k, 2k, 3k... do
2: {r
k
, s
t+k
} = K-STEP(s
t
, θ,
¯
ω
a
,
√
Cov
a
, γ, r
k
=
0, itr = 0)
3: Store {s
t
, a
t
, r
k
, s
t+k
} into replay buffer RB
4: Sample a mini-batch {s
i
, a
i
, r
k
, s
i+k
} from the
latest N steps to alleviate off-policyness bias
5: Update the parameters of θ with DDQN, where
r = r
k
, s
′
= s
i+k
and keep
¯
ω
a
,Cov
a
fixed
6: Every M steps: Update the GP posterior
{
¯
ω
a
,Cov
a
} for all actions
7: if Q-variance <
ˇ
ε: k+=1; Empty RB.
else if Q-variance >
ˇ
ε: k-=1; Empty RB.
8: Every N steps: reset θ
target
= θ,
¯
ω
target
a
=
¯
ω
a
9: end for
Algorithm 2: K-STEP( s
t
, θ,
¯
ω
a
,
√
Cov
a
, γ, r
k
, itr).
Input: s
t
it the current state; θ,
¯
ω
a
and Cov
a
are
parameters of Q-function, γ is the discounted factor;
r
k
is the discounted sum of k-step rewards; itr is the
number of steps in the k loop.
Output: the discounted sum of k-step rewards r
k
and
the last state after k steps.
1: if itr=k: return r
k
, s
t+1
2: Sample z
t
∼ N(0, I) and then get a deterministic
Q(s, a) = Q
θ
(s, a) + φ
θ
(s)
T
√
Cov
a
z
t
3: Take action a
t
= argmax
a
Q(s, a)
4: Get next state s
t+1
and reward r
t
by interacting
with the environment.
5: r
k
+ = γ
itr
∗r
t
6: return K-STEP( s
t+1
, θ,
¯
ω
a
,
√
Cov
a
, γ, r
k
, itr + 1)
state from the environment. As shown in Algorithm 2,
we recursively deploy the process for k steps and get
the last state s
t+k
and the discounted sum of k-step re-
wards r
k
, where the k-step uncertainties information
is stored.
The pseudocode of the whole learning process
for discrete action cases is shown in Algorithm 1.
Instead of saving the one-step state and action tu-
ple, we get k-step state s
t+k
and reward r
k
from Al-
gorithm 2. For continuous action cases, the work-
flow is similar to discrete action cases; we provide
the pseudocode in the Appendix. For multi-step up-
dates, we keep the update rule same as one-step up-
dates as mentioned in Sec. 4.2 and 4.3. We only
change the way to calculate the target value, y =
r + γ
k
Q(s
′
, arg max
a
′
Q(s
′
, a
′
, θ), θ
target
), where r is the
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
384

🍎
🚗
(a) Illustration of the
environments.
(b) Learning curve of
different estimators.
(c) Performance of
different estimators.
(d) Heatmap for
BDQN.
(e) Heatmap for
OB2I.
(f) Heatmap for Far-
sighter.
(g) The change of
variance.
Figure 1: Validation of the effectiveness of multi-step uncertainty.
discounted sum of k-step rewards r
k
and s
′
is the last
state after k steps s
t+k
. Thus, our multi-step uncer-
tainty estimation would not increase the computation
and the memory complexity. Moreover, to alleviate
the bias introduced by off-policyness in multi-step
learning, the network is trained using the latest N-step
samples, where N is the target network update period,
as suggested in (Mnih et al., 2016). In addition, since
the k-step reward and state are obtained from recur-
sive Thompson sampling and they contain the uncer-
tainty information of the future k steps, the learned
Q function also contains the uncertainty information,
which is represented on the variance of the posterior.
The variance helps us quantify the uncertain impact
of the next k-step in turn.
4.5 Adaptive K
Empirically, to learn a good policy as soon as pos-
sible, it is desirable to have more exploration at the
beginning stage and then gradually decrease explo-
ration to increase exploitation. As shown above, the
amount of uncertainty is represented by the variance
of the Bayesian posterior (Eq. 6). In principle, we can
set a large initial k to enlarge the exploration at the
beginning stage and then set posterior variance tar-
get to mantain a certain level of exploration. Based
on this intuition, we have developed an adaptive Far-
sighter. In the adaptive Farsighter, we initial k to be
a large number and set a target to the variance. If the
variance is smaller than the target, we increase k, oth-
erwise, we decrease it. In this manner, the agent can
keep exploring the environment. The pseudocode for
discrete action cases is shown in the Algorithm 1. We
show the affects of different k in Sec. 5.3.
5 EXPERIMENTS
In this section, we investigate the following properties
of Farsighter: 1) We illustrate the insight of multi-step
uncertainty exploration using a toy example, 2) We
compare the performance of Farsighter with SOTA,
on a large range of RL tasks, including Atari games
and continuous control tasks, and 3) We investigate
the effect of a different number of future steps.
5.1 K-Step Uncertainty Insight
To illustrate the idea of multi-step uncertainty, we de-
sign a toy maze task as shown in Fig. 1a. The agent
(car) starts from the bottom left corner. In each step,
the car can go either up, down, left, or right. The car
wants to get the apple (top right corner) and it can-
not pass the black wall area. The bridge is the only
way that connects the left and right sides. The reward
is 100 if the car reaches the apple, and -1 otherwise
each step.
We further compare the local uncertainty explo-
ration (e.g., BDQN), uncertainty propagation (e.g.,
OB2I) and k-step uncertainty exploration(Farsighter)
under same interaction steps, 40k, where all algo-
rithms have converged, as shown in Fig 1b. The op-
timal Q-value Q
g
for the car from the bottom left
corner is 75. From Fig. 1c, we can see that the Q-
estimation of BDQN is highly biased, as we discussed
in Sec. 4.1: the mean is around 62 which is far from
the optimal 75 and the variance is low. On the other
hand, the OB2I Q-estimation is less biased, but the
variance of OB2I Q-estimation is very large. In com-
parison, the bias of Farsighter is the smallest and the
variance is lower than OB2I.
In addition, we show the heatmap of the number of
state visited times during learning process for BDQN
(Fig. 1d), OB2I(Fig. 1e), and Farsighter (Fig. 1f) . For
BDQN, fewer visits occur on the right side of the map
and most of the interactions remain on the left side be-
cause the car does not cross the bridge often enough
and repeatedly explore the left familiar side (uncer-
tainty vanishing). On the other hand, it is easier for
the car to cross the bridge with OB2I and Farsighter.
More visits occur on the right, which enhances the
car reaching to the apple more frequently. However,
OB2I performs too much exploration, which can be
observed from the action selection process where ac-
tion varies in the same state, e.g., all the episode traces
are different even with same Bayesian Q function.
The visited times for both sides are similar. In com-
parison, Farsighter visits more on the right and fre-
quently reaches the apple, since in the later learning
Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement Learning
385

(a) Montezuma’s Revenge. (b) Gravitar. (c) Beam Rider.
Figure 2: The game score for Atari Games.
phase the policy has converged and the agent leans
to access the right side. Intuitively, multi-step un-
certainty explorations (Farsighter and OB2I) consider
more exploration for further locations. When the car
is at the bridge, it is easier to find the new locations on
the right, which encourages the car to explore more
on the right side. In comparison, the one-step agent
(BDQN) takes the left as the local optima area and
sticks to it more often. Thus the Q-estimation is bi-
ased since the agent cannot explore the environment
enough. However, the OB2I performs too much ex-
ploration, since the variance is high, which leads to
slow converge speed. Farsighter balances the bias-
variance trade-off by explicitly choosing an appropri-
ate k.
Moreover, we also study the changes of posterior
variance among these exploration methods in Fig. 1g.
In the beginning, variances are low because the net-
works are randomly initialized. When the learning
starts, the variances increase rapidly to award explo-
ration. After that, the posterior variance in BDQN
gradually decreases because as the agent gathers more
samples, the uncertainty is vanishing. In compari-
son, in the Farsighter, even the posterior variance de-
creases as well earlier, it becomes larger later on (be-
cause the agent accesses more states on the right side)
and then decreases finally when the learning is con-
verged. The results show that Farsighter alleviates
the uncertainty vanishing problem because Farsighter
learns high uncertainties on the right side by consid-
ering future steps. The OB2I can also help to alleviate
the uncertainty vanishing. But it is hard to converge,
since the variance is high.
5.2 Exploration Performance
Environments: Farsighter can work on a wide range
of RL tasks with high/low-dimensional states, dis-
crete/continuous actions, and sparse/dense rewards.
We empirically study Farsighter on a variety of
Atari games in the Arcade Learning Environment
(ALE) (Bellemare et al., 2013) and robotic con-
trol tasks using MuJoCo physics engine (Liu et al.,
2020b). The states in ALE are high-dimensional im-
ages and the action space is discrete. In comparison,
the robotic control tasks are in low-dimension but the
action space is continuous. We evaluate Farsighter
on 49 Atari suite of games including hard-explored
games with sparse rewards (e.g., Montezuma’s Re-
venge, Gravitar, and Venture) and games with dense
rewards (e.g., Beam Rider, Atlantis, and Freeway);
two challenging robot control tasks (FetchPickAnd-
Place and HandManipulateBlock) with sparse re-
wards and a control task (Walker2D) with dense re-
wards.
Baselines: We compare Farsighter to four base-
lines in discrete action environments: DDQN with ε-
greedy exploration and BDQN, a parametric posterior
based exploration, which only considers one-step un-
certainty. Moreover, to study the effects of multi-step
learning, we also compare Farsighter with ‘k-DDQN’
which uses ε-greedy exploration in each step but con-
siders k steps. We also compare with OB2I, which
is the SOTA uncertainty propagation method that use
non-parametric posterior based exploration. Simi-
larly, for continuous control tasks, we select three
baselines: standard one-step NAF with random explo-
ration, multi-step NAF with random exploration, one-
step NAF with Bayesian uncertainty exploration. To
be fair, we keep the shared parts of the methods to be
the same for different exploration methods, e.g., the
state representation layers, and the hyper-parameters.
Performance: Farsighter outperforms DDQN,
BDQN and OB2I in 36 out of 49 Atari games. We
show parts of the evaluation results in Fig. 2 and
Fig. 5. More detailed results (e.g., game scores for
49 Atari games) are available in the appendix. We run
each experiment 10 times with different random seeds
and show the average performance. The shaded area
is the standard deviation in the Figures.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
386

(a) Fetch Pick And Place. (b) Hand Manipulate Block.
Figure 3: The effects of differ-
ent uncertainty steps in Mon-
tezuma’s Revenge.
Figure 4: The effects of dif-
ferent initial k and uncertainty
target.
Figure 5: The mean success rate for continue robotic tasks.
Figure 2 compares the game scores with the
four baselines in Atari Games. Farsighter achieves
higher scores substantially. In the notoriously hard
exploration game Montezuma’s Revenge, Farsighter
achieve positive results, while others achieve zero
score. The reason is that we initial k=150, which
accumulates the uncertainty over k timesteps before
performing an update. A higher initial k leads to the
agent to explore more in the game and encounter in-
formative state faster. other methods (e.g., BDQN,
DDQN) cannot explore enough in the game and most
of the reward feedback is zero, thus it is hard to get
positive score. On the contrary, OB2I performs prodi-
gious exploration because the uncertainty is very large
in Atari Games with thousands of steps, which results
in the agent almost taking random actions and hard
to get positive rewards. In Gravitar and Beam Rider,
DDQN and BDQN show comparable performance.
BDQN performs a little better since the agent can
explore with one-step uncertainty and k-DDQN can-
not improve the performance compared with DDQN,
which means k-step learning without uncertainty can-
not improve the exploration either. Interestingly, the
OB2I increases faster at early and then degenerates.
This is because OB2I performs unnecessary explo-
ration which may guide a direction that is unrelated
to the environment reward. In comparison, Farsighter
performs enough exploration and exploit it efficiently.
Figure 5 shows the performance comparison for
continuous robotic tasks. The results show that the
multi-step uncertainty exploration also outperforms
one-step uncertainty exploration and random explo-
ration in continuous action tasks. In the Fetch-
PickAndPlace task, Farsighter achieves almost 100%
success rate and it only takes around 100 million
steps. The success rate in HandManipulateBlock is
also the best and it takes the least samples for the
sample success rate. Overall, we can conclude that
Farsighter is an effective exploration method by con-
sidering multi-step uncertainty and it works on gen-
eral RL tasks.
5.3 The Impact of K
Figure 3 shows the impact of k in Montezuma’s Re-
venge, where the performance increases with k ini-
tially and then drops, with k = 150 achieving the best
score. This trend exists for other environments al-
though the optimal k value varies. An interesting ob-
servation is that the increased velocity of the scores
at the earlier stage is positively proportional to the
number of uncertainty steps. This illustrates the im-
portance, in particular in the early stages, of multi-
step exploration. The number of uncertainty steps is a
trade-off between exploitation and exploration. When
k is large, (e.g., k=500), the agent considers more cu-
mulative uncertainty, and large uncertainty forces the
agent to explore more about the environment, which
could be desirable in the early stages, but at the risk
of too much exploration and thus difficulties in con-
vergence. This might explain why uncertainty propa-
gation methods (e.g., OB2I, WQL) which accumulate
uncertainties for all the remaining steps in an episode
are outperformed by our method. On the contrary,
when k is small (e.g., k=10), the agent only considers
the uncertainty of the next few steps. The uncertainty
is easy to vanish and the agent tends to exploit.
Farsighter can explicitly balance the bias-variance
trade-off by adjusting the number of k. As discussed
in Sec. 4.5, we can use an adaptive k by seting a vari-
ance target. From Fig. 3, we can see the adaptive
Farsighter achieves the best result, where the score
increases quickly initially and also finishes with the
highest value. Moreover, in Fig. 4, we show the im-
pact of different initial k and variance target. When
the initial k is too small, e.g., 10, Farsighter performs
worst, since the exploration is not enough even though
the k is increasing to catch up with the variance tar-
get. On the contrary, when the initial k is large enough
(e.g., 150, 500), the initial exploration is adequate.
A suitable variance target that maintains the explo-
ration to a certain level in the learning process can in-
crease the performance, such as in the Montezuma’s
Revenge, the variance target 0.2 outperforms 0.5.
Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement Learning
387

6 CONCLUSION
In this paper, we propose Farsighter, an multi-step un-
certainty exploration framework in DRL and we can
explicitly adjust the number of future steps to bal-
ance the Q-estimation bias-variance trade-off. Far-
sighter helps to alleviate the sparse reward and un-
certainty vanishing problem. Moreover, it avoids the
uncertainty to be too large in the uncertainty propaga-
tion methods. It outperforms SOTA on a wide range
of RL tasks with high/low-dimensional states, dis-
crete/continuous actions, and sparse/dense rewards,
including high-dimensional Atari games and contin-
uous control robotic manipulation tasks.
ACKNOWLEDGEMENTS
The work was partially supported through grant
USDA/NIFA 2020-67021-32855, and by NSF
through IIS-1838207, CNS 1901218, OIA-2134901.
REFERENCES
Antos, A., Szepesv
´
ari, C., and Munos, R. (2008). Learn-
ing near-optimal policies with bellman-residual mini-
mization based fitted policy iteration and a single sam-
ple path. Machine Learning, 71(1):89–129.
Azizzadenesheli, K., Brunskill, E., and Anandkumar, A.
(2018). Efficient exploration through bayesian deep
q-networks. In 2018 Information Theory and Appli-
cations Workshop (ITA), pages 1–9. IEEE.
Bai, C., Wang, L., Han, L., Hao, J., Garg, A., Liu, P., and
Wang, Z. (2021). Principled exploration via optimistic
bootstrapping and backward induction. In Interna-
tional Conference on Machine Learning, pages 577–
587. PMLR.
Bellemare, M. G., Naddaf, Y., Veness, J., and Bowling, M.
(2013). The arcade learning environment: An evalua-
tion platform for general agents. Journal of Artificial
Intelligence Research, 47:253–279.
Blei, D. M., Kucukelbir, A., and McAuliffe, J. D.
(2017). Variational inference: A review for statisti-
cians. Journal of the American statistical Association,
112(518):859–877.
Ecoffet, A., Huizinga, J., Lehman, J., Stanley, K. O.,
and Clune, J. (2019). Go-explore: a new ap-
proach for hard-exploration problems. arXiv preprint
arXiv:1901.10995.
Gu, S., Lillicrap, T., Sutskever, I., and Levine, S. (2016).
Continuous deep q-learning with model-based accel-
eration. In International conference on machine learn-
ing, pages 2829–2838. PMLR.
Janz, D., Hron, J., Mazur, P., Hofmann, K., Hern
´
andez-
Lobato, J. M., and Tschiatschek, S. (2019). Successor
uncertainties: exploration and uncertainty in temporal
difference learning. Advances in Neural Information
Processing Systems, 32.
Kononenko, I. (1989). Bayesian neural networks. Biologi-
cal Cybernetics, 61(5):361–370.
Liu, Y., Chen, J., and Chen, H. (2018). Less is more:
Culling the training set to improve robustness of deep
neural networks. In International Conference on De-
cision and Game Theory for Security, pages 102–114.
Springer.
Liu, Y., Ding, J., and Liu, X. (2020a). A constrained rein-
forcement learning based approach for network slic-
ing. In 2020 IEEE 28th International Conference on
Network Protocols (ICNP), pages 1–6. IEEE.
Liu, Y., Ding, J., and Liu, X. (2020b). Ipo: Interior-point
policy optimization under constraints. In Proceedings
of the AAAI Conference on Artificial Intelligence, vol-
ume 34, pages 4940–4947.
Liu, Y., Ding, J., and Liu, X. (2021a). Resource alloca-
tion method for network slicing using constrained re-
inforcement learning. In 2021 IFIP Networking Con-
ference (IFIP Networking), pages 1–3. IEEE.
Liu, Y., Ding, J., Zhang, Z.-L., and Liu, X. (2021b).
Clara: A constrained reinforcement learning based re-
source allocation framework for network slicing. In
2021 IEEE International Conference on Big Data (Big
Data), pages 1427–1437. IEEE.
Liu, Y., Halev, A., and Liu, X. (2021c). Policy learning
with constraints in model-free reinforcement learning:
A survey. In The 30th International Joint Conference
on Artificial Intelligence (IJCAI).
Liu, Y. and Liu, X. (2021). Cts2: Time series smooth-
ing with constrained reinforcement learning. In Asian
Conference on Machine Learning, pages 363–378.
PMLR.
Liu, Y. and Liu, X. (2023a). Adventurer: Exploration with
bigan for deep reinforcement learning. Applied Intel-
ligence.
Liu, Y. and Liu, X. (2023b). Constrained reinforcement
learning for autonomous farming: Challenges and op-
portunities. In AI for Agriculture and Food Systems.
Lu, L., Liu, L., Hussain, M. J., and Liu, Y. (2017). I sense
you by breath: Speaker recognition via breath biomet-
rics. IEEE Transactions on Dependable and Secure
Computing, 17(2):306–319.
Lu, L. and Liu, Y. (2015). Safeguard: User reauthen-
tication on smartphones via behavioral biometrics.
IEEE Transactions on Computational Social Systems,
2(3):53–64.
Metelli, A. M., Likmeta, A., and Restelli, M. (2019).
Propagating uncertainty in reinforcement learning via
wasserstein barycenters. Advances in Neural Informa-
tion Processing Systems, 32.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,
Harley, T., Silver, D., and Kavukcuoglu, K. (2016).
Asynchronous methods for deep reinforcement learn-
ing. In International conference on machine learning,
pages 1928–1937. PMLR.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
388

level control through deep reinforcement learning.
Nature, 518(7540):529.
Osband, I., Van Roy, B., and Wen, Z. (2016). Generalization
and exploration via randomized value functions. In In-
ternational Conference on Machine Learning, pages
2377–2386. PMLR.
O’Donoghue, B., Osband, I., Munos, R., and Mnih, V.
(2018). The uncertainty bellman equation and ex-
ploration. In International Conference on Machine
Learning, pages 3836–3845.
Qu, H., Xie, X., Liu, Y., Zhang, M., and Lu, L. (2015). Im-
proved perception-based spiking neuron learning rule
for real-time user authentication. Neurocomputing,
151:310–318.
Rasmussen, C. E. (2003). Gaussian processes in machine
learning. In Summer school on machine learning,
pages 63–71. Springer.
Tesauro, G. et al. (1995). Temporal difference learning and
td-gammon. Communications of the ACM, 38(3):58–
68.
Van Hasselt, H., Guez, A., and Silver, D. (2016). Deep re-
inforcement learning with double q-learning. In Pro-
ceedings of the AAAI conference on artificial intelli-
gence, volume 30.
Yang, E. and Gu, D. (2004). Multiagent reinforcement
learning for multi-robot systems: A survey. Techni-
cal report, tech. rep.
Yang, T., Tang, H., Bai, C., Liu, J., Hao, J., Meng, Z.,
and Liu, P. (2021). Exploration in deep reinforcement
learning: a comprehensive survey. arXiv preprint
arXiv:2109.06668.
Zhu, Z., Bıyık, E., and Sadigh, D. (2020). Multi-agent safe
planning with gaussian processes. In 2020 IEEE/RSJ
International Conference on Intelligent Robots and
Systems (IROS), pages 6260–6267. IEEE.
APPENDIX
EMPIRICAL RESULTS
As stated in the paper, Farsighter can work on a
wide range of RL tasks with high/low-dimensional
states, discrete/continuous actions, and sparse/dense
rewards. We show the performance for sparse reward
tasks in the main paper. In Table 2 and 3, we show
the performance for all the atari games and dense re-
ward continue task(Walker2D), where Farsighter out-
performs the SOTA.
PSEUDOCODE FOR CONTINUOUS
TASKS
The pseudocode for continuous one-step uncertainty
driven Q-Learning is shown in Alg. 3. To extend
Algorithm 3: Continuous one-step uncertainty driven Q-
Learning with NAF.
Given NAF, we have
Q(s, a|θ
Q
) = A(s, a|θ
A
) +V (s|θ
V
);
A(s, a|θ
A
) = −
1
2
(a −µ(s|θ
a
))
T
P(s|θ
P
)(a −µ(s|θ
a
))
and BNN µ(s|θ
va
)
Randomly initialize normalized Q network and BNN
Initialize target network Q
′
with weight θ
Q
′
← θ
Q
Initialize replay buffer R
1: for episode=1, M do
2: Receive initial observation state s
1
3: for t = 1,T do
4: Select a variance ε from BNN layer µ(s|θ
va
)
and action a
t
= µ(s|θ
a
) + ε
5: Execute a
t
and observe r
t
and s
t+1
6: Store transition (s
t
, a
t
, r
t
, s
t+1
) into R
7: for iteration=1,I do
8: Sample a random minibatch of m transi-
tions from R
9: Update θ
a
, θ
V
, θ
P
as normal NAF with
fixing θ
va
.
10: Every M steps: Update the BNN layer
µ(φ(s)|θ
va
)
11: Every N steps: Update the target network:
θ
Q
′
← τθ
Q
+ (1 −τ)θ
Q
′
12: end for
13: end for
14: end for
the process to multi-step, we can recursively deploy
Thompson sampling on the BNN layer of µ(φ(s)|θ
va
)
to get multi-step samples, which is similar with Alg. 2
in the main paper.
EXPERIMENT DETAILS
Network Architecture
Discrete Action Tasks
For discrete action tasks, the input observations are
raw images (e.g., Atari games). The input to the net-
work is 4 × 84 × 84 tensor with a re-scaled and aver-
aged over channels of the last four observations. The
first convolution layer has 32 filters of size 8 with a
stride of 4. The second convolution layer has 64 fil-
ters of size 4 with stride 2. The last convolution layer
has 64 filters of size 3 followed by a fully connected
layer of size 512.
Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement Learning
389

Table 1: Hyperparameters.
Hyperparameter Value
Number of Seeds 10
Optimizer RMSProp
Learning rate 0.0025
Momentum 0.95
Discount factor 0.99
Representation network update frequency 4 steps
Representation network update mini-batch 32 tuples
Target network update frequency (N) 10k steps(Atari Games); 1k (Robotic controls)
Posterior update frequency (M) 10*N;
Posterior update mini-batch 100k tuples(Atari Games); 1k tuples(Robotic controls)
BLR noise variance σ
ε
1
BLR prior variance σ 0.1
Replay buffer size 1M tuples
Continuous Action Tasks
For continuous action tasks, the input observations are
low dimensional sensor data (e.g., robotic control).
The inputs are different from domain to domain. We
use two fully connected layers with hidden size 64
and 32 for the representation layer, which works in
general for different continuous domains.
Hyper-Parameters
In table 1, we show the hyper-parameters for the al-
gorithms to run. We randomly initialize the param-
eters of the networks. Since our methods are based
on DDQN (NAF), most hyper-parameters are equiv-
alent to ones in DDQN(NAF) setting. To optimize
for this set of hyper-parameters we set up a sim-
ple, fast, and cheap hyper-parameter tuning proce-
dure. For example, for Atari Games, we used a pre-
trained DDQN model for the game of Montezuma’s
Revenge, and removed the last fully connected layer
in order to have access to its already trained state
representation. Then we tried combination of M =
{N, 10∗N}, σ = {1, 0.1, 0.001}, and σ
ε
= {1, 10} and
test for 10000 episodes of the game. The procedure
is cheap and fast since it requires only a few times of
posterior update. We set these parameters to their best
M = 10 ∗N, σ = 0.1, σ
ε
= 1.
COMPLEXITY ANALYSES
Farsighter vs BDQN (One-step Bayesian NAF): As
mentioned Sec. 4.4, we did not change the update rule
for multi-step updates. We only change the data sam-
ples used to do the optimization. So Farsighter would
not change the computation cost compared to BDQN
(One-step Bayesian NAF). Moreover, multi-step up-
dates store the sum of discounted rewards and final
states after k steps to the replay buffer. The transmis-
sion tuples are in the same format with one-step up-
dates, thus Farsighter would not increase the memory
complexity either.
BDQN vs DDQN: For a given period of game
time, the number of the backward pass in both BDQN
and DQN are the same whereas for BDQN it is
cheaper since there is no backward pass for the final
layer. BDQN has more forward passes compared with
DDQN. To update the posterior distribution, BDQN
draws samples from the replay buffer and needs to
compute their feature vectors, as it is mentioned in
Sec. 4.2,The increased number is based on the update
frequency and posterior update batch size. One can
easily relax it by parallelizing this step along the main
body of BDQN or deploying online posterior update
methods.
One-step Bayesian NAF vs NAF: The update of
the BNN layer µ(φ(s)|θ
va
) is complex then a liner
layer. While for continuous action tasks the dimen-
sion of BNN layer is low thus it is easy to train. As
mentioned in the Sec. 6, the input dimension for the
BNN layer is 32. Empirically, we run experiences on
Fetch Pick And Place task. The running time is simi-
lar for both cases, which is around six hours.
In summary, we would not increase the computa-
tional and memory cost. Farsighter can work appro-
priately in complex real-world domains.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
390

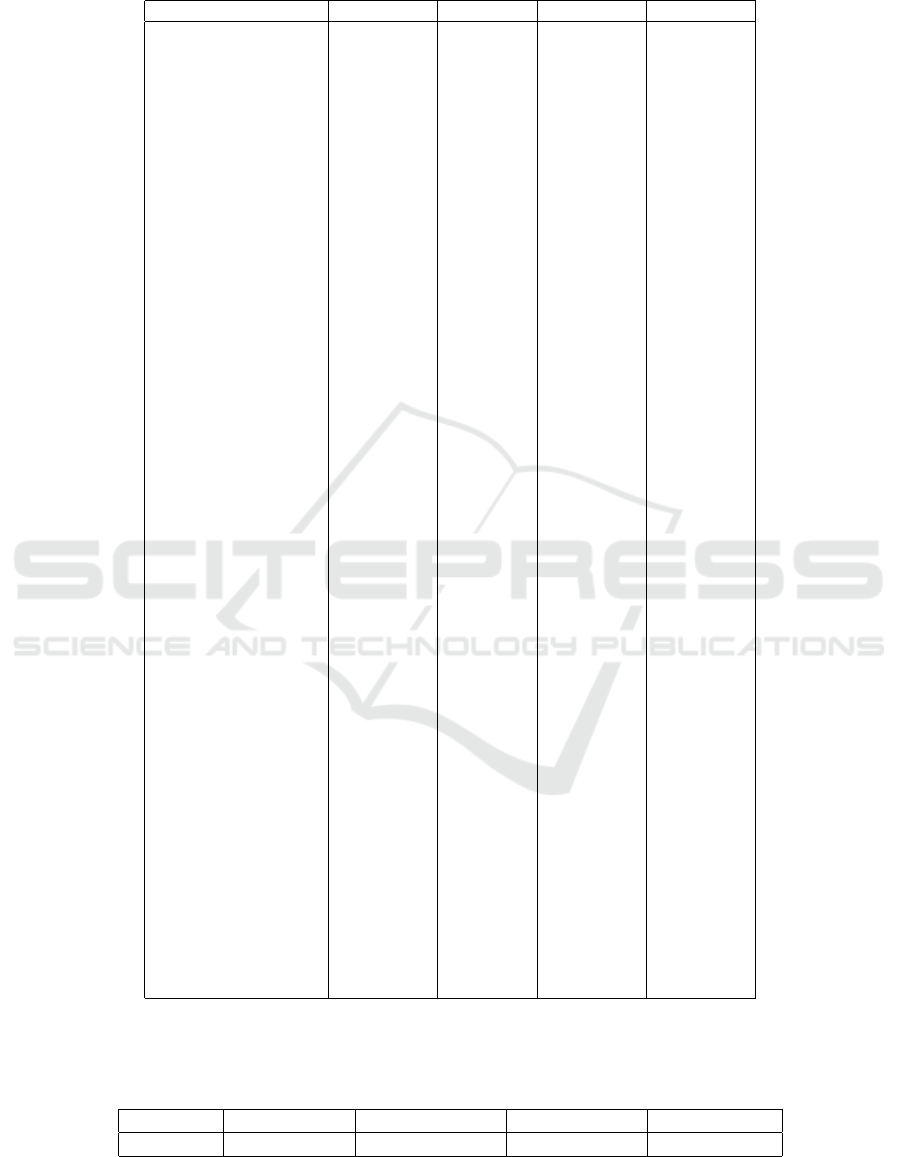
Table 2: Raw scores for Atari games. The performance of OB2I is from (Bai et al., 2021).
Farsighter DDQN BDQN OB2I(20M)
Alien 3762.50 1620.00 3167.20 916.90
Amidar 1934.20 978.00 1815.30 94.00
Assault 7439.30 4280.40 5439.40 2996.20
Asterix 39556.40 4359.00 44438.30 2719.00
Asteroids 2603.70 1364.50 2363.20 959.90
Atlantis 3959257.80 279987.00 2823842.40 3146300.00
Bank Heist 983.70 455.00 834.50 378.60
Battle Zone 47936.70 29900.00 45348.40 13454.50
Beam Rider 19504.80 8627.50 9456.30 3736.70
Bowling 54.62 50.40 38.40 30.00
Boxing 91.77 88.00 79.30 75.10
Breakout 597.20 385.50 392.60 423.10
Centipede 5936.10 4657.70 7134.70 2661.80
Chopper Command 13940.60 6126.00 17363.60 1100.30
Crazy Climber 149507.70 110763.00 137693.80 53346.70
Demon Attack 32233.61 12149.40 23595.40 6794.60
Double Dunk 3.50 -6.60 -1.30 -18.20
Enduro 1604.70 729.00 1496.50 719.00
Fishing Derby 3.80 -4.90 27.30 -60.10
Freeway 48.02 30.80 30.10 32.10
Frostbite 1795.30 797.40 1643.60 1277.30
Gopher 19418.90 8777.40 13742.80 6359.50
Gravitar 1175.81 473.00 589.30 393.60
H.E.R.O. 22010.70 20437.80 21532.70 3302.50
Ice Hockey -0.70 -1.90 -2.70 -4.20
James Bond 1707.25 768.50 1593.70 434.30
Kangaroo 14651.80 7259.00 13596.30 2387.00
Krull 13263.91 8422.30 9643.60 45388.80
Kung-Fu Master 38734.99 26059.00 40563.70 16272.20
Montezumas Revenge 413.60 0.00 0.00 0.00
Ms. Pac-Man 3796.19 3085.60 3295.50 1794.90
Name This Game 12312.80 8207.80 10536.70 8576.80
Pong 20.25 19.50 19.80 18.70
Private Eye 494.50 146.70 149.70 1174.10
Q*Bert 20788.47 13117.30 19530.60 4275.00
River Raid 12597.50 7377.60 15830.70 2926.50
Road Runner 55823.20 39544.00 51062.70 21831.40
Robotank 66.61 63.90 60.70 13.50
Seaquest 6880.48 5860.60 7934.70 332.10
Space Invaders 5684.02 1692.30 7830.80 904.90
Star Gunner 96013.91 54282.00 79403.70 1290.20
Tennis 19.10 12.20 -1.00 -1.00
Time Pilot 6402.11 4870.00 7932.70 3404.50
Tutankham 201.70 68.10 230.60 297.00
Up and Down 17328.92 9989.90 23056.90 5100.80
Venture 951.36 163.00 693.80 16.10
Video Pinball 529524.60 196760.40 47246.80 80607.00
Wizard Of Wor 7429.40 2704.00 9450.80 480.70
Zaxxon 8934.95 5363.00 8394.70 2842.00
Table 3: The score for dense reward continue tasks (30k steps).
NAF Multi-step NAF Bayesian NAF Farsighter
Walker2D -75.8 ± 631.0 -68.2 ± 649.0 160.1 ± 493.0 230.2 ± 566.8
Farsighter: Efficient Multi-Step Exploration for Deep Reinforcement Learning
391