Playstyle Generation for Geister With Genetic Algorithm and Clustering

Keisuke Tomoda and Koji Hasebe

Department of Computer Science, University of Tsukuba, Japan

Keywords:

Imperfect Information Game, Genetic Algorithm, Playstyle, Geister.

Abstract:

Studies on game-playing agents have made various attempts to develop agents with characteristic playstyle.

Most of these studies either generated agents with predetermined playstyles or simultaneously generated dif-

ferent playstyles without deﬁning a speciﬁc playstyle for single-player complete information games. However,

the generation of agents with different playstyles for multi-player imperfect information games has not been

thoroughly investigated. Therefore, in this study, we have proposed an automatic playstyle generation method

for a two-player imperfect information game called Geister. The basic idea is to use a genetic algorithm to

optimize agents whose genes represent parameters that determine the manner of guessing hidden information.

By clustering the genes with high ﬁtness, obtained using this process, agents with different playstyles are

generated simultaneously. From the results of the experiments, our proposed method generated ﬁve different

playstyles with cyclic dominance relationships.

1 INTRODUCTION

Research on game-playing agents is developing

rapidly, with the performance of some agents, such as

AlphaZero (Silver et al., 2018) and Libratus (Brown

and Sandholm, 2018), surpassing professional human

players. In addition, there are signiﬁcant interests

in developing these agents to achieve broader ob-

jectives, not just their strengths (Lara-Cabrera et al.,

2015; Hoover et al., 2019; Fan et al., 2019). Among

these, there exist studies on the generation of agents

with characteristic playstyles (Tychsen and Canossa,

2008; Tampuu et al., 2017; Ishii et al., 2018). A

playstyle refers to a set of characteristic behaviors of

the player. However, most of these studies predeﬁned

the playstyles they wanted to generate, which makes it

difﬁcult to identify playstyles that cannot be assumed

in advance.

To address this issue, Iwasaki et al. (Iwasaki and

Hasebe, 2021) proposed a framework called C-NEAT

to generate different playstyles simultaneously with-

out predeﬁning any styles. This framework consisted

of an evolutionary computation called NeuroEvlution

of Augmenting Topologies (NEAT) (Stanley and Mi-

ikkulainen, 2002) and clustering, which optimizes

gameplay while classifying the characteristic behav-

ior of the agents by clustering. However, that study

focused on a roguelike game, which is a complete

information game for a single player. Generation of

agents with different playstyles for multiplayer imper-

fect information games has not yet been thoroughly

investigated.

In this study, we have proposed an automatic

playstyle generation framework for a two-player im-

perfect information game. Here, we focus on Geis-

ter, a chess like game, in which the colors of the

pieces (red and blue) are hidden from the opponent.

In this game, the optimal action varies depending on

the color of the the opponent’s pieces; therefore, it is

important to advance the game while guessing them.

However, it is not possible to perfectly identify the

color of the piece using only the revealed information,

and the effective guessing method changes depending

on the opponent’s strategy. Based on the above obser-

vations, we focus on the playstyles that determine the

guessing manner.

To simultaneously generate the playstyles deﬁned

above, we propose a framework using genetic al-

gorithms and clustering based on the concept of C-

NEAT. Speciﬁcally, many agents are generated that

have parameters of a function for guessing the color

of the opponent’s piece and, while they are played

against each other, agents with a high winning rate

(i.e., high ﬁtness) are repeatedly retained. After natu-

ral selection, the set of genes possessed by the elites

from all generations are clustered. Then, for each

cluster, the average value of the genes was evaluated,

resulting in different playstyles.

916

Tomoda, K. and Hasebe, K.

Playstyle Generation for Geister With Genetic Algorithm and Clustering.

DOI: 10.5220/0011801400003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 916-922

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

To demonstrate the effectiveness of the proposed

method, an experiment was conducted using a sim-

pliﬁed Geister with 4 × 5 board. We observed that

ﬁve different playstyles with dominant cyclic relation-

ships were generated.

The remainder of this study is organized as fol-

lows. Section 2 presents the related work. Section

3 provides an overview of the rules of Geister. Sec-

tion 4 describes the proposed framework for gener-

ating playstyles for a Geister. Section 5 presents the

experimental results. Finally, Section 6 concludes the

paper and presents future work.

2 RELATED WORK

Signiﬁcant research has been conducted to develop

agents capable of playing games with characteristic

playstyles. One of the earliest studies on playstyles

in games was conducted by Tychsen et al. (Tychsen

and Canossa, 2008). The authors deﬁned a player’s

playstyle to be a set of their characteristic behav-

iors. Based on this deﬁnition, they focused on the

game, Hitman: Blood Money, and identiﬁed different

playstyles by analyzing various playlogs.

Ishii et al. (Ishii et al., 2018) developed agents

with different characteristic playstyles (personas) for

the ﬁghting game, FightingICE. Their fundamental

idea was to determine the agent’s actions via Puppet-

Master Monte Carlo Tree Search (MCTS), which is

an extension of general MCTS, using evaluation func-

tions pertaining to one of two playstyles: short-range

attack and long-range attack.

Tampuu et al. (Tampuu et al., 2017) generated

agents with two playstyles, cooperative and adversar-

ial, for the video game called Pong. They demon-

strated that both cooperative and adversarial game-

play can be achieved by agents based on Deep-Q-

Network (Mnih et al., 2013) using a uniﬁed reward

scheme.

In all of the aforementioned studies, playstyles

were predeﬁned based on the authors’ expectations.

Therefore, generation of playstyles not deﬁned in ad-

vance is difﬁcult using these methods. In contrast we

attempt to generate multiple playstyles automatically

without deﬁning them in advance.

Studies on similar topics have been conducted by

Iwasaki et al. (Iwasaki and Hasebe, 2021; Iwasaki and

Hasebe, 2022). They generated multiple playstyles

for the roguelike game, MiniDungeons, using evolu-

tionary computation and clustering. The game was a

single-player complete-information game so the envi-

ronment of the game visible to the player was ﬁxed.

In contrast, we focus on applying the framework pro-

Figure 1: Board of Geister (left) and an example of the ini-

tial board setting from the viewpoint of the player on the

bottom (right).

posed by Iwasaki et al. to a two-player imperfect-

information game. This challenge raises several new

issues, such as changes in ﬁtness depending on the op-

ponent even with the same pointing, and appropriate

handling of imperfect information.

3 OVERVIEW OF GEISTER

Geister is a two-player chess-like game in which play-

ers take turns moving their pieces on a 6 × 6 board.

However, in this study, in order to reduce computa-

tional time, the size of the board is reduced to 4 × 5,

as depicted in Figure 1, without loss of generality.

On the board, the left- and right-most cells (indi-

cated by icons in the left picture in Figure 1) of the

farthest row of the board, as seen by each player, are

special cells called “exits.” Each player initially con-

trols four pieces, two of which are blue and the other

two are red. The color of each piece is only visible

to its owner. Before starting the game, each player

places two of their four pieces in the 2 × 2 region at

the center of the two rows closest to them (marked in

gray in the left picture in Figure 1 for the player on the

bottom). An example of an initial board conﬁguration

from the perspective of the player on the bottom is de-

picted in the right picture in Figure 1.

During the game, the players take turns moving

their pieces. During each player’s turn, they can move

any one piece to a vertically or horizontally adjacent

square, unless it takes the piece outside the board or

onto a square already occupied by another of their

pieces. If a piece is moved onto a square occupied

by an opponent’s piece, the latter is removed from the

game and may not be reused (henceforth referred to

as being captured). Further, each player can make a

special move called “escape” on the following turn if

one of their pieces is on one of their exits during the

current turn.

The ﬁrst player to achieve any of the following

conditions wins.

1. Have one of their blue pieces escape.

Playstyle Generation for Geister With Genetic Algorithm and Clustering

917

2. Capture all of their opponent’s blue pieces.

3. Have their opponent capture all of their red pieces.

4 FRAMEWORK FOR

PLAYSTYLE GENERATION

4.1 Overview

In Geister, the optimal move on a given board state

depends on the colors of the opponent’s pieces, thus

guessing them is integral to one’s strategy. However,

since it is not possible to deduce the colors of the

opponent’s pieces based only on the revealed infor-

mation, there is no single correct method of guess-

ing. Thus, the usefulness of guessing methods is

likely to depend on the opponent’s guessing strategy.

Therefore, optimization of play is not expected in-

duce convergence to a single guessing method, but,

instead, yield multiple methods of guessing. Based

on the above considerations, in this study, we deﬁne

playstyle in terms of the guessing method used to es-

timate the colors of the opponent’s pieces.

A more detailed deﬁnition of the playstyle is pre-

sented below. The agent determines its move on each

turn by evaluating the likelihoods of the opponent’s

pieces being of certain colors and searching for the

best move on the probabilistic board. The former is

determined using a special function (called a guess-

ing function), which involves some parameters, that

takes into account the speciﬁc movements of enemy

pieces on the board. The latter is performed using

the Expectimax algorithm (Michie, 1966), which is

a variant of the Min-Max search algorithm with in-

corporated probabilistic state transitions. The evalua-

tion function for Expectimax is taken to be one whose

usefulness has been conﬁrmed in preliminary exper-

iments. Therefore, the moves of the agent are deter-

mined based solely on the parameters of the guessing

function and the search algorithm.

We obtain the desired playstyles using genetic al-

gorithm and clustering by considering the parameters

of the guessing function used by the agent as genes.

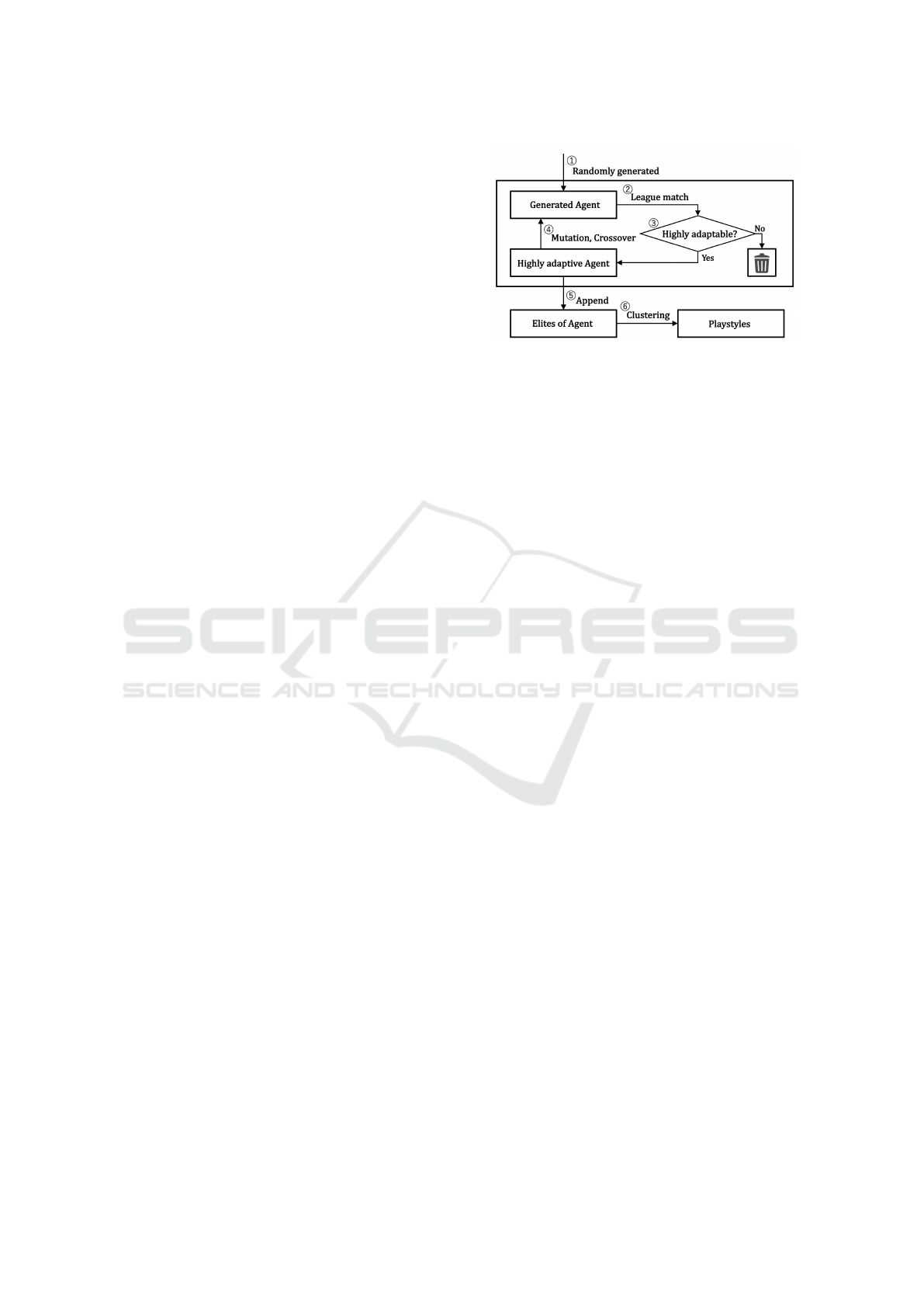
The detailed procedure is given by the following al-

gorithm. (Figure 2 illustrates the procedure, where

the numbers correspond to the step numbers presented

below.)

1. Generate multiple agents with random guessing

parameters.

2. Match the generated agents with other agents se-

quentially and measure the corresponding win-

ning rates, which are considered to be measures

of ﬁtness.

Figure 2: Procedure for obtaining playstyles.

3. Retain agents with high ﬁtness and remove others.

4. Create a new generation of agents based on the

retained agents via mutation and crossover.

5. Repeat steps 2-4 and save all agents with high ﬁt-

ness in each generation.

6. Cluster the parameters of all saved agents as fea-

ture values.

7. Determine individual playstyles based on the av-

erage values of all parameters in each cluster.

4.2 Guessing Colors of Opponent’s

Pieces

In Geister, the colors of one’s opponent’s pieces can-

not be guesses solely by considering one’s own per-

spective. That is, the opponent’s estimation of the

colors of one’s own pieces must also be accounted for.

Therefore, the proposed agent formulates one guess,

e(p

opp

), for the color of each piece, p

opp

(1 ≤ i ≤ 4),

of the opponent, and another, e(p

pro

), for the oppo-

nent’s guess for the color of each piece, p

pro

(1 ≤ i ≤

4), owned by themselves. The guessed values lie in

the range, [0, 1], with values close to 1 correspond-

ing to guesses of blue with high conviction, and those

close to 0 corresponding to guesses of red with high

conviction. Each initial value is set to 0.5.

Guessed values are updated after the movement

of pieces during each turn. In particular, each agent

involves three parameters g

, g

, and g

, with values

in the range, [−0.5, 0.5], which correspond to the fol-

lowing movements.

• g

: Move to a cell adjacent to an enemy piece.

• g

: Move away from an adjacent enemy piece.

• g

: Move closer to the exit.

These three actions are related to Geister’s victory

conditions, and various playstyles can be deﬁned by

combining different conﬁgurations of the parameters.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

918

During the updating process, the availability of

actions corresponding to these parameters are veri-

ﬁed for each move. In case of availability, the value

of the corresponding parameter is added to the guess

value of the piece moved. For example, if the oppo-

nent’s move on their t-th turn is to move the piece,

opp

, adjacent to a piece of the agent, the guess value,

opp

), is updated using the following formula:

opp

) := g

+ e

t−1

opp

Then, the guess values are adjusted to satisfy:

i=1

e(p

) = 2 (for s ∈ {opp, pro}) and ∀ie

) ∈

[0, 1].

However, in the exceptional case in which a piece

adjacent to an exit is not moved to the exit, the cor-

responding guess value is set to 0 and is not changed

thereafter. This is because, if the color of the piece

were blue, the only rational move would have been to

move it to the exit.

4.3 Decision of Moves

Based on the guess values, the agent determines

the optimal move during each turn using an exten-

sion of the Expectimax algorithm. Expectimax is

an exhaustive, depth-ﬁrst game tree search algorithm,

which is often used to determine moves in imperfect-

information games. Both Expectimax and its exten-

sion are described below.

The nodes in the search tree of the Min-Max al-

gorithm are classiﬁed into two types: Max nodes and

Min nodes. Nodes of the former type represent the

player’s turn and transition to a child node with the

maximum evaluation value, while those of the latter

type represent the opponent’s turn and transition to a

child node with the minimum evaluation value. In ad-

dition, in Expectimax, a chance node is inserted be-

tween Min and Max nodes when the transition des-

tination node changes depending on the probability.

The evaluation value of a chance node is given by a

weighted sum of evaluation values, with the transition

probabilities of its child nodes as coefﬁcients. In Ex-

pectimax, the evaluation value, V(n), of a node, n, is

calculated using the following formula.

V (n) =

∑

∈C(n)

P(n, c

) ×V (c

where C(n) represents the set of child nodes of node

n, P(n, c) represents the probability of reaching node c

from node n, and V (c) represents the evaluation value

for node c.

We now consider applying Expectimax to Geis-

ter. If a move reveals the color of an opponent’s piece

(e.g., when an opponent’s piece is captured), the state

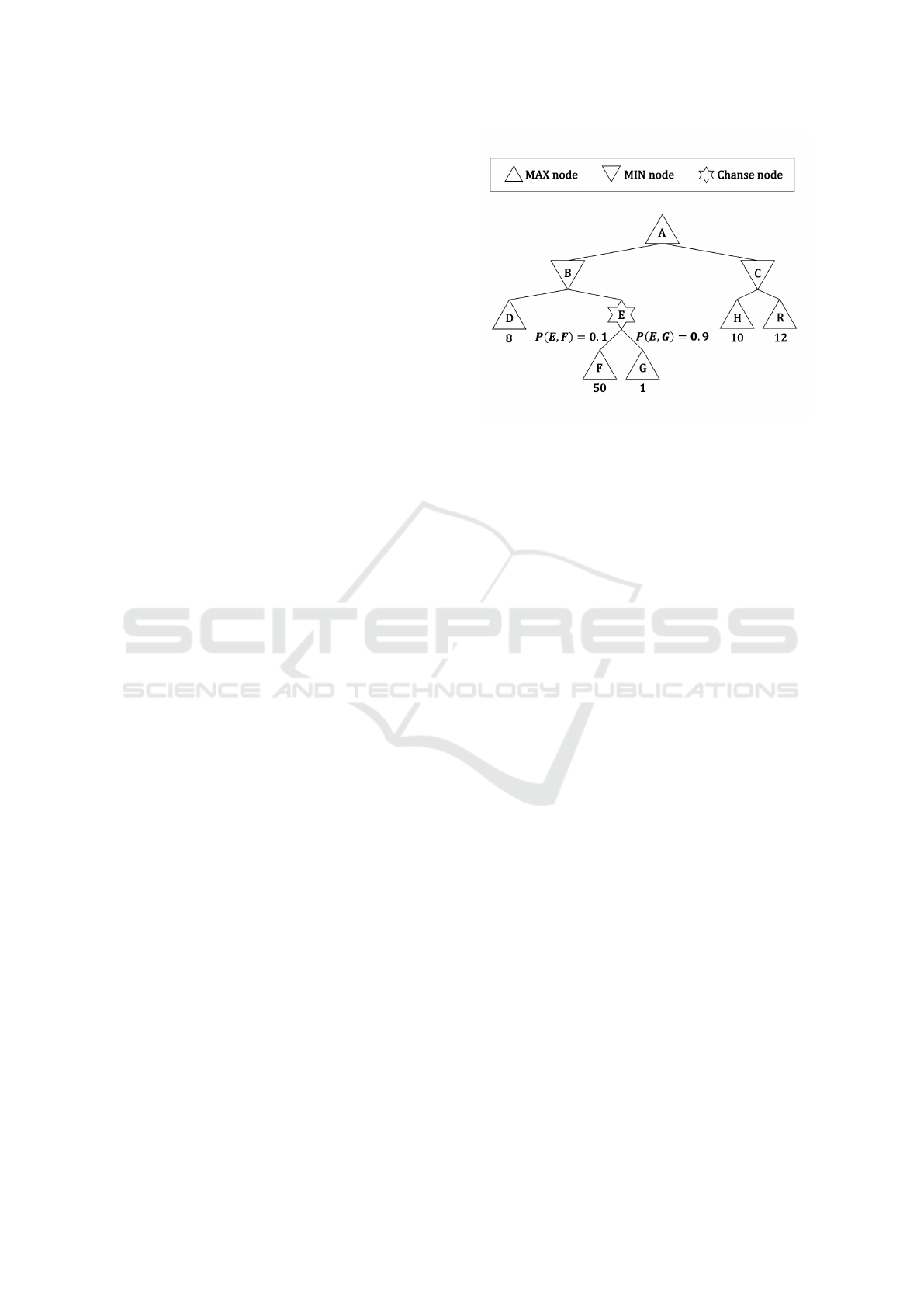
Figure 3: Expectimax game tree.

after the move transitions stochastically depending on

the likelihood of the color of the opponent’s piece.

Thus, a chance node is inserted after such a move.

As explained previously, Expectimax can be used

to determine moves in this way. However, better

moves can be found by considering the information

regarding the colors of one’s own pieces. For exam-

ple, let us consider the search tree depicted in Fig-

ure 3. If the color of the piece, say p, is red and

the opponent chooses a move that induces a transi-

tion from node B to node E, then the transition node

is known to be F. At this time, from the opponent’s

perspective, V (E) = 5.9, as they do not know the

color of p. However, from the player’s perspective,

V (E) = V (F) = 50, as the color of p is known to be

red. Therefore, if the opponent chooses a move to

transition to node E from node B, it is possible to tran-

sition to a state where it is better to choose the move

to transition to node B from node A.

In order to utilize the aforementioned information

asymmetry between the proponent and the opponent

during optimal move search, we extend Expectimax

by incorporating the real value, which is the evalua-

tion value from one’s own perspective, and the pre-

tense value, which is the evaluation value from the

opponent’s perspective.

In the extended Expectimax, nodes are selected to

increase the real value at the MAX node and reduce

the pretense value at the MIN node. If the transition

destination at a chance node is known, its real value

becomes the real value of the transition destination

node. The pretense value of the chance node is always

a weighted sum of the pretense values, with the tran-

sition probabilities of the child nodes of the chance

node as coefﬁcients.

Playstyle Generation for Geister With Genetic Algorithm and Clustering

919

Figure 4: Evaluation tables for blue (left) and red (right)

pieces.

4.4 Genetic Manipulation and

Clustering

In our framework, genetic manipulation is performed

based on mutation and crossovers, as in several exist-

ing genetic algorithms. As depicted in Figure 2, in

Step 5 of the genetic algorithm, individuals with high

ﬁtness are saved. Once a sufﬁcient number of agents

with high ﬁtness have been generated, the parameters

of guessing functions of all stored agents are clustered

using the k-means method. Further, the average value

of the parameters of all agents within each cluster is

representative of the playstyle corresponding to that

cluster.

5 EXPERIMENTS

5.1 Parameter Conﬁguration

In this research, the following experiments are per-

formed to verify that the proposed framework actually

generates multiple playstyles in Geister.

5.1.1 Optimal Move Search

In our experiments, the depth of optimal move search

is set to 3. The evaluation function used in the search

is deﬁned as the sum of values assigned to each piece

by its position. In particular, values are assigned to

blue and red pieces as depicted in Figure 4. As ex-

plained previously, in Geister, the ﬁrst player to move

a blue piece to the exit wins. Therefore, we assume

that high proximity between the blue pieces and the

exits is desirable. Further, we assume that the value

of a red piece is high when it is positioned to protect

a blue piece near the exit without blocking its course

to it. The table depicted in Figure 4 lists the highest

winning rates in matches conducted during prelimi-

nary experiments using various similar tables.

On the other hand, we assume low proximity be-

tween the opponent’s pieces and the exits to be de-

sirable. Therefore, during the evaluation of the oppo-

Figure 5: Clustering result.

nent’s pieces, we used the inverted version of Figure

4, with negative values weighted by the guess value.

5.1.2 Agent Generation

During the execution of genetic algorithm, the num-

ber of agents in each generation is taken to be 100,

and 30 agents with high ﬁtness are retained in each

subsequent generation. During the generation of new

agents based on agents with high ﬁtness, mutation and

crossover are performed with probabilities of 0.6 and

0.4, respectively. Moreover, generation of excessively

weak agents is avoided by allowing each generated

agents to play against an agent taking random actions

100 times in advance, and deleting those with win

rates less than 90%.

5.1.3 Clustering

The parameters of 1,500 experimentally obtained

agents over 50 generations are subsequently classiﬁed

via clustering. A non-hierarchical k-means method is

adopted as the clustering algorithm. Preliminary ex-

periments varying the number of clusters conﬁrmed

that only 3-5 playstyles with a high winning rate were

generated even when the number of clusters was in-

creased, so the number of clusters was set to 5 in this

study. This process yields ﬁve agents with different

playstyles. We also determine the compatibilities be-

tween these playstyles via round-robin matches.

5.2 Results

Figure 5 depicts the three-dimensional plot obtained

by color-coding the 30 individuals with highest ﬁt-

ness in each generation via clustering. Figure 6 illus-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

920

Figure 6: Change in the ratio of the number of agents for

each playstyle.

Table 1: Parameters of cluster representative.

Estimated Parameters

Adjacent Distancing GoalDirected

Cluster A 0.2685 -0.2646 -0.2592

Cluster B 0.3847 0.2832 -0.3515

Cluster C -0.0794 0.1240 -0.3194

Cluster D 0.1012 0.2411 0.1975

Cluster E -0.3819 0.0200 0.1309

trates the variation in the ratios of different playstyles

in each generation.

The representative parameters of the generated

clusters are presented in Table 1. In this table, a posi-

tive (negative, resp.) value is adopted while determin-

ing that a piece that has made a move corresponding

to each parameter is a blue (red, resp.) piece.

Further, Table 2 presents the results of matches

performed using the representative parameters of each

generated cluster. The table lists the winning rates

of all possible initial placements after 72 matches

in aggregate, with the ﬁrst and second player roles

switched once each. Figure 7 depicts a graphical rep-

resentation of the dominance relationships between

the identiﬁed playstyles. In this ﬁgure, the nodes rep-

resent the generated playstyles and an edge from X to

Y indicates that X wins (dominates) against Y in 60%

or more instances.

Based on Table 1, the characteristics of the

playstyles can be interpreted as follows.

Cluster A: A piece that is adjacent to another of the

same player is considered to be blue, and one that

has moved away from another of the same player

is considered to be red.

Cluster B: A piece that is adjacent or has moved

away from another of the same player is consid-

Table 2: Match results between playstyles.

Opponent’s playstyle

A B C D E

A 0.375 0.312 0.625 0.813

B 0.625 0.437 0.406 0.563

C 0.688 0.563 0.250 0.688

D 0.375 0.594 0.750 0.625

E 0.187 0.437 0.312 0.375

Figure 7: Dominant relations between playstyles.

ered to be blue, and one that is close to an exit is

considered to be red.

Cluster C: A piece approaching an exit is considered

to be red.

Cluster D: A piece that has moved away from an-

other of the same player and a piece that is close

to an exit are considered to be blue.

Cluster E: A piece that is adjacent to another of the

same player is considered to be blue.

Based on the above results, the following conclu-

sions can be drawn regarding the pairwise compat-

ibilities of these playstyles. In general, agents are

more likely to capture pieces that they consider to be

blue, and less likely to capture pieces that they con-

sider to be red. Therefore, Playstyle A prefers to play

slowly, only capturing adjacent pieces instead of chas-

ing pieces moving away. Playstyles B and C prefer to

aim for the goal early, thinking that their pieces will

not be captured even if they approach the goal. Fi-

nally, Playstyles D and E prefer to play slowly, with-

out aiming for the goal.

As depicted in Figure 7, a cyclic dominance re-

lationship is observed. More speciﬁcally, a performs

favorably against C, C performs favorably against D,

and D performs favorably against A. Further, as il-

lustrated in Figure 6, for no playstyle does the num-

ber of individuals monotonically increase with each

generation. The number of individuals following a

playstyle with a high winning rate is observed to trend

upwards. Based on these results, we can conclude that

no playstyle is always optimal when playstyles are de-

ﬁned based on the guessing strategy utilized. Also,

Playstyle Generation for Geister With Genetic Algorithm and Clustering

921

the effective playstyles may change dynamically de-

pending on the playstyle of the majority of the players

in each generation.

6 CONCLUSIONS AND FUTURE

WORK

In this study, we proposed a framework using ge-

netic algorithms and clustering to generate multiple

playstyles for Geister, a two-player imperfect infor-

mation game. Speciﬁcally, many agents with genes

are generated as the parameters of a function to guess

the color of the opponent’s piece. While these are

played against each other, agents with high ﬁtness are

obtained. Furthermore, by clustering the genes pos-

sessed by the elites of all generations, we can obtain

our target multiple playstyles. As a result of the exper-

iment, we observed that ﬁve playstyles with circular

dominance relationships were generated.

In this experiment, we have considered playstyles

that focused only on the guessing manner; however,

in the future, we would like to generate more di-

verse playstyles determined by the border evaluation

functions. In addition, based on methods such as re-

inforcement learning, we investigated an improved

framework that allowed agents to play better with

characteristic playstyles.

REFERENCES

Brown, N. and Sandholm, T. (2018). Superhuman ai for

heads-up no-limit poker: Libratus beats top profes-

sionals. Science, 359(6374):418–424.

Fan, T., Shi, Y., Li, W., and Ikeda, K. (2019). Position

control and production of various strategies for deep

learning go programs. In 2019 International Confer-

ence on Technologies and Applications of Artiﬁcial In-

telligence (TAAI), pages 1–6. IEEE.

Hoover, A. K., Togelius, J., Lee, S., and de Mesentier Silva,

F. (2019). The many ai challenges of hearthstone. KI

- K

unstliche Intelligenz, 34:33–43.

Ishii, R., Ito, S., Ishihara, M., Harada, T., and Thawon-

mas, R. (2018). Monte-carlo tree search implemen-

tation of ﬁghting game ais having personas. In 2018

IEEE Conference on Computational Intelligence and

Games (CIG), pages 1–8. IEEE.

Iwasaki, Y. and Hasebe, K. (2021). Identifying playstyles

in games with neat and clustering. In 2021 IEEE Con-

ference on Games (CoG), pages 1–4. IEEE.

Iwasaki, Y. and Hasebe, K. (2022). A framework for gen-

erating playstyles of game ai with clustering of play

logs. In ICAART (3), pages 605–612.

Lara-Cabrera, R., Nogueira-Collazo, M., Cotta, C., and

Fern

andez-Leiva, A. (2015). Game artiﬁcial intel-

ligence: Challenges for the scientiﬁc community.

CEUR Workshop Proceedings, 1394:1–12.

Michie, D. (1966). Game-playing and game-learning au-

tomata. In Advances in programming and non-

numerical computation, pages 183–200. Elsevier.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing atari with deep reinforcement learn-

ing. arXiv preprint arXiv:1312.5602.

Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,

M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,

Graepel, T., et al. (2018). A general reinforcement

learning algorithm that masters chess, shogi, and go

through self-play. Science, 362(6419):1140–1144.

Stanley, K. O. and Miikkulainen, R. (2002). Evolving neu-

ral networks through augmenting topologies. Evolu-

tionary computation, 10(2):99–127.

Tampuu, A., Matiisen, T., Kodelja, D., Kuzovkin, I., Korjus,

K., Aru, J., Aru, J., and Vicente, R. (2017). Multiagent

cooperation and competition with deep reinforcement

learning. PloS one, 12(4):e0172395.

Tychsen, A. and Canossa, A. (2008). Deﬁning personas in

games using metrics. In Proceedings of the 2008 con-

ference on future play: Research, play, share, pages

73–80.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

922