A Comparison of Synchronous and Asynchronous Distributed Particle

Swarm Optimization for Edge Computing

Riccardo Busetti, Nabil El Ioini, Hamid R. Barzegar and Claus Pahl

Free University of Bozen-Bolzano, Bolzano, Italy

Keywords:

Edge Cloud, Optimization, Particle Swarm Optimization, Distributed PSO, Synchronous PSO, Apache Spark,

Kubernetes, Docker.

Abstract:

Edge computing needs to deal with concerns such as load balancing, resource provisioning, and workload

placement as optimization problems. Particle Swarm Optimization (PSO) is a nature-inspired stochastic opti-

mization approach that aims at iteratively improving a solution of a problem over a given objective. Utilising

PSO in a distributed edge setting would allow the transfer of resource-intensive computational tasks from a

central cloud to the edge, this providing a more efﬁcient use of existing resources. However, there are chal-

lenges to meet performance and fault tolerance targets caused by the resource-constrained edge environment

with a higher probability of faults. We introduce here distributed synchronous and asynchronous variants of

the PSO algorithm. These two forms speciﬁcally target the performance and fault tolerance requirements in

an edge network. The PSO algorithms distribute the load across multiple nodes in order to effectively realize

coarse-grained parallelism, resulting in a signiﬁcant performance increase.

1 INTRODUCTION

Edge computing aims at reducing the overload on

cloud resources by distributing compute and storage

resources nearer to the edge and its devices (Hoang

et al., 2019). This proximity to data sources also

decreases latency (Mahmud et al., 2020). Unlike

cloud data centers, edge devices are geographically

distributed, resource-constrained, often even highly

dynamic in their environment. This in turn creates

problems (Bonomi et al., 2012) that require tailored

solutions to address load balancing, workload place-

ment or resource provisioning (Salaht et al., 2020).

Various optimization problems have emerged for

the edge (Scolati et al., 2019; Pahl, 2022) that

require intelligent solutions. Here, speciﬁcally

meta-heuristics nature-inspired methods like Particle

Swarm Optimization (PSO) provide suitable solutions

(Rodriguez et al., 2021). Nonetheless, most existing

PSO-based solutions are designed to be run on sin-

gle machines, which is often not adequate for edge

devices’ limited resources and reliability. Thus, in or-

der to improve performance but also fault-tolerance

of a PSO solution for the edge, we need to horizon-

tally scale the computation to combine resources of

multiple nodes into one transparent distributed edge

architecture.

Due to the lack of computational resources, but

also a higher probability of faults in edge architec-

tures, we need a PSO variant that combines compu-

tational power of multiple edge nodes while also of-

fering resilience to deal with nodes failures. A char-

acteristic of the PSO algorithm is its distributed na-

ture since the algorithm is essentially a swarm-based

evolutionary algorithm (Wang et al., 2018), allow-

ing for coarse-grained parallel implementation in a

parallel or distributed computational network. The

PSO algorithm has two primary variants that differ

in the update sequence of the particles’ velocities and

positions. These variants are the Synchronous PSO

and Asynchronous PSO. These variants can be im-

plemented in both a centralized or distributed man-

ner. While some distributed PSO variants have been

proposed, our objective is here a comparison of dis-

tributed synchronous and asynchronous PSO algo-

rithms as two variants that aim to enhance perfor-

mance and fault tolerance. We also highlight their

suitability for different application settings.

194

Busetti, R., El Ioini, N., Barzegar, H. and Pahl, C.

A Comparison of Synchronous and Asynchronous Distributed Particle Swarm Optimization for Edge Computing.

DOI: 10.5220/0011815500003488

In Proceedings of the 13th International Conference on Cloud Computing and Services Science (CLOSER 2023), pages 194-203

ISBN: 978-989-758-650-7; ISSN: 2184-5042

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 PARTICLE SWARM

OPTIMIZATION

Particle Swarm Optimization (PSO) is a nature-

inspired stochastic optimization algorithm (Kennedy

and Eberhart, 1995). The PSO algorithm centres

around a population of entities composed of so-called

particles. A particle is an abstraction of an entity that

moves with a given velocity and acceleration. Each

particle in a swarm keeps track of both its best per-

sonal position and best global position. The latter po-

sition represents the best position found by any parti-

cle in the swarm. The concept of the “best” position

can be measured with a ﬁtness function, which we

aim to optimize. The term “best” refers here to the

minimum or maximum value found during an evalua-

tion of the particle’s position with the deﬁned ﬁtness

function. PSO works in iterations, during which all

particles are evaluated based on their ﬁtness function

in terms of best personal and global positions.

Our ﬁrst variant, the synchronous PSO, is the most

common variant and uses the concept of iterations.

Each iteration is composed of four steps: evaluate the

ﬁtness function with each particle’s position as input,

the evaluation of the best personal position for every

particle, the determination of the best global position

among all particles, and updating each particle’s ve-

locity and position based on the best positions com-

puted earlier.

Our second variant, the asynchronous PSO, is dif-

ferent ii that in the asynchronous variant particles are

updated based on the current state of all the swarm,

i.e., each particle’s velocity and position is updated as

soon as the ﬁtness function is evaluated (that means it

is considering the best global position found until that

moment). This creates full independence between the

particles, which are moved to their next position with

the information available at the time of the evaluation.

3 RELATED WORK

Using parallel PSO algorithms has generally the aim

of alleviating high computational costs that are asso-

ciated with the algorithm. Most of the parallel al-

gorithms, however, are not distributed, which means

they consist of multiple processing components that

communicate using shared memory, rather than mul-

tiple computers communicating over a network (Ven-

ter and Sobieszczanski-Sobieski, 2006). Further-

more, most of the parallel implementations of PSO

are based on synchronous interaction (Schutte et al.,

2004; Azimi et al., 2020). In order to solve result-

ing performance issues, (Venter and Sobieszczanski-

Sobieski, 2006) propose a distributed asynchronous

PSO solution based on a Message Passing Interface

(MPI), but do not consider fault tolerance sufﬁciently.

PSO has been investigated for edge optimization

concerns (Li et al., 2022; Zedadra et al., 2018). A

PSO example tailored for edge computing to demon-

strate the problem is (Rodriguez et al., 2021). Here

a Binary Multi-Objective PSO (BMOPSO) solution

with a matrix-based encoding is used to solve a work-

load placement problem. In this encoding, a parti-

cle’s position and velocity is represented in the form

of matrices which encode the placement of a module

to an edge node. The BMPOSO algorithm does re-

quire considerable time to ﬁnd an optimal placement,

causing a problem for latency-sensitive applications,

e.g., workload placement. Furthermore, the optimiza-

tion problem is solvable when sufﬁcient time and re-

sources are provided, but this is often not possible in

an edge architecture.

4 DISTRIBUTED SYNCHRONOUS

AND ASYNCHRONOUS PSO

When using PSO with coarse-grained paralleliza-

tion, a swarm is split into multiple large sub-swarms

that are evaluated in parallel either on the same

multi-processor machine or in a distributed system

composed of multiple nodes. For each iteration,

all particles are independent of each other and can

therefore be easily evaluated in parallel (Venter and

Sobieszczanski-Sobieski, 2006).

Our experiments showed that the ﬁtness func-

tion evaluation is for many of the problem encodings

the most computationally intensive part. In (Schutte

et al., 2004) a medium-scale biomechanical system

identiﬁcation problem is presented, where the ﬁtness

function evaluation took about 1 minute. It is clear

that a standard sequential PSO algorithm could re-

sult in a signiﬁcant time required for adequate re-

sults. Thus there is a need to parallelize the algorithm

around the ﬁtness function evaluation.

The proposed solution for the distributed PSO al-

gorithm involves the design and implementation of

two variants of the distributed PSO algorithm, namely

synchronous and asynchronous. For synchronous and

asynchronous forms, timing assumptions are neces-

sary when designing a distributed algorithm. In gen-

eral, synchronous algorithms are simpler to design

because all the nodes are synchronized, whereas in

the asynchronous model there is no minimum waiting

time for synchronization between nodes, thus mak-

ing the design more complicated. In synchronous

PSO, there is a need to synchronize all the particles

A Comparison of Synchronous and Asynchronous Distributed Particle Swarm Optimization for Edge Computing

195

around iterations, whereas in the asynchronous PSO

each particle can move right after its ﬁtness function

has been evaluated.

4.1 Distributed Synchronous PSO

We introduce here the high-level design of the dis-

tributed synchronous PSO algorithm, without pre-

senting all implementation details. The design aims

at supporting different settings rather than identifying

a one-size-ﬁts-all solution.

In synchronous PSO, we need to synchronize all

particles using iterations. Here, we selected the mas-

ter/slave paradigm with two types of nodes; a master

node is responsible for coordinating and slave nodes

that are responsible for carrying out the computa-

tions dispatched by the master node. The choice of

master/slave is particularly suitable for a synchronous

PSO since the algorithm ﬂow is controlled by a mas-

ter node and the functions evaluations are carried out

by slave nodes.

We have implemented two variants of the DSPSO:

the Local Update (LU) and Distributed Update (DU).

The local variant performs the update of the particles

entirely in the master, which results in faster perfor-

mance; however, it does decrease the fault tolerance.

The distributed variant performs the update of the par-

ticles by parallelizing the collection of particles across

the slave nodes.

The distributed synchronous PSO algorithm is

characterized by the following components:

• i-th particle position vector X

• i-th particle velocity vector V

• i-th particle personal best position vector P

• best global position vector P

• ﬁtness function f

The tasks performed by master and slave nodes

are the following: Process of the master node:

1. Initializes the problem encoding parameters, po-

sitions and velocities;

2. Initializes the state of the swarm including current

iteration and received particles;

3. Starts the iteration by distributing all the particles

to the available slave nodes;

4. Waits to receive back all particles with function

evaluation and best personal position P

;

5. Computes for each incoming particle the best

global position P

until all particles are received;

6. Updates the velocity V

and position X

vectors of

each particle i based on the best personal P

and

global position P

found by all the particles;

7. Back to step 3 if last iteration is not reached;

8. Returns the best global position P

Process of a slave node:

1. Waits for a particle from the master node;

2. Evaluates the ﬁtness function f and updates the

personal best position P

;

3. Sends evaluated particle back to master node;

4. Goes back to step 1 if the master is not ﬁnished.

The pseudocode of SDSPSO with DU is shown in

Figure 1, where I is the number of iterations, P is the

number of particles, N and M are the lengths of the

dimensions of the encoding.

Figure 1: Pseudocode DSPSO Distributed Update (DU).

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

196

4.2 Distributed Asynchronous PSO

The distributed asynchronous PSO also follows the

master/slave paradigm similar to the synchronous

variant. It differs in the synchronization since there

are no iterations that link together all particles. In

asynchronous PSO, each particle is independently

evaluated and moved from the other particles.

For efﬁciency reasons we implemented an abstrac-

tion called SuperRDD, which is essentially a collec-

tion of particles that are all dependent on each other

and are executed on the cluster as a single sub-swarm.

This means that instead of sending each single par-

ticle independently, we are grouping them into sub-

swarms of variable size [1, n], where n is the num-

ber of particles. The smaller the sub-swarm size, the

more reduced the asynchrony of the algorithms is.

However, this allows for better performance, due to

the reduced communication happening within the dis-

tributed system.

The distributed asynchronous PSO algorithm is

characterized by the following components as the

synchronous variant above. The tasks performed by

master and slave nodes are in this variant as follows:

• Master node

1. Initializes the problem encoding parameters,

positions, and velocities;

2. Initializes the state of the swarm including a

queue of particles to send to slave nodes;

3. Loads the initial particles into the queue;

4. Distributes the particles in sub-swarms from the

queue to the available slave nodes;

5. Waits and receives each sub-swarm containing

particles with their ﬁtness function evaluation

result and best personal position;

6. Updates the best global position P

based on

each incoming particle;

7. Updates velocity V

and position P

vectors of

each incoming particle i based on best personal

and global position P

found so far;

8. Pushes particle back into queue and goes back

to step 4 if stopping condition is not met;

9. Returns the best global position P

• Slave node : same as for the synchronous variant

but is waits for a sub-swarm.

The pseudocode of DAPSO is shown in Figure 2,

where I is the number of iterations, P is the number of

particles, N and M are the lengths of the dimensions

of the encoding.

Figure 2: Pseudocode of the DAPSO algorithm.

4.3 Discussion

Even if the high-level ﬂow the two algorithms is sim-

ilar, they are quite different both from an execution

A Comparison of Synchronous and Asynchronous Distributed Particle Swarm Optimization for Edge Computing

197

ﬂow and accuracy perspective. The synchronous al-

gorithm requires the master to wait for all particles

to be evaluated before starting a new iteration, which

results in some slave nodes being idle especially if

the load on the cluster is imbalanced (e.g., some slave

nodes might ﬁnish before others). Moreover, it allows

for faster convergence, because the whole swarm will

converge faster towards the best global position found

by any of the particles in the previous iteration. This is

in contrast to the asynchronous algorithm, which up-

dates velocity and position of each particle as soon as

its ﬁtness function is evaluated, effectively using the

best global position available until that point. This

results in better usage of cluster resources and more

exploration made by the swarm which can be either a

positive or a negative depending on the optimization

problem’s domain.

We now summarize key characteristics and the

discuss implementation concerns.

4.3.1 Distributed Synchronous PSO (DSPSO)

The synchronous algorithm proposed in this research

is the Distributed Synchronous PSO (DSPSO), which

is a synchronous PSO designed to be distributed

with Apache Spark in two variants with local and

distributed updates. The DSPSO algorithm realizes

coarse-grained parallelization in which each executor

node in the cluster will compute a large task, com-

posed of multiple particles whose ﬁtness functions

will be evaluated.

4.3.2 Distributed Asynchronous PSO (DAPSO)

DAPSO is an asynchronous PSO designed to be dis-

tributed with Apache Spark. DAPSO realizes both

coarse-grained and ﬁne-grained parallelization de-

pending on the conﬁguration parameters, which will

make the algorithm more ﬂexible for certain use-

cases. DAPSO differs from existing implementa-

tions such as the asynchronous PSO from (Venter and

Sobieszczanski-Sobieski, 2006), because it does not

use the parallel scheme of Message Passing Interface

(MPI) and is designed around a completely different

programming model (Spark), but uses the same mas-

ter/slave paradigm.

4.3.3 Implementation Differences

Both of the proposed algorithms are designed around

Apache Spark’s RDDs, also known as Resilient Dis-

tributed Datasets. A RDD is a partitioned distributed

memory abstraction that allows the execution of in-

memory computations on large clusters in a fault-

tolerant manner. It is the core primitive of Apache

Spark and aims at efﬁciently providing fault tolerance

with the use of coarse-grained transformations that

are applied in parallel to all the partitions of the RDD

DAPSO is built on top of Kotlin coroutines, which

allow the concurrent execution of multiple Spark jobs

on the cluster. In the case of DAPSO, a Spark job

is a parallel computation consisting of multiple tasks

that are executed on the cluster. Each job contains

a group of particles whose ﬁtness function is evalu-

ated by the executor nodes. The usage of coroutines

requires a more careful design of the algorithm funda-

mentals and especially shared mutable structures such

as the best global position.

The asynchronous DAPSO algorithm is also more

complicated than its synchronous DSPSO counterpart

because the programming model of Apache Spark is

not totally suitable for asynchronous use-cases. How-

ever, it allows multiple jobs to be executed concur-

rently on the same cluster. This aspect of Spark re-

quired an implementation that involved new ideas in

order to balance efﬁciency and asynchrony.

Speciﬁc lessons learned show a trade-off between

asynchrony and performance. The ﬁrst design of

the asynchronous algorithm was based on two corou-

tines, one to schedule Spark jobs each with a Spark

RDD that contained a single particle, and run the ﬁt-

ness evaluation on the cluster, while the other asyn-

chronously collects result of each job, update particle

velocity/position locally and send back the particle as

a new Spark job. This ﬁrst implementation realized

full asynchrony because each particle was fully inde-

pendent of the others and was evaluated as soon as an

executor was free. Nonetheless, this design was rather

inefﬁcient, because it ended up creating several Spark

jobs that were executed only for a few milliseconds.

A large number of Spark jobs resulted in signiﬁcant

overhead which was especially noticeable on simpler

optimization problems. For the aforementioned rea-

sons, we had to reconsider more efﬁcient ways of re-

ducing the number of jobs, but at the same time keep-

ing a good level of asynchrony. The speciﬁc remedy

is presented in the next subsection.

4.3.4 Asynchrony vs. Performance: SuperRDDs

In order to solve the above performance issue, we pro-

pose an abstraction called SuperRDD. This is a col-

lection of particles, which are all dependent on each

other and that are executed on the cluster as a single

Spark RDD. The idea of SuperRDD aims to improve

the efﬁciency of the algorithm by reducing the degree

of asynchrony. In the context of Apache Spark, this

could be solved by grouping multiple particles within

a single RDD which was evaluated by the cluster. Su-

perRDDs result in fewer Spark jobs to be scheduled,

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

198

but at the cost of less asynchrony, as particles belong-

ing to one SuperRDD must wait for all other particles

to be evaluated.

We allow more ﬂexibility by making the size of

a SuperRDD conﬁgurable in the interval [1, n] with

1 being full asynchrony and n no asynchrony at all

(n denotes the number of particles). A SuperRDD

of size 1 thus essentially resembles the initially in-

troduced idea of having one Spark job for each par-

ticle. Then, a SuperRDD of size n is similar to the

synchronous PSO, where each particle waits for all

other particles to be evaluated ﬁrst before proceeding

to update its own velocity and position. The differ-

ence between DSPSO and DAPSO with SuperRDDs

of size n is only the way in which the particles are

updated. In the ﬁrst case, we update velocities and

positions once a single best global is computed for all

particles. This results in all particles to update their

velocities and positions with the same global best po-

sition. In the second case, we update velocities and

positions with an ever-changing best global position

updated after each particle evaluation.

4.4 Conceptual Comparison

The main strength of DSPSO is in the exploitation of

the information, meaning that we always have to wait

for each particle to conclude exploring, hence leading

up to a possible better global position. On the other

hand, the main strength of DAPSO is that particles are

updated using partial information, leading to stronger

exploration. A major problem of SPSO, which will

be even more evident when distributing the algorithm,

is that the ﬁrst evaluated particle will be idle for the

longest time, hence if we consider an imbalance in

the cluster resources, we might have nodes waiting in-

stead of performing useful work. This problem does

not apply to DAPSO because the progress made by

any particle does not depend on other particles or it-

erations. Therefore, cluster resources can be used to

their maximum capacity at any point during execu-

tion.

5 EVALUATION AND

DISCUSSION

The focus of the evaluation is now the performance

of the different algorithms in terms of performance

time, while also taking into consideration fault toler-

ance properties of the PSO algorithms in the context

of the platforms used.

5.1 Evaluation Methodology

The goal of this evaluation is to understand, ﬁrstly, if

the distributed algorithms are more performant than

non-distributed counterparts and, secondly, to distin-

guish synchronous and asynchronous variants. The

evaluation of the performance has been done by tak-

ing into consideration the time needed for the execu-

tion. In order to make measurements suitably accu-

rate, we created a benchmarking abstraction that uses

the monotonic clock. The usage of this clock guar-

antees that the time always moves forward and is not

impacted by any variations such as the clock skew.

We ran our experiments multiple times and took the

best measurements out of the runs. Multiple experi-

ments allowed us to notice and isolate any outlier ex-

ecutions.

The algorithms evaluated include the traditional

PSO, DSPSO with local velocity/position update and

DSPSO with distributed velocity/position update and

also DAPSO as the asynchronous variant. In order to

test performance, we used various scenarios in which

only one of the parameters was increased at a time and

others kept unchanged (e.g., increase only the number

of the particles). This helps to identify bottlenecks

and how the algorithms react to an increase in com-

plexity in certain parts.

In order to test the performance of the four al-

gorithms, we implemented our distributed algorithms

for workload placement problem encoding from (Ro-

driguez et al., 2021) that was also introduced earlier.

We used a matrix data structure D for this which is

composed of the set of nodes F and the set of mod-

ules M. Furthermore, the ﬁtness function here aims

to minimize the maximal amount of resources needed

by a given set of modules if deployed at speciﬁc edge

node.

The encoding implementation in total required an

adaptation of data structures, the ﬁtness function and

also the particle velocity/position update formulas,

but did not require changes to the high-level ﬂow of

the algorithms. We chose this speciﬁc encoding for

the evaluation since it provides a meaningful applica-

tion of distributed PSO in an edge computing archi-

tecture, i.e., it is a relevant challenge to be solved at

the edge.

5.2 Evaluation Setup

The evaluation of the distributed algorithms has been

accomplished by executing the algorithm in a virtual-

ized Kubernetes cluster. The goal of the cluster was to

simulate an edge computing environment with multi-

ple nodes connected to each other.

A Comparison of Synchronous and Asynchronous Distributed Particle Swarm Optimization for Edge Computing

199

For a virtualized Kubernetes cluster, we used

minikube, which implements a local Kubernetes clus-

ter. The Kubernetes cluster was provisioned on a

MacBook Pro 2017 using minikube. The conﬁgura-

tion of minikube was set to use 8 virtual CPUs and

8192MB of RAM.

The cluster topology used for the expirement was

composed of a set of four pods that were scheduled

on a single minikube virtual node. One pod was used

as the driver and had one core, whereas the remain-

ing three pods were executor nodes with two cores

each. In total, we used 7 CPUs/cores. We could not

utilize all 8 cores provisioned because the remaining

core was taken by the pods concurrently running, such

as the Spark, Kubernetes dashboard, and other sup-

porting services.

5.3 Evaluation Results

As a performance measure we use the elapsed time

needed by an algorithm to perform the optimization

until a stopping condition is met. This differs from

the convergence speed – another performance metric

which represents how quickly an optimization algo-

rithm converges towards an optimal value.

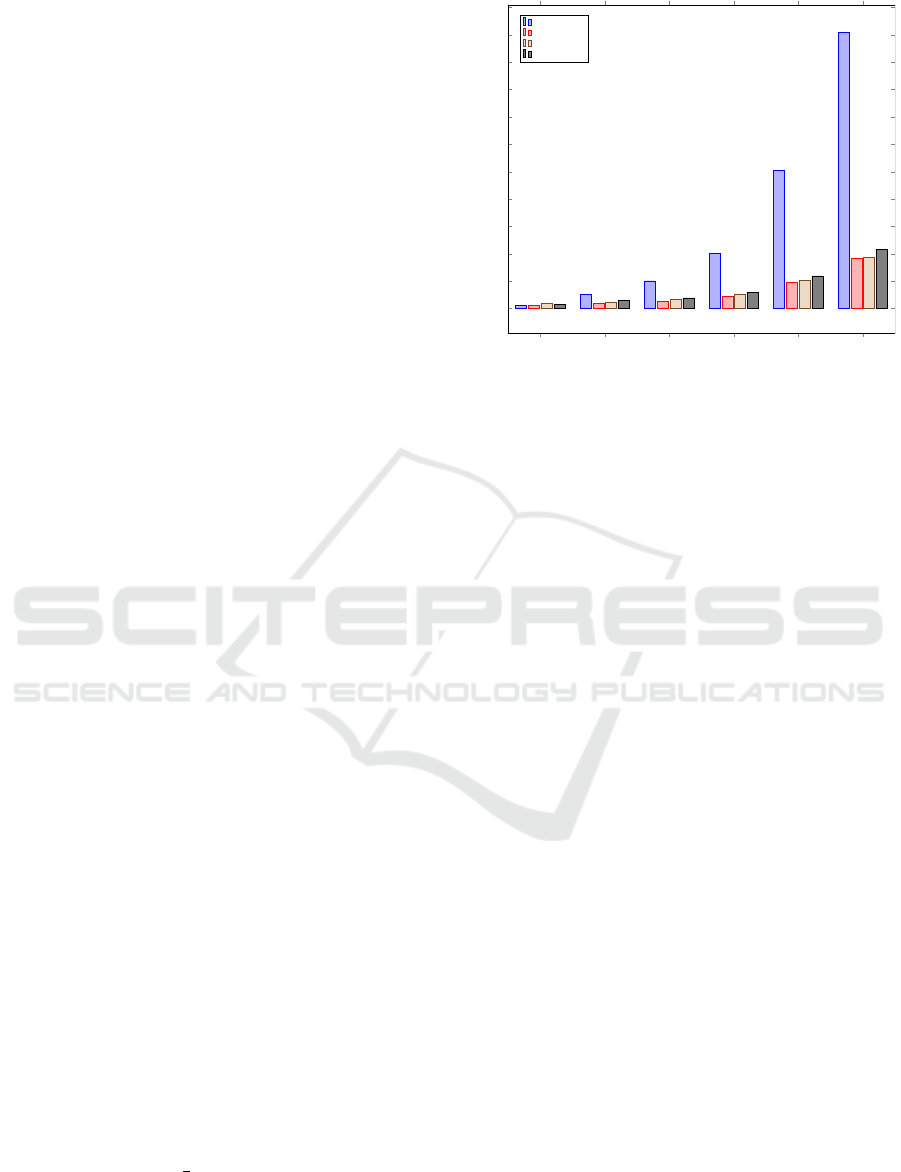
5.3.1 Particles Increase Benchmark

The ﬁrst evaluation part considers the algorithms ex-

ecuted with an increasing number of particles while

other parameters are ﬁxed. The goal is to under-

stand the effects of increasing only the particle num-

ber since each algorithm handles the particles differ-

ently. We aim to verify if these differences impact

on performance. The experiment setup was the fol-

lowing: # particles = 10, 50, 100, 200, 500, 1000; #

iterations = 10; # edge nodes = 10; # modules = 10;

and 50ms ﬁtness function artiﬁcial delay.

The observations in Fig. 3 indicate that for 10

particles the three distributed algorithms perform

marginally worse than a traditional PSO algorithm.

This can be expected as the overhead introduced by

Spark is here noticeable for a small optimization

problem. When the number of particles increases, the

distributed algorithms do get signiﬁcantly faster than

a traditional PSO implementation. On average, the

speedup achieved is ﬁve times, which is correlated to

the number of CPUs used for execution, which are in

this case six (3 pods with 2 cores each). This correla-

tion exists since if we have an amount of work x and

we spread this over n executors, this will result in the

best case scenario in a

amount of work per executor.

There are other differences between the dis-

tributed algorithms. Between DSPSO with the LU

and DU variants, there is a some performance gain

10 particles 50 particles 100 particles 200 particles 500 particles 1000 particles

100

150

200

250

300

350

400

450

500

550

Elapsed Time (seconds)

Traditional PSO

SDSPSO with LU

SDSPSO with DU

SDAPSO

Figure 3: Performance evaluation: change # of particles.

for the LU variant because of the in-memory update

of particles, which is slightly faster despite being at

the same time less fault-tolerant. The DAPSO algo-

rithm results in comparison to be the slowest of the

distributed algorithms because the synchronous algo-

rithms produce 1 job or 2 jobs per iteration depending

on the variant. The asynchronous algorithm produces

a number of jobs that is directly proportional to the

number of particles and iterations, thus introducing

additional overhead. An important aspect to note is

that DAPSO used on average more particles than the

other algorithms, caused by the rounding performed

by the algorithm.

5.3.2 Iterations Increase Benchmark

The second of the evaluations considers the algo-

rithms executed using an increasing number of iter-

ations and other parameters being ﬁxed. The goal

is to determine if more Spark jobs generated by the

synchronous algorithms impact on their performance.

This is caused, because we create 1 job or 2 jobs per

iteration, ultimately resulting in more Spark jobs be-

ing executed. The experiment setup was the follow-

ing: # particles = 20; # iterations = 10, 50, 100, 200,

500; # edge nodes = 10; # modules = 10; and 50ms

ﬁtness function artiﬁcial delay.

The observed results shown in Fig. 4 demon-

strate similar behavior to the earlier increase in par-

ticle numbers. However, one difference concerns the

further reduced performance of synchronous DSPSO

with DU compared to DSPSO with LU. With the

increase of iterations, the number of Spark jobs in-

creased signiﬁcantly. As an example, for 500 it-

erations the number of Spark jobs results in 1000

for DSPSO with DU and 500 for DSPSO with LU.

The observed performance difference is not signiﬁ-

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

200

10 iterations 50 iterations 100 iterations 200 iterations 500 iterations

100

150

200

250

300

350

400

450

500

550

Elapsed Time (seconds)

Traditional PSO

SDSPSO with LU

SDSPSO with DU

SDAPSO

Figure 4: Performance evaluation: change # of iterations.

cant, but indicates that the overhead of Spark must

be taken into account when choosing the right vari-

ant. As above, In general, we obtained here also a

ﬁve times speedup of the distributed algorithms com-

pared to the implemented traditional PSO. A similar

speedup shows that the algorithms perform equally

well irrespective of the speciﬁc parameters that have

been increased.

5.3.3 Dimensionality Increase Benchmark

The third evaluation form considers algorithms exe-

cuted with an increasing number of nodes and mod-

ules and again other parameters ﬁxed. The goal is

here to understand if an increase in problem dimen-

sionality affects the algorithm, especially because the

broadcast variables and accumulators can propagate

data that is tied to the dimensionality of the problem

(such as the accumulator that keeps track of the best

global position, which includes the entire matrix of

placements and errors). The experiment setup was the

following: # particles = 20; # iterations = 10; # edge

nodes = 5, 10, 20, 50, 70, 100, 200; # modules = 5,

10, 20, 50, 70, 100, 200; and 50ms ﬁtness function

artiﬁcial delay.

The results shown in Fig. 5 indicate that the num-

ber of nodes and modules does impact on the perfor-

mance of the algorithms. The impact on performance

is more noticeable for the distributed algorithms, due

to their usage of shared variables and the continuous

data transfer between nodes, that all internally per-

form serialization and deserialization activities. Fur-

thermore, there is also a slight increase in the elapsed

time across all algorithms because each stage of the

algorithm does effectively take more time, caused by

the quadratically increasing number of combinations

to be considered.

5 x 5 10 x 10 20 x 20 50 x 50 70 x 70 100 x 100 200 x 200

Elapsed Time (seconds)

Traditional PSO

SDSPSO with LU

SDSPSO with DU

SDAPSO

Figure 5: Performance evaluation: change # of nodes.

For this evaluation the number of particles is also

rounded for the DAPSO algorithm and it is more ev-

ident in this experiment due to the small number of

particles used.

5.4 Final Considerations

5.4.1 Discussion for DSPSO

Our DSPSO algorithms were designed to address the

performance problem of the traditional PSO, but also

through the technology stack fault tolerance. The per-

formance of the DSPSO algorithm is improved by

using multiple executor nodes that can evaluate the

ﬁtness function in parallel. The performance bene-

ﬁts are more clear for complex optimization problems

since here the overhead caused by Spark is less of a

concern. We can also note that the performance in-

crease is dependent on the cluster conﬁguration, in-

cluding the number of executor nodes, communica-

tion channels, the partitioning scheme, and also the

computational resources at each node. This does,

however, not imply that more nodes and partitions re-

sults in better algorithm performance, only because

the overhead introduced by Spark increases.

An important aspect regarding performance is that

the chosen problem encoding for DSPSO must take

into account the communication cost. This is notably

more than a traditional PSO solution. The most no-

ticeable improvement is to reduce the size and amount

of data propagated within the cluster (simpler data

structures or more efﬁcient serialization as examples)

as much as possible.

Fault tolerance is improved in comparison with

the non-distributed PSO due to the resiliency of

Spark’s RDDs. The RDD for the ﬁtness function eval-

uation and also velocity/position update can easily be

A Comparison of Synchronous and Asynchronous Distributed Particle Swarm Optimization for Edge Computing

201

redone if failures occur in the executor nodes. The

re-execution of the function evaluation produces de-

terministic results, while the re-execution of the latter

results in non-deterministic results due to the stochas-

tic nature of parameters used in velocity and position

updates. The non-determinism does not create prob-

lems but results in different positioning of some parti-

cles. Furthermore, the DU variant of the algorithm is

more fault-tolerant but less performant, caused by the

added distributed collection. This variant suits when

the velocity/position update is computationally more

demanding and more fault tolerance is needed.

The only possible point of failure of the DSPSO

variant is the driver program that manages the full al-

gorithm lifecycle including the state. Spark does not

provide a resiliency mechanisms for the driver, this

resiliency needs to be achieved at node level. A driver

failure could result in a full loss of data.

5.4.2 Discussion for DAPSO

The DAPSO implementation is designed to address

the performance problem, and also fault tolerance

compared to the traditional PSO while being executed

in an edge computing environment. The main ob-

servations of the DSPSO algorithm do also apply to

DAPSO. However, some further observations shall be

made.

The performance of DAPSO is dependent on the

SuperRDD size. This implies that a smaller Super-

RDD results in the lower performance but more asyn-

chrony as a trade-off, whereas a larger SuperRDD

results in better performance but lower asynchrony.

The choice of the SuperRDD size depends on avail-

able cluster resources, because an asynchronous algo-

rithm can be expected to perform better compared to a

synchronous variant when executed in an imbalanced

cluster. This performance difference becomes clear in

an imbalanced cluster because some nodes could re-

main idle while waiting for other slower nodes to end

with the ﬁtness evaluation of particles in their parti-

tion. Consequently, the more imbalanced the cluster

is, the fewer particles should be set within a Super-

RDD.

The algorithm’s fault tolerance is also on similar

to DSPSO. The fault tolerance of the driver can be

improved with a state replication of the driver across

multiple devices. However, this is out of scope for

this work as it would require a considerable amount

of exploration.

5.5 Synchronous vs Asynchronous

In conclusion, the synchronous and asynchronous de-

signs have proved to be both valid solutions during

our evaluations. However, they have slight differ-

ences that will play an important role when decid-

ing on the algorithm to use. Due to the mostly non-

deterministic nature of distributed systems, it is not

always possible to decide upfront which algorithm to

use, initial real-world testing could identify some sys-

tem characteristics for the decision.

The synchronous algorithm is simpler and more

efﬁcient in general because it runs a single Spark job

per iteration (two in the case of DSPSO with DU),

which translates to less overhead by Spark because

it will need to perform fewer optimizations, DAG

management, and lineage maintenance. Nevertheless,

DSPSO uses one more shared variable in contrast to

DAPSO, which is the accumulator used to keep track

of each best local position of each sub-swarm and to

compute the ﬁnal best global position. The usage of

an accumulator is certainly an additional overhead,

but in our tests we did not observe it to be noticeably

inﬂuential on the performance. DSPSO is also sim-

pler than the asynchronous design because it is based

on strict iterations and clearly deﬁned sequences of

operations that do not require any tricky implementa-

tion. The simplicity aspect as stated earlier is an im-

portant property of both algorithms, especially con-

sidering that they need to be adapted each time a new

problem encoding needs to be implemented.

The asynchronous algorithm, on the other hand,

is more complex and in general less efﬁcient than the

synchronous counterpart, however, it is meant to be

ﬂexible and suitable for speciﬁc use cases. Given the

fact that DAPSO has near to complete independence

between particles, depending on the conﬁgured Su-

perRDD size, it has the ability to work well in clus-

ters where the resources are imbalanced. An imbal-

anced cluster is characterized by a heterogeneous set

of nodes that have all different computational capa-

bilities and therefore will take different amounts of

time to perform the same tasks dispatched by Spark.

With the asynchronous algorithm, we are able to re-

alize ﬁne-grained parallelism, using a small Super-

RDD size in order to have several Spark jobs with

fewer particles executed concurrently. When faced

with multiple concurrent jobs, Spark will automati-

cally try to optimize as much as possible the available

cluster resources. For example, if a node is idle be-

cause it is faster than the others then Spark will start a

task that might belong to a different Spark job on the

idle node. A problem of DAPSO, besides the over-

head introduced by the high number of Spark jobs,

is the complexity of the implementation. The asyn-

chronous algorithm uses a multitude of concurrent

primitives and techniques to manage multiple jobs

and shared mutable states, therefore it is more com-

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

202

plex to work on and requires a careful modiﬁcation of

the core components.

In conclusion, both variants of the distributed

PSO algorithm have their advantages and disadvan-

tages. Due to the multitude of conﬁguration param-

eters available (e.g., SuperRDD size, number of par-

titions, nodes in the cluster, cores per node) it is not

possible to identify one as the "best" one. Therefore

only a real production setting will be able to identify

the most suitable variant for a speciﬁc use case – for

which we have given some indicators.

6 CONCLUSIONS

In this paper, we proposed distributed variants of

the PSO algorithm that were implemented on top of

Apache Spark, speciﬁcally an asynchronous variant

called DAPSO and two synchronous variants called

DSPSO with Local Update (LU) and Distributed Up-

date (DU). The variants provide options for different

performance and fault tolerance needs.

In our evaluation, we compared our solutions ex-

perimentally with the traditional PSO. We demon-

strated that our distributed algorithms perform bet-

ter than the traditional PSO, resulting on average in

a ﬁve times speed improvement. Only in small cases,

the traditional PSO solution performs better concern-

ing elapsed time, but does not provide either adequate

fault tolerance. Fault tolerance is also considered by

tailoring our distributed variants to speciﬁc features

offered by the implementation platforms. We pro-

vided indications in which particular situations one

of the three distributed variants would be most bene-

ﬁcial.

In the future, we intend to improve the perfor-

mance of our distributed algorithms by ﬁne-tuning

their implementation better to Apache Spark features.

In conclusion, also testing the algorithms in real-

world scenarios should be performed, to fully validate

our assumptions.

REFERENCES

Azimi, S., Pahl, C., and Shirvani, M. H. (2020). Parti-

cle swarm optimization for performance management

in multi-cluster iot edge architectures. In CLOSER,

pages 328–337.

Bonomi, F., Milito, R., Zhu, J., and Addepalli, S. (2012).

Fog computing and its role in the internet of things. In

MCC workshop. ACM.

Hoang, K. D., Wayllace, C., Yeoh, W., and et al. (2019).

New Distributed Constraint Satisfaction Algorithms

for Load Balancing in Edge Computing: A Feasibility

Study.

Kennedy, J. and Eberhart, R. (1995). Particle swarm op-

timization. In ICNN’95 International Conference on

Neural Networks. IEEE.

Li, A., Li, L., and Yi, S. (2022). Computation Ofﬂoad-

ing Strategy for IoT Using Improved Particle Swarm

Algorithm in Edge Computing. Wireless Communica-

tions and Mobile Computing, 2022:1–9.

Mahmud, R., Ramamohanarao, K., and Buyya, R. (2020).

Application Management in Fog Computing Environ-

ments: A Taxonomy, Review and Future Directions.

ACM Computing Surveys, 53(4):88:1–88:43.

Pahl, C. (2022). Research challenges for machine learning-

constructed software. Service Oriented Computing

and Applications.

Rodriguez, O., Le, V., Pahl, C., El Ioini, N., and Barzegar,

H. (2021). Improvement of Edge Computing Work-

load Placement using Multi Objective Particle Swarm

Optimization. In (IOTSMS’21).

Salaht, F. A., Desprez, F., and Lebre, A. (2020). An

Overview of Service Placement Problem in Fog

and Edge Computing. ACM Computing Surveys,

53(3):65:1–65:35.

Schutte, J. F., Reinbolt, J. A., Fregly, B. J., Haftka, R. T.,

and George, A. D. (2004). Parallel global optimiza-

tion with the particle swarm algorithm. Intl Jrnl for

Numerical Methods in Eng, 61(13):2296–2315.

Scolati, R., Fronza, I., El Ioini, N., Elgazazz, A. S. A., and

Pahl, C. (2019). A containerized big data streaming

architecture for edge cloud computing on clustered

single-board devices. In CLOSER.

Venter, G. and Sobieszczanski-Sobieski, J. (2006). Paral-

lel Particle Swarm Optimization Algorithm Acceler-

ated by Asynchronous Evaluations. Jrnl of Aerospace

Comp, Inform, and Comm, 3(3):123–137.

Wang, D., Tan, D., and Liu, L. (2018). Particle swarm

optimization algorithm: an overview. Soft Comp.,

22(2):387–408.

Zedadra, O., Guerrieri, A., Jouandeau, N., Spezzano,

G., Seridi, H., and Fortino, G. (2018). Swarm

intelligence-based algorithms within IoT-based sys-

tems: A review. Jrnl of Par and Distr Comp, 122:173–

187.

A Comparison of Synchronous and Asynchronous Distributed Particle Swarm Optimization for Edge Computing

203