Automata-Based Study of Dynamic Access Control Policies
Ahmed Khoumsi
a
Department of Electrical & Computer Engineering, Universit
´
e de Sherbrooke, Sherbrooke, Canada
Keywords:
Dynamic Access Control Policies, Deterministic and Nondeterministic Policies, Complete Policy,
Nonblocking Policy, Conflict-Free Policy, Automata-Based Design and Analysis.
Abstract:
Access control policies (more briefly: policies) are used to filter accesses to resources. A policy is usually
defined by a table of rules that specify which access requests (more briefly: requests) must be accepted and
which ones must be rejected. In this paper, we study dynamic policies which do not have a common definition
in the scientific community, but whose basic intuition is that the decision to accept or reject a request rq
depends not only on rq, but also on the history of what have preceded rq. In our case, it is the history of events
and requests that precede rq. An event indicates that a specific condition has just been met, for example “it is
midnight”. We formally specify the history of events and requests by associating a guard and an assignment
to each rule, and an assignment to each event. We show how to model, execute and analyze dynamic policies
using an automata-based approach. In the analysis, we verify several properties of a dynamic policy, such as
nonblocking, completeness, and absence of conflict. Deterministic as well as nondeterministic policies are
considered.
1 INTRODUCTION
Access control policies (more briefly: policies) are
used to filter access to resources and are usually de-
fined by a table of rules that specify which access
requests (more briefly: requests) are accepted and
which ones are rejected. The correct design and anal-
ysis of policies is paramount and has been addressed
by many researchers, such as (Sandhu et al., 1996;
Schneider, 2000; Mayer et al., 2000; Naldurg et al.,
2002; Kamara et al., 2003; Kalam et al., 2003; Al-
Shaer and Hamed, 2004; Wool, 2004; Fong, 2004;
Hoffman and Yoo, 2005; Yuan et al., 2006; Tschantz
and Krishnamurthi, 2006; Agarwal and Wang, 2007;
Chen and Feng, 2007; Mallouli et al., 2007; Liu
and Gouda, 2007; Sistla and Zhou, 2007; Bertolissi
et al., 2007; Liu and Gouda, 2008; Garcia-Alfaro
et al., 2008; Al-Shaer et al., 2009; Ligatti et al.,
2009; Acharya and Gouda, 2010; Acharya et al.,
2010; Liu and Gouda, 2010; Acharya and Gouda,
2011; Pozo et al., 2012; Cuppens et al., 2012; Mans-
mann et al., 2012; Madhuri and Rajesh, 2013; Garcia-
Alfaro et al., 2013; Karoui et al., 2013; Krombi et al.,
2014; Khoumsi et al., 2014; Elmallah and Gouda,
2014; Idrees et al., 2015; Reaz et al., 2015; Pardo
et al., 2016; Khoumsi et al., 2018; Khoumsi and Er-
a
https://orcid.org/0000-0003-4850-477X
radi, 2018; Reaz et al., 2019).
In this paper, we study dynamic policies which do
not have a common definition in the scientific com-
munity, but whose basic intuition is that the decision
to accept or reject a request rq depends not only on
rq, but also on the history of what have preceded rq.
In our case, it is the history of events and requests that
precede rq. An event indicates that a specific condi-
tion has just been met, for example “it is midnight”
or “the weekend begins”. We formally specify the
history of events and requests by associating a guard
and an assignment to each rule, and an assignment
to each event. Guards and assignments are formu-
lated using integer variables. Event Calculus (Kowal-
ski and Sergot, 1986) has been developed to study for-
mally events, but we do not need this framework for
the purpose of our study.
We show how to model and execute a dynamic
policy P by an automaton A
P
. Deterministic as well
as nondeterministic policies are considered. In the
case of a nondeterministic policy P , the obtained au-
tomaton A
P
is nondeterministic and is then trans-
formed in some way into a deterministic automaton
DA
P
. Then, by analyzing A
P
and DA
P
, we verify
whether P satisfies properties such as nonblocking,
completeness, and absence of conflict.
This is the organization of the paper: Sect. 2
presents dynamic policies, and Sect. 3 shows how to
218
Khoumsi, A.
Automata-Based Study of Dynamic Access Control Policies.
DOI: 10.5220/0011819700003405
In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 218-227
ISBN: 978-989-758-624-8; ISSN: 2184-4356
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

model and execute a deterministic dynamic policy us-
ing an automaton. In Sect. 4, we consider the case of
nondeterministic policies. Sect. 5 shows how to verify
properties of a dynamic policy, whether deterministic
or nondeterministic, by analyzing its automata-based
model. In Sect. 6, we present related work. A conclu-
sion is given in Sect. 7.
2 DYNAMIC POLICIES
2.1 Static Policies
A static policy is defined by a set of rules, where each
rule is noted c/d, d is the decision Accept or Reject,
and c is a condition. c is specified by sets of values
F
1
,··· , F
m
of several (say m) fields, and every ac-
cess request rq is specified by m values f
1
,· ·· , f
m
.
c is said to be satisfied by rq (which is termed as: rq
matches the rule c/d), if for every j = 1,···m: f
j
be-
longs to F
j
. The semantics of applying a rule c/d is
that: if a request rq satisfies c, then take decision d for
rq.
The decision to accept or reject a given rq takes
into account all the rules that are matched by rq. For
example, let us consider a firewall policy where the
requests correspond to packets arriving at the firewall.
The condition of each rule is defined by four fields
IPsrc, IPdst, Port and Protocol and is specified in the
form (u, v,x, y) where u, v, x and y are sets of values of
the four fields, respectively. A rule is therefore speci-
fied in the form (u,v,x,y)/d which means: Apply de-
cision d to any request rq that comes from an address
in u, is destined to an address in v, and is transmitted
through a port in x by a protocol in y. Table 1 shows
two examples of that type of rules.
2.2 Dynamic Policies: Generalization of
Static Policies
The intuition of a dynamic policy is that the decision
to accept or reject a request rq depends not only on
rq, but also on the history of events and requests that
precede rq. Formally, we specify a dynamic policy by
a table of rules and events based on a set of integer
variables V = {v
1
,· ·· , v
p
} which are initially equal to
0. A rule is defined by c/d (as in the static case) and
by a guard g and an assignment a defined as follows,
where k is a positive integer:
g is a set of Boolean expressions in the forms “v
i
≥
k” and “v
i
<k”. g is said to be true if all the Boolean
expressions that compose it are true. A rule is said to
be enabled if its guard is true. The absence of guard
(i.e. emptiness of g) in a rule R is noted “-” and means
that R is enabled whatever the history.
a is a set of assignments in the forms “v
i
:=v
i
+1”
and “v
i
:=0”. The absence of assignment (i.e. empti-
ness of a) in a rule R is noted “-” and means that the
application of R does not modify any variable of V ,
and hence is not taken into account in the history of
requests and events.
As in the static case, applying a rule R defined by
(c/d, g, a) means: taking the decision d for an access
request rq, if rq satisfies c. The difference with the
static case is that:
• a rule R is applied to rq, only if it is enabled; (i.e.
its g is true);
• when R is applied to rq, the assignment a is ap-
plied.
In addition to rules, a dynamic policy also has events.
An event indicates that a condition has just been met
(e.g. “it is midnight”). An event has an assignment,
but not a guard.
Table 2 shows an example of an event and two
rules R
1
and R
2
of a dynamic policy based on two
integer variables u and v. u counts the number of
times R
1
is applied in a complete day (i.e. between
two events “it is midnight”). v counts the number
of times R
2
is applied between two applications of
R
1
. Concretely: among all requests in a full day (i.e.
from 0:00 to the next 0:00) that meet the conditions of
R
1
, the policy accepts the first 2 requests; and among
all requests which meet the conditions of R
2
between
these first 2 acceptances, the policy rejects the first 3
requests.
3 AUTOMATA-BASED
MODELING AND EXECUTION
OF DYNAMIC POLICIES
In order to analyze and execute a dynamic policy P
(in Sect. 5), we will first model its table of rules and
events by an automaton A
P
that executes P . We pro-
ceed in three steps described in the following subsec-
tions. To clarify the “mechanics” of each step, we
will use the simple example of Table 3 with a single
field “Type” that corresponds to the type of document
(image, video, audio) desired by a request. The vari-
able v counts the number of times R
2
is applied be-
tween two applications of R
1
. The dynamic policy
of Table 3 specifies that between two applications of
R
1
, there may be: at most two applications of R
2
fol-
lowed by any number of applications of R
3
. More
concretely, the policy specifies that between two ac-
Automata-Based Study of Dynamic Access Control Policies
219

Table 1: Example of two rules of a static policy.
Rule IPsrc IPdst Port Protocol Decision
R
1
190.170.15.0/24 80.15.15.0/24 25, 81 TCP Accept
R
2
190.170.15.0/24 80.15.15.0/24 25, 83 UDP Reject
Table 2: Example of an event and two rules of a dynamic policy.
Event assignment
It is midnight u := 0
Rule IPsrc IPdst Port Protocol Decision guard assignment
R
1
190.170.15.0/24 80.15.15.0/24 25,81 TCP Accept u< 2 u := u+1
v := 0
R
2
190.170.15.0/24 80.15.15.0/24 25,83 UDP Reject v< 3 v:=v+1
cesses to a video or an image, there may be at most
two accesses to an audio.
Table 3: Illustrative example of dynamic policy.
Rule Type Decision guard assignment
R
1
Image, Video Accept - v := 0
R
2
Audio Accept v < 2 v := v + 1
R
3
Audio Reject v ≥ 2 -
3.1 Step 1: Specifying the Policy by a
1-Location Automaton
The table of rules and events of P is rewritten in
the form of a node (called location) with selfloop
transitions as follows: each rule defined by c/d, g
and a is represented by a selfloop transition labeled
(c/d, g, a); and each event e with an assignment a
is represented by a selfloop transition labeled (e, a).
The two types of transitions are naturally called rule-
transitions and event-transitions, respectively. Such a
description is named 1-location automaton and noted
L
P
.
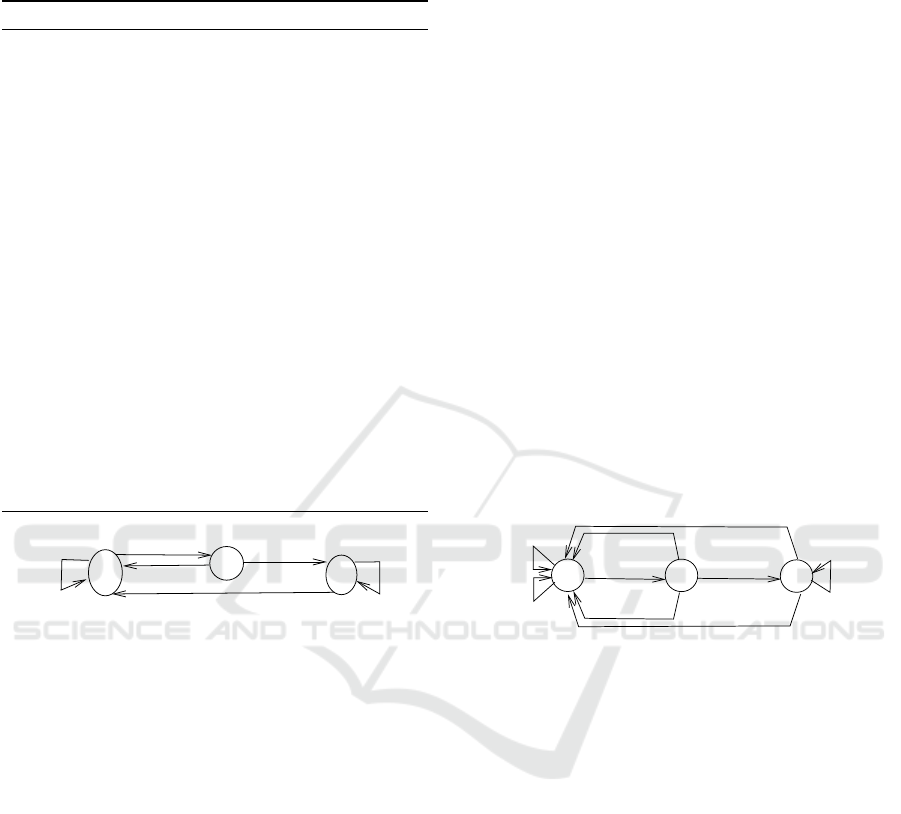
For example, the 1-location automaton of Fig. 1
is obtained from Table 3. The label of each rule-
transition is written in two lines: c/d in line 1, and
g,a in line 2. An empty g or a is noted -. A and R
mean Accept and Reject, respectively. Im, Vid and
Aud denote the three types of resources. This exam-
ple has no event-transition.
{Im,Vid}/A
-, v := 0
{Aud}/R
v>2, -
{Aud}/A
v<2, v := v+1
Figure 1: Step 1: 1-location automaton modeling the policy
of Table 3.
3.2 Step 2: Constructing an Automaton
A
∗
P
The 1-location automaton L
P
is transformed into a fi-
nite state automaton A
∗
P
which specifies explicitly all
the possible sequences of rules and events. Before
continuing, we redefine the assignments of the vari-
ables used in P as follows: For every variable v
i
, let
k
i
be the greatest value to which v
i
is compared in the
guards of L
P
. When v
i
has the value k
i
, its increment-
ing is useless because it has no effect on the guards of
L
P
. Hence, we redefine the assignment “v
i
:= v
i
+ 1”
as:
• if v
i
< k
i
then v
i
:= v
i
+ 1
This redefinition allows to obtain a finite state automa-
ton.
Let V = {v
1
,· ·· , v
p
} be the set of integer vari-
ables used in P . Each state of A
∗
P
is defined by
a p-tuple (`
1
,· ·· ,`
p
), where `
i
is a value of v
i
, for
i = 1, ·· · , p. A
∗
P
is constructed iteratively from L
P
as
shown in Algorithm 1. Firstly, we construct the ini-
tial state q
0
=(0,· ·· , 0), because every variable is ini-
tially equal to 0. Then, we consider every enabled
rule-transition of L
P
(labeled (c/d, g, a)), and every
event-transition of L
P
(labeled (e, a)). For each con-
sidered transition, we construct the state r obtained by
applying a to q
0
, and then we construct the transition
q
0
x
−→ r, where x is in the form c/d or e, depending
on the transition. These operations are iterated to ev-
ery constructed state, until all constructed states are
treated. The number of iterations is finite because, as
explained above, each variable v
i
of V takes its value
in the finite domain {0,1, ·· · ,k
i
}.
Fig. 2 represents the automaton A
∗
P
obtained from
the 1-location automaton L
P
of Fig. 1. As already ex-
plained, since v is compared uniquely to 2, then when
v is equal to 2, its incrementation does not change its
value. Therefore, v takes uniquely the values 0, 1,
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
220

and 2, that correspond respectively to the three states
of the automaton of Fig. 2.
Algorithm 1: Construction of the automaton A
∗
P
.
Input: Single-location automaton L
P
Output: Finite state automaton A
∗
P
1: A
∗
P
is initialized with the p-tuple state q
0
= (0,· ·· , 0)
2: The set S of states to be treated is initialized as {q
0
}
3: while S 6=
/
0 do
4: Select a state q = (x
1
,x
2
,· ·· , x
p
) in S
5: Remove q from S
6: for each rule-transition of L
P
labeled c/d, g, a do
7: if g is True for the valuation (x
1
,· ·· , x
p
) then
8: Let r = (y
1
,· ·· , y
p
) be the result of applying a to q
9: if A
∗
P
does not contain r then
10: Add the state r to A
∗
P
and S
11: end if
12: Add to A
∗
P
the transition q
c/d
−−→ r
13: end if
14: end for
15: for each event-transition of L
P
labeled e and a do
16: Let r =(y
1
,· ·· , y
p
) be the result of applying a to q
17: if A
∗
P
does not contain r then
18: Add the state r to A
∗
P
and S
19: end if
20: Add to A
∗
P
the transition q
e
−→ r
21: end for
22: end while
{Aud}/A
{Im,Vid}/A
{Aud}/R
{Aud}/A
1
0
2
{Im,Vid}/A
{Im,Vid}/A
Figure 2: Step 2: automaton A
∗
P
obtained from L
P
of Fig. 1.
3.3 Step 3: Constructing an Automaton
A
P
That Executes P
In this step, we consider only the rule-transitions of
A
∗
P
, i.e. which are labeled in the form c/d, where
d is a decision Accept or Reject (noted A or R), and
c is a condition defined by a m-tuple (F
1
,· ·· , F
m
),
where each F
j
is a set of values of one of the m
fields. Equivalently, c represents the Cartesian prod-
uct F
1
×···×F
m
. For simplicity, we do not distinguish
c and its corresponding Cartesian product.
We determine in A
∗
P
a basis B = (b
1
,· ·· , b
p
) that
respects the following three points: 1) every b
i
is a
Cartesian product of sets of values of the m fields;
2) b
i
and b
j
are disjoint for every i 6= j; 3) for every
label c/d of a rule-transition, the Cartesian product
corresponding to c is a union of some (maybe all) of
the b
i
of B.
Then, every rule-transition q
c/d
−−→ r of A
∗
P
is split
into the rule-transitions q
c
1
/d
−−→ r,··· ,q
c
k
/d
−−→ r, where
c
1
,· ·· , c
k
are the components of B that constitute c,
i.e. c = c
1
∪ ·· · ∪ c
k
and every c
i
is one of the b
j
of B.
Let A
P
denote the obtained automaton.
For example, from A
∗
P
of Fig. 2, we obtain A
P
of
Fig. 3, where the basis B consists of the singletons
{Im}, {Vid} and {Aud}. Since only one field is con-
sidered, the Cartesian product is not used. For clarity,
the number 1, 2 or 3 in each transition indicates that
the corresponding rule is R
1
, R
2
or R
3
, respectively.
We have the following definition and result:
Definition 1. The automaton A
P
obtained at step 3 is
said to be nondeterministic, if from some state there
exist two or more rule-transitions with the same label
(in the form b
k
/d) that lead to different states. Other-
wise, A
P
is deterministic.
Proposition 1. Provided that it is deterministic, A
P
executes (or implements) the policy P .
Since A
P
of Fig. 3 is deterministic, let us explain
in an example how it executes the policy P of Ta-
ble 3. Consider that a request to an image is followed
by two consecutive requests to an audio. In the corre-
sponding A
P
of Fig. 3, the first request (to an image)
is accepted by executing the selfloop 0
Im/A
−−−→ 0, then
the following two requests (to an audio) are accepted
by executing 0
Aud/A
−−−−→ 1 and 1
Aud/A
−−−−→ 2.
0
1
2
Aud/A
Vid/A
Aud/R
Im/A
Aud/A
Vid/A
Im/A
Im/A
Vid/A
1
1
1
1
1
2
3
1
2
Figure 3: Step 3: automaton A
P
obtained from A
∗
P
of Fig. 2.
4 HOW TO PROCESS
NONDETERMINISTIC
DYNAMIC POLICIES
In Sect. 3, we studied the case of deterministic dy-
namic policies, that is, every policy P for which we
obtain a deterministic automaton A
P
. Let us now sug-
gest how to deal with a nondeterministic policy P .
i.e. whose automaton A
P
is nondeterministic. We
will illustrate our proposition with the policy of Ta-
ble 4, which specifies that between two applications
of R
1
, there may be: at most two applications of R
2
followed by any number of applications of R
3
. Intu-
itively, this policy is nondeterministic because there
are situations (satisfying v < 2) where a request to an
image is accepted by both R
1
and R
2
which affect the
future differently (since they have different effects on
v).
If we apply the three steps of Sect. 3 to the policy
of Table 4, we obtain the automaton A
P
of Fig. 4. This
Automata-Based Study of Dynamic Access Control Policies
221

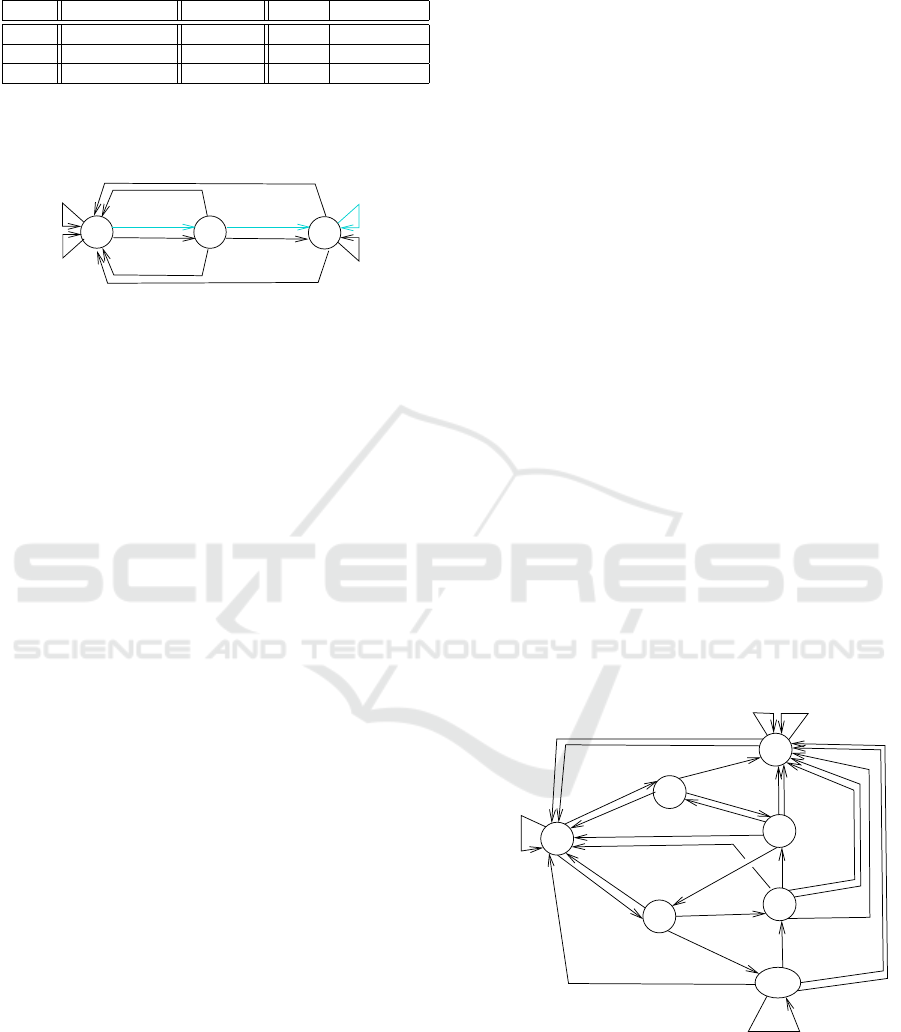
Table 4: Illustrative example of nondeterministic dynamic
policy.
Rule Type Decision guard assignment
R
1
Image, Video Accept - v := 0
R
2
Image, Audio Accept v < 2 v := v + 1
R
3
Image, Audio Reject v ≥ 2 -
automaton is nondeterministic, because state 0 (resp.
1) has two transitions labeled Im/A that lead to states
0 and 1 (resp. 0 and 2).
0
1
2
Aud/A
Im/A
Vid/A
Aud/R
Im/A
Im/R
Aud/A
Im/A
Vid/A
Im/A
Im/A
Vid/A
1
1
1
1
1
2
2
3
3
1
2
2
Figure 4: Nondeterministic automaton A
P
obtained from
Table 4.
As we will see in Sect. 5, a nondeterministic A
P
can be used to analyze properties of P , but it cannot
be used to execute P . A solution is therefore to trans-
form A
P
in some way into a deterministic automaton
DA
P
. We see two possible transformation methods
which are presented in Sects. 4.1 and 4.2, respectively.
If A
P
is deterministic, DA
P
denotes A
P
.
4.1 Method 1 to Obtain a Deterministic
Automaton
This method is applicable if there is a total priority
order between the rules, for example each R
i
has more
priority than R
j
if j > i. Concretely, if a request rq
matches several enabled rules, only the most priority
of them is applied to rq. Formally, in each state q
of A
P
, among any set of outgoing rule-transitions of
q with the same b
k
in their labels, we keep only the
most priority of these transitions (i.e. the transition
corresponding to the most priority rule).
Let us consider A
P
of Fig. 4, assuming that the
rules are ordered in decreasing priority. In state 0,
among the two transitions labeled “Im/A” (of R
1
and
R
2
), we remove the transition of R
2
. In state 1, among
the two transitions labeled “Im/A” (of R
1
and R
2
), we
remove the transition of R
2
. In state 2, among the
two transitions labeled “Im/A” and “Im/R” (of R
1
and
R
3
), we remove the transition of R
3
. We obtain the
deterministic automaton of Fig. 3. That is, if we apply
a decreasing order to the rules of the nondeterministic
policy of Table 4, we obtain the policy of Table 3.
The difference between the nondeterministic policy
(Table 4 and Fig. 4) and the resulting deterministic
policy (Table 3 and Fig. 3) is represented in blue.
4.2 Method 2 to Obtain a Deterministic
Automaton
This method is applicable if there is no priority be-
tween the rules, i.e. all the rules have the same prior-
ity. Intuitively, if a request rq matches several enabled
rules, all these rules are applied to rq at the same time.
Formally, DA
P
is computed by applying the automa-
ton determinization procedure to A
P
.
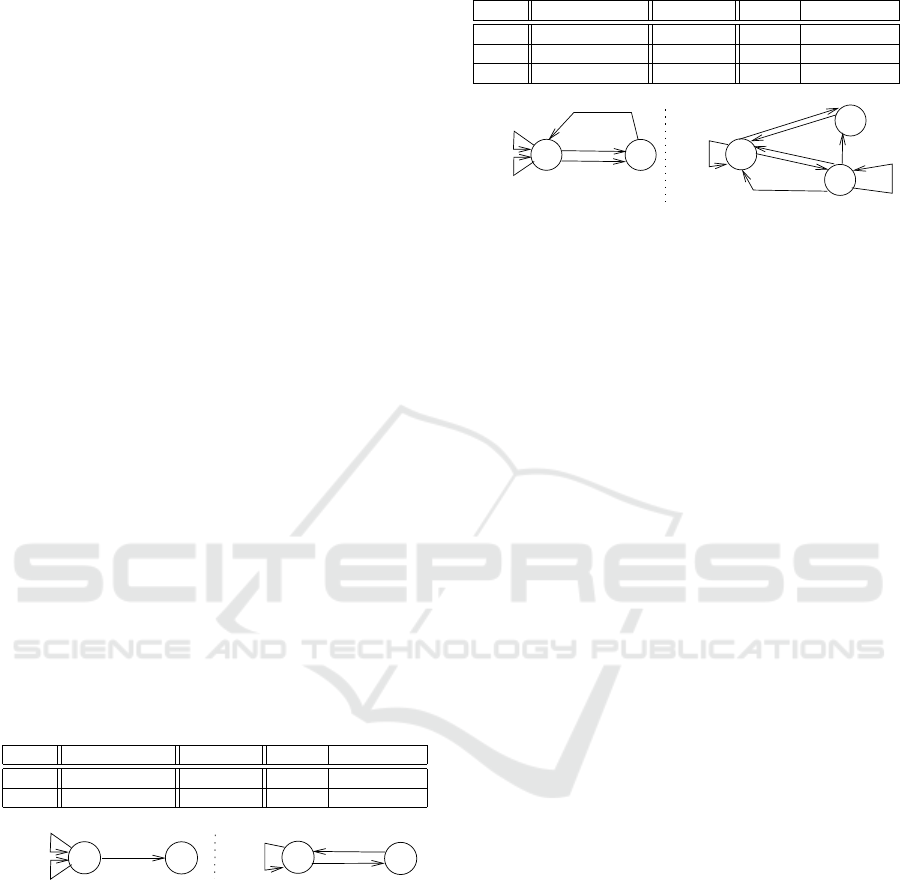
For example, determinization of A
P
of Fig. 4 gen-
erates the deterministic automaton DA
P
represented
in Fig. 5. Consider the same scenario as in Sect. 3.3,
i.e. a request to an image is followed by two con-
secutive requests to an audio. In the corresponding
DA
P
of Fig. 5, the first request (to an image) is ac-
cepted by executing 0
Im/A
−−−→ (0,1), then the follow-
ing request (to an audio) is accepted by executing
(0,1)
Aud/A
−−−−→ (1,2). Finally, the third request (to an
audio) might be accepted by executing (1,2)
Aud/A
−−−−→ 2,
or rejected by executing (1,2)
Aud/R
−−−−→ 2. Concretely,
both R
1
and R
2
are applied to the first request which
implies that v has a “superposition” of values 0 and
1 (hence the state (0,1)). Then, R
2
is applied to the
second request which implies an incrementation of v
(from (0, 1) to (1,2)), hence v has a “superposition”
of values 1 and 2. Then, R
2
(resp. R
3
) is enabled to be
applied to the third request, due to the value 1 (resp.
2) of v. The fact that the audio can be both accepted
and rejected from state (1,2) corresponds to a conflict
which is studied in Sect. 5.3.
2
1
0
Im/A
Im/R Aud/R
Vid/A
Aud/A
0,1
0,2
1,2
0,1,2
Vid/A
Vid/A
Vid/A
Vid/A
Vid/A
Vid/A
Im/A
Im/A
Im/A
Im/A
Im/A
Im/A
Im/R
Im/R
Im/R
Aud/A
Aud/A
Aud/A
Aud/A
Aud/A
Aud/R
Aud/R
Aud/R
Figure 5: Method 2: DA
P
obtained by determinizing A
P
of
Fig. 4.
An inconvenient of method 2 is that the deter-
minization procedure can be very costly.
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
222

5 DYNAMIC POLICY ANALYSIS
We have seen in Sects. 3 and 4 how to construct a de-
terministic automaton DA
P
that models and executes
a dynamic policy P . We will first show how to ver-
ify properties of P by analyzing its automaton DA
P
.
Then we will show that A
P
can be used to verify prop-
erties of a nondeterministic P treated using Method 2.
5.1 Verifying Nonblocking
Definition 2. A dynamic policy is said to be blocked
when it is in a situation (reached after a sequence of
requests and events) where all its rules are disabled
and remain disabled for ever, hence the policy be-
comes totally unapplicable forever. A dynamic policy
is said to be nonblocking if there exists no situation
where it is blocked.
Blocking is therefore an undesirable property
which must be detected. The following Prop. 2 pro-
vides a necessary and sufficient condition on DA
P
so
that P is nonblocking.
Proposition 2. A dynamic policy is nonblocking if
and only if: DA
P
has no deadlock state
1
and no cy-
cle of states from which only events (and no rule) are
executable.
For example, the dynamic policy of Table 4 is non-
blocking with both methods 1 and 2, because there is
no event in this example and there is no deadlock in
automata DA
P
of Figs. 3 and 5 obtained with meth-
ods 1 and 2, respectively.
5.2 Verifying Completeness
Definition 3. A dynamic policy is said to be complete,
if for every request rq that follows any execution of
sequence of requests and events, there exists one or
more enabled rules that match rq.
Definition 4. The basis B = (b
1
,· ·· , b
p
) (defined in
Sect. 3.3) is said to be complete, if b
1
∪ ··· ∪ b
p
is
equal to the set of all possible values of the m fields.
The following Prop. 3 provides a necessary and
sufficient condition on DA
P
for completeness of P .
Proposition 3. A dynamic policy P is complete if and
only if: the basis B is complete, and every state of
DA
P
has an outgoing transition labeled b
k
/A or b
k
/R
for every component b
k
of B.
Consider for example the policy P of Table 4,
whose basis is B = ({Im},{Vid},{Aud}). With both
methods 1 and 2, every state of DA
P
of Figs. 3 and 5
1
A deadlock state is a state without outgoing transitions.
has outgoing transitions labeled Im/d, Vid/d and
Aud/d. Therefore, from Prop. 3, the policy is com-
plete with both methods if and only if B is complete,
i.e. if and only if Im, Vid and Aud are the only types
supported by the system whose access is controlled
by P .
Remark 1. If a policy is complete, then it is non-
blocking.
5.3 Conflict Detection
Definition 5. Two rules of a dynamic policy P are
said to be conflicting if the following four points hold:
1) both rules have the same priority, 2) there exists a
request rq that matches both rules, 3) there exists a
situation (reached after a sequence of requests and
events) where the guards of both rules are true, and
4) the decisions of the two rules are different (one is
Accept, the other is Reject). A policy is said to be
conflicting if it has conflicting rules. Otherwise, the
policy is said to be nonconflicting.
Intuitively, two rules R
i
and R
j
are conflicting if
after the policy has processed a sequence λ of requests
and events, R
i
and R
j
do not agree on the decision to
take for some request following λ.
The following Prop. 4 provides a necessary and
sufficient condition on DA
P
for the existence of con-
flicts in P .
Proposition 4. A dynamic policy P contains conflict-
ing rules, if and only if DA
P
has a state with a pair of
outgoing transitions labeled b
k
/A and b
k
/R respec-
tively.
For example, when treated with method 2, the
nondeterministic policy of Table 4 contains conflicts
because in each of the states (0,2), (1, 2) and (0, 1,2)
of the deterministic automaton DA
P
of Fig. 5, there
exist two transitions labeled Im/A and Im/R and two
transitions labeled Aud/A and Aud/R. Also, in state
2, there exist two transitions labeled Im/A and Im/R.
Remark 2. A nondeterministic dynamic policy which
is treated using method 1 is conflict-free, because its
rules do not satisfy the first condition of Def. 5.
5.4 Additional Results Related to
Method 2
With method 2, the nondeterministic A
P
is equivalent
to the deterministic DA
P
that executes the policy, in
the sense that the two automata accept the same lan-
guage. A question that arises with method 2 is then:
Why use DA
P
instead of A
P
for verifying nonblock-
ing, completeness and conflicts? The answer is that if
Automata-Based Study of Dynamic Access Control Policies
223

we use A
P
, we obtain the following Props. 5, 6 and 7,
which are more restrictive than Props. 2, 3 and 4 that
were obtained using DA
P
. Indeed, the latter have
necessary and sufficient conditions, while the former
have sufficient conditions.
Proposition 5. With method 2, a dynamic policy is
nonblocking, if A
P
has no deadlock state.
Proposition 6. With method 2, a dynamic policy P is
complete if: the basis B is complete, and every state of
A
P
has an outgoing transition labeled b
k
/A or b
k
/R
for every component b
k
of B.
Proposition 7. With method 2, a dynamic policy P
contains conflicting rules, if A
P
has a state with a
pair of outgoing transitions labeled b
k
/A and b
k
/R
respectively.
Let us illustrate the fact that the sufficient condi-
tions of Props. 5, 6 and 7 (which are related to A
P
) are
not necessary.
Consider the toy policy P of Table 5 and assume
that images and videos are the only supported types.
We obtain the automata A
P
and DA
P
of Fig. 6. From
Prop. 2, P is nonblocking because DA
P
has no dead-
lock. However, the sufficient condition of Prop. 5 is
not satisfied, because state 1 of A
P
is a deadlock.
From Prop. 3, P is complete because the ba-
sis B = ({Im},{Vid}) is complete, and every state
of DA
P
has outgoing transitions labeled Im/A and
Vid/A. However, the sufficient condition of Prop. 6
is not satisfied because state 1 of A
P
has no outgoing
transition Im/d and Vid/d.
Table 5: Example to illustrate the fact that the sufficient
conditions of Props. 5 and 6 are not necessary.
Rule Type Decision guard assignment
R
1
Image, Video Accept v < 1 v := 0
R
2
Image Accept v < 1 v := v + 1
0
1
0
0,1
Im/A
Im/A
Vid/A
Im/A
Vid/A
Vid/A
(a)
(b)
Figure 6: Automata obtained from Table 5: (a) A
P
;
(b) DA
P
.
Consider now the toy policy P of Table 6 and
assume that the only supported types are image, au-
dio and video. We obtain the automata A
P
and DA
P
of Fig. 7. From Prop. 4, P is conflicting because
state (0,1) of DA
P
has outgoing transitions labeled
Im/A and Im/R. However, the sufficient condition of
Prop. 7 is not satisfied because in the automata A
P
,
state 0 has only transitions with the decision Accept,
and state 1 has a unique transition.
Table 6: Example to illustrate the fact that the sufficient
condition of Prop. 7 is not necessary.
Rule Type Decision guard assignment
R
1
Image, Video Accept v < 1 v := 0
R
2
Image, Audio Accept v < 1 v := v + 1
R
3
Image Reject v ≥ 1 v := 0
0
1
0
0,1
1
Im/A
Im/A
Vid/A
Im/A
Vid/A
(a)
(b)
Aud/A
Im/R
Im/A
Aud/A
Aud/A
Im/R
Im/R
Vid/A
Figure 7: Automata obtained from Table 6: (a) A
P
;
(b) DA
P
.
6 RELATED WORK
There exist several methods that provide practical al-
gorithms of logical analysis of policies, for example
for testing (Hoffman and Yoo, 2005), configuration
error analysis (Wool, 2004) and vulnerability detec-
tion (Kamara et al., 2003). Other more fundamental
methods provide analysis algorithms with estimations
of time complexities, such as (Acharya and Gouda,
2011; Liu and Gouda, 2010; Acharya and Gouda,
2010; Al-Shaer et al., 2009; Liu and Gouda, 2008).
(Elmallah and Gouda, 2014) show that the analyses
of several problems of policies are NP-hard. Several
methods are based on the automata model (Schneider,
2000; Fong, 2004; Ligatti et al., 2009).
There exist several approaches to design and ana-
lyze policies, such as those used in (Liu and Gouda,
2008; Acharya et al., 2010; Reaz et al., 2015; Reaz
et al., 2019), which are respectively referred to as
“diverse policy design”, “divide-and-conquer”, “step-
wise refinement” and “bottom-up design”.
(Pozo et al., 2012) propose CONFIDDENT, a
model-driven design, development and maintenance
framework for firewalls.
(Mallouli et al., 2007) propose a framework to
generate test sequences to check the conformance of
a policy to a specification. The system behavior is
described by an extended automaton (Lee and Yan-
nakakis, 1996) and the policy that we wish to apply
to this system is described by OrBAC (Kalam et al.,
2003).
Several methods have been developed to detect
anomalies in policies or discrepancies between poli-
cies, such as in (Madhuri and Rajesh, 2013; Al-Shaer
and Hamed, 2004; Karoui et al., 2013; Garcia-Alfaro
et al., 2013; Cuppens et al., 2012; Garcia-Alfaro et al.,
2008; Liu and Gouda, 2008). (Madhuri and Rajesh,
2013) defines an anomaly in a policy by the exis-
tence of at least one request that matches several rules
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
224

of the policy. (Al-Shaer and Hamed, 2004; Karoui
et al., 2013) present techniques to detect anomalies
in a policy, where a policy is specified by a Policy
tree in (Al-Shaer and Hamed, 2004) and a Decision
tree in (Karoui et al., 2013). (Garcia-Alfaro et al.,
2013; Cuppens et al., 2012) propose methods to study
stateful anomalies. (Garcia-Alfaro et al., 2008) pro-
poses mechanisms to detect anomalies in configura-
tion rules of policies. (Liu and Gouda, 2008) shows
how to detect discrepancies between several designs
of the same policy, where the policy is modeled by
a Firewall Decision Diagram (FDD) defined in (Liu
and Gouda, 2007).
Interesting work is also found in (Khoumsi et al.,
2018; Reaz et al., 2019; Khoumsi and Erradi, 2018).
(Khoumsi et al., 2018) suggests an automata-based
method to design and analyze policies. (Reaz et al.,
2019) suggest a bottom-up design method of policies
specified as policy expressions. A policy expression
looks like a boolean expression, where policies are
composed using three operators: ¬, ∧, ∨. (Khoumsi
and Erradi, 2018) adapt the automata-based method
of (Khoumsi et al., 2018) to the context of (Reaz et al.,
2019), i.e. to design policies specified as policy ex-
pressions.
Several tools have been developed to analyze and
design policies, such as the engines Fireman (Yuan
et al., 2006) and Fang (Mayer et al., 2000). In (Mans-
mann et al., 2012), a tool is proposed to visualize and
analyze firewall configurations. (Tschantz and Krish-
namurthi, 2006) investigate the suitability of various
policy languages (e.g. XACML) to reason on proper-
ties, and hence to analyze policies by checking their
properties.
The above references study static policies. Dy-
namic policies have been studied by several re-
searchers, e.g. (Naldurg et al., 2002; Agarwal and
Wang, 2007; Chen and Feng, 2007; Idrees et al.,
2015; Sistla and Zhou, 2007; Pardo et al., 2016). Al-
though there is no common definition of a dynamic
policy, the various suggested definitions have in com-
mon that a dynamic policy is evolutive, in the sense
that its behavior depends on the history. The authors
of (Bertolissi et al., 2007) use term rewriting (Baader
and Nipkow, 1998) to develop Dynamic Event-Based
Access Control (DEBAC) which is a dynamic ver-
sion of Role-Based Access Control (RBAC) (Sandhu
et al., 1996). We have adopted a different approach
which uses the automata model and is based more on
Attribute-Based Access Control (ABAC) than RBAC.
Other researchers have also adopted the automata
model, but their automata describe quite different as-
pects than our automata. For example, in the au-
tomata of (Pardo et al., 2016), each state corresponds
to a whole policy and a transition models the passing
from one policy to another. To our best knowledge, no
work has studied in detail nondeterministic dynamic
policies where rules have the same priority (i.e. our
method 2).
7 CONCLUSION
We suggest a simple and precise definition of dynamic
policies and develop an automata-based method to
study them. More precisely, we show how to model
and execute a dynamic policy P by an automaton A
P
.
In the case of a nondeterministic policy P , the ob-
tained automaton A
P
is nondeterministic and is then
transformed in some way into a deterministic automa-
ton DA
P
. We consider the case where the rules of the
policy are prioritized, as well as the case where all
rules have the same priority. We show how to verify
properties of P by analyzing DA
P
and A
P
. In the anal-
ysis, we verify three properties of a dynamic policy:
nonblocking, completeness, and absence of conflict.
We plan to: 1) investigate how to develop dynamic
policies that are intrinsically deterministic, to avoid
the computational cost of determinization; 2) imple-
ment our method and investigate the relevance of us-
ing dynamic policies in concrete examples; 3) study
dynamic policies with more general guards and as-
signments.
REFERENCES
Acharya, H., Joshi, A., and Gouda, M. (2010). Firewall
Modules and Modular Firewalls. In IEEE Int. Confer-
ence on Network Protocols (ICNP), pages 174–182.
Acharya, H. B. and Gouda, M. G. (2010). Projection and
Division: Linear Space Verification of Firewalls. In
30th IEEE Int. Conf. on Distributed Computing Sys-
tems (ICDCS), pages 736–743, Genova, Italy.
Acharya, H. B. and Gouda, M. G. (2011). Firewall Ver-
ification and Redundancy Checking are Equivalent.
In 30th IEEE Int. Conf. on Computer Communication
(INFOCOM), pages 2123–2128, Shanghai, China.
Agarwal, A. and Wang, W. (2007). DSPM: Dynamic Secu-
rity Policy Management for Optimizing Performance
in Wireless Networks. In Military Communications
Conference(MILCOM 2006).
Al-Shaer, E. and Hamed, H. (2004). Modeling and Man-
agement of Firewall Policies. IEEE Transactions on
Network and Service Management, 1(1):2–10.
Al-Shaer, E., Marrero, W., El-Atawy, A., and Elbadawi,
K. (2009). Network Configuration in a Box: To-
wards End-to-End Verification of Networks Reacha-
bility and Security. In 17th IEEE Int. Conf. on Net-
Automata-Based Study of Dynamic Access Control Policies
225

work Protocols (ICNP), pages 736–743, Princeton,
NJ, USA.
Baader, F. and Nipkow, T. (1998). Term rewriting and all
that. Cambridge University Press, Great Britain.
Bertolissi, C., Fernandez, M., and Barker, S. (2007). Dy-
namic event-based access control as term rewriting. In
S. Barker and G.J. Ahn, editor, Data and Applications
Security XXI (DBSec), Lecture Notes in Computer
Science 4602, Redondo Beach, CA, USA. Springer,
Berlin, Heidelberg.
Chen, L. and Feng, D. (2007). Dynamic Security Policy for
Credential-based Storage Systems. In International
Conference on Convergence Information Technology),
Gyeongju, South Korea.
Cuppens, F., Cuppens-Boulahia, N., Garcia-Alfaro, J.,
Moataz, T., and Rimasson, X. (2012). Handling State-
ful Firewall Anomalies. In 27th IFIP International
Information Security and Privacy Conference (SEC),
pages 174–186, Heraklion, Crete, Greece.
Elmallah, E. and Gouda, M. G. (2014). Hardness of Fire-
wall Analysis. In Intern. Conf. on NETworked sYS-
tems (NETYS), Marrakesh, Morocco.
Fong, P. (2004). Access control by tracking shallow exe-
cution history. In IEEE Symposium on Security and
Privacy (S&P), Berkeley, CA, USA.
Garcia-Alfaro, J., Cuppens, F., and Cuppens-Boulahia, N.
(2008). Complete Analysis of Configuration Rules to
Guarantee Reliable Network Security Policies. Inter-
national Journal of Information Security, 7(2):103–
122.
Garcia-Alfaro, J., Cuppens, F., Cuppens-Boulahia, N.,
Perez, S. M., and Cabot, J. (2013). Management of
Stateful Firewall Misconfiguration. Computers and
Security , 39:64–85.
Hoffman, D. and Yoo, K. (2005). Blowtorch: A Frame-
work for Firewall Test Automation. In Proc. 20th
IEEE/ACM Int. Conf. on Automated Software Engi-
neering (ASE), pages 96–103, Long Beach, Califor-
nia, USA.
Idrees, M., Ayed, S., and Cuppens-Boulahia, N. (2015). Dy-
namic Security Policies Enforcement and Adaptation
Using Aspects. In IEEE Trustcom/BigDataSE/ISPA,
Helsinki, Finland.
Kalam, A. A. E., Baida, R. E., Balbiani, P., Benferhat,
S., Cuppens, F., Deswarte, Y., Mi
`
ege, A., Saurel, C.,
and Trouessin, G. (2003). Organization Based Access
Control. In IEEE 4th International Workshop on Poli-
cies for Distributed Systems and Networks (POLICY),
Lake Come, Italy.
Kamara, S., Fahmy, S., Schultz, E., Kerschbaum, F., and
Frantzen, M. (2003). Analysis of Vulnerabilities in In-
ternet Firewalls. Computers and Security, 22(3):214–
232.
Karoui, K., Ftima, F. B., and Ghezala, H. B. (2013). For-
mal Specification, Verification and Correction of Se-
curity Policies Based on the Decision Tree Approach.
International Journal of Data & Network Security,
3(3):92–111.
Khoumsi, A. and Erradi, M. (2018). Automata-Based
Bottom-Up Design of Confict-Free Policies Specified
as Policy Expressions. In Intern. Conf. on NETworked
sYStems (NETYS), Essaouira, Morocco.
Khoumsi, A., Erradi, M., and Krombi, W. (2018). A Formal
Basis for the Design and Analysis of Firewall Security
Policies. Journal of King Saud University-Computer
and Information Sciences, 30(1):51–66.
Khoumsi, A., Krombi, W., and Erradi, M. (2014). A Formal
Approach to Verify Completeness and Detect Anoma-
lies in Firewall Security Policies. In 7th Intern. Sym-
posium on Foundations & Practice of Security (FPS),
Montreal, Canada.
Kowalski, R. and Sergot, M. (1986). A logic-based calculus
of events. New Gener Comput, 4:67–95.
Krombi, W., Erradi, M., and Khoumsi, A. (2014).
Automata-Based Approach to Design and Analyze
Security Policies. In Intern. Conf. on Privacy, Security
and Trust (PST), Toronto, Canada.
Lee, D. and Yannakakis, M. (1996). Principles and Methods
of Testing Finite State Machines - A Survey. Proceed-
ing of the IEEE, 84:1090–1126.
Ligatti, J., Bauer, L., and Walker, D. (2009). Run-time En-
forcement of Nonsafety Policies. ACM Transactions
on Information and System Security (TISSEC), 12(3).
Liu, A. and Gouda, M. (2008). Diverse Firewall Design.
IEEE Transactions on Parallel and Distributed Sys-
tems, 19(9):1237–1251.
Liu, A. and Gouda, M. (2010). Complete Redundancy
Removal for Packet Classifiers in TCAMs. IEEE
Transactions on Parallel and Distributed Systems,
21(4):424–437.
Liu, A. X. and Gouda, M. G. (2007). Structured Firewall
Design. Computer Networks: The International Jour-
nal of Computer and Telecommunications Network-
ing, 51(4):1106–1120.
Madhuri, M. and Rajesh, K. (2013). Systematic Detection
and Resolution of Firewall Policy Anomalies. Inter-
national Journal of Research in Computer and Com-
munication Technology (IJRCCT), 2(12):1387–1392.
Mallouli, W., Orset, J., Cavalli, A., Cuppens, N., and Cup-
pens, F. (2007). A Formal Approach for Testing Secu-
rity Rules. In 12th ACM symposium on Access control
models and technologies (SACMAT), Sophia Antipo-
lis, France.
Mansmann, F., T. G
¨
obel, and Cheswick, W. (2012). Visual
Analysis of Complex Firewall Configurations. In 9th
International Symposium on Visualization for Cyber
Security (VizSec), pages 1–8, Seattle, WA, USA.
Mayer, A., Wool, A., and Ziskind, E. (2000). Fang: A Fire-
wall Analysis Engine. In Proc. of the IEEE Sympo-
sium on Security and Privacy, pages 177–187, Berke-
ley, California, USA.
Naldurg, P., Campbell, R., and Mickunas, M. (2002). De-
veloping dynamic security policies. In DARPA Active
Networks Conference and Exposition.
Pardo, R., Colombo, C., Pace, G., and Schneider, G. (2016).
An Automata-based Approach to Evolving Privacy
Policies for Social Networks. In International Con-
ference on Runtime Verification (RV 2016), Madrid,
Spain.
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
226

Pozo, S., Gasca, R., Reina-Quintero, A., and Varela-Vaca,
A. (2012). CONFIDDENT: A Model-Driven Con-
sistent and Non-Redundant Layer-3 Firewall ACL
Design, Development and Maintenance Framework.
Journal of Systems and Software, 85(2):425–457.
Reaz, R., Acharya, H., Elmallah, E., Cobb, J., and Gouda,
M. (2019). Policy Expressions and the Bottom-
Up Design of Computing Policies. Computing,
101:1307–1326.
Reaz, R., Ali, M., Gouda, M., Heule, M., and Elmallah, E.
(2015). The implication Problem of Computing Poli-
cies. In Int. Symposium on Stabilization, Safety, and
Security of Distributed Systems, pages 109–123, Mar-
rakesh, Morocco.
Sandhu, R., Coyne, E., Feinstein, H., and Youman, C.
(1996). Role-based access control models. IEEE
Computer, 29(2):38–47.
Schneider, F. B. (2000). Enforceable Security Policies.
ACM Transactions on Information and System Secu-
rity (TISSEC), 3(1).
Sistla, A. and Zhou, M. (2007). Analysis of dynamic poli-
cies. Information and Computation, 206:185–212.
Tschantz, M. and Krishnamurthi, S. (2006). Towards rea-
sonability properties for access-control policy lan-
guages. In ACM Symposium on Access control mod-
els and technologies (SACMAT), pages 160–169, Lake
Tahoe, CA, USA.
Wool, A. (2004). A Quantitative Study of Firewall Config-
uration Errors. Computer, 37(6):62–67.
Yuan, L., Mai, J., Su, Z., Chen, H., Chuah, C.-N., and Mo-
hapatra, P. (2006). FIREMAN: A Toolkit for FIRE-
wall Modeling and Analysis. In IEEE Symposium on
Security and Privacy (S&P), Berkeley/Oakland, CA,
USA.
Automata-Based Study of Dynamic Access Control Policies
227