Novel Topic Models for Content Based Recommender Systems

Kamal Maanicshah, Manar Amayri and Nizar Bouguila

Concordia Institute for Information Systems Engineering, Concordia University, Montreal, Quebec, Canada

Keywords:

Topic Biterm Models, Generalized Dirichlet Distribution, Beta-Liouville Distribution, Mixture Allocation,

Recommender Systems.

Abstract:

Content based recommender systems play a vital role in applications related to user suggestions. In this paper,

we introduce novel topic models which help tackle the recommendation task. Being one of the prominent

approaches in the ﬁeld of natural language processing, topic models like latent Dirichlet allocation (LDA) try

to identify patterns of topics across multiple documents. Due to the proven efﬁciency of generalized Dirichlet

allocation and Beta-Liouville allocation in recent times, we use these models for better performance. In

addition, since it is a known fact that co-occurences of words are commonplace in text documents, the models

have been designed with this reality in mind. Our models follow a mixture based design to achieve better

topic quality. We use variational inference for estimating the parameters. Our models are validated with two

different datasets for recommendation tasks.

1 INTRODUCTION

Recommendation systems have become an insepa-

rable part of a variety of online services like web

search, news articles, movies, etc. in recent years

(Pazzani and Billsus, 2007). Most of the recent ad-

vancement in this ﬁeld is centred on collaborative ﬁl-

tering (Bobadilla et al., 2011) and content based ﬁl-

tering (Pazzani and Billsus, 2007). While the for-

mer method is based on modelling the activities of

users with similar behaviour in a platform, the later

works on modelling the likes of an individual user in

the platform. Both approaches have their own merits

and are used depending on the task at hand. In this

article, we explore a content based recommender sys-

tem based on novel topic models. Topic modelling

refers to an unsupervised learning approach that ex-

tracts topics from documents and groups the words

belonging to each topic. Latent Dirichlet allocation

(LDA) is one of the most famous topic models used

for this purpose (Blei et al., 2003). Since the intro-

duction of LDA a number of research ideas have been

proposed to improve the vanilla model to suit differ-

ent applications. For example, there is demonstra-

tion of LDA being used to model multilingual top-

ics simultaneously (Mimno et al., 2009). This would

help in tagging documents appropriately irrespective

of language. Another improvement over LDA which

can be used for supervised classiﬁcation of images

has also proved to be effective (Chong et al., 2009).

LDA has also been used for creating recommenda-

tion systems (Nagori and Aghila, 2011). LDA can

extract topics from the description of user activity

which could help suggest new items that the user

might be interested in. It is well known that models

which take into account, the co-occurrences of words,

tend to give a boost for topic modelling tasks (Opper

and Saad, 2001). This made us to choose a design

which incorporates the possibility of bigram words

such as ‘Thank you’, ‘high school’, etc. Recent re-

search has shown that using mixture models in con-

junction with LDA helps in extracting better topics

(Opper and Saad, 2001). In our models we will in-

tegrate this idea to improve recommendations. There

has also been studies, involving the use of alternative

priors other than Dirichlet for the prior of topic pro-

portions in a document. Generalized Dirichlet (GD)

and Beta-Liouville (BL) distributions have proved to

be efﬁcient substitutes for Dirichlet (Bakhtiari and

Bouguila, 2016; Bakhtiari and Bouguila, 2014). Gen-

eralized Dirichlet (GD) distribution has a general co-

variance structure which might help to better ﬁt the

data, as compared to Dirichlet which has a nega-

tive covariance structure. The drawback of GD how-

ever, is that twice the number of parameters have to

be estimated than Dirchlet distribution. BL distribu-

tion helps to overcome this drawback and also sports

a general covariance matrix. Based on these theo-

138

Maanicshah, K., Amayri, M. and Bouguila, N.

Novel Topic Models for Content Based Recommender Systems.

DOI: 10.5220/0011826700003467

In Proceedings of the 25th International Conference on Enterprise Information Systems (ICEIS 2023) - Volume 1, pages 138-145

ISBN: 978-989-758-648-4; ISSN: 2184-4992

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

retical grounds and experimental proofs, we decided

to use these distributions as priors in our model to

provide a better ﬁt to the data. Parameters estima-

tion plays a crucial role in machine learning models.

Most of the approaches on LDA based models men-

tion variational inference and Gibbs sampling as ef-

fective methods for estimating the parameters (Blei

et al., 2003; Liu et al., 2020). However, in the case of

pure Bayesian approaches such us Gibbs sampling,

computations are not always tractable for complex

priors (Attias, 1999). Variational inference on the

other hand, approximates the posterior probability in-

stead of calculating it which gives guaranteed conver-

gence (Hu et al., 2019). Hence, we choose variational

inference as our parameter estimation method. Fur-

thermore, as opposed to the frequently used method

for inferring the variational solutions as established

in (Blei et al., 2003), we employed the method used

for mixture models in (Fan et al., 2012). This makes

the mathematical computation of variational solutions

easier. We evaluate our model, with two challenging

datasets. One of them is for anime recommendation

and the other is for recommendation of movies from

netﬂix. We estimate the performance of the model

based on coherence score for both datasets. In addi-

tion, since we had enough ground truth data to vali-

date the netﬂix dataset, we estimate the accuracy of

predictions as well. The rest of the paper is organized

as follows: The description of the proposed models is

given in Section 2. This is followed by the variational

algorithm to estimate the parameters in Section 3. The

experiments performed on the datasets with our mod-

els are detailed in Section 4. We ﬁnally conclude in

Section 5 with our ﬁndings.

2 MODEL DESCRIPTION

Let us assume that we have a set of D documents in

a corpus. We denote the number of words in a doc-

ument d = 1, 2,...,D by N

. For the n

word among

words in a document d, w

can be represented as

a V dimensional indicator vector, where w

dnv

= 1 if

the word w

is the v

word in the vocabulary and

0 otherwise. We also have another latent variable

Z = {~z

} which speciﬁes, to which among the K

topics the word has maximum afﬁnity. z

dnk

follows a

similar convention that z

dnk

= 1 if the word belongs to

the k

topic of the K different topics and 0 otherwise.

The distribution of words for a topic k is given by a

multinomial with parameters

which has a Dirichlet

prior with parameter

. p(

θ | Φ) is the distribution of

the prior for the topic proportions for the documents

and takes the form of GD or BL distributions with

parameter Φ. In addition to this, we also have an-

other latent variable Y = (~y

,~y

,...,~y

) correspond-

ing to the mixture model which is an L dimensional

one hot encoded indicator vector showing which com-

ponent the document belongs to. Hence, y

= 1 if

the document is sampled from the l

component and

0 if not. Y in turn is sampled from a multinomial

distribution with parameters

π = (π

,π

,...,π

) with

the constraints, 0 ≤ π

≤ 1 and

∑

l=1

. According

to these assumptions, for a corpus W containing D

documents, we can write the marginal as,

p(W |

π,

Φ,

β) =

∏

d=1



∑

| y

Φ)p(y

π)



∏

n=1

∑

p(w

d(n−1)

| z

β)

p(z

)

(1)

where

Φ,

β are the parameters of the prior distribu-

tion for document topic proportions and topic word

proportions respectively. Here, w

d(n−1)

= v

n−1

and

= v

incorporates the dependency of adjacent

words to the topic latent variable. Based on this gen-

eral structure, we can deﬁne the priors based on GD

and BL distributions as mentioned in the following

subsections.

2.1 Latent Generalized Dirichlet

Bi-Term Mixture Allocation

(Bi-LGDMA)

In the case of Bi-LGDMA, the prior for the topic

proportions is generated from a GD distribution.

Let us consider a GD distribution with parameters

(σ

,σ

,...,σ

,τ

,...,τ

). The probability den-

sity function of the topic proportions can be written

as,

) =

∏

k=1

Γ(τ

+ σ

)

Γ(τ

)Γ(σ

)

−1

1−

∑

j=1

d j

(2)

where, γ

= τ

−τ

l(k+1)

−σ

l(k+1)

for k = 1, 2, ...,K −

1 and γ

= σ

− 1 for k = K. As mentioned ear-

lier, owing to the fact that using a mixture model over

the topic proportions helps improve the model (Chien

et al., 2018), we introduce mixture models as,

|~y

σ,

τ) =

∏

l=1

∏

k=1

Γ(τ

+ σ

)

Γ(τ

)Γ(σ

)

−1

1 −

∑

j=1

d j

(3)

Novel Topic Models for Content Based Recommender Systems

139

The latent variable Y is governed by a multinomial

distribution with parameter

π which is the mixing

weights for the mixture model. This is denoted by

p(y

π) =

∏

l=1

. Contrary to bigrams where the

probability of two words occurring together is consid-

ered, we take into account that logically these bigrams

end up belonging to the same topic and consider them

as bi-terms associated with the same topic. This gives

us,

p(w

d(n−1)

| z

β) =

∏

k=1



∏

v=1

d(n−1)(v−1)

dnv



dnk

(4)

The relation between the topic proportions and la-

tent variable ~z

is given by the multinomial p(z

) =

∏

k=1

dnk

. In general, it is well known that

introducing conjugate prior over the undetermined

parameters helps improve parameter estimation (Fan

et al., 2012). However, in the case of GD the conju-

gate priors are intractable. Due to this reason, we in-

troduce Gamma prior for the parameter

σ as p(σ

) =

G(σ

| υ

,ν

) =

Γ(υ

)

−1

−ν

, where G(·)

indicates a Gamma distribution. Similarly, follow-

ing the same convention, the prior for

τ is given by,

p(τ

) = G(τ

| s

). In addition, we also apply

variational smoothing as mentioned in (Blei et al.,

2003) which helps to eliminate problems that arise

due to sparsity in data. Assuming a Dirichlet prior

over

β we can deﬁne,

) =

Γ(

∑

v=1

)

∏

v=1

Γ(λ

)

∏

v=1

−1

(5)

We assume a GD distribution over

given by the

equation,

|~g

) =

∏

k=1

Γ(g

+ h

)

Γ(g

)Γ(h

)

−1

1 −

∑

j=1

d j

(6)

where, ζ

= h

− g

d(k−1)

− h

d(k−1)

while k ≤

K −1 and ζ

= h

− 1 when k = K. This helps us in

deriving the variational solutions. Thus, considering

the parameters Θ = {Z,

β,

θ,

σ,

τ,~y}, the joint poste-

rior distribution can be written as,

p(W,Θ) =p(

W | Z,

β)p(~z |

θ)p(

θ |

σ,

τ,~y)p(~y |

π)

× p(

θ |~g,

h)p(

β |

λ)p(

σ |

υ,

ν)p(

τ |

(7)

2.2 Latent Beta-Liouville Bi-Term

Mixture Allocation (Bi-LBLMA)

By following similar assumptions, we can construct

our Bi-LBLMA model with some changes. The basic

idea here is to replace the prior for topic proportions

with BL distribution. Considering a BL distribution

with parameters (µ

,µ

,...,µ

,σ

,τ

), we can write

the prior as,

|~µ,

σ,

τ) =

∏

l=1

∏

k=1

Γ(

∑

k=1

)

∏

k=1

Γ(µ

)

Γ(σ

+ τ

)

Γ(σ

)Γ(τ

)

−1

∑

k=1

−

∑

k=1

1 −

∑

k=1

−1

(8)

Assuming Gamma priors for the parameters quot-

ing the same reasons for Bi-LGDMA, the priors ar

given by, G(µ

| υ

,ν

), G(σ

| s

) and G(τ

Ω

,Λ

) respectively. The variational distribution for

the topic proportions in the case of Bi-LBLMA con-

sequently takes the form,

) =

∏

k=1

Γ(

∑

k=1

)

∏

k=1

Γ( f

)

Γ(g

+ h

)

Γ(g

)Γ(h

)

−1

∑

k=1

−

∑

k=1

1 −

∑

k=1

−1

(9)

The rest of the equations are the same as men-

tioned in previous subsection. Making these changes,

we can write the posterior joint probability for Bi-

LBLMA as,

p(W,Θ) =p(

W | Z,

β)p(~z |

θ)p(

θ |~µ,

σ,

τ,~y)p(~y |

π)

× p(

θ |

f ,~g,

h)p(

β |

λ)p(~µ |

υ,

ν)

× p(

σ |

t)p(

τ |

Ω,

Λ) (10)

where Θ = {Z,

β,

θ,~µ,

σ,

τ,~y} represents the parame-

ters of the model.

3 VARIATIONAL INFERENCE

Having deﬁned the model, the next step is to estimate

the parameters. In this article we use the variational

method used in (Fan et al., 2012). The basic idea

of variational inference is to assume a distribution

Q(Θ) which is bound to be the approximation of the

true posterior p(W | Θ) and then minimize the differ-

ence between the two distributions until they are sim-

ilar. This is done by calculating the Kullback-Leibler

(KL) divergence between the two distributions. The

equation to ﬁnd KL divergence between Q(Θ) and

p(W | Θ) can be written as,

KL(Q || P) = −









W | Θ









dΘ (11)

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

140

We can simplify this equation as,

KL(Q || P) = ln p(W ) − L(Q) (12)

where, L(Q) =









W,Θ









dΘ is the lower

bound. Theoretically, when KL(Q || P) is 0 the dis-

tributions must be identical. Hence, maximizing the

lower bound L(Q) will minimize the value of KL di-

vergence and consequently bring the value closer to

0. By following mean-ﬁeld theory (Opper and Saad,

2001) we consider the parameters to be independent

of each other since the true posterior becomes in-

tractable otherwise. Q(Θ) can now be written as the

product of the individual parameters as Q(Θ) =

∏

j=1

with J being the total number of parameters.The opti-

mal solution for each of the parameters can be found

by calculating the expectations of all the parameters

except the current parameter. This can be expressed

as,





exp



ln p



W,Θ



6= j

exp



ln p



W,Θ



6= j

dΘ

(13)

Once initiated with some random values, the varia-

tional solutions are updated iteratively and thus low-

ering the lower bound. The optimal variational so-

lutions for all the parameters are obtained at conver-

gence. The variational solutions for our models are

given in the following subsections.

3.1 Variational Solutions for

Bi-LGDMA

Calculating the variational solutions for Eq. 7 yields

the following equations:

Q(Y ) =

∏

d=1

∏

l=1

,Q(Z) =

∏

d=1

∏

N=1

∏

k=1

dnk

(14)

σ) = G(

σ |

∗

),Q(

τ) = G(

τ |

∗

) (15)

β) =

∏

k=1

∏

v=1

Γ(

∑

v=1

∗

)

∏

v=1

Γ(λ

∗

)

∗

−1

(16)

θ) =

∏

d=1

∏

k=1

Γ(g

∗

+ h

∗

)

Γ(g

∗

)Γ(h

∗

))

∗

−1

1−

∑

j=1

d j

∗

(17)

where,

∑

l=1

,φ

dnk

∑

k=1

dnk

,π

∑

d=1

(18)

=exp

(

lnπ

∑

k=1

(σ

−1)



lnθ



+γ

1−

∑

j=1

d j

)

(19)

dnk

= exp





d(n−1)(v−1)

+ w

dnv



lnβ





lnθ





(20)

Here, R is the taylor series approximations of



Γ(σ+τ)

Γ(σ)Γ(τ)



and is given by,

R = ln

Γ(σ + τ)

Γ(σ)Γ(τ)

+ σ



Ψ(σ + τ) − Ψ(σ)



(



lnσ



− ln σ)

+ τ



Ψ(σ + τ) − Ψ(τ)



(



lnτ



− ln τ)

+ 0.5σ



(σ + τ) − Ψ

(σ)



(lnσ − ln σ)



+ 0.5τ



(σ + τ) − Ψ

(τ)



(lnτ − ln τ)



+ σ τΨ

(σ + τ)(



lnσ



− ln σ)(



lnτ



− ln τ)

(21)

∗

=υ

∑

d=1







+ τ



− Ψ





+ τ



+ τ



lnτ



− ln τ



(22)

∗

∑

d=1







+ σ



− Ψ





+ σ



+ σ



lnσ



− ln σ



(23)

∗

= ν

−

∑

d=1





lnθ



(24)

∗

= t

−

∑

d=1





1 −

∑

j=1

d j

(25)

∗

= g

∑

n=1



dnk



∑

l=1





(26)

∗

= h

∑

l=1





∑

kk=k+1

dn(kk)

(27)

∗

= λ

∑

d=1

∑

n=1

∑

v=1

dnk



d(n−1)v

+ w

dnv



(28)

∑

d=1

(29)

In the above equations,





indicates the expectation

of the variable, whose values are detailed in (Maan-

icshah et al., 2023). We calculate equations 14 - 17

by repetitively updating the parameters until there is

no considerable change in the lower bound estimates.

At this point of convergence, we will have the optimal

values for the variational solutions.

Novel Topic Models for Content Based Recommender Systems

141

3.2 Variational Solutions for LBLMA

Similar to the previous section, we can derive the fol-

lowing variational solutions for Eq. 10. The only dif-

ference is the apparent change in Q(

θ) and some def-

initions of related variables. The variational solutions

are hence given by,

Q(Y ) =

∏

d=1

∏

l=1

,Q(Z) =

∏

d=1

∏

N=1

∏

k=1

dnk

(30)

Q(~µ) = G(~µ

∗

υ∗,

∗

),Q(σ

) = G(σ

| s

) (31)

Q(τ

)=G(τ

| Ω

,Λ

),Q(

β)=

∏

k=1

∏

v=1

Γ(

∑

v=1

∗

)

∏

v=1

Γ(λ

∗

)

∗

−1

(32)

θ) =

∏

d=1

∏

k=1

Γ(

∑

k=1

∗

)

Γ( f

∗

)

Γ(g

∗

+ h

∗

)

Γ(g

∗

)Γ(h

∗

)

∗

−1

∑

k=1

∗

−

∑

k=1

∗

1 −

∑

k=1

∗

−1

(33)

where,

∑

l=1

,φ

dnk

∑

k=1

dnk

,π

∑

d=1

(34)

=exp

(

lnπ

+ R

+ S

+ (µ

− 1)



lnθ





−

∑

k=1

D



∑

k=1



+ (τ

− 1)

1 −

∑

k=1

)

(35)

Due to intractability, we use Taylor series expansions

for



Γ(

∑

k=1

)

Γ(σ

)



and



Γ(σ+τ)

Γ(σ)Γ(τ)



denoted by R and

S respectively. The approximations are given as,

=ln

Γ(

∑

k=1

)

∏

k=1

Γ(µ

)

∑

k=1



∑

k=1



− Ψ(µ

)



lnµ



− ln µ



∑

k=1



∑

k=1



− Ψ

(µ

)



(lnµ

− ln µ

)



∑

a=1

∑

b=1,a6=b



∑

k=1





lnµ



− ln µ



lnµ



− ln µ



S =ln

Γ(σ + τ)

Γ(σ)Γ(τ)

+ σ



Ψ(σ + τ) − Ψ(σ)



(



lnσ



− ln σ)

+ τ



Ψ(σ + τ) − Ψ(τ)



(



lnτ



− ln τ)

+ 0.5σ



(σ + τ) − Ψ

(σ)



(lnσ − ln σ)



+ 0.5τ



(σ + τ) − Ψ

(τ)



(lnτ − ln τ)



+ σ τΨ

(σ + τ)(



lnσ



− ln σ)(



lnτ



− ln τ)

(36)

∗

=υ

∑

d=1







∑

k=1



− Ψ(µ

)

+ Ψ



∑

k=1



∑

a6=k



lnµ



− ln µ



(37)

∗

= ν

−

∑

d=1







lnθ



−

∑

k=1

(38)

∗

∑

d=1







+ τ



− Ψ





+ τ



+ τ



lnτ



− ln τ



(39)

∗

= t

−

∑

d=1





∑

k=1

(40)

Ω

∗

=Ω

∑

d=1







+ σ



− Ψ





+ σ



+ σ



lnσ



− ln σ



(41)

∗

= Λ

−

∑

d=1





1 −

∑

k=1

(42)

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

142

∗

= f

∑

n=1



dnk



∑

l=1





(43)

∗

= g

∑

n=1

∑

k=1



dnk



∑

l=1





(44)

∗

= h

∑

l=1





(45)

The expectations in these equations are deﬁned with

respect to BL distribution in (Maanicshah et al.,

2022). Similar to Bi-LBLMA, we calculate equations

30 - 33 repeatedly until convergence to ﬁnd the opti-

mal solutions.

4 EXPERIMENTAL RESULTS

To evaluate the performance of our model, we build a

system for anime recommendation based on a dataset

in Kaggle containing information about anime

and

another for recommending movies based on data from

netﬂix prize data

. We compare our model with

widely used LDA and examine how our models weigh

up against unmodiﬁed latent generalized Dirichlet al-

location (LGDA) and latent Beta-Liouville allocation

(LBLA) models. The idea of our recommendation

system is that we ﬁnd the Euclidean distance between

the document topic proportions φ

of the query doc-

ument and the rest of the documents. We can then

ﬁnd the top N recommendations for that query. The

following subsections detail our experiments for the

two datasets.

4.1 Anime Recommendation

This dataset consisted of 2 ﬁles containing informa-

tion about anime, reviews of users and user proﬁle

details. The anime ﬁle had around 16K anime de-

tails like, title, synopsis, genre, airing date, etc. The

proﬁles ﬁle had details of users and the anime they

have added as favourites. The reviews ﬁle has infor-

mation on the reviews the user has written for differ-

ent anime. All these data has been extracted from

https://myanimelist.net. From the anime details ﬁle,

the data that helps for content based recommenda-

tion is mainly the synopsis. However, the synopsis

was not available for some of the anime within the

data. Hence we used the myanimelist API to extract

https://www.kaggle.com/datasets/marlesson/myanimelist-

dataset-animes-proﬁles-reviews

https://www.kaggle.com/datasets/netﬂix-inc/netﬂix-

prize-data

missing synopsis. There were cases in which some

of the titles refer to a parent anime and the descrip-

tion of parent anime was taken in these cases. We

ignore anime where the synopsis is too short. After

applying these constraints we were left with around

1126 anime to use for our content based recommen-

dation system. In the case of this dataset, there were

a very few user proﬁles who had more than 20 anime

in their favourites list which was not enough to eval-

uate our models. To understand the relevance of the

topics that have been extracted by our model, we cal-

culated UMass coherence score(Mimno et al., 2011)

which takes into account, the probability of two words

within a topic occurring in the corpus. It is given by,

score

UMass

(k) =

∑

i=2

−1

∑

j=1

log

p(w

) + 1

p(w

)

(46)

in the above equation indicates the number of top

words taken into consideration for the topic. In our

case this value is 10. The equation basically calcu-

lates the relevancy of words within a topic by ﬁnding

the ratio of the probability of two words w

and w

occurring together to the probability of word w

for

which the score is being calculated. Table 1 shows the

coherence scores of topics derived from LDA, latent

generalized Dirichlet allocation (LGDA), latent Beta-

Liouville allocation (LBLA) and Bi-LGDMA and Bi-

LBLMA for different values of L. It can be seen that

using a GD and BL prior helps in obtaining better top-

ics with a higher coherence score. Bi-LBLMA per-

forms better than Bi-LGDMA according to our ex-

periments, which is due to the fact that choosing the

parameters for Bi-LGDMA is a little harder than Bi-

LBLMA. We calculated the coherence scores for dif-

ferent values of K to ﬁnd the correct number of top-

ics for the model. The best results were observed

when K was set to 5 as observed in Figure 1. Both

Bi-LGDMA and Bi-LBLMA performed well when

L = 3. In the case of Bi-LBLMA we see that the

coherence is very close when L = 3 and L = 4. In

these situations choosing the L as 3 or 4 will give

similar recommendations. This being a quantitative

assessment of the model, to qualitatively see how the

model performs, Table 1 and 2 shows few of the top

ten suggestions for a query anime for the two models.

‘Bleach’ is an anime based on travelling between

worlds through portals in the action genre. The anime

suggested by Bi-LGDMA aligns with this concept

of inter-dimensional portals and magic. Similarly,

the test query for Bi-LBLMA was an anime called

‘Dragon Ball’ which involves super-human ﬁghting.

It is interesting to see that our model identiﬁed the

sequel to the original anime followed by a few other

anime like ‘Boku no Hero Academia’ which also falls

Novel Topic Models for Content Based Recommender Systems

143

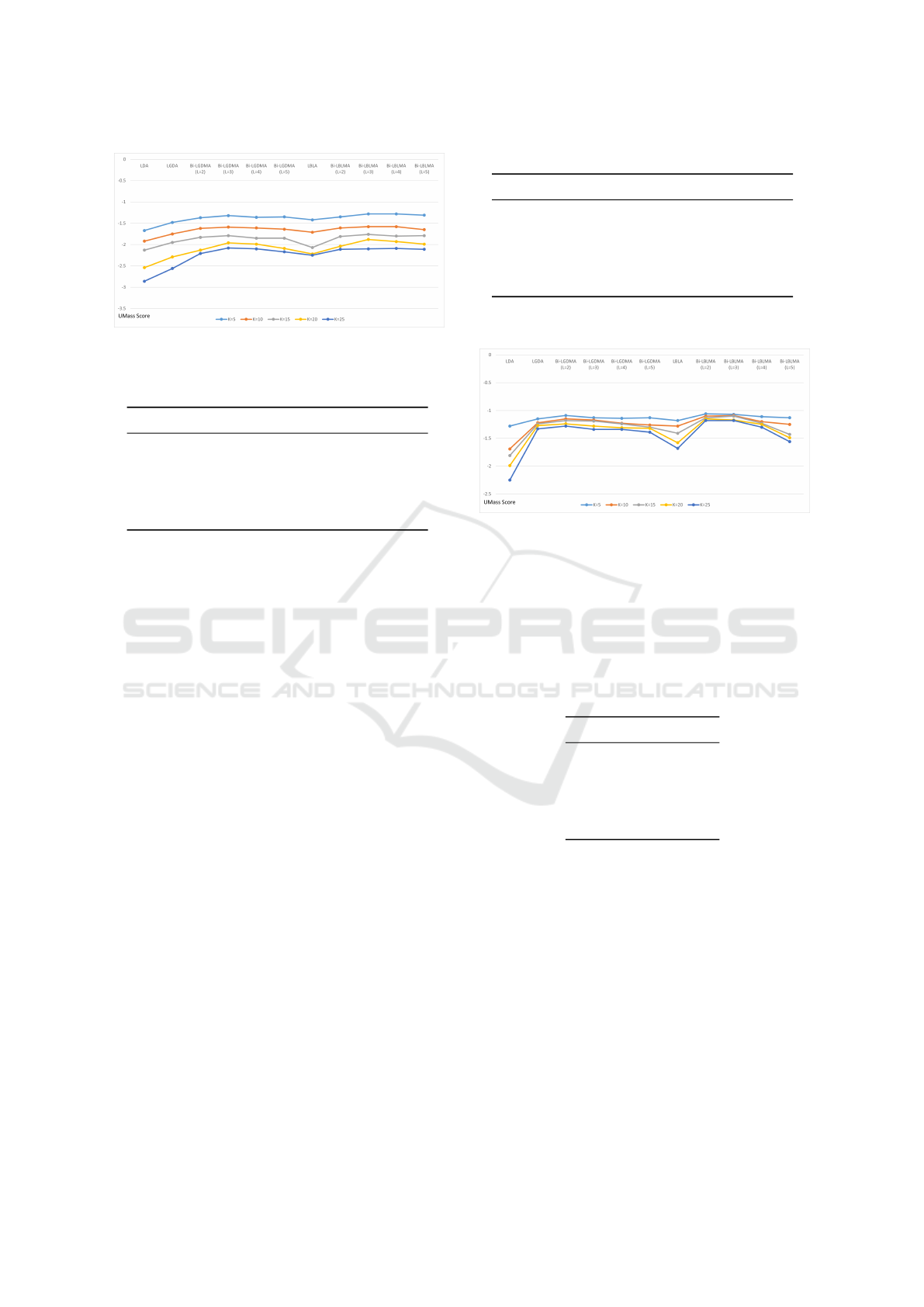
Figure 1: Coherence score for anime dataset for different

values of K and L.

Table 1: Query results for Anime data with Bi-LGDMA.

S. No. Bleach

1 Fullmetal Alchemist

2 Rosario to Vampire

3 World Trigger

4 FLCL

5 Tenjou Tenge

under the same category.

4.2 Netﬂix Movie Recommendation

The Netﬂix dataset is bigger compared to the anime

datset. The dataset consists of details pertaining to

ratings fo different users for around 17000 movies

released before the year 2006. However, the prob-

lem with this dataset is that the synopsis of movies

were not available. Hence, we scraped the data from

wikipedia pages to get this details and then used it

for content based recommendation. We selected the

movies released after 2000 so that we are aware of

them to test qualitatively. This gave us around 4000

movies with description. From the user details, we

consider that a user likes a movie when they rate it as

4 or 5. We selected users who had liked at least 300

movies. This left us with 900 users as ground truth.

These conditions are only to quantitatively access our

models and can be ignored in realtime applications.

When queried with a movie that an user likes, if one

of the top N recommendations by our model is present

in the list of movies liked by that user, then we con-

sider it as a hit. By using this logic, we can calcu-

late the accuracy of our model by calculating the ra-

tio of total number of hits to total number of queries.

We also calculate the coherence score of our topics as

in the previous subsection which is graphed in Fig-

ure 2. We can see that both our models perform the

best when L = 2 and K = 5. The performance im-

provement achieved by our models compared to the

widely used LDA model proves the efﬁciency of our

Table 2: Query results for Anime data with Bi-LBLMA.

S. No. Dragon Ball

1 Dragon Ball Z

2 Dragon Ball Super Movie: Broly

3 Boku no Hero Academia

4 Yu-Gi-Oh Duel Monsters

5 Fate/stay night

model to represent the topics better. In addition to

Figure 2: Coherence score for anime dataset for different

values of K and L.

these analysis Table 3 shows the accuracy of differ-

ent models. Though both Bi-LGDMA and Bi-LBLA

give comparatively better accuracy for our model, the

improvement for Bi-LGDMA is not that much when

compared to Bi-LBLA. Similar to the last experiment,

Table 3: Accuracy of recommendation at N = 15 for Netﬂix

Data.

Model Accuracy

LDA 85.59

LGDA 84.40

Bi-LGDMA 86.00

LBLA 86.50

Bi-LBLMA 87.36

we also check the quality of recommendations for two

sample queries. This is shown in Table 4 and 5. We

can see that Bi-LGDMA recommends a set of teenage

and kids action movies like ‘Agent Cody Banks’ when

queried with the movie ‘The Paciﬁer’ which is a kids

action comedy. In the case of Bi-LGDMA ‘Resident

Evil’ is a zombie movie where the virus causes the

people to attack the non-infected people. The recom-

mendations from our model found similar plot lines

like ‘Dawn of the dead’, ‘Sasquatch’, etc which are

movies based on virus outbreak, hunted by animals

and so on.

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

144

Table 4: Query results for Netﬂix data.

S. No. The Paciﬁer

1 Agent Cody Banks

2 Agent Cody Banks 2: Destination London

3 Lilo and Stitch 2

4 101 Dalmations II: Patch’s London

Adventure

5 Mean Creek

Table 5: Query results for Netﬂix data with Bi-LBLMA.

S. No. Resident Evil

1 Dawn of the Dead

2 Sasquatch

3 Wrong Turn

4 Evil Remains

5 Dead Birds

5 CONCLUSION

We have introduced two novel models for topic mod-

elling and applied it for recommendation tasks. The

models are found to be effective when compared to

widely used models such as LDA. From the exam-

ple queries, we see that our models are able to deliver

promising suggestions that the user might like. The

improvement achieved by using GD and BL distribu-

tions is also clearly seen. Using biterms in conjunc-

tion with our models tend to improve the results con-

siderably. Especially, the Bi-LBLMA model proves

to be a good alternative to LDA based on the results

from both the experiments.

REFERENCES

Attias, H. (1999). A variational baysian framework for

graphical models. In Solla, S., Leen, T., and M

uller,

K., editors, Advances in Neural Information Process-

ing Systems, volume 12, Cambridge, Masschusetts.

MIT Press.

Bakhtiari, A. S. and Bouguila, N. (2014). Online learning

for two novel latent topic models. In Linawati, Ma-

hendra, M. S., Neuhold, E. J., Tjoa, A. M., and You, I.,

editors, Information and Communication Technology,

pages 286–295, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Bakhtiari, A. S. and Bouguila, N. (2016). A latent beta-

liouville allocation model. Expert Systems with Appli-

cations, 45:260–272.

Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent

dirichlet allocation. Journal of machine Learning re-

search, 3(Jan):993–1022.

Bobadilla, J., Hernando, A., Ortega, F., and Bernal, J.

(2011). A framework for collaborative ﬁltering rec-

ommender systems. Expert Systems with Applica-

tions, 38(12):14609–14623.

Chien, J.-T., Lee, C.-H., and Tan, Z.-H. (2018). Latent

dirichlet mixture model. Neurocomputing, 278:12–

22. Recent Advances in Machine Learning for Non-

Gaussian Data Processing.

Chong, W., Blei, D., and Li, F.-F. (2009). Simultaneous im-

age classiﬁcation and annotation. In 2009 IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 1903–1910.

Fan, W., Bouguila, N., and Ziou, D. (2012). Variational

learning for ﬁnite dirichlet mixture models and appli-

cations. IEEE transactions on neural networks and

learning systems, 23(5):762–774.

Hu, C., Fan, W., Du, J.-X., and Bouguila, N. (2019). A

novel statistical approach for clustering positive data

based on ﬁnite inverted beta-liouville mixture models.

Neurocomputing, 333:110–123.

Liu, Y., Du, F., Sun, J., and Jiang, Y. (2020). ilda: An

interactive latent dirichlet allocation model to im-

prove topic quality. Journal of Information Science,

46(1):23–40.

Maanicshah, K., Amayri, M., and Bouguila, N. (2022).

Improving topic quality with interactive beta-liouville

mixture allocation model. In 2022 IEEE Symposium

Series on Computational Intelligence (SSCI), pages

1143–1148.

Maanicshah, K., Amayri, M., and Bouguila, N. (2023).

Interactive generalized dirichlet mixture allocation

model. In Structural, Syntactic, and Statistical Pattern

Recognition: Joint IAPR International Workshops, S+

SSPR 2022, Montreal, QC, Canada, August 26–27,

2022, Proceedings, pages 33–42. Springer.

Mimno, D., Wallach, H. M., Naradowsky, J., Smith, D. A.,

and McCallum, A. (2009). Polylingual topic models.

In Proceedings of the 2009 Conference on Empirical

Methods in Natural Language Processing: Volume 2 -

Volume 2, EMNLP ’09, page 880–889, USA. Associ-

ation for Computational Linguistics.

Mimno, D., Wallach, H. M., Talley, E., Leenders, M., and

McCallum, A. (2011). Optimizing semantic coher-

ence in topic models. In Proceedings of the Confer-

ence on Empirical Methods in Natural Language Pro-

cessing, Proceedings of the Conference on Empirical

Methods in Natural Language Processing; EMNLP

’11, page 262–272, USA. Association for Computa-

tional Linguistics.

Nagori, R. and Aghila, G. (2011). Lda based integrated

document recommendation model for e-learning sys-

tems. In 2011 International Conference on Emerging

Trends in Networks and Computer Communications

(ETNCC), pages 230–233.

Opper, M. and Saad, D. (2001). Advanced mean ﬁeld meth-

ods: Theory and practice. MIT press, Cambridge,

Masschusetts.

Pazzani, M. J. and Billsus, D. (2007). Content-Based

Recommendation Systems, pages 325–341. Springer

Berlin Heidelberg, Berlin, Heidelberg.

Novel Topic Models for Content Based Recommender Systems

145