A Deep Learning Approach for Estimating the Rind Thickness of

Trentingrana Cheese from Images

Andrea Caraffa

∗1

, Michele Ricci

2,3 a

, Michela Lecca

1 b

, Carla Maria Modena

1 c

Eugenio Aprea

2,3 d

, Flavia Gasperi

2,3 e

and Stefano Messelodi

1 f

Bruno Kessler Foundation, Digital Industry, Via Sommarive 14, 38123 Trento, Italy

Edmund Mach Foundation, Research and Innovation Centre, Via E. Mach 1, 38098 San Michele all’Adige (TN), Italy

University of Trento, Center Agriculture Food Environment, Via E. Mach 1, 38098 San Michele all’Adige (TN), Italy

ﬂ

Keywords:

Food Quality Assessment, Cheese Rind Thickness, Deep Learning, Regression.

Abstract:

Checking food quality is crucial in food production and its commercialization. In this context, the analysis

of macroscopic visual properties, like shape, color, and texture, plays an important role as a ﬁrst assessment

of food quality. Currently, such an analysis is mostly performed by human experts, who observe, smell,

taste the food, and judge it based on their training and experience. Such an assessment is usually subjective,

time-consuming, and expensive, so it is of great interest to support it with automated and objective advanced

computer vision tools. In this paper, we present a deep learning method to estimate the rind thickness of

Trentingrana cheese from color images acquired in a controlled environment. Rind thickness is a key feature

for the commercial selection of this cheese and is commonly considered to evaluate its quality. We tested our

method on 90 images of cheese slices, where we deﬁned the ground-truth rind thickness using the measures

provided by a panel of 12 experts. Our method achieved a Mean Absolute Error (MAE) of ≈ 0.5 mm, which

is half the ≈ 1.2 mm error produced on average by the experts with respect to the deﬁned ground-truth.

1 INTRODUCTION

Food quality control is a crucial step in the food pro-

duction and selling chain since it grants the customer

to get safe and good products. Many efforts have been

made to automatize food quality evaluation. Never-

theless, in several areas, this task is best performed

by human experts, who assess the quality of food

by analyzing various characteristics perceived by the

ﬁve senses, such as visual appearance, texture, hard-

ness, crispness, and chemical properties perceived by

smell and taste. In this framework, visual inspection

plays an important role since the appearance of food

is highly correlated with its quality. Visual character-

istics of food are usually investigated both at a micro-

scopic and a macroscopic scale. Microscopic analy-

sis is performed using technologically advanced in-

https://orcid.org/0000-0002-1114-1672

https://orcid.org/0000-0001-7961-0212

https://orcid.org/0000-0001-7015-8768

https://orcid.org/0000-0003-3648-0459

https://orcid.org/0000-0003-0055-9464

https://orcid.org/0000-0002-4673-9607

struments, e.g., near-infrared imaging systems, spec-

troscopy and hyper-spectral imaging systems, and X-

ray imaging sensors, that provide objective measures

regarding micro-structures (Russ, 2015; Lei and Sun,

2019). The macroscopic analysis often represents the

ﬁrst step to judging the food quality and thus gen-

erally precedes the microscopic analysis. However,

unlike the latter, it is usually performed by humans

without the help of any tools. Speciﬁcally, experts ob-

serve the product focusing on macro visual properties

such as color, shape, and texture and judge it based

on their expertise and experience (Brosnan and Sun,

2004). Because they are subjective, sensory evalu-

ations can be affected by high inter-individual vari-

ability. This variability is partially limited by using

a well-designed experimental protocol, following ba-

sic rules of good practice for sensory analysis, and

carefully selecting, training, and monitoring judges.

Besides that, sensory evaluations are usually time-

consuming and expensive, and only a limited number

of samples can be analyzed in an evaluation session.

For this reason, an automated instrumental evaluation

of one or more sensory parameters is an attractive

tool to support a panel. Computer vision techniques,

Caraffa, A., Ricci, M., Lecca, M., Modena, C., Aprea, E., Gasperi, F. and Messelodi, S.

A Deep Learning Approach for Estimating the Rind Thickness of Trentingrana Cheese from Images.

DOI: 10.5220/0011830000003497

In Proceedings of the 3rd International Conference on Image Processing and Vision Engineering (IMPROVE 2023), pages 76-83

ISBN: 978-989-758-642-2; ISSN: 2795-4943

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

in which the visual properties of food are analyzed

through image processing algorithms, have proven to

be a promising tool for objective, effective, sustain-

able, cheaper, and faster assessment of food qual-

ity (Du and Sun, 2004; Turgut et al., 2014; Ma et al.,

2016; Jackman and Sun, 2013; Sun, 2016).

This work concerns assessing the quality of Trent-

ingrana, a Protected Designation of Origin (PDO)

cheese, with the help of advanced computer vision

techniques. The quality assessment of cheese pro-

duced seasonally by a cheese dairy is sample-rated

by a panel of experts. Some wheels are opened along

their diameter and visually screened by the experts.

One of the parameters they consider for a global judg-

ment is the rind thickness. This is important because

pieces of cheese with a thick or uneven rind are not

appreciated on the market. Here, we present a novel

method that estimates the cheese rind thickness on six

points of the wheel using a deep learning approach.

Computer vision has already been applied to

cheese quality evaluation. An interesting case study

is the assessment of the degree of conformity to

the quality standards of a protected cheese brand

(Bosakova-Ardenska et al., 2020; Badaro et al.,

2021), while an overview of computer vision methods

applied to quality control cases of speciﬁc cheeses,

along with the limitations of using simple image anal-

ysis techniques, can be found in (Lukinac et al.,

2018). However, to the best of our knowledge, there

is no previous method using deep learning. Therefore,

this work represents the ﬁrst attempt to assist cheese

quality control by leveraging advanced computer vi-

sion based on neural networks and, more precisely,

to estimate cheese rind thickness from images in the

visible spectrum.

For our purpose, we acquired with an industrial

camera several images of Trentingrana cheese slices

obtained from a half-wheel by wire-cutting a piece

and then dividing it into left and right slices. Then

we asked a pool of 12 experts to observe each pic-

ture and measure the rind thickness in the upper and

lower faces of the cheese slice and in the heel. The

use of two slices per wheel and multiple thickness

measurements on the rind are introduced to provide

a more accurate assessment of the overall rind qual-

ity. We used this data to train and test a deep neural

network that estimates the thicknesses reported by the

experts. Experiments show that the proposed method

can accurately predict the rind thickness. As a base-

line, we developed a purpose-driven algorithm with

traditional computer vision that relies on detecting

contrast between rind and paste areas. With respect

to the mean thicknesses reported by the experts, the

Mean Absolute Error (MAE) for the hand-crafted al-

gorithm stands at 1.10 mm, while the MAE for the

deep learning method is 0.51 mm, which is less than

half the MAE produced on average by the pool of hu-

man experts.

The rest of the paper is organized as follows. Sec-

tion 2 provides a brief overview of the method. In

Section 3, we describe the preparation of the dataset

of images, along with their annotations, necessary to

train the model, while in Section 4, we describe the

proposed deep learning method in more detail. We

present experimental results in Section 5, including

the comparison with a fairly elaborate baseline tech-

nique we implemented using classical image analysis.

2 OVERVIEW OF THE METHOD

A block diagram of the proposed method is illustrated

in Figure 1. As input, it takes a color image I de-

picting a wire-cut cheese slice acquired under a ﬁxed,

controlled light against a white background. A Re-

gion Extractor automatically localizes and crops I in

three rectangular regions R

, R

around the cen-

ter points of the upper face A, the heel B, and the

lower face C of the cheese slice. Each sub-image

, p ∈ {A, B,C}, is fed in turn to the Thickness Es-

timator that produces a value as an estimation of the

rind thickness. The Thickness Estimator is learning-

based and, more precisely, implements a regression

technique exploiting a deep neural network.

3 DATA PREPARATION

The learning process requires the preparation of a

dataset of images representing the regions of inter-

est extracted from the original cheese images labeled

with a value representing the rind thickness. The work

is structured in the following steps.

3.1 Image Acquisition

We considered 45 cheese wheels from 15 dairy facto-

ries related to Trentingrana Consortium. Each wheel

was opened along its diameter with a special knife. A

piece about 2.5 cm thick was wire-cut and divided into

a left and a right slice (Figure 2(a)). Using a visual

analyser (Iris, AlphaMos, Tolouse France) under top

and bottom lighting (D65 compliant, 6700°K color

temperature), we acquired N = 90 images I

, . . . , I

with dimension 1024 × 768 pixels, each depicting a

slice of cheese.

A calibration step was performed to estimate the

conversion factor from pixels to millimeters. For this

A Deep Learning Approach for Estimating the Rind Thickness of Trentingrana Cheese from Images

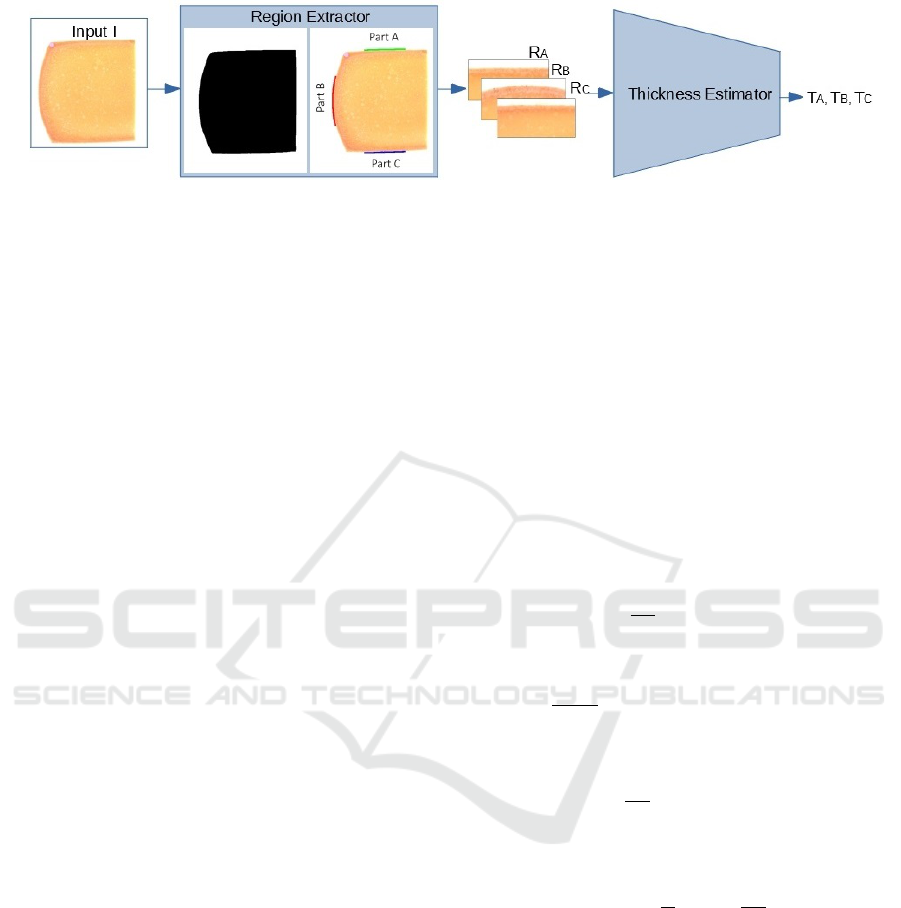
Figure 1: Overview: the Region Extractor focuses on three parts of interest in the input image and crops the regions

, R

. In turn, the learning-based Thickness Estimator to predict the thickness in these regions runs three times,

every time being fed with a single region.

purpose, an image was captured depicting an object of

known dimensions (in millimeters), and its size in the

image (in pixels) was extracted, resulting in 1 pixel

corresponding to 0.29 mm.

3.2 Image Annotation

The subjective evaluation has been performed through

an online questionnaire created using EyeQues-

tion® (EyeQuestion, 2022), submitting all the im-

ages in randomized order to a jury of K = 12 experts

, . . . , E

. The experts quantitatively estimated the

rind thickness of each cheese slice in three regions.

For each image, every expert provided an estimate of

the rind thickness in centimeters measured on the up-

per face A, heel B, and lower face C. A set of three

rulers were superimposed on each image to assist the

task of the experts. Each region received K subjective

measurements of rind thickness. The analysis of these

estimates shows the presence of outliers and, because

of the smooth transition from rind to paste, different

experts provided different thickness values. We re-

mark that this was a new procedure for the experts

since they usually measure the rind thickness by ob-

serving the physical cheese and not from images.

3.3 Region Extraction

The Region Extractor receives in input an image I. It

identiﬁes three parts on the cheese border and three

regions where the experts performed their measure-

ments. To this end, it computes the foreground mask

F corresponding to the cheese area in I and local-

izes the upper and lower faces A, C, and the heel B

by analyzing the concavities along its boundary ∂F

(Figure 2(b)). One-thick-pixel parts P

, P

and P

are extracted from ∂F around the middle point of

the three sides (Figure 2(c)). Three rectangular re-

gions R

, R

around these parts are then cropped

and used as input to the Thickness Estimator (Fig-

ure 2(d)). The size of the rectangles was chosen to

roughly match the area observed by the experts to pro-

vide their measurements (280 × 150 pixels). Regions

and R

were rotated to appear as R

, i.e., with the

white background at the top of the region.

3.4 Ground-Truth Deﬁnition

We deﬁned a method to associate each region R

i,p

where i = 1, . . . , N and p ∈ {A, B,C}, with a ground-

truth thickness value taking into account the intrinsic

variability of the annotations provided by the differ-

ent experts. Given the set of measures T

i,p

, where

k = 1, . . . , K, we ﬁrst compute coefﬁcients M

, expert-

dependent, and a global coefﬁcient M, as follows:

∑

i=1

∑

p∈{A,B,C}

i,p

(1)

i,p

K − 2

(

∑

k=1

i,p

− max

k=1...K

i,p

− min

k=1...K

i,p

)

(2)

M =

∑

i=1

∑

p∈{A,B,C}

i,p

(3)

Then, we deﬁned the ground-truth for region R

i,p

as:

i,p

∑

k=1

i,p

(4)

The dataset was organized in order to keep track of

the slice/wheel from which each region came.

4 THE PROPOSED NETWORK

We used the ResNet18 model (He et al., 2016), a well-

known architecture for image recognition tasks. We

replaced the ﬁnal layer with a fully connected layer

returning a single value and we trained the whole

network from scratch as we experimented lower per-

formance by ﬁne-tuning a backbone pre-trained on

ImageNet (Russakovsky et al., 2015). We tried a

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

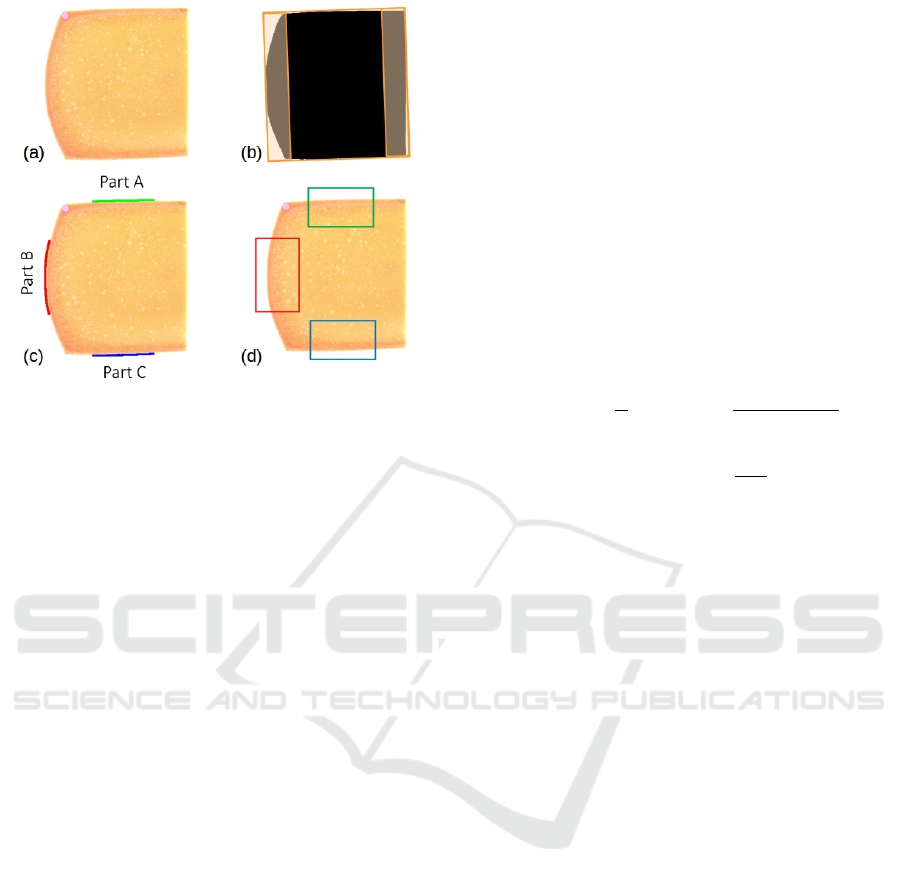
Figure 2: In (a) a wire-cut left slice of a cheese wheel. In

(b) the mask F of the cheese area (possibly rotated to align

its minimum bounding rectangle with the axes) with the two

stripes where to focus for the localization of the heel side.

In (c) the 1-pixel-thick parts P

, P

along the border ∂F.

In (d) the ﬁnal regions R

, R

and R

, around, respectively,

, P

and P

, corresponding to the areas observed by the

experts; they are used for training and testing the proposed

network.

deeper network, such as ResNet50, without achiev-

ing better results. As ResNet18 resulted superior to

the deeper ResNet50, we tried a shallower network,

i.e., a ResNet variant with only 10 layers. However,

this network did not boost the performance. We also

tried more recent and sophisticated architectures and

approaches, such as ShufﬂeNet (Zhang et al., 2018),

RegNet (Radosavovic et al., 2020), ConvNeXt (Liu

et al., 2022) and CLIP (Radford et al., 2021). How-

ever, we did not obtain any improvement. A more

in-depth investigation into why this is the case is left

for future work.

4.1 Data Augmentation

Data augmentation plays a central role in overcoming

the small number of available samples. We adopted

different data augmentation techniques, some more

beneﬁcial than others. Overall, the best results were

achieved using color jittering, random rotation (from

−5 to +5 degrees), horizontal ﬂipping, and random

cropping. The latter was the most relevant: from

an input region randomly extracts smaller and dif-

ferent patches of a ﬁxed size. The smaller the crop-

ping size, the higher the number of different patches

is. Nevertheless, a too-small patch forces the net-

work to focus only on a speciﬁc subpart of the rind,

while the ground-truth represents the average of the

whole side and the thickness is not perfectly uniform.

For this reason, the size of 180 × 130 pixels (about

52 × 38 mm) used for random cropping had to be ac-

curately determined.

4.2 Customized Loss

As described in Section 3, the ground-truth was ob-

tained using measures from a panel of 12 experts.

However, there are regions for which the experts

agree more than others. For a given region, the Mean

Absolute Deviation (MAD) around the ground-truth

is a measure of how much the experts actually agree

on the thickness of that region. To get the most out

of this information, we deﬁned a custom loss based

on the Mean Squared Error (MSE) but incorporating

ground-truth uncertainty as follows:

L(Y, T ) =

∑

p∈{A,B,C}

i,p

− T

i,p

)

i,p

(5)

C =

∑

p∈{A,B,C}

i,p

(6)

where C is a normalization factor, Y the set of predic-

tions, T the set of ground-truths, and D

i,p

the MAD

for region R

i,p

. The deﬁned loss helps the network

focus on the regions for which experts agree the most

and, therefore, those for which the assigned ground-

truth is more signiﬁcant.

5 EVALUATION

In this section, we present the results of the experi-

ments of the proposed method, including the evalua-

tion protocol, the experimental setup, and an alterna-

tive estimation algorithm, based on a classical image

analysis approach, for performance comparison.

5.1 Evaluation Protocol

The major limitation in validating our method was

the small number of images available. Splitting the

dataset into standard train, validation, and test sets

would have resulted in too small sets. Therefore, we

employed a nested cross-validation strategy using an

ensemble of models to validate our method in a fair

yet exhaustive way.

First, we divided the 90 images into nine folds,

each containing 10 images, i.e., ﬁve pairs of left and

right slices. Since the left and the right slices be-

long to the same wheel, they could be correlated, both

in terms of ground-truth and image content. Mix-

ing them up in different folds could introduce poten-

tial bias. For this reason, we created nine folds so

A Deep Learning Approach for Estimating the Rind Thickness of Trentingrana Cheese from Images

that every wheel appears in one and only one fold.

For every split, we therefore had 80 images for train-

ing/validation and 10 for testing. Again, we split the

80 images into ten different folds, each containing

four pairs of slices. We used nine folds for training

and left one out for validation. We selected the best

model according to the validation set and repeated the

same procedure ten times every time holding out a dif-

ferent 8-images fold for validation. Therefore, lever-

aging the 80 images for training/validation, we got ten

different models. We then made inferences for each of

them on the 10-images test set and averaged the pre-

dictions through model ensembling. Finally, we repli-

cated the entire procedure for all nine initial splits to

obtain a prediction for each region in the dataset.

5.2 Experimental Setup

We trained every model for 200 epochs using as op-

timizer AdamW (Loshchilov and Hutter, 2018) (β

0.9, β

= 0.999, λ = 0.001), a batch size of 32, and a

cosine annealing schedule with an initial learning rate

of 0.001. For each training, we then chose the model

with the lowest MAE according to the 8-images hold-

out validation set after the ﬁrst 100 epochs. All the ex-

periments involving neural networks were performed

on a GPU NVIDIA 1070 Ti.

5.3 An Hand-Crafted Algorithm

We compared our deep learning method with the

baseline provided by a “traditional” computer vision

method we previously implemented for detecting the

rind: a speciﬁc hand-crafted algorithm, shortly called

HCA. We devised such an algorithm based on the em-

pirical evidence that the rind of the cheese is darker

than the interior because of its higher density and that

the paste has a fairly uniform coloring, although not

constant. Thus, the rind thickness can be detected by

searching for a color variation in the image analyzing

adjacent regions close to the three parts of interest.

HCA takes as input the image of a slice and ex-

tracts the 1-pixel-thick parts P

, P

as done in the

data preparation step for the deep learning method.

To highlight as much as possible the variation be-

tween rind and paste, and to attenuate an illumination

gradient due to the acquisition device, the image is

pre-processed by means of a color edge-preserving

smoothing followed by an intensity normalization

step. HCA works on this last image, named G. Let P

be an element in {P

, P

} and R the corresponding

rectangular region in {R

, R

}. HCA computes

n + 1 regions P

:= P, P

= S(P, 1), . . . , P

= S(P, n),

where P

is obtained by shifting P

by i pixels towards

the cheese interior. n was ﬁxed in such a way to en-

sure the scanning of a sufﬁciently large area to in-

clude both rind and paste, i.e., approximately 5 cm

expressed in pixels. For each i, HCA computes the

median of G’s values along P

and plots it with respect

to i (Figure 3). In this way, HCA builds up the projec-

tion function f : {0, . . . , n} → [0, 255] such that f (i) is

the median value of the G values over P

. We choose

to compute the median as it is not affected by outlier

values due, for example, to the presence of crystals in

the paste.

The plot of f usually shows a shape that starts with

low values at the very ﬁrst part of the rind (darker),

increasing inside the rind and sub-rind area, followed

by a ﬂat area generated when scanning the paste re-

gion. HCA estimates the rind thickness for each part

of interest P by analyzing the generated f as follows.

1. Compute the value V

of f in the plateau zone. V

is estimated as the median of all the pixels belong-

ing to the zone obtained by a strong shrink of the

mask F (corresponding to 2 cm, to overpass the

rind) and the rectangle R of the part P, in order to

capture a paste-only zone.

2. Compute the local minima of S

and the depth

of their basins, where S

indicates a Gaussian

smoothing of f . Discard the minima with low

depth and those with ordinate too close to V

;

select the minimum M = (M

, M

) having the

greater abscissa i.

3. Determine the transition point U = (U

) with

> M

. The transition point should deﬁne the

end of the rind zone. Depending of the cheese

slice this can be more or less marked: this is ex-

pressed by the slope of f between M and the start-

ing point of plateau V .

In the current implementation of HCA U

is de-

ﬁned as:

= (1 − µ)M

+ µV

, (7)

where µ is a real-valued coefﬁcient ranging be-

tween 0 and 1. In this implementation, µ has been

set empirically to 0.3.

The end of the rind region is determined in HCA

by selecting in the set f

−1

) the point in the in-

terval (M

) with greater abscissa. We observe

that the value of µ has little inﬂuence on the posi-

tion of U

if the ramp between M and V is steep,

i.e., when the separation between rind and paste

is quite clear. The position of U

can be inﬂu-

enced more signiﬁcantly by the choice of µ in the

case where the transition between rind and paste

is very smooth. This agrees with the uncertainty

of different annotators in cheese slices that exhibit

a gradual transition.

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

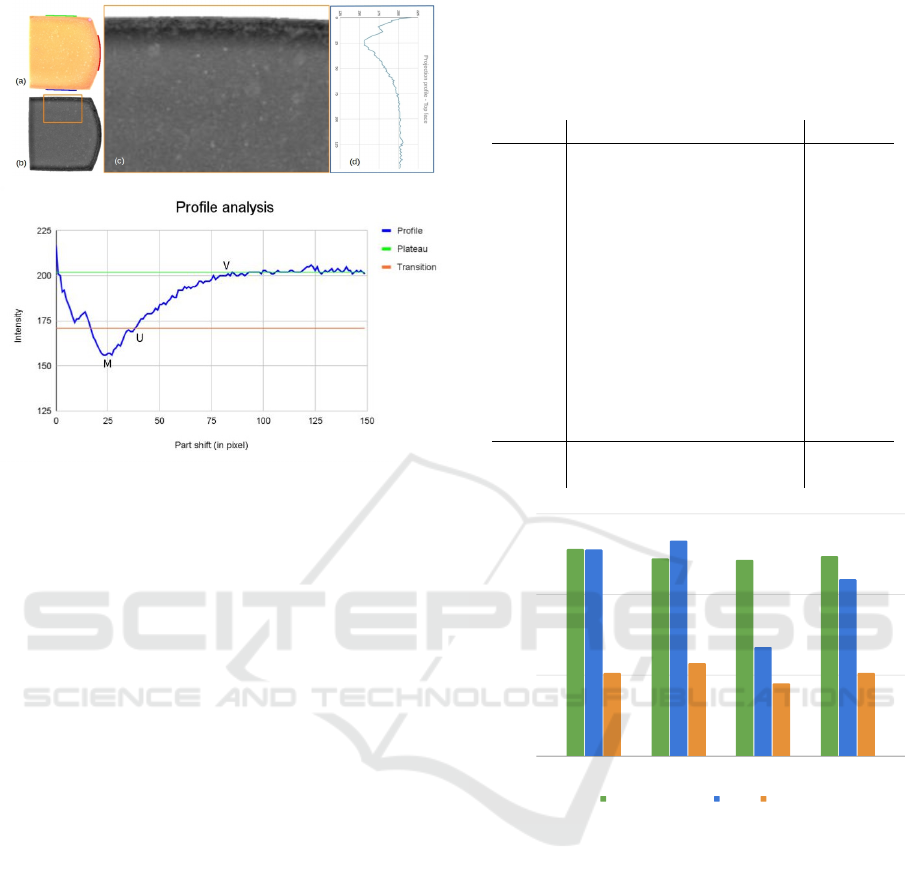
Figure 3: In (a) a right slice, where the parts A, B and C

are marked in color. In (b) an intensity normalization of

(a). In (c), the intensity values of a region adjacent to part

A are considered to build the plot f , in (d). Below is an

illustration of the proﬁle analysis: the green line highlights

the plateau, while the estimated transition line, between the

plateau and the selected minimum M of f , is depicted in

orange. Finally, U indicates the point used to compute the

rind thickness, which corresponds to its abscissa.

5.4 Results of the Experiments

In this section, we present the results of the proposed

deep learning-based method and we compare it with

HCA and the pool of 12 human experts in terms of

MAE (Table 1).

Figure 4 summarizes the performance of the pro-

posed deep learning method and compared it with

HCA for the three slice regions and globally. The ﬁg-

ure includes also the average error of the 12 experts.

It is noteworthy to specify that the ground-truth was

deﬁned as the average prediction of the 12 experts,

which is different from the average error of the ex-

perts. Considering globally all the three regions, the

MAE for the deep learning method is 0.51 mm, while

for HCA it is 1.10 mm, which is in line with the MAE

for the human experts, about 1.24 mm.

The comparison with a classical method based

on manual, albeit accurate, feature selection was

introduced to highlight how, in this case, the deep

learning approach achieves signiﬁcantly better per-

formance while avoiding the critical task of selecting

features and setting thresholds and parameters typical

of traditional methods.

Table 1: Mean Absolute Error (MAE) in millimeters

achieved by the pool of human experts (E), the Hand-

Crafted Algorithm (HCA) and the Neural Network (NN).

MAE

represents the MAE for region i, where i ∈ {A, B,C}.

E–avg is the average error produced by the 12 experts.

MAE

avg

E–01 1.06 1.10 0.84 1.00

E–02 0.87 1.17 1.07 1.04

E–03 1.53 1.24 1.43 1.40

E–04 1.13 1.07 1.32 1.17

E–05 1.02 1.09 1.07 1.06

E–06 1.23 1.30 0.84 1.12

E–07 1.22 0.97 1.09 1.10

E–08 1.28 1.46 1.34 1.36

E–09 0.93 1.12 0.81 0.95

E–10 1.68 1.87 1.83 1.79

E–11 1.93 1.49 1.54 1.65

E–12 1.49 0.79 1.38 1.22

E–avg 1.28 1.22 1.21 1.24

HCA 1.28 1.33 0.67 1.10

NN 0.51 0.58 0.45 0.51

Mean Absolute Error (mm)

0.5

1.5

A B C Average

Human Experts HCA NN

Figure 4: Graphical comparison of the error produced by

the pool of human experts (average), the Hand-Crafted Al-

gorithm (HCA) and the proposed Neural Network (NN).

Mean Absolute Error (in millimeters) is reported separately

for regions A, B,C and their average.

Moreover, to check whether the network actually

learned how to measure rind thickness, we visualize,

in Figure 5, the areas of the input images that most

inﬂuenced the ﬁnal prediction. We used a Grad-CAM

variant for visual explanations of network decisions in

regression problems (Akikawa and Yamamura, 2021).

The two depicted examples show how the network,

indeed, relies on reasonable areas of the input images

for predicting the thickness.

In Figure 6, we highlight how the estimates pro-

vided by the neural network follow the ground-truth

by sorting the ground-truth thickness of the regions

in increasing order (blue) and plotting the correspon-

A Deep Learning Approach for Estimating the Rind Thickness of Trentingrana Cheese from Images

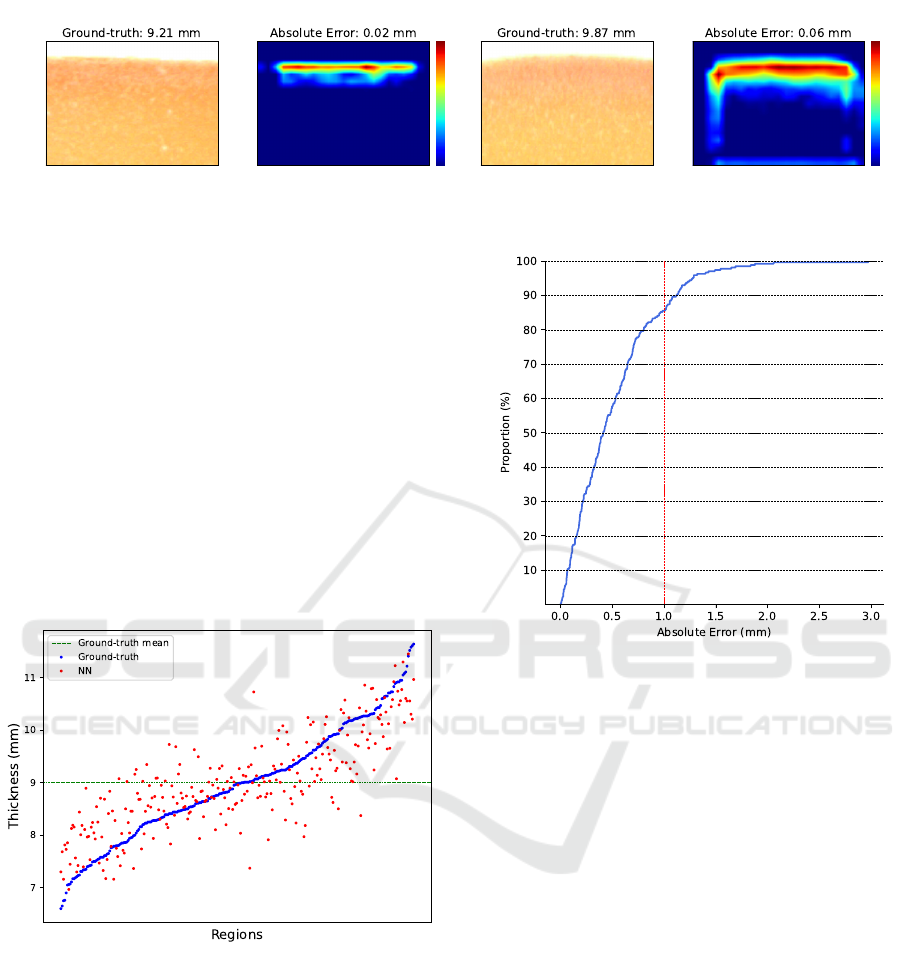
Figure 5: Grad-CAM visualizations for two different input images. Colors from blue to red indicate the increasing importance

of the corresponding areas to determine the ﬁnal estimation.

dent network estimates (red). We can observe that

the network maintains, in trend, the ordering of mea-

sures. Indeed, the network does not predict a mean

value for all the samples but, instead, tends to raise

the prediction for regions with a thicker rind and to

lower it for regions with a thinner rind. This is also

supported by the R2-Score achieved, which is 0.68,

meaning that the MSE for the network is less than a

third of the MSE for a constant model always pre-

dicting the ground-truth mean regardless of the input

images (green dashed line in Figure 6).

Finally, Figure 7 shows the cumulative curve in-

dicating for a given absolute error (x-axis) the per-

centage of regions whose estimation error is below it

(y-axis). We can observe that up to 85% of the cases

exhibits an error lower than 1.0 mm.

Figure 6: Comparison between the Neural Network (NN)

predictions and the ground-truth. On the x-axis, the regions

are ordered by their ground-truth thickness to highlight the

correlation between the real and the predicted thickness.

6 CONCLUSIONS AND FUTURE

WORKS

This paper focused on the quality assessment of PDO

Trentingrana cheese, and, in particular, it proposed

an innovative deep learning-based method to estimate

the thickness of its rind. Currently, this estimation is

performed by a pool of experts by observing the phys-

Figure 7: Empirical Cumulative Density Function (ECDF)

of the error for the deep learning-based approach.

ical object, but their work requires time, the simulta-

neous presence of the team at the lab, is subjective,

and is rather expensive. Automation of this process

is therefore desired to support panels in visual inspec-

tion. The proposed method implements a regression

technique that learns the cheese thickness from a set

of measurements collected by human experts. In ma-

chine learning approaches, the number and quality of

data used for training determine the accuracy of the

results. In this regard, we had very little data at our

disposal.

In our work, we carefully devised a procedure

to automatically extract rectangular regions around

points of interest from an image of a cheese slice. We

applied different augmentation stages to overcome the

lack of available data. The network was then thor-

oughly tested using a nested cross-validation proce-

dure on 90 cheese slice images, i.e., 270 regions, re-

porting highly satisfactory results. Indeed, as shown

in Section 5, the MAE reported by our method is

0.51 mm, i.e., less than half the MAE produced on

average by the experts. Moreover, our deep learning-

based approach enabled better results than a hand-

crafted method, which was speciﬁcally implemented

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

to localize accurately the transition between cheese

rind and paste.

Future work will be devoted to providing a more

comprehensive characterization of the rind thickness,

for instance, by measuring it in other parts of the

cheese wheel, like in the angles formed by the heel

and the upper and lower faces. We are furthermore

interested in investigating the estimation of the rind

thickness using images depicting rock-cracked cheese

slices rather than wire-cut. In this new scenario, the

hand-crafted algorithms have little chance of success

because there are even fewer visual changes in the

transition from the rind to the paste.

Finally, rind thickness is only one of the features

considered by the internal quality panel of Trentin-

grana Consortium. Automatic estimation of other vi-

sual characteristics, such as paste color and texture,

could be a topic for future research to provide more

comprehensive support to experts.

ACKNOWLEDGEMENTS

The research was funded by Trentingrana - Consorzio

dei Caseiﬁci Sociali Trentini, Italy and by the Au-

tonomous Province of Trento, Italy (as part of the

ADP funding prot. n. 244380 dd 04/05/2020 and

the TRENTINGRANA project - RDP 201-202, CUP

C66D17000180008).

REFERENCES

Akikawa, M. and Yamamura, M. (2021). Materializing

Architecture for Processing Multimodal Signals for

a Humanoid Robot Control System. Journal of Ad-

vanced Computational Intelligence and Intelligent In-

formatics, 25(3):335–345.

Badaro, A., de Matos, G., Karaziack, C., et al. (2021). Au-

tomated Method for Determination of Cheese Melta-

bility by Computer Vision. Food Analytical Methods,

14:2630–2641.

Bosakova-Ardenska, A., Panayotov, P., Boyanova, P., and

Pashova, E. (2020). Application of Images Segmenta-

tion for Evaluation Structure of White Brined Cheese.

In International Conference on Information Technolo-

gies, pages 1–4.

Brosnan, T. and Sun, D.-W. (2004). Improving Quality In-

spection of Food Products by Computer Vision - A

Review. Journal of Food Engineering, 61(1):3–16.

Du, C.-J. and Sun, D.-W. (2004). Recent Developments in

the Applications of Image Processing Techniques for

Food Quality Evaluation. Trends in Food Science &

Technology, 15(5):230–249.

EyeQuestion (Accessed: Dec 2022). https://eyequestion.nl.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep Resid-

ual Learning for Image Recognition. In IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 770–778.

Jackman, P. and Sun, D.-W. (2013). Recent Advances in Im-

age Processing using Image Texture Features for Food

Quality Assessment. Trends in Food Science & Tech-

nology, 29(1):35–43.

Lei, T. and Sun, D.-W. (2019). Developments of Nonde-

structive Techniques for Evaluating Quality Attributes

of Cheeses: A review. Trends in Food Science & Tech-

nology, 88:527–542.

Liu, Z., Mao, H., Wu, C., et al. (2022). A ConvNet for the

2020s. In IEEE Conference on Computer Vision and

Pattern Recognition, pages 11966–11976.

Loshchilov, I. and Hutter, F. (2018). Decoupled Weight De-

cay Regularization. In International Conference on

Learning Representations.

Lukinac, J., Juki

c, M., Mastanjevi

c, K., and Lu

can, M.

(2018). Application of Computer Vision and Image

Analysis Method in Cheese-Quality Evaluation: a Re-

view. Ukrainian Food Journal, 7(2):192–214.

Ma, J., Sun, D.-W., Qu, J.-H., et al. (2016). Applications

of Computer Vision for Assessing Quality of Agri-

Food Products: A Review of Recent Research Ad-

vances. Critical Reviews in Food Science and Nutri-

tion, 56(1):113–127.

Radford, A., Kim, J. W., Hallacy, C., et al. (2021). Learn-

ing transferable visual models from natural language

supervision. In International Conference on Machine

Learning, pages 8748–8763.

Radosavovic, I., Kosaraju, R. P., Girshick, R., et al. (2020).

Designing network design spaces. In 2020 IEEE/CVF

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 10425–10433.

Russ, J. C. (2015). Image analysis of foods. Journal of Food

Science, 80(9):E1974–E1987.

Russakovsky, O., Deng, J., Su, H., et al. (2015). Imagenet

large scale visual recognition challenge. International

journal of computer vision, 115(3):211–252.

Sun, D.-W. (2016). Computer Vision Technology for Food

Quality Evaluation. Academic Press.

Turgut, S. S., Karacabey, E., K

uc¸

oner, E., et al. (2014).

Potential of image analysis based systems in food

quality assessments and classiﬁcations. In 9th Baltic

Conference on Food Science and Technology, pages

8–12.

Zhang, X., Zhou, X., Lin, M., and Sun, J. (2018). Shuf-

ﬂeNet: An extremely efﬁcient Convolutional Neural

Network for mobile devices. In IEEE Conference

on Computer Vision and Pattern Recognition, pages

6848–6856.

A Deep Learning Approach for Estimating the Rind Thickness of Trentingrana Cheese from Images