Hybrid Optimal Traffic Control: Combining Model-Based and
Data-Driven Approaches
Urs Baumgart and Michael Burger
Fraunhofer Institute for Industrial Mathematics ITWM, Fraunhofer-Platz 1, D-67663 Kaiserslautern, Germany
Keywords:
Traffic Control, Model Predictive Control, Optimal Control, Imitation Learning.
Abstract:
We study different approaches to use real-time communication between vehicles, in order to improve and to
optimize traffic flow in the future. A leading example in this contribution is a virtual version of the prominent
ring road experiment in which realistic, human-like driving generates stop-and-go waves.
To simulate human driving behavior, we consider microscopic traffic models in which single cars and their
longitudinal dynamics are modeled via coupled systems of ordinary differential equations. Whereas most
cars are set up to behave like human drivers, we assume that one car has an additional intelligent controller
that obtains real-time information from other vehicles. Based on this example, we analyze different control
methods including a nonlinear model predictive control (MPC) approach with the overall goal to improve
traffic flow for all vehicles in the considered system.
We show that this nonlinear controller may outperform other control approaches for the ring road scenario but
intensive computational effort may prevent it from being real-time capable. We therefore propose an imitation
learning approach to substitute the MPC controller. Numerical results show that, with this approach, we
maintain the high performance of the nonlinear MPC controller, even in set-ups that differ from the original
training scenarios, and also drastically reduce the computing time for online application.
1 INTRODUCTION
Increasing traffic volumes, accompanied by traffic
jams and negative environmental aspects, have led to
a high demand for intelligent mobility solutions that
should guarantee efficiency, safety, and sustainability.
Intelligent vehicles that communicate with other
road users may contribute to these solutions if they
not only maximize their own goals (e.g. minimizing
travel time) but aim to increase and stabilize traffic
flow for all vehicles in certain traffic situations, for
instance, in stop-and-go waves and congestion that
emerge because of inefficient human driving behav-
ior. With intelligent vehicle control these inefficien-
cies may be outbalanced if we can directly affect other
vehicles’ driving behavior.
A crucial point is the design of such controllers.
While models that describe traffic dynamics and hu-
man driving behavior have been studied since the last
century (Lighthill and Whitham, 1955; Gazis et al.,
1961), nowadays, an increasing amount of data is be-
ing collected by vehicles and infrastructure systems,
such that a huge amount of real-time traffic data is
available. That means, besides approaches that re-
quire, at least partially, understanding of the vehi-
cle dynamics, like optimal control theory and model
predictive control (MPC), also purely data-driven ap-
proaches may be applied in traffic control.
1.1 Related Work
For most of the time, traffic flow has been con-
trolled by infrastructure objects like speed lim-
its (Hegyi et al., 2008) or switching through traf-
fic light phases (McNeil, 1968; De Schutter and
De Moor, 1998). But since driver assistance sys-
tems as well as (semi-) autonomous vehicles have
been developed, new ways to control traffic flows
have emerged. By communicating with other vehi-
cles such intelligent vehicle controllers may increase
traffic flow, e.g., with cruise control systems (Orosz
et al., 2010; Orosz, 2016).
One specific scenario, in which these controllers
may be applied, tested, and optimized is the artificial
ring road scenario based on the experiment described
in (Sugiyama et al., 2008). Here, human-like driv-
ing behavior leads to stop-and-go waves without the
presence of bottleneck situations. Further, it has been
Baumgart, U. and Burger, M.
Hybrid Optimal Traffic Control: Combining Model-Based and Data-Driven Approaches.
DOI: 10.5220/0011838000003479
In Proceedings of the 9th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2023), pages 85-94
ISBN: 978-989-758-652-1; ISSN: 2184-495X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
85

shown in another real-world experiment that with one
intelligently controlled vehicle the traffic flow can be
stabilized (Stern et al., 2018). Different modeling set-
ups and control strategies have been proposed to an-
alyze the stability and controllability of the ring road
network (Cui et al., 2017; Wang et al., 2020; Zheng
et al., 2020).
While in these works, the underlying dynamical
system that describes the dynamics of all vehicles
in the system is linearized, we present an MPC ap-
proach that preserves the nonlinear vehicle dynamics
and show that a linearization may decrease the con-
troller’s performance.
Further, we apply an imitation learning approach
that mimics the nonlinear MPC controller with the
goal to reduce the computing time for online appli-
cations while keeping the high performance of the
nonlinear MPC controller. We compare our approach
with several other controllers and show that it dras-
tically reduces the required training time in compari-
son to other ML-based approaches that have been ap-
plied to this problem, like reinforcement learning (Wu
et al., 2017; Baumgart and Burger, 2021).
Accordingly, the remaining part of this contribu-
tion is organized as follows. In Section 2, we intro-
duce microscopic traffic models and set up the spe-
cific traffic control problem for the ring road. Then, in
Section 3, we present solution approaches for the con-
trol problem and compare their results in Section 4.
We also analyze the robustness of the imitation learn-
ing approach in different scenarios and close the con-
tribution in Section 5 with a short summary and po-
tential open problems.
2 TRAFFIC MODELING AND
CONTROL
To set up the specific traffic control problem, we
model human-like driving behavior with microscopic
traffic models - and, more precisely, car-following (or
follow-the-leader) models (Helbing, 1997; Kessels,
2019). With these models, we can describe traf-
fic flows of individual driver-vehicle units on single
lanes. To reflect human decision making, the acceler-
ation behavior of each vehicle i depends on the head-
way h
i
towards its leading vehicle i + 1 and both the
own speed v
i
and the leader’s speed v
i+1
.
We define the headway between the two vehicles in
terms of the bumper-to-bumper distance as follows
h
i
= s
i+1
−s
i
−l
i+1
with s
i
and s
i+1
being the (front bumper) lane posi-
tions of both vehicles and l
i+1
the length of the lead-
ing vehicle. Then, the dynamics of each vehicle i
can be described by a system of ordinary differential
equations (ODEs):
˙
h
i
(t) = v
i+1
(t) −v
i
(t),
˙v
i
(t) = f (h
i
(t),v
i
(t),v
i+1
(t)).
(1)
The right hand side f , that determines the ac-
celeration, depends on the specific car-following
model. One choice is the Intelligent Driver Model
(IDM) (Treiber and Kesting, 2013), in which the right
hand side is given by
f (h
i
,v
i
,v
i+1
)
= a
max
"
1 −

v
i
v
des

δ
−

h
∗
i
(v
i
,∆v)
h
i

2
#
,
h
∗
i
(v
i
,∆v) = h
min
+ max

0,v
i
T +
v
i
∆v
2
√
a
max
b

,
(2)
with ∆v = v
i
−v
i+1
. The model depends on a set of
parameters
β
IDM
= [v
des
,T,h
min
,δ,a
max
,b] (3)
which may be fitted to real-world traffic data or be
used to model different driver types.
Remark 1. In our set-up, other car-following mod-
els may be used to describe the acceleration behav-
ior of the human-driven vehicles as well. We choose
the IDM because it realistically describes human driv-
ing behavior, including its inefficiencies which makes
it an adequate choice for the comparison of different
control approaches. Further, it avoids crashes and we
can introduce heterogeneous driving behavior by as-
signing each vehicle i an individual set of parameters
β
i
IDM
(cf. Section 4). Typical parameter values as well
as other traffic models can be found in (Treiber and
Kesting, 2013).
2.1 Ring Road Control
In real-world experiments of the ring road (Sugiyama
et al., 2008; Stern et al., 2018), it has been shown
that human-driving behavior can be inefficient and
that connected autonomous vehicles (AVs) may be
able to improve traffic flow for all vehicles in the sys-
tem. As it is a closed scenario, the number of ve-
hicles is fixed which facilitates the mathematical de-
scription of the system. However, despite being an ar-
tificial scenario, similar inefficiencies (congestion and
stop-and-go-waves) as in real-world scenarios occur.
Therefore, the ring road experiment has proven to be
an effective benchmark scenario for developing and
testing new traffic control strategies.
In this work, we focus on scenarios with a total
number of N vehicles including one AV and N −1 hu-
man drivers (HDs). We assume that the dynamics of
VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems
86

Figure 1: Visualization of the Ring Road in Matlab (The
MathWorks, Inc., 2021) with 21 HDs and one AV.
the HDs (i = 1,...,N −1) are given by a car-following
model (cf. (1)) and cannot be controlled directly. But
for the AV (i = N), we can set the acceleration behav-
ior with controls u such that the dynamics are given
by
˙
h
N
(t) = v
1
(t) −v
N
(t),
˙v
N
(t) = u(t).
Then, we define the system’s state as
x =



x
1
.
.
.
x
N



,x
i
=

h
i
v
i

and the dynamics can be described as an ODE initial
value problem (IVP) problem:
˙x(t) = F(t,x(t),u(t)) =






v
2
(t) −v
1
(t)
f (h
1
(t),v
1
(t),v
2
(t))
.
.
.
v
1
(t) −v
N
(t)
u(t)






,
x(t
0
) = x
0
,t ∈ [t
0
;t
f
]
(4)
with initial value x
0
. To set up the control problem,
first, we define two constraints for the AV such that
certain safety criteria are satisfied.
A box constraint to include physical limitations for
acceleration and deceleration of the AV,
u(t) ∈ [a
N
min
,a
N
max
] =: U, (5)
and a safety distance, induced by Gipps’ model
(Gipps, 1981; Treiber and Kesting, 2013), to keep the
AV from crashing into its leading vehicle
h
N
(t) ≥ h
min
+ v
N
∆t
N
+
v
2
N
2a
N
min
−
v
2
1
,
2a
N
min
(6)
with AV reaction time ∆t
N
and deceleration bound
a
N
min
. For the other vehicles, the IDM (cf. (2)) is
known to prevent crashes for all HDs (Treiber and
Kesting, 2013).
While keeping these constraints satisfied, we aim to
find such controls for the AV, that the traffic flow for
all vehicles in the system is maximized. One ap-
proach to measure the traffic flow in the system is the
average speed over all vehicles. We therefore define
the running cost l as
l(x,u) = r ·u
2
+ q · v
∗
−
1
N
N
∑
i=1
v
i
!
2
(7)
with r,q ≥ 0 to penalize high actuations u of the AV
and steer the average speed of the system to an equi-
librium speed v
∗
. We can summarize Eqs. (4)-(7)
to state the following nonlinear ODE optimal control
problem (OCP)
min
x,u
J(x,u) =
Z
t
f
t
0
l(x(t), u(t))dt
s.t. ˙x(t) = F(t,x(t),u(t)), x(t
0
) = x
0
,
u(t) ∈ U, x(t) ∈ X , t ∈ [t
0
,t
f
],
(8)
in which X ⊂R
2N
denotes the set of states x such that
constraint (6) is satisfied.
3 CONTROL METHODS
To find optimal controls u for the AV, in this sec-
tion, we present different methods. First, we present
a model predictive control approach that iteratively
computes optimal controls for certain time periods.
As a second model-based controller, we also set up a
linear quadratic regulator.
Then, we present an approach to substitute the
MPC controller by an imitation learning approach that
mimics the MPC controller’s behavior, but requires
much less computing time. Further, we compare this
approach with another ML-based techniques, rein-
forcement learning.
3.1 Model Predictive Control
To set up the MPC scheme, first, we define a time
horizon T , a time shift τ such that τ < T < t
f
, and a
time grid
t
k
= {t
0
,...,t
f
}, t
k+1
−t
k
= τ.
Hybrid Optimal Traffic Control: Combining Model-Based and Data-Driven Approaches
87

Figure 2: Visualization of the MPC scheme.
The MPC idea is visualized in Figure 2 and can be
summarized as follows: at each sampling step k, we
observe the current state x
k
and optimize the system
over time interval [t
k
,t
k
+ T]. The resulting optimal
control sequence u
|[t
k
,t
k
+τ]
up to time τ is then used
as a feedback control for the next sampling inter-
val (Gr
¨
une and Pannek, 2011). That means, at each
step, we have to solve an updated version of the OCP
stated in (8):
min
x,u
J(x,u) =
Z
t
k
+T
t
k
l(x(t),u(t))dt
s.t. ˙x(t) = F(t, x(t), u(t)), x(t
k
) = x
k
,
u(t) ∈ U, x(t) ∈ X , t ∈ [t
k
,t
k
+ T ].
(9)
Typically, the resulting OCP (9) has to be solved nu-
merically at each time instance which may be time
consuming in dependence of time horizon T . In this
work, we apply a reduced discretization approach,
cf. (Gerdts, 2011).
3.2 Linear Quadratic Regulator
Instead of solving OCP (9) numerically, another
approach is to transform the problem to a linear
quadratic problem. For these problems, we can solve
the resulting differential Riccati equation analytically
(Sontag, 1998; Locatelli, 2001). Here, the running
cost
l(x,u) = u
⊤
Ru + x
⊤
Qx
with R ∈R and Q ∈R
2N×2N
is quadratic and the right
hand side of the ODE is linear
˙x(t) = Ax(t) + Bu(t)
with A ∈ R
2N×2N
and B ∈ R
2N
.
In the following, we set up a linear quadratic regula-
tor (LQR) similar to (Cui et al., 2017; Wang et al.,
2020). First, we define an equilibrium state in which
all vehicles travel with constant speed v
∗
. Depending
on the set of parameters β
i
IDM
(cf. (3)), the constant
equilibrium headways h
∗
i
may differ for each HD. As
all vehicles i travel with constant speed at the equilib-
rium state, the accelerations equal zero:
˙v
i
= f (h
i
,v
i
,v
i+1
) = f (h
∗
i
,v
∗
,v
∗
) = 0, i = 1,...,N.
Then, we define a state that indicates the deviation
from (h
∗
i
,v
∗
),
x
i
=

˜
h
i
˜v
i

=

h
i
−h
∗
i
v
i
−v
∗

and apply a first-order Taylor expansion around
f (h
∗
i
,v
∗
,v
∗
)
f (h
i
,v
i
,v
i+1
)
≈
∂ f
∂h
i
(h
∗
i
)(
˜
h
i
) +
∂ f
∂v
i
(v
∗
)( ˜v
i
) +
∂ f
∂v
i+1
(v
∗
)( ˜v
i+1
)
= α
i1
˜
h
i
+ α
i2
˜v
i
+ α
i3
˜v
i+1
.
Here, α
i1
,α
i2
,α
i3
denote the directional derivatives of
the IDM function (cf. (2)) at the equilibrium state for
each vehicle and, similar to (1), we can describe the
dynamics of the HDs as follows
˙
˜
h
i
= ˜v
i+1
− ˜v
i
,
˙
˜v
i
= α
i1
˜
h
i
+ α
i2
˜v
i
+ α
i3
˜v
i+1
,
for i = 1,. . . , N −1. Again, the acceleration behavior
of the AV (i = N) is determined by the control input
u:
˙
˜
h
N
= ˜v
1
− ˜v
N
,
˙
˜v
N
= u.
Finally, the linear dynamics for all vehicles are given
by
˙x(t) = Ax + Bu,
with matrices A and B defined as
A =









C
1
D
1
0 ... 0
0 C
2
D
2
0
.
.
.
.
.
. 0
.
.
.
.
.
.
0
0
.
.
. 0 C
N−1
D
N−1
D
N
0 ... 0 C
N









,B =




0
.
.
.
0
B
N




,
and where the submatrices C
i
and D
i
are given by
C
i
=

0 −1
α
i1
α
i2

,D
i
=

0 1
0 α
i3

,i = 1,...,N −1,
C
N
=

0 −1
0 0

,D
N
=

0 1
0 0

,B
N
=

0
1

.
Still, we aim on keeping low control values and a high
average speed. By setting
R = r ∈ R,Q = diag [0,q,0,q,...,0, q] ∈ R
2N×2N
we obtain the same running cost as in the previous
section (cf. (7)). The LQR is then defined as follows:
min
x,u
J(x,u) =
Z
t
k
+T
t
k
u(t)
⊤
Ru(t) +x(t)
⊤
Qx(t)dt
s.t. ˙x(t) = Ax(t) + Bu(t), x(t
k
) = x
k
,
t ∈ [t
k
,t
k
+ T ].
VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems
88

Remark 2. For the LQR, the optimal control u can be
computed analytically by solving the differential Ric-
cati equation for the tuple (A,B,Q,R), which, in gen-
eral, is much faster than solving the nonlinear OCP
(9) numerically. However, due to the linearization,
the description of the vehicle dynamics lacks in accu-
racy which may lead to an unsatisfying performance
of the computed controls.
Further, for the LQR set-up, constraints as (5) and
(6) have to be neglected such that infeasible solutions
may be computed. There are, however, approaches
for constrained LQRs based on constrained quadratic
programming (Nocedal and Wright, 2006). But, in
general, this requires additional constraint handling
and typically leads to much higher computational
loads as well. In this work, we combine the LQR ap-
proach with a so-called safe speed controller based on
Gipps’ safe speed model (Gipps, 1981; Treiber and
Kesting, 2013), such that at each time step constraint
(6) is satisfied and crashes are avoided.
3.3 Imitation Learning
In this section, we introduce a controller based on im-
itation learning (IL) with the goal to keep the high
performance of the nonlinear MPC approach but to
decrease the required computing time. The general
idea of IL is to imitate (or mimic) another controller
at a certain task. This controller, for the ring road sce-
nario, could be either an intelligent human driver or,
in our applications, a controller that has been realized
using MPC.
In particular, by solving the control problem over
a certain timer period [t
0
,t
f
] numerically, we obtain
for each time step t of a time grid [t
0
,...,t
f
] a state
x
t
∈ X of state space X and a corresponding optimal
control u
t
∈ U of control space U. Now, we aim to
find a function
π
θ
: X → U
with parameters θ that maps optimally from state
space to control space. Optimally, in this context,
means as similar as possible to the other controller.
This can, e.g., be achieved by optimizing θ such that
ˆ
θ = argmin
θ
t
f
∑
t=t
0
∥
π
θ
(x
t
) −u
t
∥
2
. (10)
That is, for all states x
t
, the resulting function out-
put π
θ
(x
t
) should be as close as possible to the MPC-
based controls u
t
.
3.3.1 Neural Nets
A typical choice for π
θ
are multi-layer feed-forward
neural nets (NNs) because they are well known for
their capability of approximating nonlinear func-
tions (Cybenko, 1989; Hornik et al., 1989; Bishop,
2006). In general, they can be described by a com-
position of K layers, k = 1,... K, that all consist
of M
k
neurons. Additionally, an activation function
σ
k
: R → R for each layer has to be specified. All
of these quantities, the number of layers K, the num-
ber of neurons for each layer M
k
and the activation
functions σ
k
are hyperparameters that are chosen pre-
liminary. Further, each layer has a weight matrix W
k
and bias vector b
k
that have to be optimized by a so-
called training procedure. That means, if we choose
a NN for π
θ
in the optimization problem (10), then θ
consists of W
1
,b
1
,..., W
K
,b
K
.
While the optimization (or training) may require
significant computing time, the NN outputs of a
trained net, i.e., the controls, can be computed very
fast in comparison to solving nonlinear control prob-
lems (cf. Section 4).
3.4 Extended Imitation Learning
So far, we have introduced an IL controller that shall
mimic the MPC controller for one specific scenario.
However, we aim to find a controller that performs
well in different situations. Consequently, in the fol-
lowing, we assume that we have solved L different
problems leading to a data set of states and controls
D = {(x
l
t
,u
l
t
)} over time steps t ∈ {t
0
,...,t
f
} and tra-
jectories l = 1,...,L. These problems may differ in
their initial values x
0
and set-ups of the dynamical
system (4) induced by car-following parameters β
IDM
,
cf. (3). Then, similar to (10), we aim to optimize the
parameters of a function π
θ
such that
ˆ
θ = argmin
θ
L
∑
l=1
t
f
∑
t=t
0



π
θ
(x
l
t
) −u
l
t



2
. (11)
Again, the function outputs π
θ
(x
t
) should be as simi-
lar as possible to the controls u
t
. But, by summing not
only over time steps t but also trajectories l, different
set-ups of the dynamical system can be taken into ac-
count. The goal of our approach is to be able to com-
pute controls u even for states x that have not been
observed exactly during training. To achieve this, it
is therefore crucial for the controller’s performance to
define a diverse and substantial dataset D induced by
the L different scenarios.
3.5 Reinforcement Learning
As an additional alternative to the approaches
presented here, we have applied a model-free rein-
forcement learning (RL) approach to the ring road
control problem. In RL, we optimize a control
Hybrid Optimal Traffic Control: Combining Model-Based and Data-Driven Approaches
89

mapping (often called policy in the RL context)
π
θ
which could be, e.g., a neural net. The main
difference to the other control approaches is that,
in general, the dynamical system, induced by the
ODE of (1), is unknown. Thus, several simulations
of the dynamical system are needed such that the
controller can observe different states and apply
different controls. By interacting with the dynamical
system, i.e., by observing the system’s response, the
goal is to find such policy parameters θ that a certain
objective function, called reward, is maximized.
Remark 3. In our implementation, we have optimized
the RL agent with the Matlab Reinforcement Learn-
ing Toolbox and an actor-critic algorithm (The Math-
Works, Inc., 2021). The policy π
θ
is represented by
a neural net with two hidden layers, 32 neurons for
each layer and the tanh activation function.
For a more detailed description of RL in general,
some common algorithms, and its application for traf-
fic control, we refer to, e.g., (Sutton and Barto, 2018),
(Duan et al., 2016), and (Wu et al., 2017; Baumgart
and Burger, 2021), respectively.
4 RESULTS
In this section, we compare the different control ap-
proaches of Section 3 in terms of accuracy, robust-
ness, performance, and computational efficiency. We
show that the MPC controller performs well even if
the dynamical system is not completely known and
we study for the extended IL controller how many ve-
hicles have to send data to achieve desirable results.
General Set-Up
For all scenarios, we let the vehicles start with equal
headways and slightly vary each HD’s driving behav-
ior such that over time a stop-and-go wave occurs. To
obtain different driving behavior, first, we introduce a
nominal IDM parameter set β
nom
IDM
= [16,1,2,4,1,1.5]
(cf. (3)). Then, before each simulation, we draw sam-
ples from a Gaussian distribution with the entries of
β
IDM
as mean values and standard deviation σ. Thus,
each HD’s i current characteristics can be described
by the corresponding IDM parameter set β
i
IDM
defined
as
β
i
IDM
∼ N (β
nom
IDM
,σ). (12)
For each simulation l, we draw new parameters which
may be summarized by
B
l
=
h
β
1,l
IDM
,β
2,l
IDM
,...,β
22,l
IDM
i
. (13)
0 100 200 300 400 500 600
time [s]
0
2
4
6
8
Average Speed [m/s]
HD
AV NLMPC
AV LQR
HD baseline
AV control start
0 100 200 300 400 500 600
time [s]
0
5
10
15
Speed AV [m/s]
Figure 3: Comparison of the MPC solution approaches in
terms of the average speed over all vehicles and the AV’s
speed.
At the beginning, all vehicles are controlled by HDs
with their corresponding parameters β
i
IDM
to observe
the emerging stop-and-go wave caused by heteroge-
neous driving behavior. Then, at t = 300s the AV con-
trol for vehicle i = N is switched on with the goal to
stabilize the traffic flow.
4.1 Comparison of Controllers
At first, we compare the model-based solution ap-
proaches of Sections 3.1 and 3.2. For both, the non-
linear MPC (NLMPC) and the LQR approach, the re-
sulting OCP is solved for time horizon T = 30s and
then the resulting controls are applied with time shift
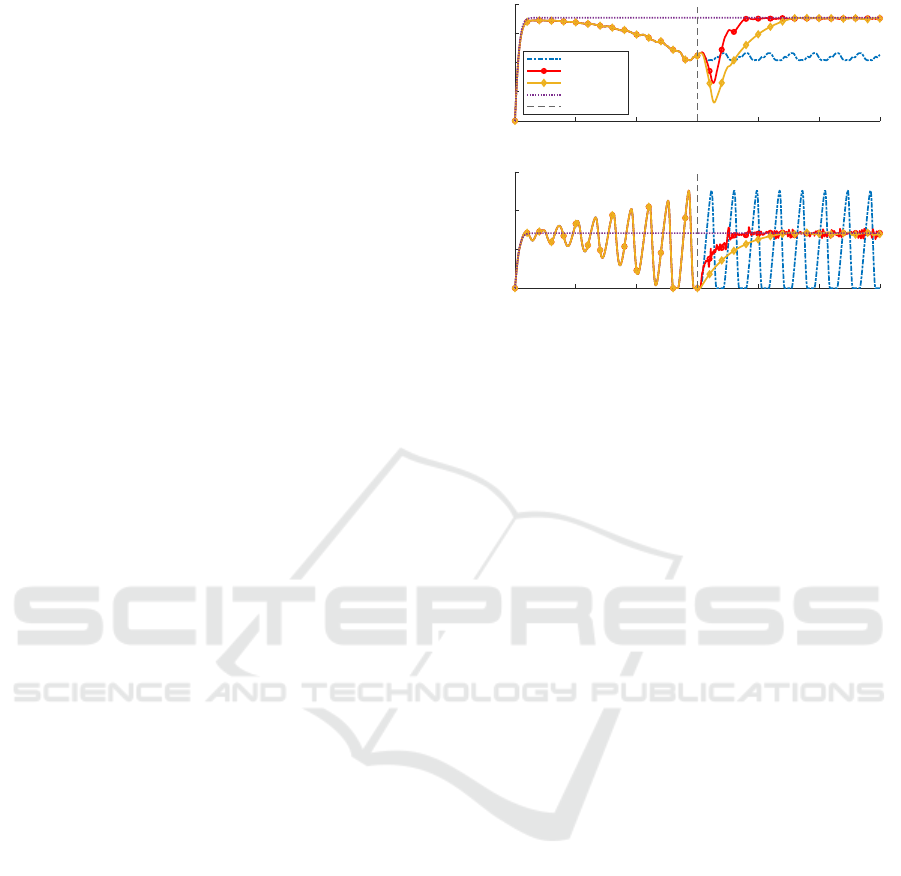
τ = 2s. In Figure 3, results are shown in terms of av-
erage speeds over all vehicles and the AV’s speeds for
the following controllers for one set of parameter B
l
:
• HD Baseline: First, all vehicles are controlled
by HDs with homogeneous parameters β
nom
IDM
such
that no stop-and-go wave occurs.
• HD: All vehicles are controlled by HDs but with
heterogeneous parameters β
i
IDM
. Without AV con-
trol the the stop-and-go wave evolves and does not
vanish over time.
• NLMPC and LQR: For both controllers, the
same stop-and-go wave evolves until the AV con-
trol start. Then, the controllers are switched on to
stabilize the traffic flow for the rest of the time pe-
riod. For the running cost of (7), we set q = 1 and
r = 5.
The results show that both controllers, after the AV
control start, slow down at the beginning, but then
increase their speed which stabilizes the traffic flow
and leads to an average speed similar to the HD base-
line scenario. However, the controllers differ in their
VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems
90

performance (cf. Figure 3 and Table 1): while the
NLMPC approach reaches a high average speed after
the control starts and stabilizes the traffic flow earlier,
the LQR approach has much faster computing times.
Further, for the NLMPC controller, the computing
time clearly exceeds the time shift of τ = 2s. That
means, at least with our implementation of the con-
troller, the NLMPC approach is not capable of being
applied as a real-time feedback controller.
Extended Imitation Learning Controller
To achieve a similar high performance as the NLMPC
approach while reducing the computing time for each
control, in Section 3.4, we have presented an ap-
proach to imitate the MPC controller. Thus, we gen-
erate a data set of L = 10 trajectories in which the
control problem is solved with the NLMPC approach.
For all trajectories l, we draw parameter sets B
train
=
{B
train
1
,...,B
train
10
} according to (13) such that the HD
driving behavior varies in each scenario and the con-
troller is confronted with different stop-and-go situa-
tion at the control start. Then, we optimize the param-
eters θ of a NN according to (11).
The resulting NN of the extended IL controller is
then applied to five test scenarios with parameter sets
B
test
= {B
test
1
,...,B
test
5
} (that all differ from the pa-
rameter sets used to generate the training data). Addi-
tionally to the controllers of Figure 3, in Table 1, we
compare the following controllers for test scenarios
B
test
:
• extIL: Extended IL controller of Section 3.4.
Here, we train a NN that consists of two layers
K = 2, M
1
= M
2
= 10 neurons for each layer, and
the tanh activation function (cf. Section 3.3.1).
• RL: RL controller of Section 3.5 with hyperpa-
rameters and training algorithm as described in
Remark 3. To achieve desirable results, experi-
ments have shown, that we require at least a num-
ber of 1000 episodes (system simulations).
• PI sat PI with saturation controller of (Stern et al.,
2018).
We compare the average speed and the standard devi-
ation (SD) of the speed after the control start as well
as average times for stabilization and for computing
the next control over all test scenarios B
test
. For the
NLMPC approach the next control is computed on-
line, whereas the ML-based techniques consist of an
offline optimization (training) and an online compu-
tation of the controls.
We stress, that our extended IL approach, that has
been trained without direct knowledge of the dynam-
ical system and training data that differs from the test
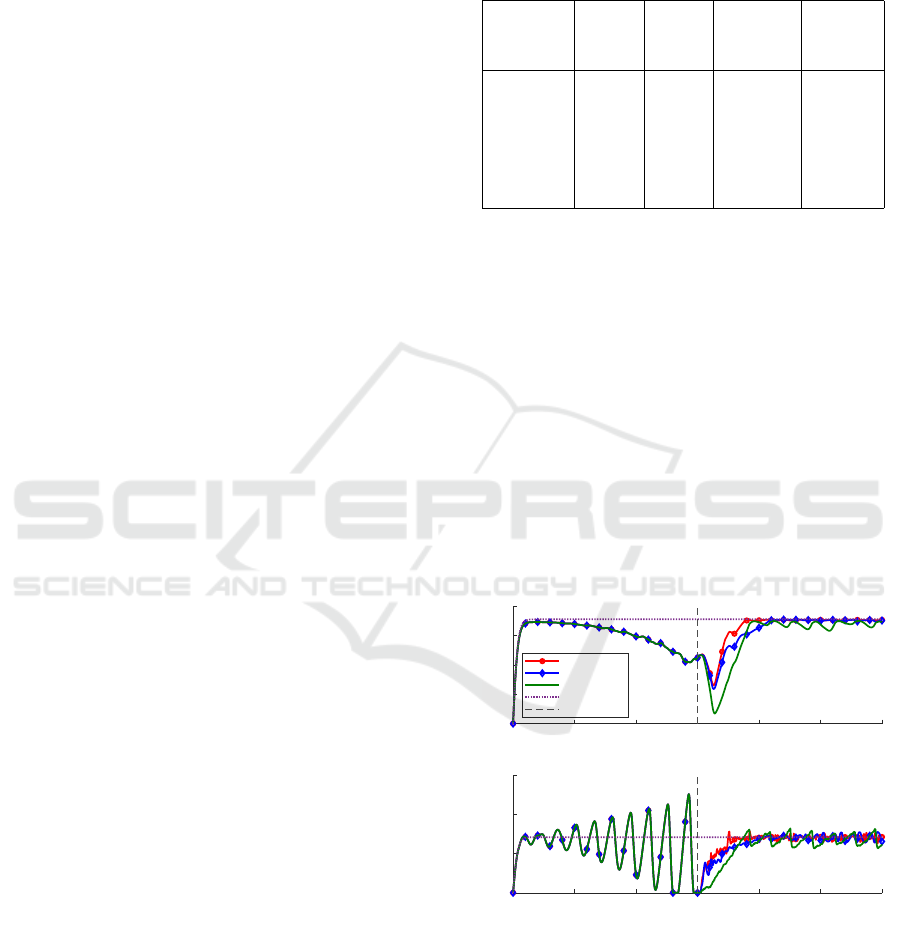
Table 1: Comparison of different controllers at the ring road
scenario in terms of average values over test scenarios B
test
.
The average time to stabilize the system is defined as the
time until all speeds v
1
,.. .,v
N
are within ±0.3m/s of the
equilibrium speed.
Control- Av. SD Av. Av.
speed speed time for comp.
[m/s] [m/s] stab. [s] time [s]
HD 4.60 3.98 - -
NLMPC 6.61 1.35 72.1 8.1
LQR 5.82 2.02 246.5 0.053
extIL 6.57 1.40 131.2 0.0041
RL 5.65 2.10 191.1 0.0026
PI Sat 6.41 1.60 181.5 0.0007
data, performs almost as good as the NLMPC ap-
proach at least in terms of the average speed. How-
ever, in contrast to the NLMPC approach, it is real-
time capable, because we only have to feedforward
the current state through the NN to obtain the next
control in contrast to solving an OCP numerically.
Further, it can be observed that satisfying results can
already be achieved with 10 training trajectories, thus,
it requires much less forward runs than, e.g., RL. The
latter is due to the fact that, with the used MPC tra-
jectory data, expert system knowledge is induced into
the training procedure.
In Figure 4, we show resulting trajectories of the
two ML-based techniques, extIL and RL, as well as of
the NLMPC approach for the same set of parameters
B
l
as in Figure 3 that is part of the test data set B
test
.
0 100 200 300 400 500 600
time [s]
0
2
4
6
8
Average Speed [m/s]
AV NLMPC
AV ExtIL
AV RL
HD baseline
AV control start
0 100 200 300 400 500 600
time [s]
0
5
10
15
Speed AV [m/s]
Figure 4: Comparison of the NLMPC approach with extIL
and RL in terms of the average speed over all vehicles and
the AV’s speed.
4.2 Analysis of Robustness
In this section, we analyze the robustness of the ex-
tended IL approach in terms of the training data and
Hybrid Optimal Traffic Control: Combining Model-Based and Data-Driven Approaches
91

the observed data of other vehicles that is required
for an online application.
4.2.1 Incorrect Description of the Underlying
Dynamical System
For the NLMPC approach, we require to know the
underlying dynamics of OCP (9). However, in real-
world situations, it is a challenging task to find car-
following parameters β
i
IDM
that exactly describe the
driving behavior of HDs. If we have enough obser-
vation data, we can calibrate the parameters of the
car-following model (Kesting and Treiber, 2008). But
even then, their driving behavior may change over
time.
To simulate this situation, we let all HDs travel
with one of the parameters sets B
test
l
as in Section 4.1
such that the same stop-and-go wave occurs at each
simulation. But now, we draw new parameters sets
B
σ
= {B
σ
1
,...,B
σ
10
} for different standard deviations
σ according to (12) and (13). That means, at each
instance, the controller optimizes a system with pa-
rameters B
σ
l
that differs from the simulated system
induced by parameters B
test
l
. By increasing the stan-
dard deviation σ ∈ {0, 0.1, 0.2, 0.3, 0.4, 0.5}, we an-
alyze how much the optimized system is allowed to
differ from the simulated system. Table 2 shows aver-
age values over all vehicles and parameter sets B
σ
.
Desirable results up to σ = 0.3 indicate a certain
robustness of the NLMPC approach against incorrect
description of the underlying dynamics. This may be
explained by the fact, that the MPC scheme allows to
observe the real state at each sampling step and to take
this real state as initial value for the next optimization.
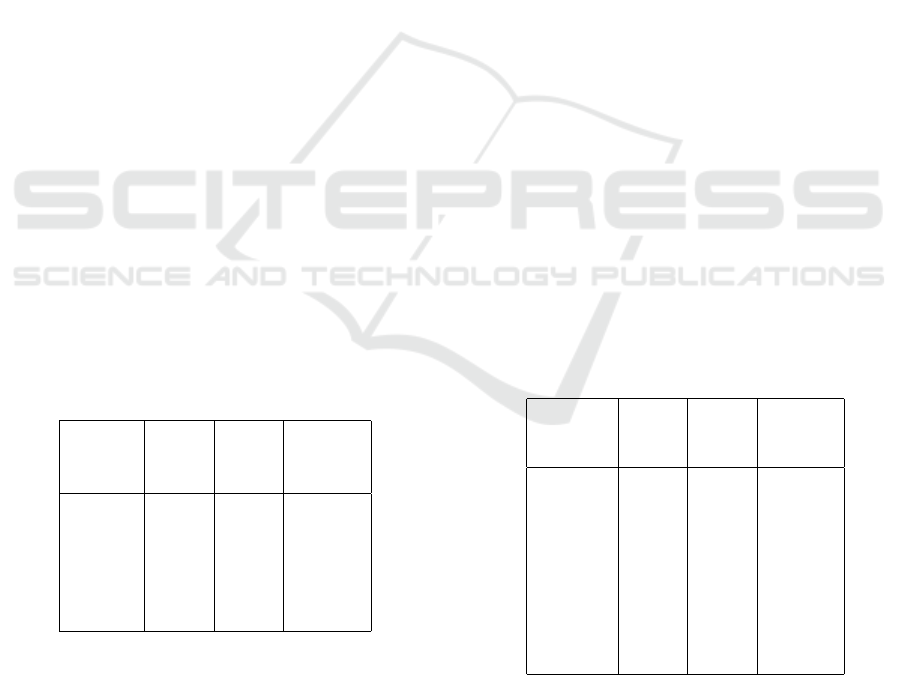
Table 2: Influence of wrong parameters B
σ
on the perfor-
mance of the NLMPC approach.
SD σ Av. SD Av.
for speed speed time for
ˆ
β
i
IDM
[m/s] [m/s] stab [s]
σ = 0 6.52 1.72 97.5
σ = 0.1 6.40 1.69 90.1
σ = 0.2 6.23 1.65 96.8
σ = 0.3 6.24 1.69 102.5
σ = 0.4 5.76 1.83 140.9
σ = 0.5 4.92 1.91 210.6
4.2.2 Data-Availability
In a real-world application, we may not obtain real-
time data from all other vehicles, for instance, be-
cause they are unwilling or physically unable to send
data. But even if (in the near future) we overcome
these problems, it is not guaranteed to observe all ve-
hicles at a certain traffic situation. We therefore ana-
lyze the impact of data-availability of preceding vehi-
cles for the extended IL controller.
In the following, we use the same training data
set obtained with parameters B
train
and same hyper-
parameters for the NNs as in Section 4.1, but now the
controller only obtains data from a limited number of
leading vehicles during the training. That means, ad-
ditionally to the NN in which data from all leaders
is available, further NNs with only input data from a
limited number of leading vehicles are trained. Then,
all of them are applied to the test scenarios, induced
by B
test
. In Table 3, we compare average values over
all scenarios for different numbers of leading vehi-
cles.
The results show that, indeed, the number of ve-
hicles sending data may affect the controller’s per-
formance. Up to four leaders the controller’s perfor-
mance in terms of the average speed increases and the
highest performance is reached when all data is avail-
able.
For the time to stabilize the system, the interpre-
tation is not completely clear because low values are
not always achieved for the NNs with high average
speed. One explanation is the fact, that in some sce-
narios the controller dampens the stop-and-go wave
relatively fast which directly increases the averages
speed, but may require some significant time to reach
a completely stable traffic flow.
Consequently, as for a small number of leaders the
results are already satisfying, it seems that not all data
is necessary for an application of the extended IL con-
troller.
Table 3: Influence of the number of the number of leading
vehicles sending data in terms of average values over test
scenarios B
test
.
Num. of Av. SD Av.
cons. speed speed time for
leaders [m/s] [m/s] stab [s]
1 6.25 1.52 155.8
2 6.42 1.40 156.3
3 6.43 1.44 178.3
4 6.55 1.48 124.6
6 6.44 1.43 122.6
8 6.41 1.32 99.1
10 6.38 1.36 115.1
16 6.30 1.54 177.2
all 6.57 1.40 131.2
Remark 4. To obtain the results of Table 3, we choose
the same hyperparameters for each NN with K = 2
layers, M
1
= M
2
= 10 neurons for each layer, and the
tanh activation function. But, feedforward networks
are typically initialized with random weights and bi-
ases. Depending on the parameter initialization, typ-
VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems
92

ical training algorithms may lead to locally instead
of globally optimal solution for the objective function
(11). We therefore use a Monte-Carlo type approach
with 50 parameter initializations for each of the NNs
to make them more comparable.
5 SUMMARY AND CONCLUSION
We have presented different model-based and data-
driven solution approaches to solve the ring road
control problem. While the highest performance is
reached for the NLMPC approach and it performs
well even if the dynamical system differs from the
real system (cf. Section 4.2.1), its computing times
may prevent it from being real-time applicable. Thus,
we have replaced the MPC controller by an imitation
learning approach which can be extended to include
several different training scenarios. With this exten-
sion, the controller can perform well even in scenarios
that have not been observed exactly during the train-
ing and may not even require data from all vehicles in
the system (cf. Section 4.2.2). By imitating another
controller, expert knowledge about the dynamical sys-
tem is induced which leads to much faster training
than for other ML techniques like RL.
For the training, we require an, at least basic, un-
derstanding of the HD dynamics induced by the car-
following model. But to run it in real-world appli-
cation, we need real-time data from other vehicles.
We expect that current developments in communica-
tion technologies will enable the realization of such
controllers in real-world traffic situations in the near
future.
Although its performance depends on the ob-
served training data, there are advantages of apply-
ing data-driven controllers such as the extIL approach
in real-world situations. That is, while the presented
NLMPC controller is only valid for the closed ring
road in which we are able to describe the dynamics,
the extIL controller may be applied in all set-ups in
which data of one or several leading vehicles is avail-
able. As the occurring stop-and-go waves and traffic
jams in, for instance, city traffic are similar to the ones
at the ring road, we expect our extIL controller to per-
form well in these situations, too.
Like in other applications, in which ML tech-
niques show promising results, there are still open
questions regarding the application of NN-based con-
trollers in safety critical situations like steering a ve-
hicle. While we have shown a certain robustness of
our approach, guaranteed accuracy and stability are
still hard to prove and, at least partially, open tasks.
Further, the tuning of hyperparameters and the repro-
ducibility of training results of Neural Nets are crit-
ical as well and may be overcome by using other
structures like radial basis function (RBF) networks
(Bishop, 2006).
In this work, we have focused on scenarios with
only one intelligently controlled vehicles to empha-
size that already one of these suffices to outbalance
the emerging stop-and-go wave. However, taking into
account several AVs may further improve the results
and may lead to a more efficient outbalancing effect,
cf. (Chou et al., 2022).
In future work, we aim to further analyze the robust-
ness and stability of our approach and other AI-based
techniques. Especially, to guarantee certain safety cri-
teria such that the controller can be applied not only in
artificial but also realistic real-world traffic situations.
REFERENCES
Baumgart, U. and Burger, M. (2021). A reinforcement
learning approach for traffic control. In Proceedings
of the 7th International Conference on Vehicle Tech-
nology and Intelligent Transport Systems - VEHITS,,
pages 133–141. INSTICC, SciTePress.
Bishop, C. M. (2006). Pattern Recognition and Machine
Learning. Springer-Verlag New York.
Chou, F.-C., Bagabaldo, A. R., and Bayen, A. M. (2022).
The Lord of the Ring Road: A Review and Evaluation
of Autonomous Control Policies for Traffic in a Ring
Road. ACM Transactions on Cyber-Physical Systems
(TCPS), 6(1):1–25.
Cui, S., Seibold, B., Stern, R., and Work, D. B. (2017). Sta-
bilizing traffic flow via a single autonomous vehicle:
Possibilities and limitations. In 2017 IEEE Intelligent
Vehicles Symposium (IV), pages 1336–1341.
Cybenko, G. (1989). Approximation by superpositions of a
sigmoidal function. Mathematics of Control, Signals
and Systems, 2(4):303–314.
De Schutter, B. and De Moor, B. (1998). Optimal Traf-
fic Light Control for a Single Intersection. European
Journal of Control, 4(3):260 – 276.
Duan, Y., Chen, X., Houthooft, R., Schulman, J., and
Abbeel, P. (2016). Benchmarking Deep Reinforce-
ment Learning for Continuous Control. In Proceed-
ings of The 33rd International Conference on Ma-
chine Learning, volume 48 of Proceedings of Machine
Learning Research, pages 1329–1338.
Gazis, D. C., Herman, R., and Rothery, R. W. (1961). Non-
linear Follow-the-Leader Models of Traffic Flow. Op-
erations Research, 9(4):545–567.
Gerdts, M. (2011). Optimal Control of ODEs and DAEs.
De Gruyter.
Gipps, P. (1981). A behavioural car-following model for
computer simulation. Transportation Research Part
B: Methodological, 15(2):105–111.
Gr
¨
une, L. and Pannek, J. (2011). Nonlinear Model Predic-
tive Control. Springer-Verlag, London.
Hybrid Optimal Traffic Control: Combining Model-Based and Data-Driven Approaches
93

Hegyi, A., Hoogendoorn, S., Schreuder, M., Stoelhorst, H.,
and Viti, F. (2008). SPECIALIST: A dynamic speed
limit control algorithm based on shock wave theory.
In 2008 11th International IEEE Conference on Intel-
ligent Transportation Systems, pages 827–832.
Helbing, D. (1997). Verkehrsdynamik. Springer-Verlag
Berlin Heidelberg.
Hornik, K., Stinchcombe, M., and White, H. (1989). Multi-
layer feedforward networks are universal approxima-
tors. Neural Networks, 2(5):359–366.
Kessels, F. (2019). Traffic Flow Modelling. Springer Inter-
national Publishing.
Kesting, A. and Treiber, M. (2008). Calibrating car-
following models by using trajectory data: Method-
ological study. Transportation Research Record,
2088(1):148–156.
Lighthill, M. J. and Whitham, G. B. (1955). On kinematic
waves. II. A theory of traffic flow on long crowded
roads. Proc. R. Soc. Lond. A, 229:317–345.
Locatelli, A. (2001). Optimal Control: An Introduction.
Birkh
¨
auser Verlag AG Basel.
McNeil, D. R. (1968). A Solution to the Fixed-Cycle Traffic
Light Problem for Compound Poisson Arrivals. Jour-
nal of Applied Probability, 5(3):624–635.
Nocedal, J. and Wright, S. (2006). Numerical Optimization.
Springer Series in Operations Research and Financial
Engineering. Springer New York.
Orosz, G. (2016). Connected cruise control: modelling, de-
lay effects, and nonlinear behaviour. Vehicle System
Dynamics, 54(8):1147–1176.
Orosz, G., Wilson, R. E., and St
´
ep
´
an, G. (2010). Traffic
jams: dynamics and control. Philosophical Transac-
tions of the Royal Society A: Mathematical, Physical
and Engineering Sciences, 368(1928):4455–4479.
Sontag, E. D. (1998). Mathematical Control Theory: Deter-
ministic Finite-Dimensional Systems. Springer-Verlag
New York.
Stern, R. E., Cui, S., Delle Monache, M. L., Bhadani, R.,
Bunting, M., Churchill, M., Hamilton, N., Haulcy,
R., Pohlmann, H., Wu, F., Piccoli, B., Seibold, B.,
Sprinkle, J., and Work, D. B. (2018). Dissipation
of stop-and-go waves via control of autonomous ve-
hicles: Field experiments. Transportation Research
Part C: Emerging Technologies, 89:205 – 221.
Sugiyama, Y., Fukui, M., Kikuchi, M., Hasebe, K.,
Nakayama, A., Nishinari, K., Tadaki, S.-i., and
Yukawa, S. (2008). Traffic jams without bottle-
necks—experimental evidence for the physical mech-
anism of the formation of a jam. New Journal of
Physics, 10(3):033001.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-
ing: An Introduction. Adaptive Computation and Ma-
chine Learning. MIT Press, 2nd edition.
The MathWorks, Inc. (2021). Matlab R2021b. Natick, Mas-
sachusetts, United State.
Treiber, M. and Kesting, A. (2013). Traffic Flow Dynamics.
Springer-Verlag Berlin Heidelberg.
Wang, J., Zheng, Y., Xu, Q., Wang, J., and Li, K.
(2020). Controllability Analysis and Optimal Control
of Mixed Traffic Flow With Human-Driven and Au-
tonomous Vehicles. IEEE Transactions on Intelligent
Transportation Systems, pages 1–15.
Wu, C., Kreidieh, A., Parvate, K., Vinitsky, E., and Bayen,
A. M. (2017). Flow: Architecture and Benchmarking
for Reinforcement Learning in Traffic Control. arXiv:
1710.05465.
Zheng, Y., Wang, J., and Li, K. (2020). Smoothing Traf-
fic Flow via Control of Autonomous Vehicles. IEEE
Internet of Things Journal, 7(5):3882–3896.
VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems
94