Which Approach Best Predicts Dropouts in Higher Education?

Kerstin Wagner

1 a

, Henrik Volkening

, Sunay Basyigit

Agathe Merceron

1 b

, Petra Sauer

and Niels Pinkwart

3 c

Berliner Hochschule für Technik, Berlin, Germany

Deutsches Zentrum für Luft- und Raumfahrt, Berlin, Germany

Deutsches Forschungszentrum für Künstliche Intelligenz, Berlin, Germany

Keywords:

Predicting Dropouts, Global / Local Feature Set, Evaluation, Balanced Accuracy, Explainability, Fairness.

Abstract:

To predict whether students will drop out of their degree program in a middle-sized German university, we

investigate ﬁve algorithms — three explainable and two not — along with two different feature sets. It turns out

that the models obtained with Logistic Regression (LR), an explainable algorithm, have the best performance.

This is an important ﬁnding to be able to generate explanations for stakeholders in future work. The models

trained with a local feature set and those trained with a global feature set show similar performance results.

Further, we study whether the models built with LR are fair with respect to both male and female students as

well as the study programs considered in this study. Unfortunately, this is not always the case. This might

be due to differences in the dropout rates between subpopulations. This limit should be taken into account in

practice.

1 INTRODUCTION

Although the number of students in Germany who

drop out of their ﬁrst degree program is decreasing

overall, it is still 27% of students on average when

comparing ﬁrst-year students in 2014 with graduates

in 2018. Depending on the subject groups, the degree

aimed at, and the type of university, the proportion

varies, e.g. for bachelor’s degree programs (under-

graduate study programs), between 17% at universi-

ties of applied sciences in the area of law, economics

and social sciences and 39% in the natural sciences

and mathematics area (DZHW, 2020). In order to be

able to take targeted measures that address directly

students who are at risk of dropping out of their stud-

ies, it is necessary to detect these students as exactly

and as early as possible. For example, Berens et al.

(2019) and Manrique et al. (2019) have predicted de-

gree dropout at the end of the 1st, 2nd, 3rd, and 4th

semester with an accuracy approaching or sometimes

surpassing 90%. However, achieving a high accuracy

or recall is not enough for the prediction to be useful.

We agree with Williamson and Kizilcec (2021, p. 1)

https://orcid.org/0000-0002-6182-2142

https://orcid.org/0000-0003-1015-5359

https://orcid.org/0000-0001-7076-9737

that "educators and learners will not trust a model that

cannot easily be explained to them." Stakeholders like

students and counselors need to understand the pre-

diction and be empowered to judge for themselves the

factors that explain the outcome to take action, as ex-

pressed by our students (Wagner et al., 2021) and ar-

gued by Cohausz (2022).

In this paper, we investigate ﬁve algorithms and

two different feature sets based on academic perfor-

mance data only to predict whether students will drop

out of their degree program in a middle-sized German

university. We chose algorithms that have been re-

ported to give good results (Aulck et al., 2019; Berens

et al., 2019; Dekker et al., 2009; Kemper et al., 2020;

Manrique et al., 2019): three algorithms are explain-

able (Molnar, 2022) and two algorithms are not. Ex-

plainable algorithms would make the generation of

explanations for our stakeholders in future work more

straightforward. We trained different models using

the different feature sets and different steps of data

transformation to predict degree dropout after the ﬁrst

four semesters. The models are evaluated, using pri-

marily balanced accuracy, from several perspectives:

algorithms, features, semester, and study program.

Furthermore, we compared the predictions of the best

models using the McNemar test (McNemar, 1947) to

determine signiﬁcant differences.

Wagner, K., Volkening, H., Basyigit, S., Merceron, A., Sauer, P. and Pinkwart, N.

Which Approach Best Predicts Dropouts in Higher Education?.

DOI: 10.5220/0011838100003470

In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023) - Volume 2, pages 15-26

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Additionally, especially when the sizes of sub-

groups in the data differ, one should check whether

these subgroups are equally well predicted as, for ex-

ample, investigated by Gardner et al. (2019). We eval-

uated whether the obtained models are fair with re-

spect to male and female students and with respect to

the study programs considered in this study.

In summary, our research questions are:

RQ1. Are models built with a local feature set more

performant than models built with a global feature set

in our context?

RQ2. Are explainable algorithms as performant re-

garding balanced accuracy as more complex algo-

rithms?

RQ3. How fair are the best models regarding gender

and study program?

RQ4. What are the important features of the most

performant, interpretable model?

The paper is organized as follows. The next sec-

tion describes related works. In the third section, we

present our data and methodology, and the results and

their discussion in the follower section. The last sec-

tion concludes the paper and presents future works.

Excerpts of the data and code are publicly available.

2 RELATED WORKS

Researchers have used diverse data sources to solve

the task of predicting dropouts: pre-entry data like the

grade of entrance degree, demographic data like gen-

der or age, and academic performance data like course

grades or course enrollments. Good prediction results

have been obtained using a mix of academic and de-

mographic data by Kemper et al. (2020) while Man-

rique et al. (2019) have achieved good scores using

academic performance data only. Aulck et al. (2019)

and Berens et al. (2019) have shown that adding de-

mographic data hardly improved the results. In order

to avoid inferences about the students as far as pos-

sible in terms of data protection and because of the

good results of Manrique et al. (2019), we have con-

sidered only data related to the academic performance

of students to build predictors in this work.

Various students’ representations can be calcu-

lated from academic performance data to predict

whether students will drop out. In the work of Man-

rique et al. (2019), three student representations are

distinguished, which the authors referred to as fol-

lows: global features, local features, and time series.

The local feature set contains only courses and their

grades, which are directly part of the academic data.

https://kwbln.github.io/csedu23/

The global feature set contains features that are cal-

culated from the academic data such as average grade

or the number of failed courses; the generation of this

set requires a feature engineering step. Dekker et al.

(2009) and Kemper et al. (2020) have used in this

sense a mix of local and global academic performance

features while the research of Aulck et al. (2019) and

Berens et al. (2019), as well as our own previous work

(Wagner et al., 2020) have been limited to global fea-

tures. An advantage of models based on global fea-

tures is that they can be trained for multiple study pro-

grams together; however, Manrique et al. (2019) have

reported that all their models trained with the local

feature sets had a better performance than the other

models. We do not consider the authors’ third ap-

proach of representing a student as a multivariate time

series in this work because such features are more dif-

ﬁcult for humans to understand; this would be in con-

tradiction to understandability, which is an important

goal of our research.

All ﬁve algorithms used in the present work have

been reported in other works to give good results;

three of them are explainable – decision trees, k-

nearest neighbors, logistic regression (Aulck et al.,

2019; Berens et al., 2019; Dekker et al., 2009; Kem-

per et al., 2020; Manrique et al., 2019) – while the

two others are ensemble methods, which in some

works give better results, but are non-explainable –

AdaBoost and Random Forests (Aulck et al., 2019;

Berens et al., 2019; Dekker et al., 2009; Manrique

et al., 2019). Although there are ways to explain

the predictions of black-box models (Cohausz, 2022;

Molnar, 2022), the work of Swamy et al. (2022)

shows that these methods do not necessarily work as

expected and should be chosen with care: comparing

several approaches reveals that the selected approach

has a far greater impact on feature importances used

to explain the prediction than the underlying data.

Related work has taken different approaches to

improve their models by preprocessing the train-

ing data. Kemper et al. (2020), for example,

have removed unpopular exams with fewer than 15

scores each for dropouts and graduates based on the

observation-variable rate from the data. Manrique

et al. (2019), in contrast, have included only manda-

tory courses based on the assumption of at least 20

enrollments per semester. In both cases, the same ap-

proach has been used for all programs and semesters.

Since the programs used in this study have differ-

ent numbers of elective courses at different points

in the study, we developed a program-speciﬁc ap-

proach to ﬁnd the courses that might be critical for

predicting dropout. Kemper et al. (2020) and Man-

rique et al. (2019) have used SMOTE to balance the

CSEDU 2023 - 15th International Conference on Computer Supported Education

ratio using synthetically generated data sets because

dropouts and graduates were not equally distributed

in the data. Aulck et al. (2019, p. 5), in contrast,

have intentionally trained the models using data "in

its original, unaltered form." For the present work, we

have used Borderline-SMOTE, a further development

of SMOTE (Han et al., 2005).

Regarding the evaluation of the models, the afore-

mentioned studies have used accuracy, i.e. the pro-

portion of correct predictions to all predictions, as a

common metric. A distinctive characteristic of our

evaluation is that we have considered balanced accu-

racy as our key metric. This choice is primarily moti-

vated by the feedback of our students who expressed

that false positives, in our context false alarms, can

be destabilizing (Wagner et al., 2022). Balanced ac-

curacy as the mean of the true positive rate and the

true negative rate gives equal attention to the correct

prediction of dropouts and graduates.

In summary, we contribute to the ﬁeld of dropout

prediction in higher education with:

– an investigation of whether the use of local feature

sets outperforms the use of global feature sets in

another context different from the context of Man-

rique et al. (2019),

– an extensive usage of different processing steps

to improve the models’ performance, including an

expert-based course selection,

– an in-depth comparison of models using the

McNemar test to investigate whether a model

emerges as the best model,

– a fairness investigation in terms of study programs

and gender.

3 DATA AND METHODOLOGY

3.1 Data

The data for this study included three six-semester

bachelor’s degree programs, Architecture coded AR,

Computer Science and Media (CM), and Print and

Media Technology (PT), the three degree programs

with the most students from a medium-sized German

university. The initial dataset contained 3,476 stu-

dents who started their study program between the

winter semester of 2012 and the summer semester

of 2019. Data from 15 so-called fast lane outliers

who completed their degree in three semesters or less

were removed. Fast lane outliers are not represen-

tative since they received credit points for courses

completed in previous study programs and thus may

have completed their studies in much less than six

semesters; the semester threshold of three is based

on our experience. Finally, our dataset contained the

course results from 2,231 students: 995 students who

graduated and 1,236 students who dropped out, see

Table 1. Students who were still active at the time of

consideration were not included in further exploration

and prediction.

Table 1: Number of students per study program (P), gender

(GE), and status (A: active, D: dropout, G: graduate) at the

time of observation.

P GE A D G All GE %

M 205 253 176 634 43

W 286 256 301 843 57

All 491 509 477 1,477

M 360 368 223 951 71

W 120 183 88 391 29

All 480 551 311 1,342

M 100 90 83 273 43

W 159 86 124 369 57

All 259 176 207 642

All

M 665 711 482 1,858 54

W 565 525 513 1,603 46

All 1,230 1,236 995 3,461

We used the enrollments and exam results of the

students. The grading scale is [1.0, 1.3, 1.7, 2.0, 2.3,

2.7, 3.0, 3.3, 3.7, 4.0, 5.0], where the best grade is

1.0, the worst is 4.0, and 5.0 means failing. Students

may enroll in courses without taking the exam. In this

case, they get no grade, but the enrollment is recorded.

Table 2 shows the median number of courses a student

passes in a semester as well as the median grade ob-

tained, distinguishing students who dropped out from

students who completed the program. For example,

the ﬁrst line shows that a student of the program AR

who dropped out passes four courses and has an aver-

age grade of 2.7 in the ﬁrst semester while a student

who completed the program passes ﬁve courses and

has an average grade of 2.0. Generally, the students

who dropped out pass fewer courses and get worse

grades than the students who graduated in all pro-

grams and semesters. We conjecture that algorithms

can learn these differences and predict whether stu-

dents will drop out of their studies.

The study handbook of the given university

provides a suggested course schedule for the six

semesters. Students may or may not follow this

schedule: for example, they may enroll in courses

in their 1st semester that are scheduled for the 2nd

semester, and vice versa. Students must pass all

mandatory courses and a program-speciﬁc number of

elective courses to graduate. Speciﬁcally, students

Which Approach Best Predicts Dropouts in Higher Education?

Table 2: Median number of courses passed (MCP) and me-

dian grades (MG) per study program (P), semester (S), and

student status (D: dropped out, G: graduated).

P S

MCP MG

D G D G

AR 1 4 5 2.7 2.0

2 3 5 2.7 2.0

3 3 6 2.7 2.0

4 2 5 3.0 2.0

CM 1 3 5 2.7 2.0

2 3 5 3.0 2.0

3 3 5 3.0 1.7

4 2 5 2.7 1.7

PT 1 5 6 2.3 1.7

2 3 5 2.3 1.7

3 4 6 2.7 1.7

4 4 6 2.7 1.7

who were not enrolled or failed a mandatory course

in their 1st semester must repeat it in a later semester

to graduate. It is worth mentioning that the pro-

grams are structured differently in terms of elective

courses. Roughly, AR has no electives in the ﬁrst

four semesters, CM has two elective courses sched-

uled in semesters 4 and 5, while PT has ﬁve electives

in semesters 3 and 4.

3.2 Methodology

Preliminary data explorations have shown that 75% of

the students who drop out do so during their three ﬁrst

semesters in the AR study program, in their four ﬁrst

semesters in the CM study program, and during their

ﬁve ﬁrst semesters in the PT program. Thus, this work

investigates dropout prediction after the 1st, 2nd, 3rd,

and 4th semesters. As already mentioned, this work

uses two student representations: one based on a local

feature set, and the other on a global feature set.

We used a series of data transformation steps for

the local and global features to determine which com-

bination gives the best performance for balanced ac-

curacy (BACC). These steps include: handling miss-

ing values, course selection, outlier removal, stan-

dardization, balancing data, and feature selection.

They are shortly explained in subsection 3.2.3.

3.2.1 Local Feature Set

As students do not have to follow the study hand-

book and are quite free in their enrollments, the

courses used as features have to be determined for

each semester and each study program. The baseline

Table 3: Number of selected courses for the prediction

task per study program (P) and semester (S) as the sum of

the number of mandatory courses (MC) and the number of

courses from the enrollment ranking list (ERL).

P AR CM PT

S MC ERL MC ERL MC ERL

1 5 2 5 3 6 2

2 11 3 10 6 12 1

3 17 3 15 4 13 7

4 23 3 18 5 14 7

BL for the local program-speciﬁc feature set included

all courses in which at least one student was enrolled

in a semester. As this gives a large number, between

32 and 44 courses, we tested an automatic course se-

lection that is described in subsection 3.2.3.

Further, we devised a course selection especially

tailored to our context, which we call CS. It includes

three aspects: courses that are passed in a semester,

mandatory courses, and courses in which students en-

roll in a semester:

1. First, we calculated the number of courses stu-

dents passed each semester and detected the out-

liers based on the interquartile range: our upper

fence is the sum of the upper quartile and 1.5

times the interquartile range. Depending on the

semester and the study program, this gave a num-

ber between 6 and 10 as the upper fence, a num-

ber always bigger than the number of mandatory

courses of the current semester.

2. The sum of this upper fence and the number of

mandatory courses from previous semesters gives

the number of courses that we want to use.

3. The courses that are ﬁnally selected are at ﬁrst

the mandatory courses of the current and pre-

vious semesters, supplemented by other courses

with the highest numbers of enrollments in the re-

spective study program and semester (enrollment

ranking list).

This selection approach led to more features for

higher semesters as in Manrique et al. (2019). Ta-

ble 3 gives an overview of the number of courses used.

For example, in the study program PT, six mandatory

courses and two according to the enrollment ranking

list were used at the end of the 1st semester to predict

dropout, and 14 mandatory courses and seven from

the enrollment ranking list were used at the end of the

4th semester. Table 7 shows the courses selected for

CM and PT using this approach.

A natural approach is to represent students with

a vector containing all their grades in each course.

However, some students may not have grades for

CSEDU 2023 - 15th International Conference on Computer Supported Education

some courses. This is the case for courses that stu-

dents did not enroll in or enrolled in but did not

sit the exam. We distinguished what we call post-

poned courses: mandatory courses from the current

semester or from an earlier semester that do not have

any grades are called postponed. A student has to pass

such a course at some point to graduate. Postponed

courses were coded with 7.0, which falls outside the

grading scale and acts as a penalty. Other missing val-

ues, i.e., elective courses or mandatory courses sched-

uled for higher semesters, were coded with 5.1, a

value slightly different from 5.0 (failed). Looking at

Table 7: If, for example, students in the CM program

had not taken the course M05 in their 1st semester,

this course was penalized with 7.0. However, for

M06, which is scheduled for the 2nd semester, 5.1

was imputed.

In the following, we refer to models built with the

local features set as local models.

3.2.2 Global Feature Set

Based on the local features, i.e., with already im-

puted values when grades were missing, global fea-

tures were generated. They are general in nature and

applicable to every study program.

We tested two different course sets to generate

them: including all courses from the local baseline

BL and including only the courses selected with our

own devised method CS.

The lists BL and CS served as the basis to calculate

quantities per student such as the number of passed,

failed, postponed, and enrolled courses. Based on the

number of courses in BL and CS, the features are cal-

culated as proportions to obtain values that are com-

parable across semesters and study programs. Con-

sider for example the feature P_Passed. If a student

in the program CM passed four courses out of the 16

possible courses of CS in the second semester, this fea-

ture gets a value of 0.25. If a student in the program

PT passed four courses out of 13 possible courses, this

feature gets a value of 0.31.

We also created aggregated features based on the

non-standardized grades of the local features like the

mean grade and the mean absolute deviation taking

the grades of all courses and of passed courses only.

If a student passed no course, a value of 6.1 — a value

between 5.1 and 7.0 that has been used for the local

features — was imputed for the average grades and a

value of 0 for the mean absolute deviation.

The following 12 features have been created:

1. Mean_O_Gr: Mean grade of all courses

2. Median_O_Gr: Median grade of all courses

3. MAD_O_Gr: Mean absolute deviation of all courses

4. Mean_P_Gr: Mean grade of courses passed

5. Median_P_Gr: Median grade of courses passed

6. MAD_P_Gr: Mean absolute deviation of courses

passed

7. P_Passed: Proportion of the number of passed

courses out of the number of courses

8. P_Not_Passed: Proportion of the number of

courses failed, postponed, and enrolled

9. P_Failed: Proportion of the number of courses

with a grade of 5.0

10. P_Postponed: Proportion of the number of post-

poned courses out

11. P_Enrolled: Proportion of the number of courses

without grade that are not postponed

12. P_Not_Enrolled: Proportion of the number of

courses without enrollment

In the following, we refer to models built with the

global features set as global models.

3.2.3 Training and Testing

Train Test Split. The data set of the students was

sorted by the semester they started to study and then

split into training (80%) and test sets (20%) with-

out shufﬂing. Hence the test set contained the stu-

dents who started their studies the latest, reﬂecting

the use of prediction in a practical setting: data on

past students are used to predict whether incoming

students are at risk of dropping out. Table 4 shows

the number of students with the status Dropout (D)

or Graduate (G) per semester (S) and study program

(P). The semester-speciﬁc global models have been

trained with all training data for the three programs

and evaluated on the test set of each program sepa-

rately. The test data always contain the same students

in all experiments, although the features differ.

Outlier Handling. We identiﬁed outliers with re-

spect to the number of courses passed per semester

and study program based on the interquartile range.

Models were trained with and without outliers.

Centering/Standardization. Regarding standardiza-

tion, we considered two approaches: centered and

standardized features, where centering and standard-

ization are based on the training data, and the test data

are subsequently transformed.

Balancing Training Data. Since some of the original

training sets were unbalanced, see Table 4, we used

Borderline-SMOTE (Han et al., 2005), implemented

by the python package Imbalanced-learn (Lemaître

et al., 2017), to generate samples for the training data.

Borderline-SMOTE ignores the minority records that

have only neighbors that belong to the majority for

Which Approach Best Predicts Dropouts in Higher Education?

Table 4: Number of students by status (D: dropped out, G:

graduated) of training and test data set per semester (S) and

study program (P).

Training Testing Overall

S P D G D G D G

AR 329 413 149 38 478 451

CM 370 288 155 10 525 298

PT 105 184 63 11 168 195

AR 159 394 70 69 229 463

CM 222 268 94 30 316 298

PT 63 174 39 22 102 196

AR 98 381 43 81 141 462

CM 156 260 68 38 224 298

PT 38 165 21 30 59 195

AR 68 374 27 86 95 460

CM 104 244 41 50 145 294

PT 26 163 15 33 41 196

the synthetic generation of data records. Instead, it

chooses records with both minorities and majorities

as neighbors, i.e., those that are borderline. We tested

two different orders in the pipeline: balancing the

training data before or after centering/standardization.

Feature Selection. To include only important fea-

tures in the models, feature selection is necessary in

the following cases: for local models trained with all

courses BL, and for global models in both cases: us-

ing features calculated with all courses BL or with

courses selected with our own method CS. We im-

plemented two approaches: based on SelectFrom-

Model SFM from Python’s scikit-learn library (Pe-

dregosa et al., 2011) with Logistic Regression as the

estimator and based on correlation.

Algorithms. The following ﬁve algorithms were used

for the prediction: (i-iii) are interpretable algorithms,

see the work of Molnar (2022) for more details, and

(iv-v) are non-interpretable algorithms, so-called en-

semble methods.

(i) Decision Tree (DT): This algorithm builds a tree

from the training data. The root of the tree con-

tains the full training set. Then, features are se-

lected recursively to divide the data into subsets

that are more homogeneous for the class to be

predicted. To classify an element, a path is sim-

ply followed in the tree starting with the root till

a leave is reached. At each node, the decision is

made according to the value that the element has

for the given feature. The majority class of the

leave determines the prediction.

(ii) K-Nearest Neighbors (KNN): To classify an ele-

ment, this algorithm looks in the training data for

the nearest neighbors of this element and predicts

the class of the majority of the neighbors. Be-

cause all the values of all features are numbers,

we chose the Euclidean distance to determine the

nearest neighbors.

(iii) Logistic Regression (LR): This algorithm calcu-

lates optimal weights to all features using the

training data; to classify an element, it performs

a linear combination of the values of the features

for this element using the weights and then applies

the logistic function.

(iv) AdaBoost (AB): This algorithm builds several

classiﬁers by sampling the training data. Each el-

ement in the sample has a probability. At ﬁrst,

the probabilities are all equal. Then, the probabil-

ities of the elements that are correctly classiﬁed

decrease, so that the sample for the next model

is more likely to contain elements that were mis-

classiﬁed. Each classiﬁer is assigned a weight de-

termined by its performance. The ﬁnal prediction

is also given by the majority vote calculated after

taking the weights of each model into account, see

Han et al. (2012) for more details. In our setting,

the models are decision trees.

(v) Random Forest (RF): A random forest is a set of

decision trees; each decision tree is built with a

random sample of the data and a random subset

of the features. The prediction of each tree is a

vote. The ﬁnal prediction of an element is given

by the majority vote.

The implementation was done in the Python

scikit-learn library (Pedregosa et al., 2011). The mod-

els have been trained by optimizing the hyperparam-

eters using grid search with 5-fold cross-validation

against balanced accuracy.

3.2.4 Model Evaluation

The following metrics have been used to evaluate the

models:

– Accuracy (ACC): proportion of correct predic-

tions.

– Recall (REC), also called true positive rate

(TPR): proportion of students who dropped out

and are correctly predicted to drop out.

– False positive rate (FPR): proportion of students

who graduated and are wrongly predicted to drop

out.

– Speciﬁcity (SPEC), also called true negative rate

(TNR): proportion of students who graduated and

are correctly predicted to graduate.

CSEDU 2023 - 15th International Conference on Computer Supported Education

– Balanced Accuracy (BACC): mean of REC (TPR)

and SPEC (TNR).

As already argued in section 2, the most important

metric in this work is BACC. ACC and REC are added

for comparison as many other works use them. For

the fairness evaluation described below, we needed

BACC, ACC, REC (TPR), and SPEC (FPR).

McNemar Test. When two models have a similar

balanced accuracy on the same test set, we used the

McNemar test to further distinguish them (McNemar,

1947) based on a p-value of 0.05.

Fairness Evaluation. Finally, we have evaluated the

fairness of the global models trained with all data with

respect to the three study programs as well as the fair-

ness of the local and global models with respect to the

subgroups of male and female students using slicing

analysis and equalized odds. Slicing analysis is eval-

uating the model performance by "slicing the results

of that model across different dimensions of the test

set" (Gardner et al., 2019); in our case, the dimensions

are the study programs and gender and the considered

metrics BACC, ACC, and REC. Equalized odds com-

pares a model’s true positive rates (TPR) and its false

positive rates (FPR) regarding subgroups. TPR and

FPR of two subgroups often correlate to a sensitive

attribute such as gender (Hardt et al., 2016).

4 RESULTS AND DISCUSSION

We present the overall performance of the ﬁve algo-

rithms, discuss fairness issues, and look at the impor-

tant features found with Logistic Regression.

4.1 General Performance Evaluation

To determine the best feature engineering approach

separately for local and global models, we looked at

the best mean BACC across all algorithms, programs,

and semesters. The best approach for local models

was to use our own course selection CS, see 3.2.1, to

balance the training data and to standardize the data

(mean BACC = 0.8509 across all models, study pro-

grams, and semesters). The highest mean BACC for

global models has been achieved by excluding the

outliers, taking all courses into account (BL), ﬁrst cen-

tering the data and balancing the training data after-

ward, and by selecting the features using SFM (mean

BACC = 0.8850 across all models, study programs

and semesters).

Table 5 shows the performance of each algorithm

when predicting dropout at the end of the 1st, 2nd,

3rd, and 4th semesters for the three study programs

AR, CM, and PT, and the two feature sets. The global

models have been built with all training data for the

three programs and evaluated on the test set of each

program separately. The best BACC scores across

programs, semesters, and feature sets are underlined.

Note that, for example, in semester 1 and program

CM two models, KNN and RF, reach the same best

score. The cell colors correspond to the scores: from

red for values >=0.3 over nuances to dark green for

values >=0.9. In the following, we discuss these re-

sults from different perspectives.

4.1.1 Algorithms Perspective

We consider our key metric BACC. When global fea-

tures are used, the models built with DT obtains the

best value in ﬁve cases out of 12, followed by KNN

in four cases, LR in three cases, and AB as well as

RF in two cases. The algorithms achieve the follow-

ing mean BACC across the different degree programs

and semesters: AB: 0.8807, DT: 0.892, KNN: 0.8762,

LR: 0.8905, RF: 0.8857.

When local features are used, the models built

with LR have the best value in ﬁve cases out of 12,

followed by RF in three cases, then AB and DT in

two cases each, and KNN in one case. The algorithms

achieve the following mean BACC: AB: 0.8528,

DT: 0.813, KNN: 0.8532, LR: 0.8787, RF: 0.8567.

Overall, LR achieves the best value eight times, has

the best mean when local features are used, and the

second best mean when global features are used.

One notices that the BACC values are not far apart

for each program and semester. For example, in the

1st semester, BACC line LR in the global setting and

AR program (column AR GF) is 0.8857 while the

best score 0.8990 appears line RF. We have used the

McNemar test to compare the best of the explainable

algorithms (DT, KNN, LR) with the best of the en-

semble methods (AB, RF). In all but one case, an ex-

plainable model has either the best score or does not

perform signiﬁcantly differently, according to the Mc-

Nemar test, from a non-explainable model.

Further, we have also used the McNemar test to

compare the three explainable models between them.

LR always either performs better or does not perform

signiﬁcantly differently from KNN; and LR always

performs better or does not perform signiﬁcantly dif-

ferently from DT in all but one case while DT per-

forms signiﬁcantly worse than LR in four cases. Thus,

in our context, LR emerges as the algorithm which,

generally, gives the best results. Further, since our

stakeholders need to understand the prediction, ex-

plainable models based on LR should be preferred.

In the literature, there is still no agreement on

which algorithms perform the best, though ensem-

ble methods (Manrique et al., 2019) and AB (Berens

Which Approach Best Predicts Dropouts in Higher Education?

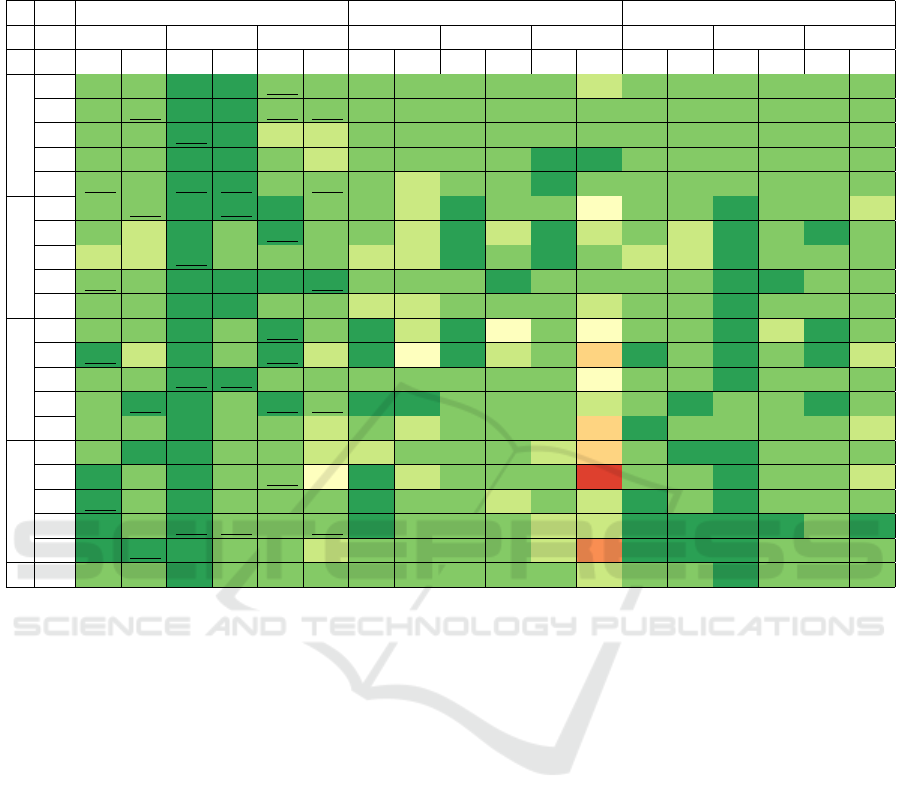
Table 5: Evaluation of the best models based on the metric balanced accuracy (BACC) for global (GF) and local features (LF)

per study program (P) for each semester (S) and algorithm (A) and the corresponding scores for recall (REC) and accuracy

(ACC): best BACC scores per program, feature set and semester are underlined.

BACC REC ACC

P AR CM PT AR CM PT AR CM PT

S A GF LF GF LF GF LF GF LF GF LF GF LF GF LF GF LF GF LF

AB 0.804 0.879 0.938 0.935 0.846 0.815 0.844 0.838 0.877 0.870 0.859 0.797 0.828 0.854 0.884 0.878 0.855 0.803

DT 0.879 0.889 0.932 0.910 0.846 0.831 0.838 0.857 0.864 0.821 0.859 0.828 0.854 0.870 0.872 0.831 0.855 0.829

KNN 0.883 0.843 0.944 0.914 0.763 0.789 0.844 0.818 0.889 0.827 0.859 0.828 0.859 0.828 0.895 0.837 0.829 0.816

LR 0.886 0.886 0.941 0.923 0.828 0.786 0.877 0.851 0.883 0.846 0.906 0.906 0.880 0.865 0.890 0.855 0.882 0.868

RF 0.899 0.847 0.944 0.941 0.828 0.831 0.851 0.799 0.889 0.883 0.906 0.828 0.870 0.818 0.895 0.890 0.882 0.829

AB 0.811 0.848 0.926 0.911 0.903 0.825 0.822 0.767 0.918 0.888 0.850 0.650 0.811 0.846 0.922 0.898 0.889 0.778

DT 0.803 0.798 0.914 0.831 0.907 0.844 0.877 0.740 0.929 0.796 0.900 0.775 0.804 0.797 0.922 0.812 0.905 0.825

KNN 0.797 0.791 0.931 0.889 0.885 0.872 0.795 0.753 0.929 0.878 0.900 0.875 0.797 0.790 0.930 0.883 0.889 0.873

LR 0.832 0.833 0.916 0.904 0.903 0.903 0.836 0.808 0.898 0.908 0.850 0.850 0.832 0.832 0.906 0.906 0.889 0.889

RF 0.827 0.841 0.916 0.900 0.891 0.866 0.753 0.753 0.898 0.867 0.825 0.775 0.825 0.839 0.906 0.883 0.873 0.841

AB 0.898 0.847 0.924 0.819 0.903 0.826 0.930 0.791 0.901 0.690 0.870 0.652 0.888 0.864 0.917 0.780 0.907 0.852

DT 0.910 0.783 0.924 0.828 0.903 0.729 0.930 0.651 0.901 0.761 0.870 0.522 0.904 0.824 0.917 0.807 0.907 0.759

KNN 0.863 0.876 0.930 0.908 0.870 0.832 0.860 0.814 0.859 0.817 0.870 0.696 0.864 0.896 0.908 0.881 0.870 0.852

LR 0.899 0.916 0.903 0.875 0.903 0.853 0.907 0.930 0.859 0.803 0.870 0.739 0.896 0.912 0.890 0.853 0.907 0.870

RF 0.899 0.865 0.909 0.889 0.865 0.761 0.884 0.767 0.845 0.831 0.826 0.522 0.904 0.896 0.890 0.872 0.870 0.796

AB 0.841 0.918 0.929 0.877 0.846 0.735 0.786 0.893 0.857 0.833 0.750 0.500 0.870 0.930 0.935 0.880 0.880 0.820

DT 0.907 0.846 0.930 0.855 0.847 0.612 0.964 0.750 0.881 0.810 0.812 0.312 0.878 0.896 0.935 0.859 0.860 0.720

KNN 0.924 0.865 0.920 0.813 0.803 0.846 0.929 0.821 0.881 0.786 0.812 0.750 0.922 0.887 0.924 0.815 0.800 0.880

LR 0.918 0.894 0.940 0.895 0.816 0.875 0.929 0.857 0.881 0.810 0.750 0.750 0.913 0.913 0.946 0.902 0.840 0.920

RF 0.900 0.935 0.919 0.885 0.831 0.719 0.893 0.893 0.857 0.810 0.750 0.438 0.904 0.957 0.924 0.891 0.860 0.820

All All 0.869 0.860 0.927 0.885 0.859 0.807 0.867 0.808 0.885 0.827 0.845 0.700 0.865 0.866 0.910 0.861 0.873 0.832

et al., 2019) are mentioned to perform better. By con-

trast, the explainable model obtained with DT gives

a good performance in (Dekker et al., 2009; Kemper

et al., 2020). Since the balanced accuracy does not

reach 100% regardless of the setting, we consider the

choice of algorithms as a limitation of our work: we

did not investigate other non-explainable algorithms

such as gradient-boosted trees or support vector ma-

chines that have also been reported as giving good

results in dropout prediction (Manrique et al., 2019).

Models built with those algorithms, however, should

reach a balanced accuracy well above 90% to be eligi-

ble for consideration in our context. It is worth men-

tioning that any intervention or any system targeting

speciﬁc students has to take the prediction imperfec-

tion into account.

4.1.2 Local Versus Global Features Perspective

Again, we focus on BACC and compare for each

study program and each semester, whether the global

model has a higher value than the local model. For

example, in column AR GF and semester 4, BACC

for LR is 0.9183 while it is 0.8941 in the LF column.

Because LR emerges as the preferred algorithm, we

focus on it from this perspective.

We observe that the values of BACC obtained with

global and local models in the three study programs

and the four semesters are not far apart. As above,

we have used the McNemar test to compare the global

LR model to the local LR model. The result is that the

performance of the two models is not signiﬁcantly dif-

ferent. Thus, both approaches appear equally success-

ful and could be used in practice. The choice could be

decided with some other criteria, like the availability

of the data or the effort required to build a model per

study program. Our ﬁndings are different from those

of Manrique et al. (2019), who found that the models

built with the local feature set are consistently better

than the other models.

4.1.3 Semester Perspective

We do not observe any particular trend in the three

metrics BACC, REC, and ACC across semesters,

study programs, and settings, i.e., using local or

global features. By contrast, Kemper et al. (2020),

Manrique et al. (2019), and Berens et al. (2019) have

observed a performance increase as the semesters get

higher. Manrique et al. (2019) argue "that with the

CSEDU 2023 - 15th International Conference on Computer Supported Education

increase of information about the student, better re-

sults should be obtained" but recognize that others do

not share this observation; indeed, with an increased

number of semesters, there are less data to train the

models, which can lead to poorer performance.

4.1.4 Study Program Perspective

The values of all metrics for global and local models

tend to be lower in the program PT than in the other

programs, especially in semesters 3 and 4. This might

be due to the fact that this program is structured differ-

ently than the other two and has many elective courses

in semesters 3 and 4, see also Table 7.

Interestingly, the data exploration shows that stu-

dents in this program tend to drop out less than in the

two other programs (Table 1). This fact could play a

role, as could the fact that, in the global setting, stu-

dents who drop out from the PT program are under-

represented (AR: 41%, CM: 45%, PT: 14%).

One can also notice that the values of all met-

rics are a bit lower in the second semester of the AR

program. Exploring our data, we have observed that

students tend to not follow the study handbook in

semester 2, hence many students have a value of 7.0

for the courses planned in that semester. This could

explain the poorer prediction results in that semester

for this program.

4.2 Fairness

As already written, we evaluate the fairness of our

models using slicing analysis and equalized odds. All

metrics should have the exact same value for the sub-

populations that we consider to qualify our models as

fair. However, this is not the case. Can we tolerate

some differences between subpopulations? Given our

context, we have consulted our students to help clar-

ify this issue. In a machine learning class involving

about 50 students over two semesters, we have asked

the following questions:

"Suppose your best model to predict dropout has

an accuracy of 77.5% for male students and an accu-

racy of 76.7% for female students. Would you ﬁnd

this model to be fair? If not, who are disadvantaged,

male students or female students? And what if your

best model has an accuracy of 75.5% for male stu-

dents and an accuracy of 83.7% for female students?"

Unanimously, students found that the ﬁrst differ-

ence does not matter while male students are disad-

vantaged in the second case. Based on that opinion

and generalizing it to other metrics, in this study, we

consider a performance difference of up to 2% for the

following analysis as fair. Compared, for example,

to the work of Zhang et al. (2022), 2% appears to be

a conservative threshold since Zhang et al. judge a

difference ranging from 1-11% for the AUC metric

between male and female students as small.

We focus on LR in the following because it ended

up being the algorithm that performed best overall.

4.2.1 Study Program Perspective

As already written, the global models for each

semester have been built with all training data for the

three programs and evaluated on the test set of each

program separately. Here, we discuss whether these

models are fair with respect to the dimension study

program. Such a discussion is not relevant for the lo-

cal models as they have been built with training data

of each respective study program.

Slicing Analysis. The GF columns of Table 5 show

a slicing analysis of the global models across the di-

mension study program. As already written, we focus

ﬁrst on LR. One notices, for example, that BACC of

the line LR in semester 1 varies from 0.8281 (column

PT) to 0.9414 (column CM). This difference is bigger

than 2%, the value discussed above, and we transfer

that to all metrics. Inspecting the three metrics BACC,

REC, and ACC across programs and semesters, one

observes that the differences are mostly above 2% for

the models built with the different algorithms: we can

consider LR as fair in 6 out of 36 cases (three met-

rics × three degree programs × four semesters); note

that the other algorithms reach fairness in fewer cases

(AB: 0, DT: 2, KNN: 3, RF: 3).

Equalized Odds. We have further compared the

TPR, which is also known as REC, and the FPR and

found that only in one case out of 24 (two metrics ×

three study programs × four semesters) there was a

difference below 2%: the difference between REC in

semester 3 for AR and CM using the KNN models.

All other differences are over 2%.

Overall, it appears that the performance of all

global models, not only LR, varies by program, and

this variation may be perceived as unfair by students.

Therefore, if global models are used, their perfor-

mance with respect to each degree program should be

checked if data are available.

4.2.2 Gender Perspective

In our data, there are more male students than female

students and also differences in distribution between

programs (Table 1). While AR and PT have 43% male

students, CM has 71%. From all students who drop

out, we have noticed differences in the proportions of

male and female students: 50% are male in the AR

program, 67% in CM, and 51% in PT. We investi-

gated whether these two subpopulations are equally

Which Approach Best Predicts Dropouts in Higher Education?

Table 6: Result of the fairness evaluation: Number of fair

cases out of 12 per algorithm and feature set (GF, LF) re-

garding gender.

BACC ACC REC/TPR FPR

GF LF GF LF GF LF GF LF

AB 4 3 4 3 3 4 3 3

DT 3 3 4 0 2 1 1 2

KNN 1 3 3 1 1 3 5 3

LR 3 2 1 3 3 3 2 5

RF 4 2 5 3 1 1 1 3

well predicted.

Table 6 shows the number of cases that we con-

sider as fair regarding gender, i.e., the cases where the

absolute score difference between women and men is

less than 2%. The overall picture given by the slicing

analysis is that all models exceed the threshold value

of 2% in the majority of cases.

Further work is needed to understand these re-

sults and their reasons. The question of the thresh-

old value requires further investigation. We assume

that exactly equal values between subpopulations will

seldom happen in practice and we have chosen a con-

servative threshold of 2%. Considering an increase of

the threshold from 2% to 3%, for example, would re-

sult in the global LR models being considered fair in

twice as many cases. A threshold of 11% as given by

Zhang et al. (2022) would change the results of Ta-

ble 6 and show LR fair in all but seven cases across

all columns (96 cases in total). Thus, further work

is needed to understand which threshold suits which

stakeholders. We argue that these ﬁndings are impor-

tant and that any practical use of a classiﬁer has to

take fairness considerations into account.

4.3 LR and Important Features

Perspective

Since LR provides the best mean BACC overall, i.e.,

for both global and local models, we have a closer

look at the coefﬁcients of the models.

In LR, the exponential of a coefﬁcient gives the

estimated odd change when the value of the feature is

increased by one unit assuming the other features re-

main the same (Molnar, 2022). Consequently, the val-

ues of features with positive coefﬁcient impact much

more the probability of the prediction to be dropout

than the values of features with negative coefﬁcients.

4.3.1 Local Models

Table 7 shows the coefﬁcients of the different courses,

our local features, for the study programs CM and PT

per semester. The program AR is omitted because

of ﬁndings similar to CM. Courses whose code be-

gins with M are mandatory and with E elective. One

can see that the models for CM have ﬁve mandatory

courses in the ﬁrst plan semester, M01 till M05, while

PT has six: M06 is a mandatory course in the 1st

semester for PT and in the 2nd semester for CM.

It is interesting to observe that three mandatory

courses of the ﬁrst semester have positive coefﬁcients

and, therefore, impact the prediction "dropout" across

all semesters and study programs. Exploring the data,

some courses appear easier for students because they

have a higher proportion of good grades, and some ap-

pear more difﬁcult, because they have a smaller pro-

portion of good grades, higher proportion of fail or

of students not sitting the exam. Examples of easier

courses are M03 in CM, and M05 in PT. Examples

of more difﬁcult courses are M05 in CM, and M02

in PT. One notice that both kinds of courses can have

high coefﬁcients compared to the other coefﬁcients in

semester 1.

Another observation is that some of the 1st and

2nd semester’s courses achieve relatively high coefﬁ-

cients in semester 3 or 4. This is the case of M04 and

M06 in CM, and M02 and M08 in PT. These courses

could be courses that students keep postponing and,

thus, could be brought to the attention of advisors and

program heads. More research is needed to check this

supposition.

From semester 2 onward, the number of features

with existing coefﬁcient is large, probably too large

to communicate them all to users. Some work will be

needed to derive explanations that are enlightening to

stakeholders.

4.3.2 Global Models

Table 8 shows the features selected by SFM for each

semester and their coefﬁcients used for predicting

dropout in the four semesters.

In the ﬁrst semester, the mean grade of all course

Mean_O_Grade highly inﬂuences the dropout prob-

ability. This feature remains important in the sub-

sequent semesters. The most important feature for

semesters 2 to 4 is the proportion of failed courses

P_Failed. In the 3rd semester, P_Not_Passed also

inﬂuences the probability to drop out, but is balanced

byP_Passed which in principle has the inverse value.

Here we can see that the automated feature selection

based on SFM could have been limited to one of these

two features. Thus, further analysis is needed here.

Overall, it is probably easier to derive explana-

tions for users of the predictions from the small num-

ber of global features compared to the local features.

CSEDU 2023 - 15th International Conference on Computer Supported Education

Table 7: Coefﬁcients of local features, i.e. courses, with planned semesters (PS) from the study handbook per study program

(top: CM, bottom: PT) and semester (S): elective courses are recommended for two semesters, e.g. 34 means plan semester 3

or 4; red cells highlight positive values, blue cells negative values, and white cells indicates that this course was not included

to build the model; values equal or higher than 1 are in bold.

PS 1 2 3 4 5 45

CM M01 M02 M03 M04 M05 M06 M07 M08 M09 M10 M13 M14 M15 M16 M17 M18 M19 M20 M23 M24 E01 E02 E03 E05 E06

S1 0.1 0.4 0.4 0.8 0.6 -0.2 -0.0 0.5

S2 -0.4 0.2 0.3 0.4 0.5 0.5 -0.0 0.3 0.5 0.6 -0.1 0.2 -0.1 0.2 0.1 0.2

S3 -0.1 -0.2 0.3 0.7 0.6 0.2 -0.4 -0.6 0.3 0.1 0.0 0.0 0.8 0.5 1.0 0.0 0.0 0.4 0.4

S4 -0.2 0.0 0.2 0.7 0.3 0.6 0.0 0.0 0.2 -0.3 0.0 0.1 0.4 0.5 1.1 0.1 -0.0 0.4 -0.1 -0.2 -0.1 0.1 0.4

PS 1 2 3 4 34

PT M01 M02 M03 M04 M05 M06 M07 M08 M09 M10 M11 M12 M13 M19 E02 E05 E09 E10 E12 E16 E17 E22 E23 E25 E26

S1 0.7 0.3 0.2 0.1 1.0 0.5 0.1 -0.2

S2 0.9 0.1 0.4 -0.3 0.1 -0.5 0.6 0.3 -0.2 0.0 0.7 0.8 1.3

S3 0.4 0.3 0.1 -0.5 0.5 -0.0 0.6 1.1 0.4 0.3 0.3 -0.0 1.3 0.3 0.0 -0.3 0.2 -0.2 0.4 0.1

S4 0.2 0.8 0.0 -0.4 0.1 -0.1 0.3 1.1 0.5 0.2 0.1 -0.2 0.1 1.1 0.2 0.2 0.7 -0.1 0.5 0.0 -0.2

Table 8: Coefﬁcients of global features: red cells high-

light positive values, blue cells negative values, and white

cells indicates that this course was not included to build the

model; values higher than 1 are in bold.

S 1 2 3 4

MAD_O_Gr -0.73 0.00 -2.15 -1.14

Mean_O_Gr 7.01 3.93 0.93 3.23

Mean_P_Gr -0.62 -0.83

P_Failed 12.73 22.15 16.98

P_Not_Enrolled -16.40

P_Not_Passed 0.00 4.01 0.00

P_Passed 0.00 -4.01 0.00

P_Postponed -2.65

5 CONCLUSION, LIMITS AND

FUTURE WORKS

In this paper, we have investigated several algorithms

and two types of feature sets to predict whether a stu-

dent will drop out of a degree program at a medium-

sized German university. Our results show that pre-

dicting whether students will drop out is possible with

a balanced accuracy and also an accuracy approach-

ing or surpassing 90% in many cases; these results are

comparable to those obtained by others, sometimes

with more data. Thus, such studies bring insight even

in the context of medium-sized universities. However,

as stated in section 4.1.1, we consider it a limitation

of the work that we did not investigate additional non-

explainable algorithms.

Our research shows that the explainable algorithm

Logistic Regression gives the best overall results. It

shows further that the performance of the models

based on Logistic Regression built with a global fea-

ture set is comparable to the performance of the mod-

els built with a local feature set, which differs from the

results obtained by Manrique et al. (2019). It should

be noted, however, that not all study programs are pre-

dicted equally well in a semester when a single model

built using the global feature set is used. The inﬂu-

ence that the different structure of study programs re-

garding elective courses has on the prediction quality

needs to be analyzed in the future. A limitation of

this study is that we have considered three study pro-

grams only. Future work should include more pro-

grams, also programs with fewer students.

Further, our models do not predict male and fe-

male students equally well. More research is needed

to understand why this is the case and whether the

models can be made fairer without losing balanced

accuracy. Future work includes discussing with dif-

ferent stakeholder groups to understand which differ-

ence between subpopulations is acceptable in our con-

text, and whether the threshold value of 2% adopted

in section 4.2 is too conservative or not. When such

prediction models are used in practice, their fairness

in terms of study programs and gender should be an-

alyzed and considered.

As an explainable algorithm, Logistic Regression

can be used to generate explanations for academic

advisors on the one hand and for the students them-

selves on the other hand. Future work also includes

discussing the results of section 4.3 with deans of

studies and program heads to generate explanations

helpful to them. An interesting future line of research

would be to convert explanations into student recom-

mendations. Indeed, our students think that informing

them about the possibility of dropping out has both

advantages and disadvantages, and there is no agree-

ment on which of these is more important (Wagner

et al., 2021). They have, however, expressed a need

for more guidance, especially in their ﬁrst semesters.

Which Approach Best Predicts Dropouts in Higher Education?

Building on our results, we are currently devel-

oping a course recommender system to support espe-

cially students at risk of dropping out (Wagner et al.,

2022). Indeed, if students enroll properly and pass

more courses, they may be less likely to drop out as

Table 2 and 8 suggest. Students may need guidance

for enrolling in the appropriate courses as well as the

appropriate number of courses. Our recommender

system supports these two aspects.

REFERENCES

Aulck, L., Nambi, D., Velagapudi, N., Blumenstock, J., and

West, J. (2019). Mining university registrar records to

predict ﬁrst-year undergraduate attrition. In Proceed-

ings of the 12th International Conference on Educa-

tional Data Mining, page 9–18.

Berens, J., Schneider, K., Gortz, S., Oster, S., and Burghoff,

J. (2019). Early detection of students at risk - predict-

ing student dropouts using administrative student data

from german universities and machine learning meth-

ods. Journal of Educational Data Mining, 11(3):1–41.

Cohausz, L. (2022). When probabilities are not enough -

a framework for causal explanations of student suc-

cess models. Journal of Educational Data Mining,

14(3):52–75.

Dekker, G., Pechenizkiy, M., and Vleeshouwers, J. (2009).

Predicting students drop out: A case study. In Pro-

ceedings of the 2nd International Conference on Edu-

cational Data Mining, pages 41–50.

DZHW (2020). Veröffentlichungen, hochschul-IT,

hochschulforschung, hochschulentwicklung.

Gardner, J., Brooks, C., and Baker, R. (2019). Evaluat-

ing the fairness of predictive student models through

slicing analysis. In Proceedings of the 9th Interna-

tional Conference on Learning Analytics & Knowl-

edge, pages 225–234.

Han, H., Wang, W.-Y., and Mao, B.-H. (2005). Borderline-

smote: A new over-sampling method in imbalanced

data sets learning. In Advances in Intelligent Comput-

ing, pages 878–887.

Han, J., Kamber, M., and Pei, J. (2012). Data Mining -

Concepts and Techniques. Morgan Kaufmann.

Hardt, M., Price, E., and Srebro, N. (2016). Equality

of opportunity in supervised learning. In 30th Con-

ference on Neural Information Processing Systems,

(NIPS 2016).

Kemper, L., Vorhoff, G., and Wigger, B. U. (2020). Predict-

ing student dropout: A machine learning approach.

European Journal of Higher Education, pages 28–47.

Lemaître, G., Nogueira, F., and Aridas, C. K. (2017).

Imbalanced-learn: A python toolbox to tackle the

curse of imbalanced datasets in machine learning.

Journal of Machine Learning Research, 18(17):1–5.

Manrique, R., Nunes, B. P., Marino, O., Casanova, M. A.,

and Nurmikko-Fuller, T. (2019). An analysis of stu-

dent representation, representative features and clas-

siﬁcation algorithms to predict degree dropout. In

Proceedings of the 9th International Conference on

Learning Analytics & Knowledge, pages 401–410.

McNemar, Q. (1947). Note on the sampling error of the

difference between correlated proportions or percent-

ages. Psychometrika, 12:154–166.

Molnar, C. (2022). Interpretable machine learning. https:

//christophm.github.io/interpretable-ml-book/. Last

checked on Dec 07, 2022.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Swamy, V., Radmehr, B., Krco, N., Marras, M., and Käser,

T. (2022). Evaluating the explainers: Black-box ex-

plainable machine learning for student success predic-

tion in MOOCs. In Proceedings of the 15th Interna-

tional Conference on Educational Data Mining, pages

98–109.

Wagner, K., Hilliger, I., Merceron, A., and Sauer, P. (2021).

Eliciting students’ needs and concerns about a novel

course enrollment support system. In Companion

Proceedings of the 11th International Conference on

Learning Analytics & Knowledge LAK20, pages 294–

304.

Wagner, K., Merceron, A., and Sauer, P. (2020). Accuracy

of a cross-program model for dropout prediction in

higher education. In Companion Proceedings of the

10th International Learning Analytics & Knowledge

Conference (LAK 2020), pages 744–749.

Wagner, K., Merceron, A., Sauer, P., and Pinkwart, N.

(2022). Personalized and explainable course recom-

mendations for students at risk of dropping out. In

Proceedings of the 15th International Conference on

Educational Data Mining, pages 657–661.

Williamson, K. and Kizilcec, R. (2021). Effects of algorith-

mic transparency in bayesian knowledge tracing on

trust and perceived accuracy. In Proceedings of the

14th International Conference on Educational Data

Mining, pages 338–344.

Zhang, J., Andres, J. M. A. L., Hutt, S., Baker, R. S.,

Ocumpaugh, J., Mills, C., Brooks, J., Sethuraman,

S., and Young, T. (2022). Detecting SMART model

cognitive operations in mathematical problem-solving

process. In Proceedings of the 15th International Con-

ference on Educational Data Mining, pages 75–85.

CSEDU 2023 - 15th International Conference on Computer Supported Education