A Novel Method for InSAR Phase Unwrapping with Single Baseline
Chenxi Tian and Guoman Huang
Chinese Academy of Surveying and Mapping, Haidian District, Beijing, China
Keywords: Interferometric Synthetic Aperture Radar (InSAR), Single-Baseline (SB), Multi-Baseline (MB), Phase
Unwrapping (PU).
Abstract: The precision of phase unwrapping (PU), one of the primary methods used in interferometric synthetic
aperture radar (InSAR), has a direct impact on the accuracy of the digital elevation model (DEM) that InSAR
produces. The phase continuity assumption restricts single-baseline (SB) PU, and it is frequently hard to
achieve optimal PU results in complex terrain areas with significant gradient variations. Fortunately, by
utilizing numerous InSAR interferograms, or the elevation changes corresponding to each interference fringe
in the interferogram, multi-baseline (MB) PU can totally overcome the restriction of the phase continuity
assumption. Therefore, this paper proposes a virtual-baseline (VB) PU based on the two-stage programming
(TSPA) MB PU approach to transform the SB PU problem into a MB PU problem. The novel method can be
referred to as VB-TSPA. First, the effect of baseline length on MB PU is comprehensively considered to
determine the virtual baseline length. Then a corresponding interferogram is simulated according to the length.
Finally, the TSPA method is used for the MB PU. The experimental results from simulated and real data
demonstrate that the novel PU method has a better effect than the traditional SB PU algorithm and can obtain
higher precision DEM.
1 INTRODUCTION
Interferometric synthetic aperture radar (InSAR) is a
technique for tracking ground deformation even in
inclement weather or at night. It has been widely used
in building digital elevation model (DEM) for
topographic mapping and extracting deformation
fields for surface deformation monitoring (Wang, Ch,
Zhang, H, & Liu, Z, 2002). InSAR technology can
retrieve terrain elevation information through phase
(Liao, M & Lin, H, 2003). However, the temporal and
spatial decoherence contribute to generating the
phase noise easily. Phase undersampling and
spectrum aliasing are major issues that have a direct
impact on the accuracy, solvability, and reliability of
elevation information inversion in complicated
terrain areas, such as those with steep slopes and
discontinuities (Jin, G, Zhang, H, & Xu, Q, 2015).
Phase unwrapping (PU) is one of the key steps of
InSAR, and its precision directly affects the accuracy
of the DEM generated by InSAR.
At present, single-baseline (SB) PU methods can
be divided into three categories: path-following
methods, optimization-based methods, integrated
denoising and unwrapping methods. Path-following
algorithms mainly include branch-cut method
(Goldstein, R, Zebker, H, & Werner, C, 1988),
quality-guided method (Anand, A & Zhou, W, 1988;
Zhong, H & Li, H, 2021), etc. Generally, the path-
following methods have high efficiency when the
interferograms with high signal-noise ratio. Yet,
when processing interferograms with low quality, the
methods result in unwrapping failure. The minimum
cost flow (MCF) algorithm (Costantini, M, 1988), a
typical example of the optimization-based methods,
transforms the PU problem into the network cost
minimization problem, which can obtain relatively
robust PU results from the interferogram with litle
noise. There are also some methods, such as
weighting least square method (Ghiglia, D & Romero,
L, 1994) and the least squares based on the fast
Fourier transform method (Pritt, M. & Shipman, J,
1994) that can unwrap continuously and smoothly.
Unfortunately, the dynamic range of unwrapping
phase is quickly reduced, resulting in serious
distortion of fringe details. Integrated denoising and
unwrapping methods include extended Kalman
filtering PU algorithm (Estahbanati, A. & Dehghani,
M, 2018), unscented Kalman filtering PU algorithm
(XIE, X., 2016), can retrieve ideal unwrapping results
60
Tian, C. and Huang, G.
A Novel Method for InSAR Phase Unwrapping with Single Baseline.
DOI: 10.5220/0011839300003473
In Proceedings of the 9th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2023), pages 60-68
ISBN: 978-989-758-649-1; ISSN: 2184-500X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

taking long time. Moreover, the deep learning
algorithm has also been applied to the field of PU
(Sica, F, Calvanese, F, & Scarpa, G, 2020; Ferraioli,
G., 2021 ), and excellent unwrapping results have
been obtained in some examples. These methods are
conducive to expanding the application field of PU
technology.
The majority of the SB PU methods mentioned
above rely on the assumption of phase continuity,
which necessitates that the observation region have
enough spatial continuity. Sadly, the prerequisites of
this hypothesis cannot be met by valleys, steep peaks,
cliffs, and other complex terrain, which frequently
prevents the optimum PU results. The multi-baseline
(MB) InSAR technology performs microwave
imaging in the same area under different baseline
conditions, resulting in the formation of multiple
interferograms (Yu, H., Lan, Y., & Yuan, Z., 2019).
It can effectively overcome or reduce the adverse
effects caused by the surge of target height, large
noise interference and other factors, so that it has the
potential to access high precision DEM in the
reconstruction of discontinuous terrain elevation. The
MB PU method can be divided into two main
categories : parameter-based methods and non-
parameter-based methods. The first set of methods
adopt InSAR probability density functions to
construct a statistical framework, using maximum
likelihood (ML) or maximum a posteriori (MAP)
criteria to estimate PU results (Pascazio &
Schirinzi,G, 2000; Fornaro,G, Monti, G., Pauciullo,
A, & DeZan, F, 2006). The method of the second
group transformed MB PU problem into an
unsupervised learning problem; then, cluster analysis
(CA) is used to estimate the unentanglement results
group by group (Jiang, J, Wang, Q, & Zhou, Z, 2017).
It is worth noting that the two-stage programming
(TSPA) method (Yu, H. & Lan, Y, 2016) establishes
the connection between SB PU and MB PU. In the
first stage, TSPA estimates the difference in
ambiguity number between adjacent pixels using
interferograms of different baseline lengths based on
the formulation of the Chinese remainder theorem
(CRT). In the second stage, the SB PU methods are
used to calculate the MB residues.
In order to obtain reliable PU results for complex
terrain in the instance of the SB InSAR system, this
study suggests a virtual-baseline (VB) PU based on
the two-stage programming MB PU approach
(TSPA), referred to as VB-TSPA. By
comprehensively considering the impact of baseline
length on the PU performance of multiple baselines,
an appropriate virtual baseline length is selected.
Afterwards, a simulated interferogram with the
baseline length is created. The double-baseline (DB)
PU is employed with the TSPA approach as a last step.
In order to get over the restriction of the phase
continuity assumption and determine the true phase
of complicated terrain, the SB PU problem is turned
into the MB PU problem in this paper. The approach
is capable of successfully addressing the PU problem
of complex terrain, according to experimental results.
2 VB-TSPA PU METHOD
2.1 SB PU Converts to DB PU
The primary goal of PU is to choose a pixel in the
interferogram as a reference point in order to recover
the true phase of the other pixels (relative to the
reference point) from the wrapped interferogram (that
is, the phase of the interferogram range cycling
between -π and π). As follows:
Ψ
(
𝑠
)
=𝜑
(
𝑠
)
+2𝑘
(
𝑠
)
𝜋
(1
)
where Ψ
(
𝑠
)
is the absolute phase of the sth pixel,
𝜑
(
𝑠
)
is the wrapped phase of the sth pixel and 𝑘
(
𝑠
)
is called the ambiguity number of the sth pixel (Gao,
Y., Tang, X., & Li, T., 2022).
It can be seen from equation (1) that SB PU is an
ill-posed inverse problem, hence, almost all SB PU
methods make a hypothesis, namely phase continuity
assumption, to overcome this problem. However,
system noise and sudden terrain changes often lead to
the failure of the hypothesis in practical applications.
Promisingly, MB PU can significantly increase the
fuzzy interval of the interference phase by using the
diversity of the baseline, which completely
overcomes the limitation of the phase continuity
assumption. The VB-TSPA PU method is described
in detail below.
For the InSAR system, the relation between the
terrain height and the absolute phase is
ℎ
(
𝑠
)
=
𝜆∙𝑅
(
𝑠
)
∙𝑠𝑖𝑛
(
𝜃
)
𝐵∙4
𝜋
∙Ψ
(
𝑠
)
(2
)
where ℎ
(
𝑠
)
is the terrain height of the sth pixel, 𝜆 is
the wavelength, 𝑅
(
𝑠
)
is the slant range of the target
from the master channel of the sth pixel, 𝜃 is the
incidence angle, and 𝐵 is the vertical baseline
(referred to as baseline) (Baselice, F, Ferraioli, G,
Pascazio, V, & Schirinzi, G, 2014; Liu, H, Xing, M,
& Bao, Z, 2015).
Then, the VB length B
2
is selected to form the
optimal baseline combination with the baseline length
B
1
of the original interferogram. After simulating an
A Novel Method for InSAR Phase Unwrapping with Single Baseline
61

interferogram with the length of B
2
, we can link the
true phase of the two interferograms by combining (1)
and (2):
𝐵

(𝜑

(
𝑠
)
+2𝑘

(
𝑠
)
𝜋)
=𝐵

(𝜑

(
𝑠
)
+2𝑘

(
𝑠
)
𝜋)
(3
)
where 𝑘

(
𝑠
)
and 𝑘

(
𝑠
)
are the ambiguity numbers of
the sth pixel in original interferogram and simulated
interferogram, respectively. 𝜑

(
𝑠
)
and 𝜑

(
𝑠
)
are the
wrapped phase of the sth pixel in the original
interferogram and simulated interferogram,
respectively.
If choosing a neighboring pixel s-1 of pixel s,
from (3), and letting (3) subtract it, we will get
𝐵

((𝜑

(
𝑠
)
−𝜑

(
𝑠−1
)
)+2(𝑘

(
𝑠
)
−𝑘

(
𝑠−
1
)
𝜋)) = 𝐵

((𝜑

(
𝑠
)
−𝜑

(
𝑠−1
)
)+
2(𝑘

(
𝑠
)
−𝑘

(
𝑠−1
)
𝜋))
(4)
If we let 𝑘

(
𝑠
)
−𝑘

(
𝑠−1
)
=∆

𝑘

(
𝑠,𝑠 −1
)
and
𝑘

(
𝑠
)
−𝑘

(
𝑠−1
)
=∆

𝑘

(
𝑠,𝑠 −1
)
, (4) will become
𝐵

((𝜑

(
𝑠
)
−𝜑

(
𝑠−1
)
)+2∆

𝑘

(
𝑠,𝑠 −
1
)
𝜋)) = 𝐵

((𝜑

(
𝑠
)
−𝜑

(
𝑠−1
)
)+
2(∆

𝑘

(
𝑠,𝑠 −1
)
𝜋))
(5)
Using the CRT method, ∆

𝑘

(
𝑠,𝑠 −1
)
and
∆

𝑘

(
𝑠,𝑠 −1
)
can be obtained as new gradient
information between adjacent pixels of two
interferograms, respectively. Next, the MCF method
is adopted to solve the DB PU residues.
2.2 Principle of VB Length Selection
The VB-TSPA PU method is a subset of DB PU
methods, and any combination of baselines of the
problem can be solved by using the CRT.
Nevertheless, the CRT are sensitive to baseline length.
Even if the same PU method is chosen, varied
baseline lengths will result in different PU
performance. Obviously, the SB PU problem is
unable to transform from ill-posed to well-posed by
simply increasing the number of interferograms
without any restriction on the baseline length.
Yu, H., Lee, H., Cao, N., & Lan, Y (2019),
proposed a nonlinear mixed-integer programming-
based baseline design criterion (referred to NIP
criterion) to maximize the MB PU's CRT-based
measurement deviation tolerance.
𝐵

(𝜑

(
𝑠
)
+𝑛

(𝑠)+2𝑘

(
𝑠
)
𝜋) =
𝐵

(𝜑

(
𝑠
)
+𝑛

(𝑠) +2𝑘

(
𝑠
)
𝜋)
(6
)
Where 𝑛

(𝑠)(𝑖=1,2)represents the general system
observation noise of the sth pixel in the interferogram
i.
𝑎𝑟𝑔 min


(

)
,

(

)
|
𝐵

(𝜑

(
𝑠
)
+𝑛

(𝑠) +2𝑘

(
𝑠
)
𝜋)
−𝐵

(𝜑

(
𝑠
)
+𝑛

(𝑠)
+2𝑘

(
𝑠
)
𝜋)
|
𝑟


(

)

≤𝑘

(
𝑠
)
≤𝑟


(

)

𝑟


(

)

≤𝑘

(
𝑠
)
≤𝑟


(

)

𝑘

(
𝑠
)
,𝑘

(
𝑠
)
∈𝑖𝑛𝑡𝑒𝑔𝑒𝑟
(7)
where 𝑘

(
𝑠
)
and 𝑘

(
𝑠
)
are the decision variables,
(
𝑟
𝑘
1
(
𝑠
)

, 𝑟
𝑘
1
(
𝑠
)

) and ( 𝑟
𝑘
2
(
𝑠
)

, 𝑟
𝑘
2
(
𝑠
)

) are the CRT
searching windows of 𝑘

(
𝑠
)
and 𝑘

(
𝑠
)
, respectively.
𝑊

=𝑟


(

)

+𝑟


(

)

(i = 1,2)
(8
)
According to the NIP requirement, CRT prefers
MB InSAR baseline lengths that increase
correspondingly as the size of the available CRT
searching windows increases. Only the length of the
CRT search window in the long baseline is relevant
to the OPT requirement of the NIP criterion. When




≥W

+1, the results of MB PU are optimal.
Where B

is the long baseline, B

is the short baseline,
and W
2
is the CRT search window size of the long
baseline (Yu, H., Lee, H., Cao, N., & Lan, Y, 2019).
The size of the search window can be estimated
by using some prior knowledge, such as rough terrain
information (Yu, H., Lee, H., & Cao, N., 2018). If the
terrain changes greatly, the search window should
also be large. In addition, the search window W
2
corresponding to the long baseline can be estimated
by the following formula:
W

=2∙round



∙∙

∙∙()

(0<α≤1)
(9
)
where α is a scaling factor and in some systems, is
believed to be 0.1(Moreira, A., Prats-Iraola, P., &
Younis, M., 2013).
g

is the maximum gradient (i.e.
the maximum height difference between adjacent
pixels) in the observation area. B
c
is known as the
critical baseline for which the two SAR images
become completely decorrelated.
Additionally, in order to reduce the PU error
sensitivity of MB InSAR system, the longer B
i
(i = 1,
2), the better the performance. Also, the increase of
B
i
(i = 1, 2) can minimize the impact of baseline error
on DEM accuracy (Yu, H., Xing, M., & Yuan, Z,
2021). Summarily, appropriate baseline length should
be chosen comprehensively to achieve the best
performance.
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
62

3 EXPERIMENTAL RESULTS
In order to confirm the viability of the suggested
method, the performance of the VB-TSPA PU
method was tested on simulated data and real data,
respectively, and compared to the conventional SB
PU method. As one of the most widely used SB PU
methods at present, the MCF PU method has
advantages in operation time and PU precision, which
can improve the computational efficiency. Moreover,
the algorithm can limit the error to a small range,
prevent the error transmission, and the PU result is
more accurate. Consequently, the MCF PU method is
chosen in this paper for comparison.
3.1 Simulated Data
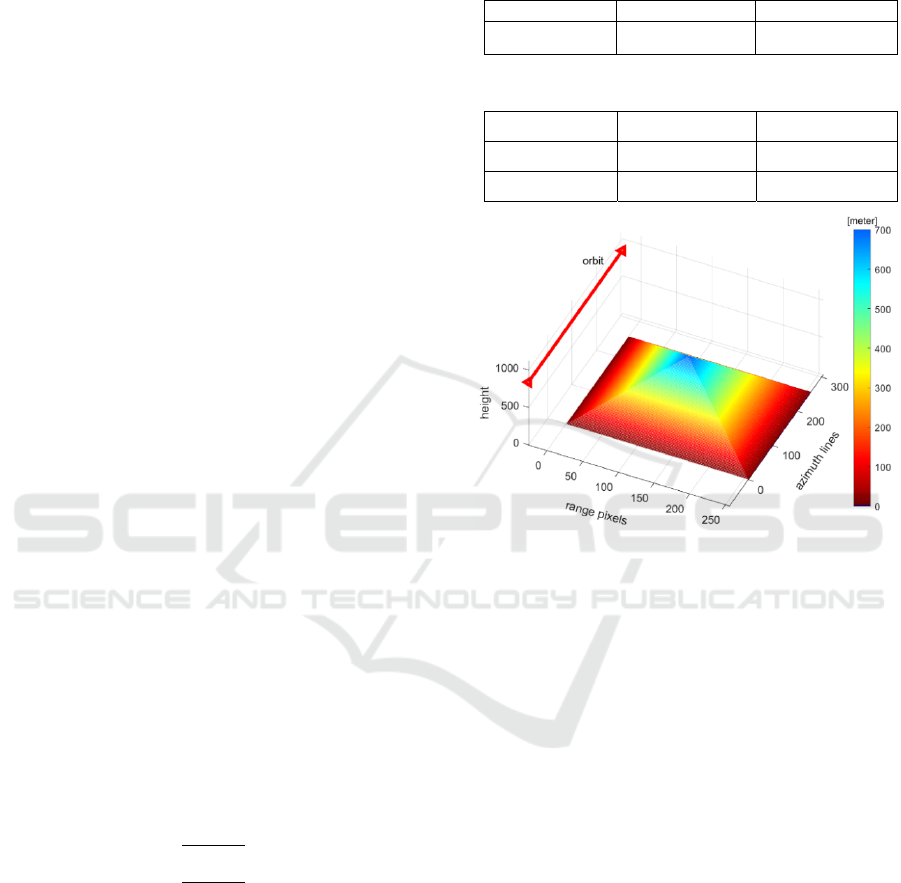
Fig. 1 is a 3D view of the simulated mountain terrain
with a size of 256 ×256 pixels and an elevation range
of 0-700 meters. Fig. 2 is the interferogram
corresponding to the terrain in Fig. 1 obtained by
simulating the system parameters in Table 1. Fig. 2(a)
and (b) show the reference unwrapping phase and the
wrapping phase containing noise, with the baseline
length of 700 meters, respectively. Meanwhile, Fig.
2(b) is also the interferogram to be unwrapped. Fig.
2(c) is a noiseless wrapping phase with a baseline
length of 100 meters determined according to the
baseline length selection principle of the VB-TSPA
method.
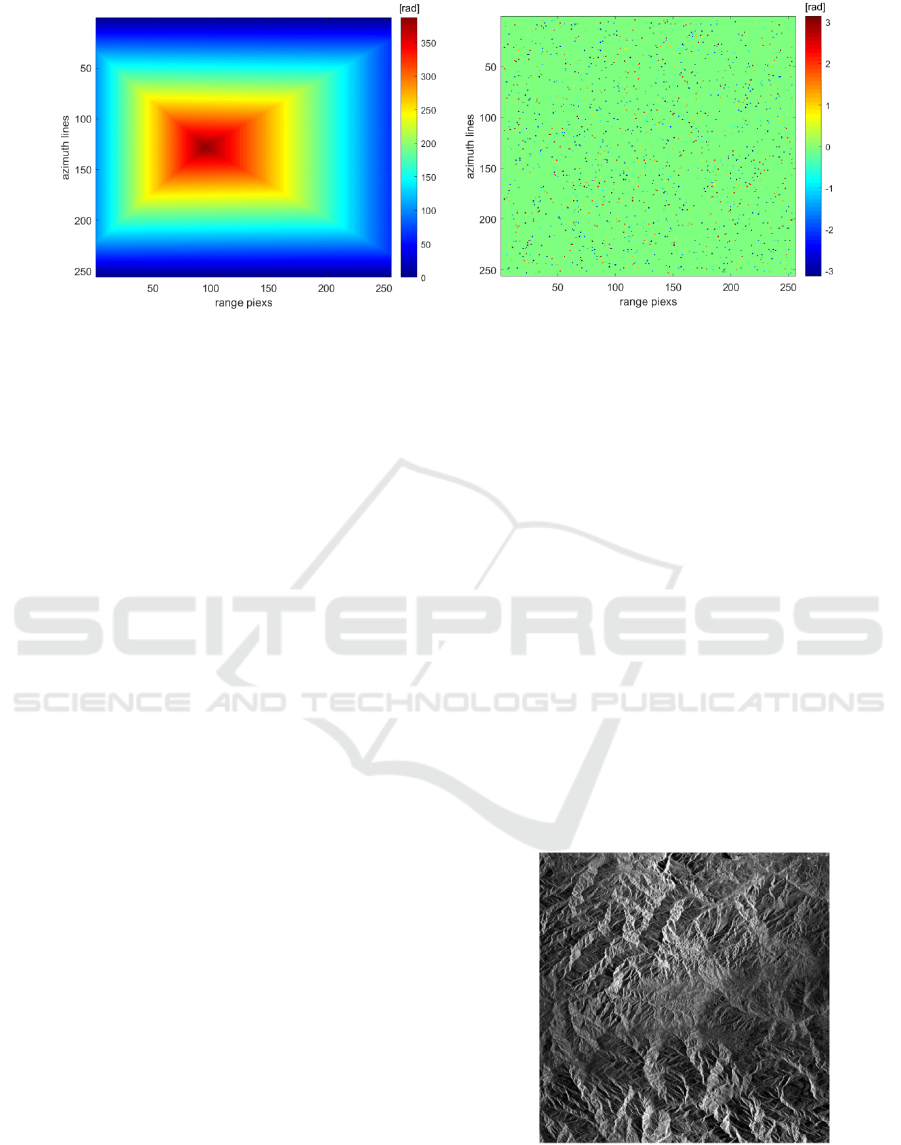
Fig. 3 and Fig. 4 are the results obtained by using
the MCF and VB-TSPA methods to unwrap Fig. 2(b),
respectively. From Fig. 3(a), we can clearly see
discontinuous terrain changes (marked by rectangular
boxes), while Fig. 4(a) has continuous phase changes.
From a visual interpretation perspective, the method
presented in this paper yields a better unwrapping
result. For further quantitative evaluation of the
performance, the normalized root-mean-square error
(NMSE) of the PU accuracy is defined as:
ξ =

ψ

ψ


ψ


(10)
where ψ is the vector collecting from the reference
unwrapped phase, ψ

is the vector collecting from the
estimated unwrapped phase, and
‖‖

is the
quadratic norm. The smaller the ξ is, the higher the
unwrapping precision is generated and the better the
unwrapping result is achieved. Therefore, it can be
seen from Table 2 that the NMSE of the unwrapping
result of the VB-TSPA method is lower than that of
the MCF method, and the error range is also narrower,
confirming the method's efficacy.
Table 1: Major parameters of simulated InSAR system.
Orbit Altitude Incidence Angle Wavelength
785km 19° 5.7cm
Table 2: Evaluation results of the simulation data set.
PU method NMSE Error range(rad)
MCF 0.1312 [-9.3,6.2]
VB-TSPA 0.0156 [-3.1,3.1]
Figure 1: Reference terrain height.
3.2 China-TH2 InSAR Data
In the real data experiment of this study, the data is
by the China_TH2 system, and its main parameters
are shown in Table 3. The amplitude image of the
experiment area, shown in Fig. 5, reveals that the
region is geographically distinguished by a
significant amount of mountainous and rough terrain.
In this situation, the phase continuity assumption
may not be effective, making it challenging to achieve
correct results for SB PU methods. Fig. 6 depicts the
simulated unwrapped phase of the region after
removing the flat-earth phases.
A Novel Method for InSAR Phase Unwrapping with Single Baseline
63

(a) (b)
(c)
Figure 2: Simulated interferograms: (a) reference unwrapped phases with long baseline; (b) simulated noise-containing
wrapped phases with long baseline; (c) simulated noise-free wrapped phases with short baseline.
(a) (b)
Figure 3: PU results of Fig. 2(b) obtained by MCF: (a) unwrapped phases; (b) errors between (a) and Fig.2(a).
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
64

(a) (b)
Figure 4: PU results of Fig. 2(b) obtained by VB-TSPA: (a) unwrapped phases; (b) errors between (a) and Fig.2(a).
Fig. 7 is the coherence coefficient of the data,
whose interferometric coherence coefficient is 0.38.
The low coherent images limit the accuracy of the
interferometric phase measurement. Fig. 8 is the
flattened interferogram and its local magnification
obtained from the real data. Meanwhile, it is the
interferogram to be unwrapped. Next, the MCF
method and the VB-TSPA method will be used for PU
of Fig. 8(a). According to the principle of virtual
baseline length selection, the length in this
experiment is 83.8780 meters, and the simulated
interferogram is displayed in Fig. 9(a).
Fig. 10 and Fig. 11 show the PU results accessed
by the MCF and VB-TSPA method, respectively. It
can be seen from the figures that the interference
pattern fringe details got by the MCF method are
seriously distorted, while the unwrapping result
obtained by the VB-TSPA method is similar to the
reference unwrapping result. The error range is
substantially narrower than that of the MCF approach,
and the NMSE of the PU result acquired by the VB-
TSPA method is much closer to 0. For long baseline
interferogram and rapid phase change in complex
terrain, the VB-TSPA PU method displays better
performance than the MCF PU method. Evidently, it
can be concluded that the VB-TSPA method
suggested in this paper is more accurate and reliable.
The DEM of this region was created by an
elevation inversion of the unwrapping phase achieved
by the VB-TSPA method, as shown in Fig. 12.
Additionally, the accuracy of the DEM inversion
produced by the PU solution was further assessed
using 221 control points taken from an external DEM,
and the final median error was 22.45m. Apparently,
the VB-TSPA method can produce high precision
DEM.
4 CONCLUSIONS
The VB-TSPA PU proposed in this study transforms
the SB PU problem into the MB PU problem, breaks
through the limitation of phase continuity assumption,
and can obtain the unwrapped phase of complicated
terrain in the case of SB InSAR system. The
efficiency of the VB-TSPA PU algorithm has been
demonstrated by experimental findings using real and
simulated data. Compared with the MCF PU method,
it can achieve more accurate results under the
conditions of dense interference fringes and complex
terrain, and produce high-precision DEM of the
region. Although the influence of noise on the PU
results is reduced by global optimization in this paper,
there is still room for improving the robustness of this
method as the mathematical basis of the method is
CRT.
Figure 5: Amplitude image.
A Novel Method for InSAR Phase Unwrapping with Single Baseline
65

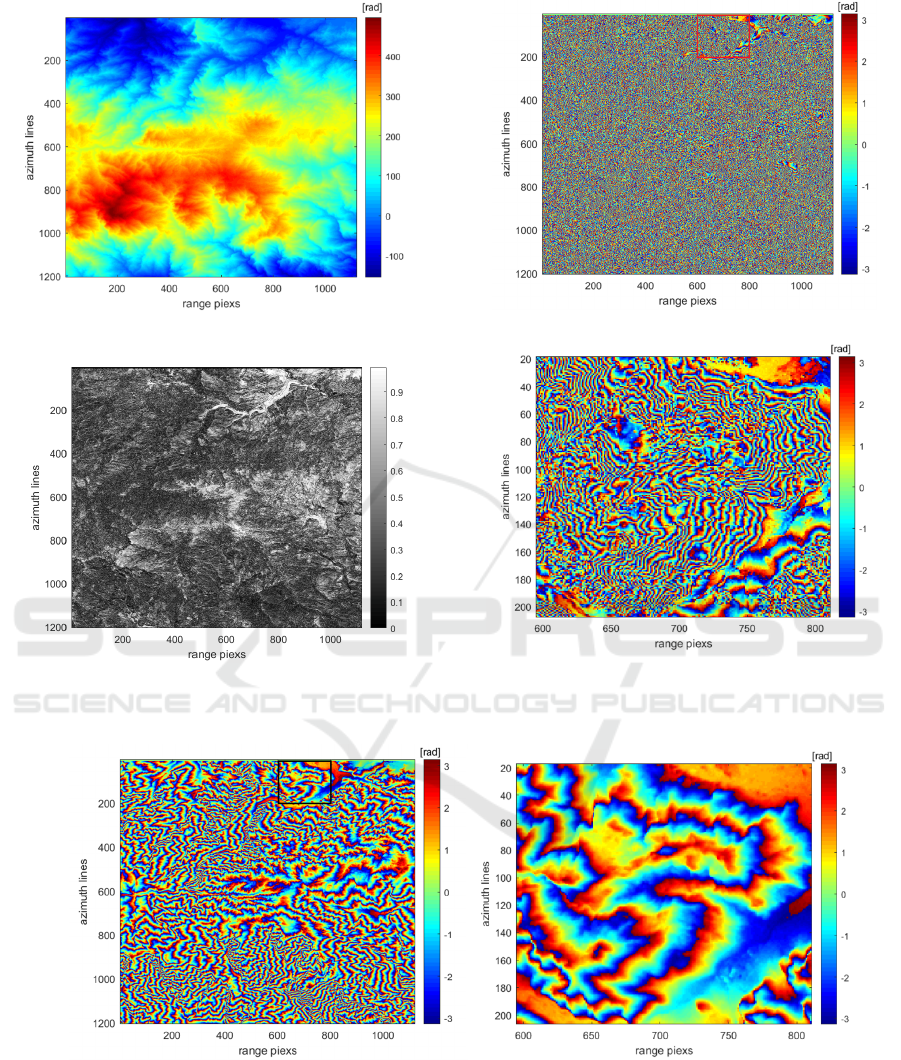
Figure 6: Simulated unwrapped phase (flattened).
Figure 7: Coherence image.
(a) Wrapped phases (flattened).
(b) Marked by rectangular boxes in (a).
Figure 8: Interferogram of China-TH2 data set.
(a) (b)
Figure 9: Simulated Interferogram: (a) Wrapped phases (flattened); (b) Marked by rectangular boxes in (a).
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
66

(a) (b)
Figure 10: PU results of Fig. 8(a) obtained by MCF: (a) unwrapped phases (flattened) ; (b) errors between (a) and Fig. 8(a).
(a) (b)
Figure 11: PU results of Fig. 8(a) obtained by VB-TSPA: (a) unwrapped phases (flattened); (b) errors between (a) and Fig. 8(a).
Figure 12: Terrain height estimated by the PU solution of
the VB-TSPA method.
Table 3: Major parameters of China-TH2 InSAR system.
Orbit Altitude 517.597km
Wavelength 3.12cm
Latitude
9.65°
longitude -83.80°
Incidence Angle 41.19°
Normal Baseline 587.1457m
Table 4: Evaluation results of the China-TH2 data set.
PU metho
d
NMSE Error ran
g
e
(
rad
)
MCF 0.8677 [-332.8,464.8]
VB-TSPA 0.3617 [-76.4,97.3]
ACKNOWLEDGEMENTS
This work was supported in part by National Key
Research and Development project
(2022YFB3901604) and CSAM FUNDING : 3D
A Novel Method for InSAR Phase Unwrapping with Single Baseline
67

information construction of array SAR point cloud
research (AR2206).
REFERENCE
Anand, A, & Zhou, W. (1988). Fast phase-unwrapping
algorithm based on a gray-scal mask and flood fill.
Applied optics, 37(23): 5416-5420.
Baselice, F, Ferraioli, G, Pascazio, V, & Schirinzi, G.
(2014). Contextual information-based multichannel
synthetic aperture radar interferometry: Addressing
DEM reconstruction using contextual information.
IEEE Signal Process. Mag, vol. 31, no. 4, pp. 59–68.
Costantini, M. (1988). A novel phase unwrapping method
based on network programming. IEEE Trans. Geosci.
Remote Sense, 813–821.
Estahbanati, A., & Dehghani, M. (2018). A Phase
Unwrapping Approach Based on Extended Kalman
Filter for Subsidence Monitoring Using Persistent
Scatterer Time Series Interferometry. IEEE Journal of
Selected Topics in Applied Earth Observations and
Remote Sensing, vol. 11, no. 8, pp. 2814-2820, Aug.
Ferraioli, G. (2021). Joint Phase Unwrapping and Speckle
Filtering by Using Convolutional Neural Networks.
IEEE International Geoscience and Remote Sensing
Symposium IGARSS, 2021, (pp. 3376-3379).
Fornaro,G, Monti, G., Pauciullo, A, & DeZan, F. (2006).
Maximum likelihood multi-baseline SAR
interferometry. Proc. Inst. Electr. Eng., vol. 153, no. 3,
pp. 279–288.
Gao, Y., Tang, X., & Li, T. (2022). A Phase Slicing 2-D
Phase Unwrapping Method Using the L 1 -Norm. IEEE
Geoscience and Remote Sensing Letters, 19, 1–5.
Ghiglia, D, & Romero, L. (1994). Robust two-dimensional
weighted and unweighted phase unwrapping that uses
fast transforms and interative methods. Journal of the
optical society of America, 11(1): 107-117.
Goldstein, R, Zebker, H, & Werner, C. (1988). Satellite
radar interferometry: two-dimensional phase
unwrapping. Radio science, 23(4): 713-720.
Jiang, J, Wang, Q, & Zhou, Z. (2017). A refined
clusteranalysis-based multibaseline phase-unwrapping
algorithm. IEEE Geosci. Remote Sens. Lett., vol. 14,
no. 9, pp. 1565–1569.
Jin, G, Zhang, H, & Xu, Q. (2015). Radar photogrammetry.
Beijing: Surveying and Mapping Press.
Liao, M, & Lin, H. (2003). Synthetic aperture radar
interferometry: principle and signal processing.
Beijing: Surveying and Mapping Press.
Liu, H, Xing, M, & Bao, Z. (2015). A cluster-analysis-
based noise-robust phase-unwrapping algorithm for
multibaseline interferograms. EEE Trans. Geosci.
Remote Sens., vol. 53, no. 1, pp. 494–504.
Moreira, A., Prats-Iraola, P., & Younis, M. (2013). A
tutorial on synthetic aperture radar. IEEE Geoscience
and Remote Sensing Magazine, 1(1), 6–43.
Pascazio, & Schirinzi,G. (2000). Multifrequency InSAR
height reconstruction through maximum likelihood
estimation of local planes parameters. IEEE Trans.
Image Process, vol. 11, no. 12, pp. 1478–1489.
Pritt, M., & Shipman, J. (1994). Least-squares two-
dimensional phase unwrapping using FFT's. IEEE
Transactions on Geoscience and Remote Sensing.
Sica, F, Calvanese, F, & Scarpa, G. (2020). A CNN-Based
Coherence-Driven Approach for InSAR Phase
Unwrapping. IEEE Geoscience and Remote Sensing
Letters, 99.
Wang, Ch, Zhang, H, & Liu, Z. (2002). Space borne
synthetic aperture radar interferomet. Bejing: Science
press.
XIE, X. (2016). Iterated unscented Kalman filter for phase
unwrapping of interferometric fringes. Optics Express,
24(17): 18872-18897.
Yu, H., Lee, H., & Cao, N. (2018). A novel method for
deformation estimation based on multibaseline InSAR
phase unwrapping. IEEE Trans. Geosci. Remote Sens.,
vol. 56, no. 9, pp. 5231–5243.
Yu, H., & Lan, Y. (2016). Robust Two-Dimensional Phase
Unwrapping for Multibaseline SAR Interferograms: A
Two-Stage Programming Approach. IEEE
Transactions on Geoscience and Remote Sensing,
54(9), 5217–5225.
Yu, H., Lan, Y., & Yuan, Z. (2019). Phase Unwrapping in
InSAR: A Review. IEEE Geoscience and Remote
Sensing Magazine, 7(1), 40–58.
Yu, H., Lee, H., Cao, N., & Lan, Y. (2019). Optimal
Baseline Design for Multibaseline InSAR Phase
Unwrapping. IEEE Transactions on Geoscience and
Remote Sensing, 57(8), 5738–5750.
Yu, H., Xing, M., & Yuan, Z. (2021). Baseline Design for
Multibaseline InSAR System: A Review. IEEE Journal
on Miniaturization for Air and Space Systems, 2(1),
17–24.
Zhong, H, & Li, H. (2021). Path-following Phase
Unwrapping Algorithm based on Priority-guided Map.
2021 14th International Congress on Image and Signal
Processing, BioMedical Engineering and Informatics
(CISP-BMEI), (pp. 1-6).
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
68