A Path-Depended Passenger Flow Forecasting Model for Metro Rail

Systems Using LSTM Neural Network

Jaison Paul Mulerikkal

1 a

, Deepa Merlin Dixon

and Sajanraj Thandassery

2 b

Dept. of Information Technology, Rajagiri School of Engineering and Technology,Kochi, 682 039, Kerala, India

Dept. of Computer Science and Engineering, Rajagiri School of Engineering and Technology,

Keywords:

Passenger Flow, Short-Term, Long Short-Term Memory Network, Support Vector Regression.

Abstract:

The primary goal of this work is to develop a framework for short term passenger ﬂow prediction for metro rail

transport systems. A reliable prediction of short-term passenger ﬂow could greatly support metro authorities’

decision process. Both inﬂow and outﬂow of the metro stations are strongly associated with the travel demand

within metro networks. Sequestered station-wise analysis ignores the spatial correlations existing between

the stations. This paper tries to merge the spatial with the temporal by employing an indirect method of

computing ﬂow through O-D estimates for the same. Path-depended station-pairs of O-D ﬂow are considered

for employing a customized LSTM network. Experimental results indicate that the proposed passenger ﬂow

prediction model is capable of better generalization on short-term passenger ﬂow than standard models of

learning compared. This work also establishes that O-D prediction provides an indirect estimation procedure

for passenger ﬂow. The speciﬁc use case for this work is Kochi Metro Rail Limited (KMRL). A highlight of

the work is that the whole analytics and modelling procedures are written on a customized scalable big-data

platform (Jaison Paul Data Analytics Platform) JP-DAP which was developed prior to this work.

1 INTRODUCTION

Metro railways are one of the new additions to intel-

ligent transportation systems. Due to increasing pop-

ulation and ever extending city coverage, commuters

rely more on public transit systems such as metro rail-

ways. Recently, with efﬁcient, reliable and safe ser-

vice, metro networks are experiencing a sharp hike in

ridership. Short term trafﬁc ﬂow prediction is an in-

tegral component of the operational decision making

pipeline. Short term passenger ﬂow prediction aims

at estimating the number of commuters given a spe-

ciﬁc station and a time interval, which is an important

problem to address in metro transportation manage-

ment (Li et al., 2017). Prediction of passenger ﬂow

information is of immense value in facility improve-

ment, operation planning, revenue management, and

even emergency evacuation. The literature supports

both parametric and non-parametric models, paramet-

ric models include Auto-Regressive Moving Aver-

age(ARMA), seasonal ARMA, Kalman ﬁltering, etc.,

https://orcid.org/0000-0002-5266-2159

https://orcid.org/0000-0003-2899-0184

while some frequently used non-parametric models

are k-Nearest Neighbors algorithm (kNN) and spec-

tral analysis. Recently, with incredible developments

in artiﬁcial intelligence and explosive growth in com-

putational power, there is a signiﬁcant leap from ana-

lytical to data-driven modelling.

Since the operations of the metro, with an expand-

ing user base, is a source of big data, analytical sand-

boxes designed to perform inferential procedures can-

not be deployed as a real time solution as long as the

scalability aspect is left unaddressed. The analytics

presented here were therefore preceded by develop-

ing a customized distributed and scalable platform,

JP-DAP. The models presented here were developed

and run on the platform. The system is populated us-

ing the data received from KMRL (The project has

a data sharing agreement with KMRL). In this work,

propose an efﬁcient and reliable travel pattern predic-

tion through Origin-Destination (O-D) matrix estima-

tion. This indirect approach is better than direct esti-

mation of travel patterns which overlooks the spatial

interconnections between stations. O-D distribution

is distinct for different station-pairs since the usage

distributions of stations are not identical.

Mulerikkal, J., Dixon, D. and Thandassery, S.

A Path-Depended Passenger Flow Forecasting Model for Metro Rail Systems Using LSTM Neural Network.

DOI: 10.5220/0011840800003479

In Proceedings of the 9th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2023), pages 257-264

ISBN: 978-989-758-652-1; ISSN: 2184-495X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

257

In the current trend most of the algorithms con-

sider either entry ﬂow or the exit. In this case, we

have included origin-destination ﬂow to make the

ﬂow path dependency between two stations. Here the

case study has included the path from station A to sta-

tion B, and also considered the direction ﬂow from B

to A. So that the mapping become 1:1.

The proposed model outperforms some widely

used forecasting models such as the Support Vector

Regressor (SVR), Bayesian regressor and Regression

Tree.

The remainder of the paper is organized as fol-

lows. Section 1.1 describes the related work in the

area. This section gives a comprehensive review of

big data analytics in railway transportation. The fol-

lowing section 2 provides an intuitive analysis of the

data, formats and basic architecture of JP-DAP. Sec-

tion 3 provides a detail explanation about the fare card

based learning for short term passenger ﬂow predic-

tion. Section 3.1 explains the proposed network archi-

tecture and passenger ﬂow prediction model based on

long short term memory (LSTM). Comparative anal-

yses of the prediction performances are provided in

Section 4. Finally, conclusions drawn and future re-

search directions are discussed in Section 5.

1.1 Related Works

In recent years, Intelligent transportation systems

(ITS) have a signiﬁcant role in smart cities. Short

term trafﬁc ﬂow prediction plays an indispensable

role in ITS (Ci et al., 2017). Hence considerable ef-

fort is made to develop efﬁcient trafﬁc ﬂow prediction

methods, which is backed by a large number of pub-

lications in this ﬁeld. The purpose of short term traf-

ﬁc ﬂow prediction is to facilitate dynamic trafﬁc con-

trol proactively by monitoring the present trafﬁc and

foreseeing its immediate future (Tang et al., 2019).

Apart from that, it provides accurate and timely traf-

ﬁc volume information for individual travelers, busi-

ness sectors and government agencies (Tian and Pan,

2015). At the same time, any transportation net-

work is a very complex system composed of many

other factors such as weather conditions, region, etc..

Hence, the short-term trafﬁc ﬂow is highly non-linear

and stochastic, which makes it a huge challenge to

be predicted accurately (Tian and Pan, 2015). From

previous studies, diverse deep learning methods have

been applied to trafﬁc ﬂow prediction as they can cap-

ture the complex non-linear relations and the latent

correlation features in trafﬁc ﬂow data. Furthermore,

short-term passenger ﬂow prediction for metro rail

systems is a relatively new research ﬁeld when com-

pared to trafﬁc prediction for ground transport.

A seminal work, Ahmed et al. (1979) proposed

a model for short-term prediction of freeway trafﬁc

ﬂow using Autoregressive Integrated Moving Aver-

age (ARIMA) (Ahmed and Cook, 1979). In 2009,

Tsai et al. (Tsai et al., 2009) constructed two types

of improved neural network models based on distinc-

tive railway data for short-term railway passenger de-

mand forecasting. The ﬁrst is a neural network with

several temporal units that interprets raw material us-

ing speciﬁc connections inside the network. The sec-

ond method uses a parallel ensemble neural network,

which processes various input data using various in-

dividual models. Both neural networks outperform

traditional multilayer perception neural networks, ac-

cording to the data. Later in 2013, Teresa Pamuła

(Pamuła, 2013) developed a neural network model

for accurate short term trafﬁc ﬂow forecasting with

the data obtained from two video detectors located

at the ends of a transit road in the city of Gliwice.

In this work, tests were performed using three dis-

tinct classes of time series corresponding to: working

days, Saturdays and Sundays. In (Sun et al., 2015)

proposed a hybrid model of Wavelet Support Vector

Machine (SVM). The method ﬁrst decomposes the

passenger ﬂow data into different high frequency and

low frequency series by wavelet and then prediction

performed using SVM.

In 2018, Xiaoqing Dai et al. (Dai et al., 2018)

developed a data-driven framework for short-term

metro passenger ﬂow prediction which utilizes spatio-

temporal correlations. The travel demand within the

metro networks are closely related to inﬂow and out-

ﬂow of the metro stations. Hence, in this work they

collect the O-D information from the smart-card data

to explore the passenger ﬂow patterns and propose a

data driven framework for short-term metro passenger

ﬂow prediction. This method utilizes two forecasts as

basic models, adaptive boosting and k-Nearest Neigh-

bors (kNN) and then uses a probabilistic model se-

lection method to combine the two outputs for better

forecast.

From the literature survey, it was evident that

LSTM based sequence prediction systems have not

received much attention in metro related studies.

Also, there are some existing gaps in metro passen-

ger ﬂow forecast such as unclear inﬂuencing factors,

low accuracy, passenger congestion, unbalanced ca-

pacity and demand etc.(Zhang et al., 2020). A metro

path deﬁned to a travel from the origin station to

alighting station of a passenger, which indicates the

movement of a commuter within the metro network.

Thus O-D ﬂows is a potential feature to boost pre-

diction (Dai et al., 2018). Therefore, in this work

the O-D ﬂows extracted from AFC data can be suc-

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

258

cessfully utilized to describe different metro rail travel

patterns. Hence the proposed forecasting framework,

especially the LSTM method, can improve the per-

formance of short-term transportation forecasting for

metro rail.

2 EXPERIMENTAL

ENVIRONMENT AND DATA

SET

Kochi Metro rail (KMRL) (Metro Rail, 2017) net-

work in Kerala, India, is selected as the use case for

this research work. During the time interval consid-

ered, the metro line in the city covered only 16 sta-

tions with an average daily passenger volume of about

50,000. This dataset provides an insight into typical

growth and demand pattern of a new-built metro sys-

tem. The dataset is collected from Automatic Fare

Collection (AFC)(Ampelas, 2001) system and covers

667 days, from 2017 (from June), 2018 and 2019 with

a size of 5GB. A detailed description of AFC is given

in Section 2.1.

The software ecosystem on which the experimen-

tal procedure and analysis were conducted consists of

• Customized Hadoop based platform with Apache

Spark integration and GPU support (JP-DAP)

• Python 3 with associated packages including Ten-

sorﬂow, Keras and Scikit-learn for implementa-

tion of the analytic models.

On the hardware side, the computational nodes were

conﬁgured with Intel Xeon E3 series server-grade

processor with 4 cores and 32 GB RAM and NVIDIA

Quadro P1000 graphics card with 4GB of GPU mem-

ory. The data are received through system APIs and

are appropriately transformed into forms suitable for

analysis and visualization. The structured informa-

tion is stored in Hive database. Spark (Zaharia et al.,

2010) is responsible for the computation and transfor-

mation process, with distributed memory computing.

Details of JP-DAP is provided in Section 2.2.

2.1 Automated Fare Card Data

The compiled data used for this research work is pro-

vided by by the AFC Analysis Department of KMRL.

The data is stripped of sensitive private attributes and

anonymized by the department before making it avail-

able for analysis. The detail data format is shown in

Table 1.

2.2 Big Data Platform

In this section, the description of the big data plat-

form called Jaison Paul Data Analytics Platform (JP-

DAP)(Mulerikkal et al., 2022) built on Hadoop with

supporting analytics components is given. This is

a prior work done which is already communicated.

The system accepts data from a spectrum of distinct

sources associated with the metro presently. The ar-

chitecture has been designed to provide enough lee-

way to seamlessly integrate other modes of transport

as well as the future expansions in the metro itself.

The data is received through system APIs. The core

analysis covered by a set of internal APIs within the

platform .

3 SHORT TERM PASSENGER

FLOW PREDICTION FROM

O-D FORECAST

Short term passenger ﬂow prediction is an important

aspect of usage trend analysis and provides a very

useful feature for deciding stafﬁng pattern and train

schedules. For effective metro system management

and to help commuters adjust their travel timings or

in extreme cases, assist emergency management an

effective passenger ﬂow prediction is required (Dai

et al., 2018). The passenger counts in both up and

down directions of each station provide its distinct be-

havioral travel pattern. The passenger count can be

station wise or pair-wise total entry and total exit. For

the analysis of passenger ﬂow, different time frames

are considered and day-wise prediction is performed.

An accurate short term passenger ﬂow at each (O-

D) path can be predicted by combining the legacy in-

formation of both inﬂow and outﬂow of each metro

station (Dai et al., 2018). Hence, for time series

forecasting for each path, the O-D information is ex-

tracted from AFC data. The entire travel paths, both

forward and backward of the metro system is shown

in Fig. 1(a) and Fig. 1(b). In the ﬁgure, S

and S

are the target origin and destination stations. Hence

the path connecting S

and S

is the targeted path.

The proposed model is trained for predicting the pas-

senger ﬂow of the targeted O-D based on legacy O-D

data. The O-D matrix of the metro system consisting

of m stations is shown in equation 1. Where P

i j

rep-

resents the total count of passengers from station i to

station j for a predeﬁned time window.

A Path-Depended Passenger Flow Forecasting Model for Metro Rail Systems Using LSTM Neural Network

259

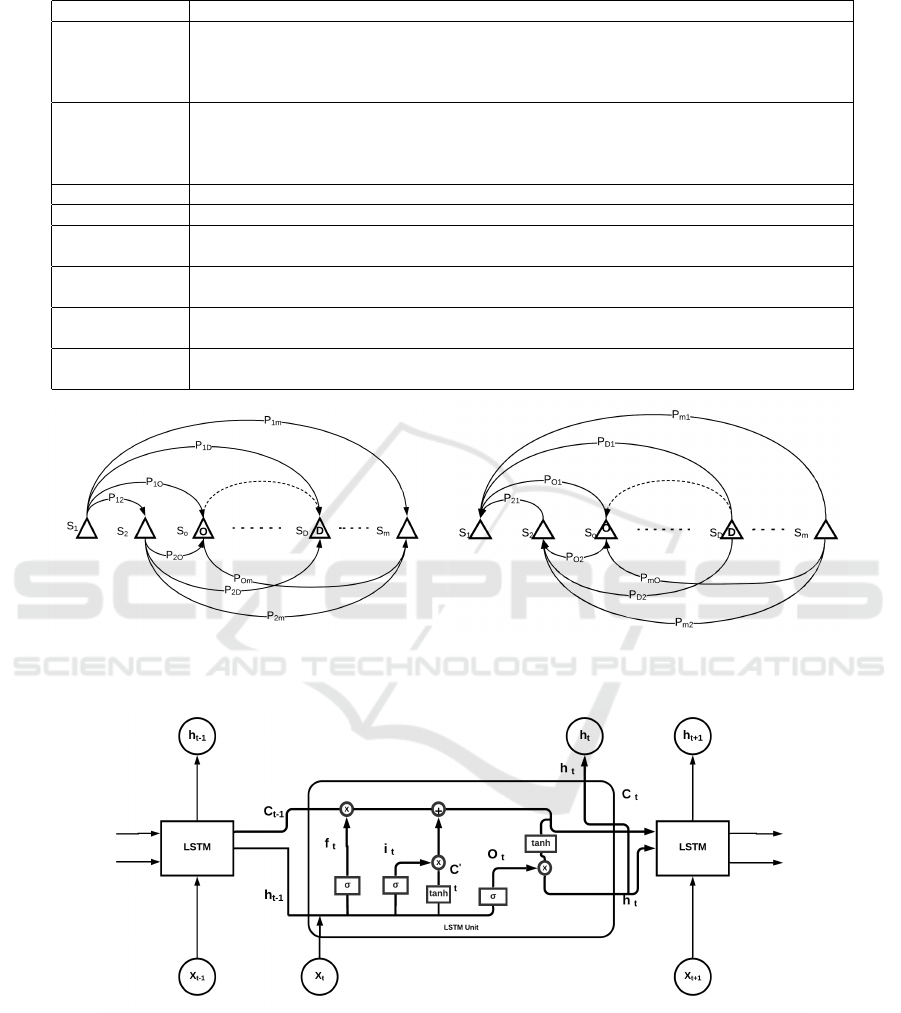
Table 1: Dataset Description.

Database Entry Description / Contents

Stations

All working station information (till Feb 2019)

Aluva, Pulinchodu, Companypady, Ambattukavu,Muttom, Kalamassery, Cochin University,

Pathadipalam, EdapallyChangampuzha Park, Palarivattom, JLN Stadium, Kaloor,

Lissie, M.G Road, Maharaja’s College

Equipment

Type

Mode of Taking Tickets have done (3 Modes)

EFO (Excess Fare Ofﬁce)

TOM (Ticket Ofﬁce Machine)

GATE (AFC Gates)

Equipment ID Unique ID of each Machines

Fare Product E-Purse, SJT (Single Journey Ticket), Free Exit Ticket, Paid Exit Ticket, Staff Card

Fare

Media

EMV (using Kochi One Card) , QR (Normal Paper Ticket), RPT (RF-ID Paper Ticket)

Ticket

Card Number

Unique Ticket ID Information

Transaction

Type

Top-up, Issue , Adjustment, Entry, Exit ,Cancel

Transaction

Time

YYY-MM-DD HH:MM:SS Format

(a) Forward Path of Passengers for Different O-D’s (b) Backward Path of Passengers for Different O-D’s

Figure 1: Passenger Flow Paths in Metro System.

Figure 2: Illustration of the Inner Structure of an LSTM Layer.

Matrix







0 P

1,2

1,3

.....P

1,m

2,1

0 P

2,3

.....P

2,m

3,1

3,2

0......P

3,m

. . .

m,1

m,2

m,3

.....0







(1)

In the proposed method, a feature matrix com-

prised of O-D information based on the time win-

dow is computed over a period of time, forming a 2-D

time sequence. A Recurrent Neural Network (RNN)

is trained to make short term O-D predictions from a

sequence collected over a span of d consecutive time

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

260

windows.

Feature

Matrix







1,1

t−d+1

··· P

1,m

. ·· ·

1,m

t−d+1

·· · P

1,m

2,1

t−d+1

·· · P

2,1

m,m

t−d+1

·· · P

m,m







(2)

3.1 Long Short-Term Memory (LSTM)

Neural networks outperform most of the traditional

machine learning techniques because of its unique

non-linear adaptive processing ability(Xiao and Yin,

2019). The inability of traditional neural networks in

handling long sequences due to undesirable behaviour

of training gradients hindered their application on

structured learning problems until the path-breaking

invention of LSTM networks (Hochreiter and

Schmidhuber, 1997). Literature amply supports the

application of LSTM for trafﬁc ﬂow prediction(Xiao

and Yin, 2019). The architectural checks to prevent

gradients from going haywire are implemented using

input, output and forget gates, which regulate the ﬂow

of gradients through the neural units (LSTM cells) (Ci

et al., 2017). The LSTM cell unit is depicted in Fig. 4.

With reference to Figure 2, the equations listed be-

low describe how an LSTM unit works at every time

step t. The expressions f

, i

, O

and C

represent

the forget gate, input gate, candidate cell state, output

gate and cell state respectively. C

combines past in-

formation with present input. The ﬁnal cell output is

represented by h

where the typically used activation

function is tanh (Xiao and Yin, 2019). σ(x) and tanh

are the standard activation functions used in neural

networks as given in equation 9 and 10. And W and

b are the weight vector matrix and bias vector respec-

tively.

= σ(w

.[h

t−1

, x

] + b

) (3)

= σ(w

.[h

t−1

, x

] + b

) (4)

= tanh(w

.[h

t−1

, x

] + b

) (5)

= f

∗C

t−1

+ i

∗

(6)

= σ(w

.[h

t−1

, x

] + b

) (7)

= O

∗tanh(C

) (8)

σ(x) =

1 + e

−x

(9)

tanh(x) =

− e

−x

+ e

−x

(10)

The transmission of information in the hidden state

are controlled by the input gate, the forget gate and the

output gate (Han et al., 2019). The input and forget

gates decide the strength of input and previous state

signals used in deciding the state of the cell. The out-

put gate modulates the non-linearly transformed state

and can helps local control of the output signal prop-

agated. LSTMs are highly effective in passenger ﬂow

prediction as observed in (Han et al., 2019). The goal

of this work is to implement a path-dependent pas-

senger ﬂow forecasting model. The detailed explana-

tion of proposed LSTM network for path-dependent

passenger ﬂow forecasting is given in the following

Section.

Figure 3: Architecture of LSTM.

3.2 Path-Dependent Passenger Flow

Prediction Model Based on LSTM

The passenger ﬂow forecasting is deﬁned as predict-

ing future passenger volume y, from the historical

passenger ﬂow at each station. Localized passenger

ﬂow analysis of O-D pairs is an important technique

in spatio-temporal trafﬁc analysis and is of great as-

sistance in service scheduling and logistics manage-

ment. We use LSTM model to forecast the trafﬁc

through O-D paths. Suppose the input passenger ﬂow

sequence of a certain O-D path is x = (x

, x

...x

the vector sequence of the memory cell in LSTM is

h = (h

, h

...h

), the output predicted y is the ﬁ-

nal predicted passenger ﬂow sequence for the O-D

path. For training the model, feature matrix is col-

lected from O-D information as given in equation 2.

The inﬂow and outﬂow of at each station is the ag-

gregated result of predicted path-dependent passen-

ger ﬂows. The feature matrix is scaled in the range of

0to1 before being fed to the model. The architecture

of the proposed LSTM neural network is shown in ﬁg

3. The input layer size is same as the input feature

matrix sequence length.

The proposed model consists of an LSTM layer

followed by a dense layer. The intermediate output

of the LSTM does a revealing representation of the

temporal correlations existing in the passenger ﬂow

sequence. Hence the dense layer performs better than

when the sequence is directly fed to it. The dense

functions as a regressor for the scaled passenger ﬂow

output. The network requires a single neuron in the

A Path-Depended Passenger Flow Forecasting Model for Metro Rail Systems Using LSTM Neural Network

261

output layer with a linear activation to predict the

passenger ﬂow at the next time step. The optimiza-

tion of the dense layer is gradient descent and the

loss function is Mean Squared Error (MSE). Since

it is a single dense layer network the computation

done by it can be summarized by the equations below:

f inal

= f (W

∗ X

+ B)

: input matrix

: weight matrix, B : bias

(11)

All the analytical procedures are performed in JP-

DAP software platform using relevant APIs and

deep learning libraries such as Google TensorFlow(Ci

et al., 2017). The other internal libraries used from the

JP-DAP platforms are ML-lib, Scikit-learn, OpenCV.

The LSTM model can be generalized to other com-

plex metro systems connecting other modes of trans-

port with O-D matrix providing relevant insights for

the future research.

4 EXPERIMENTAL RESULTS

AND ANALYSIS

This section presents the experiment outcomes of the

proposed model and discusses them in comparison

with other conventional machine learning algorithms

like SVR, Regressor and Regression Tree.

LSTM model is implemented using Keras library

(Chollet et al., 2015) on top of Google’s TensorFlow

machine learning framework (Abadi et al., 2016). To

analyze the passenger ﬂow at each station and also to

ﬁnd the anomalies present in the data, box plot analy-

sis is performed. All those points outside the min and

max are considered to be the outliers in the data. Out-

lier removal is performed as part of pre-processing.

Figure 4: Heat-map of Origin-Destination Matrix.

Further, the heatmap of O-D matrix for Kochi

metro stations per day is shown in Fig 4. From

the heatmap for a single day it is can be in-

ferred that, the frequent travel paths in the

Kochi metro network or the path-dependent stations

are (Edappally-Aluva), (Maharajas-Aluva), (Aluva-

Edappally), (Aluva-Maharajas), (Edappally- Mahara-

jas), (Maharajas-Edappally). Different machine

learning models such as the SVR, Bayesian Regres-

sor and Regression Tree are trained along with LSTM

network using scaled metro data. For training the

models, 60% from the whole data set is selected ran-

domly and the rest 40% is used for validation and

testing the network. LSTM is trained using stochastic

gradient descent algorithm. For more efﬁcient passen-

ger ﬂow prediction model, the maximum number of

epochs set to be 1000. From the experimental analysis

of the fare card dat based learning (AFC), the model

is best ﬁt when it has 250, 40 and 6 neurons respec-

tively. Conventionally, the model training is stopped

if the loss of validation dataset does not decrease af-

ter ﬁve loops. The single step training and validation

loss of the proposed LSTM model is shown in Fig-

ure 5(a). Figure 5(b) provides the valid versus pre-

diction result of data points. Moreover, we train our

models by minimizing the mean square error for 500

epochs with a batch size of 100. The optimizer learn-

ing rate is experimentally ﬁxed to 0.05. In any time

series forecasting method, performance metric is an

indispensable part. The accuracy assessment methods

for passenger ﬂow prediction is given in the following

subsection.

4.1 Performance Metric

The statistical test indicators that we used to compare

the performance of the trafﬁc ﬂow prediction models

are Mean Squared Error (MSE), Root Mean Squared

Error (RMSE) and Mean Absolute Error (MAE). It is

deﬁned as follows:

MSE =

∑

i=1

− x

)

(12)

RMSE =

∑

i=1

− x

)

(13)

MAE =

∑

i=1

− x

| (14)

4.2 Evaluation and Inferences

The evaluation results of different models using O-D

is shown in Table 2. The model is compared with

a trained SVR model, Bayesian Regressor and Re-

gression Tree. With reference to Table 2, it is ob-

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

262

(a) Single-step Training and Validation Loss (b) Vaild vs Prediction based on the data-

points(Passenger Day Count)

Figure 5: Single-step Training and Validation Loss of LSTM and Valid vs Predction on datapoints.

(a) Short Term Path-wise Passenger Flow Prediction us-

ing LSTM

(b) Short Term Station-wise Passenger Flow Prediction

using LSTM

Figure 6: Path-wise and Station-wise Passenger Flow Prediction using LSTM.

Table 2: Accuracy Metrics for Time Series Forecast.

Model MSE RMSE MAE

SVR(kernel)

Linear 0.0023 0.0486 0.0476

Polynomial 0.0084 0.0924 0.0899

RBF 0.0031 0.0553 0.0541

Bayesian Regressor 0.00018 0.01376 0.003435

Regression Tree 0.00072 0.02688 0.01099

LSTM 0.00015 0.01253 0.003539

served that the best kernel for the SVR model is linear.

Also, the performance of the model is evaluated us-

ing accuracy measuring metrics such as MSE, Root

Mean Square error (RMSE), Mean Absolute Error

(MAE). From the experimental analysis and results

obtained, proposed passenger ﬂow prediction model

using LSTM outperforms most of the traditional ma-

chine learning techniques. The LSTM model is de-

signed using all possible paths existing in the current

metro system. The time series prediction of passen-

ger count using the LSTM neural network is shown

in Figure 6(a). The inﬂow and outﬂow of each sta-

tion is the aggregated result of predicted O-D ﬂows as

depicted in Figure 6(b).

5 CONCLUSION AND FUTURE

WORK

This work attempts to tackle the problem of ﬂow pre-

diction for metro rail transport using path-dependent

station pairs to increase the accuracy of the predic-

tion. By examining the observations it was found

that LSTM network in conjunction with a non-linear

dense prediction layer performed better than other

models. Experimental results have derived that that

incorporation of spatial information is a performance

enhancer and blazes a direction worth further explo-

ration. Moreover unlike conventional ML methods

the intermediate features generated by the LSTM con-

vey the temporal structure more effectively. The ex-

A Path-Depended Passenger Flow Forecasting Model for Metro Rail Systems Using LSTM Neural Network

263

traction of OD matrix is computational bottleneck in

this process. We identify employment of distributed

computational methods as a potential future work for

solving this problem. Another intended area of future

work is to further explore is the effect of external fac-

tors like weather conditions and bring them into the

scope of the model.

ACKNOWLEDGEMENTS

This research is supported by Interdisciplinary Cyber

Physical Systems Division of Department of Science

and Technology (DST), Government of India (Project

ID : DST/ ICPS/ CPS Individual/2018/1091).

REFERENCES

Abadi, M., Agarwal, A., and Barham, P. (2016). Tensor-

Flow: Large-scale machine learning on heterogeneous

systems. Software available from tensorﬂow.org.

Ahmed, M. S. and Cook, A. R. (1979). Analysis of free-

way trafﬁc time-series data by using Box-Jenkins tech-

niques. Number 722.

Ampelas, A. (2001). Automatic fare collection. IEEE Con-

ference on Intelligent Transportation Systems, Pro-

ceedings, ITSC.

Chollet, F. et al. (2015). Keras. https://keras.io.

Ci, Y., Xiu, G., and Wu, L. (2017). A short-term trafﬁc ﬂow

prediction method based on long short-term memory

network. In International Conference on Green Intel-

ligent Transportation System and Safety, pages 601–

608. Springer.

Dai, X., Sun, L., and Xu, Y. (2018). Short-term origin-

destination based metro ﬂow prediction with prob-

abilistic model selection approach. Journal of Ad-

vanced Transportation, 2018.

Han, Y., Wang, C., Ren, Y., Wang, S., Zheng, H., and Chen,

G. (2019). Short-term prediction of bus passenger

ﬂow based on a hybrid optimized lstm network. ISPRS

International Journal of Geo-Information, 8(9):366.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural computation, 9(8):1735–1780.

Li, Y., Wang, X., Sun, S., Ma, X., and Lu, G. (2017).

Forecasting short-term subway passenger ﬂow under

special events scenarios using multiscale radial basis

function networks. Transportation Research Part C:

Emerging Technologies, 77:306–328.

Metro Rail (2017). Kochi metro rail Ltd., Kerala, India.

Mulerikkal, J., Thandassery, S., Dixon K, D. M., Rejathalal,

V., and Ayyappan, B. (2022). Jp-dap: An intelligent

data analytics platform for metro rail transport sys-

tems. IEEE Transactions on Intelligent Transporta-

tion Systems, 23(7):9146–9156.

Pamuła, T. (2013). Short-term trafﬁc ﬂow forecasting

method based on the data from video detectors using a

neural network. In International Conference on Trans-

port Systems Telematics, pages 147–154. Springer.

Sun, Y., Leng, B., and Guan, W. (2015). A novel wavelet-

svm short-time passenger ﬂow prediction in beijing

subway system. Neurocomputing, 166:109–121.

Tang, L., Zhao, Y., Cabrera, J., Ma, J., and Tsui,

K. L. (2019). Forecasting short-term passenger

ﬂow: An empirical study on shenzhen metro. IEEE

Transactions on Intelligent Transportation Systems,

20(10):3613–3622.

Tian, Y. and Pan, L. (2015). Predicting short-term traf-

ﬁc ﬂow by long short-term memory recurrent neural

network. In 2015 IEEE international conference on

smart city/SocialCom/SustainCom (SmartCity), pages

153–158. IEEE.

Tsai, T.-H., Lee, C.-K., and Wei, C.-H. (2009). Neural

network based temporal feature models for short-term

railway passenger demand forecasting. Expert Sys-

tems with Applications, 36(2):3728–3736.

Xiao, Y. and Yin, Y. (2019). Hybrid lstm neural network

for short-term trafﬁc ﬂow prediction. Information,

10(3):105.

Zaharia, M., Chowdhury, M., Franklin, M. J., Shenker, S.,

Stoica, I., et al. (2010). Spark: Cluster computing with

working sets. HotCloud, 10(10-10):95.

Zhang, Z., Wang, C., Gao, Y., Chen, J., and Zhang, Y.

(2020). Short-term passenger ﬂow forecast of rail

transit station based on mic feature selection and st-

lightgbm considering transfer passenger ﬂow. Scien-

tiﬁc Programming, 2020.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

264