A Carbon-Neutral, Community-Based, Reactive and Scalable

Ride-Sharing Service

Avinash Nagarajan

1 a

, Alan McGibney

2 b

, Pio Fenton

3 c

and Ignacio Casti

neiras

1 d

Department of Computer Science, Munster Technological University, Cork, Ireland

NIMBUS Centre, Munster Technological University, Cork, Ireland

Teaching & Learning Unit, Munster Technological University, Cork, Ireland

Keywords:

Ride-Sharing, Smart Energy Communities, Green Computing, Optimisation.

Abstract:

This paper presents the design, implementation and evaluation of a community-based, reactive ride-sharing

service that promotes carbon-neutral management of city commutes using autonomous vehicles. The problem

is formulated as a variant of the classical Dynamic Vehicle Routing problem with Time Windows, considering

both dynamic resources and requests over a simulated time horizon. A solution approach is provided, based

on an algorithm following a reactive-based simulation on top of a greedy decision-making process. A pa-

rameterised instance generator is developed to align existing benchmarks (i.e. Google HashCode) and public

datasets (i.e. NYC taxis) to the proposed problem formulation and to enable testing of the solution under

various conﬁgurations. The ride-sharing service is proven to scale well, when applied to very large instances,

it provides fast and competitive results, both in terms of trip petitions satisﬁed and overall distance traversed.

1 INTRODUCTION

The European Green Deal has set the vision for a

climate neutral continent by 2050 (EU Green Deal,

2020). For transportation systems to meet the afore-

mentioned goal, a sustained transition to mass electric

vehicles (EV) and a fully Renewable Energy Sources

(RES)-based energy market to power them is critical

(Xiang et al., 2016). There is an onus on all citi-

zens to play a role in this green transition, for exam-

ple Smart Energy Communities (SEC) are emerging

to enable distributed energy generation and storage at

a local level, representing a step further to the reali-

sation of the term ‘Energy Citizen’ (Diamantoulakis

et al., 2015).

Ride-sharing has presented new opportunities for

the SEC sector to be productive with energy usage

(Agatz et al., 2012). Dynamic ride-sharing systems

aim to match riders and drivers with similar itineraries

and time schedules on short-notice (Furuhata et al.,

2013). These systems can reduce the number of

cars used for personal travel (improving the utilisa-

https://orcid.org/0000-0002-4533-0527

https://orcid.org/0000-0002-0665-2005

https://orcid.org/0000-0002-1673-9737

https://orcid.org/0000-0002-3875-4460

tion of available seat capacity) as well as the total

distance for such travels, thus reducing the environ-

mental impact. The research presented in this pa-

per includes the design, implementation and evalu-

ation of a ride-sharing service operating in a Smart

City environment to align with the ambition of the

EU Green Deal goals, and therefore envisioning an al-

ternative carbon-neutral, community-based, reactive

transportation approach for managing city commutes

using autonomous vehicles. Emphasis is placed on in-

dividual citizens (rather than on haulage/commercial

transportation) that collectively aim to minimise their

impact on the environment through the use of ride-

sharing commutes relying on 100% EVs operating

solely on RES.

Speciﬁcally, the paper includes the following con-

tributions:

• The formulation of a ride-sharing simulation ser-

vice with the aforementioned conditions, pre-

sented as a variant of the classical Dynamic Ve-

hicle Routing Problem with Time Windows (Jail-

let and Wagner, 2008). The dynamic resources

are provided by a number of SECs spread across

a city, each of them owning a number of au-

tonomous EVs and using its own RES generation

function to dynamically charge (and release) them

Nagarajan, A., McGibney, A., Fenton, P. and Castiñeiras, I.

A Carbon-Neutral, Community-Based, Reactive and Scalable Ride-Sharing Service.

DOI: 10.5220/0011842500003491

In Proceedings of the 12th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2023), pages 28-39

ISBN: 978-989-758-651-4; ISSN: 2184-4968

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

over time. The dynamic requests are provided

via trip petitions released over time, each of them

with its own location and pick-up/drop-off times.

The formulation of the ride-sharing service inte-

grates energy generation, allocation and reactive

re-routing constraints, with the objective function

of maximising the overall number of trip petitions

being served.

• The design and implementation of a ride-sharing

service, based on an algorithm following a

reactive-based simulation approach on top of a

greedy-based decision-making process. The al-

gorithm favours scalability over optimality, there-

fore evaluating its applicability to real-world in-

stances based on the transportation of large cities.

• The evaluation of the solution approach us-

ing a parameterised instance generator, allow-

ing for the ﬁne-grained customisation of a Vehi-

cle Routing Problem benchmark and of a pub-

lic transportation-based dataset to the speciﬁc re-

quirements and format of the ride-sharing prob-

lem. A problem-speciﬁc benchmark is generated,

testing the performance and scalability of the al-

gorithm over a number of conﬁgurations.

The structure of the paper is as follows: Sec-

tion 2 positions the paper w.r.t. existing ride-sharing

approaches and solutions. Section 3 formalises the

problem for the carbon-neutral, community-based re-

active ride-sharing service being proposed, Section 4

presents the solution approach and Section 5 its eval-

uation. Finally, Section 6 provides the main conclu-

sions and future work.

2 RELATED WORK

In (Hasan et al., 2018) the authors argue the viabil-

ity of a ride-sharing service is dependent on six core

principles: spatial and temporal proximity of the rid-

ers, low coordination costs, guaranteed to ride back

home, low trust concerns and clear commuter roles.

Spatial and temporal proximity reduces per-trip costs

by matching customers with similar schedules and

locations. The other four principles come down to

psychological factors that make the service reliable.

Their approach focuses on one of the passengers own-

ing the vehicle, and therefore is explicitly attached to

the trips of the vehicle like taxis. The optimisation

criteria centres around maximising the incentives of

key stakeholders.

The authors in (Agatz et al., 2012) focus on dy-

namic ride-sharing from the point of view of its shar-

ing cost mechanism. Uncertainty in trip petitions

is considered, with trip applications ranging from a

few minutes to a few hours before departure time.

The algorithm then evaluates different re-optimisation

frequencies for ﬁnding ride-share arrangements each

time a new trip petition arrives or at ﬁxed time inter-

vals. Drivers are considered private entities, thus en-

abling vehicle availability only when aligned to their

trip needs. The ride-sharing service focuses on op-

timising the total distance or the total travel time of

each individual ride.

In (Hasan and Hentenryck, 2020) the authors fo-

cus on dynamic ride-sharing from the point of view of

enabling the scheduling of ride-sharing trips in real-

time. Their approach reuses the idea of re-assessment

over a time horizon for matching trip petitions re-

quested just a few minutes before its departure. Al-

though the authors focus on clustering drivers and

passengers of the same neighbourhood together (to

provide a set of possible feasible trips), it is intended

to address the return trip of a population for which an

outbound trip has already been provided. The optimi-

sation criteria is the quality of service where once a

passenger has been assigned to a trip session, they are

guaranteed a ride back.

In (Serra et al., 2019) the authors focus on dy-

namic ride-sharing for the last-mile from the point of

view of integrating it as part of a multi-modal trans-

portation system. The paper considers the routing of

passengers who have nearly completed their commute

after having reached a central station by using pub-

lic transport and are now in a position of scattering

to their ﬁnal destination points. The goal is to reduce

the number of vehicles on road by efﬁcient passenger-

vehicle allocation.

The authors of (Al-Abbasi et al., 2019) focus on

ride-sharing from the point of view of trust and pri-

vacy. They propose a co-util framework based on

Game Theory, which requires all involved parties to

beneﬁt by being an active part of the solution. In the

proposed ride-sharing service, the passengers beneﬁt

from low travel costs. The goal is to reduce the num-

ber of vehicles on the road and the cost of mitigating

trafﬁc congestion.

The study of community-based reactive ride-

sharing systems has shown signiﬁcant potential in

mitigating the impact of conventional transportation

on the environment and promoting the use of RES.

The key factor contributing to this potential is the

scalability, robustness and uncertainty of such sys-

tems. By leveraging the power of autonomous electric

vehicles, community-based reactive ride-sharing sys-

tems can be tailored to meet the diverse and evolving

transportation needs of modern society while reduc-

ing their carbon footprint.

A Carbon-Neutral, Community-Based, Reactive and Scalable Ride-Sharing Service

3 PROBLEM DEFINITION

This section formalises the problem for a carbon-

neutral, community-based reactive ride-sharing ser-

vice as a variant of the classical Dynamic Vehicle

Routing Problem with time windows. It integrates

energy generation, allocation and reactive re-routing

constraints as both the trip petitions and the number

of available vehicles evolve during a simulated time

horizon. The ride-sharing service aims to maximise

the number of trip petitions being served. It is also

intended to be highly scalable to facilitate transporta-

tion in large cities.

The ride-sharing service contains the following

features:

• The grid dimensions of the city c

, c

and the time

horizon for the simulation th. W.l.o.g., Manhat-

tan distances among the locations of the city are

assumed.

, c

,th)

• A set S of SECs, each of them with an id s

, a

location in the city s

, s

, a lexicographic-ordered

list of the vehicles belonging to it s

, the amount

of vehicles ready at the start of the simulation

(i.e., at time unit 0) s

and an energy function

f s

: NxN with the energy produced per time

unit of the simulation, which will be used to re-

lease(in order) each new vehicle from s

as soon

as enough energy to ﬁll its battery capacity is gen-

erated.

, s

, f s

)∀s ∈ S

• A set E of EVs, each of them with its own id e

the id of the SEC it belongs to s

, its release time

during the simulation e

(either 0 or when enough

energy is generated) and its battery and passenger

capacities (e

and e

). A mapping from E to S

is assumed, such that each e

belongs to one s

, e

)∀e ∈ Es

• A set T of trip petitions (TPs), each of them with

its id t

, its release time during the simulation t

and its pick-up (resp. drop-off) locations t

, t

(resp. t

, t

) and time-windows t

, t

l p

(resp. t

l p

)∀t ∈ T

The ride-sharing service is intended to provide an

output containing the following features:

• A set Alloc, representing an allocation mapping

from T to E.

∀t ∈ T Alloc[t

] =

(

, if t

is allocated to e

−1, otherwise

• A set Sched, representing a scheduling mapping

from E to its sequence of movements (in chrono-

logical order) over the entire time horizon.

∀e ∈ E Sched[e

] = (m

, m

, . . . , m

n−1

)

Each movement m

of a vehicle is represented as

≡ {(TA

, T B,

, AY

, BX

, BY

, PS

, ES

, EE

, T L

, LW

, T D

)}

with:

– TA

(resp. T B

) represent the start time (resp.

end time) of m

– AX

and AY

(resp. BX

and BY

) represent the

coordinates of the vehicle at the start (resp.

end) of m

– PS

(resp. PE

) represents the number of pas-

sengers in the vehicle at the start time (resp. end

time) of m

– ES

(resp. EE

) represents the battery left in the

vehicle at the start time (resp. end time) of m

– T l

represents a label to identify the purpose of

the trip.

A movement for picking-up (resp. dropping

off) the passenger of t

is marked as +t

(resp. −t

An idle movement (resting at a given location)

is marked as idle.

A last movement, returning to its home SEC

is marked as ret.

– LW

represents the leeway of the movement,

i.e., the maximum delay that could be applied

to the movement while still accomplishing the

action is intended to.

– T D

represents the movement duration.

3.1 Instance Example

To highlight the approach taken, an example of a

problem instance is presented here. A possible in-

stance represents a city of dimensions 3 x 4 (w.l.o.g,

3km x 4km) and a simulated time horizon of 10 units

(w.l.o.g., 10 minutes).

= 3, c

= 4,th = 10)

The city contains just 1 SEC, with id SEC

and

placed at location (1,2), with a list of 2 vehicles

≡ [EV

, EV

], one vehicle ready to go at the start

of the simulation, and a constant energy generation

function of 2kWh per time unit f SEC

= 2.

S ≡ {(SEC

, 1, 2, [EV

, EV

], 1, f SEC

)}

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

A constant speed is assumed, making each vehicle to

traverse 1 block of the city every time unit, while con-

suming 1 unit of its battery capacity (w.l.o.g., 60km/h

constant speed and 60kWh constant consumption).

Both EVs have a battery capacity of 10kWh and room

for 5 passengers. Whereas EV

is released at the start

of the simulation (time unit 0), EV

is released when

its battery capacity is generated by SEC

(i.e., given

the constant energy generation of 2kWh per time unit,

the vehicle is generated at time unit 5). If SE C

had

had more vehicles in S

, they would have been re-

leased (in order) at time units 10, 15, and so on.

E ≡ {(SEC

, EV

, 0, 10, 5), (SEC

, EV

, 5, 10, 5)}

The city receives 3 TPs, with ids T P

, T P

and TV

T P

is announced at time unit 0, to pick-up the pas-

senger at location (2,3) between time units 0 and 4,

and to drop-off at location (0,0) between time units 5

and 7. T P

is announced at time unit 2, to pick-up the

passenger at location (2,2) between time units 3 and

4, and to drop-off at location (1,1) between time units

5 and 6. T P

is announced at time unit 6, to pick-up

the passenger at location (2,3) between time units 6

and 7, and to drop-off at location (1,3) between time

units 7 and 9.

T ≡ {(T P

, (0, 2, 3, 0, 0, 0, 4, 5, 7)),

(T P

, (2, 2, 1, 1, 1, 3, 4, 5, 6)),

(T P

, (6, 2, 3, 1, 3, 6, 7, 7, 9))}

A feasible solution to this instance allocates T P

and

T P

to EV

, while T P

is not allocated.

Alloc ≡ {(T P

, EV

), (T P

, EV

), (T P

, −1)}

In the allocation above, the vehicles have the fol-

lowing schedules:

Sched ≡ {(EV

, [(0, 2, 1, 2, 2, 3, 0, 1, 10, 8, +T P

, 2, 2),

(2, 4, 2, 3, 2, 1, 1, 2, 8, 6, +T P

, 0, 2),

(4, 5, 2, 1, 1, 1, 2, 1, 6, 5, −T P

, 1, 1),

(5, 7, 1, 1, 0, 0, 1, 0, 5, 3, −T P

, 0, 2),

(7, 10, 0, 0, 1, 2, 0, 0, 3, 0, ret, 0, 3)]),

(EV

, [(5, 10, 1, 2, 1, 2, 0, 0, 10, 10, idle, 5, 0)]}

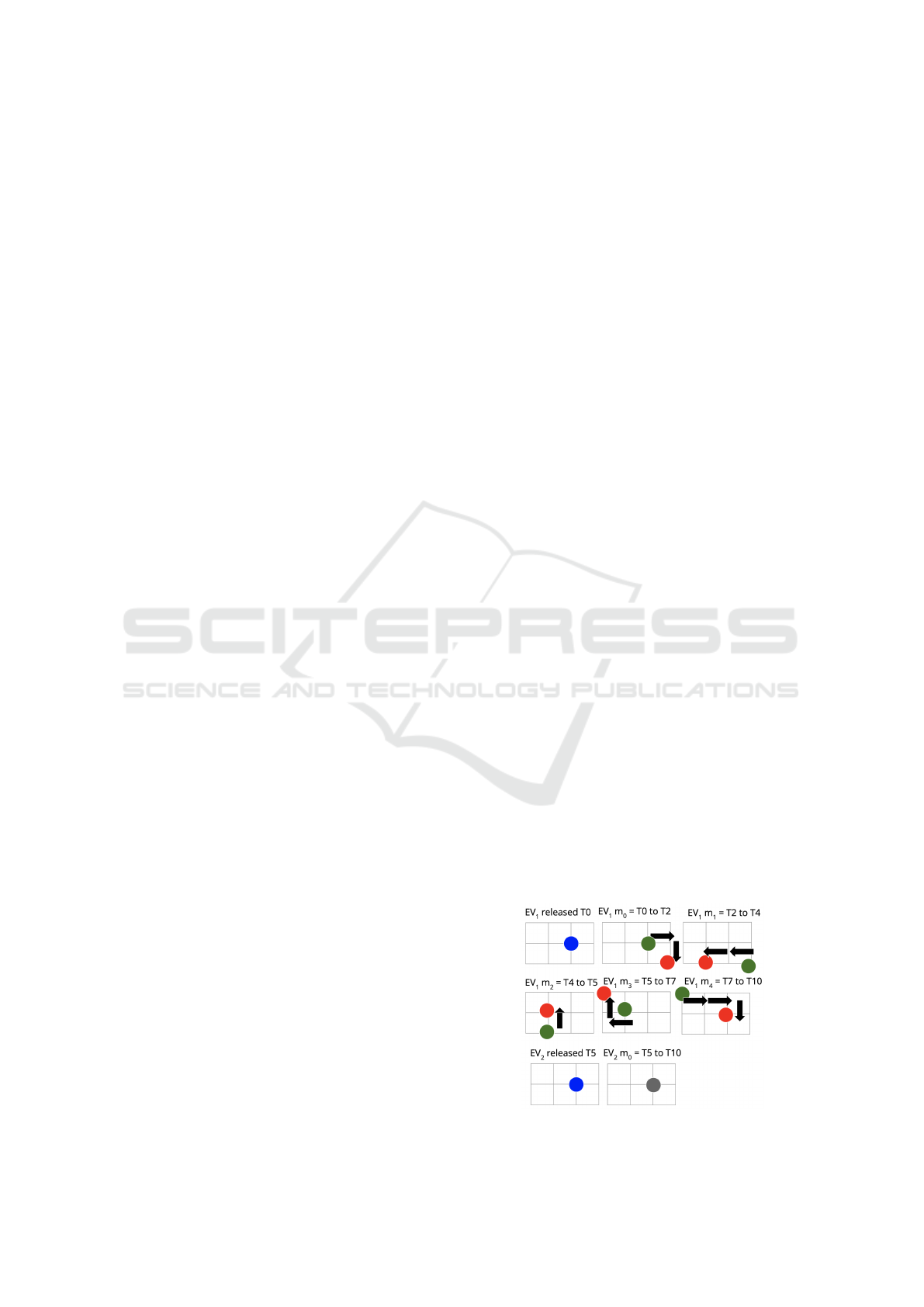
Figure 1 displays the route of EV

and EV

Sched. W.l.o.g., the coverage of the Manhattan dis-

tance between two points is assumed to be traversed

always by covering ﬁrst the distance of the x-axis fol-

lowed up by the distance in the y-axis. The release of

an EV is highlighted in blue, an idle movement in grey

and an active movement by its starting point (green)

and destination one (red).

The route of EV

is composed of 5 movements:

1. From time unit 0 to time unit 2, it leaves the SEC

to serve the pick-up of T P

. On doing so, it goes

from (1,2) to (2,3), increases its number of pas-

sengers from 0 to 1, and reduces its battery capac-

ity from 10 to 8. As the pick-up of T P

must be

within time units 0 and 4 and EV

arrives at time

unit 2, a leeway of 2 time units is associated to the

movement, as it could have been re-scheduled by

delaying it up to 2 time units in case the vehicle

had needed any re-routing.

2. From time unit 2 to time unit 4, the vehicle serves

the pick-up of T P

. On doing so, it goes from

(2,3) to (2,1), increases its number of passengers

from 1 to 2, and reduces its battery capacity from

8 to 6. As the pick-up of T P

must be within time

units 3 and 4 and EV

arrives at time unit 4, a lee-

way of 0 time units is associated to the movement,

as it cannot be further delayed by any re-routing.

3. From time unit 4 to time unit 5, the vehicle serves

the drop-off of T P

. On doing so, it goes from

(2,1) to (1,1), decreases its number of passengers

from 2 to 1, and reduces its battery capacity from

6 to 5. As the drop-off of T P

must be within time

units 5 and 6 and EV

arrives at time unit 5, a lee-

way of 1 time unit is associated to the movement.

4. From time unit 5 to time unit 7, the vehicle serves

the drop-off of T P

. On doing so, it goes from

(1,1) to (0,0), decreases its number of passengers

from 1 to 0, and reduces its battery capacity from

5 to 3. As the drop-off of T P

must be within

time units 5 and 7 and EV

arrives at time unit

7, a leeway of 0 time units is associated to the

movement.

5. From time unit 7 to time unit 10, the vehicle re-

turns to SEC

before the end of the simulation.

On doing so, it goes from (0,0) to (1,2), stays at 0

passengers, and reduces its battery capacity from

3 to 0. As the end of the time horizon is at time

unit 10, and the vehicle arrives to SEC

at time

unit 10, a leeway of 0 time units is associated to

the movement.

Figure 1: S ched Outputted as Solution.

A Carbon-Neutral, Community-Based, Reactive and Scalable Ride-Sharing Service

The route of EV

is composed of just 1 movement,

as the vehicle remains idle since it is released at time

unit 5 until the end of the time horizon.

4 SOLUTION APPROACH

This section presents an initial algorithm to solve the

problem formalised in Section 3. Subsections 4.1 and

4.2 present the algorithm and analyse its complexity,

respectively.

4.1 Algorithm Overview

Given a valid instance of a city with its SECs, vehi-

cles, energy generation and trip petitions, the algo-

rithm aims to maximise the number of trip petitions

being served, outputting both the allocation of each

trip to a vehicle and the routing of each vehicle over

the entire simulated time horizon. For doing so, the

algorithm implements a reactive-based simulation ap-

proach on top of a greedy decision making process for

trip allocations. Algorithm 1 presents the pseudocode

of the solution approach, which is explained in detail

next.

Algorithm 1: Ride-Sharing.

function allocate(e, t, Alloc[t], Sched[e])

is allocated ← f alse

m ≡ [m

, . . . , m

k−1

] ← copy(Sched[e])

for i ∈ 0, . . . , k − 1 do

if pick up(m, t, i) then

m ← [m

, . . . , m

′

, m

′

i+1

, . . . , m

′

r−1

]

for j ∈ i + 1, . . . , r − 1

′

if drop o f f (m, t, j) then

m ← [m

, . . . , m

′′

, m

′′

j+1

, . . . , m

′′

w−1

]

if ret sec(m, w − 1) then

m ← [m

, . . . , m

′′

w−1

, m

′′

]

(Alloc[t], Sched[e]) ← (e, m)

is allocated ← true

Break

return is allocated

function reactive simulation(S, E, T , th)

(Alloc, S ched) ← init(S, E, T,th)

for t ∈ sorted(T ) do

for e ∈ E do

if allocate(e, t, Alloc[t], Sched[e]) then

Break

return (Alloc, Sched)

4.1.1 Reactive-Based Simulation

First, the algorithm initialises Alloc, considering each

trip as initially not allocated. It also initialises Sched,

considering the route of each vehicle as, initially,

resting at its home SEC from its release time e

to the end of the time horizon of the simulation th.

Therefore, even at the beginning of the simulation

(time unit 0), all vehicles have an associated schedule

(even if such schedule does not start until a release

time unit e

in the future).

∀t ∈ T Alloc[t

] = (e

, −1)

∀e ∈ E ∃s

∈ S with s

, s

, e ∈ s

s.t. Sched[e

] =

[(e

,th, s

, s

, 0, 0, e

, e

, idle,th − e

, 0)]

For example, given the instance of Section 3.1,

the initial value of Al loc and Sched is as follows:

Alloc ≡ {(T P

, −1), (T P

, −1)}

Sched ≡ {(EV

, [(0, 10, 1, 2, 1, 2, 0, 0, 10, 10, idle, 10, 0)]

(EV

, [(5, 10, 1, 2, 1, 2, 0, 0, 10, 10, idle, 5, 0)]}

The algorithm then simulates a reactive-based

ride-sharing service by simply sorting all trip peti-

tions by their increasing release time (referred to as

sorted(T )), thus attempting to serve each trip petition

as soon as it is released. For each t ∈ sorted(T ), the

algorithm iterates for each e ∈ E, attempting to allo-

cate the trip to the vehicle by dynamically re-routing

its schedule (i.e., by ﬁtting both the pick-up and drop-

off of t as new movements into the existing schedule

of the vehicle Sched[e]. As soon as the algorithm suc-

cessfully allocates t to a vehicle e, the search stops

(i.e., the trip is not attempted to be allocated to any

other vehicle). On the other hand, if no vehicle can

allocate t, then the attempt to serve the trip petition is

considered as not successful, and no further attempt

for allocating it is made for the rest of the simulation.

For example, given the instance of Section 3.1, the

trips T P

, T P

and T P

are released in time units 0, 2

and 6, respectively. Therefore:

1. The algorithm simulates that T P

is attempted to

be allocated ﬁrst, at time unit 0. On that moment,

the schedule of EV

and EV

is the initial one

described above. If EV

can be successfully re-

routed to ﬁt T P

, then it is allocated to it. Other-

wise EV

is attempted. If T P

can not be serviced

by either EV

or EV

, then T P

is not allocated. In

any case, these allocation attempts lead to a new

updated state Sched

′

and Alloc

′

2. The algorithm continues by attempting to allocate

T P

over EV

ﬁrst and EV

otherwise with their

current updated schedules Sched

′

at time unit 2,

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

further leading to a new updated state Sched

′′

and

Alloc

′′

3. Finally, the algorithm continues by attempting to

allocate TP

over EV

ﬁrst and EV

otherwise

with their current updated schedules Sched

′′

time unit 6, leading to the ﬁnal state (the one re-

ported as output) Sched

′′′

and Alloc

′′′

4.1.2 Trip Petition Allocation

The allocation of t to e (speciﬁcally, to its schedule

Sched[e]) is deﬁned to be successful iff:

1. The updated Sched[e]

′

incorporates one new

movement ensuring the pick-up (resp. drop-off)

of t within its deﬁned time window t

and t

l p

(resp. t

and t

). The functions pick up (resp.

drop o f f ) ensure this (cf. Algorithm 1).

2. The updated Sched[e]

′

contains a very last active

movement, labelled as ret, ensuring the vehicle

returning to its home SEC before the end of the

time horizon th. The functions ret sec ensures this

(cf. Algorithm 1).

3. The addition of these new pick-up, drop-off and

ret movements to Sched[e]

′

(to serve t) might de-

lay the actual pick-up and drop-off times of any

other previous trips t

the vehicle e had previously

committed to. For t to be successfully allocated to

e, such these additional delays on serving t

must

not break the pick-up and drop-off time windows

of t

. In other words, once a vehicle e commits

to a trip t

, no further trip allocation t can delay

e enough to make it not serving t

in time. The

functions pick up (resp. drop o f f ) ensure this

(cf. Algorithm 1).

4. The updated Sched[e]

′

contains no movement

where the number of passengers exceeds its ca-

pacity e

or where the battery capacity e

goes

below 0.

To ﬁt t into Sched[e] = [m

, . . . , m

k−1

] the algo-

rithm iterates through its movements (which are in

chronological order). When considering a movement

≡ (TA

, T B

, ...), the algorithm only considers its

starting time unit TA (i.e., the decision of whether to

re-route or not e to serve t is considered just at TA, not

at any other given time in the interval (TA, . . . , T B].

First, the algorithm searches for a movement m

ﬁtting the pick-up of t. As soon as such movement

is found, no further movement m

with j > i of

e is considered for picking-up t, and the algorithm

moves on into searching for a movement m

ﬁtting

the drop-off of t. Again, as soon as such movement

is found, no further movement m

with k > j of e

is considered for dropping-off t.

Needless to say, both policies of (1) considering

just the starting time TA of each movement and (2)

considering just one valid pair (m

, m

) of picking-

up and dropping-off movements search to be incom-

plete. That is, the search is not considering other (m

′

) valid combinations and any other valid re-routing

times for such combinations other than TA

′

and TA

′

Any such alternatives might lead not only to the allo-

cation of t, but to an overall higher number of trips

allocated, which is the goal aimed by the algorithm.

However, these policies are designed to favour scala-

bility over optimality for the algorithm (more detail in

Section 4.2). Moreover, although not leading to opti-

mality, the above non-complete search still leads to a

very competitive trip allocation rate when applied to

real-world very large instances, as it is discussed in

more detail in Section 5.2.

Given the instance of Section 3.1, the following

analyses the attempt to ﬁt TP

into EV

at time unit 2.

T P

≡ (2, 2, 1, 1, 1, 3, 4, 5, 6)

As described previously, at this stage in the simu-

lation, TP

had been successfully allocated to EV

making its Sched[EV

Sched[EV

] = [

≡ (0, 2, 1, 2, 2, 3, 0, 1, 10, 8, +T P

, 2, 2),

≡ (2, 7, 2, 3, 0, 0, 1, 0, 8, 3, −T P

, 0, 5),

≡ (7, 10, 0, 0, 1, 2, 0, 0, 3, 0, ret, 0, 3)]

The window of opportunity for allocating the

pick-up of T P

is from T P2

= 2 to T P2

l p

= 4.

The algorithm ﬁrst attempts to ﬁt the pick-up on

, but fails, as the time of the movement TA

is 0,

even before T P

is announced, and therefore outside

of its window of opportunity.

The algorithm then attempts m

, and it succeeds.

spans from time unit TA

= 2 to T B

= 7, going

from (2,3) to (0,0) for dropping-off T P

. The total

distance covered is 5. It must be at (0,0) at time unit

7 at the latest (T P1

= 7), so it cannot be further de-

layed. Re-routing m

to serve pick-up of T P

involves

(1) going from (2,3) to (2,1); (2) arrive there between

time units 3 and 4; (3) going from (2,1) to (0,0); (4)

still arrive there on time (i.e., time unit 7 + 0 leeway =

7). The total distance of re-route to pick-up T P

while

still dropping-off TP

from there is 2 + 3 = 5; if leav-

ing straight-away at time unit 2, it will reach (2,1) to

pick-up T P

at time unit 4, still within the window of

opportunity, and leading to a leeway of 0, as this new

movement cannot be any further delayed.

A Carbon-Neutral, Community-Based, Reactive and Scalable Ride-Sharing Service

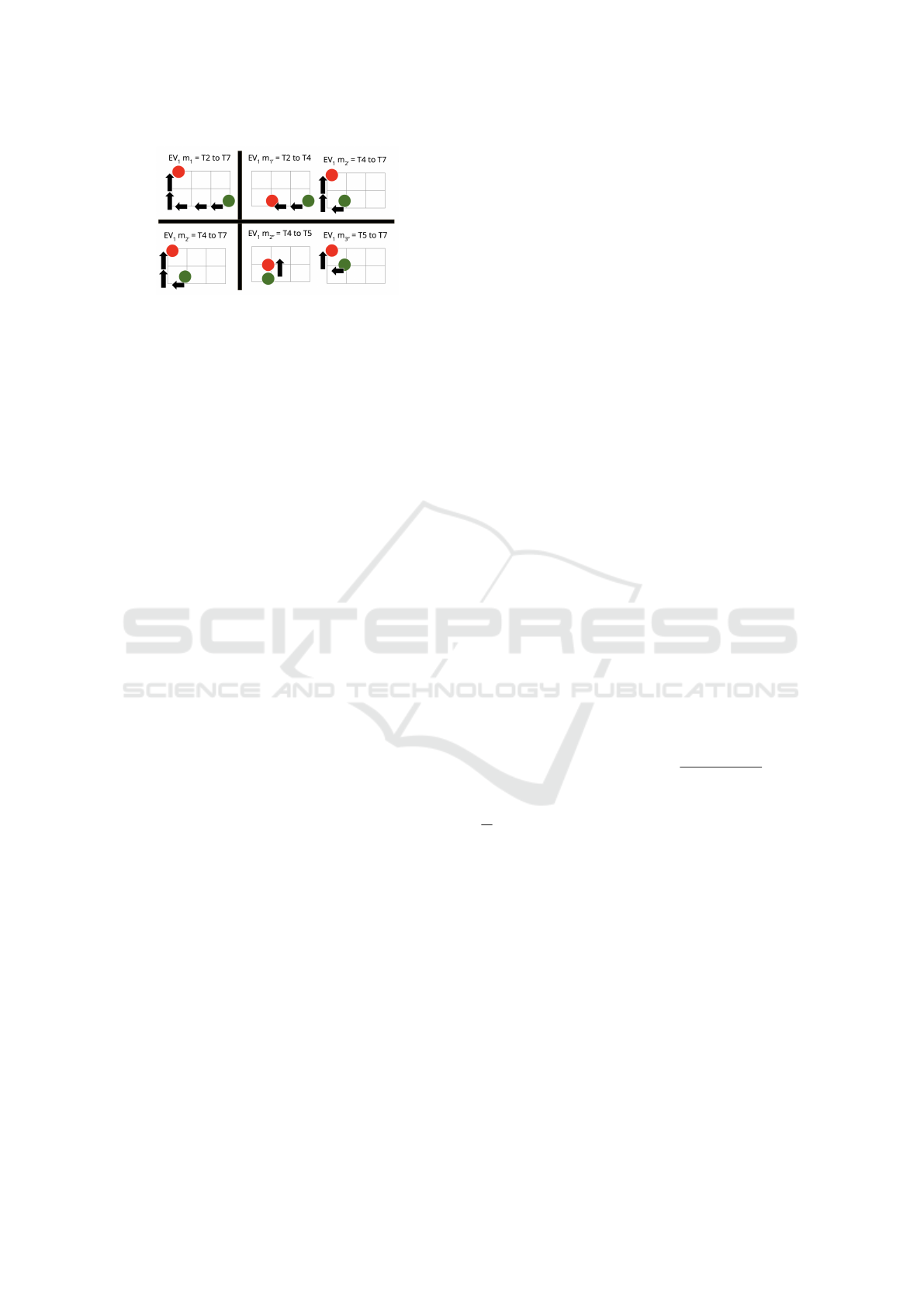
Figure 2: S ched[EV

] when Fitting T P

The new state of Sched

′

[EV

] is:

Sched

′

[EV

] = [

′

≡ (0, 2, 1, 2, 2, 3, 0, 1, 10, 8, +T P

, 2, 2),

′

≡ (2, 4, 2, 3, 2, 1, 1, 2, 8, 6, +T P

, 0, 2),

′

≡ (4, 7, 2, 1, 0, 0, 2, 1, 6, 3, −T P

, 0, 3)

′

≡ (7, 10, 0, 0, 1, 2, 0, 0, 3, 0, ret, 0, 3)]

The window of opportunity for allocating drop-off

of T P

is from the next time unit to its pick-up (5) to

T P2

= 6.

The algorithm ﬁrst attempts m

′

(as it does not start

attempting the drop-off allocation any earlier than the

pick-up movement), and it succeeds. m

′

spans from

time unit TA

′

= 5 to T B

′

= 7, going from (2,1) to

(0,0) for dropping-off T P

. The total distance cov-

ered is 3. It must be at (0,0) at time unit 7 at the lat-

est (T P1

= 7), so it cannot be further delayed. Re-

routing m

′

to serve drop-off of T P

involves (1) go-

ing from (2,1) to (1,1); (2) arrive there between time

units 5 and 6; (3) going from (1,1) to (0,0); (4) still

arrive there on time (i.e., time unit 7 + 0 leeway = 7).

The total distance of re-route to drop-off T P

while

still dropping-off TP

from there is 1 + 2 = 3; if leav-

ing straight-away at time unit 4, it will reach (1,1) to

drop-off T P

at time unit 5, still within the window of

opportunity and leading to a leeway of 1 as the time

window for dropping TP

ends at time unit 6

The new state of Sched”[EV

] is:

Sched”[EV

] = [

” ≡ (0, 2, 1, 2, 2, 3, 0, 1, 10, 8, +T P

, 2, 2),

” ≡ (2, 4, 2, 3, 2, 1, 1, 2, 8, 6, +T P

, 0, 2),

” ≡ (4, 5, 2, 1, 1, 1, 2, 1, 6, 5, −T P

, 1, 1)

” ≡ (5, 7, 1, 1, 0, 0, 1, 0, 5, 3, −T P

, 0, 2)

” ≡ (7, 10, 0, 0, 1, 2, 0, 0, 3, 0, ret, 3, 0)]

Figure 2 displays the re-routing of EV

to ﬁt

T P

. Whereas its top-left (resp. bottom-left) display

the movements before the re-routing for the pick-up

(resp. drop-off), the top-right (resp. bottom-right)

display the movements after the re-routing.

Finally, if a re-routing movement m

or m

serving

t implies a delay of d units, this delay must be sup-

ported by any further movement in the schedule. Idle

movements use their own leeway to reduce d (until

eventually reduce it to 0), and any non further move-

ment serving t

must have a leeway of, at least, the

remaining delay when reaching it.

4.2 Complexity Analysis

An evaluation of the algorithm reveals its complexity

to be, at worst, O(n

), where n is the number of trips,

m the number of vehicles and n > m.

A movement-centric reasoning is used. Given m

vehicles, at the start of the simulation each of them

has a schedule with a single (very large) idle move-

ment (c.f., 4.1.1). From then on-wards, each trip is

attempted to be allocated, by iterating through the ve-

hicles and, for each vehicle, by iterating through its

movements. This means that, in the worst case, ﬁrst

trip will need to explore m × 1 = m movements. If

successful, two new movements will be added to the

schedule of the vehicle allocating it (one for pick-up

and one for drop-off). Thus, after allocating 1 trip, the

overall amount of movements of all vehicles will be

m + 2 (the m movements being there before and the 2

new ones). The same rationale applies over the next

trips attempted to be allocated; for the second trip, a

worst-case scenario of m + 2 movements will be at-

tempted before allocating it, leading to a new overall

amount of m+4 movements, and so on. Given n trips,

this leads to an overall amount of

n−1

∑

n=0

m + 2n

which can be decomposed as

n−1

∑

n=0

m +

n−1

∑

n=0

2n = (nm) +

) − 3n − 2

n > m, the above expression is dominated by the term

, which leads to a worst-case scenario of O(n

5 EVALUATION

Section 5.1 presents a parameterised instance gener-

ator. The parametric generation enables ﬁne-grained

customisation of the instances, which is then used in

sections 5.2 and 5.3 for respectively analysing the per-

formance and scalability of the solution approach de-

ﬁned in Section 4.

Section 5.4 applies the parametric instance gener-

ator to a wider context, in this case customising the

well-known, real-world-based data-set of NYC Taxis

to valid ride-sharing problem-based instances. This

includes a mapping process from the areas and time-

line of the original data-set to the grid dimensions and

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

simulation time horizon required by the ride-sharing

problem deﬁned in Section 3. The newly generated

benchmark is then used in Section 5.5, analysing the

performance of the ride-sharing service from the per-

spective of the amount of distance covered and the

number of vehicles used compared to more classical

taxi-based services or even individual private vehicle

transportation-based systems.

5.1 Parameterisable Instance Generator

Google HashCode (Google HashCode, 2018) is per-

haps the most popular team-based programming com-

petition in the world, with more than 100,000 pro-

grammers participating on each edition. On the quali-

ﬁcation round of 2018, a self-driven-based transporta-

tion system (a variant of the classical Vehicle Rout-

ing Problem with Time Windows) was proposed as a

challenge. Its very-large complex instances make it an

ideal candidate for testing the performance and scala-

bility of the solution approach described in Section 4.

However, although the challenge was also based on a

grid-based city and a simulated time horizon, the fol-

lowing features of the ride-sharing problem of Section

3 were not included in the challenge:

• The model does not include a set S of SECs, nor

an ownership mapping from E to S. Instead, a

single depo at location (0,0) is placed.

• The model does not include dynamic availability

of requests T and resources E over time. Instead,

all vehicles and trip petitions are available (e

and

) at time unit 0.

• The vehicles have unlimited battery capacity e

and room for just one passenger e

• The pick-up and drop-off windows of the trips

contain t

and t

, but not t

l p

nor t

Therefore, all the above must be incorporated

when customising the instances of Google HashCode

to the ride-sharing problem. To enable a ﬁne-grained

customisation allowing the solution approach to be

tested under different conﬁgurations, an instance gen-

erator is implemented, including:

Num SECs. A conﬁgurable integer number of

SECs |S| is created across the city, distributed uni-

formly among its areas. The vehicles E are also dis-

tributed uniformly across S, with each SEC

having a

same amount of vehicles |s

Energy Generation Factor. Let sum dist be the

sum of the distance from pick-up to drop-off loca-

tions for all trips in T . A ﬂoat value is passed to

specify the total energy generated, collectively, by

all SECs as a factor of sum dist. Thus, if factor is

2.0, then total energy = sum dist ∗ 2. A full use of

total energy is assumed, as well as its uniformly dis-

tribution among all SECs and vehicles. Therefore, the

factor ultimately impacts the battery capacity of all

vehicles, setting e

total energy

|E|

Dispatch Mode. A unique energy generation

function f s is assumed to be applied to all SECs, with

a constant energy generation per time unit. A boolean

value is passed to specify such function. If f alse is

passed (let’s call it START ), then all vehicles of a SEC

are released at time unit 0, and f s = 0, producing no

further energy afterwards. Otherwise, if true is passed

(let’s call it SPREAD), a constant energy production

f s =

×|s

is used, releasing a ﬁrst vehicle per SEC

at time unit 0, and each of the remaining |s

| − 1 ve-

hicles at a constant pace across the time horizon, with

one new vehicle each

time units.

Trip Flexibility Factor. As discussed, each trip

petition includes t

and t

, but not t

, t

l p

nor t

. In

the case of t

, it is simply computed as t

+ dist,

where dist is the Manhattan distance from pick-up

to drop-off location. A ﬂoat value between 0 and 1

f lex is passed, representing the ﬂexibility percent-

age for computing t

= t

− (t

∗ f lex) and t

l p

+ ((t

− t

) ∗ f lex). If ﬂexibility factor tends to

1.0 (i.e., 100% ﬂexible), then t

tends to 0 (early an-

nouncement) and t

l p

tends to t

(late pick-up far from

early pick-up). In other words, plenty of time to re-

route vehicles to accommodate the trip. On the other

hand, if the ﬂexibility factor tends towards 0.0 (i.e.,

0% ﬂexible), then both t

and t

l p

tend to t

(with

very little time to react from the announcement of the

trip and a very short time window for its pick-up.)

5.2 Analysis - Performance

The instance d metropolis.in from Google HashCode

is selected for its customisation to the ride-sharing

problem. The instance is very-large, representing

a city of 10,000 x 10,000 distance units, a simula-

tion time horizon of 50,000 time units, 400 vehi-

cles and 10,000 trip petitions. The instance gen-

erator is used for the ﬁne-grained customisation of

d metropolis.in, leading to a new benchmark of 72

instances, coming from the 72 different combinations

of values for NumSECs, EnergyGenerationFactor,

DispatchMode and TripFlexibilityFactor below:

• Num SECs: 1, 4, 16.

• Energy Generation Factor: 0.5, 1.0, 2.0.

• Dispatch Mode: false (START ), true (SPREAD).

• Trip Flexibility Factor: 0.02 (2%), 0.10 (10%),

0.25 (25%), 0.50 (50%).

The 72 instances are run using the solution ap-

proach of Section 4 to evaluate the performance of

A Carbon-Neutral, Community-Based, Reactive and Scalable Ride-Sharing Service

the algorithm (i.e., the number of trip petitions being

allocated to vehicles).

Interestingly, a wide range of results are reported

for the 72 instances, from some successful with up to

8,969 trip petitions allocated (an 89,69% of the peti-

tions) to unsuccessful with 0 trip petitions allocated

(a 0% of the petitions). The set of results is discussed

below, to identify the factors (conﬁgurations) having

a bigger impact in the performance of the algorithm.

The best conﬁguration is the one with < maximum

ﬂexibility, max energy, earlier release of EV > and,

given that the number of SECs might have an impact,

the more SECs the better.

1. (F - 50%; SECs - 16; ST; EF - 2.0) ≡ 89.69%

2. (F - 50%; SECs - 4; ST; EF - 2.0) ≡ 89.55%

3. (F - 50%; SECs - 1; ST; EF - 2.0) ≡ 82.53%

The next 3 top results have the same conﬁguration

as before, but now with energy factor 1.0. Therefore,

it seems that the best conﬁguration is the one with

< maximum ﬂexibility, earlier release of EV>, and

given that, the energy factor does have an impact, with

the more energy the better. After that, once again, the

number of SECs seems irrelevant.

4. (F - 50%; SECs - 1; ST; EF - 1.0) ≡ 77.69%

5. (F - 50%; SECs - 4; ST; EF - 1.0) ≡ 76.95%

6. (F - 50%; SECs - 16; ST; EF - 1.0) ≡ 76.40%

The next 6 results conﬁrm that, among the duo <

maximum ﬂexibility, earlier release of EV>, the ear-

lier release of EVs seems to be the top factor, as all

the 11 top results have START release. But, it can

also be observed the crucial importance of ﬂexibil-

ity, as by reducing it from 50% to 25% the algo-

rithm passes from the previous range of TPs satisﬁed

of [76.40, 89.69] to a reduced performance result of

[49.45, 61.84].

7. (F - 25%; SECs - 1; ST; EF - 1.0) ≡ 61.84%

8. (F - 25%; SECs - 1; ST; EF - 2.0) ≡ 61.67%

9. (F - 25%; SECs - 16; ST; EF - 2.0) ≡ 56.26%

10. (F - 25%; SECs - 4; ST; EF - 2.0) ≡ 55.20%

11. (F - 25%; SECs - 16; ST; EF - 1.0) ≡ 51.19%

12. (F - 25%; SECs - 4; ST; EF - 1.0) ≡ 49.45%

The next 8 results conﬁrm that, among the duo <

maximum ﬂexibility, earlier release of EV>, the ear-

lier release of EVs seems to be the top factor, followed

by the ﬂexibility. If top ﬂexibility is maintained at

50%, but release the EVs over the time horizon, the

decrease in total TPs satisﬁed continues, from the pre-

vious range [49.45, 61.84] to a new one of [41.73,

49.09]. If ﬂexibility decreases again back to 25%,

then the range decreases even a bit more, to 35.57%

of the petitions satisﬁed.

13. (F - 50%; SECs - 16; SP; EF - 2.0) ≡ 49.09%

14. (F - 50%; SECs - 1; SP; EF - 2.0) ≡ 48.82%

15. (F - 50%;SECs - 4; SP; EF - 2.0) ≡ 47.76%

16. (F - 50%; SECs - 4; SP; EF - 1.0) ≡ 45.02%

17. (F - 50%; SECs - 16; SP; EF - 1.0) ≡ 42.06%

18. (F - 50%; SECs - 1; SP; EF - 1.0) ≡ 41.73%

19. (F - 25%; SECs - 1; SP; EF - 2.0) ≡ 35.86%

20. (F - 25%; SECs - 1; SP; EF - 1.0) ≡ 35.57%

The next 16 results show that, all the above analy-

sis state when there is enough energy being produced.

In the case of scarcity of energy, then this turns out to

be the most important factor, as the range of TPs satis-

ﬁed decreases dramatically, to [15.38, 30.31]. That is,

if there is a scarcity of energy, the best conﬁguration

satisﬁes the 30.31% of the TPs. However, when look-

ing only at SPREAD, there is a conﬁguration leading

to 49.09% of TPs satisﬁed. Likewise, when looking

only at ﬂexibility 25%, there is a conﬁguration lead-

ing to 61.84% of TPs satisﬁed.

21. (F - 50%; SECs - 1; ST; EF - 0.5) ≡ 30.31%

22. (F - 25%; SECs - 1; ST; EF - 0.5) ≡ 29.94%

35. (F - 50%; SECs - 16; SP; EF - 0.5) ≡ 17.07%

36. (F - 25%; SECs - 16; SP; EF - 0.5) ≡ 15.38%

The next 24 results show that, all the above analysis

state when there is enough ﬂexibility. If ﬂexibility be-

comes very low, with the TPs having very little mar-

gin (2% or even 10%), then the vast majority of the

TPs cannot be satisﬁed, even with an earlier release

of EV and plenty of energy.

37. (F - 10%; SECs - 4; ST; EF - 0.5) ≡ 12.77%

38. (F - 10%; SECs - 16; ST; EF - 0.5) ≡ 12.61%

39. (F - 10%; SECs - 16; SP; EF - 0.5) ≡ 9.95%

58. (F - 10%; SECs - 4; SP; EF - 1.0) ≡ 4.30%

59. (F - 10%; SECs - 16; SP; EF - 2.0) ≡ 3.93%

60. (F - 2%; SECs - 16; SP; EF - 1.0) ≡ 3.93%

Interestingly, the lack of ﬂexibility can even lead

to 0 TPs satisﬁed. This is the case when there is just

1 SEC, placed in the centre of the city. Irrespective

of the early or spread release of the EVs, a very tight

ﬂexibility in the TPs can make it impossible for an EV

to leave from the centre of the city, and reach both the

pick-up and drop-off in time. This situation does not

happen at all when there are 4 or even 16 SECs, as

this the EV is closer to extreme pick-up or drop-off

points, making it possible to reach to the destination

even with a very tight ﬂexibility.

61. (F - 10%; SECs - 1; ST; EF - 2.0) ≡ 0.06%

72. (F - 2%; SECs - 1; SP; EF - 0.5) ≡ 0.00%

All in all, the analysis above leads to the following

conclusions:

• The most important factor is to have enough ﬂex-

ibility in the TPs (of at least 25%).

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

• This is followed by having enough energy (of at

least 1.0 times the one required to accomplish all

the TPs).

• With enough ﬂexibility and energy, the most rele-

vant factor is to have earlier release of the EVs.

• On top of that, the more ﬂexibility the better (50%

better than 25%).

• If all SECs are uniform in terms of their number

of vehicles and energy production, then the num-

ber of SECs does not have an impact in the results,

except for the extreme cases with very few ﬂexi-

bility and a unique SEC placed in the centre of the

city.

5.3 Analysis - Scalability

The same 72 instances of the benchmark of Section

5.2 (referred to as d 10000 400 due to its 10,000 trip

petitions and 400 vehicles) are considered again to

evaluate the scalability of the algorithm. Also, smaller

versions by factor f of such benchmark are achieved

by simply removing

trips and vehicles from the in-

stances of the original d 10000 400. Table 1 shows

the total running time (resp. average running time per

instance) in seconds as the size of the instances scale

from 1,000 trips and 40 vehicles to 10,000 trips and

400 vehicles. Benchmarks have been run in a Mac

OS Ventura, Intel i7 Quad Core 2.3Ghz processor and

16GB RAM memory. The algorithm has been imple-

mented in Python and run with Python 3.10.5.

The results conﬁrm the scalability of the solution

approach of Section 4, as it is able to solve very large

instances (as the ones of d 10000 400) in less than 2

minutes. Together with the previous ones of Section

5.2, it is concluded that the algorithm provides both

good performance and scalability.

5.4 NYC Taxi Instances

The data-set (NYC Green Taxi data, 2018) covers the

entire ﬂeet of taxi operators in NYC and comprises a

total of 1,048,575 trips. The records include ﬁelds to

capture pick-up and drop-off dates/times, pick-up and

drop-off locations and trip distances. The data used

were collected and provided by the NYC Taxi and

Table 1: Scalability of the Algorithm.

Benchmark Total Time Avg. Time

d 40 1000 40.82 0.54

d 100 2500 221.29 2.91

d 200 5000 933.2 12.28

d 400 10000 9038.0 118.92

Limousine commission by technology providers au-

thorised under the Taxi cab and Livery management

enhancements program. The NYC taxi data models

a wide array of attributes such as tip amount, pay-

ment type, and fare amount. However, for the exper-

iments conducted, the attributes considered are men-

tioned in Table 2.

The ride-sharing service allows various vital pa-

rameters to be dynamically adjusted, as presented in

Section 5.1. On top of the conﬁguration described

then, the customisation of the NYC taxis uses a ﬁxed

battery capacity per vehicle, and then allows to pa-

rameterise the total amount of vehicles as a factor of

such battery capacity and the total energy being pro-

duced.

5.4.1 Grid-Generation

A grid-based mapping approach is used. This ap-

proach signiﬁcantly decreases the time required to

analyse data compared to a spatial resolution of near-

continuous coverage data (Ramsdale et al., 2017).

Grid-based mapping provides a consistent and stan-

dardised approach to spatial data collection. A grid

map is a set of cells where the users can customise

their geometries, and visual representations (Ferreira

et al., 2013). An example of a grid map of taxi zones

in NYC is shown in Figure 3. To divide the spatial

polygon of the NYC map with 262 taxi zones (NYC

Taxi Zones, 2023) into a grid, Quantum Geospatial

Information System(QGIS) is used. The OGC coor-

dinate reference system (OGC: EPSG7326-WGS84),

proposed in the world geodetic system 1984 ensem-

ble (EPSG:7326), is used to form the grids. The

average trip distance from the NYC taxi data set

is 2.7 miles, with the shortest trip being 0.2 miles.

Therefore, the horizontal and vertical spacing is set

at 0.01 miles, and a ‘420X556’ grid map is gener-

ated. A GeoJSON ﬁle is generated for the grid lay-

out of the NYC map. The instance generator com-

putes the pick-up and drop-off locations of passengers

based on the ‘PULocationID’, the ‘DOLocationID’

and trip distance of the passengers from Table 2.

Table 2: NYC Attributes.

Attribute Eg.Value

!pep pickup datetime 01/01/2018 12:18:50 AM

!pep dropoff datetime 01/01/2018 12:24:39 AM

PULocationID 236

DOLocationID 236

trip distance 0.7

A Carbon-Neutral, Community-Based, Reactive and Scalable Ride-Sharing Service

Figure 3: Taxi zones in Bronx, New York (NYC Green Taxi

data, 2018).

5.5 Analysis - Ride-Sharing Vehicles

and Distance Traversed

Interestingly, when running a large-scale instance for

the NYC taxis, the best conﬁguration turns out to be

the very same one as reported in Section 5.2. This

conﬁrms the conﬁguration observations reported then,

in this case observed when applying the ride-sharing

service over a real-world data-set:

(F − 50%; SECs − 16; ST ; EF − 2.0)

This time, the experiments are focused on analysing

the performance of the ride-sharing service when

compared to both a more classical taxi-based service

and to an individual, private vehicle transportation-

based service. In this case, both the amount of dis-

tance covered and the number of vehicles used are

analysed.

• Taxi Mode: In this mode, EVs aim to pick-up

and drop-off passengers sequentially, as opposed

to the ride-sharing mode, where several passen-

gers might, temporarily, share a vehicle during

their trips.

• Individual Mode: This mode represents a private

mode of transportation. Each passenger uses a

privately owned EV to commute from the pick-up

to the drop-off point.

The overhead of both taxi and ride-sharing modes

w.r.t. individual mode is for the extra distance tra-

versed by the EV from the drop-off point to the pick-

up point of subsequent requests. Whereas in ride-

sharing mode the possibility of having multiple pas-

sengers sharing the vehicle might reduce this extra

distance, in the case of the taxi mode the extra dis-

tance becomes non-avoidable.

Table 3 shows the results when running a large

instance with thousands of trip petitions. The ride-

sharing service is conﬁgured to use 704 vehicles, and

it manages to serve 4,514 trip petitions. When com-

pared to individual mode, the use of the ride-sharing

Table 3: Ride-share vs Taxi vs Individual.

Mode Vehicles Distance(miles)

Ride-share 704 70360

Taxi 718 71164

Individual 4514 57909

service would have allowed to put 4,514 - 704 = 3,810

vehicles out of the road, a reduction of an 84.4%.

The algorithm is then re-run for taxi mode. This

time it is set to contain: only the 4,514 petitions that

were served above; an unlimited amount of vehicles

(to ensure that all 4,514 trip petitions are indeed sat-

isﬁed); and a single passenger capacity on each vehi-

cle (to ensure that no two trip petitions might share

a vehicle while being served). The focus is now on

the actual number of vehicles used by the algorithm,

which turns out to be slightly higher than before (718,

an increase of 1.9% w.r.t. ride-sharing mode).

In terms of the overall distance traversed, the ride-

sharing mode has an overhead of 70,360 - 57,909 =

12,451 extra miles, representing an increase of 21.5%

in the distance on the individual mode. In the case

of taxi-mode, this increase is even higher, conﬁrming

the beneﬁts of the ride-sharing mode vs. the taxi sim-

ulation also.

6 CONCLUSIONS AND FUTURE

WORK

This paper has presented the design, implementation

and evaluation of a carbon-neutral, community-based,

reactive ride-sharing service for a Smart City with a

100% EVs operating solely over RES.

The ride-sharing service has been formulated as

a variant of the classical Dynamic Vehicle Routing

Problem with Time Windows, with both dynamic re-

sources and requests. The objective function has

been set to maximise the overall number of trip pe-

titions being served. The problem has been solved

via a reactive-based simulation approach on top of a

greedy-based decision-making process.

An instance generator has been developed to cre-

ate conﬁgurable scenarios to evaluate the proposed

approach. It was used to extend existing existing

benchmarks (Google HashCode) and public datasets

(NYC taxis) to the problem formulation and testing

the proposed algorithm under different settings.

The ride-sharing service has proven to scale well,

with a quadratic algorithm complexity over its num-

ber of trips, allowing to solve an instance of about

1,000 trips in less than a second, and an instance of

about 10,000 trips in less than two minutes. Although

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

favouring scalability over optimality, the service has

proven to be able to solve up to 90% of the in-

stances for some conﬁgurations of d metropolis.in, a

complex instance from the Google HashCode. When

applied to the real-world data-set of the NYC taxis

and compared to an individual private transportation,

the ride-sharing approach has been proven to offer

a good trade-off between the amount of vehicles re-

duced (84%) and its overhead in terms of distance tra-

versed (21%). The complete code can be accessed via

GitHub (Nagarajan, 2023).

Future work will include the analysis of the ride-

sharing service under diversity on its SECs speciﬁ-

cation, i.e., diversity in the number of vehicles and

energy produced by each SEC. Coupled with the as-

sociation of each trip petition to a given SEC, this will

allow to evaluate the ride-sharing service under unbal-

anced resources and requests for different SECs. Re-

search will then investigate the possibility of trading

services among SECs, ultimately exploring a decen-

tralised solution approach where each SEC competes

for serving a trip petition. This decentralised setting

will be explored in both reactive and proactive modes,

simulating that all trips were known beforehand. Fi-

nally, it is intended to integrate the ride-sharing ser-

vice as part of an existing simulation-tool, as Sumo

(Alazzawi et al., 2018).

ACKNOWLEDGEMENTS

This research work is supported by Science Foun-

dation Ireland Centre for Research Training focused

on Future Networks and the Internet of Things (Ad-

vanceCRT), under Grant number 18/CRT/6222.

REFERENCES

Agatz, N. A. H., Erera, A. L., Savelsbergh, M. W. P., and

Wang, X. (2012). Optimization for dynamic ride-

sharing: A review. Eur. J. Oper. Res., 223(2):295–303.

Al-Abbasi, A. O., Ghosh, A., and Aggarwal, V. (2019).

Deeppool: Distributed model-free algorithm for ride-

sharing using deep reinforcement learning. IEEE

Trans. Intell. Transp. Syst., 20(12):4714–4727.

Alazzawi, S., Hummel, M., Kordt, P., Sickenberger, T.,

Wieseotte, C., and Wohak, O. (2018). Simulating the

impact of shared, autonomous vehicles on urban mo-

bility – a case study of milan. In SUMO’18, volume 2

of EPiC Series in Engineering , pages 94–110. Easy-

Chair.

Diamantoulakis, P. D., Kapinas, V. M., and Karagiannidis,

G. K. (2015). Big data analytics for dynamic energy

management in smart grids. Big Data Res., 2(3):94–

101.

EU Green Deal (2020). https://ec.europa.eu/info/strategy/

priorities-2019-2024/european-green-deal en.

Ferreira, N., Poco, J., Vo, H. T., Freire, J., and Silva, C. T.

(2013). Visual exploration of big spatio-temporal ur-

ban data: A study of new york city taxi trips. IEEE

Trans. Vis. Comput. Graph., 19(12):2149–2158.

Furuhata, M., Dessouky, M., Ord

nez, F., Brunet, M.-E.,

Wang, X., and Koenig, S. (2013). Ridesharing: The

state-of-the-art and future directions. Transportation

Research Part B: Methodological, 57:28–46.

Google HashCode (2018). https://codingcompetitions.

withgoogle.com/hashcode/archive/2018.

Hasan, M. H. and Hentenryck, P. V. (2020). The ﬂexible and

real-time commute trip sharing problems. Constraints

An Int. J., 25(3-4):160–179.

Hasan, M. H., Hentenryck, P. V., Budak, C., Chen, J., and

Chaudhry, C. (2018). Community-based trip sharing

for urban commuting. In AAAI’18, pages 6589–6597.

AAAI Press.

Jaillet, P. and Wagner, M. (2008). Online Vehicle Routing

Problems: A Survey, volume 43, pages 221–237.

Nagarajan, A. (2023). https://github.com/Nasheor/reactive

rideshare.git.

NYC Green Taxi data (2018). https://data.cityofnewyork.

us/Transportation/2018-Green-Taxi-Trip-Data/

w7fs-fd9i.

NYC Taxi Zones (2023). https://data.cityofnewyork.us/

Transportation/NYC-Taxi-Zones/d3c5-ddgc.

Ramsdale, J., Balme, M., Conway, S., Gallagher, C., Gas-

selt, S., Hauber, E., Orgel, C., S

ejourn

e, A., Skin-

ner Jr, J., Costard, F., Johnsson, A., Losiak, A., Reiss,

D., Swirad, Z., Kereszturi, A., Smith, I., and Platz, T.

(2017). Grid-based mapping: A method for rapidly

determining the spatial distributions of small features

over very large areas. Planetary and Space Science,

140.

Serra, T., Raghunathan, A. U., Bergman, D., Hooker, J. N.,

and Kobori, S. (2019). Last-mile scheduling under

uncertainty. In CPAIOR’19. LNCS 11494, Springer.

Xiang, Y., Liu, J., Li, R., Li, F., Gu, C., and Tang, S. (2016).

Economic planning of electric vehicle charging sta-

tions considering trafﬁc constraints and load proﬁle

templates. Applied Energy, 178:647–659.

A Carbon-Neutral, Community-Based, Reactive and Scalable Ride-Sharing Service