Towards a Transition Matrix-Based Concept Drift Approach:

Experiments on the Detection Task

Antonio Carlos Meira Neto, Rafael Gaspar de Sousa, Marcelo Fantinato and Sarajane Marques Peres

School of Arts, Science and Humanities, University of S

ao Paulo, S

ao Paulo, Brazil

Keywords:

Concept Drift, Process Mining, Transition Matrix, Event Log, Process Drift, Data Mining.

Abstract:

Contemporary process mining techniques commonly assume business processes are in a steady state. How-

ever, business processes are prone to change and evolution in response to various factors, which can happen

at any time, in a planned or unplanned way. This phenomenon of business process evolution and change is

known as concept drift, and identifying and understanding is of paramount relevance for business process

management, so that organizations can respond and adapt to the new challenges they face. The goal of this

paper is to introduce the use of transformed transition matrices as a data structure to support the treatment

of concept drifts in process mining, given its efﬁciency, simplicity, and expandability. The proposed data

structure allows to handle different concept drift aspects in an integrated way. Three concept drift detection

methods are ﬁrst adapted to work on transformed transition matrices. The results obtained in the experiments

are compared with a state-of-the-art method (baseline), and the three methods used achieved good results,

showing an encouraging potential for future planned work.

1 INTRODUCTION

Business processes are prone to continuous, unex-

pected changes in response to many factors, including

changes in the competitive environment, regulations,

supply, demand, and technology resources, as well as

seasonal factors (Maaradji et al., 2015). This is an in-

herent characteristic of the business, which can hap-

pen at any time and whether planned or not. Changes

impact the dynamics of operations and affect business

process performance (Ostovar et al., 2016). Conse-

quently, the changes impact the process mining anal-

yses, especially the quality of the process model dis-

covered based on the event log (Sato et al., 2021).

This phenomenon of change in business process

behavior over time is called concept drift (or process

drift). Concept drift refers to when the business pro-

cess changes during analysis (van der Aalst and et al.,

2012) or, more speciﬁcally, when there is a statis-

tically signiﬁcant difference in the business process

behavior (Maaradji et al., 2015). Nonetheless, con-

temporary process mining techniques assume busi-

ness processes are in steady state (Sato et al., 2021).

E.g., when discovering a process model from an event

log, the business process at the beginning of the event

logged period is assumed to be the same as the one

at the end of the event logged period. Identifying and

understanding concept drift is of paramount impor-

tance in business process management, so that organi-

zations can respond and adapt to the associated chal-

lenges (Bose et al., 2014).

Process mining has supported organizations to

handle business processes in descriptive, predictive,

and prescriptive ways. As summarized by de Sousa

et al. (2021), following van der Aalst (2014, 2016)’s

deﬁnitions, process mining relies primarily on the

concepts of event, case, trace, log, and attribute. An

event is the occurrence of a business process activity

at a given time, performed by a given resource, at a

given cost. A case corresponds to a process instance

and comprises events such that each event relates ex-

actly to a case. A trace is a mandatory attribute of

a case and corresponds to a ﬁnite sequence of events

such that each event appears only once. An event log

is a set of cases such that each event appears only

once in the entire event log. Each event in the event

log comprises a set of non-mandatory attributes such

as identiﬁer, timestamp, activity, resource, and cost.

Cases can also have non-mandatory attributes, often

related to domain-speciﬁc data.

To deal with concept drift in process mining, the

following aspects (or dimensions) should be consid-

ered (Sato et al., 2021): tasks (detection, localization,

characterization, and explanation), types of change

Neto, A., Gaspar de Sousa, R., Fantinato, M. and Peres, S.

Towards a Transition Matrix-Based Concept Drift Approach: Experiments on the Detection Task.

DOI: 10.5220/0011843600003467

In Proceedings of the 25th International Conference on Enterprise Information Systems (ICEIS 2023) - Volume 2, pages 361-372

ISBN: 978-989-758-648-4; ISSN: 2184-4992

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

361

(sudden, gradual, recurring, and incremental), pro-

cess perspectives (control-ﬂow, time, resource, and

data), and data scenario (online and ofﬂine). For a

complete, end-to-end analysis of the concept drift, a

holistic view is required that fully considers all as-

pects (Manoj Kumar et al., 2015).

Success in dealing with a wide range of differ-

ent aspects of concept drift in process mining may

rely on the features (Maaradji et al., 2015) and hence

the data structure used. Data structure is the format

used to store, represent, organize, and manage data

extracted from event logs, such as vector, list, matrix,

tree, graph, etc. Features refer to values represented

in these data structures, such as event frequency, av-

erage time, total of a resource, etc. Data structure and

features are the means to represent the business pro-

cess behavior (called here process representation) and

hence are crucial to identify and understand concept

drifts. However, most studies have addressed in a very

limited way the different aspects of concept drifts.

The main goal of this paper is to introduce a com-

prehensive concept drift approach for process mining

based on a transformed transition matrix as a single,

simple, effective, and expandable data structure. The

transformed transition matrix allows the proposed ap-

proach to be potentially used to fully deal with all

concept drift aspects in process mining. In this pa-

per, we ﬁrst show the good results of the proposed ap-

proach for the task of detecting sudden changes from

the control-ﬂow perspective for an ofﬂine scenario.

The remainder of this paper is organized as fol-

lows. Section 2 discusses related work on concept

drift in process mining. Section 3 details the proposed

approach. Section 4 reports the undertaken experi-

ments. Finally, section 5 concludes the paper.

2 RELATED WORK

Table 1 summarizes the representations used in re-

lated work, as well as the concept drift aspects cov-

erage. Some works are put together as they are pub-

lished as an evolution or addition of a single approach.

Several types of representations (data structures

and features) have been proposed, each with beneﬁts

and drawbacks depending on its purpose. The repre-

sentation choice should consider which aspects’ items

are addressed. E.g., if the approach aims to handle

only the detection task, the chosen data representa-

tion may not be suitable for handling other tasks. On

the other hand, different data representations speciﬁc

for each aspect item (e.g., one for detection and an-

other for localization) may result in a complex, non-

integrated solution, making a holistic analysis difﬁ-

cult or even impossible (de Sousa et al., 2021).

Moreover, if the features that can capture a pro-

cess change cannot be expressed in the chosen data

structure, then such a change cannot be identiﬁed, re-

gardless of the detection method used. In addition,

each representation may be different in terms of, e.g.,

processing cost to transform raw data into the chosen

representation, supportability for each item of the dif-

ferent aspects of concept drift (i.e., tasks, types, pro-

cess perspectives, and data scenario), and supporta-

bility for user interpretation of data. Thus, the choice

of representation used by the concept drift approach

is of paramount relevance.

Per Table 1, of the few works addressing several

aspects’ items, Yeshchenko et al. (2021) stands out for

its larger coverage as it addresses three tasks and all

types of change. However, only the control-ﬂow per-

spective in the ofﬂine scenario is handled. In addition,

their experiments are not clearly reported (Sato et al.,

2021). They compare their method effectiveness with

Ostovar et al. (2016)’s, but without using the same

full set of public synthetic event logs made available

and without deﬁning the F-score calculation. Cer-

avolo et al. (2022) compare several concept drift de-

tection methods and cite Yeshchenko et al. (2021)’s

study with the worst effectiveness and efﬁciency re-

sults when increasing the size of event logs due to the

many pre-processing steps before the detection task.

Adams et al. (2021) also present great coverage,

addressing two tasks and all perspectives. However,

only the sudden type in the ofﬂine scenario is handled.

Moreover, the data representation comprises disjoint

features (i.e., not necessarily extracted using a sin-

gle data structure) and transformed into time series.

An approach expansion to handle the other two tasks,

which need more data detail, might be unfeasible.

The studies presented by Maaradji et al. (2015,

2017) and Ostovar et al. (2016, 2017, 2020) are

considered state-of-the-art due to their effectiveness,

although featuring low coverage of aspects’ items.

Maaradji et al. (2015, 2017) address one task, one per-

spective, and two types, only in the ofﬂine scenario,

while Ostovar et al. (2016, 2017, 2020) address three

tasks, one perspective, and one type, in the online sce-

nario. Data representations of both studies are spe-

ciﬁc to the control-ﬂow perspective (i.e., Alpha con-

currency and frequency of Alpha plus relations).

As for our approach, it is designed to be used for

all aspects’ items, as it is based on a data structure

that centralizes the data used, allowing full integra-

tion. However, in this ﬁrst paper, only one item per

aspect is being tested. Moreover, the approach does

not use any costly pre-processing and the data struc-

ture is simple and efﬁcient.

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

362

Table 1: Comparison of related work.

Work Representation Task Perspective Type Scenario

Bose et al. (2011, 2014); Martju-

shev et al. (2015)

Relation type count, relation entropy, local window

count, J-measure

D, L C S, G Off

Weber et al. (2011) Probabilistic deterministic ﬁnite automata, Alpha

relations

D C S On*

Luengo and Sep

ulveda (2012) Maximal repeat (a special substring in a sequence),

trace starting time

D C G Off

Accorsi and Stocker (2012) Distance between pair of activities D, L C S Off

Carmona and Gavald

a (2012) Trace as Parikh vectors D C S On*

Manoj Kumar et al. (2015) Event class correlation D C S Off

Hompes et al. (2015, 2017) Stochastic similarity matrix between cases D C, D S Off

Maaradji et al. (2015, 2017) Alpha concurrency (runs) D C S, G Off

Ostovar et al. (2016, 2017, 2020) Frequency of Alpha plus relations, Process tree model D, L, C C S On

Seeliger et al. (2017) Graph metrics from Heuristic miner D, L C S Off

Zheng et al. (2017) Directly-follows and weak order relations D C S Off

Richter and Seidl (2017) Time interval between activities D, L T S, I, R On

Barbon Junior et al. (2018);

Tavares et al. (2019)

Frequency of activities, Graph-distance (trace and

time)

D C, D S, G On

Liu et al. (2018) Alpha relations matrix, Process model D, L, C C S, G, I, R On*

Stertz and Rinderle-Ma (2018) Process model D, C C S, G, I, R On

Pauwels and Calders (2019) Extended dynamic Bayesian network D C, D, R N/D Off

Hassani (2019) Directly-follows relations D C S On

Kurniati et al. (2019, 2020) Metrics of process model, trace and activity levels D C N/D Off

Yeshchenko et al. (2019a,b,

2020, 2021)

DECLARE constraints conﬁdence D, L, C C S, G, I, R Off

Brockhoff et al. (2020) Trace and time as stochastic languages D C, D S Off

Impedovo et al. (2020) Dynamic networks D, L C S Off

Adams et al. (2021) Several measures extracted over time D, E C, T, D, R S Off

Lu et al. (2021b) Directly-follows relations D, L C S Off

Lu et al. (2021a) Exclusive choice splits from process model D, L C S Off

de Sousa et al. (2021) Activity and transitions trace vector proﬁle D, L C S On*

Lin et al. (2022) Directly-follows relations D C S Off

Our approach Transition features in transformed transition matrix All (D) All (C) All (S) All (Off)

Legend: Task (Detection, Localization, Characterization, and Explanation); Perspective (Control-ﬂow, Time, Data, and Resources);

Type (Sudden, Gradual, Incremental, and Recurring); Scenario (Offline and Online).

* Online methods that work with trace stream instead of event stream.

N/D: when the aspect item is not speciﬁed by the study.

3 PROPOSED APPROACH

The proposed approach is organized as a sequence of

integrated steps (illustrated in Figure 1). The ﬁrst step

refers to receiving the event log, which can be batch,

for the ofﬂine scenario, or stream, for the online sce-

nario. The second refers to applying a windowing

strategy, where the event log is split into samples over

time (windows). The third refers to instantiating the

proposed data structure (i.e., a transition matrix) for

each window, containing all the necessary informa-

tion to represent the process (i.e., process features),

considering the different perspectives (control-ﬂow,

time, resources, or data). The fourth refers to compar-

ing the windows over time, obtaining information that

can represent the change over time (change features).

The ﬁfth refers to detecting the existence of change in

a given window. The detection method with the win-

dowing strategy impacts the types of change (sudden,

gradual, recurring, and incremental) which can be de-

tected. Finally, the sixth refers to executing the other

tasks (i.e., localization, characterization, and explana-

tion) that allow a better understanding of the detected

drift, which are not explored herein.

The approach is proposed as a conceptual frame-

work based on the transition matrix. The other com-

ponents are ﬂexible, i.e., different methods are eligi-

ble for the windowing strategy and detection, local-

ization, characterization, and explanation tasks. Also,

different features can be chosen for extraction from

both the event log (process features) and the compar-

ison between windows (change features).

The approach’s components are described below,

emphasizing the data structure and detection method.

Towards a Transition Matrix-Based Concept Drift Approach: Experiments on the Detection Task

363

Figure 1: Overview of the proposed approach steps.

3.1 Windowing Strategy

Windowing strategies serve to sample data over time,

i.e., to create data windows for analysis. These win-

dows act as a picture of the data at different points in

time. Each windowing strategy perform this sampling

in a speciﬁc way. There are typically two windows,

the reference window and the detection window. At

each iteration, the data in these two windows are com-

pared with each other aiming to detect concept drifts.

Some characteristics and parameters that differ

among the windowing strategies are: window size for

ﬁxed-size windows, minimum and maximum window

size for adaptive-size windows, ﬁxed or sliding refer-

ence window, windows with or without overlapping

slides and with or without continuous slides, slide

size for windows with overlapping slides, and gap

size for windows with non-continuous slides. Osto-

var et al. (2016), e.g., used a non-overlapping, con-

tinuous, adaptive-size, and sliding reference window.

Each windowing strategy has strengths and weak-

nesses, depending on the speciﬁc purpose of use (Lu

et al., 2019; Gemaque et al., 2020; Sato et al., 2021).

Some strategies combine two or more basic window-

ing strategies in order to complement the results.

The choice of the windowing strategy, as well as

the choice of values for its parameters, is crucial when

using the proposed approach, as this choice reﬂects on

the effectiveness and delay in detecting concept drifts.

Furthermore, certain windowing strategies may allow

all or only some of the types (sudden, gradual, recur-

ring, and incremental) to be detected.

3.2 Process Representation

The execution of the different concept drift tasks (i.e.,

detection, localization, characterization, and explana-

tion) is based on features describing the process be-

havior over time. Thus, features showing what is hap-

pening in the process over time need to be extracted

from event logs as part of the proposed approach. Ex-

amples of such features are activity frequency, tran-

sition average time, total of a resource, etc. Each

feature represents a process perspective (control-ﬂow,

time, resources, and data). However, a given feature

does not necessarily allows to fully represent a pro-

cess perspective. E.g., the feature number of process

activities allows to represent changes that add or re-

move activities to/from the process, but it does not

allow to represent any change in activity transitions.

As a result, to provide a full representation of a given

process perspective, a set of features that complement

each other may be required. Moreover, the choice of

feature (or set of features) to be extracted is crucial

when using the proposed approach in order to iden-

tify the desired perspectives. These features extracted

in this step are named process features.

Process feature values must be represented in a

data structure. We introduce here transition matri-

ces for this purpose. First, the values of each chosen

process feature are extracted as a transition matrix.

Then all transition matrices are combined into a single

transformed transition matrix containing all process

features. A transition matrix is a granular structure,

as it stores data in a high level of detail, i.e., transi-

tions between activities according to the event log

A transition matrix is a square matrix, containing

n rows and n columns, where n is the number of pro-

cess activities. Each value in a transition matrix repre-

sents some process feature value that refers to a transi-

tion between two activities according to the event log,

This matrix would more correctly be called directly-

follows relation matrix rather than transition matrix, as one

activity directly followed by another in an event trace does

not necessarily represent a transition in a process (van der

Aalst, 2016). However, for simplicity, as done by de Sousa

et al. (2021), we kept the nomenclature used by previous

authors (Song et al., 2009; Appice and Malerba, 2016).

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

364

i.e., a transition from an activity represented by a row

in the matrix to an activity represented by a column

in the matrix. E.g., a transition matrix can contain

the values for the process feature transition frequency

that occurred between activity n

and activity n

. This

process feature value can refer to data extracted di-

rectly from the event log (e.g., frequencies) or derived

data calculated from data in the event log (e.g., infor-

mation derived from Alpha relations). Figure 2 illus-

trates how transition matrices are created. From an

event log, four transition matrices are created, repre-

senting four process features from a process perspec-

tive, namely: the transition probability (probability

column) and the transition frequency (frequency col-

umn) from control-ﬂow perspective; the average tran-

sition time (average time column) and the transition

time variance (time variance column) from time per-

spective; among all activities in the event log.

As stated earlier, the proposal consists of extract-

ing each process feature chosen to be used in the ap-

proach, as a transition matrix, and in the end com-

bining them into a single transformed transition ma-

trix, containing all process features. The transforma-

tion of the transition matrices is a way of represent-

ing the same information but arranged in a different

format. This new format has two columns with the

transition matrix indices (the transition activities) and

a single column containing the process feature infor-

mation (probability, frequency, etc.).

Figure 2 also illustrates how occurs the transfor-

mation of a set of transition matrices into a single

transformed transition matrix (a snippet of the trans-

formed transition matrix is shown). A transformed

transition matrix is a n

× (2 + m) matrix, where n

is the number of activities in the process and m is

the number of input transition matrices which in turn

refers to the number of extracted features. Each of

the columns refers to: (column 1) the row index of

the input transition matrix representing the transition

source activity, (column 2) the column index of the

input transition matrix representing the transition tar-

get activity, and (columns 3...2 + m) the feature val-

ues at those two indices that represent the transition in

the input transition matrices. In the example of Fig-

ure 2(c), the following features are extracted: transi-

tion probability, transition frequency, average transi-

tion time, and transition time variance.

This single data structure is designed to contain

data with such a high level of detail it allows to han-

dle all four tasks of concept drift (i.e., detection, lo-

calization, characterization, and explanation). Also,

the transition matrix is a simple data structure that al-

lows efﬁcient storage and update operations, which

makes its use feasible in the online scenario, as it can

be updated with each new event at low cost.

Extracting features from the event log can be as

simple as counting the transitions from one activity to

another in the window, or more complex operations

such as getting the type of relationship between two

activities in a transition according to the Alpha algo-

rithm. The more features are extracted, the more pro-

cess perspectives related to concept drift can be ana-

lyzed. On the other hand, more operations should be

performed to process the data and the data structure,

which can impact the approach execution time.

The extracted features must always be represented

by numerical values. Categorical features (such as Al-

pha algorithm’s relationship types of each transition)

must be transformed into indicator variables (binary

or frequency). For features associated with individ-

ual activities rather than activity transitions, such as

the role of who performed the activity, the features

associated with each of the two activities part of the

transition must be concatenated, generating v

indica-

tor variables, where v is the number of distinct values

in the window. For the role feature example, an in-

dicator variable could be analyst-manager, making it

possible to count transitions from activities performed

by an analyst to activities performed by a manager.

3.3 Change Representation

We assume the transformed transition matrix can rep-

resent changes in the process over time. Thus, for two

windows representing two moments between which

there is a concept drift, when comparing the trans-

formed transition matrices for both windows, signiﬁ-

cant differences can be observed in the values of one

or more process features represented in such matrices.

Figure 3 exempliﬁes the comparison of trans-

formed transition matrices from different periods be-

tween which there is a concept drift in the control-

ﬂow. Two process models are shown at the top of the

ﬁgure: the one on the left represents a process that

occurs before t

(moment in time when a concept drift

occurs) and the one on the right represents the pro-

cess that occurs after t

. The respective transformed

transition matrices generated from the event log for

each of the two processes are shown at the bottom

of the ﬁgure, where different values can be observed

for the activity transitions where the concept drift oc-

curs (highlighted with a red rectangle). Regardless of

the windowing strategy used, each window is com-

pared with some other window over time, which are

called reference and detection windows, respectively.

For each comparison, features (change features) can

be extracted based on the process features differences

(or changes) between the transformed transition ma-

Towards a Transition Matrix-Based Concept Drift Approach: Experiments on the Detection Task

365

Figure 2: Illustrative example of creating a set of transition matrices from a event log and combining them into a single

transformed transition matrix snippet.

trix from the reference window and the transformed

transition matrix from the detection window, e.g., fre-

quency difference. The way of extracting, storing and

using the change features depends on the technique

used in the concept drift tasks step.

3.4 Concept Drift Detection Task

Our approach is designed to allow different concept

drift detection methods to be used in the detection

task. We describe below three strategies that are

adapted for this purpose, namely: time series strategy,

statistical test strategy, and threshold strategy.

3.4.1 Time Series Strategy

At the change representation step, change features can

be extracted in multivariate time series format, such as

the total transition frequency difference between win-

dows over time. Features like multivariate time series

can be used as input to time series techniques special-

ized in concept drift detection. Such techniques are

focused on a more complete analysis of temporal fea-

tures, which represent a relevant combination for the

concept drift detection task. We prioritized the time

series techniques known as change point detection,

mainly because such techniques have been used and

considered effective by state-of-the-art studies in pro-

cess mining (Yeshchenko et al., 2021; Adams et al.,

2021). Change point detection aims to estimate the

point at which the statistical properties of a sequence

of observations change (Truong et al., 2020).

To transform window comparisons into multivari-

ate time series, the absolute difference between the

windows must be calculated through a modulus sub-

traction (|x − y|) for each process feature and activity

transition. In the sequence, the total difference of each

change feature can be obtained and then concatenated

with the totals of the other comparisons.

3.4.2 Statistical Test Strategy

Change features can also be calculated as a result of

hypothesis testing on a given feature of both windows

being compared. Hypothesis testing results over time

can be used to identify when different windows show

statistically signiﬁcant differences.

In Figure 3, the chi-square test can be applied to

test the independence of the two samples using the

frequency variable. In this hypothesis testing, the

null hypothesis is “there is no signiﬁcant difference

between the distributions”, while the alternative hy-

pothesis is “there is a signiﬁcant difference between

the distributions”. The result of the hypothesis test is

the p-value, or probability of signiﬁcance. A p-value

greater than a chosen threshold, usually 0.01 or 0.05,

means the null hypothesis cannot be rejected. A p-

value less than or equal to the threshold means the null

hypothesis can be rejected, thus assuming the samples

are different, i.e., the event log data come from differ-

ent processes, conﬁguring a concept drift.

Pre-processing may be required depending on the

type of hypothesis test used to ensure the conditions

and assumptions of the test. By the example above,

the two samples from each window need to be com-

bined in a pairwise way into a contingency matrix, in

the format 2×d, where d is the number of distinct ac-

tivity transitions with frequency greater than 0 in any

of the windows. Moreover, for some types of hypoth-

esis testing, the windowing strategy should result in

windows of the same or similar amount of transitions.

3.4.3 Threshold Strategy

The change features can be seen as simple metrics,

i.e., a quantiﬁable measure of behavior observed.

Thus, one can use a metric threshold to trigger a pos-

sible concept drift when the threshold is crossed.

There are many ways to set a threshold value, e.g.,

if the difference of a change feature is greater than a

ﬁxed value x at any time, or if the value of a change

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

366

Figure 3: Illustrative comparison of transformed transition matrices.

feature increases by at least y% at time i compared to

time i-1. These values often rely on prior knowledge

of the operating environment. At the change repre-

sentation step, interpretable features can be obtained,

such as the total differences of transition frequencies

over time, which can help a process manager to deﬁne

a threshold based on the business risk appetite.

4 EXPERIMENTS

In this ﬁrst experiment, only the concept drift detec-

tion task is evaluated as our ﬁrst goal to evaluate the

proposed approach. In addition, the following as-

pects’ items are considered: sudden changes from the

control-ﬂow perspective for an ofﬂine scenario.

4.1 Planning and Setup

Each of the steps of the proposed approach, as de-

scribed in Section 3 (and summarized in Figure 1) are

addressed. Figure 4 summarizes the decisions made

including the choice of windowing strategy, process

and change features, and concept drift detection meth-

ods. The solution is coded in Python.

A set of public synthetic event logs called Busi-

ness Process Drift, created by Maaradji et al. (2015),

is used as input. This dataset has been used in several

other studies on this subject in the literature. As done

by Maaradji et al. (2015), event logs with 2,500 events

are not considered in the experiments, given the short

distance between the concept drifts and the window

size tested (about 250 traces or 2,500 transitions), not

allowing stability between the concept drifts.

As for the windowing strategy, the following def-

initions are chosen: the windows have a ﬁxed size of

4,000 transitions each; the reference window is ﬁxed

as the ﬁrst window of the event log; the detection win-

dows follow a sliding strategy, with overlap and in a

continuous way; the size of the sliding is 200 transi-

tions, where for each window is added this number of

newer transitions and the same number of the older

transitions is deleted.

As the data structure (transformed transition ma-

trix) has a high granularity, being process transitions,

it is expected detection strategies need a large number

of samples to represent the process and its changes.

Therefore, as the goal is to test whether the strategies

can have good effectiveness, a window size of 4,000

transactions and a sliding of 200 transitions was cho-

sen for the experiment to use the largest possible win-

dow size but still be able to use the Business Process

Drift logs with 5,000 events with some stability be-

tween the concept drifts.

The third step is process representation. For this

experiment, transition frequency (named Freq) and

probability (named Prob) are extracted as process fea-

tures and stored in the transformed transition matrix.

The fourth step is the change representation,

where each detection window is compared with the

ﬁxed reference window. In order to test the three de-

tection strategies mentioned in the previous section,

some actions are carried out. First, for the time se-

ries strategy, an operation to get the absolute differ-

ence is applied for each transition and feature in the

transformed transition matrix comparison, resulting

in a transformed transition matrix containing the dif-

ferences between the windows (named Delta matrix).

A feature derived from the product of the frequency

Towards a Transition Matrix-Based Concept Drift Approach: Experiments on the Detection Task

367

Figure 4: Summary of the strategies, techniques and features used in the experiments.

and probability differences (named Prob-Freq) is cre-

ated. This derived feature is a way of giving weight

to the differences that occur in both original features.

In sequence, each feature in Delta matrix is aggre-

gated using the sum function, resulting in a vector

containing the total differences for the transition fre-

quency (named Freq-change), transition probability

(named Prob-change) and Prob-Freq change features.

Second, for the statistical test strategy, the statistical

hypothesis test G-test (McDonald and of Delaware,

2009) is applied, based on the work of Ostovar et al.

(2016), using Freq of both windows being compared

to get the test p-value. Finally, for the threshold strat-

egy, the Freq-change is divided by the total amount of

transitions from both windows, resulting in the per-

centage of changes in transition frequency (named %

Freq-change), to be used in the threshold strategy.

The ﬁfth step is the concept drift detection task.

For the time series strategy, based on the work of

Yeshchenko et al. (2021), the values of Freq-change

and Prob-Freq are used as input data, separately, for a

change point detection technique, named Pruned Ex-

act Linear Time (PELT) (Killick et al., 2012). PELT

performs an exact search, capable of detecting abrupt

changes and it can be used in cases where the exact

number of changes is not known. For the hypothesis

testing strategy, the test p-value result is used for de-

tecting concept drift, with the threshold of 2.5% lower

being considered a drift. In addition, a smoothing

treatment is applied to avoid outlier variations in the

p-value which could result in a false detection. Sim-

ilarly, for the threshold strategy, a threshold of 5%

higher in % Freq-change is used to detect a drift, as

well as a smoothing treatment is applied to avoid out-

lier variations in the feature.

4.2 Results

The results for the three detection strategies are re-

ported for effectiveness (through F1-score) and de-

tection delay and compared with the state of the art.

Table 2 and Table 3 summarize all results, which are

detailed in the following sections.

Table 2: Effectiveness results through F1-score for the three

strategies including comparison with baseline.

Change Base-

Time series Stat test Threshold

pattern line

strategy strategy strategy

Prob-

Freq

Freq-

change

Freq % Freq-

change

cb 0.92 1.00 1.00 1.00 1.00

cd 0.88 1.00 1.00 1.00 1.00

cf 0.98 1.00 1.00 1.00 1.00

cm 1.00 1.00 1.00 1.00 1.00

cp 1.00 1.00 1.00 1.00 1.00

fr 0.75 1.00 0.92 1.00 0.87

lp 1.00 1.00 1.00 1.00 0.84

pl 1.00 1.00 1.00 1.00 1.00

pm 1.00 1.00 1.00 1.00 1.00

re 1.00 1.00 1.00 1.00 0.87

rp 0.96 1.00 1.00 1.00 1.00

sw 1.00 1.00 1.00 1.00 1.00

IOR 1.00 1.00 1.00 1.00 1.00

IRO 1.00 1.00 1.00 1.00 1.00

OIR 0.97 1.00 1.00 1.00 1.00

ORI 1.00 1.00 1.00 1.00 1.00

RIO 0.98 1.00 1.00 1.00 1.00

ROI 1.00 1.00 1.00 1.00 1.00

Mean 0.969 1.000 0.996 1.000 0.976

F1-score is the result of the combination (har-

monic mean) of two other measures, precision and re-

call. Precision is given by the number of true positive

results divided by the number of all positive results,

even incorrect ones. The recall is given by the num-

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

368

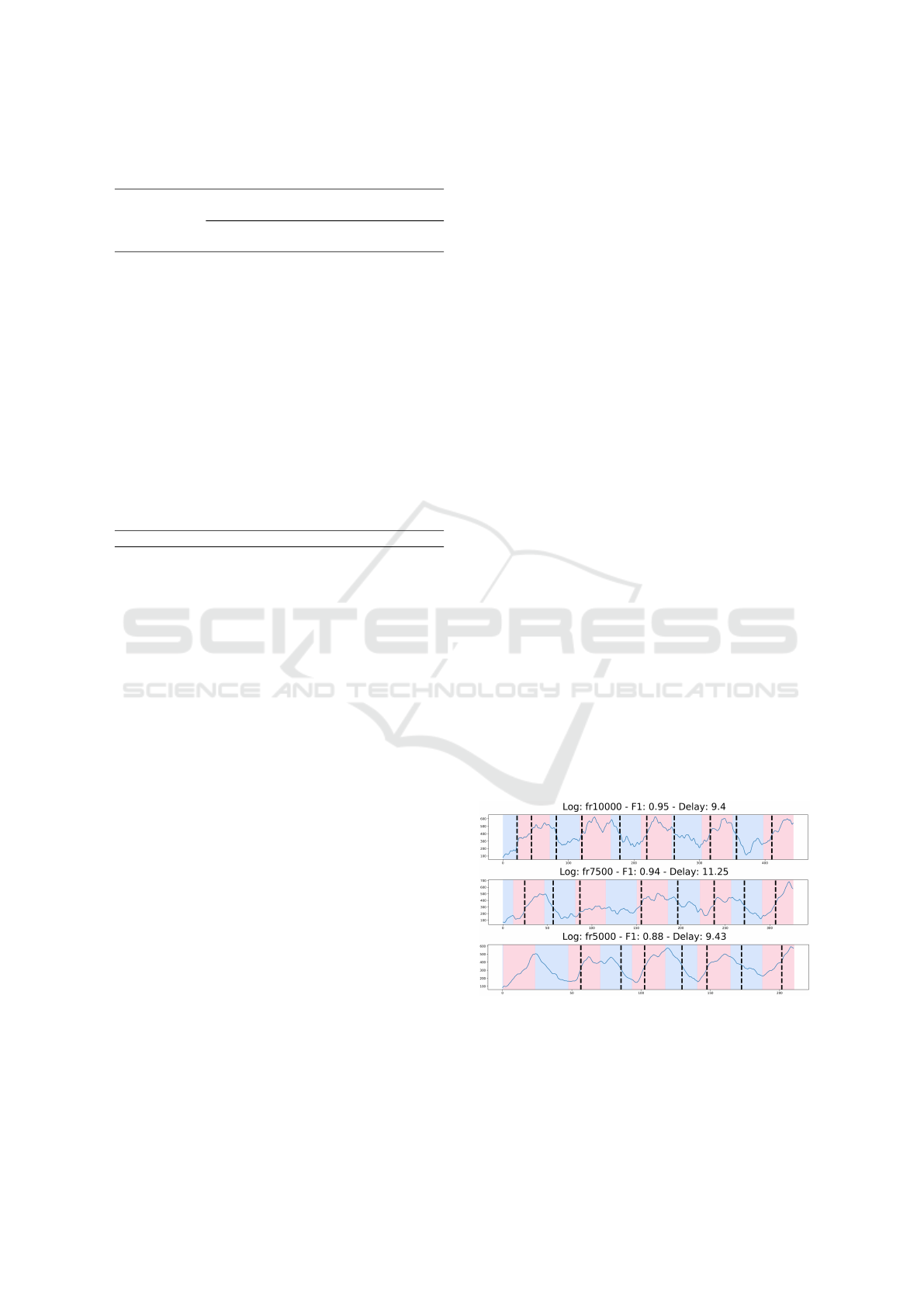
Table 3: Detection delay for the three strategies (in win-

dows) including comparison with baseline (in traces).

Change Base-

Time series Stat test Threshold

pattern line

strategy strategy strategy

Prob-

Freq

Freq-

change

Freq % Freq-

change

cb 52 10.82 10.41 8.96 9.33

cd 30 11.07 10.96 8.30 8.41

cf 28 11.26 10.45 7.59 8.70

cm 44 10.85 10.48 7.56 8.33

cp 32 11.15 10.81 7.00 8.04

fr 67 11.00 10.03 10.00 9.35

lp 54 11.70 11.44 9.48 8.14

pl 45 10.74 10.85 7.82 7.89

pm 32 10.93 10.66 7.26 8.18

re 28 11.63 11.00 8.89 8.25

rp 33 10.96 11.00 7.30 8.52

sw 30 11.00 10.85 6.67 7.44

IOR 24 11.56 11.33 7.26 8.92

IRO 47 10.78 10.44 7.63 9.18

OIR 19 11.22 11.15 6.48 6.93

ORI 32 11.29 11.11 6.89 8.37

RIO 37 11.04 11.04 7.48 9.44

ROI 18 11.22 11.07 6.33 7.11

Mean 36.22 11.12 10.84 7.72 8.36

ber of true positive results divided by the number of

all samples that should be classiﬁed as positive. A

detection is given as a true positive if at least one pos-

itive result is within the margin of error of the actual

concept drift (ground truth). F1-score is a normalized

measure, its highest possible value is 1 (or 100%) and

the smallest 0 (or 0%). Thus, methods with higher

F-scores are preferable.

Detection delay is a relevant point for the interpre-

tation of the validation criterion. The delay represents

the number of detection delay windows. As the win-

dowing strategy uses a sliding strategy, one can multi-

ply the detection delay value by the number of sliding

steps to arrive at the number of delay transitions. E.g.,

a delay of 10, using 200 transitions as sliding steps,

results in 2,000 detection delay transitions.

Moreover, the chosen windowing strategy has

window overlap, i.e., only the number of sliding

steps are new transitions from one window to an-

other. Therefore, when a concept drift occurs, it is

only present in the new transitions that have just ar-

rived. To know how many steps/windows are needed

to have a window with all new transitions, one can di-

vide the window size by the number of sliding steps.

E.g., for window size of 4,000 transitions and sliding

steps of 200 transitions, 20 steps/windows are taken

to have a window with all new transitions. This is im-

portant to evaluate the detection delay because, for the

same example above, a delay of 10 windows means

detection is performed in a window where half of the

transitions are from the new concept and the other half

from the old one; thus, getting a window with all tran-

sitions in the new concept was not necessary.

Finally, a margin of error of three windows is set

from the actual window starting the concept drift, plus

the number of slides needed until the window is com-

plete with new data. For the example above again,

the window takes 20 steps/windows to complete with

new data, adding three more steps result in 23 steps

of margin of error or acceptable distance to be con-

sidered a true positive.

4.2.1 Time Series Strategy

Table 2 shows the results of the time series strategy of

the Freq-change and Prob-Freq. The F1-score and

delay values represent the mean value in the three

event logs of different sizes (5,000, 7,500 and 1,0000

events) for each change pattern. The only change pat-

tern with F1-score different than 1.0 is fr, using Freq-

change. However, Prob-Freq is successful in per-

fectly capturing changes in this change pattern, most

likely because it considers changes in probability in

addition to frequency. Change pattern fr has more

subtle changes than the other change patterns, as they

only change the frequency of ﬂows, which is probably

best represented by Prob-Freq.

Figures 5 and 6 illustratively show Freq-change

and Prob-Freq, respectively, over time for the event

logs of change pattern fr. The blue background rep-

resents the period in which the event log is composed

by the original process and the pink background rep-

resents the period where the event log is composed

by the process with the process changed. Vertical

dashed lines represent the concept drift detected by

the strategy. One can notice Prob-Freq better repre-

sents change pattern fr in a more stable way.

Figure 5: Time series strategy with Freq-change in change

pattern fr.

Figure 7 shows Freq-change for change pattern lp,

with F1-score of 1.0. One can notice the changes are

clearly represented by the feature, unlike change pat-

tern fr. All other change patterns with F1-score of 1.0

Towards a Transition Matrix-Based Concept Drift Approach: Experiments on the Detection Task

369

Figure 6: Time series strategy with Prob-Freq in change

pattern fr.

have change representations similar to Figure 7.

Figure 7: Time series strategy with Freq-change in change

pattern lp.

As for the detection delay in Table 3, both features

have similar results, with a slightly longer delay for

Prob-Freq. Overall, both features can detect changes

when the sliding window has about a little more than

half of the transitions with the new concept.

4.2.2 Statistical Test Strategy

Table 2 and Table 3 also shows the results of the statis-

tical test strategy using Freq. The strategy has perfect

F1-Score and the lowest mean delay. The mean delay

of change pattern fr stands out as above the rest and

similar to the delay of the same change pattern in the

time series strategy using Freq-change (i.e., 10.03),

which may mean a certain detection difﬁculty for this

change pattern. However, unlike the time series strat-

egy, which had an F1-score of 0.92, all concept drifts

are correctly detected for this strategy.

4.2.3 Threshold Strategy

Table 2 and Table 3 also shows the results of the

threshold strategy with % Freq-change, using 5% as

threshold. The results are very good, considering de-

tection is a ﬁxed rule. Only three change patterns did

not have F1-score 1.0: fr, lp and re. Figure 8 shows a

result example for each of these change patterns.

Figure 8: Threshold strategy with % Freq-change in change

patterns fr, lp and re.

The % Freq-change has the same behavior as

Freq-change (cf. Figure 5), i.e., change pattern fr is

not well represented. Therefore, the threshold strat-

egy also has difﬁculties in detecting this change pat-

tern. The change patterns lp and re are well repre-

sented; however, at certain windows, the 5% thresh-

old is exceeded although there is no concept drift.

With a slightly higher threshold (e.g., 10%), the strat-

egy would detect all concept drifts for these two

change patterns, while a 10% threshold would detect

no concept deviations for the change pattern fr.

4.2.4 Baseline Comparison

Table 2 also shows the F1-score results of all strate-

gies tested compared with the results of the best

method (AWIN) from Maaradji et al. (2015)’s work

used as a baseline. In general, our experiments re-

sulted in better F1-scores than the baseline, which did

not obtain 100% in 7 of the 18 change patterns. In-

terestingly, change pattern fr is the worst result in the

baseline, showing it is a really difﬁcult change pattern

to detect perfectly. However, our experiments only

focused on ensuring a better F1-score using a larger

window size, while the baseline looked for the best

balance between F1-score and detection delay.

Table 3 also shows the detection delay results

of the three tested strategies along with the baseline

results, although they are not directly comparable.

Despite different metrics, one can note the baseline

method manages to achieve a good balance between

the F1-score and the detection delay as it presents an

overall mean delay of 36 traces. As for our experi-

ments, the best result was achieved by the statistical

test strategy, with an overall mean delay of 7.72 win-

dows (equivalent to about 154 traces). However, from

the perspective of the percentage of the new concept

data in relation to the window size that were neces-

sary for the method to detect concept drift, the results

are equivalent. The baseline averages 36% (i.e., 36.22

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

370

traces of mean delay per window of 100 traces), while

the statistical test strategy used with our approach av-

erages about 38% (i.e., about 154 traces of mean de-

lay per window of about 400 traces).

5 CONCLUSION

We propose a concept drift approach in process min-

ing that use a single, simple, effective and expand-

able (i.e., that can handle different aspects’ items)

data structure – the transformed transition matrix. We

showed how easy is to create the transformed transi-

tion matrix, to store different features extracted from

the event log, the window comparison to extract fea-

tures that represent the changes in the process, and

how to use these features in the detection task. We

showed how the approach and the data structure per-

forms in the task of detecting abrupt changes in the

control-ﬂow and in an ofﬂine scenario, with three dif-

ferent detecting strategies (time series strategy, statis-

tical test strategy, and threshold strategy). The three

strategies had good results in the tested experiments,

showing an encouraging potential of the approach.

Two issues are relevant to be considered: (i) as

the approach use the transformed transition matrix, all

features must be at the transition level (e.g., activity

and trace data must be adapted); and (ii) as the transi-

tion matrix features are at a granular level of detail, a

minimum window size dependency may be required

to ensure effectiveness.

As future work, we plan to run more experiments

to evaluate the impact of the parameters and test the

approach on other synthetic public event logs. We

also plan to expand the approach to consider the other

items of concept drift aspects, starting with localiza-

tion and characterization tasks, using the time process

perspective in an online scenario.

REFERENCES

Accorsi, R. and Stocker, T. (2012). Discovering workﬂow

changes with time-based trace clustering. In Data-

driven Proc. Discov. and Anal., pages 154–168.

Adams, J., van Zelst, S., Quack, L., Hausmann, K., van der

Aalst, W., and Rose, T. (2021). A framework for ex-

plainable concept drift detection in process mining. In

Bus. Process Manage., pages 400–416.

Appice, A. and Malerba, D. (2016). A co-training strategy

for multiple view clustering in process mining. IEEE

Trans. Serv. Comput., 9(6):832–845.

Barbon Junior, S., Tavares, G., Da Costa, V., Ceravolo, P.,

and Damiani, E. (2018). A framework for human-in-

the-loop monitoring of concept-drift detection in event

log stream. In Companion The Web Conf. 2018, page

319–326.

Bose, R., Van Der Aalst, W., Zliobaite, I., and Pechenizkiy,

M. (2014). Dealing with concept drifts in process min-

ing. IEEE Trans. on Neural Networks and Learning

Syst., 25(1):154–171.

Bose, R., Van Der Aalst, W.,

Zliobaite, I., and Pechenizkiy,

M. (2011). Handling concept drift in process mining.

In Adv. Inf. Syst. Eng., pages 391–405.

Brockhoff, T., Uysal, M., and Van Der Aalst, W. (2020).

Time-aware concept drift detection using the earth

mover’s distance. In Int’l Conf. Process Mining, pages

33–40.

Carmona, J. and Gavald

a, R. (2012). Online techniques for

dealing with concept drift in process mining. In Adv.

in Intel. Data Anal. XI, pages 90–102.

Ceravolo, P., Tavares, G., Barbon Junior, S., and Damiani,

E. (2022). Evaluation goals for online process min-

ing: A concept drift perspective. IEEE Trans. Serv.

Comput., 15(4):2473–2489.

de Sousa, R. G., Peres, S. M., Fantinato, M., and Reijers,

H. A. (2021). Concept drift detection and localiza-

tion in process mining: An integrated and efﬁcient ap-

proach enabled by trace clustering. In ACM Symp.

Appl. Computing, page 364–373.

Gemaque, R. N., Costa, A. F. J., Giusti, R., and dos Santos,

E. M. (2020). An overview of unsupervised drift de-

tection methods. WIREs Data Mining and Knowledge

Discovery, 10(6):e1381.

Hassani, M. (2019). Concept drift detection of event

streams using an adaptive window. In Eur. Conf.

Model. Simul., pages 230–239.

Hompes, B., Buijs, J., Van Der Aalst, W., Dixit, P., and Bu-

urman, J. (2015). Detecting change in processes us-

ing comparative trace clustering. In Data-driven Proc.

Discov. and Anal., pages 95–108.

Hompes, B., Buijs, J., Van Der Aalst, W., Dixit, P., and Bu-

urman, J. (2017). Detecting changes in process behav-

ior using comparative case clustering. In Data-driven

Proc. Discov. and Anal., pages 54–75.

Impedovo, A., Mignone, P., Loglisci, C., and Ceci, M.

(2020). Simultaneous process drift detection and char-

acterization with pattern-based change detectors. In

Discovery Science, pages 451–467.

Killick, R., Fearnhead, P., and Eckley, I. A. (2012). Optimal

detection of changepoints with a linear computational

cost. Journal of the American Statistical Association,

107(500):1590–1598.

Kurniati, A., McInerney, C., Zucker, K., Hall, G., Hogg,

D., and Johnson, O. (2019). A multi-level approach

for identifying process change in cancer pathways. In

Bus. Process Manage. Workshops, pages 595–607.

Kurniati, A., McInerney, C., Zucker, K., Hall, G., Hogg,

D., and Johnson, O. (2020). Using a multi-level pro-

cess comparison for process change analysis in can-

cer pathways. Int’l J. Environ. Res. Public Health,

17(19):1–16.

Lin, L., Wen, L., Lin, L., Pei, J., and Yang, H. (2022). Lcdd:

Detecting business process drifts based on local com-

Towards a Transition Matrix-Based Concept Drift Approach: Experiments on the Detection Task

371

pleteness. IEEE Trans. Serv. Comput., 15(4):2086–

2099.

Liu, N., Huang, J., and Cui, L. (2018). A framework

for online process concept drift detection from event

streams. In IEEE Int’l Conf. Serv. Comput., pages

105–112.

Lu, J., Liu, A., Dong, F., Gu, F., Gama, J., and Zhang, G.

(2019). Learning under concept drift: A review. IEEE

Trans. on Knowledge and Data Eng., 31(12):2346–

2363.

Lu, Y., Chen, Q., and Poon, S. (2021a). Detecting and un-

derstanding branching frequency changes in process

models. In Enterprise, Business-Proc. and Inf. Syst.

Modeling, pages 39–46.

Lu, Y., Chen, Q., and Poon, S. (2021b). A robust and

accurate approach to detect process drifts from event

streams. In Bus. Process Manage., pages 383–399.

Luengo, D. and Sep

ulveda, M. (2012). Applying clustering

in process mining to ﬁnd different versions of a busi-

ness process that changes over time. In 7th Int’l Wks.

on Bus. Proc. Intel., pages 153–158.

Maaradji, A., Dumas, M., La Rosa, M., and Ostovar, A.

(2015). Fast and accurate business process drift detec-

tion. In Bus. Process Manage., pages 406–422.

Maaradji, A., Dumas, M., Rosa, M., and Ostovar, A. (2017).

Detecting sudden and gradual drifts in business pro-

cesses from execution traces. IEEE Trans. on Knowl.

and Data Engin., 29(10):2140–2154.

Manoj Kumar, M., Thomas, L., and Annappa, B. (2015).

Capturing the sudden concept drift in process mining.

In Int’l Works. on Algor. & Theories for the Anal. of

Event Data, pages 132–143.

Martjushev, J., Jagadeesh Chandra Bose, R., and van der

Aalst, W. (2015). Change point detection and deal-

ing with gradual and multi-order dynamics in process

mining. In Perspectives in Bus. Inform. Research,

pages 161–178.

McDonald, J. and of Delaware, U. (2009). Handbook of

Biological Statistics. Sparky House Publishing, 2 edi-

tion.

Ostovar, A., Leemans, S., and Rosa, M. (2020). Robust

drift characterization from event streams of business

processes. ACM Trans. Knowl. Discov. Data, 14(3).

Ostovar, A., Maaradji, A., La Rosa, M., and Ter Hofstede,

A. (2017). Characterizing drift from event streams of

business processes. In Adv. Inf. Syst. Eng., pages 210–

228.

Ostovar, A., Maaradji, A., La Rosa, M., ter Hofstede, A.,

and van Dongen, B. (2016). Detecting drift from event

streams of unpredictable business processes. In 35th

Int’l Conf. on Conceptual Modeling, pages 330–346.

Pauwels, S. and Calders, T. (2019). An anomaly detection

technique for business processes based on extended

dynamic bayesian networks. In ACM/SIGAPP Symp.

Appl. Computing, page 494–501.

Richter, F. and Seidl, T. (2017). Tesseract: Time-drifts in

event streams using series of evolving rolling averages

of completion times. In Bus. Process Manage., pages

289–305.

Sato, D. M. V., De Freitas, S. C., Barddal, J. P., and Scal-

abrin, E. E. (2021). A survey on concept drift in pro-

cess mining. ACM Comput. Surv., 54(9).

Seeliger, A., Nolle, T., and M

uhlh

auser, M. (2017). De-

tecting concept drift in processes using graph metrics

on process graphs. In Conf. on Subject-Oriented Bus.

Process Manage.

Song, M., G

unther, C. W., and van der Aalst, W. (2009).

Trace clustering in process mining. In Int’l Wks. on

Bus. Proc. Intel., pages 109–120.

Stertz, F. and Rinderle-Ma, S. (2018). Process histories - de-

tecting and representing concept drifts based on event

streams. In Int’l Conf. on Coop. Inform. Sys., pages

318–335.

Tavares, G., Ceravolo, P., Da Costa, V., Damiani, E., and Ju-

nior, S. (2019). Overlapping analytic stages in online

process mining. In IEEE Int’l Conf. Serv. Comput.,

pages 167–175.

Truong, C., Oudre, L., and Vayatis, N. (2020). Selective re-

view of ofﬂine change point detection methods. Signal

Processing, 167.

van der Aalst, W. (2014). Process mining in the large: A

tutorial. In 3rd Eur. Summer Sch. on Bus. Intell., pages

33–76.

van der Aalst, W. (2016). Process Mining: Data Science in

Action. Springer Berlin, Heidelberg, 2 edition.

van der Aalst, W. and et al. (2012). Process mining man-

ifesto. In 7th Int’l Wks. on Bus. Proc. Intel., pages

169–194.

Weber, P., Bordbar, B., and Ti

no, P. (2011). Real-time de-

tection of process change using process mining. In

Imp. Coll. Comput. Stud. Wks, pages 108–114.

Yeshchenko, A., Ciccio, C., Mendling, J., and Polyvyanyy,

A. (2019a). Comprehensive process drift analysis with

the visual drift detection tool. In 38th Int’l Conf. on

Conceptual Modeling, pages 108–112.

Yeshchenko, A., Di Ciccio, C., Mendling, J., and

Polyvyanyy, A. (2019b). Comprehensive process drift

detection with visual analytics. In 38th Int’l Conf. on

Conceptual Modeling, pages 119–135.

Yeshchenko, A., Di Ciccio, C., Mendling, J., and

Polyvyanyy, A. (2021). Visual drift detection for event

sequence data of business processes. IEEE Trans. Vi-

sual Comput. Graphics, 28(8):3050–3068.

Yeshchenko, A., Mendling, J., Di Ciccio, C., and

Polyvyanyy, A. (2020). VDD: A visual drift detection

system for process mining. In ICPM Doc. Consort.

and Tool Demo. Track, pages 31–34.

Zheng, C., Wen, L., and Wang, J. (2017). Detecting process

concept drifts from event logs. In Int’l Conf. on Coop.

Inform. Sys., pages 524–542.

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

372