Discrete-Time MDP Policy for Energy-Aware Data Center
L
´
ea Bayati
Laboratoire d’Algorithmique Complexit
´
e et Logique, Universit
´
e Paris-Est Cr
´
eteil (UPEC),
Keywords:
Data Center, Markov Decision Process, Energy Saving, Performance, Queues.
Abstract:
This paper presents a stochastic model for Dynamic Power Management (DPM) that consists in dynamically
switching-on/off servers in the data center to ensure a reasonable energy consumption with a good Quality of
Services (QoS). In this work, arrival jobs are specified with histograms which are discrete identically indepen-
dently distributions obtained from real traces, empirical data, or incoming traffic measurements. We model
a data center by a queue, then we formulate the optimization problem by a discrete time Markov Decision
Process (MDP) to find the optimal policy. We prove also some structural properties of the optimal policy.
Our approach was applied and tested for several data center parameters with arrivals modeled by histograms
obtained from real Google traffic traces.
1 INTRODUCTION
The recent expansion of Clouds and Data Centers
is causing energetic problems and digital pollution
issues. More than 1.3% of the global energy con-
sumption is due to the electricity used by data cen-
ters. Additionally, one data center server can produce
more than 10 kg of CO
2
per day, rates that are in-
creasing, revealed by surveys conducted in (Koomey,
2011), saying a lot about the increasing evolution of
data centers. Data centers are designed to support
the expected peak traffic load, however the global
load is about 60% of the peak load (Benson et al.,
2010). In fact, an important number of servers are
not under load and still consume about 65%-70% of
the maximal energy consumption (Greenberg et al.,
2009). Studies like (Lee and Zomaya, 2012) show
that much of the energy consumed in the data center
is mainly due to the electricity used to run the servers
and to cool them (70% of total cost of the data cen-
ter). Thus, the main factor of this energy consumption
is related to the number of operational servers. Many
efforts have focused on servers and their cooling.
Works have been done to build better components and
low-energy-consumption processors (Grunwald et al.,
2000), more efficient energy network (Benson et al.,
2010), more efficient cooling systems (Patel et al.,
2003), and optimized kernels (Jin et al., 2012). That
being said, another complementary saving energy ap-
proach is to consider a power management strategy
to manage the switching-on/off of servers in a data
center to ensure both a good performance of services
offered by these data centers and reasonable energy
consumption. Two requirements are in conflict: (i) In-
creasing the Quality of the Service (QoS). (ii) Saving
energy. For the first requirement we need to turn-on a
large number of servers which consume more energy
and leads to less waiting time and decreases the rate
of losing jobs but requires a high energy consump-
tion. For the second requirement we need to turn-on
a small number of servers which leads to less energy
consumption, but causes more waiting time and in-
creases the rate of losing jobs. Thus, the goal is to de-
sign better power management algorithms which take
into account these two constraints to minimize wait-
ing time, loss rate and energy consumption.
In a data center every job may generates a profit,
and the average profit per job can be computed as
a ratio of the total profit over the number of served
jobs. For instance, 10
6
requests (page views) may
bring $1000 of revenue. Thus, it can be said that each
job brings $10
−3
on average. Work in (Dyachuk and
Mazzucco, 2010) suggests that each successfully pro-
cessed job generates a profit around 6.2 × $10
−6
. In
this case, a lost job costs 6.2 × $10
−6
. Otherwise, ac-
cording to research published by Dell and Principled
Technologies, a single server consumes around some-
thing between 384 and 455 Watts. Other works evalu-
ate that the power consumption of each server ranges
between 238 and 376 Watts (Mazzucco et al., 2010).
Rajesh et al. (Rajesh et al., 2008) estimate the cost
Bayati, L.
Discrete-Time MDP Policy for Energy-Aware Data Center.
DOI: 10.5220/0011846300003491
In Proceedings of the 12th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2023), pages 89-97
ISBN: 978-989-758-651-4; ISSN: 2184-4968
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
89

of one kWh of energy to $0.0897. These values may
vary depending on where the data center is located
and how electricity is generated. Using that baseline
a one server costs around $300 per year to run.
In order to save energy, the strategy presented by
Mazzucco et al in (Mazzucco and Dyachuk, 2012) is
a dynamic allocation policy that checks the system
periodically, collects statistics, estimates arrival rate
and average service time, and finally allocates a mini-
mal number of servers which should meet the QoS re-
quirements. Numerical experiments and simulations
based on Wikipedia traces (November 2009) show a
significant improvement of energy saving.
Works as in (Mitrani, 2013) present a theoreti-
cal queuing model to evaluate the trade-off between
waiting time and energy consumption if only a sub-
set of servers is active all the time and the remaining
servers (reserve-servers) are enabled when the num-
ber of jobs in the system increases and exceeds some
threshold Up. The reserve-servers will be turned-off
again if the number of jobs decreases and becomes
less than another threshold Down. Jobs arrive accord-
ing to an identically independently distributed (i.i.d)
Poisson process then served according to an exponen-
tially distributed service time. Analytic equation and
experimental simulation results show that energy con-
sumption is significantly reduced (from 20% to 40%)
while still having an acceptable waiting time.
In (Bayati et al., 2016) we present, with other co-
authors, a tool to study the trade-off between energy
consumption and performance evaluation. The tool
is based on threshold policy. It is numerical rather
than analytical or simulation. Some measurements
of real traffic are used to model the job arrivals in a
more accurate manner. The arrival process is assumed
to be stationary for short periods of time and change
between periods. This allowed us to model for in-
stance hourly variations of the job arrivals. The tool
uses real traffic traces to produce a discrete distribu-
tion that models arrival jobs. Threshold policy checks
every slot the number of waiting jobs in the buffer,
then turn-on more additional servers if this number
exceeds threshold U, and turn off some server if it’s
less then threshold D. The tool analyzes all possible
couples (U, D) then returns the best couple that min-
imize a cost function combining performance mea-
sures and energy consumption.
All previous works and others (Gebrehiwot et al.,
2016) consider models under specific management
mechanisms, that leads to suboptimal strategies. In
(Maccio and Down, 2015), MDP based models were
considered in order to device optimal strategies.
More recent works can be found in (Khan, 2022;
Rteil et al., 2022; Peng et al., 2022; An and Ma,
2022).
Markov Decision Process (MDP) is a formalism
allowing to model a decision-making system. Ba-
sically it is a Markov chain augmented by a set of
decision-making actions. Applying an action moves
the system from a state to another state and gives rise
to some cost. Thus, the probability that the system
moves into its new state is influenced by the chosen
action. In the context of Dynamic Power Manage-
ment, the cost of the consumed energy depends on the
number of operational servers and the QoS cost de-
pends on the number of waiting and/or rejected jobs.
Additionally, from every state of the system we have
to consider all the following actions: {turn off all
servers, turn on only 1 server, turn on only 2 servers,
... , turn on all servers}. The optimal strategy consists
in finding the best sequence of actions to minimize the
total cost accumulated during a finite period of time,
or to minimize the expected cost for an infinite period
of time.
MDP models can be considered in continuous
or discrete time context. In the case of discrete
time MDP the value iteration algorithm that im-
plements the Bellman’s backup equations (Bellman,
1957) computes the optimal policy. However, con-
tinuous time MDP are considered when the arrival
jobs are modeled by a continuous time distribution
obtained by fitting the empirical data or by asserting
some assumptions that leads usually to a Poisson dis-
tribution (Maccio and Down, 2015).
One of the main uses of Markov decision process
methods is to establish the existence of optimal poli-
cies with simple structure. The importance of found-
ing structured policy among optimal strategies lies in
its advantage in making decisions, in its implementa-
tion facility, and in its efficient computation. When
the optimal policy has a simple form, specialized al-
gorithms can be device to search only among policies
that have the same form as the optimal policy. This
avoids the need for using iteration algorithm. Works
as in (Topkis, 1978; Lu and Serfozo, 1984; Serfozo,
1979; Hipp and Holzbaur, 1988; Plum, 1991) inves-
tigate the structure of optimal policy in the context
of Markovian control process and give conditions to
check properties like hysteresis, monotony, or isotony
of the policy.
In our work, real incoming traffic traces are sam-
pled then used directly to build an empirical discrete
distribution called histogram that may model the job
arrivals in a more accurate way. In fact, we can ac-
commodate less regular processes than the Poisson
process considered in several works like in (Mitrani,
2013; Schwartz et al., 2012). Thus, the Markovian
assumptions (Poisson arrivals, exponential services)
SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems
90

and the infinite buffer capacity are not required for
our approach analysis and its optimization procedure.
We already used histograms in (Bayati, 2016; Bayati
et al., 2016), and similar works as in (Tancrez et al.,
2009) used them for network traffic.
The target of our approach is request based ser-
vices data center. A data center is modeled by a dis-
crete time queue with a finite buffer capacity where
we set the length of the time slot to the length of
the sampling time used to sample the traffic traces
to obtain the histogram. We formulated the problem
of energy-QoS optimization by a discrete time MDP
without passing by uniformization process. Then we
study the energy consumption and its evolution over a
finite (hour, day, month) or infinite period of time. As
value iteration algorithm is an efficient dynamic pro-
gramming implementation for solving an MDP model
(for both finite and infinite horizon), we used it to
compute the optimal control policy of our MDP. We
assume identical servers, identical job duration, job
duration largely higher than time to switch on a server,
and servers switch-on immediately which is particu-
larly a strong assumption.
The rest of this paper is organized as follows. Sec-
tion 2 models the system by simple queue. Then,
Section 3 formulates the optimization problem as dis-
crete time MDP. After that, in Section 4 we prove
some structural properties related to the optimal pol-
icy. Finally, Section 5 analyzes systems with arrivals
modeled by discrete distribution obtained from real
Google traffic traces (Wilkes, 2011).
2 QUEUE MODEL
Here we deal with discrete time model. Let DC be a
data center composed of max identical servers work-
ing under the FIFO
1
discipline. DC receives jobs re-
questing the offered service. The maximal number of
jobs that can be served by one server in one slot is
assumed to be constant and denoted by d. Thus, the
queuing model is a batch arrival queue with constant
services and finite capacity buffer b (buffer size). In
practice, data centres handle jobs of varying service
tiers, each with its own revenue model. In this work
we assume that the data centre handles only one tier of
jobs. We model arrival jobs by finite structure called
histogram which is based on discrete distribution.
Definition 1 (histogram). Let A be a discrete ran-
dom variables taking values in N. The couple H
A
=
(S
A
, P
A
) denotes the histogram of A where P
A
: N →
[0, 1] is the probability mass function of A and S
A
=
1
First In First Out.
S
S
S
S
d × m
i: job arrivals
b: Buffer size
n: Waiting jobs
m: Number of operational servers
d: Number of jobs served by a server per slot
Figure 1: Illustration of the queuing model.
{i ∈ N : P
A
(i) > 0} is the support of P
A
.
Thus, the number of jobs arriving to the data cen-
ter during a slot is modeled by a histogram H
A
where
P
A
(i) gives the probability to have i arrival jobs per
a slot. Note that in this paper, arrival jobs are as-
sumed independent, and their distribution P
A
is ob-
tained from real traces, empirical data, or incoming
traffic measurements.
Example 1. Assume that, per slot, we have a prob-
ability of 0.59 to receive one arrival job, and 0.41 to
receive no arrival jobs. In this case, arrivals are mod-
eled by histogram H
A
= (S
A
, P
A
) where S
A
= {0, 1},
P
A
(0) = 0.41, and P
A
(1) = 0.59.
The number of waiting jobs in the buffer is de-
noted by n. The number of operational servers is de-
noted by m. The number of rejected (lost) jobs is de-
noted by l. We assume that initially the number of op-
erational servers, the number of waiting jobs, and the
number of rejected jobs are 0. The maximal number
of servers that can be operational is max. The num-
ber of waiting jobs n can be computed by induction
where the exact sequence of events during a slot have
to be described. First, the jobs are added to the buffer
then they are executed by the servers. The admission
is performed per job according to the Tail Drop pol-
icy: a job is accepted if there is a place in the buffer,
otherwise it is rejected. The following equations give
the number of waiting jobs in the buffer and the lost
jobs. For a number of i arrival jobs, we have:

n ← min{b, max{0, n + i − d × m}}
l ← max{0, n + i − d × m − b}
(1)
It is assumed that the input arrivals are i.i.d. and under
these assumptions, the model of the queue is a time-
homogeneous Discrete Time Markov Chains.
The problem we have to consider is to find a trade-
off between the performance (i.e. waiting and loss
jobs) and the energy consumption (i.e. number of op-
erational servers). However, as the number of servers
Discrete-Time MDP Policy for Energy-Aware Data Center
91

changes with time, the system becomes more com-
plex to analyze. The number of servers may vary ac-
cording to the traffic and performance indexes. More
precisely, n, l and m are considered and then some de-
cisions are taken according to a particular cost func-
tion.
The energy consumption takes into account the
number of operational servers. Each server consumes
some units of energy per slot when a server is oper-
ational and it costs an average of c
M
∈ IR
+
monetary
unit. A server may consume a very low amount of
energy when it is turned-off. However, during the
latency period a server may consume an additional
amount of energy that costs an average of c
On
∈ IR
+
monetary unit which is the energetic cost needed to
switch-on a server. Additionally, we consider that a
server switches-on immediately. The total consumed
energy is the sum of all units of energy consumed
among a specific period. QoS takes into account the
number of waiting and lost jobs. Each waiting job
costs c
N
∈ IR
+
monetary unit per slot, and a rejected
job costs c
L
∈ IR
+
monetary unit. Notice that in prac-
tice energy costs may vary with time of day, depend-
ing on the prevailing demand from other users, how-
ever in this work we assume that there is no variation
energy costs over a day.
3 MARKOV DECISION PROCESS
In order to find the optimal strategy and then analyze
the performance and the energy consumption of the
data center under this optimal strategy, we will use
the concept of Markov Decision Process to formulate
our optimization problem. Notice that (n, l) and m are
mutually dependent. If we decrease m, we save more
energy, but both n and l increase, so we will have an
undesirable diminution of QoS and vice versa.
Let (S , A, P , C ) be an MDP where S is the state
space, A is the set of actions, P is the transition prob-
ability, and C the immediate cost of each action. Let
H
A
= (S
A
, P
A
) be the histogram used to model the ar-
rival jobs. The state of the system is defined by the
couple (m, (n, l)) where m is the number of opera-
tional servers, n is the number of waiting jobs, and
l is the number of lost job. Indeed the state space S is
defined as:
S = {(m, (n, l)) | m ∈ [0..max], n ∈ [0..b],
l ∈ [0.. max(S
A
)]}
(2)
At the beginning of each slot, and based on the current
state of the system, an action α
j
∈ A will be made to
determine how many servers will be operational dur-
ing the current slot. In fact the action space A is de-
fined as A = {α
j
| 0 ≤ j ≤ max}, where action α
j
consists of keeping exactly j operational servers dur-
ing the current slot. We have a probability of P
α
j
ss
′
to
move from state s = (m, (n, l)) to s
′
= ( j, (n
′
, l
′
)) un-
der action α
j
. This probability is defined as:
P
α
j
ss
′
=
∑
i∈S
A
P
A
(i) (3)
For each i ∈ S
A
satisfying:

n
′
= min{b, max{0, n + i − d × j}}
l
′
= max{0, n + i − d × j − b}
Consequently moving from state s = (m, (n, l)) to
s
′
= ( j, (n
′
, l
′
)) under action α
j
induces immediately
a cost C
α
j
s
defined as:
C
α
j
s
= j ×c
M
+max{0, j −m}×c
On
+n ×c
N
+l ×c
L
(4)
The immediate cost C
α
j
s
includes four parts:
1. The first part is j ×c
M
, where c
M
is the cost of en-
ergy consumption of one working server per slot
and j is the number of working servers during the
current slot. This part presents the total cost of en-
ergy consumed by the operational servers during
the current slot.
2. The second part is max{0, j − m} × c
On
, where
c
On
is the energetic cost of switching-on one
server from stopping mode to working mode and
max{0, j − m} is the number of servers switched-
on at the beginning of the slot. This part presents
the total cost of energy used to switch-on servers
at the beginning of the current slot.
3. The third part is n × c
N
, where c
N
is the cost of
keeping one job in the buffer during the current
slot and n is the number of waiting jobs. This part
presents the total cost of maintaining waiting jobs
in the buffer during the current slot.
4. The last part is l ×c
L
, where c
L
is the cost of loos-
ing one job during the current slot and l is the
number of lost jobs. This part presents the total
cost of loosing jobs during the current slot.
Notice that the number of state of the MDP is in
O(max × b × max(S
A
)), and the number of transition
of the MDP is in O(max
2
×b × |S
A
|×max(S
A
)). This
can be proved as following. Every state of the MDP
includes three element:
1. the number of operational servers which is be-
tween 0 and max,
2. the number of waiting jobs in the buffer which is
bounded by b, and
3. the number of rejected jobs which can be at most
equals to the maximum number of arrival jobs
given by max(S
A
).
SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems
92

So, |S | is bounded by (max + 1) × (b + 1) ×
(max(S
A
) + 1). Additionally from each state of the
MDP we have at most (max + 1) action, and each
action leads to a number of transition equals to |S
A
|
(one transition for each bin in the support of the ar-
rival distribution). In fact, as the number of state is
in O(max × b × max(S
A
)), we deduce that the num-
ber of transition is bounded by max × b × max(S
A
) ×
(max + 1) × |S
A
|.Table 1 resumes parameters used in
our model and our MDP formulation.
Table 1: Model and MDP Parameters.
Parameters Description
h duration of analysis
max total number of servers
d processing capacity of a server
b buffer size
m number of operational servers
n number of waiting jobs
l number of rejected jobs
H
A
histogram of job arrivals
c
On
energetic cost of switching-on 1 server
c
M
energetic cost of 1 working server during 1 slot
c
N
cost of 1 waiting job in buffer during 1 slot
c
L
cost of 1 lost job during 1 slot
S set of all possible states
A set of all possible actions
s = (m, (n, l)) system state
s
0
= (0, (0, 0)) starting state
α
j
action to keep exactly j operational servers
P
α
j
ss
′
probability transition from s to s
′
under action α
j
C
α
j
s
immediate cost from s under action α
j
Example 2. To illustrate our formalization let’s show
an MDP for a very simple data center of one server
with a buffer size equals one. Which means that
max = 1 and b = 1. Job arrivals are modeled by his-
togram of Example 1. So, MDP= (S, A, P , C ) where:



S = {(0, (0, 0)), (0, (1, 0)), (0, (1, 1)), (1, (0, 0))
, (1, (1, 0)), (1, (1, 1))}
A = {α
0
, α
1
}
and P can be deduced from the graph of Figure 2.
4 OPTIMAL STRATEGY
STRUCTURE
As we formulate our optimization problem as an
MDP, an action consists in turning-on each unit of
time a specific number of servers and turning-off the
rest of the servers. The optimal strategy is the best se-
quence of actions to be done in order to minimize the
overall cost during a finite period of time called hori-
zon and noted h. More generally, the value function
s
0
(0, (0, 0))
s
1
(0, (1, 0))
s
2
(0, (1, 1))
s
3
(1, (0, 0))
s
4
(1, (1, 0))
s
5
(1, (1, 1))
α
1
α
0
α
1
α
0
α
1
α
0
α
1
α
0
α
1
α
0
α
1
α
0
.41
.59
.41
.59
.41
.59
.41
.59
.41
.59
.41
.59
1
1
.41
.59
.41
.59
.41
.59
.41
.59
Figure 2: MDP example. For instance, state s
3
= (1, (0, 0))
means that the system is running by one server, and no wait-
ing jobs are in the buffer nor lost jobs. Action α
0
switches-
off the server and α
1
switches-on the server.
V : S × [0..h] → IR
+
has as objective minimizing the
expected sum of costs over time:
V (s, t) = min
π
E
"
t
∑
k=0
C
π(s
k
,k)
s
k
#
(5)
The value function can be seen as a Bellman equa-
tion (Bellman, 1957; Puterman, 1994; Bertsekas,
1995):
V (s, t) = min
α
j
(
C
α
j
s
+
∑
s
′
∈S
P
α
j
ss
′
V (s
′
,t − 1)
)
(6)
Where α
j
is the action taken by the system, and P
α
j
ss
′
is the transition probability from state s to state s
′
. In
this case the optimal policy for each state s is:
π
∗
(s,t) = argmin
α
j
∈A
(
C
α
j
s
+
∑
s
′
∈S
P
α
j
ss
′
V (s
′
,t − 1)
)
(7)
As the value iteration algorithm is an efficient dy-
namic programming, implementation for solving
Bellman equation, we used it to compute the optimal
control policy of our MDP.
As shown previously, the size of the MDP is im-
portant, and the computation of the optimal policy can
be hard even impossible for a big data center. In fact,
it is essential to analyze the structural properties of
the optimal policy to make the computation efficient.
In the following we will be interested in some prop-
erties around the optimal policy, and we show in par-
ticular that the property of the double-threshold struc-
ture does not hold for our heterogeneous data center
model.
Definition 2 ((Hipp and Holzbaur, 1988)). A pol-
icy π is called to be hysteretic if ∀t ∈ [0..h], ∃m ∈
Discrete-Time MDP Policy for Energy-Aware Data Center
93

[0..max], ∃α
j
∈ A such as π((m, (n, l)), t) = α
j
=⇒
π(( j, (n, l)),t) = α
j
.
Theorem 1. The optimal policy (7) is hysteretic.
Proof. For each slot t, let’s define function f
t
(m, j) :
[0..max] × [0..max] → IR
+
as the cost for switching
the number of operational servers from m to j. And
function w
t
(m, (n, l)) : S → IR
+
presents the expected
and the possibly future cost starting with n waiting
jobs in the buffer, losing l jobs, serving with m oper-
ational servers during one slot, and then following an
optimal policy. So, the our optimal policy (7) can be
formulated as:
π
∗
(s,t) = argmin
α
j
∈A
{ f
t
(m, j) + w
t
( j, (n, l))} (8)
Where:





w
t
( j, (n, l)) = j × c
M
+ n × c
N
+ l × c
L
+
∑
s
′
P
α
j
ss
′
V (s
′
,t)
f
t
(m, j) = max{0, j − m} × c
On
(9)
According to Theorem 1 of (Hipp and Holzbaur,
1988), if the function f
t
satisfies the following con-
dition:

∀m ∈ [0..max] : f
t
(m, m) = 0
∀m, p, q ∈ [0..max] : f
t
(m, q) ≤ f
t
(m, p) + f
t
(p, q)
(10)
then the optimal policy π
∗
is a hysteretic policy. Thus,
to prove that our optimal policy is hysteretic we need
just to prove that f
t
satisfies conditions 10. We have
f
t
(m, m) = max{0, m − m} × c
On
= 0 which implies
the first condition of 10, and the following resumes
all possible cases for the second condition of 10:
1. if m ≥ q we have f
t
(m, q) = 0 and as f
t
is posi-
tive then ∀p ∈ [0..max] : f
t
(m, p) + f
t
(p, q) ≥ 0 =
f
t
(m, q) =⇒ f
t
(m, q) ≤ f
t
(m, p) + f
t
(p, q).
2. if m ≤ p ≤ q we have f
t
(m, p) + f
t
(p, q) = (p −
m) × c
On
+ (q − p) × c
On
= (q − m) × c
On
=
f
t
(m, q) =⇒ f
t
(m, q) ≤ f
t
(m, p) + f
t
(p, q).
3. if m ≤ q ≤ p we have f
t
(m, p) + f
t
(p, q) = (p −
m) × c
On
+ 0 = (p − m) × c
On
≥ (q − m) × c
On
=
f
t
(m, q) =⇒ f
t
(m, q) ≤ f
t
(m, p) + f
t
(p, q).
4. if p ≤ m ≤ q we have f
t
(m, p) + f
t
(p, q) = 0 +
(q − p) × c
On
= (q − p) × c
On
≥ (q − m) × c
On
=
f
t
(m, q) =⇒ f
t
(m, q) ≤ f
t
(m, p) + f
t
(p, q).
In conclusion, conditions 10 hold and our optimal pol-
icy is hysteretic.
Definition 3 ((Lu and Serfozo, 1984)). A policy π is
called to be monotone if π is hysteretic and, ∀t ∈
[0..h], ∀m ∈ [0..max], ∃ D
m
,U
m
∈ [−1..b + 1], and
D
m
≤ U
m
such that for every s = (m, (n, l)) we have:
π((m, (n, l)),t) =



π((max{0, m − 1}, (n, l)), t) if n < D
m
α
m
if D
m
≤ n ≤ U
m
π((min{max, m + 1}, (n, l)),t) if U
m
< n
(11)
Theorem 2. The optimal policy (7) is not monotone.
Proof. In this proof we give a counterexample that
shows that monotony of the optimal policy (7) does
not hold in general. Let’s model the arrival by the his-
togram of Example 1. We set b = 5, max = 5, c
M
= 9,
c
N
= 8, c
On
= 7, d = 1, and h = 7. In order to sim-
plify the counter example
2
, we set c
L
= 0 so we don’t
need to consider rejected job in the MDP model. Un-
der this parameters, solving the optimality equation 6
leads to the following optimal policy for t = 5:
Observed state (m,(n, l)) Action
(m = 0, (n = 0, l = 0)) → α
1
(m = 0, (n = 1, l = 0)) → α
2
(m = 0, (n = 2, l = 0)) → α
2
(m = 0, (n = 3, l = 0)) → α
3
(m = 0, (n = 4, l = 0)) → α
4
(m = 0, (n = 5, l = 0)) → α
5
Observed state (m,(n, l)) Action
(m = 1, (n = 0, l = 0)) → α
1
(m = 1, (n = 1, l = 0)) → α
1
(m = 1, (n = 2, l = 0)) → α
2
(m = 1, (n = 3, l = 0)) → α
2
(m = 1, (n = 4, l = 0)) → α
3
(m = 1, (n = 5, l = 0)) → α
4
Observed state (m,(n, l)) Action
(m = 2, (n = 0, l = 0)) → α
1
(m = 2, (n = 1, l = 0)) → α
1
(m = 2, (n = 2, l = 0)) → α
1
(m = 2, (n = 3, l = 0)) → α
2
(m = 2, (n = 4, l = 0)) → α
2
(m = 2, (n = 5, l = 0)) → α
3
Observed state (m,(n, l)) Action
(m = 3, (n = 0, l = 0)) → α
1
(m = 3, (n = 1, l = 0)) → α
1
(m = 3, (n = 2, l = 0)) → α
1
(m = 3, (n = 3, l = 0)) → α
1
(m = 3, (n = 4, l = 0)) → α
2
(m = 3, (n = 5, l = 0)) → α
3
2
The counter example holds even for some positive
value of c
L
.
SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems
94

Observed state (m,(n, l)) Action
(m = 4, (n = 0, l = 0)) → α
1
(m = 4, (n = 1, l = 0)) → α
1
(m = 4, (n = 2, l = 0)) → α
1
(m = 4, (n = 3, l = 0)) → α
1
(m = 4, (n = 4, l = 0)) → α
1
(m = 4, (n = 5, l = 0)) → α
2
Observed state (m,(n, l)) Action
(m = 5, (n = 0, l = 0)) → α
1
(m = 5, (n = 1, l = 0)) → α
1
(m = 5, (n = 2, l = 0)) → α
1
(m = 5, (n = 3, l = 0)) → α
1
(m = 5, (n = 4, l = 0)) → α
1
(m = 5, (n = 5, l = 0)) → α
1
It is clear that lower and upper thresholds of the opti-
mal policy for m = 2 should be D
2
= 3 and U
2
= 4. If
the policy is monotone, the following must hold:
if n < D
2
=⇒ π
∗
((m = 2, (n, l)), t) = π
∗
((m =
1, (n, l)),t). Let’s check that for n = 2. We have
n < D
2
, if the optimal policy is monotone we have
to conclude that π
∗
((m = 2, (n = 2, l)), t) = π
∗
((m =
1, (n = 2, l)),t). Unfortunately this last equality does
not hold, because from the above tables we have
π
∗
((m = 2, (n = 2, l)),t) = α
1
however: π
∗
((m =
1, (n = 2, l)),t) = α
2
.
Corollary 1. The optimal policy (7) is not isotone.
Proof. From Definition of isotony of (Serfozo, 1979),
monotony is a necessary condition for isotony. How-
ever form Theorems 1 and 2, we deduce that the opti-
mal policy (7) is not isotone.
5 EXPERIMENTAL RESULTS
To model arrivals, this work uses real traffic traces
based on the open clusterdata-2011-2 trace (Wilkes,
2011). We focus on the part that contains the job
events corresponding to the requests destined to a spe-
cific Google data center for the whole month of May
2011. The job events are organized as a table of eight
attributes; where column timestamps refers to the ar-
rival times of jobs expressed in µ-sec. This traffic
trace is sampled with a sampling period equal to the
slot duration. Thus, we consider frames of one minute
to sample the trace and construct one empirical distri-
bution. The obtained distributions are formed respec-
tively of a number of bins between 20 and 100. And
the average of arrival jobs is around 46 jobs per slot.
As PRISM can be used for the specification and anal-
ysis of a Markov decision process (MDP) model, in
Number of jobs
Probability
0 40 80 120
160
200 240 280 320
360
400
0.00
1.24·10
−3
2.49·10
−3
3.74·10
−3
4.99·10
−3
6.24·10
−3
7.49·10
−3
8.74·10
−3
1·10
−2
1.13·10
−2
1.25·10
−2
Number of jobs
Probability
0 40 80 120
160
200 240 280 320
360
400
0.00
1.24·10
−3
2.49·10
−3
3.74·10
−3
4.99·10
−3
6.24·10
−3
7.49·10
−3
8.74·10
−3
1·10
−2
1.13·10
−2
1.25·10
−2
Figure 3: Example of arrival jobs distribution P
A
for two
different days.
this section we use this probabilistic model-checker
software tool to perform our experimentations. In
the following of this section we use PRISM to model
and then analyze data centers with various parame-
ters shown in Table 2. Notice that the buffer sizes are
small because to avoid a hug PRISM model.
Table 2: Settings of different data centers parameters.
Setting DC # servers Buffer # bins
First Small max = 21 b = 31 |S
A
| = 23
Second Medium max = 51 b = 59 |S
A
| = 47
Third Big max = 103 b = 111 |S
A
| = 98
An analysis period of a day (h = 1440 slots) is
considered. Initially, in order to have an experimen-
tation in which the importance of energy and QoS is
the same, we set the unitary costs to the same value:
Discrete-Time MDP Policy for Energy-Aware Data Center
95

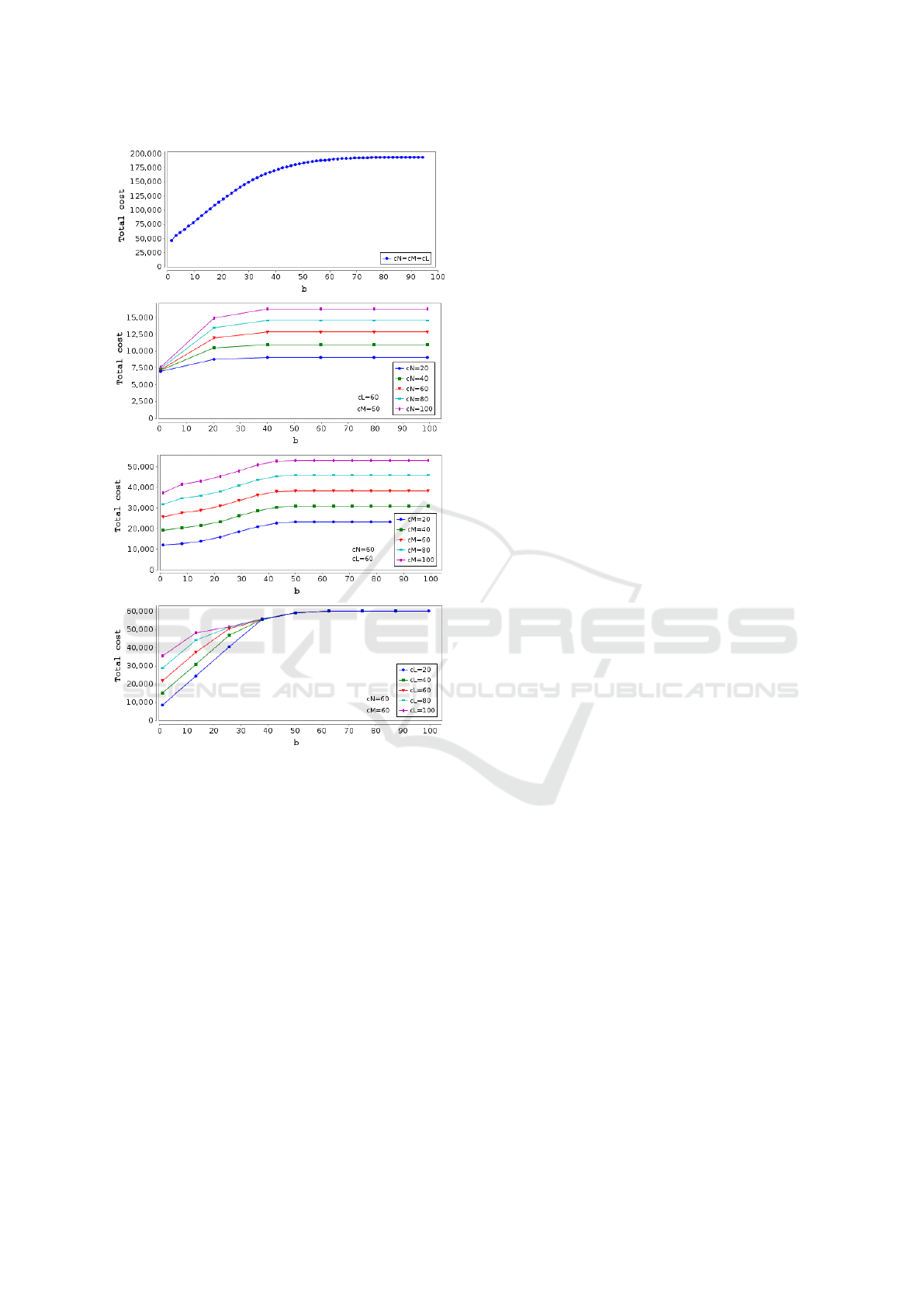
Figure 4: Value of total cost when varying buffer size b for
several values of c
M
, c
N
and c
L
.
c
M
= c
N
= c
L
. Figure 4 resumes the obtained results
for this configuration. However, we have done other
experimentations to analyze the impact of varying the
unitary costs c
M
, c
N
, and c
L
on the total cost. Figure 4
resume the obtained results. The first sub-figure of
Figure 4 shows the result of experiments in which we
are analyzing the total cost over one day when vary-
ing the buffer size b. The second sub-figure presents
analysis for several values of c
N
where keeping c
M
and c
L
constants. The third sub-figure shows an anal-
ysis for several values of c
M
where keeping c
N
and c
L
constants. The last sub-figure shows an analysis for
several values of c
L
where keeping c
N
and c
M
con-
stants.
Observation 1. Total cost increase when b is less
than some value. However, when b is bigger than this
value the total cost seams to be convergent.
We can explain this behavior as following: for a
small size of the buffer, the number of waiting jobs is
low. This leads to a small number of served jobs. In
fact the system switches-on a less number of servers.
So the energetic and also the waiting jobs are low.
When the buffer size is bigger, the number of wait-
ing jobs is more important. Which leads to a bigger
number of served jobs. In fact the system switches-on
more servers. So the energetic and also the waiting
jobs increase. As the arrival jobs are bounded, when
the buffer size is bigger than some value, the number
of waiting jobs and the number of served job become
stationary which leads to a stationary number of run-
ning servers and necessarily to a stationary total cost.
Observation 2. For big values of b, unitary cost for
loosing jobs c
L
does not affect the behavior of the sys-
tem, especially the total cost.
We can explain that by the fact that large value of b
leads to a low rejection rate. In fact the total cost will
not increase so much even if we increase c
L
. How-
ever, for small value of b the rejection rate is more
important and increasing c
L
leads to a higher overall
cost.
6 CONCLUSION
In this work we present an approach based on
discrete-time Markov Decision Process to save en-
ergy in a data center. The system is modeled by a
a queue where job arrivals are modeled by histograms
obtained from an empirical trace. The optimal control
policy is computed by value iteration algorithm. This
optimal policy is used to define the Dynamic Power
Management to insure the trade-off between perfor-
mance and energy consumption. We prove that the
optimal policy is hysteretic but neither isotone nor
monotone, consequently, the optimal policy can not
be designed as a double-threshold structure.
REFERENCES
Alagoz, O. and Ayvaci, M. U. Uniformization in markov
decision processes. Wiley Encyclopedia of Operations
Research and Management Science.
An, H. and Ma, X. (2022). Dynamic coupling real-time en-
ergy consumption modeling for data centers. Energy
Reports, 8:1184–1192.
Bayati, M. (2016). Managing energy consumption and
quality of service in data centers. In Proceedings of
the 5th International Conference on Smart Cities and
Green ICT Systems, pages 293–301.
SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems
96

Bayati, M., Dahmoune, M., Fourneau, J., Pekergin, N., and
Vekris, D. (2016). A tool based on traffic traces and
stochastic monotonicity to analyze data centers and
their energy consumption. EAI Endorsed Trans. En-
ergy Web, 3(10):e3.
Bellman, R. (1957). Dynamic Programming. Princeton
University Press, Princeton, NJ, USA, 1 edition.
Benini, L., Bogliolo, A., Paleologo, G. A., and De Micheli,
G. (1999). Policy optimization for dynamic power
management. IEEE Transactions on Computer-Aided
Design of Integrated Circuits and Systems, 18(6):813–
833.
Benson, T., Akella, A., and Maltz, D. A. (2010). Network
traffic characteristics of data centers in the wild. In
Proceedings of the 10th ACM SIGCOMM conference
on Internet measurement, pages 267–280. ACM.
Bertsekas, D. P. (1995). Dynamic programming and optimal
control, volume 1. Athena Scientific Belmont, MA.
Dyachuk, D. and Mazzucco, M. (2010). On allocation
policies for power and performance. In 2010 11th
IEEE/ACM International Conference on Grid Com-
puting, pages 313–320. IEEE.
Gebrehiwot, M. E., Aalto, S., and Lassila, P. (2016). Op-
timal energy-aware control policies for fifo servers.
Performance Evaluation, 103:41–59.
Greenberg, A. G., Hamilton, J. R., Maltz, D. A., and Patel,
P. (2009). The cost of a cloud: research problems in
data center networks. Computer Communication Re-
view, 39(1):68–73.
Grunwald, D., Morrey, III, C. B., Levis, P., Neufeld, M.,
and Farkas, K. I. (2000). Policies for dynamic clock
scheduling. In Proceedings of the 4th Conference on
Symposium on Operating System Design & Implemen-
tation - Volume 4, OSDI’00, pages 6–6, Berkeley, CA,
USA. USENIX Association.
Hipp, S. K. and Holzbaur, U. D. (1988). Decision pro-
cesses with monotone hysteretic policies. Operations
Research, 36(4):585–588.
Jin, Y., Wen, Y., and Chen, Q. (2012). Energy efficiency
and server virtualization in data centers: An empirical
investigation. In Computer Communications Work-
shops (INFOCOM WKSHPS), 2012 IEEE Conference
on, pages 133–138. IEEE.
Khan, W. (2022). Advanced data analytics modelling for
evidence-based data center energy management.
Koomey, J. (2011). Growth in data center electricity use
2005 to 2010. A report by Analytical Press, completed
at the request of The New York Times, page 9.
Lee, Y. C. and Zomaya, A. Y. (2012). Energy efficient uti-
lization of resources in cloud computing systems. The
Journal of Supercomputing, 60(2):268–280.
Lu, F. and Serfozo, R. F. (1984). M/m/1 queueing decision
processes with monotone hysteretic optimal policies.
Operations Research, 32(5):1116–1132.
Maccio, V. J. and Down, D. G. (2015). On optimal con-
trol for energy-aware queueing systems. In Teletraf-
fic Congress (ITC 27), 2015 27th International, pages
98–106. IEEE.
Mazzucco, M. and Dyachuk, D. (2012). Optimizing cloud
providers revenues via energy efficient server alloca-
tion. Sustainable Computing: Informatics and Sys-
tems, 2(1):1–12.
Mazzucco, M., Dyachuk, D., and Dikaiakos, M. (2010).
Profit-aware server allocation for green internet ser-
vices. In Modeling, Analysis & Simulation of Com-
puter and Telecommunication Systems (MASCOTS),
2010 IEEE International Symposium on, pages 277–
284. IEEE.
Mitrani, I. (2013). Managing performance and power con-
sumption in a server farm. Annals OR, 202(1):121–
134.
Patel, C. D., Bash, C. E., Sharma, R., and Beitelmal, M.
(2003). Smart cooling of data centers. In Proceedings
of IPACK.
Peng, X., Bhattacharya, T., Mao, J., Cao, T., Jiang, C., and
Qin, X. (2022). Energy-efficient management of data
centers using a renewable-aware scheduler. In 2022
IEEE International Conference on Networking, Archi-
tecture and Storage (NAS), pages 1–8. IEEE.
Plum, H.-J. (1991). Optimal monotone hysteretic markov
policies in anm/m/1 queueing model with switching
costs and finite time horizon. Mathematical Methods
of Operations Research, 35(5):377–399.
Puterman, M. L. (1994). Markov Decision Processes. J.
Wiley and Sons.
Rajesh, C., Dan, S., Steve, S., and Joe, T. (2008). Profiling
energy usage for efficient consumption. The Architec-
ture Journal, 18:24.
Rteil, N., Burdett, K., Clement, S., Wynne, A., and
Kenny, R. (2022). Balancing power and perfor-
mance: A multi-generational analysis of enterprise
server bios profiles. In 2022 International Conference
on Green Energy, Computing and Sustainable Tech-
nology (GECOST), pages 81–85. IEEE.
Schwartz, C., Pries, R., and Tran-Gia, P. (2012). A queuing
analysis of an energy-saving mechanism in data cen-
ters. In Information Networking (ICOIN), 2012 Inter-
national Conference on, pages 70–75.
Serfozo, R. F. (1979). Technical note—an equivalence be-
tween continuous and discrete time markov decision
processes. Operations Research, 27(3):616–620.
Tancrez, J.-S., Semal, P., and Chevalier, P. (2009). His-
togram based bounds and approximations for produc-
tion lines. European Journal of Operational Research,
197(3):1133–1141.
Topkis, D. M. (1978). Minimizing a submodular function
on a lattice. Operations research, 26(2):305–321.
Wilkes, J. (2011). More Google cluster data. Google re-
search blog. Posted at http://googleresearch.blogspot.
com/2011/11/more-google-cluster-data.html.
Yang, Z., Chen, M.-H., Niu, Z., and Huang, D. (2011).
An optimal hysteretic control policy for energy saving
in cloud computing. In Global Telecommunications
Conference, pages 1–5. IEEE.
Discrete-Time MDP Policy for Energy-Aware Data Center
97