Effects of Early Warning Emails on Student Performance

Jens Klenke

1 a

, Till Massing

1 b

, Natalie Reckmann

, Janine Langerbein

, Benjamin Otto

Michael Goedicke

and Christoph Hanck

Faculty of Business Administration and Economics, University of Duisburg-Essen, Germany

paluno - The Ruhr Institute for Software Technology, University of Duisburg-Essen, Germany

Keywords:

Learning Analytics, Exam Predictions, Early Warning Systems.

Abstract:

Individual support for students in large university courses is often difﬁcult. To give students feedback regarding

their current level of learning at an early stage, we have implemented a warning system that is intended to

motivate students to study more intensively before the ﬁnal exam. For that purpose, we use learning data

from an e-assessment platform for an introductory mathematical statistics course to predict the probability

of passing the ﬁnal exam for each student. Subsequently, we sent a warning email to students with a low

predicted probability of passing the exam. Using a regression discontinuity design (RDD), we detect a positive

but imprecisely estimated effect of this treatment. Our results suggest that a single such email is only a weak

signal – in particular when they already receive other feedback via midterms, in-class quizzes, etc. – to nudge

students to study more intensively.

1 INTRODUCTION

Introductory courses at universities are often attended

by a large number of students. Many such courses

are in the ﬁrst academic year, with students struggling

with increased anonymity and distributing their work-

load. It is not easy for lecturers to support each stu-

dent individually. One can, however, inform students

if their performance throughout class indicates a high

probability of them failing the ﬁnal exam. (Massing

et al., 2018b) show that it is possible to predict stu-

dents’ outcome in the ﬁnal exam at a relatively early

stage of an introductory statistics course. These early-

warning procedures may help students to better assess

their level of proﬁciency.

For such prediction, it is attractive to use data from

e-learning platforms to gain insights into the students’

learning behavior. In this paper, we use a logit model

to predict the probability of a student passing the ﬁ-

nal exam. For model building, we use data from a

previous cohort of the course. To establish the early-

warning system, we send emails to students of the cur-

rent cohort of the course with a low predicted proba-

bility of passing the ﬁnal exam. This intervention is to

serve as a wake-up call for students who may improp-

https://orcid.org/0000-0001-6292-3968

https://orcid.org/0000-0002-8158-4030

erly assess their level of proﬁciency. We investigate

the effectiveness of said warning emails by using a

regression discontinuity design (RDD). We ﬁnd that

the emails have a positive but imprecisely estimated

effect on the students’ performance in the ﬁnal exam.

The remainder of this paper is organized as fol-

lows: Section 2 describes the statistics course investi-

gated in the study. Section 3 provides a brief overview

of related work. We present the available data and the

models used in section 4. Section 5 discusses the em-

pirical results. Section 6 concludes.

2 COURSE DESCRIPTION

This section outlines the structure of the Inferential

Statistics course at the University of Duisburg-Essen

in 2019, in which students at risk received a warning

email. The course is compulsory for several business

and economics programs and teachers’ training, and

hence we gathered information on 802 students from

JACK and Moodle. Of these 802 students, 337 took

an exam at the end of the semester.

Note that the 802 students’ data in our platforms do not

imply that all of them actively followed the course. JACK

and Moodle are open to many students, not only those who

want or need to participate in the class.

Klenke, J., Massing, T., Reckmann, N., Langerbein, J., Otto, B., Goedicke, M. and Hanck, C.

Effects of Early Warning Emails on Student Performance.

DOI: 10.5220/0011847800003470

In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023) - Volume 1, pages 225-232

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

225

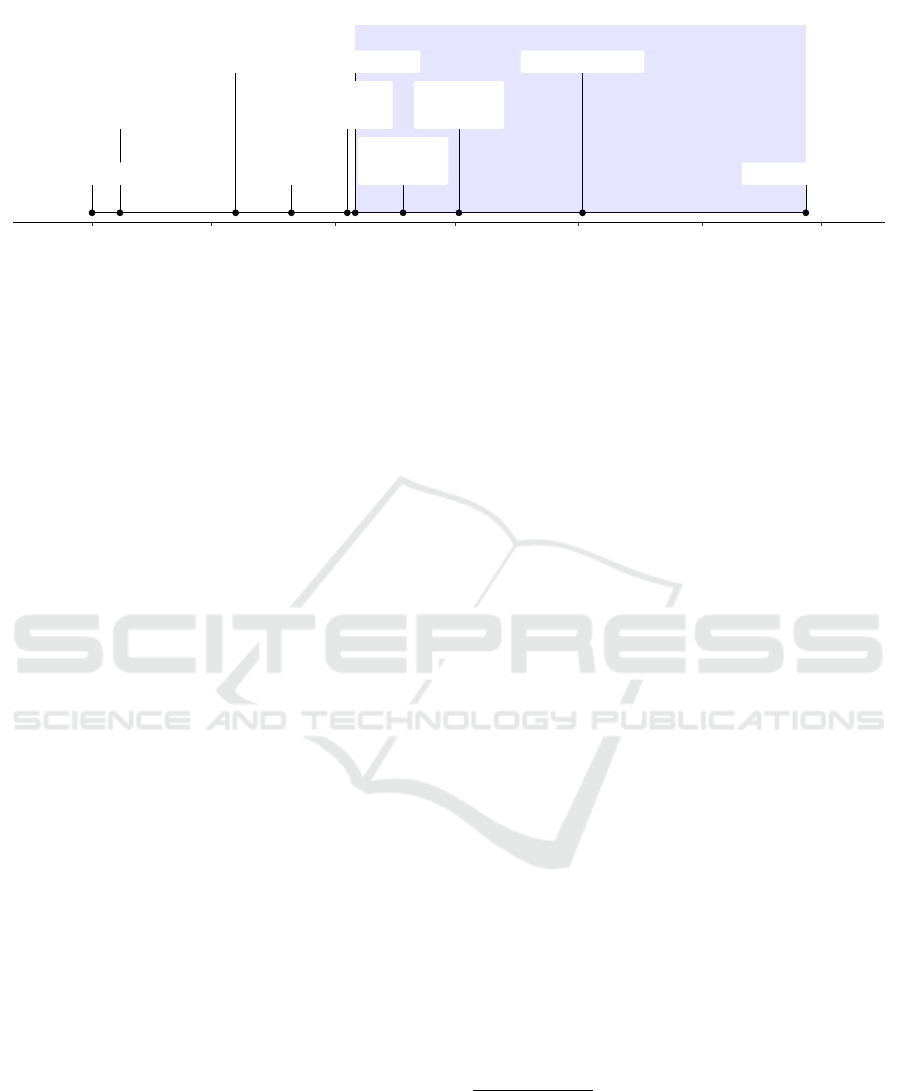
Semester start

Lecture start

Online

test

Online

test

Online

test

Warning mail

Online

test

Online

test

Final exam

Apr Mai Jun Jul Aug Sep Okt

Figure 1: Timeline for the key events in the 2019 summer term course Inferential Statistics (treatment cohort). The shaded

area indicates the period after treatment. There were 57 days between the warning email and the ﬁrst opportunity to take the

exam and 113 days between the warning email and the second opportunity.

The course consisted of a weekly 2-hour lecture,

which introduced concepts, and a 2-hour exercise,

which presented explanatory exercises and problems.

We conducted at least one Kahoot! game in every lec-

ture and exercise. These games were short quizzes

related to the subject of the current class. Students

were able to earn up to 2 bonus points. Both classes

were held classically in front of the auditorium. Be-

cause these classes have many students, they are lim-

ited in their ability to address students’ varying learn-

ing speeds and individual questions. To overcome this

and to encourage self-reliant learning and support-

ing students who had difﬁculties attending classes, all

homework was offered on the e-assessment system

JACK, where the correctness of students’ answers is

automatically assessed.

In addition to classical ﬁll-in and multiple-choice

exercises, the course also introduces the statistics

software R. Individual learning success is supported

by offering speciﬁc automated feedback and optional

hints. Students were able to ask additional questions

in a Moodle help forum.

We offered ﬁve online tests using JACK to en-

courage students to study continuously during the

semester and not only in the weeks prior to the ex-

ams. These tests lasted 40 minutes at ﬁxed time slots.

These summative assessments allowed students to as-

sess their individual state of knowledge during the

lecture. Students did not need to participate in online

tests to take the ﬁnal exam at the end of the course. In-

stead, we offered up to 10 bonus points to encourage

participation. The bonus points were only added to

ﬁnal exam points if students passed the exam without

the bonus. Students may earn up to 60 points in the

exam. We provide more detail on the data in section

Kahoot! games, exercises on JACK, and online

tests already provide students with some feedback

during the semester.

Before the last online test of the previous cohort in

2017

, the points students reached in JACK exercises

and the previous online tests were analyzed to predict

individual probabilities of passing the ﬁnal exams. In

the current cohort in 2019, we split students into three

groups according to the trained model: students with a

high probability of passing the exam, one group with

a moderate probability and the last group with a low

probability of passing the exam. The students in the

last two groups received a warning email, which was

formulated more strictly for those with a low proba-

bility of passing the course.

Students received the warning email shortly after

the third online test on June 6

. The ﬁrst possibility

to take the ﬁnal exam was on August 2

. The sec-

ond and last possibility to take the ﬁnal exam was on

September 27

. Students who did not pass the ﬁnal

exam on the ﬁrst attempt were allowed to retake the

ﬁnal exam. Section 5 will analyze the effectiveness

of the email regarding the passing probability of the

ﬁnal exam.

The ﬁnal exams were also held electronically.

While online tests during the semester could be solved

at home with open books, the ﬁnal exams were of-

fered exclusively at university PC pools and proctored

by academic staff. Students can only retake an exam

if they failed or did not take the previous one (so that

students can pass at most once) but can fail several

times.

The maximum number of points a student

achieves in an exam (over both exams per semester)

determines the ﬁnal grade. We denote the correspond-

ing exam as the ﬁnal exam.

The course is jointly offered by two chairs, and there-

fore held on a rotating basis. Hence, the course is only com-

parable every two years.

Students obtain 6 “malus points” for each failed exam,

of which they may collect up to 180 during their whole

bachelor’s program. This has the side effect that showing

up unprepared and hence failing (many) single exams has

limited consequences. Predicatively, this relates into rela-

tively low passing rates in our program.

CSEDU 2023 - 15th International Conference on Computer Supported Education

226

We summarize the timeline of the main events of

the course in Figure 1.

3 RELATED WORK

Students’ general interest and participation are among

the strongest factors for successful studies (Koc¸ak

et al., 2021; Schiefele et al., 1992). (Sosa et al.,

2011) show in a meta-study that the additional use of

e-assessment in traditional face-to-face courses posi-

tively affects student success. (Massing et al., 2018b)

measure learning effort and learning success via the

total number of (correct) entries on the e-assessment

platform JACK during the course. They can show that

this positively inﬂuences the ﬁnal exam grade.

The literature has identiﬁed a number of important

predictors. (Gray, G. et al., 2014) show the impor-

tance of socioeconomic and psychometric variables

as well as pre-high school grades, which may vary

across countries (Oskouei and Askari, 2014). Vari-

ables that arise after admission to the program, such

as credits earned, degree of exam participation, and

exam success rate in previous courses, are also related

to student success (Baars et al., 2017). (Macfadyen

and Dawson, 2010; Wolff et al., 2013) analyze stu-

dent activity in learning management systems to ac-

curately predict student performance. (Burgos et al.,

2018; Huang and Fang, 2013; Massing et al., 2018a)

use the activity in e-learning frameworks and the re-

sults of midterm exams to predict student success in

the ﬁnal exam, which is particularly useful as these

predictors are related to the exam under consideration.

Some researchers have already worked on identi-

fying students at risk in higher education. (Akc¸apınar

et al., 2019a; Akc¸apınar et al., 2019b; Chen et al.,

2020; Chung and Lee, 2019; Lu et al., 2018) study the

identiﬁcation of students at risk in different contexts

of e-learning systems. They all show that it is pos-

sible to achieve high accuracy in predicting student

success early in the semester. Furthermore, (Ba

neres

et al., 2020) implemented an early warning system.

However, they did not analyze the effect of the sys-

tem on students’ performance.

To summarize, data on student learning activity

can be used for the implementation of early warn-

ing systems. Purdue University (West Lafayette), In-

diana, developed the early warning system Course

Signals, see (Arnold, 2010). Email notiﬁcations and

signal lights (red, yellow, and green) inform stu-

dents of their learning status. (Arnold and Pistilli,

2012) analyze the retention and performance out-

comes achieved since the introduction of Course Sig-

nals. They ﬁnd that using this early warning system

substantially affects students’ grades and retention be-

havior. (S¸ahin and Yurdug

ul, 2019) developed, based

on learning analytics, an intervention engine called

the Intelligent Intervention System (In2S). In this sys-

tem, students see signal lights for each assessment

task, representing a direct intervention in the class-

room. The system uses gamiﬁcation elements such

as a leaderboard, badges, and notiﬁcations as an ad-

ditional motivational intervention. Learners who use

In2S emphasize the system’s usefulness.

(Mac Iver et al., 2019) examined the effects of

a ninth-grade early warning system on student at-

tendance and percentage of credits earned in ninth

grade. They could not ﬁnd a statistically signiﬁcant

impact of the intervention. (Edmunds and Tancock,

2002; Stanﬁeld, 2008) investigate the effects of dif-

ferent incentives on third or fourth-graders’ reading

motivation. (Edmunds and Tancock, 2002; Mac Iver

et al., 2019; Stanﬁeld, 2008) ﬁnd no signiﬁcant dif-

ferences in reading motivation between students who

received incentives and those who did not. (Parkin

et al., 2012) used a range of technical interventions

that can encourage the effort level. They can show

that online posting of grades, feedback and adaptive

grade release signiﬁcantly improve students’ engage-

ment with their feedback.

Most researchers analyze the corresponding early

warning system qualitatively via questionnaires using

linear regression (OLS). (Laur

ıa et al., 2013) show

that their warning system leads to a higher dropout

rate of students receiving a warning. An increased

dropout rate is often viewed negatively. However,

they argue that there are also many positive aspects

from the perspective of students and instructors, such

as a higher focus on other courses, less sunk cost, and

fewer students to supervise, which may increase sup-

port for other students.

OLS cannot be used in our settings. The issue is

that the warning is inherently not assigned randomly

but instead based on student performance. Therefore

a standard OLS regression of student success on, e.g.,

variables such as whether a warning was issued would

not identify the causal effect of the warning. Such a

regression would be confounded with unobserved in-

ﬂuences such as general ability or motivation, which

both affect the outcome, student success, as well as

whether a student receives a warning as the warning

is issued to those students, which will be less quali-

ﬁed/motivated on average compared to students who

have not received a warning.

However, regression discontinuity designs (RDD)

may be suitable in such settings as the method can

isolate the potential effect from other inﬂuences. In

this design, there are two groups of individuals, in

Effects of Early Warning Emails on Student Performance

227

which one group receives a speciﬁc treatment, such

as an early warning. A running variable, W , gives

the individual probability for each student to pass the

exam. The value of this running variable lying on ei-

ther side of a ﬁxed threshold determines the assign-

ment to the two groups. Comparing individuals with

values of the running variable below the threshold to

those just above can be used to estimate the causal ef-

fect of the treatment on a speciﬁc outcome. (McEwan

and Shapiro, 2008) use regression discontinuity ap-

proaches to estimate the effect of delayed school en-

rollment on student outcomes, as these students will

be similar w.r.t. observed as well as unobserved con-

founders such as those mentioned below.

(Angrist, J. D. and Lavy, V., 1999) use the RDD

approach to estimate the effect of class size on test

scores. (Jacob and Lefgren, 2004) studied the effect

of remedial education on student achievement. More

details on RDD will be provided in the next section.

4 DATA AND MODEL

This section presents the data and model used for the

analysis. The raw data is collected from three differ-

ent sources. First, we collected each student’s home-

work submissions on JACK, where we monitored the

exercise ID, student ID, the number of points (on a

scale from 0 to 100) and the time stamp with a minute-

long precision. The second data source comprises

the online tests, whereby the student may earn ex-

tra points for their ﬁnal grade, see section 2. Until

the treatment was assigned, three out of ﬁve online

tests were conducted. Lastly, the response variable

is given by their ﬁnal exam result. For students’ ﬁ-

nal grades, which consist of the ﬁnal exam result and

earned bonus points, the following grading scheme

was applied: very good (“1”), good (“2”), satisfactory

(“3”), sufﬁcient to pass (“4”), and failed (“5”). We

assigned “6” to 465 students who participated in the

course but did not take any ﬁnal exams.

This reﬂects

our view that students who did not take any exam

were even less prepared than students who failed the

exams.

Over the whole course, JACK registered 175, 480

submissions of homework exercises from students.

For each student, we compute the score (JACK score

in Table 1) as the sum of the points of the latest sub-

mission over all subtasks.

To determine who should receive a treatment

(warning email), we mainly considered the results

Postponing exams to later semesters is possible and

common in our program.

from the ﬁrst three online tests, which had been con-

ducted until then. We used a logit model to predict

the probability that a student with these online test re-

sults would pass the exam. The model was trained

with the data obtained from the same course given

two years earlier, see (Massing et al., 2018b; Massing

et al., 2018a). The predicted probability will serve as

our running variable W in the RDD, see equation (1)

below. These predictions were transformed to an or-

dinal variable. If the predicted probability of passing

the exam was larger than 0.4, the student was be sup-

plied with no message (0 in Table 1), and with less

than 0.4 with a warning message (1 in Table 1).

However, as the online tests were not mandatory,

we further considered the students’ general activity

during the course and thus modiﬁed the decision on

whether an email was sent for a subset of the students.

By taking into account activity during the course, we

eliminate two disadvantages that could arise if we

solely built the treatment on the online tests.

First, the online tests were not mandatory, and not

all students took the online test – despite the high in-

centive to earn extra points for their ﬁnal grade.

Second, the students were allowed to cooperate

during the online tests, although all students were

graded individually. This could potentially lead to a

student performing well in the online tests, although

he did not comprehend the course content that well.

Given our data and treatment design, which were

not distributed randomly but rather based on the prob-

ability to pass the exam, we use the RDD to analyze

the effectiveness of our intervention.

The method allows us to compare students around

the cutoff point and hence to causally identify a pos-

sible treatment effect. Our identifying assumption is

that the participants around the cutoff are similar with

respect to other (important) properties. Such determi-

nants, for example, include the general or quantitative

ability. To distinguish between the different RD de-

signs, ﬁrst consider

= β

+ αT

+ βW

+ u

(1)

and let

(

1, W

≤ c,

0, W

> c,

(2)

where T

indicates if a student received an email,

which is determined by the threshold c, in our case

There are several possible explanations for that. E.g.,

perhaps some students could not participate due to other

commitments since the online tests were held at a ﬁxed date

and time.

We also investigated alternative modeling approaches

like propensity score matching. However, the results were

similar, and RDD seems most suitable given the problem.

CSEDU 2023 - 15th International Conference on Computer Supported Education

228

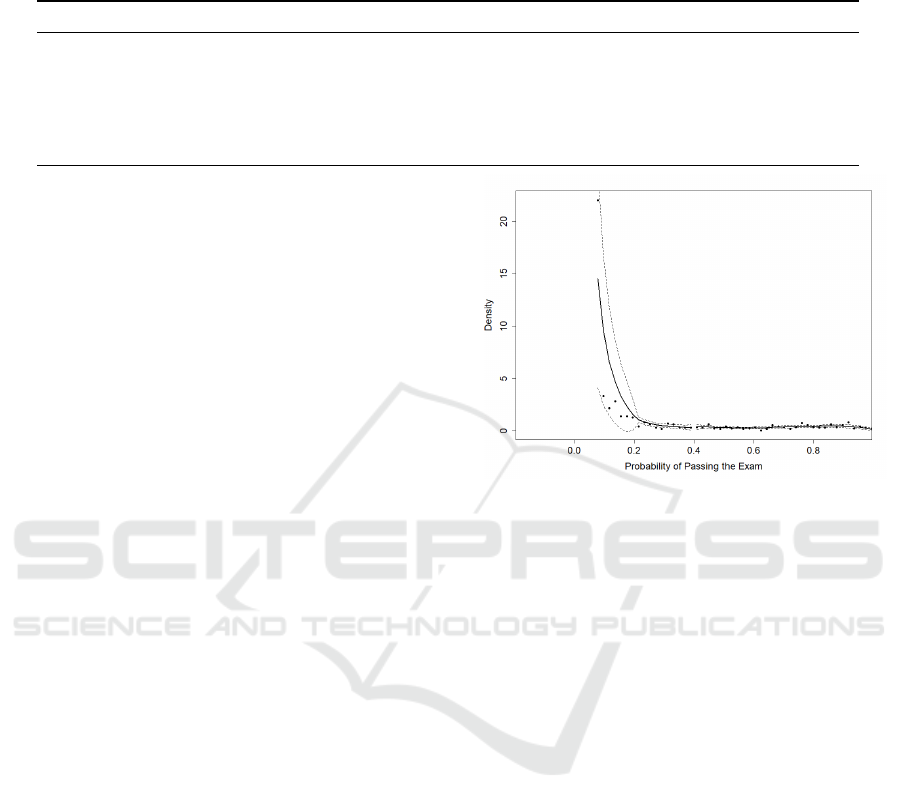
Table 1: Overview of empirical quartiles, mean and standard deviation for the response variable and considered covariates.

Exam points describes the points reached in the ﬁnal exam. Online test is the sum of the ﬁrst four online tests, while the JACK

score describes the score until the warning mail was sent.

variable warning count min Q0.25 median mean Q0.75 max sd

Exam points 0 151 3.40 17.50 25.30 23.80 30.00 47.00 8.20

1 183 0.00 8.55 15.60 16.10 23.10 39.20 9.52

Online test 0 191 341.00 579.00 755.00 761.00 900.00 1425.00 221.00

1 607 0.00 0.00 0.00 98.50 167.00 700.00 133.00

JACK score 0 191 0.00 2216.00 3520.00 3799.00 5174.00 11580.00 2206.00

1 425 0.00 200.00 983.00 1347.00 2033.00 8385.00 1363.00

0.4 of the predicted probability to pass the exam W

is the sum of points of student i in their (latest) ﬁnal

exam, and u

is an error term. For the analysis, only

students who attended at least one ﬁnal exam were

included (n = 337). This design deterministically as-

signs the treatment, which means that only if W

≤ c

will the student receive the treatment. The treatment

effect is represented by α.

The approach sketched above is a sharp RDD

since the two groups (treatment, no treatment) are per-

fectly separated by the cutoff.

However, as explained above, this is not the case

in our design as we also wanted to consider the stu-

dent’s activity in the course in our decision. Thus, the

groups are no longer perfectly separated.

We, therefore, employed an extension of this de-

sign, called fuzzy RDD. In this case, only the prob-

ability of receiving the treatment needs to increase

considerably at the cutoff and not from 0 to 1, as

in the sharp design. This non-parametric approach

estimates a local average treatment effect (LATE) α

in equation (3) through an instrumental variable (IV)

setting (Angrist et al., 1996).

More speciﬁcally, consider the following model

= β

+ α

+ δ

+ X

β + u

(3)

= γ

+ γ

+ ν

, (4)

where equation (4) represents the ﬁrst stage of the IV

estimation with T

denoting if a student received the

treatment, the instrument Z

= 1 [W

≤ c] indicating if

a student is below or above the cutoff of c = 0.4 (as

in the sharp RDD), W

remains the predicted proba-

bility to pass the exam from the logit model, while

represents an error term. The ﬁtted values

of T

are inserted into equation (3), where Y

again repre-

sents the sum of points of student i in their (latest)

ﬁnal exam. u

represents the error term, X

a covariate

– here the sum of points of online tests – and α the

treatment effect.

The following assumptions must be met to iden-

tify a potential treatment effect; (i) the running vari-

able W needs to be continuous around the cutoff, see

(McCrary, 2008). If this assumption is not met, it

Figure 2: The McCrary sorting test for the running variable

W predicted probability to pass the exam (x-axis). There

is no jump in the density around the cutoff point of 0.4,

i.e., the density left, and right of the cutoff do not differ

substantially.

could indicate that participants can manipulate the

treatment. Furthermore, the general assumptions for

IV estimation must hold. Therefore, (ii) instrument Z

only appears in equation (4) for T and not in equation

(3) for Y (the exclusion restriction). (iii) Instrument Z

must be correlated with the endogenous explanatory

variable T (Cameron and Trivedi, 2005, pp. 883-885).

We will return to assumption (i) in section 5. The

exclusion restriction for the instrument variable Z

holds since the variable is only an indicator variable

showing whether a student is to the left or right of

the cutoff (c = 0.4), and the probability of passing the

exam is also already included in the second stage of

the design. Assumption (iii) is satisﬁed in an RDD

model by the construction of the approach as the in-

strument is a nonlinear (step) transformation of the

running variable (Lee and Lemieux, 2010).

5 EMPIRICAL RESULTS AND

DISCUSSION

Table 1 shows that the treatment (warning = 1) and

control (warning = 0) groups, as expected, differ sub-

Effects of Early Warning Emails on Student Performance

229

Figure 3: Graphical illustration of the RDD with the proba-

bility to pass the exam W on the x-axis and the exam points

Y on the y-axis. At the cutoff point of c = 0.4, we cannot

see any (major) decrease in earned exam points.

stantially. The performances in the online tests and

JACK score

, are much lower in the treatment group.

This also illustrates that a single OLS regression of Y

on T

would fail to identify the effect of the interven-

tion.

We ﬁrst check that the assumption (i) of a continu-

ous running variable with no jump at the cutoff is met.

For this, we perform the (McCrary, 2008) sorting test,

which tests the continuity of the density of our run-

ning variable W – the predicted probability of passing

the exam – around the cutoff. In order to estimate the

effect α correctly, there must not be a jump in the den-

sity at the cutoff. Otherwise, some participants could

have manipulated the treatment, and the results would

no longer be reliable.

The McCrary sorting test indicates no discontinu-

ity of the density around the cutoff with a p-value of

0.509; see Figure 2. Since there is no jump around

the cutoff and the students were not informed before-

hand about the warning email, we can be relatively

conﬁdent that the students were not able to manipu-

late the treatment. In any case, the incentive to worsen

one’s own performance to receive the treatment seems

rather small as there is no direct beneﬁt from receiv-

ing the warning. The idea and a possible effect of the

email lie in a change in the effort students invest from

that time on.

We employed the non-parametric local average

treatment effect (LATE) method to estimate the causal

effect. This RDD method only compares the local av-

erage around the cutoff (c = 0.4) rather than ﬁtting

a polynomial regression.

This method is more efﬁ-

Note that students may partially or entirely study out-

side of the JACK framework. However, since the ﬁnal exam

was taken via JACK, students have a strong incentive to

mainly learn on the platform to get used to the framework.

We also performed the RDD using polynomial regres-

Table 2: Model 1 summarises the RDD model without and

Model 2 with covariates. LATE describes the Local Average

Treatment Effect. The bandwidth and F-statistics report the

(Imbens and Kalyanaraman, 2009) bandwidth and the F-

statistics for the non-parametric estimation. N is the number

of observations used.

Model 1 Model 2

LATE

0.193

(4.889)

0.146

(4.852)

Bandwith 0.255 0.255

F-statistics 0.257 0.257

N 126 126

Note: Standard errors are indicated within parenthesis.

∗

p < 0.1,

∗∗

p < 0.05,

∗∗∗

p < 0.01.

cient than polynomial regression since the estimation

involves fewer parameters. Furthermore, we avoid the

common concerns of ﬁtting polynomial regressions,

e.g., determining the polynomial degree and the ten-

dencies to extremes at the edges (Lee and Lemieux,

2010). We performed all RDD regressions with and

without covariates, which is usually not necessary in

the sharp setting but is often recommended in the

fuzzy design to get a more precise estimate of the

treatment effect. Including covariates can increase the

explained variance of the model (Huntington-Klein,

2022, p. 515).

The effect point estimates (LATE) in Table 2 of

the two non-parametric RDD models are positive but

not signiﬁcant (parameter α in equation (3)). Figure 3

gives a graphical illustration of the model. The LATE

is 0.193 for the estimation without covariates (model

1 in Table 2) and 0.146 if we include the covariates

(model 2 in Table 2), with corresponding standard

errors of 4.889 and 4.852. An estimate of 0.193 or

0.146 means that students who received the warning

email achieved 0.193 or 0.146 points more than com-

parable students who did not. Compared to the 60-

point ﬁnal exam, the effect size seems limited.

The bandwidth of 0.255 was determined with the

data-driven approach of (Imbens and Kalyanaraman,

2009). The method ﬁts the bandwidth as widely as

possible without introducing other confounding ef-

fects, e.g., general ability. Therefore, only students

with a predicted probability between 0.145 and 0.655

,0.4 (cutoff) ± 0.255 (bandwidth), are included in the

analysis. This leads to a sample size for the estimation

of 126 students (N). Other bandwidths were consid-

ered in the estimation process but were too conserva-

tive or violated the assumption that the groups around

the cutoff must be comparable. We provide further

sion. The results were essentially identical to those of the

LATE method.

CSEDU 2023 - 15th International Conference on Computer Supported Education

230

discussion in section 6.

Hence, our RDD results do not provide evidence

that the warning email has a signiﬁcant effect on the

students’ results (or behavior). This might have sev-

eral reasons. For instance, many participants who re-

ceived a warning did not participate in any ﬁnal exam.

Of the 608 students who received a warning, only

183 sat the exam. This likely compromises the de-

tection of an effect. A possible explanation is that the

warning might lead weak students to postpone par-

ticipation to a later semester. The email could give

students the impression that the chances of getting a

good grade are already relatively low. Therefore, stu-

dents might be more likely to repeat the course a year

later. In a sense, this can also be viewed as a positive

outcome, as we then at least prevent students from

collecting malus points, cf. footnote 2.

The non-parametric method used here has the dis-

advantage that (many) students, which are relatively

far from the cutoff, are not included in the analysis.

This reduces the effective sample size, and thus pre-

cise estimation of the treatment becomes more difﬁ-

cult. Figure 3 suggests another potential issue: both

groups’ variance around the cutoff (c = 0.4) is rather

high.

Another important aspect of this analysis is that

students can get feedback on their proﬁciency JACK

homework and earn extra points through the online

tests and the Kahoot! games. From the perspective of

the students, this is probably an even bigger incentive

than the warning email. Hence, the incremental effect

of the warning email may be limited. Further incen-

tives and feedback combined with the warning emails

during the semester, might have a greater effect on

student performance than the warning emails alone.

6 CONCLUSIONS

In this paper, we analyzed whether students who per-

form relatively poorly in a current course can be pos-

itively inﬂuenced by a warning email. Even though

we did not ﬁnd a signiﬁcant effect of the treatment,

we see the open and transparent communication of

the student’s performance to the students as a posi-

tive aspect of the system. Furthermore, we are con-

sidering expanding the system further. One possible

approach we are currently viewing is implementing

an automatic repeatedly system for detecting inactive

students or students whose submissions show little

progress, which will regularly notify students at risk.

One more aspect that requires attention in the fu-

ture is the investigation of a possible effect of the

warning system on the dropout rate, i.e., whether the

email leads to more students withdrawing from the

exam beforehand and thus increasing the pass rate.

However, a higher dropout rate is not inherently neg-

ative. Students can focus on other courses and thus

achieve higher grades.

To conclude, we do not detect a signiﬁcant effect

of the warning emails in our design. This is still note-

worthy because the successful motivation of weak and

modest students remains challenging for instructors.

ACKNOWLEDGMENTS

We thank all colleagues who contributed to the course

“Induktive Statistik” in the summer term 2019.

Part of the work on this project was funded by the

German Federal Ministry of Education and Research

under grant numbers 01PL16075 and 01JA1910 and

by the Foundation for Innovation in University Teach-

ing under grant number FBM2020-EA-1190-00081.

REFERENCES

Akc¸apınar, G., Altun, A., and As¸kar, P. (2019a). Using

learning analytics to develop early-warning system for

at-risk students. International Journal of Educational

Technology in Higher Education, 16(1):1–20.

Akc¸apınar, G., Hasnine, M. N., Majumdar, R., Flanagan, B.,

and Ogata, H. (2019b). Developing an early-warning

system for spotting at-risk students by using ebook in-

teraction logs. Smart learning environments, 6(1):1–

15.

Angrist, J. D., Imbens, G., and Rubin, D. B. (1996). Iden-

tiﬁcation of causal effects using instrumental vari-

ables. Journal of the American Statistical Association,

91(434):444–455. Publisher: Taylor & Francis.

Angrist, J. D. and Lavy, V. (1999). Using maimonides’

rule to estimate the effect of class size on scholas-

tic achievement. The Quarterly journal of economics,

114(2):533–575.

Arnold, K. E. (2010). Signals: Applying academic analyt-

ics. Educause Quarterly, 33(1):10.

Arnold, K. E. and Pistilli, M. (2012). Course signals at pur-

due: using learning analytics to increase student suc-

cess. In ACM International Conference Proceeding

Series, LAK ’12, pages 267–270. ACM.

Baars, G. J. A., Stijnen, T., and Splinter, T. A. W. (2017).

A model to predict student failure in the ﬁrst year of

the undergraduate medical curriculum. Health profes-

sions education, 3(1):5–14.

neres, D., Rodr

ıguez, M. E., Guerrero-Rold

an, A. E., and

Karadeniz, A. (2020). An early warning system to de-

tect at-risk students in online higher education. Ap-

plied Sciences, 10(13):4427.

Burgos, C., Campanario, M., de la Pe

na, D., Lara, J. A.,

Lizcano, D., and Mart

ınez, M. A. (2018). Data min-

Effects of Early Warning Emails on Student Performance

231

ing for modeling students’ performance: A tutoring

action plan to prevent academic dropout. Computers

& Electrical Engineering, 66:541–556.

Cameron, A. C. and Trivedi, P. K. (2005). Microecono-

metrics : methods and applications. Cambridge Univ.

Press.

Chen, Y., Zheng, Q., Ji, S., Tian, F., Zhu, H., and Liu,

M. (2020). Identifying at-risk students based on the

phased prediction model. Knowledge and Information

Systems, 62(3):987–1003.

Chung, J. Y. and Lee, S. (2019). Dropout early warning sys-

tems for high school students using machine learning.

Children and Youth Services Review, 96:346–353.

S¸ ahin, M. and Yurdug

ul, H. (2019). An intervention en-

gine design and development based on learning an-

alytics: the intelligent intervention system (in 2 s).

Smart Learning Environments, 6(1):18.

Edmunds, K. and Tancock, S. M. (2002). Incentives: The

effects on the reading motivation of fourth-grade stu-

dents. Reading Research and Instruction, 42(2):17–

37.

Gray, G., McGuinness, C., and Owende, P. (2014). An

application of classiﬁcation models to predict learner

progression in tertiary education. In International

Advance Computing Conference (IACC), pages 549–

554. IEEE.

Huang, S. and Fang, N. (2013). Predicting student academic

performance in an engineering dynamics course: A

comparison of four types of predictive mathematical

models. Computers & Education, 61:133–145.

Huntington-Klein, N. (2022). The effect : an introduction

to research design and causality. Chapman & Hall

book. CRC Press, Taylor & Francis Group, Boca Ra-

ton ; London ; New York, ﬁrst edition edition.

Imbens, G. and Kalyanaraman, K. (2009). Optimal band-

width choice for the regression discontinuity esti-

mator. National Bureau of Economic Research,

1(14726).

Jacob, B. A. and Lefgren, L. (2004). Remedial ed-

ucation and student achievement: A regression-

discontinuity analysis. Review of economics and

statistics, 86(1):226–244.

Koc¸ak,

O., G

oksu,

I., and G

oktas, Y. (2021). The factors

affecting academic achievement: A systematic review

of meta analyses. International Online Journal of Ed-

ucation and Teaching, 8(1):454–484.

Laur

ıa, E. J., Moody, E. W., Jayaprakash, S. ., Jonnala-

gadda, N., and Baron, J. D. (2013). Open academic

analytics initiative: initial research ﬁndings. In Pro-

ceedings of the Third International Conference on

Learning Analytics and Knowledge, pages 150–154.

Lee, D. S. and Lemieux, T. (2010). Regression discontinu-

ity designs in economics. 48(2):281.

Lu, O. H. T., Huang, A. Y. Q., Huang, J. C. H., Lin, A.

J. Q., Ogata, H., and Yang, S. J. H. (2018). Applying

learning analytics for the early prediction of students’

academic performance in blended learning. Journal of

Educational Technology & Society, 21(2):220–232.

Mac Iver, M. A., Stein, M. L., Davis, M. H., Balfanz, R. W.,

and Fox, J. H. (2019). An efﬁcacy study of a ninth-

grade early warning indicator intervention. Journal

of Research on Educational Effectiveness, 12(3):363–

390.

Macfadyen, L. P. and Dawson, S. (2010). Mining LMS

data to develop an ”early warning system” for edu-

cators: A proof of concept. Computers & Education,

54(2):588–599.

Massing, T., Reckmann, N., Otto, B., Hermann, K. J.,

Hanck, C., and Goedicke, M. (2018a). Klausurprog-

nose mit Hilfe von E-Assessment-Nutzerdaten. In

DeLFI 2018 - Die 16. E-Learning Fachtagung Infor-

matik, pages 171–176.

Massing, T., Schwinning, N., Striewe, M., Hanck, C., and

Goedicke, M. (2018b). E-assessment using variable-

content exercises in mathematical statistics. Journal

of Statistics Education, 26(3):174–189.

McCrary, J. (2008). Manipulation of the running variable

in the regression discontinuity design: A density test.

Journal of Econometrics, 142(2):698–714.

McEwan, P. J. and Shapiro, J. S. (2008). The beneﬁts of

delayed primary school enrollment discontinuity esti-

mates using exact birth dates. The Journal of human

Resources, 43(1):1–29.

Oskouei, R. J. and Askari, M. (2014). Predicting Academic

Performance with Applying Data Mining Techniques

(Generalizing the results of Two Different Case Stud-

ies). Computer Engineering and Applications Jour-

nal, 3(2):79–88.

Parkin, H. J., Hepplestone, S., Holden, G., Irwin, B., and

Thorpe, L. (2012). A role for technology in enhancing

students’ engagement with feedback. Assessment &

Evaluation in Higher Education, 37(8):963–973.

Schiefele, U., Krapp, A., and Winteler, A. (1992). In-

terest as a predictor of academic achievement: A

meta-analysis of research, chapter 8, pages 183–212.

Lawrence Erlbaum Associates, Inc, New York, 1 edi-

tion.

Sosa, G. W., Berger, D. E., Saw, A. T., and Mary, J. C.

(2011). Effectiveness of computer-assisted instruction

in statistics: A meta-analysis. Review of Educational

Research, 81(1):97–128.

Stanﬁeld, G. M. (2008). Incentives: The effects on reading

attitude and reading behaviors of third-grade students.

The Corinthian, 9(1):8.

Wolff, A., Zdrahal, Z., Nikolov, A., and Pantucek, M.

(2013). Improving retention: Predicting at-risk stu-

dents by analysing clicking behaviour in a virtual

learning environment. In Proceedings of the Third

International Conference on Learning Analytics and

Knowledge, LAK ’13, pages 145–149, New York, NY,

USA. ACM.

CSEDU 2023 - 15th International Conference on Computer Supported Education

232