Exploiting Context in Handwriting Recognition Using Trainable

Relaxation Labeling

Sara Ferro

2,1,∗ a

, Alessandro Torcinovich

3,∗ b

, Arianna Traviglia

1 c

and Marcello Pelillo

2,1 d

Center for Cultural Heritage Technology, Italian Institute of Technology, Venice, Italy

DAIS, Ca’ Foscari University of Venice, Venice, Italy

Department of Computer Science, ETH Z

urich, Z

urich, Switzerland

Keywords:

Handwriting Recognition, Relaxation Labeling Processes, Generalisation.

Abstract:

Handwriting Text Recognition (HTR) is a fast-moving research topic in computer vision and machine learning

domains. Many models have been introduced over the years, one of the most well-established ones being

the Convolutional Recurrent Neural Network (CRNN), which combines convolutional feature extraction with

recurrent processing of the visual embeddings. Such a model, however, presents some limitations such as a

limited capability to account for contextual information. To counter this problem, we propose a new learning

module built on top of the convolutional part of a classical CRNN model, derived from the relaxation labeling

processes, which is able to exploit the global context reducing the local ambiguities and increasing the global

consistency of the prediction. Experiments performed on three well-known handwritten recognition datasets

demonstrate that the relaxation labeling procedures improve the overall transcription accuracy at both character

and word levels.

1 INTRODUCTION

The increased availability of digitized large collec-

tions of ancient and historical manuscripts in the

form of digital images is increasingly providing the

opportunity to convert past scripts into machine-

readable text formats and create digital storages of

editable content. Advancements both in layout analy-

sis and text recognition are currently paving the way

for making digitized manuscript content fully ma-

chine searchable and readable. Automatic letter/word

recognition of ancient and historic texts, however, still

has many inherent complexities. Besides the broad

range of handwriting across several centuries, there

are also many varieties in the shape of the letters due

to the writing tool type and width within the same

group of scripts; in addition, individual scribes might

have had different handwriting (e.g. in letters shape

and size), this being a common feature, especially

https://orcid.org/0000-0001-9937-7112

https://orcid.org/0000-0001-8110-1791

https://orcid.org/0000-0002-4508-1540

https://orcid.org/0000-0001-8992-9243

∗

Equal contributions, authors listed in alphabetical or-

der

for historical documents. Transcription of handwrit-

ten text from badly preserved documents is also made

more difﬁcult by the deterioration of the writing sup-

port (paper, parchment or others).

Even though, at present, handwriting transcrip-

tion has shown promising performances (Teslya and

Mohammed, 2022), (Lombardi and Marinai, 2020),

thanks to both the development of sequential mod-

els which are compatible with the sequential nature

of handwriting scripts, attention-based models, and

a mixture of both there still is a long way to go.

During the processing of the input text image, recur-

rent sequential models take into account past informa-

tion, as Long-Short Term Memory (LSTM) networks

(Hochreiter and Schmidhuber, 1997), past and future

information, as Bidirectional LSTM (BLSTM) net-

works, and multi-directional information, as Multi-

Directional LSTM (MDLSTM) networks. These

models have improved thanks to the inclusion of con-

volutional layers, which proved to be able to extract

informative features from data (Puigcerver, 2017)

(Retsinas et al., 2022). Sequential model capabili-

ties have been enhanced by using attention mecha-

nisms that weigh more the “most important” input

data (Bluche et al., 2017). Gating mechanisms bor-

rowed from LSTMs and GRUs were also used to-

574

Ferro, S., Torcinovich, A., Traviglia, A. and Pelillo, M.

Exploiting Context in Handwriting Recognition Using Trainable Relaxation Labeling.

DOI: 10.5220/0011849300003411

In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 574-581

ISBN: 978-989-758-626-2; ISSN: 2184-4313

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

gether with Convolutional Neural Networks (CNNs)

to retain relevant information, showing competitive

results compared to more classical Convolutional Re-

current Neural Network (CRNN) models (Coquenet

et al., 2019). However, non-sequential models with

attention mechanisms have outperformed sequential

ones (Li et al., 2021).

Relaxation labeling procedures are parallel it-

erative processes able to simultaneously take data

into account. Data is therefore processed in a non-

sequential manner. This feature enables the model to

learn the context in relation to all characters in the

text line. In addition, they are able to reﬁne the out-

puts concurrently, and not just one at a time. These

characteristics were introduced with attention-based

non-sequential models based on the (Vaswani et al.,

2017) Transformer architecture.

Although the models mentioned above are efﬁ-

cient at solving the problem of sequence labeling (as

in the case of handwriting recognition), how to prop-

erly embed and use contextual information is still an

open question. Relaxation labeling processes proved

to be able to include useful contextual information, as

they reduce both local ambiguities and achieve global

consistency. These are in fact parallel iterative label-

ing processes capable of performing the exploitation

of contextual information.

Relaxation labeling processes for consistent label-

ing represented a fundamental model in the past in

solving tasks such as text recognition (Goshtasby and

Ehrich, 1988). Research, however, shifted its focus

to neural network-based approaches (Lombardi and

Marinai, 2020). This was probably due to one of the

main disadvantages of these processes: the need to

deﬁne the compatibility coefﬁcients a-priori. To ad-

dress this problem, (Pelillo and Reﬁce, 1994) showed

that a forward propagation error strategy is effective

in learning good compatibilities in the ﬁeld of Natural

Language Processing.

In this paper, we include relaxation labeling pro-

cesses in a well-established neural network architec-

ture in the HTR ﬁeld, the CRNN, to further reﬁne the

labeling output. We use a novel learning scheme for

the parameters, i.e. the compatibility coefﬁcients, of

relaxation labeling processes to be learned together

with those of the neural network. We conducted ex-

periments which demonstrated the ability of relax-

ation labeling processes to improve the model gen-

eralisation capability.

2 HANDWRITING

RECOGNITION MODEL

In this Section, we revise the theoretical framework

of relaxation labeling and describe our proposed so-

lution for handwritten text recognition.

2.1 Consistent Labeling Problem

Many models have been introduced to solve the so-

called consistent labeling problem, a class of prob-

lems widely studied in computer vision, pattern

recognition and artiﬁcial intelligence ﬁelds (Haralick

and Shapiro, 1979). These problems involve label-

ing a set of objects such that certain domain-speciﬁc

constraints must be satisﬁed: given a set of objects,

there exist labeling conﬁgurations that are impossible.

For example, in the case of character-level labeling in

a line of English text, if we were to decide to label

with a character knowing that the preceding charac-

ter is a comma, we would choose a space. Indeed,

the character space always follows such punctuation.

Attempts in formalizing the notion of consistent la-

beling culminated in the seminal paper of Hummel

and Zucker (Hummel and Zucker, 1983), who devel-

oped a formal theory of consistency that later turned

out to have intimate connections with non-cooperative

game-theory (Miller and Zucker, 1991). The theory

generalizes the classical constraint satisfaction prob-

lem, where the constraints are boolean, to soft com-

patibility measures and probabilistic labeling assign-

ments (Rosenfeld et al., 1976). It is possible to solve

the ﬁrst kind of problem through discrete relaxation

labeling processes instead continuous relaxation la-

beling, also named probabilistic relaxation labeling

processes, can solve the second one. We will use this

second name in the case of soft compatibility mea-

sures.

In this paper, the second case scenario is consid-

ered, as it is better suited for unsegmented data. La-

bel pairs cannot be fully compatible or incompatible.

Compatibility coefﬁcients must not be logical asser-

tions but weighted values representing relative prefer-

ences.

To consistently label our data, the classical relax-

ation labeling procedures of (Rosenfeld et al., 1976)

are used, as they present funded theoretical properties

(Pelillo, 1997): when a speciﬁc condition of symme-

try is met, such processes possess a Lyapunov func-

tion which drives them towards the nearest consistent

solution. Furthermore, even if the symmetry condi-

tion is relaxed, more of the essential dynamical prop-

erties of the algorithm continues to hold.

Exploiting Context in Handwriting Recognition Using Trainable Relaxation Labeling

575

2.1.1 Relaxation Labeling Processes

Here we introduce some necessary information about

the relaxation labeling algorithms of (Rosenfeld et al.,

1976).

As stated in the previous Section, relaxation la-

beling processes are iterative procedures that can take

advantage of contextual information to label in a con-

sistent manner a set of objects. The contextual in-

formation is embedded in the so-called compatibil-

ity coefﬁcients. The compatibility coefﬁcients are the

non-negative real-valued elements in the matrix of

compatibility coefﬁcients, which we name R. Given

B =

{

, . . . , b

}

the set of objects to label and Λ =

{

1, . . . , m

}

the set of possible labels, R is deﬁned in

terms of a n ×n block matrix:

R =







. . . R







, (1)

where each R

i j

, with i and j = 1, . . . , n, is a m × m

matrix:

i j







i j

(1, 1) . . . r

i j

(1, m)

i j

(m, 1) . . . r

i j

(m, m)







. (2)

Each coefﬁcient r

i j

(λ, µ) measures the strength of

compatibility between λ assigned to object b

and µ

to object b

. High values correspond to compatibility,

and low values correspond to incompatibility.

Let’s assume p

(λ) to be the probability of an ob-

ject i to be labeled with λ. The relaxation labeling

processes are deﬁned by the two formulas:

(τ)

(λ) =

∑

i j

(λ, µ)p

(τ)

(µ), (3)

(τ+1)

(λ) =

(τ)

(λ)q

(τ)

(λ)

∑

(τ)

(µ)q

(τ)

(µ)

, (4)

with τ the iteration step of the processes. (Formula 3)

is the relaxation operator that considers the context

coded into the compatibility coefﬁcients in R. q

(τ)

(λ)

represents the support of the context to labeling object

with label λ.

Iterating (Formulas 3-4), we would obtain a re-

ﬁned probability distribution for the objects, resulting

in a less ambiguous labeling output.

The iterative procedure can be stopped after the

updates become small in the norm or after a prede-

ﬁned number of steps.

2.1.2 Proposed Model and Learning Scheme

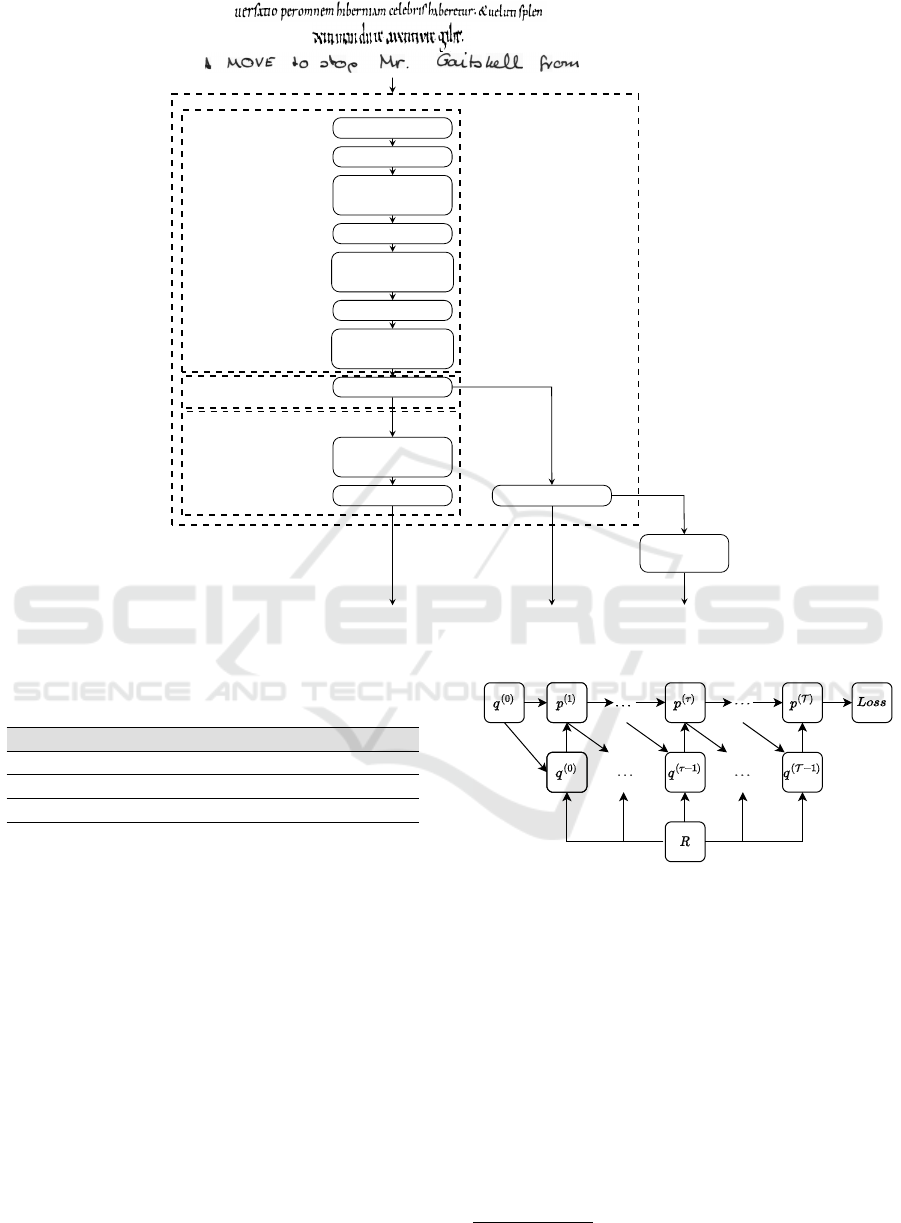
The proposed model is depicted in Figure 1. The ar-

chitecture is composed of a neural backbone (base-

line), taken from (Retsinas et al., 2022), and the relax-

ation labeling module. The baseline model comprises

two main modules and an interface one. The ﬁrst one

is in charge of extracting visual features from images.

The second learns the sequential patterns from data.

These modules are connected through a ﬂattening one

to obtain a 1D-sequence of feature vectors from 2D-

sequence feature representations because the recur-

rent head needs 1D-sequence data as input.

The relaxation labeling module is applied before

the recurring one to avoid running into missing con-

textual information that can be present when using re-

curring layers.

To learn the parameters, we use the backward

propagation through time, which is guaranteed to pro-

duce equivalent results to the forward propagation

scheme developed in (Pelillo and Reﬁce, 1994) but

has the advantage of being computationally efﬁcient

(Baydin et al., 2018). This learning scheme is com-

monly used to train neural network models (Guo,

2013), (Werbos, 1990).

In Figure 2, we report the computational graph of

the relaxation labeling module after deﬁning the num-

ber of iterations T . In this way, it is possible to see

the architecture in the unfolded representation.

We modify the loss of (Retsinas et al., 2022) with

the term involving the relaxation labeling procedures

to train the architecture. All the used losses are

CTC losses to satisfy the unsegmented data process-

ing. The loss of (Retsinas et al., 2022) comprises two

terms, L

End

which is the loss at the end of the archi-

tecture, and L

Shortcut

which is the loss applied after the

feature extractor module, the ﬂattening one and what

the authors called ‘CTC Shortcut’, a 1D-convolution.

The ‘CTC Shortcut’, with L

Shortcut

, has been intro-

duced to assist in training the network. The new term

that we introduce to the loss, L

Relax

, allows learning

the relaxation labeling compatibility coefﬁcients to-

gether with those of the entire convolutional part of

the neural network. The loss is in fact given by the

following formula:

L (ρ

conv.

, ρ

rec.

, R;s) = L

End

(ρ

conv.

, ρ

rec.

;s)+

αL

Shortcut

(ρ

conv.

;s)+

βL

Relax

(ρ

conv.

, R;s),

(5)

with ρ

conv.

, ρ

rec.

representing a generic parameter of

the convolutional and recurrent parts of the architec-

ture, respectively. R is the compatibility matrix, and s

is the transcription of the input line. Finally, α and

β are hyperparameters, weighting the CTC loss of

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

576

FEATURE

EX T RACT OR

MODULE

FLAT T ENING

MODULE

SEQUENCE

LABELING

MODULE

BASELINE

Conv 7 × 7, 32

MaxPool 2 × 2

ResBlock 3 × 3, 64

2×

MaxPool 2 × 2

ResBlock 3 × 3, 128

4×

MaxPool 2 × 2

ResBlock 3 × 3, 256

4×

ColumnMaxPool

BLST M, 256

3×

Linear, m

Conv, 1 × 3, m

Relaxation

Labeling

End

(·)

Shortcut

(·)

Relax

(·)

Figure 1: The architecture of our model. ColumnMaxPool represents the max pooling applied vertically to ﬂatten the extracted

feature maps, and m is the number of labels.

Table 1: Cardinality for the training, validation and test sets

of the datasets.

Dataset Train. Set Valid. Set Test Set

Saint Gall 468 235 707

Parzival 2, 237 912 1, 328

IAM 6, 482 976 2, 915

the CTC Shortcut and the relaxation labeling module,

correspondingly.

3 EXPERIMENTS

In this Section we brieﬂy introduce the datasets used

and the pre-processing and data augmentation tech-

niques performed. We, then, explicitly state the set-

tings used for the experiments. Finally, a detailed ex-

planation of the baseline architecture, the relaxation

labeling module and how these are combined is re-

ported.

Figure 2: Computational graph of the unfolded relaxation

labeling module.

3.1 Datasets

We use both historical and modern datasets with line-

level transcription: the Saint Gall (Fischer et al.,

2011), the Parzival (Fischer et al., 2012) and the

IAM dataset (Marti and Bunke, 2002). Datasets are

available from the Research Group on Computer Vi-

sion and Artiﬁcial Intelligence at the University of

Bern

. The Saint Gall dataset comprises images of

manuscripts of the 9

century written in Latin, the

Parzival dataset contains manuscript images of the

century written in German, the IAM dataset con-

https://fki.tic.heia-fr.ch/databases

Exploiting Context in Handwriting Recognition Using Trainable Relaxation Labeling

577

Table 2: Experiments on the Saint Gall Dataset. Validation and test CER and WER are reported.

Model Val. CER Test CER Val. WER Test WER

Baseline 4, 56% 4, 76% 32, 70% 33, 95%

B. with Relax 4, 43% 4, 65% 31, 95% 33, 29%

Table 3: Experiments on the Parzival Dataset. Validation and test CER and WER are reported.

Model Val. CER Test CER Val. WER Test WER

Baseline 1, 29% 1, 46% 5, 60% 6, 46%

B. with Relax 1, 19% 1, 37% 5, 15% 6, 05%

Table 4: Experiments on the IAM Dataset. Validation and test CER and WER are reported.

Model Val. CER Test CER Val. WER Test WER

Baseline 4, 00% 5, 57% 14, 36% 18, 57%

B. with Relax 3, 77% 5, 50% 13, 85% 18, 50%

Table 5: Examples of reﬁnement using the relaxation labeling module for all the datasets. Grey-ﬁlled bounding boxes highlight

errors.

Sample Image (csg562-042-24)

GT Vocavit deinde unum e fribus& eum interrogavit quid

Without Relaxation Labeling

Vocavit deinde unum

efribus

& eum interrogavit qui

With Relaxation Labeling Vocavit deinde unum e fribus& eum interrogavit quid

Sample Image (d-008b-025)

GT Gahm8reth der werde man.

Without Relaxation Labeling

Gahm8reth der werde

an.

With Relaxation Labeling Gahm8reth der werde man.

Sample Image (d04-012-10)

GT word of God .

Without Relaxation Labeling

word of

With Relaxation Labeling word of God .

tains forms of handwritten modern English text from

657 different writers. The datasets have a different

alphabet cardinality: 50, 95, and 79, respectively. Ta-

ble 1 reports the cardinality of the partitions of the

datasets. Transcription errors are present in all the

datasets, a problem that is affecting the performance

of the models (Aradillas et al., 2020).

3.2 Data Augmentation

We apply the best practices deﬁned in (Retsinas et al.,

2022) as image centring, left and right padding with

the median intensity. We perform classical data aug-

mentation techniques: afﬁne transformations as rota-

tions and translations, and gaussian blur ﬁlter of ker-

nel 3 × 3 with a randomly chosen standard deviation

in the range σ ∈ [1.0, 2.0]. The images are resized to

128 ×1024 (H ×W ).

3.3 Settings

The same setting of (Retsinas et al., 2022) is used to

train the architecture: the Adam optimizer (Kingma

and Ba, 2014) with an initial learning rate of 1E − 3

and weight decay of 5E − 5, a ﬁxed number of epochs

equal to 240 while decreasing the learning rate of 0.1

at speciﬁc epoch numbers (120 and 180) and α = 0.1

weighting the CTC Shortcut contribution to the loss

(cf. Equation (5)). To perform the analysis, we ﬁrst

train the entire network considering only the baseline

architecture, then add the relaxation labeling mod-

ule with different numbers of iterations. The con-

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

578

sidered numbers of iterations are queal to 1, . . . , 5,

10 and 15. For each architecture realisation, we per-

form hyperparameter optimization varying β in the set

{

0.1, 0.3, 0.5, 1.

}

. We also set a maximum wall time

for the training of 24 hours. A batch size of 20 is used

with 4 NVidia Tesla V100 16 Gb GPUs.

3.4 Baseline Model

As already mentioned, the baseline model we used

is taken from (Retsinas et al., 2022). It is made of

a CRNN. Speciﬁcally, the ﬁrst convolutional layer

has a kernel size 7 × 7, and presents 32 ﬁlters. It is

followed by a sequence of 3 × 3 ResNet blocks: 2

ResNet blocks with 64 ﬁlters, 4 ResNet blocks with

128 ﬁlters, and 4 ResNet blocks with 256 ﬁlters. Both

the standard convolution and ResNet blocks are fol-

lowed by ReLU activations, Batch Normalization and

dropout. Between the sequences of blocks 2 × 2 max-

pooling layer with stride 2 is set to reduce the fea-

ture map dimension. Then, the 3D feature map is re-

ported to a sequence thanks to a maxpool by column.

The recurrent head takes in input the aforementioned

sequence. It consists of three stacked BLSTM lay-

ers, with a hidden size of 256. Finally, a Fully Con-

nected (FC) layer is used to report the output dimen-

sion to the number of characters in the alphabet (in

addition with the blank character, needed for the CTC

loss (Graves et al., 2006)). The scores are then re-

ported to a probability distribution thanks to the Soft-

max function (Bridle, 1989). To aid the network in

the training process, a ‘CTC Shortcut’ was also used,

consisting of a convolutional layer with kernel dimen-

sion 1 ×3 and a number of channels equal to the num-

ber of classes where another CTC loss is applied to

help training.

3.5 Relaxation Labeling Module

The probabilistic relaxation labeling procedures are

applied to the full-text line image to consider the

whole line context. We apply it after the convolu-

tional part of the architecture (see Figure 1) to in-

clude the context before the recurring part in order to

avoid missing contextual information that can occur

when training recurring layers. The ﬁnal mapping of

the convolutional part, including the 1D-convolution

1 × 3, is of dimension m × 1 × 128 (m × H × W).

The mapping elements represent the objects to label

B =

{

, . . . , b

}

, with n = 128. The labels m are all

the characters in the respective dataset’s alphabet and

the blank character necessary for the CTC loss.

The iteration number T must be chosen before-

hand. Models were released that performed optimally

even using only one iteration, T = 1 (Pelillo and

Reﬁce, 1994). As already mentioned, the iteration

number T is treated like a hyperparameter to be tuned

by doing various experiments.

3.6 Combined Architecture

The relaxation labeling module is placed at the end

of the whole convolutional part of the baseline archi-

tecture (see Figure 1). Differently from (Pelillo and

Reﬁce, 1994), we do not make simplifying assump-

tions as the neighbourhood hypothesis (i.e. assuming

that objects interact within a neighbourhood) and the

stationarity hypothesis (i.e. the compatibility coefﬁ-

cients do not depend on the absolute positions of the

objects, but on their relative distance) not to constrain

the learning of the compatibility coefﬁcients. This is

to make all objects interact with each other, without

imposing restrictions.

Given the size of the compatibility matrix, we de-

cided to remove the relaxation labeling module in in-

ference time, dealing with the CRNN, only. The re-

laxation labeling module proves to be able to drive

the network towards a more consistent labeling out-

put (see Section 4).

4 RESULTS AND DISCUSSION

4.1 Quantitative Analysis

Tables 2 - 4 report the best results for the considered

datasets. The relaxation labeling processes showed

the ability to drive the network to a more consistent

labeling, obtaining a lower validation and test CER

and WER than the baseline model. We found the best

choice for β = 0.1, for all the architectures and all the

datasets. Instead, the number of unfolds for the relax-

ation labeling module differs for each dataset. In the

case of the Saint Gall and the IAM dataset, the best

number of relaxation labeling processes iterations is

T = 15, and in the case of the Parzival dataset T = 3.

4.2 Qualitative Analysis

Table 5 reports some cases where the relaxation la-

beling module increased the transcription accuracy

for all the datasets. It is possible to notice that the

model can perform all types of modiﬁcations to the

text line: character substitutions, insertions and dele-

tions. The cases of samples csg562-042-24, d-008b-

025 and d04-012-10 report cases of substitutions. In-

sertions are present in the cases of csg562-042-24 and

Exploiting Context in Handwriting Recognition Using Trainable Relaxation Labeling

579

d04-012-10. Finally, an example of deletion is present

in the case of sample csg562-042-24. As already

mentioned, errors are present in the datasets. In the

IAM dataset, the GT transcriptions have many more

spaces than the correct ones, especially before punc-

tuation marks. Moreover, errors in the transcription

are present, such as in the case of d04-012-10 where

the GT transcription contains the ﬁnal dot not present

in the image itself.

5 CONCLUSIONS

We empirically demonstrated that relaxation label-

ing processes help in generalisation abilities for

well-established architectures in the HTR ﬁeld, the

CRNNs. Such processes can drive the network to-

wards a more consistent labeling output in all the

datasets considered. They improve the results in

terms of both validation and test CER and WER. As

a future work we consider to compare the relaxation

labeling module with attention mechanisms, which

have a similar role of contextual processing from the

context. Finally, we plan to conduct a more exten-

sive comparison of our proposed method with other

backbones, to consistently evaluate the performance

improvement provided by relaxation labeling.

ACKNOWLEDGEMENTS

We would especially like to thank Gregory Sech for

his valuable suggestions and his past work on Relax-

ation Labeling processes. Also, we want to thank the

Italian Institute of Technology (IIT) for the possibil-

ity to use their High-Performance Computing (HPC)

as it allowed for faster experimentation.

REFERENCES

Aradillas, J. C., Murillo-Fuentes, J. J., and Olmos, P. M.

(2020). Improving ofﬂine htr in small datasets by

purging unreliable labels. In 2020 17th International

Conference on Frontiers in Handwriting Recognition

(ICFHR), pages 25–30. IEEE.

Baydin, A. G., Pearlmutter, B. A., Radul, A. A., and

Siskind, J. M. (2018). Automatic differentiation in

machine learning: a survey. Journal of Marchine

Learning Research, 18:1–43.

Bluche, T., Louradour, J., and Messina, R. (2017). Scan,

attend and read: End-to-end handwritten paragraph

recognition with mdlstm attention. In 2017 14th IAPR

international conference on document analysis and

recognition (ICDAR), volume 1, pages 1050–1055.

IEEE.

Bridle, J. (1989). Training stochastic model recognition al-

gorithms as networks can lead to maximum mutual in-

formation estimation of parameters. Advances in neu-

ral information processing systems, 2.

Coquenet, D., Soullard, Y., Chatelain, C., and Paquet, T.

(2019). Have convolutions already made recurrence

obsolete for unconstrained handwritten text recogni-

tion? In 2019 International conference on document

analysis and recognition workshops (ICDARW), vol-

ume 5, pages 65–70. IEEE.

Fischer, A., Frinken, V., Forn

es, A., and Bunke, H. (2011).

Transcription alignment of latin manuscripts using

hidden markov models. In Proceedings of the 2011

Workshop on Historical Document Imaging and Pro-

cessing, pages 29–36.

Fischer, A., Keller, A., Frinken, V., and Bunke, H. (2012).

Lexicon-free handwritten word spotting using charac-

ter hmms. Pattern recognition letters, 33(7):934–942.

Goshtasby, A. and Ehrich, R. W. (1988). Contextual

word recognition using probabilistic relaxation label-

ing. Pattern Recognition, 21(5):455–462.

Graves, A., Fern

andez, S., Gomez, F., and Schmidhu-

ber, J. (2006). Connectionist temporal classiﬁcation:

labelling unsegmented sequence data with recurrent

neural networks. In Proceedings of the 23rd interna-

tional conference on Machine learning, pages 369–

376.

Guo, J. (2013). Backpropagation through time. Unpubl.

ms., Harbin Institute of Technology, 40:1–6.

Haralick, R. M. and Shapiro, L. G. (1979). The consistent

labeling problem: Part i. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, (2):173–184.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural computation, 9(8):1735–1780.

Hummel, R. A. and Zucker, S. W. (1983). On the foun-

dations of relaxation labeling processes. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

(3):267–287.

Kingma, D. P. and Ba, J. (2014). Adam: A

method for stochastic optimization. arXiv preprint

arXiv:1412.6980.

Li, M., Lv, T., Cui, L., Lu, Y., Florencio, D., Zhang, C.,

Li, Z., and Wei, F. (2021). Trocr: Transformer-based

optical character recognition with pre-trained models.

arXiv preprint arXiv:2109.10282.

Lombardi, F. and Marinai, S. (2020). Deep learning for his-

torical document analysis and recognition—a survey.

Journal of Imaging, 6(10):110.

Marti, U.-V. and Bunke, H. (2002). The iam-database:

an english sentence database for ofﬂine handwrit-

ing recognition. International Journal on Document

Analysis and Recognition, 5(1):39–46.

Miller, D. A. and Zucker, S. W. (1991). Copositive-plus

lemke algorithm solves polymatrix games. Operations

research letters, 10(5):285–290.

Pelillo, M. (1997). The dynamics of nonlinear relaxation

labeling processes. Journal of Mathematical Imaging

and Vision, 7(4):309–323.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

580

Pelillo, M. and Reﬁce, M. (1994). Learning compatibility

coefﬁcients for relaxation labeling processes. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 16(9):933–945.

Puigcerver, J. (2017). Are multidimensional recurrent lay-

ers really necessary for handwritten text recognition?

In 2017 14th IAPR International Conference on Doc-

ument Analysis and Recognition (ICDAR), volume 1,

pages 67–72. IEEE.

Retsinas, G., Sﬁkas, G., Gatos, B., and Nikou, C. (2022).

Best practices for a handwritten text recognition sys-

tem. In International Workshop on Document Analy-

sis Systems, pages 247–259. Springer.

Rosenfeld, A., Hummel, R. A., and Zucker, S. W. (1976).

Scene labeling by relaxation operations. IEEE Trans-

actions on Systems, Man, and Cybernetics, (6):420–

433.

Teslya, N. and Mohammed, S. (2022). Deep learning for

handwriting text recognition: Existing approaches and

challenges. In 2022 31st Conference of Open Innova-

tions Association (FRUCT), pages 339–346. IEEE.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. Advances in neural

information processing systems, 30.

Werbos, P. J. (1990). Backpropagation through time: what

it does and how to do it. Proceedings of the IEEE,

78(10):1550–1560.

Exploiting Context in Handwriting Recognition Using Trainable Relaxation Labeling

581