Cloud-Native Applications’ Workload Placement over the

Edge-Cloud Continuum

Georgios Kontos

1,2

, Polyzois Soumplis

1,2

, Panagiotis Kokkinos

2,3

and Emmanouel Varvarigos

1,2

School of Electrical and Computer Engineering, National Technical University of Athens, Greece

Institute of Communication and Computer Systems, Athens, Greece

Department of Digital Systems, University of Peloponnese, Sparta, Greece

Keywords: Cloud-Native, Edge-Cloud Continuum, Resource Allocation, Multi-Agent Rollout, Reinforcement Learning.

Abstract: The evolution of virtualization technologies and of distributed computing architectures has inspired the so-

called cloud native applications development approach. A cornerstone of this approach is the decomposition

of a monolithic application into small and loosely coupled components (i.e., microservices). In this way,

application’s performance, flexibility, and robustness can be improved. However, most orchestration

algorithms assume generic application workloads that cannot serve efficiently the specific requirements posed

by the applications, regarding latency and low communication delays between their dependent microservices.

In this work, we develop advanced mechanisms for automating the allocation of computing resources, in order

to optimize the service of cloud-native applications in a layered edge-cloud continuum. We initially present

the Mixed Integer Linear Programming formulation of the problem. As the execution time can be prohibitively

large for real-size problems, we develop a fast heuristic algorithm. To efficiently exploit the performance–

execution time trade-off, we employ a novel multi-agent Rollout, the simplest and most reliable among the

Reinforcement Learning methods, that leverages the heuristic’s decisions to further optimize the final solution.

We evaluate the results through extensive simulations under various inputs that demonstrate the quality of the

generated sub-optimal solutions.

1 INTRODUCTION

Monolithic applications logic is concentrated into a

single, integral, and indivisible entity (Villamizar et

al., 2015). This approach was efficient in the past

when applications consisted of a client-side user

interface, a server-side implementation, and a

database. However, with the gradual establishment of

new ICT technologies (Akbar et al., 2022; Dangi et

al., 2021; Shah et al., 2021) (virtualization, optical

networks, 5G/6G), applications’ design complexity

has become higher, while there is a constant need for

updates to meet the ever-increasing Quality of

Service (QoS) demands. The monolithic approach

stands inadequate in such a competitive and volatile

environment, thus creating the need for a novel

application architecture model. The cloud-native

approach seems to be a favorable candidate: By

taking full advantage of the cloud computing model

and decomposing the applications into microservices,

it offers the flexibility, scalability, and robustness to

thrive in the modern world (Ren et al., 2018).

The primary design principle of a cloud-native

application is its effective decomposition into

microservices; small, loosely-coupled components,

where each one packs its own code, runs

autonomously and serves a specific and unique

purpose. The execution typically takes place in

autonomous visualized computing environments

called containers (Bernstein, 2014), which reserve the

required computing, networking and storage

resources from the host operating system.

Today, new kinds of services, inter-connected

products and other digitized assets create massive

amounts of data at the network’s edge and often

require ultra-low processing delays. These include,

among others, concepts like autonomous vehicles,

smart cities, virtual/augmented reality, and

biomedical care that utilize an abundance of sensors

and other data-generating systems. In such scenarios,

moving the generated load to remote cloud data

centers can lead to network bottlenecks, while also

fails to satisfy applications’ strict requirements due to

the increased latency. To tackle these problems, the

Kontos, G., Soumplis, P., Kokkinos, P. and Varvarigos, E.

Cloud-Native Applications’ Workload Placement over the Edge-Cloud Continuum.

DOI: 10.5220/0011850100003488

In Proceedings of the 13th International Conference on Cloud Computing and Services Science (CLOSER 2023), pages 57-66

ISBN: 978-989-758-650-7; ISSN: 2184-5042

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

paradigm of edge computing has arisen (Shi et al.,

2016). With edge computing, units placed at various

locations close to the data sources, computing,

networking and storage capabilities are provided on

the spot. These units, although of lower capacity

compared to cloud infrastructures, serve time-critical

tasks and reduce the load offloaded to the central

cloud. Cloud resources are also utilized in

combination with the edge ones, e.g., serving latency-

tolerant workloads, creating a powerful edge-cloud

continuum. Software-wise, lightweight containers are

the ideal technology to enable the seamless execution

of cloud-native applications, or parts of them, on the

edge; (Goethals, n.d.) in contrast to other

virtualization approaches like virtual machines.

The present work focuses on the development of

a novel mechanism for the appropriate allocation of

the available computing and storage resources in the

various layers of an edge-cloud infrastructure, to

support incoming workload from cloud-native

applications. Our aim is to jointly optimize a

weighted combination of the average delay (per

application) and the average cost of service while

ensuring that the delay between dependent

microservices and the available resources on the

infrastructure nodes meet the requirements specified

by the applications.. We first model the problem as a

Mixed Integer Linear Programming (MILP) problem.

Then, we construct a fast heuristic algorithm, called

Greedy Resource Allocation Algorithm (GRAA),

which is also utilized by a novel Rollout technique to

further optimize the generated solution (namely

Rollout algorithm based on GRAA) relying on

Reinforcement Learning (RL) principles. We

evaluate the results through extensive simulations

under various scenarios and demonstrate the

efficiency of the proposed solutions.

The remainder of this paper is organized as

follows: In Section 2, we present the related work. In

Section 3, we analyze the considered edge-cloud

infrastructure and the cloud-native applications

workload and formulate the resource allocation

problem as a MILP. In Section 4, we present the

heuristic algorithms developed. In Section 5, we

comment on the simulation results and finally, in

Section 6 we conclude our work.

2 RELATED WORKS

The resource allocation problem in virtualized

environments is a multi-dimensional research area

that has attracted the interest of the research

community. The modeling of the problem among the

different works varies according to the considered

topology and the adopted technologies, while the

proposed solutions employ techniques from the wider

realm of mathematics and computer science.

(Li et al., 2018) examine the placement of virtual

machines (VMs) on top of physical systems in a cloud

data center to perform big-data analytics from

Internet of Things (IoT) devices. The infrastructure is

modeled as a graph, where nodes represent VMs, and

links represent the network communication between

them. The aim is to minimize the maximum

utilization across the links in order to optimally utilize

network resources and avoid congestion. A greedy,

first-fit heuristic algorithm is presented that targets

placing as many interacting VMs as possible on the

same physical systems to minimize communication

costs. Authors in (Kiran et al., 2020) introduce the

VNFPRA problem, which focuses on the optimal

placement of VNFs (Virtualized Network Functions)

in SDN-NFV-enabled Multi-Access Edge Computing

(MEC) nodes with the aim of minimizing the

deployment and resource usage cost. The MEC

topology is modeled with a weighted graph, where

each node corresponds to a MEC node, characterized

by its available resources, while each link is a

network link with a given capacity. The problem is

formulated as a Mixed Integer Programming (MIP)

problem, where the objective function is the total

service cost that considers the placement cost,

resource usage cost and link usage/replication cost.

To tackle the time-consuming process of finding the

optimal solution, the authors propose a genetic-based

heuristic algorithm. In (da Silva & da Fonseca, 2018),

the authors develop an algorithm based on Gaussian

Process Regression to predict future traffic and

minimize request blocking, especially in the case of

time-critical requests. A hierarchical infrastructure

that consists of computing layers (near edge, far edge,

cloud) is considered and the objective is to ensure that

the near/far edge resources are sufficient enough to

serve future time-sensitive demands.

Shifting our attention to more relevant works to

the one presented in this paper, authors in (Santoro et

al., 2018) developed “Foggy”, an architectural

framework based on open-source tools that handles

requests from end users in a multi-level

heterogeneous fog/edge environment. The requests

arrive in a FIFO queue, and at each stage, the

available nodes are ranked by their processing power

and their networking towards the end user to extract

the best match. The authors in (Mutlag et al., 2021)

proposed a dynamic resource scheduling scheme for

critical smart-healthcare tasks in a fog/edge-cloud

topology. Their model consists of a multi-agent

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

system (MAS) with four kinds of agents named

personal agent (PA), master personal agent (MPA),

fog node agent (FNA), and master fog node agent

(MFNA). The scheduling strategy relies on effective

prioritization of the tasks according to their criticality

and on balancing network load. In (Pallewatta et al.,

2019) a system for microservices placement in a

multi-layered fog/edge environment is implemented,

targeting to place them as close as possible to the data

sources. All related operations (e.g., service

discovery, load balancing) are also handled in a

decentralized manner by the infrastructure nodes.

Finally, reinforcement learning is a technique that

has been used in the context of resource allocation in

edge-cloud environments. The authors in (Alfakih et

al., 2020) present a deep reinforcement learning

approach, based on state-action-reward-state-action

(SARSA), for addressing the problem of task off-

loading and resource allocation in Mobile Edge

Computing (MEC) environments. They model user

requests as a sequence of sub-tasks, which can be

executed by either the nearest edge server, the

adjacent edge server, or the central cloud. The

proposed solution aims to minimize service delay and

energy consumption by dynamically making

offloading decisions and allocating resources based

on the current state of the infrastructure. (Wang et al.,

2021) present a solution for the microservice

coordination problem in mobile edge computing

environments where mobile users (e.g., autonomous

vehicles) offload computation to the edge clouds. The

authors aim to minimize a weighted combination of

delay and migration costs by determining the optimal

deployment locations for microservices. They first

propose an offline algorithm able to derive the

optimal objective and then a Q-learning-based

reinforcement learning approach that produces a

near-optimal solution in real-time. (Chen et al., 2021)

propose a deep reinforcement learning solution for

microservice deployment in heterogenous edge-cloud

environments. They consider microservices as a

service chain, in which the microservices must be

executed in a pre-specified order. Simulations are

conducted with a combination of real and synthetic

data, with the objective of minimizing the Average

Waiting Time (AWT) of the microservices.

In our work, we explore the allocation of

microservice based-applications in a distributed

hierarchical edge-cloud infrastructure considering

important aspects of their operation. None of the

mentioned works, consider the dependencies between

microservices as delay constraints between their

corresponding service nodes to guarantee their

seamless communication. This is a valid concern that

must not go unnoticed especially when

geographically dispersed infrastructures are

considered. Microservice dependencies often take the

form of information exchange requirements or even

service chains, when one microservice must complete

its execution before another starts. Hence, the latency

between the corresponding service nodes of

dependent microservices should be taken into account

in the allocation process. In addition, to the best of

our knowledge, we are the first to employ the multi-

agent Rollout technique in such a scenario. It is a very

unique optimization approach based on the principles

of Dynamic Programming and Reinforcement

Learning, where greedy heuristics can be used to

approximate future decisions and can produce

valuable results with the assistance of the Rollout

technique, which although easy to understand and

implement, can improve the solutions significantly.

Finally, most works mainly focus on the provider,

studying its economic and energy well-fare, while

often neglecting the requirements of the “clients”,

such as cloud-native applications’ owners and users.

For this reason, our work focuses on meeting the

requirements set by the applications and on

optimizing the multiple and conflicting microservice

placement objectives.

3 PROBLEM FORMULATION

We consider a hierarchical edge-cloud infrastructure,

with multiple layers of edge resources (e.g., on-

device, near-edge, far-edge) to serve the incoming

cloud-native workload. We assume that the edge

layers consist of machines with relative limited

resources, such as raspberry Pi’s, NVIDIA Jetson,

servers, mini – Datacenters, etc. while the cloud layer

has practically unlimited resources.

The hierarchical edge-cloud infrastructure is

denoted as a Undirected Weighted Graph 𝐺=(𝑉,𝐸).

Each node 𝑣∈𝑉 is described by the tuple 𝜏



[𝑐



,𝑟



,𝑜



,𝑛



], where 𝑐



is node’s 𝑣 CPU capacity

measured in CPU units, 𝑟



is the node’s RAM

capacity measured in RAM units, 𝑜



is the node’s

operating cost and 𝑛



is the node’s networking cost

coefficient. Operational cost relates to the expenses

made for purchasing, deploying, and operating the

respective computing/storage systems. This is small

for the cloud layer, since providers achieve

economies of scale, and gradually increases for the

edge layers, due to their limited resources, the small

number of customers and their geographically

dispersed placement. Networking cost coefficient 𝑛



results from the usage of any link from the nodes

Cloud-Native Applications’ Workload Placement over the Edge-Cloud Continuum

where data are generated to the node(s) 𝑣 where

computing operations take place and is multiplied by

the ingress data to deduce the actual networking cost

of service. The coefficient is minimal for the near

edge nodes, where links are shorter in distance and

cheaper to install, while it gradually increases up to

the massive links connecting the cloud nodes.

Generally, data are generated at the lower levels of

the infrastructure that can be either equipped with

computing resources (local processing) or not. As

they are typically located in the near edge, the delay

is small for transferring the data to a subset of near

edge nodes as they are located closer to the data-

source, given their plurality and thus higher

geographical density, while it increases for the higher

layer nodes (far edge, cloud). Finally, each link 𝑒∈𝐸

between two nodes 𝑣 and 𝑣′ is characterized by a

weight 𝑙

,

, representing the communication

(propagation) delay of nodes 𝑣 and 𝑣′.

The workload under consideration consists of a

set 𝐴 of cloud-native applications. Each application

𝑎∈𝐴 is described by an Undirected Weighted Graph

𝐺



=(𝑉



,𝐸



), with the nodes 𝑉



corresponding to

the microservices that make up the application and

the arcs 𝐸



the inter-dependencies (communication

requirements) among them. Each cloud native

application has a source node 𝜋



∈𝑉 and each

microservice 𝑖=1,…,|𝐼



| of application 𝑎 , has

specific resource requirements described by the tuple

[𝜀

,

,𝜌

,

,𝑠

,

], where 𝜀

,

is the microservice’s CPU

demand, 𝜌

,

is its memory demand and 𝑠

,

is the

size of the input data. Furthermore, each arc 𝑒∈𝐸



between two microservices 𝜄,𝜄



∈𝑉



has a weight

𝜆

,,

that represents the maximum acceptable delay

between the corresponding service nodes 𝑣,𝑣′ of

these microservices. This is a measure of the intensity

of the dependency between these two microservices,

in a sense that highly dependent microservices should

be served by the same or geographically approximate

nodes to reduce communication costs and guarantee

application's efficiency with in-time calculations.

3.1 MILP Formulation

In what follows, we present the mathematical

formulation of the cloud native resource allocation

problem over a cloud-edge infrastructure. The

optimization objective is a weighted combination of

the average (operational and networking) cost and the

maximum delay per application assignment, with

respect to computing and networking constraints

imposed by the applications requirements and nodes’

resource availability.

Input:

𝑉

Total number of nodes

𝐴

Total number of applications

𝐼



Total number of microservices for the

𝑎’th application, 𝑎=1,…,𝐴

𝑜



Operating cost of node 𝑣, 𝑣=1,…,𝑉

𝜆

,,

Relative upper delay limit between micro-

services 𝑖,𝑖’ of an application 𝑎, 𝑎=1,…,𝐴.

𝑙

,

Communication delay between nodes 𝑣 and

𝑣’, 𝑣,𝑣



=1,…,𝑉

𝑐



Total available CPU units of node 𝑣, 𝑣=

1,…,𝑉

𝑟



Total available memory units of node 𝑣, 𝑣=

1,…,𝑉

𝜀

,

CPU units required by the 𝑖’th microservice

𝑖=1,…,𝐼



, of application 𝑎, 𝑎=1,…,𝐴

𝜌

,

Memory units required by the 𝑖 ’th

microservice 𝑖=1,…,𝐼



, of application 𝑎 ,

𝑎=1,…,𝐴

𝑛



Networking cost coefficient of node 𝑣, 𝑣=

1,…,𝑉

𝑠

,

Size of transported data for the 𝑖 ’th

microservice, 𝑖=1,…,𝐼



, of application 𝑎 ,

𝑎=1,…,𝐴

Weighting coefficient to control the

horizontal/vertical placement of the

applications’ microservices

Variables:

𝑥

,,

Binary variable, which is equal to 1 if the 𝑖’th

microservice 𝑖=1,…,𝐼



, of application 𝑎, 𝑎=

1,…,𝐴 is assigned to node 𝑖, and 0 otherwise

𝜏



Integer variable that denotes the monetary cost

for serving cloud native application 𝑎=1,…,𝐴

𝜃



Integer variable that denotes the maximum

propagation latency of cloud native application

𝑎=1,…,𝐴

Objective Function:

min𝑤 ∙ 𝜏







+(1−𝑤)∙𝜃







(1)

Subject to the Following Constraints:

C.1. Placement of the microservices to nodes. For

each application 𝑎=1,…,𝐴 and for each

microservice 𝑖=1,…,𝐼



𝑥

,,





(2)

C.2. Respect of the relative latency between the

applications’ microservices. For each application 𝑎=

1,…,𝐴, and each pair of microservices of application

a, 𝑖,𝑖



=1,…,𝐼



CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

Figure 1: The flowchart of the GRAA heuristic.

𝑙

,



𝑥

,,

+ 𝑙

,



𝑥





,,



𝜆

,,



+𝑙

,



(3)

C.3. The allocated CPU units of the served

applications cannot surpass the number of available

CPU units at each node. For each node 𝑣=1,…,𝑉,

𝜀

,

𝑥

,,







 𝑐







(4)

C.4. The allocated Memory units of the served

applications cannot surpass the number of available

Memory units at each node. For each node 𝑣=

1,…,𝑉,

𝜌

,

𝑥

,,







 𝑟







(5)

C.5. Total monetary application cost 𝜏



calculation.

For each application 𝑎=1,…,𝐴

𝜏



=(𝑜



+𝑛



∙𝑠

,

)







∙𝑥

,,





(6)

C.6. Maximum per application latency (propagation)

calculation. For each node 𝑣=1,…,𝑉, for each

cloud native application 𝑎=1,…,𝐴, and each of its

microservices 𝑖=1,…,𝐼



𝜃



𝑥

,,

∙𝑙





,

(7)

The objective function (Eq. 1) is the weighted

sum of the maximum delay and cost per applications’

assignments, where 𝑤=0 considers purely the delay

minimization problem and thus the microservices of

the applications are preferably placed in the edge

(horizontal scaling), 𝑤=1 deals with the cost

minimization problem and thus the vertical scaling of

applications, and any intermediate value of w

considers both of the aforementioned parameters with

different contribution in the calculation of the total

cost. The first constraint (Eq. 2) is used to ensure that

every microservice is assigned to exactly one node.

The second constraint (Eq. 3) enforces that allocation

of resources among interacting applications of a

microservice is performed with respect to their

latency constraint. Constraints (3) and (4) ensure that

microservices running in a node do not use more than

the available resources, while constraints (5) and (6)

calculate the monetary cost and the maximum latency

of each application respectively. Note that our

considered formulation supports general workloads

(not strictly cloud-native applications) that can take

the form of an application with a single microservice.

Next, we examined the number of variables and

constraints required by the MILP formulation.

Assuming that the infrastructure consists of |𝑉| nodes

and |𝐴| cloud-native applications are served, each

one consisting of |𝐼| microservices, the total number

of variables is [

𝑉

∙

𝐴

∙

𝐼

+2∙|𝐴|]. It requires the

following equality constraints:

𝐴

∙

𝐼

for constraint

1 (eq.2 C.1.) and

𝐴

for constraint 5 (eq. 6). It also

requires the following inequality constraints:

𝐴

∙

|𝐼|



∙|𝑉|



for constraint 2 (eq. 3), |𝑉| for

constraint 3 (eq. 4), |𝑉| for constraint 4 (eq. 5) and

|𝑉| ∙ |𝐴| ∙ |𝐼| for constraint 6 (eq. 7).

4 RESOURCE ALLOCATION

MECHANISMS

As the considered problem belongs to the NP-hard

class of problems (Sallam & Ji, 2019) the presented

MILP is computationally intensive with prohibitively

large execution time even for small size problems.

For this reason, we developed sub-optimal

mechanisms. First, we present the Greedy Resource

Allocation Algorithm (GRRA), which is able to

Cloud-Native Applications’ Workload Placement over the Edge-Cloud Continuum

Figure 2: The multi-agent Rollout options for serving the i-th microservice of application a.

deduce the optimal placement for each microservice

individually in a greedy manner. Next, we describe

the multi-agent Rollout mechanism, a meta-heuristic

algorithm that uses GRRA to provide an improved

solution through an iterative process.

4.1 Greedy Resource Allocation

Algorithm (GRAA)

GRAA is a greedy heuristic that seeks to find a

satisfactory even-though sub-optimal solution by

serving the application demands in a best fit manner.

GRAA takes as input the infrastructure graph 𝐺=

(

𝑉,𝐸

)

along with all the applications’ demands and

its microservices described by graph 𝐺



(

𝑉



,𝐸



)

for application 𝑎 , ∀𝑎=1,…,𝐴.

Applications are served sequentially, one by one.

After selecting an application, the first microservice

of the application is selected and the candidate

infrastructure nodes with enough resources are

calculated in order to accommodate it. These nodes

are ranked based on the objective function

considering the cost and the latency introduced by the

assignment of the microservice

𝑖

=1,…,𝐼

𝑎

to each

node. The best node 𝑣∈𝑉 is selected and the

demanded by the microservice computing and

memory resources are reserved. If the application

consists of more than one microservices, the next

microservice is selected. The same process is

followed for the following microservice with the

addition of the relative latency constraint between the

communicating microservices. Hence, given the first

microservice location, the nodes

𝑣



∈𝑉

with

communication latency smaller to the limit by the

microservices are selected,

𝑙

,

𝜆



,

,

,

If more

than one node is found, it places the second

microservice in the best one (it could be the same

node as the first microservice). The same process is

repeated until the 𝐼



-th microservice of the

application is served. If it is not possible to find a node

to host an application’s microservice, the procedure

is re-initiated for the same application considering the

second-best node for the first microservice and so on.

When a solution is found the utilization of the

resources is updated and the application is marked as

served. The above process is repeated for all

applications, returning the final assignment and the

value of the objective function (Eq. 1). From the

description of the aforementioned procedure, it may

be the case where the selection of the first node can

make the execution of an application impossible due

to the latency constraint among the microservices of

the application. Although this may happen for the

edge resources which are characterized by limited

capacity of resources, this does not stand for the

abundant cloud resources, which are able to execute

the application demands at the price of increased

propagation latency. The complexity of this approach

is polynomial with a worst-case execution time of

𝑂

𝐴

∙

𝐼



∙

𝑉

, assuming that all the nodes |𝑉| are

candidate locations to serve the first microservice of

each application. A typical iteration of this algorithm

is presented in the flowchart of Fig. 1.

4.2 Multi-Agent Rollout Mechanism

To further improve the performance of the

aforementioned greedy heuristic, we also developed a

multi-agent Rollout mechanism. Rollout (Bertsekas,

2010; Bertsekas et al., 1997) is among the most

known reinforcement leaning techniques that aims to

provide a close to optimal solution by leveraging a

base policy (like GRAA). It is an iterative process that

takes each time as input an instance of the resource

assignment problem (concerning applications with

microservices) with a partial solution of the problem

(some microservices assigned to nodes) and

constructs step-by-stem the solution. This technique

becomes particularly useful when the exact methods

are too slow and/or when solutions provided by

heuristics are inefficient.

Assuming that the first (𝑎-1) applications have

been served and application 𝑎 is going to be served,

the multi-agent rollout heuristic gets as input a

solution path 𝑜=[𝑜



,…,𝑜



] of size

∑

𝑜



∙𝐼







where states 𝑜



, for 𝑘=1,…,𝑎−1 contains the

assignment of the microservices of the application

𝑘=1,….,𝑎−1 to processing nodes. Then, state 𝑜

𝑎

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

is broken down into 𝐼



stages each one corresponding

to the allocation of resources of one of the 𝐼



microservices that make up application 𝑎 to

processing nodes. Initially, a number of possible

placements 𝑃

,

for each microservice 𝑖=1,…,𝐼



that is going to be served are calculated. Next, to

decide for the placement of a microservice 𝑖, one of

the available placement options 𝑝∈𝑃

,

is selected

and the respective service cost is calculated based on

the provided objective function, while the cost for the

remaining microservices and applications is

calculated making use of the GRAA heuristic (base

policy), resulting in a total cost 𝜎



. When all the

possible placements 𝑃



of microservice i have been

performed, the one that provides the lowest cost 𝜎



selected (Fig 2.). The utilization of the node that

serves the microservice is updated accordingly, the

microservice is marked as served and the procedure

continues with the following microservice. The

placement of the microservice 𝐼



of application 𝑎

indicates the transition to state 𝑜



and the same

procedure is repeated until all the application

demands A are served. At the end, the allocation of

resources to nodes is returned along with the

weighted cost for the performed assignment.

Consider an application 𝑎 consisting of 𝐼



microservices. Each microservice can be placed (in

the general scenario) in one of the nodes of the

infrastructure, resulting in a state size of |𝑉|



for the

collective decision of the application’s placement.

When the allocation of resources of an application a

is broken down into |𝐼



| sequential decisions and by

applying one agent-at-a-time instead of all-agents-at-

once the state space is reduced into |𝑉| ∙ |𝐼



| states. In

this case, the control space complexity from the

different options when serving the applications is

traded off with state space complexity and the

computational requirements are proportional to the

number of microservices and the number of

computing nodes of the examined infrastructure.

5 SIMULATION EXPERIMENTS

To perform our experiments, we considered two

topologies for the hierarchical cloud-edge

infrastructure, with different characteristics regarding

the number of nodes at the different layers and their

computing capacity (Table 1): a basic that consists of

19 nodes and an extended that consists of 53 nodes,

with the cloud having enough capacity to serve the

examined workloads. For both topologies, we

assumed that they are organized into a hierarchical

infrastructure that consists of nodes (locations) that

belong to three different layers namely the near-edge,

far-edge and cloud. In the basic topology, we

considered (i) 15 near edge resources equipped with

an integer number of CPU and memory units taken

from the uniform distribution in the close interval

[4,8] and [4,16] respectively with an operating cost

taken in the interval [6-8], (ii) 3 far edge nodes with

[80-120] and [120-200] CPU and Memory resource

and relative cost [3,4] and (iii) 1 cloud locations with

500 CPU units and 1000 Memory units with cost in

the close interval [1,2]. The operational cost 𝑜



measured in normalized cost units to fit our

mathematical model. The network cost coefficient

values 𝑛



are drawn from (Rutledge, 2020).

The propagation delay is measured in normalized

latency units. We considered the propagation delay

between the data-source and the cloud layers to be

approximately 5 times greater than between the data-

source and near-edge. The exact distances are not

well defined nor standardized, but we used (Madden,

2020) as a guideline/estimation. The communication

delays among the layers were calculated accordingly.

Note that the basic topology was used for

performance comparison between our GRAA

heuristic, the multi-agent Rollout, and the built-in

optimal MILP solver of Matlab. The execution times

for the optimal solver became prohibitively large for

larger configurations, hence the use of the basic

topology. The extended topology considers the same

node attributes, but their numbers are scaled to 40

near-edge nodes, 10 far-edge nodes and 3 central

cloud locations. The extended topology was used for

the rest of the experiments to provide a closer-to-real-

world scenario and demonstrate the scalability of the

proposed algorithms.

Table 1: The characteristics of the computing nodes of the

basic and extended topologies.

Nea

-Edge Fa

-Edge Clou

Basic topology

(#Nodes)

3 1

Extended

topology

(#Nodes)

40 10 3

𝑐



[4, 8]

[80-120] 500

𝑟



[4, 16] [120-200] 1000

𝑜



[2, 3] [1,1.5] [0.3,0.7]

𝑛



0.1

0.25 0.5

With regards to the workload, the demands were

generated randomly at the near-edge nodes consisting

of microservices drawn from the uniform distribution

in the close interval [1,5]. The size of the workload of

each application was randomly selected in the interval

[1,5], measured in normalized size units.

Cloud-Native Applications’ Workload Placement over the Edge-Cloud Continuum

Dependencies between pairs of microservices were

created randomly with probability equal to 0.3, while

the latency constraint among them varies in the close

interval [0.5,3.5] latency units. The processing and

memory requirements of each microservice are drawn

from the uniform distribution in the close interval [1,

4] and [1, 8] respectively. The proposed mechanisms

were developed in MATLAB and the experiments

were conducted on a 6 core 2.6 GHz Intel Core i7 PC

with 12 GB of RAM.

Initially, we compared the performance of the

multi-agent rollout and the greedy heuristic with the

optimal solution provided by the MILP in means of

execution time and optimality for randomly selected

application demands (ranging from 50 to 300) and for

weighting coefficient 0.01. This coefficient

corresponds to the latency optimization problem, but

with a minimal inclusion of cost.

Table 2: The total cost and the execution time for w=0.01

for the different mechanisms.

Application

demands

MILP

Multi-agent

Rollout

GRAA

Obj.

value

Exec.

Time

(sec)

Obj.

value

Exec.

Time

(sec)

Obj.

value

Exec.

Time

(sec)

50 55.92 92.37 56.31 17.3 56.84 0.12

100 115.15 507.42 116.17 69.42 117.90 0.22

150 228.51 2453.16 236.49 147.72 252.38 0.35

200 409.94 10000 421.6 252.09 438.62 0.47

250 657.8 10000 675.42 349.74 702.37 0.67

300 - 10000 1051.8 348.82 1079.2 0.89

Regarding the performance of the proposed

mechanisms, GRAA, which is a best-fit heuristic, had

the worst performance, with a gap up to 10% from the

optimal solution, whereas the Multi-agent Rollout

managed to generate solutions within 3.5% of the

optimal in all cases. As for the execution time, GRAA

exposed the lowest execution time in the order of

milliseconds even for higher workloads, while

Rollout's execution time growth is polynomial with

the workload increment. Finally, the MILP solver had

exponentially increasing execution times, and for the

workload sizes of 200 and 250 application demands,

it finished its operation withing the time limit that was

set, while for the largest workload did not managed to

produce a feasible solution during this period.

Figure 3: The pareto efficiency chart.

In Fig. 3, we present the allocative efficiency

chart for the two objectives that are taken into

consideration, namely the monetary cost for the

application execution and the average latency per

application for the different weighting co-efficients

that are used in the objective function. As expected,

the lowest cost is achieved when cloud resources are

highly utilized and thus the propagation latency

increases as cloud resources are located in a few

distant locations to which the data are transferred.

When the single optimization criterion is the

minimization of latency, the propagation delay is

minimized by 70% compared to the previous case,

while the monetary cost is increased by almost 75%.

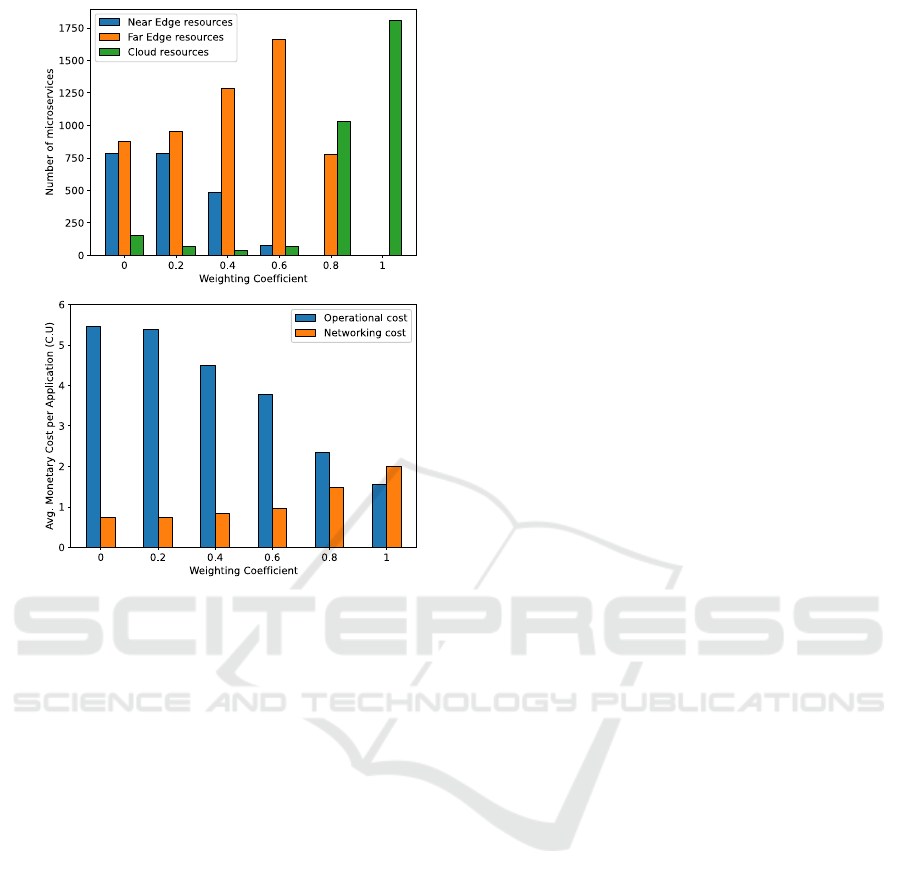
Next, we examined the utilization of edge and

cloud resources for serving 600 cloud native

application demands for the different weighting

coefficients w (Fig. 4.a). Edge resources are utilized

more in small weight values, as the objective is

approaching the delay minimization and edge layers

consist of nodes in geographic proximity to the data-

source. In this case the microservices of an

application expand over the resources of the edge

layer, which is known as horizontal scaling. On the

other hand, cloud resources are heavily utilized in

high w values, as the objective is approaching the

monetary cost minimization, thus the “cheap” cloud

nodes are preferred. For intermediate values of w,

applications microservices are allocated over the

edge-cloud continuum which is known as vertical

scaling. This showcases the importance of edge

resources in the minimization of the applications

latency for time critical operations.

Finally, in Fig.4.b we examined the contribution

of networking and operational cost for the different

weighting co-efficient values. When the objective

function targets the minimization of the monetary

cost, the cloud resources are preferred with the

operational and networking cost contributing almost

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

Figure 4: a. The number of microservices allocated at the

near/far edge and the cloud and b. the operational and

networking cost for the different objective co-efficients.

equally to the total cost, as the processing cost is low

while the networking cost increases for the

transferring the application data to the cloud. On the

other hand, when the objective is the minimization of

latency and edge resources are utilized, the

processing cost of the edge resources is the main

factor of the total monetary cost, with the networking

cost corresponding to 12% of the total cost.

6 CONCLUSIONS

In this work, we addressed the problem of resource

allocation in multi-layered edge-cloud infrastructures

for optimally serving cloud-native applications. We

considered multiple important (and often neglected)

parameters, such as the delay constraints posed by the

dependencies among microservices. GRAA was

developed to provide a sub-optimal solution and to be

used by the Rollout technique for further

optimization. We demonstrated the trade-off between

delay and monetary cost of service and proved the

quality of the Rollout technique, which provided a

significant improvement in the GRAA’s solution,

while also maintaining a low computational time. We

aspire to further investigate this problem by adding

more parameters into our objective, such as security

and bandwidth consumption. In addition, we aim to

provide a more realistic scenario by collecting real

application and infrastructure data as well as solving

the corresponding on-line problem. Finally, we aim to

fully explore the capabilities of Rollout by

implementing it with different base policies.

ACKNOWLEDGEMENTS

The work presented is supported by the EU Horizon

2020 research and innovation program under grant

agreement No. 101017171 in the context of the

MARSAL project and by the Hellenic Foundation for

Research and Innovation (H.F.R.I.) under the “2nd

Call for H.F.R.I. Research Projects to support Faculty

Members & Researchers” (Project Number: 04596).

REFERENCES

Akbar, M. S., Hussain, Z., Sheng, Q. Z., & Mukhopadhyay,

S. (2022). 6G Survey on Challenges, Requirements,

Applications, Key Enabling Technologies, Use Cases,

AI integration issues and Security aspects.

http://arxiv.org/abs/2206.00868

Alfakih, T., Hassan, M. M., Gumaei, A., Savaglio, C., &

Fortino, G. (2020). Task offloading and resource

allocation for mobile edge computing by deep

reinforcement learning based on SARSA. IEEE Access,

8, 54074–54084. https://doi.org/10.1109/ACCESS.

2020.2981434

Bernstein, D. (2014). Containers and cloud: From LXC to

docker to kubernetes. IEEE Cloud Computing, 1(3),

81–84. https://doi.org/10.1109/MCC.2014.51

Bertsekas, D. P. (2010). Rollout Algorithms for Discrete

Optimization: A Survey.

Bertsekas, D. P., Tsitsiklis, J. N., Wu, C., Bertsekas, D. P.,

Tsitsiklis, J. N., & Wu ’, C. (1997). Rollout

Algorithm For Combinatorial Optimization

ROLLOUT ALGORITHMS FOR COMBINATORIAL

OPTIMIZATION.

Chen, L., Xu, Y., Lu, Z., Wu, J., Gai, K., Hung, P. C. K., &

Qiu, M. (2021). IoT Microservice Deployment in Edge-

Cloud Hybrid Environment Using Reinforcement

Learning. IEEE Internet of Things Journal, 8(16),

12610–12622. https://doi.org/10.1109/JIOT.2020.

3014970

da Silva, R. A. C., & da Fonseca, N. L. S. (2018). Resource

allocation mechanism for a fog-cloud infrastructure.

IEEE International Conference on Communications,

2018-May. https://doi.org/10.1109/ICC.2018.8422237

Dangi, R., Lalwani, P., Choudhary, G., You, I., & Pau, G.

(2021). Study and Investigation on 5G Technology: A

Cloud-Native Applications’ Workload Placement over the Edge-Cloud Continuum

Systematic Review. Sensors (Basel, Switzerland),

22(1). https://doi.org/10.3390/s22010026

Goethals, T. (n.d.). FLEDGE: Kubernetes Compatible

Container Orchestration on Low-resource Edge

Devices.

Kiran, N., Liu, X., Wang, S., & Changchuan, Y. (2020).

VNF Placement and Resource Allocation in SDN/NFV-

enabled MEC Networks.

Li, X., Lian, Z., Qin, X., & Jie, W. (2018). Topology-aware

resource allocation for IoT services in clouds. IEEE

Access, 6, 77880–77889. https://doi.org/10.1109/

ACCESS.2018.2884251

Madden, J. (n.d.). Edge computing and transmission costs -

DCD. Retrieved December 8, 2022, from

https://www.edgecomputing-news.com/2020/10/29/an

alysis-economics-of-edge-computing/

Mutlag, A. A., Ghani, M. K. A., Mohammed, M. A.,

Lakhan, A., Mohd, O., Abdulkareem, K. H., & Garcia-

Zapirain, B. (2021). Multi-agent systems in fog–cloud

computing for critical healthcare task management

model (CHTM) used for ECG monitoring. Sensors,

21(20). https://doi.org/10.3390/s21206923

Pallewatta, S., Kostakos, V., & Buyya, R. (2019).

Microservices-based IoT application placement within

heterogeneous and resource constrained fog computing

environments. UCC 2019 - Proceedings of the 12th

IEEE/ACM International Conference on Utility and

Cloud Computing, 71–81. https://doi.org/10.1145/

3344341.3368800

Ren, Z., Wang, W., Wu, G., Gao, C., Chen, W., Wei, J., &

Huang, T. (2018, September 16). Migrating web

applications from monolithic structure to microservices

architecture. ACM International Conference

Proceeding Series. https://doi.org/10.1145/3275219.

3275230

Rutledge, K. (n.d.). Analysis_ The economics of edge

computing.

Sallam, G., & Ji, B. (2019). Joint Placement and Allocation

of VNF Nodes with Budget and Capacity Constraints.

http://arxiv.org/abs/1901.03931

Santoro, D., Zozin, D., Pizzolli, D., de Pellegrini, F., &

Cretti, S. (2018). Foggy: A Platform for Workload

Orchestration in a Fog Computing Environment.

https://doi.org/10.1109/CloudCom.2017.62

Shah, S. D. A., Gregory, M. A., & Li, S. (2021). Cloud-

Native Network Slicing Using Software Defined

Networking Based Multi-Access Edge Computing: A

Survey. In IEEE Access (Vol. 9, pp. 10903–10924).

Institute of Electrical and Electronics Engineers Inc.

https://doi.org/10.1109/ACCESS.2021.3050155

Shi, W., Cao, J., Zhang, Q., Li, Y., & Xu, L. (2016). Edge

Computing: Vision and Challenges. IEEE Internet of

Things Journal, 3(5), 637–646. https://doi.org/10.1109/

JIOT.2016.2579198

Villamizar, M., Garces, O., Castro, H., Verano, M.,

Salamanca, L., Casallas, R., & Gil, S. (2015).

Evaluating the monolithic and the microservice

architecture pattern to deploy web applications in the

cloud. 2015 10th Colombian Computing Conference,

10CCC 2015, 583–590. https://doi.org/10.1109/

ColumbianCC.2015.7333476

Wang, S., Guo, Y., Zhang, N., Yang, P., Zhou, A., & Shen,

X. (2021). Delay-Aware Microservice Coordination in

Mobile Edge Computing: A Reinforcement Learning

Approach. IEEE Transactions on Mobile Computing,

20(3), 939–951. https://doi.org/10.1109/TMC.2019.

2957804.

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science