A Computational Model for Predicting Cryptocurrencies Using

Exogenous Variables

Eduardo M. Gonc¸alves

, Eduardo N. Borges

, Bruno L. Dalmazo

, Rafael A. Berri

Giancarlo Lucca

and Vinicius M. de Oliveira

Center for Computational Sciences, Universidade Federal do Rio Grande, Rio Grande, Brazil

Keywords:

Time-Series, Cryptocurrencies, Neural Networks.

Abstract:

The recent growth of cryptocurrencies caused worldwide interest due to capitalization power and geographic

expansion. In this universe, Bitcoin is the main actor. Taking this into consideration, this paper aims to

analyze the behavior of Bitcoin during the time. To do so, we use techniques already studied in the literature

to perform the predictions and comparisons between methods jointly with exogenous variables to boost the

results. An evaluation has been performed and the best results were achieved using the Long-Short-Term-

Memory (LSTM) neural network model. Also, the experiments were carried out in different scenarios, using

datasets with more than ﬁve years of daily records and exogenous variables to improve the performance of the

models.

1 INTRODUCTION

Cryptocurrencies have been notoriously volatile in

comparison with other investments. Usually, the liter-

ature shows prediction models based on the long term

for predicting numerous assets. At the same time, the

elastic nature of cryptocurrencies means that they are

also apt to undergo sudden changes which makes it

even harder to predict their behavior. The price of vir-

tual currencies, such as Bitcoin, is still being studied

by the market, and there are several open issues about

its evolution, as observed in the work of (Chu et al.,

2015).

Several techniques have already been proposed to

perform the prediction of cryptocurrencies, such as

(Mallqui and Fernandes, 2019), (Miura et al., 2019),

and (Zoumpekas et al., 2020). Also, different types

of information are used to predict, such as the daily

prices, market cap, volume negotiated in the last 24h,

etc. However, the classic prediction models present an

apparent deﬁcit in their ability to learn the data and

make accurate forecasting. In particular, these tech-

https://orcid.org/0000-0003-3002-6386

https://orcid.org/0000-0003-1595-7676

https://orcid.org/0000-0002-6996-7602

https://orcid.org/0000-0002-5125-2756

https://orcid.org/0000-0002-3776-0260

https://orcid.org/0000-0003-3864-033X

niques demand ample tuning to improve their sensi-

tivity and achieve adequate results. As a result, the

literature lacks mechanisms that can enable it to im-

prove the accuracy of predictions while keeping low

response time.

To ﬁll these gaps, a computational model for pre-

dicting cryptocurrencies using an exogenous variable

group is proposed. Our proposal relies on analyzing

the history of the Bitcoin price to obtain features that

represent the expected appropriate behavior during

the time. This information is then used jointly with

a Long-Short-Term-Memory (LSTM) neural network

model that is supplied with these features. So, this

study aims to explore the relationship that exists be-

tween the temporal data of Bitcoin, Ethereum (Bu-

terin et al., 2013), and the exchange rate from the

dollar to the Real (USD/BRL) to predict the val-

ues of Bitcoin, using techniques of machine learn-

ing (Hochreiter and Schmidhuber, 1997).

The remainder of the paper is organized as fol-

lows. Section II covers the main concepts related to

this study. Section III describes the proposed solution

and the methodology used for this paper, whilst Sec-

tion IV presents the metrics used, the evaluation and

discusses the results. Section V concludes with some

ﬁnal remarks and prospective directions for future re-

search.

180

GonÃ

galves, E., Borges, E., Dalmazo, B., Berri, R., Lucca, G. and M. de Oliveira, V.

A Computational Model for Predicting Cryptocurrencies Using Exogenous Variables.

DOI: 10.5220/0011852000003467

In Proceedings of the 25th International Conference on Enterprise Information Systems (ICEIS 2023) - Volume 1, pages 180-186

ISBN: 978-989-758-648-4; ISSN: 2184-4992

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 PRELIMINARIES

In this section, the main concepts related to the study

are presented. Precisely, we discuss about Cryptocur-

rencies, Time-series, Neural networks, and Long-

Short-Term-Memory networks.

2.1 Cryptocurrencies

The ﬁrst cryptocurrency (Mukhopadhyay, 2016),

eCash, was a centralized system owned by DigiCash,

Inc. and later eCash Technologies. Although it was

discontinued in the late 1990s, the cryptographic pro-

tocols it employed avoided double-spending. A blind

signature was used to protect the user’s privacy and

provided good inspiration for further development.

The 2008 global ﬁnancial crisis, together with a

lack of conﬁdence in the ﬁnancial system, provoked

considerable interest in cryptocurrencies. A ground-

breaking white paper by Satoshi Nakamoto circulated

online in 2008 (Nakamoto, 2008). In the article,

this pseudonym introduced a digital currency that is

now widely known as Bitcoin. This methodology

uses blockchain (Nofer, 2017) as the public ledger for

all transactions and a scheme called Proof of Work

to avoid the need for a trusted authority or central

server for timestamp transactions (Nakamoto, 2008).

Blockchain is an open platform that records all trans-

actions in a veriﬁable and permanent way, solving the

problem of double-spending and ensuring the security

of exchanges throughout history.

Bitcoin growth led to born of new cryptocurren-

cies, such as Ethereum, Cardano

, Polygon

, among

others. There are strategies to try to regulate Bit-

coin as an ofﬁcial currency, which can be seen in

(Hughes, 2017). However, the concept of virtual cur-

rency and deﬁnitions of possible fees on currencies

are inconclusive and not general, as can also be seen

in (Castello, 2019).

2.2 Time-Series

Time series is a collection of observations made se-

quentially over time. The most important feature of

this type of data is that neighbouring observations

are dependent, and we are interested in analyzing and

modelling this dependence. While in regression mod-

els, for example, the order of observations is irrelevant

to the analysis, in time series, the order of the data is

crucial (Ehlers, 2007).

For ﬁnancial time series, according to (Morettin,

2017), it is main features: closing value, daily maxi-

https://cardano.org

https://polygon.technology

mum and minimum values of the evaluated currency.

Such information allows recognizing trends, inﬂu-

ences and other essential attributes to analyze and un-

derstand the data (Dalmazo et al., 2018). However,

even when dealing with the monetary ﬁeld, the ﬁnan-

cial time series differs from the others because they

have high volatility and suffer from various exter-

nal inﬂuences, requiring speciﬁc methods and mod-

elling (Morettin, 2017).

2.3 Neural Networks

The ﬁrst information about neurocomputing appeared

in mid-1943 (McCulloch and Pitts, 1943). In it, the

authors made an analogy between living nerve cells

and the electronic process in a published work on

”formal neurons”, simulating the behaviour that oc-

curs in human brains, in which the neuron had only

one output, which was a function of the sum of the

value of its several entries. The work consisted of a

model of variable resistors and ampliﬁers, represent-

ing synaptic connections of a biological neuron.

An Artiﬁcial Neural Network (ANN) has two ele-

mentary facets: the architecture and the learning algo-

rithm. Unlike a Von Neumann architecture computer

(Tanenbaum and Zucchi, 2009) that is programmed,

the network is trained. A neural network is basically

composed of neurons that are responsible for process-

ing information. The response of an initial neuron

with an activation function feeds the next one, and so

on, until the last node; each set of neurons represents

a layer, and the set of them forms the network.

There are several types of neural networks, and it

is worth mentioning the Recurrent Neural Networks

(RNN) (Deng and Yu, 2014), where information can

travel in different directions; in this way, one neuron,

in addition to feeding the next, manages to feed it-

self back, producing a category of short-term mem-

ory. As a result of these characteristics, RNNs can

create more complex models that are extensible to a

larger group of problems.

A special type of RNN is the Long Short-

Term Memory (LSTM) (Hochreiter and Schmidhu-

ber, 1997), which is capable of learning long-term

dependencies. This approach is considered an ideal

solution for a wide variety of problems and is widely

used today, such as pollution in the air (Tsai et al.,

2018), speech enhancement (Sun, 2017), renewable

energy sources (Abdel-Nasser and Mahmoud, 2019)

and others.

All RNNs are in the form of a chain of repeat-

ing modules in a neural network. In a standard RNN,

this module has a very simple structure, such as a

layer with a function that produces a zero-centred out-

A Computational Model for Predicting Cryptocurrencies Using Exogenous Variables

181

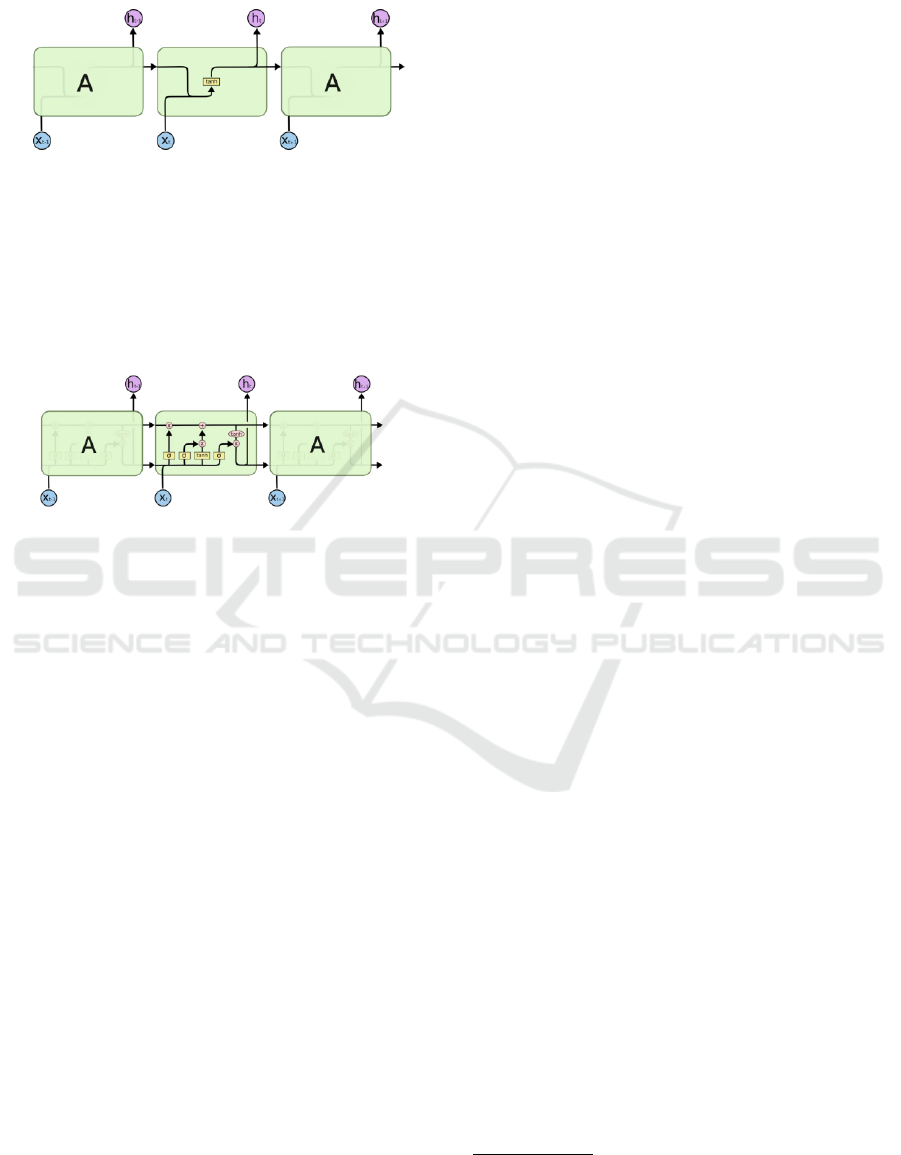
put, supporting the backpropagation process known

as tanh function, as shown in Figure 1.

Figure 1: An RNN’s module contains only a single layer.

Source: OLAH, 2015.

Following a similar structure, the LSTM networks

also have this chain structure, but the repeating mod-

ule has a different shape. Rather than having just a

single layer of a neural network, there are four, which

interact in a very speciﬁc way. Figure 2 visually

presents this concept.

Figure 2: An LSTM’s module contains four interacting lay-

ers. Source: OLAH, 2015.

The main idea of LSTM networks is to create a

representation of the cell state that traverses through

the entire structure of the network, undergoing only a

few linear interactions, making it so that information

can ﬂow without many changes.

LSTM networks also have the ability to remove or

add information to the cell state, being regulated by

structures known as gates. It is a way to let informa-

tion ﬂow in the neural network. They are composed

of a sigmoid layer of a neural network and a type

of multiplication. The sigmoid layer outputs num-

bers ranging from zero to one, which describe how

much of each component must pass through the gate.

The higher the value, the more information is passed

through this layer.

3 METHODOLOGY

This section will contextualize the data and methods

used to predict Bitcoin with the support of exogenous

time series, Ethereum and USD/BRL, in addition to

carrying out important considerations for the rest of

the study and demonstrating all proposed tests.

To ease the comprehension of the methodology,

in Figure 3, we summarize the process. It starts with

a dataset as input, and these data are pre-processed

and fed into the neural network. After the training of

the network is completed, the prediction model of the

data is generated. Finally, to evaluate the assertive-

ness of the model, the analysis is carried out through

the metrics described above. In what follows, we de-

scribe in detail the steps of the adopted methodology.

3.1 Data Collection

The datasets used were obtained from one of the

biggest investment sites in the world

. The selected

data are from January 1, 2016 to June 1, 2021, with

1,979 samples. This set consists of daily records con-

taining the following features:

• Date - Weekly Registration Date

• Open - Currency Opening Value

• Close - Currency Closing Value

• High - Maximum Currency Value in the Period

• Low - Minimum Currency Value in the Period

• Volume - Trading Amount of Currency in the Pe-

riod

• Var% - Currency Price Variation in Percentage

All analysis performed in this work was made

from the database collected. The closing value of the

coin will be used for testing and the others will be dis-

carded. In this way the study will focus on the Bitcoin

time series. Consequently, the statistical characteris-

tics of the data were observed for a better understand-

ing of the problem and were fundamental to deﬁne

some parameters of the modeling.

3.2 Pre-Processing

Before entering the data into the model, they were di-

vided between training and testing and normalized.

Normalization of datasets is a common requirement

for many machine learning estimators, and they can

misbehave if individual features don’t look like nor-

mally distributed data: Gaussian with zero mean and

unity variance. For example, many elements used in

the objective function of a learning algorithm assume

that all features are centred around zero and have vari-

ance in the same order. If a feature has a variance that

is the order of magnitude much higher than the oth-

ers, it can dominate the objective function and make

the estimator unable to learn from other’s features cor-

rectly as expected. There are several ways to split a

database. In this case, the division was done in a dif-

ferent way. Considering that the models used use the

To access and for more information about the datasets

see: https://www.investing.com

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

182

Figure 3: Overview of the proposal.

series’ own values for learning, the interval selected

for training can impact the results. In this way, incor-

porating or removing value peaks from the series dur-

ing the execution of the models can directly change

the prediction values.

First, the data was divided into 80% for training

and 20% for testing. After, for comparison purposes,

it was also performed with training and test data di-

vided into 70% and 30%. The application methods

were the same for both sets. Finally, we highlight that

the model was validate considering a 10-fold cross-

validation(Tanenbaum and Zucchi, 2009).

3.3 Experimental Setup

The analysis performed

from data collection to mod-

eling and testing, using Python language, version

3.7.10, and free machines provided by the Google

Collaboratory environment. The libraries Matplotlib

(Hunter, 2007) were used for plotting the graphs and

images, scipy (Virtanen et al., 2020) and keras library,

(Gulli and Pal, 2017), for instances of the LSTM neu-

ral network model.

3.4 Conﬁguration of the Proposal

GridSearchCV library was used to deﬁne the param-

eters, as stated in (Brownlee, 2016), hyperparameters

optimization is a big part of deep learning. The rea-

The computer that performed these tests has 8gb of

RAM memory and a core I5 8th gen processor.

son is that neural networks are notoriously difﬁcult to

conﬁgure and there are many parameters that need to

be set. Grid Search is an approach to parameter tuning

that will build and evaluate a model for each combina-

tion of algorithm parameters speciﬁed in a grid. The

key terms to know when using Grid Search CV are:

• Estimator - The model to be trained is passed to

this parameter.

• Parameter Grid - A dictionary with parameters,

they are explained in the next page. All combina-

tions of these parameters are tested to verify the

model with the best accuracy.

3.5 LSTM Network

• Optimization: Optimization refers to a procedure

for ﬁnding the input parameters or arguments to a

function that result in the minimum or maximum

output of the function. The applied optimizer is

Adam. It is a ﬁrst-order optimization algorithm,

that explicitly involve using the ﬁrst derivative

(gradient) to choose the direction to move in the

search space;

• Batch Size: The batch size is the number of pat-

terns shown to the network before the weights are

updated. It is also an optimization in the train-

ing of the network, deﬁning how many patterns to

read at a time and keep in memory. The batch size

used in the experimental is 64.

• Epochs: The number of epochs is the number of

times that the entire training dataset is shown to

A Computational Model for Predicting Cryptocurrencies Using Exogenous Variables

183

the network during training. After performing the

GridSearchCV, the model consider 25 epochs.

3.6 Evaluation Metrics

In a data modelling (Simsion and Witt, 2004) and

forecasting system (Affonso et al., 2021), it is es-

sential to use metrics that allow the evaluation and

understanding of the results obtained, through which

it is possible to suggest the adequacy of the method-

ology and processes to the problem. For evaluation,

Mean Absolute Error (MAE) and Root Mean Square

Error (RMSE) are widely adopted in several areas of

knowledge to measure performance, mainly to esti-

mate the quality of a forecasting model. Another im-

portant metric is the Mean Absolute Percent Error

(MAPE). It brings a percentage perspective of the er-

ror of the evaluated method. As can be seen in (Af-

fonso et al., 2021), the use of metrics that consider

the errors found between prediction and real value as

a form of evaluation for time series prediction is ef-

fective, in addition to facilitating the identiﬁcation of

characteristics and carrying out comparisons.

3.6.1 RMSE

The ﬁrst metric, RMSE consist in the root mean

square error of the difference between the prediction

and the actual value. Similar to the standard devia-

tion, is interpreted as a measure of the average devia-

tion between observed and predicted. Where x

is the

actual value and x

′

is the predicted value, we have:

RMSE =

(

∑

− x

′

)

) (1)

3.6.2 MAE

The Mean absolute error basically consists of the av-

erage of errors that the model obtained. Unlike the

previous metric, it penalizes large model errors less.

Where x

is the actual value and x

′

is the predicted

value, we have:

MAE =

∑

− x

′

)

(2)

3.6.3 MAPE

The MAPE differs from the metrics mentioned above

and calculates the error in percentage. It is calculated

as the average of the percent error, i.e. it expresses the

error precision as a percentage.

MAPE =

∑

− x

′

)

∗ 100 (3)

4 RESULTS

In general, evaluating the results obtained, it was pos-

sible to observe how the proposed model, as described

in the methodology, was able to make predictions of

Bitcoin time efﬁciently, with good behavior for dif-

ferent approaches of training/test split. The ﬁrst split

is presented in 4; in it, we provide the real variations

of the Bitcoin (blue line) with the prediction of the

model (yellow line) considering in the x-axis differ-

ent years and the values on the y-axis.

As we can see, the periods of 2017, 2018, and

2021 show how intense Bitcoin variations can be in

this case. Up to this point, to provide a complete

study, we perform an analysis of the data split in 70-

30%. Precisely, the behaviour of this series is pre-

sented in 5, which follows a similar structure to the

previous analysis.

When considering periods in which the behavior

of Bitcoin was unstable or more volatile, the model

did not predict this situation well. The great peaks of

value suffered by Bitcoin, whether high or low, are the

result of a set of factors. Studying and understanding

these factors is essential to proceed with the study.

Another consideration that must be made is re-

lated to the existence time of Bitcoin, the small pe-

riod of existence does not allow infer patterns yet.

The atypical situations in which the series is submit-

ted make it difﬁcult to understand, study and corrobo-

rate the large variations and lack of pattern identiﬁed.

Studying the behavior of the data and its relation

with the predictive model is an important step. How-

ever, in order to provide a more robust study, we con-

sider the application of different evaluation metrics,

RMSE and MAPE. The results related to these met-

rics and the considered model are presented in Table

1, which is divided into two different parts according

to the splits of the datasets.

Table 1: Results obtained by different evaluation metrics

considering the two datasets distributions and LSTM Neural

Network.

80%-20% 70%-30%

RMSE MAPE (%) RMSE MAPE (%)

4.320,37 6.89 5.535,53 7.03

During training, the results suggest that the net-

work, divided into 80% training and 20% testing,

presented an RMSE of 4,320.37 and a MAPE of

6.89%. The network where the data were divided into

70% training and 30% testing presented an RMSE

of 5,535.53 and a MAPE of 7.03%. In general, the

RMSE penalizes large forecast errors. Considering

the analyzed data, which have large variations, these

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

184

Figure 4: Prediction Using LSTM Network (80% - 20%).

Figure 5: Prediction Using LSTM Network (70% - 30%).

values suggest an average performance of the model.

The choice of evaluation indices take into account

both the prediction error of the model and its adapta-

tion to the time series, taking into account the penalty

of errors on a small and large scale. The selection of

evaluation indices for the ﬁnal comparison table con-

sidered the best results obtained by each model, con-

taining the same total of data for testing and training.

It is important to highlight the assignment of ran-

dom weights that happens during the training of a

neural network, making its implementation a little

more complex. It was necessary to carry out several

tests using the same input data and parameters to be

able to obtain an average of the evaluation indices.

5 CONCLUSIONS

Machine learning shows itself to be effective in mod-

eling and predicting time series. However, identifying

values or future trends is not a simple task, especially

when dealing with ﬁnancial context where the studied

context is inﬂuenced by several external factors. In

particular, cryptocurrencies, unlike conventional as-

sets, suffer unknown interferences in their value, mak-

ing their temporal evolution extremely volatile. There

are indications and studies of situations that can cause

such changes. Periods of 2017, 2018, and 2021 show

that Bitcoin’s price ﬂuctuates due to several causes

such as supply and demand, investor and user senti-

ments, government regulations, and media hype.

This work aimed to investigate the efﬁciency of

modeling and understanding the Bitcoin time series

with the use of exogenous time series, which inﬂu-

enced the main series. The selected training models

and the techniques used for prediction aimed to diver-

sify the existing content about this subject, in addition

to proposing different approaches. The results sug-

gest that the model did not behave so well, highlight-

ing a deﬁciency in the proposed analysis category.

For future work, we intend to evaluate periods

with the highest volatility of the series, considering

A Computational Model for Predicting Cryptocurrencies Using Exogenous Variables

185

social networks analysis, news, and information that

inﬂuence people’s desire to buy, for instance. In fact,

this assessment intends to identify and model other

external inﬂuences, which were not addressed in this

study, to which the currency is subject.

Combining a qualitative approach to external in-

ﬂuences, such as example, Twitter sentiment analysis,

and a quantitative approach based on the series’ own

values may be the most appropriate way to conduct

the research. Furthermore, these valuations can be a

promising study for currency forecasting.

ACKNOWLEDGEMENTS

This work was partially supported by the Brazilian re-

search funding agencies CNPq (305805/2021-5) and

FAPERGS (Programa de Apoio

a Fixac¸

ao de Jovens

Doutores no Brasil - 23/2551-0000126-8).

REFERENCES

Abdel-Nasser, M. and Mahmoud, K. (2019). Accurate pho-

tovoltaic power forecasting models using deep lstm-

rnn. Neural Computing and Applications.

Affonso, F., Dias, T. M. R., and Pinto, A. L. (2021). Finan-

cial times series forecasting of clustered stocks. Mo-

bile Networks and Applications, 26(1):256–265.

Brownlee, J. (2016). How to grid search hyperparameters

for deep learning models in python with keras. l

ınea].

Disponible en: https://machinelearningmastery.

com/grid-search-hyperparameters-deep-learning-

models-python-keras.

Buterin, V. et al. (2013). Ethereum white paper. GitHub

repository, 1:22–23.

Castello, M. G. (2019). Bitcoin

e moeda? classiﬁcac¸

ao das

criptomoedas para o direito tribut

ario. Revista Direito

GV, 15.

Chu, J., Nadarajah, S., and Chan, S. (2015). Statistical

analysis of the exchange rate of bitcoin. PloS one,

10(7):e0133678.

Dalmazo, B. L., Vilela, J. P., and Curado, M. (2018). Triple-

similarity mechanism for alarm management in the

cloud. Computers & Security, 78:33–42.

Deng, L. and Yu, D. (2014). Deep learning: methods and

applications. Foundations and trends in signal pro-

cessing.

Ehlers, R. S. (2007). An

alise de s

eries temporais. Labo-

rat

orio de Estat

ıstica e Geoinformac¸

ao. Universidade

Federal do Paran

a, 1:1–118.

Gulli, A. and Pal, S. (2017). Deep learning with Keras.

Packt Publishing Ltd.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural computation, 9(8):1735–1780.

Hughes, S. D. (2017). Cryptocurrency regulations and en-

forcement in the us. W. St. UL Rev., 45:1.

Hunter, J. D. (2007). Matplotlib: A 2d graphics environ-

ment. Computing in science & engineering, 9(03):90–

95.

Mallqui, D. C. and Fernandes, R. A. (2019). Predicting

the direction, maximum, minimum and closing prices

of daily bitcoin exchange rate using machine learning

techniques. Applied Soft Computing, 75:596–606.

McCulloch, W. S. and Pitts, W. (1943). A logical calculus

of the ideas immanent in nervous activity. The bulletin

of mathematical biophysics, 5(4):115–133.

Miura, R., Pichl, L., and Kaizoji, T. (2019). Artiﬁcial neu-

ral networks for realized volatility prediction in cryp-

tocurrency time series. In International Symposium on

Neural Networks, pages 165–172. Springer.

Morettin, P. A. (2017). Econometria ﬁnanceira: um curso

em s

eries temporais ﬁnanceiras. Editora Blucher.

Mukhopadhyay, Ujan, e. a. (2016). A brief survey of cryp-

tocurrency systems. 14th annual conference on pri-

vacy, security and trust (PST), IEEE.

Nakamoto, S. (2008). A peer-to-peer electronic cash sys-

tem. Bitcoin.–URL: https://bitcoin. org/bitcoin. pdf.

Nofer, Michael, e. a. (2017). Blockchain. Business & In-

formation Systems Engineering.

Simsion, G. and Witt, G. (2004). Data modeling essentials.

Elsevier.

Sun, Lei, e. a. (2017). Multiple-target deep learning

for lstm-rnn based speech enhancement. Hands-

free Speech Communications and Microphone Arrays

(HSCMA), IEEE.

Tanenbaum, A. S. and Zucchi, W. L. (2009). Organizac¸

estruturada de computadores. Pearson Prentice Hall.

Tsai, Y.-T., Zeng, Y.-R., and Chang, Y.-S. (2018). Air pollu-

tion forecasting using rnn with lstm. 16th Intl Conf on

Dependable, Autonomic and Secure Computing, 16th

Intl Conf on Pervasive Intelligence and Computing,

4th Intl Conf on Big Data Intelligence and Computing

and Cyber Science and Technology Congress, IEEE.

Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M.,

Reddy, T., Cournapeau, D., Burovski, E., Peterson,

P., Weckesser, W., Bright, J., et al. (2020). Scipy

1.0: fundamental algorithms for scientiﬁc computing

in python. Nature methods, 17(3):261–272.

Zoumpekas, T., Houstis, E., and Vavalis, M. (2020). Eth

analysis and predictions utilizing deep learning. Ex-

pert Systems with Applications, 162:113866.

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

186