Towards a Topological Map-Matching Algorithm for Solid Waste

Collection Systems

Carola A. Blazquez

1 a

, Roberto Le

2 b

and Luis Delgado

Department of Engineering Sciences, Universidad Andres Bello, Quillota 980, Vi

na del Mar, Chile

Departamento de Inform

atica, Universidad T

ecnica Federico Santa Mar

ıa, Av. Espa

na 1680, Valpara

ıso, Chile

Faculty of Engineering, Universidad Andres Bello, Quillota 980, Vi

na del Mar, Chile

Keywords:

GPS, Intelligent Transportation Systems, Algorithm, Waste Management.

Abstract:

Global Navigation Satellite Systems (GNSS) such as Global Positioning Systems (GPS) are employed in

different Intelligent Transportation Systems (ITS) applications to determine vehicle routes. However, the

map-matching problem emerges when GPS measurements are assigned to incorrect road segments on a digital

map due to the complexities of the road network and errors from different sources when capturing GPS data.

This study presents a Topological Map-Matching Algorithm (TMMA) for determining correct waste collection

vehicle routes using GPS measurements in an ofﬂine context to help improve solid waste collection services

and compute proper performance measures. The TMMA is applied to a real-world case study with ten waste

collection routes in the commune of Renca in Santiago, Chile. Overall, results indicate that the accuracy of the

algorithm is greater than 90%, and small percentages of false negative cases with unsnapped GPS data points

are obtained for most vehicle routes. The sensitivity analysis suggests that larger buffer sizes and higher speed

tolerances yield the best solution quality and execution times.

1 INTRODUCTION

In 2016, the estimated generation of urban solid waste

worldwide was approximately 2.01 billion tons and

was estimated to reach 3.4 billion tons by 2050 (Kaza

et al., 2018; Rojas et al., 2018). As population, ur-

banization, and industrialization increase, authorities

must address this accelerated solid waste production

rate by implementing adequate solid waste manage-

ment systems (Khandelwal et al., 2019). However,

in most developing countries, unsatisfactory policies,

regulatory structures, and inefﬁcient solid waste man-

agement negatively impact society, the environment,

and the economy. Urban solid waste is usually col-

lected using a manual approach (door-to-door) based

on ﬁeld experience and intuition, generating high op-

erational and transportation costs, low service qual-

ity, high trafﬁc congestion, a large amount of green-

house gas emissions, and high health risk (Blazquez

and Vonderohe, 2009; Blazquez and Paredes-Belmar,

2020; Letelier et al., 2022). In addition, municipali-

ties spend between 20% and 50% of their budget on

https://orcid.org/0000-0003-4760-885X

https://orcid.org/0000-0002-7164-1783

solid waste management, of which 50% to 70% cor-

responds to waste collection and transportation tasks

(Erfani et al., 2017; Blazquez and Paredes-Belmar,

2020; Letelier et al., 2022).

To overcome these issues, in the last decade,

there has been an increase in the use of informa-

tion and communication technologies for solid waste

management services as part of smart cities (Ricardo

et al., 2018; Vishnu et al., 2021). In particular, the

use of Global Positioning Systems (GPS) technology

has improved tremendously the solid waste collec-

tion process, which is the most expensive within the

solid waste value chain (Ghiani et al., 2015; Steyn and

Willemse, 2018). Various performance indicators of

the solid waste collection process may be computed

using GPS measurements such as service time, road

traversal time, unloading time, number of stops, fuel

consumption, and vehicle emissions, among others,

to improve the collection service and planning and

minimize operational and transportation costs (Han-

nan et al., 2015; Akram et al., 2021).

GPS measurements must be associated or snapped

to the correct road segment to calculate performance

measures accurately. However, due to the complex-

ities of the road network and errors from different

Blazquez, C., León, R. and Delgado, L.

Towards a Topological Map-Matching Algorithm for Solid Waste Collection Systems.

DOI: 10.5220/0011854100003479

In Proceedings of the 9th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2023), pages 95-102

ISBN: 978-989-758-652-1; ISSN: 2184-495X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

sources when capturing GPS data, GPS measure-

ments are assigned to incorrect road segments on

a digital map, causing the so-called map-matching

problem (Blazquez and Vonderohe, 2009; Blazquez

et al., 2012; Le

on et al., 2020). Figure 1 illustrates an

example of the map-matching problem, in which GPS

data points p

and p

are correctly snapped to the road

at locations represented by data points s

and s

, re-

spectively. While data point p

is incorrectly snapped

to the closest road segment indicated by point s

. The

correct snapping location of the data point p

is repre-

sented by point c

. Therefore, there is a need for map-

matching algorithms to solve this problem by identi-

fying correct GPS trajectories along the road network.

Figure 1: Example of the map-matching problem. Adapted

from Blazquez et al. (2022).

In the last decades, numerous map-matching al-

gorithms have been proposed in the literature rang-

ing from simple geometric techniques to advanced,

complex algorithms such as hidden Markov models,

Kalman ﬁlter, and fuzzy logic (Blazquez et al., 2018;

on et al., 2020). These algorithms have been imple-

mented to solve the map-matching problem in mul-

tiple Intelligent Transportation Systems (ITS) appli-

cations. For example, as part of an electronic hori-

zon in driver assistance systems, Burgstahler et al.

(2016) utilized a map-matching algorithm for map-

ping vehicle geographical positions onto the digital

road map and determining the correct road segment

being used. In another study by Klitzke et al. (2019),

a map-matching algorithm was used for matching ego

vehicle positions to a digital road map as part of the

test drives in the validation of autonomous driving

systems. Similarly, Kang et al. (2020) employed an

iterative closest point-based map-matching algorithm

for identifying GPS trajectories on a digital road map

in autonomous driving and advanced driver assistance

systems. Ricardo et al. (2018) implemented a map-

matching algorithm to determine bus lines and bus

stops from GPS measurements in Porto, Portugal. A

GIS-based map-matching algorithm was employed by

Scott et al. (2021) to determine bike share users’ route

choices along the cycling network within Hamilton,

Ontario, Canada, using hub-to-hub GPS trajectories.

Regarding solid waste management applications,

most studies employ GPS technology for identify-

ing waste bin levels (Hadria et al., 2018; Anjum

et al., 2022) and waste bin locations (Erdinc¸ et al.,

2019; Mishra and Kumar Ray, 2020; Moral et al.,

2022), monitoring waste collection routes (Steyn and

Willemse, 2018), and planning route scheduling (Wil-

son and Vincent, 2008; Ghiani et al., 2015). How-

ever, scarce studies focus on implementing a map-

matching algorithm to help improve solid waste col-

lection services and compute correct performance

measures by determining the correct route on which

vehicles travel. For instance, Ghiani et al. (2015)

implemented an automated classiﬁcation and estima-

tion algorithm for estimating service time at collec-

tion points and traversal times along different roads.

This study addresses the map-matching problem

by presenting a Topological Map-Matching Algo-

rithm (TMMA) implemented ofﬂine for determining

correct waste collection vehicle routes using mea-

sured data (position, timestamp, and vehicle speed).

The proposed TMMA uses parts or all GPS measure-

ments to resolve the map-matching problem. Addi-

tionally, computational experiences are reported us-

ing real-world GPS data collected by waste collection

vehicles in the commune of Renca in Santiago, Chile.

A sensitivity analysis is conducted to identify the im-

pact of the algorithm parameters on the solution qual-

ity and execution time.

2 TOPOLOGICAL

MAP-MATCHING ALGORITHM

Among the map-matching algorithms found in the

literature, TMMAs have been preferred in ITS ap-

plications since they are simple, efﬁcient, fast, and

easy to implement (Hashemi and Karimi, 2014; Gupta

and Shanker, 2022). TMMAs employ link connectiv-

ity and contiguity to compute the shortest paths and

travel time between pairs of GPS measurements. Nor-

mally, TMMAs use different algorithmic parameters

related to buffer size for ﬁnding snapping locations of

GPS measurements along road segments, information

on trafﬁc ﬂow or congestion, and road features such as

speed limit and the number of lanes. In this study, the

TMMA utilizes two distinct parameters (buffer size

and speed range tolerance), explained below.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

start

fw = False

→ k

alt k

→ alt k

alt k

i−1

→ k

j − i ≤ N

FID(k

) = 0

fw == False

= k

i−1

fw = False

= k

j+1

fw = True

j − i > 1

end

Assign FID to snap

points k

for each

p = i + 1, ..., j − 1

fw : dummy boolean variable (backward or forward)

→ k

: shortest path between snapped points k

and k

N : maximum amount of consecutive data points.

alt k

: alternative centerline to snapped point k

alt k

: alternative centerline to snapped point k

YES

NOYES

YES

Figure 2: Flow diagram of the TMMA. Adapted from Le

et al. (2020).

Figure 2 shows the ﬂow diagram of the TMMA

used in this study. Once road segment candidates are

selected as possible snapping locations within buffers

around GPS data points, the TMMA tests pairs of

GPS points by snapping them to the closest road seg-

ment candidate and computing shortest paths between

pairs of snapped GPS points k

and k

. Subsequently,

travel speeds are calculated using distances of the

shortest paths and time differences between times-

tamps and are compared with the average vehicle

speeds recorded with each GPS measurement. Cur-

rent snapped locations of the GPS points are accepted

when the average vehicle speeds are within a speed

range tolerance of the travel speeds. On the contrary,

current snapped locations of the GPS points are re-

jected, and other snapping locations (alt k

and alt

) on alternative road segment candidates are tested,

shortest paths are recomputed, and speeds are com-

pared again. If there are no feasible routes between

snapped locations of GPS points, then the TMMA

tests with preceding and succeeding GPS points until

the map-matching problem is solved or a predeﬁned

number of maximum consecutive GPS points (N) is

reached.

Note that those GPS points with no snapping loca-

tions on the correct road segment (i.e., false negatives

with FID(k

) = 0) are forced to snap to the closest road

segment that comprises viable routes between preced-

ing and succeeding GPS points. If GPS points k

with

p = i + 1, ..., j − 1 have no snapping locations on any

road segment (false negatives), and if a valid route ex-

ists between snapped points k

and k

, therefore, these

points are snapped to their closest road segments that

belong to this viable route and are assigned the FID

of the road.

3 CASE STUDY

3.1 Study Area

The capital city of Chile, Santiago, produces approx-

imately 43% of the total waste generated nationwide

(Rojas et al., 2018). This study focuses on the com-

mune of Renca, one of the 34 communes that consti-

tute the Great Santiago, with a population of 147,151

inhabitants and an area of 24.0 km

(INE, 2017).

Renca generates over 70,000 tons of municipal solid

waste every year, representing approximately 24.5%

more than the total average waste generation of the

country. Currently, Renca has a waste collection

system comprising a door-to-door collection using a

single-compartment compactor truck and two or three

crew members per truck responsible for collecting

waste from the curbside and throwing it in the rear

of the truck for compaction (Blazquez and Paredes-

Belmar, 2020).

3.2 Data

This study applied the TMMA to 10 waste collection

vehicle routes shown in Figure 3. This ﬁgure depicts

350 GPS measurements captured every 30 seconds in

the commune of Renca. The vehicle routes include

different types of roads (e.g., local and major roads

and highways), as shown in Table 1.

Figure 4 presents the basic statistics of the

recorded vehicle speeds for each route obtained from

the data measurements. This ﬁgure shows the ﬂuc-

tuation of vehicle speeds for different types of roads.

Overall, lower speeds are observed for vehicle routes

along local roads, while higher speeds are perceived

along major roads and highways. Note that no differ-

ential GPS or other GPS position accuracy improve-

ment methods are available in this study.

Towards a Topological Map-Matching Algorithm for Solid Waste Collection Systems

Figure 3: GPS measurements for the waste collection vehi-

cle routes.

Table 1: Road types for each route.

Route Type of Road

1 Local roads

2 Major roads/Highways

3 Local roads

4 Major roads/Highways

5 Local and major roads

6 Highways

7 Major roads/Highways

8 Major roads/Highways

9 Major roads/Highways

10 Highways

Figure 4: Distribution of vehicle speeds in km/hr for each

route.

4 RESULTS

4.1 Performance of the TMMA

The performance of the TMMA is evaluated using the

accuracy (i.e., correct snaps of GPS measurements),

error (i.e., incorrect snaps of GPS measurements),

false negative (FN) cases, and execution times. FN

cases correspond to GPS measurements that are not

associated with any road segment candidate since the

buffer size is too small when these measurements

should have snapped to a certain road segment.

The accuracy is computed with Equation (1),

where p

is a GPS measurement or data point of a

vehicle route r that is snapped to the correct road seg-

ment with c = 1, ...,C, p

is a GPS data point of a

vehicle route r with n = 1, ..., N, C is the total num-

ber of correctly snapped GPS data points, and N is the

total number of GPS data points.

Acc

∑

(1)

Similarly, Equation (2) is used to calculate the er-

ror for each vehicle route, where p

is a GPS data

point of a vehicle route r that is snapped to the incor-

rect road segment with o = 1, ..., O, and O is the total

number of GPS data points snapped to incorrect road

segments.

Error

∑

(2)

FN cases (FN

) are computed with Equation (3)

for each vehicle route, where p

is a GPS data point

of a vehicle route r that is considered an FN case with

f = 1, ..., F, and F is the total number of GPS data

points that are not snapped to any road segment.

∑

(3)

Figure 5 shows the performance results of the

TMMA for the analyzed vehicle routes using a base

case scenario with a buffer size of 20 meters and a

speed range tolerance of 20 km/hr. This ﬁgure in-

dicates that the accuracy for most vehicle routes is

greater than 90%. Errors arising from the snapping

of GPS trajectories to incorrect road segments for

Routes 2, 4, and 8 occur mainly along highways be-

cause the algorithm assigns GPS data points to viable

side roads parallel to the highways. Further research

Figure 5: Performance results of the TMMA.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

should include the revision of the TMMA for address-

ing this type of issue, perhaps by also capturing the

vehicle heading to accept those road segment candi-

dates with directions (azimuth angle) that are within

a predeﬁned heading range tolerance, as in Blazquez

et al. (2012), Blazquez et al. (2022) and Chen et al.

(2019).

A small percentage of FN cases (on average,

< 1.9%) is observed in the 10 tested routes of Fig-

ure 5. Therefore, the TMMA satisfactorily forces the

snap of most GPS points with no associated road seg-

ments to the routes between preceding and succeeding

GPS points. The remaining FN cases occur for some

routes when the vehicles enter the transfer station to

unload the collected waste, and there is no road rep-

resentation in a digital form.

Figure 5 presents the computing time per point

for each tested route. The average execution time

per GPS point among all routes is approximately 0.12

minutes. This ﬁgure suggests that the TMMA needs

a higher execution time to solve the map-matching

problem for some routes, particularly those with a

larger percentage of GPS data points that are snapped

to incorrect road segments. On the contrary, routes

that reach an accuracy of nearly 100% require smaller

times in the execution to solve the problem, such as

with Route 1.

4.2 Sensitivity Analysis

This subsection presents the results of the sensitivity

analysis of the TMMA for buffers sizes of 10, 20,

and 30 meters and speed tolerances of 15, 20, and

25 km/hr. Figures 6-15 depict the variation of the ac-

curacy and the execution times of the TMMA for each

route as the buffer size and the speed tolerance ﬂuc-

tuate. Overall, the graphs in these ﬁgures show that

better results, in terms of accuracy, are obtained with

larger buffer sizes (> 20 meters) and higher speed

tolerances (> 25 km/hr), independent of the type of

roads that comprise each route.

Additionally, the ﬁgures indicate that the execu-

tion times of the algorithm remain relatively constant

as the speed tolerance increases from 15 to 25 km/hr

and the buffer size increases from 10 to 30 meters,

except for Routes 4 and 8 (Figures 9 and 13, respec-

tively). The latter routes present a higher comput-

ing time of the TMMA in a complicated part of the

road network for two possible reasons. First, when

increasing the speed tolerance, the shortest paths be-

tween pairs of incorrect snapped GPS data points are

accepted, which are subsequently corrected by the

TMMA as preceding and succeeding GPS data points

are tested. Second, if the buffer size increases, then

a higher number of road segment candidates are se-

lected within each buffer of the GPS data point, and

more alternative snapping locations along different

road segments for the GPS points are examined.

Figure 6: Sensitivity analysis for Route 1.

Figure 7: Sensitivity analysis for Route 2.

Figure 8: Sensitivity analysis for Route 3.

Figure 9: Sensitivity analysis for Route 4.

Towards a Topological Map-Matching Algorithm for Solid Waste Collection Systems

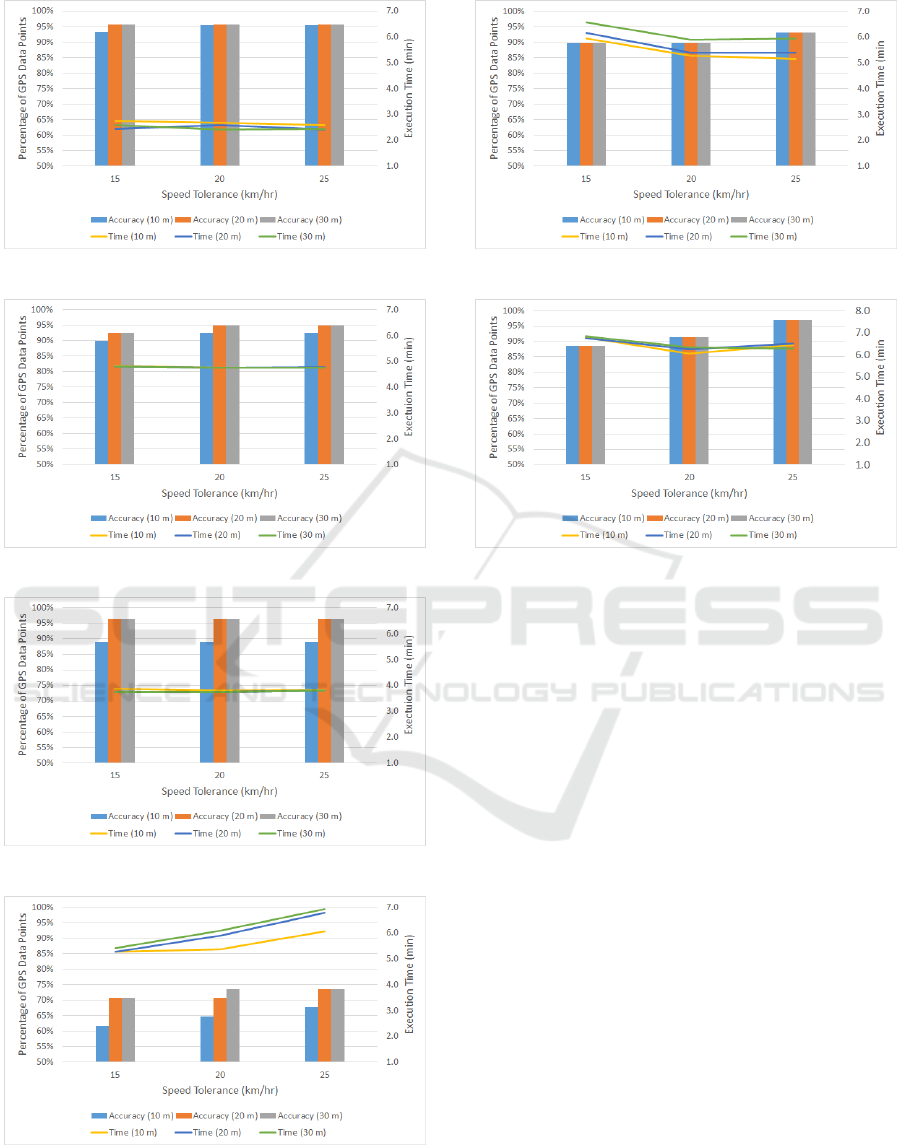
Figure 10: Sensitivity analysis for Route 5.

Figure 11: Sensitivity analysis for Route 6.

Figure 12: Sensitivity analysis for Route 7.

Figure 13: Sensitivity analysis for Route 8.

Figure 14: Sensitivity analysis for Route 9.

Figure 15: Sensitivity analysis for Route 10.

Table 2 presents the percentage of FN cases for

different speed tolerance and buffer size parameter

values. This table indicates that road segment can-

didates are assigned to GPS data points as the buffer

size increases, and thus, the percentage of FN cases

diminishes. Routes 1, 2, 3, and 7 are not listed since

these routes have no FN cases as the parameter val-

ues vary. The percentage of FN cases for most routes

does not ﬂuctuate as the speed tolerance increases.

5 CONCLUSIONS

This study employs a TMMA for determining correct

waste collection routes to improve solid waste collec-

tion services and compute appropriate performance

measures (e.g., service time, road traversal time, un-

loading time, number of stops, fuel consumption, ve-

hicle emissions, etc.). The TMMA was tested with

ten vehicle routes in the commune of Renca in Santi-

ago, Chile. Results of the TMMA are presented for a

base case and sensitivity analysis of different parame-

ter models. Overall, for the base case, more than 90%

of the GPS data points are snapped to correct road

segments for most routes, a small percentage of FN

cases exist for most routes, and the average execution

time per GPS point is approximately 0.12 minutes.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

100

Table 2: FN cases for different tested buffer sizes.

Speed Tolerance Buffer Size

10m 20m 30m

Route 4

15 km/hr 0.0% 0.0% 0.0%

20 km/hr 0.0% 2.9% 2.9%

25 km/hr 0.0% 0.0% 0.0%

Route 5

15 km/hr 4.3% 4.3% 4.3%

20 km/hr 4.3% 4.3% 4.3%

25 km/hr 4.3% 4.3% 4.3%

Route 6

15 km/hr 7.5% 5.0% 5.0%

20 km/hr 7.5% 5.0% 5.0%

25 km/hr 7.5% 5.0% 5.0%

Route 8

15 km/hr 8.8% 2.9% 2.9%

20 km/hr 2.9% 0.0% 0.0%

25 km/hr 0.0% 0.0% 0.0%

Route 9

15 km/hr 2.9% 2.9% 2.9%

20 km/hr 2.9% 2.9% 2.9%

25 km/hr 2.9% 2.9% 2.9%

Route 10

15 km/hr 0.0% 0.0% 0.0%

20 km/hr 2.9% 0.0% 0.0%

25 km/hr 0.0% 0.0% 0.0%

The sensitivity analysis suggests a tendency to

yield improved solution quality with larger buffer

sizes and higher speed tolerances. The execution

time of the TMMA remains approximately constant

as the parameters are varied, except for a couple

of routes, in which GPS measurements are captured

along parallel roads (e.g., highways and side roads).

Thus, the TMMA should be revised in future research

to address map-matching problems that arise when

there are equally viable paths between pairs of GPS

points. In addition, further research should test the

TMMA with different sampling frequencies and ve-

hicle routes from other communes or cities to identify

the appropriate algorithm parameters for each tested

data sets. Finally, future research should compare the

results of this study with a proper benchmark.

GPS technology aids in determining correct ve-

hicle routes to increase the effectiveness of waste

collection systems, which are imperative for reduc-

ing negative impacts on the environment and society.

Thus, municipal authorities must make informed de-

cisions to address the current accelerated solid waste

production rate, particularly in urban areas. A real-

time TMMA may be required to monitor and surveil

a ﬂeet of waste collection vehicles.

ACKNOWLEDGEMENTS

This study was ﬁnancially supported by the

Chilean Government through FONDEF IdeA

Grant ID22I10107 and Universidad Andres Bello

through Project N°DI-01-20/REG.

REFERENCES

Akram, S. V., Singh, R., Gehlot, A., Rashid, M., AlGhamdi,

A. S., Alshamrani, S. S., and Prashar, D. (2021). Role

of wireless aided technologies in the solid waste man-

agement: A comprehensive review. Sustainability,

13(23):13104.

Anjum, M., Sarosh Umar, M., and Shahab, S. (2022).

Iot-based novel framework for solid waste manage-

ment in smart cities. In Smys, S., Balas, V. E., and

Palanisamy, R., editors, Inventive Computation and

Information Technologies, pages 687–700, Singapore.

Springer Nature Singapore.

Blazquez, C., Le

on, R., P

erez, F., and Delgado, L. (2022).

Pre-processing techniques for improving a topological

map-matching algorithm. In 2022 41st International

Conference of the Chilean Computer Science Society

(SCCC), pages 1–6.

Blazquez, C., Miranda, P., and Ponce, A. (2012). Perfor-

mance of a new enhanced topological decision–rule

map-matching algorithm for transportation applica-

tions. Journal of applied research and technology,

10(6):929–940.

Blazquez, C. and Paredes-Belmar, G. (2020). Network de-

sign of a household waste collection system: A case

study of the commune of renca in santiago, chile.

Waste Management, 116:179–189.

Blazquez, C., Ries, J., Miranda, P. A., and Le

on, R. J.

(2018). An instance-speciﬁc parameter tuning ap-

proach using fuzzy logic for a post-processing topo-

logical map-matching algorithm. IEEE Intelligent

Transportation Systems Magazine, 10(4):87–97.

Blazquez, C. A. and Vonderohe, A. P. (2009). Effects of

controlling parameters on performance of a decision-

rule map-matching algorithm. Journal of Transporta-

tion Engineering, 135(12):966–973.

Burgstahler, D., Peusens, C., B

ohnstedt, D., and Steinmetz,

R. (2016). Horizon. kom: A ﬁrst step towards an open

vehicular horizon provider. In VEHITS, pages 79–84.

Chen, C., Ding, Y., Xie, X., Zhang, S., Wang, Z.,

and Feng, L. (2019). Trajcompressor: An online

map-matching-based trajectory compression frame-

work leveraging vehicle heading direction and change.

IEEE Transactions on Intelligent Transportation Sys-

tems, 21(5):2012–2028.

Erdinc¸, O., Yetilmezsoy, K., Ereno

glu, A. K., and Erdinc¸,

O. (2019). Route optimization of an electric garbage

truck ﬂeet for sustainable environmental and en-

ergy management. Journal of Cleaner Production,

234:1275–1286.

Towards a Topological Map-Matching Algorithm for Solid Waste Collection Systems

101

Erfani, S. M. H., Danesh, S., Karrabi, S. M., and Shad, R.

(2017). A novel approach to ﬁnd and optimize bin

locations and collection routes using a geographic in-

formation system. Waste Management & Research,

35(7):776–785.

Ghiani, G., Guerrieri, A., Manni, A., and Manni, E. (2015).

Estimating travel and service times for automated

route planning and service certiﬁcation in municipal

waste management. Waste Management, 46:40–46.

Gupta, A. K. and Shanker, U. (2022). A comprehensive

review of map-matching techniques: Empirical anal-

ysis, taxonomy, and emerging research trends. Inter-

national Journal of Web Services Research (IJWSR),

19(1):1–32.

Hadria, F. M., Jayanthy, S., Arunraja, A., and Vigneswaran,

E. E. (2018). Iot based smart waste management us-

ing top k-query scheduling. In 2018 Second Interna-

tional Conference on Intelligent Computing and Con-

trol Systems (ICICCS), pages 448–452. IEEE.

Hannan, M., Al Mamun, M. A., Hussain, A., Basri, H., and

Begum, R. A. (2015). A review on technologies and

their usage in solid waste monitoring and management

systems: Issues and challenges. Waste Management,

43:509–523.

Hashemi, M. and Karimi, H. A. (2014). A critical review

of real-time map-matching algorithms: Current issues

and future directions. Computers, Environment and

Urban Systems, 48:153–165.

INE (2017). 2017 census, instituto nacional de es-

tad

ıstica. http://www.censo2017.cl/. accessed:

18.04.2019.

Kang, J. M., Yoon, T. S., Kim, E., and Park, J. B. (2020).

Lane-level map-matching method for vehicle localiza-

tion using gps and camera on a high-deﬁnition map.

Sensors, 20(8):2166.

Kaza, S., Yao, L., Bhada-Tata, P., and Van Woerden, F.

(2018). What a waste 2.0: a global snapshot of solid

waste management to 2050. World Bank Publications.

Khandelwal, H., Dhar, H., Thalla, A. K., and Kumar, S.

(2019). Application of life cycle assessment in mu-

nicipal solid waste management: A worldwide critical

review. Journal of cleaner production, 209:630–654.

Klitzke, L., Koch, C., Haja, A., and K

oster, F. (2019). Real-

world test drive vehicle data management system for

validation of automated driving systems. In VEHITS,

pages 171–180.

on, R., Blazquez, C., and Depassier, V. (2020). Im-

provements of a topological map-matching algorithm

in post-processing mode. In 2020 39th International

Conference of the Chilean Computer Science Society

(SCCC), pages 1–5. IEEE.

Letelier, C., Blazquez, C., and Paredes-Belmar, G. (2022).

Solving the bin location–allocation problem for

household and recycle waste generated in the com-

mune of renca in santiago, chile. Waste Management

& Research, 40(2):154–164.

Mishra, A. and Kumar Ray, A. (2020). Iot cloud-based

cyber-physical system for efﬁcient solid waste man-

agement in smart cities: a novel cost function based

route optimisation technique for waste collection ve-

hicles using dustbin sensors and real-time road trafﬁc

informatics. IET Cyber-Physical Systems: Theory &

Applications, 5(4):330–341.

Moral, P., Garc

ıa-Mart

ın,

A., Escudero-Vi

nolo, M.,

Mart

ınez, J. M., Besc

os, J., Pe

nuela, J., Mart

ınez,

J. C., and Alvis, G. (2022). Towards automatic

waste containers management in cities via computer

vision: containers localization and geo-positioning in

city maps. Waste Management, 152:59–68.

Ricardo, L., Sargento, S., and Oliveira, I. C. (2018). An

information system for bus travelling and performance

evaluation. In VEHITS, volume 1, pages 395–402.

Rojas, A., Yabar, H., Mizunoya, T., and Higano, Y. (2018).

The potential beneﬁts of introducing informal recy-

clers and organic waste recovery to a current waste

management system: The case study of santiago de

chile. Resources, 7(1):18.

Scott, D. M., Lu, W., and Brown, M. J. (2021). Route

choice of bike share users: Leveraging gps data to

derive choice sets. Journal of Transport Geography,

90:102903.

Steyn, L. J. and Willemse, E. J. (2018). Using vehicle gps

data to infer ofﬂoading times of waste collection vehi-

cles at transfer stations. In 2018 International Confer-

ence on Advances in Big Data, Computing and Data

Communication Systems (icABCD), pages 1–6. IEEE.

Vishnu, S., Ramson, S. R. J., Senith, S., Anagnostopou-

los, T., Abu-Mahfouz, A. M., Fan, X., Srinivasan, S.,

and Kirubaraj, A. A. (2021). Iot-enabled solid waste

management in smart cities. Smart Cities, 4(3):1004–

1017.

Wilson, B. G. and Vincent, J. K. (2008). Estimating waste

transfer station delays using gps. Waste management,

28(10):1742–1750.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

102