Structural Analysis of the Curriculum Through a Bipartite Network

Durdica Vukic

, Alen Jakupovic

and Sanja Candrlic

University of Rijeka, Faculty of Informatics and Digital Technologies, Rijeka, Croatia

Polytechnic of Rijeka, Rijeka, Croatia

Keywords: Bipartite Network, Curriculum, Centrality Analysis, Cognitive Load.

Abstract: Investigation of curriculum elements in terms of knowledge content organisation can be based on two entities

that support the process of knowledge acquisition: concepts and learning outcomes. Motivated by this

structure of knowledge organisation, we construct curriculum knowledge content as a bipartite network of

concepts and learning outcomes. Furthermore, we examine the applicability of centrality estimates in

detecting key knowledge entities of curriculum content as well as possibilities to rethink the knowledge

organisation and teaching. Results have shown that centrality analysis is particularly suitable for identifying

concepts and learning outcomes that are key landmarks for managing cognitive load and improving learning

retention.

1 INTRODUCTION

Many real-world systems can be represented as a

large collection of interconnected elements, i.e.,

complex networks. Modelling systems as networks has

found its application in transportation and navigation,

medicine, criminology, biochemistry, electrical

engineering, computer science, operations research,

etc. Studies in educational sciences have also shown

that network science techniques can reveal the

relational nature of knowledge (Siew, 2020).

Knowledge involves the intricate relationships

among a set of knowledge elements and is not simply

a collection of unrelated facts about a subject.

How knowledge is acquired depends largely on

the curriculum model, the role of experts in

promoting knowledge acquisition, and the method of

information transfer. In this study we examine the

quality of design and relevance of outcome-based

curriculum, as well as its linkage to effective teaching

strategies, learning processes, and information

content delivery. Learners are expected to

demonstrate mastery of a number of interrelated

information, skills, and attitudes within an outcome-

based curriculum. Because curriculum plays a crucial

role in enabling high-quality learning and in defining

https://orcid.org/0000-0002-2441-0253

https://orcid.org/0000-0003-0957-8143

https://orcid.org/0000-0003-1272-093X

and supporting education, curriculum frameworks

should cover cross-cutting competencies in addition

to subject-specific capabilities.

Consequently, knowledge domains can be

perceived as complex systems consisting of clusters

and subsystems. Therefore, we opt that the complex

nature of educators’ knowledge and expertise can be

explored through network models and that the

structural properties of this knowledge representation

can lead to insights. The aim of this paper is to explore

the applicability of bipartite network representation to

curriculum knowledge design and subdomain

recognition. To this end, we construct a bipartite

network from the content of IoT educational

programme (Veleri – OI IoT School, 2021) and

perform an analysis of the corresponding network

topology. To the best of our knowledge, this is the

first work that shows how to represent and analyse the

knowledge organisation of a study programme

curriculum as a bipartite network model.

Furthermore, we examine the network science

approach to curriculum content analysis to answer the

following research questions:

RQ1 - Can curriculum knowledge content be

modelled through a bipartite network of concepts and

learning outcomes?

Vukic, D., Jakupovic, A. and Candrlic, S.

Structural Analysis of the Curriculum Through a Bipartite Network.

DOI: 10.5220/0011854700003485

In Proceedings of the 8th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2023), pages 53-60

ISBN: 978-989-758-644-6; ISSN: 2184-5034

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

RQ2 - How can centrality score indicate the key

learning outcomes and curriculum knowledge content

that can potentially overwhelm working memory and

increase cognitive load?

The difficult part in creating a quality curriculum

is integrating multidisciplinary in planning,

architecture, and design (Centre for teaching

excellence, n.d.). There are many design examples

where subject content focuses on key knowledge

areas but does not reinforce the application of

knowledge elements from one subject area to another.

Identifying strategies that allow students to develop

more consistent thinking patterns across subjects,

could support the development of skills, attitudes and

values in more than one subject or discipline.

2 RELATED WORK

The application of network science in educational

research has found numerous use cases mostly

focusing on the study of students' knowledge

structure - the internal structure of the conceptual

representations that learners acquire, the analysis of

social interactions between learners/actors in the

educational setting, the quantification of knowledge

structures and the uncovering of differences in the

structural properties of the knowledge representations

of experts and novices, and the conduct of network-

based analyses in the context of curriculum design

and education (Siew, 2019, 2022; Gera et al., 2021;

Kubsch et al., 2020, Koponen & Pehkonen, 2010;

O’Meara & Vaidya, 2021; Sun et al., 2020; Ireland &

Mouthaan, 2020)

Network structure has also been widely studied in

languages, leading to new insights in phonetics,

lexical processing, word learning, cognitive science,

syntactic structures or learning grammar (Siew &

Vitevitch, 2019; Siew, 2022; Castro et al., 2017;

Goldstein & Vitevitch, 2017; Hills & Siew, 2018;

Citraro et al., 2022; Vitevitch, 2020; Teixeira et al.,

2021; Lynn & Bassett, 2020)

Knowledge is often described as a map (diagram),

a web, or a network, in which conceptual components

are interconnected and form a comprehensive and

dynamic system (Novak, 2010; Koponen, 2021;

Monahan et al., 2019; Kubsch et al., 2020; Koponen

& Nousiainen. 2014; Lynn & Bassett, 2020; Ireland

& Mouthaan, 2020) The network science approach

aims to model a structure (e.g., a semantic relation) in

which nodes (vertices) represent different knowledge

elements or concepts and edges (or links) denote a

relationship between pairs of concepts (entities or

elements).

Educational researchers have long been interested

in understanding human cognition - particularly the

organization of knowledge, the influence of

experience on understanding, and the difference in

acquiring expert-like practices and knowledge in a

subject area. An increasing number of studies have

emphasised the need of shifting from traditional

(linear) education to an interconnected model of

education that provides a networked (nonlinear) view

of knowledge organization (Sun et al., 2020; Siew &

Guru, 2022; Gera et al., 2021; Gera et al., 2022)

Understanding the nature of expertise and expert

knowledge representations is a crucial task in

curriculum development because it greatly influences

the effectiveness of instruction and the degree to

which “educational engineering” is brought about in

the learners.

Furthermore, educational outcomes are expressed

through the flow of information and the application

of effective instructional techniques that can help

students build and organize knowledge structures

(Vukić et al., 2020). In addition, curriculum design is

complex and should be motivated by the way

knowledge is organised, especially in conjunction

with educational outcomes for more engaged, longer

lasting, and more effective learning.

A fundamental thesis of expertise research is that

experts and novices have different representations of

knowledge, while experts are able to use their

understanding of the deep structure of subject matter

to solve a wide range of problems related to their area

of expertise (Siew & Guru, 2022).

Researchers emphasise the relevance and

usefulness of centrality analysis as a means of

quantifying different levels of expertise (Siew &

Guru, 2022), identifying key nodes (Lommi &

Koponen, 2019; Koponen & Nousiainen, 2019), and

measuring the importance of concepts for cohesion

(Koponen & Nousiainen, 2014).

O’Meara & Vaidya (2021) explored the role of

network theory in an effort to outline meaningful

curricular connections and discuss the nature of

connectivity in education, illustrated by the example

of pre-calculus textbook. Textbooks can be seen as

educational repositories of information enabling

transfer of expert domain knowledge. The authors

emphasise that uncovering an inherently complex

nature of connectivity between specific curriculum

topics could improve the aggregation of successful

curricula across the subject and influence the

understanding of scientific concepts and conceptual

systems

Vukić et al. (2020) introduced the multidimen-

sional knowledge network (MKN) based on the

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk

learning outcomes (Bloom's taxonomy), key concepts

in the subject matter domain and the principles of

representation and analysis of how domain

knowledge (concepts) can be modelled across four

levels of knowledge.

Planning, organising and implementing the

teaching process requires adopting a

multidisciplinary approach. Understanding the nature

of domain-specific (or subject-specific) knowledge

structures has become an important issue in

educational science.

Recent changes due to digitization, networked

resources, and interdisciplinary shifts require a

rethinking and reconceptualization of knowledge

organization. Wheeler (1980) considers two types of

relationships between learning experiences: vertical

organization of knowledge (concepts learned within

one subject area during an academic year) and

horizontal organization of knowledge (concepts from

one subject are related to concepts in other subjects as

an attempt to develop an interrelationship between

various subjects or disciplines). According to

Thagard (1988) understanding the meaning of a

concept's significance comes from its application to

different problems and not just from studying its

definitions and rules. Therefore, Thagard (1988)

emphasizes, concepts need relate to other concepts in

”various inductive, hierarchical, non-definitional

ways. This is how meaning emerges.”. Thus,

understanding grows as networks expand and

connections are strengthened by mutually reinforcing

experiences across different subject areas and more

tightly structured networks.

In addition, representing concepts and their

interrelationships as a complex network is more

consistent with our intuition that knowledge is

inherently relational in nature, and that expertise is

reflected in an interconnected, cohesive organization

of concepts in a given domain.

Detecting modules, courses or communities of

concepts/learning outcomes, allows for quantitative

investigation of relevant knowledge subdomains that

may have different properties than the aggregate

properties of the network as a whole, e.g., monolayer

representation of knowledge organisation in

curricula. Informally, a network community is a

subgraph whose vertices are more likely to be

connected to each other than to vertices outside the

subgraph (Barber, 2007).

As mentioned earlier, most network analysis

methods and literature refer to unipartite networks, or

networks with a single node type. Consequently, it is

studied that in process of transformation from

bipartite networks into unipartite networks, the loss of

information is evident. Bipartite networks have a very

particular structure that conflicts with representation in

form of square adjacency matrices. In other words,

they consist of two different types of nodes, with each

edge connecting a node of one type to a node of the

other type. In fact, a bipartite network can be used to

represent any feature type that can be expressed by a

categorical variable. Examples of these categories

come from various research areas: scientific

publications and authors (Newman, 2001), public

transportation routes and stations served (Von Ferber,

2009), food and its ingredients (Ahn et al., 2011), paper

and author (Newman, & Park, 2003), article and

concept (Palchykov & Holovatch, 2018), etc.

As a case study, Palchykov & Holovatch (2018)

uses the structure of concept-related networks of

scientific knowledge in the field of physics where

they consider a bipartite article-to-concept network

with its two one-mode projections as the basic

network representation of the publication system. In

their research, they have shown how concept features

(e.g. subject classes) may be derived from articles and

how community detection or clustering approaches

may be used to extract groups or modules in such

knowledge systems.

3 METHODOLOGY

This paper explores unweighted directed bipartite

graph as a formal network representation of the

Veleri-OI IoT School international education

programme, which is used to identify the desirable

design of knowledge organisation. The subject of our

analysis was a collection of concepts and learning

outcomes from seven modules (courses):

M1. Business idea development

M2. Documentation of user requirements

M3. Setting up a development environment

M4. Non-relational databases

M5. Web application development

M6. Hybrid mobile applications development

M7. Arduino embedded (IoT) systems

In our previous work (Vukic et al., 2023), we

defined several steps for data collection and the

construction of a monolayer network. Following the

defined procedure and the corresponding input data,

we extracted unique entities from the aggregated IoT

education programme edge list which contains

concept pairs and associated learning outcomes. Two

types of network nodes were identified from the

module curriculum content: concepts and learning

outcomes (LO). The semantics of the connection

Structural Analysis of the Curriculum Through a Bipartite Network

between the nodes is that the concept contributes to

the achievement of the learning outcomes.

Accordingly, we created an edge list for the entire

IoT education programme - the raw data was

modified according to the use case and tool

instructions for input data.

In general, bipartite graphs are graphs in which

the set of nodes can be partitioned into two disjoint

sets such that each edge connects a vertex of one

partition to a vertex of the other partition.

The vertex set U has two types of vertices, which

represent concepts or LO. Mathematically, U = A ∪

B where A = {a

, a

, ..., a

} is the set of vertices

representing concepts, where m is the number of

concepts in this IoT education programme, and B =

, b

, ..., b

} is the set of vertices representing LO,

where n is the number of LO. According to previous

studies, three main analytic tasks have been

highlighted for this network model (Xu et al., 2014;

Yang et al., 2022): i) measuring the importance or

role of a node within a given network; ii) identifying

clusters of similar elements in one node set in terms

of their connections to elements in another node set

and vice versa; iii) understanding the connections

between clusters in both node sets A and B.

An advantage of this type of network is the ability

to quantify the connections between actors and their

relationships, rather than relying only on attribute

data. In addition, a relational model between entities

can be created that provides details about the

properties of the network and the interactions of the

actors.

Our analysis of the bipartite network of education

programme focuses on the topology analysis

quantified by the network metrics of degree

centrality. Gephi tool was used to visualize and

analyse node’s centrality for bipartite graph (Bastian

et al., 2009)

Exploring node’s number of neighbours can be

easily done by using degree centrality which simply

counts the total number of connections of a node . For

a node i, its normalised degree value is given by

(Newman, 2018):





∑











(1)

where 



is the ij-th element of the adjacency

matrix K of the graph and N is the number of vertices

in the graph.

Degree centrality is a useful indicator of a node’s

total number of connections, but it does not always

provide information about a node's importance in

terms of linkage to other nodes or its degree of

centrality within a larger group (Golbeck, 2013).

Although this preliminary research focuses only on

the analysis of node centrality and its degree, the

importance of nodes in a bipartite network can be

investigated using metrics designed specifically for

this type of network, which we will discuss in the

final chapter of this paper.

4 RESULTS

In this section, we present bipartite representation of

the IoT education programme, the application of the

defined model to the subject matter area, and the

results of the network measures.

4.1 Bipartite Network Representation

The result of the bipartite network representation

(RQ1) is partially shown in Figure 1, which

demonstrates a bipartite network in which one set of

nodes represents concepts from the teaching content

(pink) and the other set represents learning outcomes

of the teaching content (green) filtered according to

the node’s degree for the value 13-30 (maximum

number of neighbours of the node) i.e. nodes that

have between 13 and 30 connections to the nodes are

shown. We chose this interval so that we can clearly

present the nodes, i.e. two sets of nodes. The

semantics of the connection between nodes is that the

concept contributes to the achievement of learning

outcomes.

Table 1: Example of data input for bipartite network.

LO Concepts

M2.I1.1.describe

the phases of

requirements

management

user needs

user requirement

user requirement analysis

requirements management

system requirements

requirements management

requirement elicitation

requirement specification

requirement validation

requirement negotiation

M5.I3.3. Ensure

access to web

services by

creating routes

creating a route

HTTP protocol

REST

Node.js

Express

JavaScript

requirements management

HTTP protocol

API call

REST architecture

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk

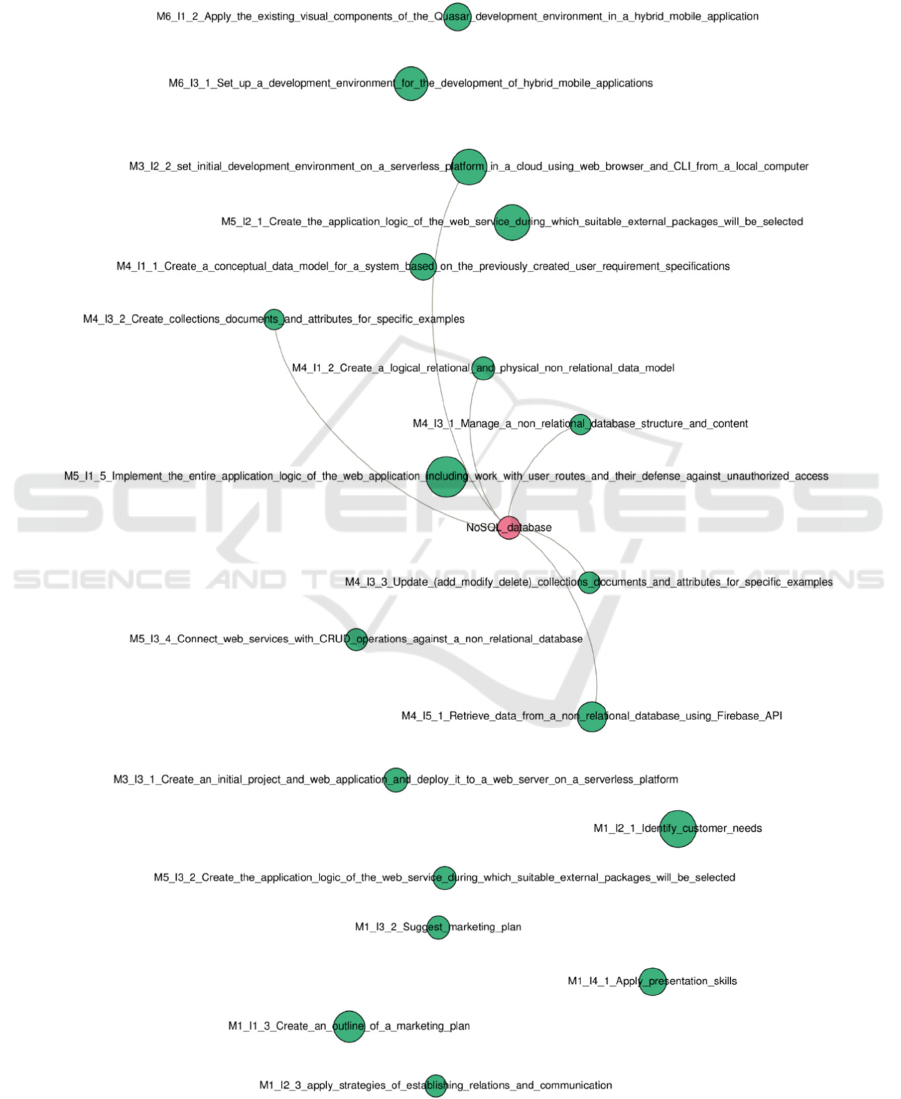
Table 1 shows an example of data input for

bipartite network pairing the learning outcome node

type with the concept node type concept. Based on

these two rows, two nodes of the learning outcome

type would be created: M2.I1.1. Describe the phases

of requirements management and M5.I3.3. Ensure

access to web services by creating routes that are

connected to ten Concept type nodes from the

corresponding line.

Figure 1: Bipartite network representation of the IoT education programme.

Structural Analysis of the Curriculum Through a Bipartite Network

Also, it is evident that among these 10 concepts is a

concept: requirements management which is a link to

both learning outcomes mentioned above.

4.2 Bipartite Network Analysis

Table 2 presents the results of the global

characterization of the structural properties for the

bipartite network of the IoT programme: total number

of learning outcomes (LO), total number of identified

concepts (C) and total number of edges (E).

Furthermore, we explore top five nodes from each set

in terms of the number of neighbours they are

connected to.

Table 2: Basic characteristics of the dataset

Bipartite

network

LO C E

IoT

education

programme

112 399 799

The subject of our analysis was a collection of LO

and concepts listed in the Veleri-OI IoT School

international education programme module’s

curriculum. The curriculum contains 511 unique

nodes. 112 of these nodes are learning outcomes and

399 are concepts.

Exploration of the module networks shows

variations in the number of nodes from network sets.

In other words, the learning outcome set has a

significantly smaller number of nodes.

Table 3: The top five ranked nodes by degree (



) for node

type: concept.

Concept





NoSQL database 15

client server architecture 9

database 9

HTTP protocol 9

Firestore 9

The degree of a node represents the largest

number of connections (neighbours) that a node has

in the network. Figure 1 presents nodes filtered by

range of degree 13-30. If a concept node is connected

with multiple links to different sets of LO, it means

that this concept contributes to different learning

outcomes at the level of the teaching unit.

Table 4: The top five ranked nodes by degree (



) for node

type: learning outcome.

Learning outcomes





M5.I1.5 Implement the entire application logic

of the web application including work with user

routes and their defense against unauthorized

access

M1.I2.1 Identify customer needs 27

M3.I2.2 set initial development environment on

a serverless platform in a cloud using web

browser and CLI from a local computer

M5.I2.1 Create the application logic of the web

service during which suitable external packages

will be selected

M6.I3.1 Set up a development environment for

the development of hybrid mobile applications

For example, the concept NoSQL database (Table

3) is associated with a large number of outcomes and

contributes to the achievement of multiple learning

outcomes. The centrality analysis shows that this

concept can be crucial in integrating a

multidisciplinary study that allows students to

develop important transferable skills such as critical

thinking and synthesis of ideas. Therefore, it can be

concluded that revisiting key concepts across

multiple learning outcomes may increase the

likelihood of retaining knowledge in a student's long-

term memory and improve learning retention (RQ2).

In addition, the LO node M5.I1.5 Implement the

entire application logic of the web application

including work with user routes and their defense

against unauthorized access (Table 4) which has a

degree value of 30 represents a learning outcome to

which 30 different concepts contribute. Using this

network approach we can determine the complexity

of LO based on the number of concepts that

contribute to this outcome.

Expert knowledge reflects structured, intricately

interwoven cognitive schemas that include one's

knowledge and abilities and are a necessary

component of a well-organized long-term memory.

Knowledge organisation which supports a reduction

in cognitive load during learning and problem

solving, leads to increased competence. Processing

new information results in “cognitive load” on

working memory and can affect learning outcomes

(Kalaš, & Mittermeir, 2011). Overload occurs in

learning settings where a large number of items are

thought of at once. For any outcome with a large

number of concepts, educators should consider

decomposing learning outcomes into less cognitively

complex learning outcomes or systematically

organising knowledge content (concepts) to facilitate

complex learning.

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk

5 CONCLUSIONS

The essential role of curriculum is to enable quality

learning and to provide a foundational framework for

achieving high-quality learning outcomes. The

curriculum as a complex network consists of several

types of elements and exhibits multiple relations

between them, which is emphasised by the fact that

the node objects are heterogeneous and the edge types

are diverse. Acknowledging the multivariate nature of

the network, we move from the simple monolayer

representation to a more powerful abstraction for

modelling – the bipartite network model. Hence, we

extract entities from the curriculum knowledge

content - concepts and LO into two sets and construct

an unweighted directed bipartite network (RQ1). To

demonstrate and apply relationships between related

subjects, learning processes should enable students to

draw meaningful connections between subjects and

integrate multiple subjects into larger learning

domains. As a result, it would also encourage the

growth of more intricate cognitive interconnections

and structures, and consequently, of competences and

skills within and across domains. Centrality analysis

has shown that achieving the learning outcomes with

large number of concepts is highly correlated with

cognitive load during learning of new and yet

strongly interwoven concepts (RQ2). Measuring the

importance of nodes in bipartite graphs could be

easily bypassed by projecting the bipartite graph onto

a unipartite network and calculating the centrality

values using, for example, the PageRank or

Eigenvector centrality algorithms, which may lead to

information loss and distortion of the network

topology, resulting in misleading results. Therefore,

in our future work, we will investigate centrality

metrics designed specifically for bipartite networks -

BiRank, HITS, CoHITS and BGRM centrality index

and their comparison with unipartite network model

for the IoT education programme. The representation

of knowledge networks as bipartite network, apart

from enabling the key entity detection, allows the

study of the effective knowledge organisation, in

terms of optimal information transfer that student can

absorb and retain effectively provided in such a way

that it does not “overload” their mental capacity.

ACKNOWLEDGEMENTS

This work has been fully supported by the University

of Rijeka under the project number uniri-drustv-18-

140.

REFERENCES

Ahn, Y. Y., Ahnert, S. E., Bagrow, J. P., & Barabási, A. L.

(2011). Flavor network and the principles of food

pairing. Scientific reports, 1(1), 1-7.

Barber, M. J. (2007). Modularity and community detection

in bipartite networks. Physical Review E, 76(6),

066102.

Bastian, M., Heymann, S., & Jacomy, M. (2009, March).

Gephi: an open source software for exploring and

manipulating networks. In Proceedings of the

international AAAI conference on web and social

media (Vol. 3, No. 1, pp. 361-362).

Castro, N., Pelczarski, K. M., & Vitevitch, M. S. (2017).

Using network science measures to predict the lexical

decision performance of adults who stutter. Journal of

Speech, Language, and Hearing Research, 60(7), 1911-

1918.

Centre for teaching excellence (n.d.). Forming a program's

structure, https://uwaterloo.ca/centre-for-teaching-

excellence/forming-programs-structure

Citraro, S., Vitevitch, M. S., Stella, M., & Rossetti, G.

(2022). Feature-rich multiplex lexical networks reveal

mental strategies of early language learning. arXiv

preprint arXiv:2201.05061.

Gera, R., BartoIf, D. M., Isenhour, M. L., & Tick, S. (2019).

Chunk: Curated heuristic using a network of

knowledge.

Gera, R., Saxena, A., Bartolf, D. M., & Tick, S. (2021). A

Network Science Perspective to Personalized Learning.

arXiv preprint arXiv:2111.01321.

Golbeck, J. (2013). Network structure and measures.

Analyzing the social web, 25-44.

Goldstein, R., & Vitevitch, M. S. (2017). The influence of

closeness centrality on lexical processing. Frontiers in

psychology, 8, 1683.

Hills, T. T., & Siew, C. S. (2018). Filling gaps in early word

learning. Nature Human Behaviour, 2(9), 622-623.

Ireland, J., & Mouthaan, M. (2020). Perspectives on

Curriculum Design: Comparing the Spiral and the

Network Models. Research Matters.

Kalaš, I., & Mittermeir, R. T. (2011). Informatics in

Schools. Contributing to 21st Century Education: 5th

International Conference on Informatics in Schools:

Situation, Evolution and Perspectives, ISSEP 2011,

Bratislava, Slovakia, October 26-29, 2011.

Proceedings. Springer.

Koponen, I. T. (2021). Systemic states of spreading

activation in describing associative knowledge

networks II: generalisations with fractional graph

Laplacians and q-adjacency kernels. Systems, 9(2), 22.

Koponen, I. T., & Nousiainen, M. (2014). Concept

networks in learning: Finding key concepts in learners'

representations of the interlinked structure of scientific

knowledge. Journal of Complex Networks, 2(2), 187-

202.

Koponen, I. T., & Nousiainen, M. (2019). Pre-service

teachers’ knowledge of relational structure of physics

concepts: finding key concepts of electricity and

magnetism. Education Sciences, 9(1), 18.

Structural Analysis of the Curriculum Through a Bipartite Network

Koponen, I. T., & Pehkonen, M. (2010). Coherent

knowledge structures of physics represented as concept

networks in teacher education. Science & Education,

19(3), 259-282.

Kubsch, M., Touitou, I., Nordine, J., Fortus, D., Neumann,

K., & Krajcik, J. (2020). Transferring knowledge in a

knowledge-in-use task—investigating the role of

knowledge organization. Education Sciences, 10(1), 20.

Lommi, H., & Koponen, I. T. (2019). Network cartography

of university students’ knowledge landscapes about the

history of science: landmarks and thematic

communities. Applied network science, 4(1), 1-24.

Lynn, C. W., & Bassett, D. S. (2020). How humans learn

and represent networks. Proceedings of the National

Academy of Sciences, 117(47), 29407-29415.

Monahan, C., Munakata, M., & Vaidya, A. (2019).

Creativity as an emergent property of complex

educational system. Northeast Journal of Complex

Systems (NEJCS), 1(1), 4.

Newman, M. E. (2001). The structure of scientific

collaboration networks. Proceedings of the national

academy of sciences, 98(2), 404-409.

Newman, M. E. (2018). Networks. Oxford university press.

Newman, M. E., & Park, J. (2003). Why social networks

are different from other types of networks. Physical

review E, 68(3), 036122.

Novak, J. D. (2010). Learning, creating, and using

knowledge: Concept maps as facilitative tools in

schools and corporations. Routledge.

O’Meara, J., & Vaidya, A. (2021). A Network Theory

Approach to Curriculum Design. Entropy, 23(10),

1346.

Palchykov, V., & Holovatch, Y. (2018, August). Bipartite

graph analysis as an alternative to reveal clusterization

in complex systems. In 2018 IEEE Second International

Conference on Data Stream Mining & Processing

(DSMP) (pp. 84-87). IEEE.

Siew, C. S. (2019). Using network science to analyze

concept maps of psychology undergraduates. Applied

Cognitive Psychology, 33(4), 662-668.

Siew, C. S. (2020). Applications of network science to

education research: Quantifying knowledge and the

development of expertise through network analysis.

Education Sciences, 10(4), 101.

Siew, C. S. (2022). Investigating cognitive network models

of learners’ knowledge representations. Journal of

Learning Analytics, 9(1), 120-129.

Siew, C. S., & Guru, A. (2022). Investigating the network

structure of domain-specific knowledge using the

semantic fluency task. Memory & Cognition, 1-24.

Siew, C. S., & Vitevitch, M. S. (2019). The phonographic

language network: Using network science to investigate

the phonological and orthographic similarity structure

of language. Journal of Experimental Psychology:

General, 148(3), 475.

Sun, H., Yen, P., Cheong, S. A., Koh, E., Kwek, D., & Tan,

J. P. L. (2020). Network science approaches to

education research. Int. J. Complex. Educ, 1, 122-149.

Teixeira, A. S., Talaga, S., Swanson, T. J., & Stella, M.

(2021). Revealing semantic and emotional structure of

suicide notes with cognitive network science. Scientific

reports, 11(1), 1-15.

Thagard P (1988) Computational Philosophy of Science.

The MIT Press, Cambridge, Massachusetts

Veleri – OI IoT School (2021). Polytechnic of Rijeka and

the University of Rijeka, Department of Informatics,

Development of the International Education Program.

https://iot-school.veleri.hr/en/home

Vitevitch, M. S. (Ed.). (2020). Network science in cognitive

psychology. Routledge, Taylor & Francis Group.

Von Ferber, C., Holovatch, T., Holovatch, Y., &

Palchykov, V. (2009). Public transport networks:

empirical analysis and modeling. The European

Physical Journal B, 68(2), 261-275.

Vukic, D., Candrlic, S., & Jakupovic, A. (2023). Monolayer

network representation and analysis of the curriculum.

Computing Conference, (Accepted for publication).

Vukić, Đ., Martinčić-Ipšić, S., & Meštrović, A. (2020).

Structural analysis of factual, conceptual, procedural,

and metacognitive knowledge in a multidimensional

knowledge network. Complexity, 2020, 1-17.

Wheeler, D. K. (1980). Curriculum process. London:

Hodder and Stoughton Ltd

Xu, K., Wang, F., & Gu, L. (2013). Behavior analysis of

internet traffic via bipartite graphs and one-mode

projections. IEEE/ACM Transactions on Networking,

22(3), 931-942.

Yang, K. C., Aronson, B., Odabas, M., Ahn, Y. Y., & Perry,

B. L. (2022). Comparing measures of centrality in

bipartite patient-prescriber networks: A study of drug

seeking for opioid analgesics. PloS one, 17(8),

e0273569.

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk