Success Factors for Mathematical e-Learning Exercises Focusing

First-Year Students

Malte Neugebauer

, Basile Tousside

and J

org Frochte

Bochum University of Applied Sciences, 42579 Heiligenhaus, Germany

Keywords:

E-Learning, Higher Education, Mathematics, Gamiﬁcation, Learning Management System.

Abstract:

How university students succeed in math courses at the beginning of their studies is of great relevance for

the overall study success in many study programs. Since the competence levels of candidates are different,

lecturers struggle to mediate knowledge to such heterogeneous audiences simultaneously. In tacit consent, a

catch-up of lower-skilled students is expected. Self-organized learning materials – which are often accessible

via e-learning – are mostly unattractive, especially to lower-skilled students. Since gamiﬁcation is success-

fully used in other areas of education to support motivation and performance, we propose gamiﬁcation as a

ﬁrst success factor for mathematical exercises. Considering infrastructural aspects of higher education, we fur-

thermore suggest the gamiﬁcation systems’ ability to be extended by lecturers, its integrability into universities

learning management systems and its affordability as success factors for mathematical e-learning exercises.

Therefore, we implemented an open-source and easy-to-extend software approach, which is integrable into

universities’ learning management systems. In an initial test run among ﬁrst-year students (n = 115), we show

how this approach improves learning and motivation at the same time. We discuss these results and propose

this approach for testing in multiple group plans, to further investigate the inﬂuence of single game elements

on motivation and learning.

1 INTRODUCTION

During the last decade, e-learning in mathematics

grew in relevance for higher education institutions.

Not only was the COVID-19 pandemic, which forced

universities into switching entirely to distance learn-

ing during 2020, of great relevance for mathematical

e-learning (Lisnani et al., 2020; Irfan et al., 2020),

but also the broader diversity of students – regard-

ing life scripts and competence levels – boosted the

importance of self-paced e-learning materials (Liang

et al., 2018; Schulmeister, 2004). Especially intro-

ductory courses are challenged to offer learning ma-

terials to their students that ﬁt learners’ different com-

petence levels (Gordon et al., 2013). Here, self-paced

learning with e-learning materials enables students to

revisit knowledge from school, helping lower-skilled

students catching up.

However, B

uchele and Marten (2022) found that

students with low math competencies fall back even

https://orcid.org/0000-0002-1565-8222

https://orcid.org/0000-0002-9332-5060

https://orcid.org/0000-0002-5908-5649

more during their studies due to a low motivation to-

wards self-regulated mathematical learning. Despite

the fact that math is of great relevance for the suc-

cess of many study programs, students have a smaller

motivation towards it. This can possibly be traced

back to a given distance of the chosen study program

(e. g. psychology, architecture or computer science) to

mathematics.

One promising method to raise motivation in dif-

ferent subjects is gamiﬁcation, which is known as “the

use of game design elements in non-game contexts”

(Deterding et al., 2011). Especially in higher educa-

tion it is widely used to raise students’ motivation, re-

duce drop-out rates or support learners’ performance

(Zainuddin et al., 2020a; Dichev and Dicheva, 2017).

Despite the fact, that most studies about gamiﬁ-

cation take place in higher education (Dicheva et al.,

2015), studies focusing on the speciﬁc case of math-

ematics in this context are rare. Surprisingly, math-

related gamiﬁcation research is more common in the

context of elementary and secondary school. One

possible reason is the size of the target group. The

number of students of the university entrance phase,

especially if one splits them up by subjects, is consid-

306

Neugebauer, M., Tousside, B. and Frochte, J.

Success Factors for Mathematical e-Learning Exercises Focusing First-Year Students.

DOI: 10.5220/0011858400003470

In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023) - Volume 2, pages 306-317

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

erably smaller than within a school year. Commercial

solutions are economically less attractive in this con-

text or would have to be managed with smaller bud-

gets. Affordability appears to be a facilitating factor.

Since many universities are using learning man-

agement systems (LMS) to facilitate self-paced

and distance learning for their students, an LMS-

based gamiﬁcation of mathematical e-learning con-

tent could be a useful alternative to commercial solu-

tions. Integrability into universities’ LMS will allow

a gamiﬁcation solution to make use of an already es-

tablished platform and, in this, support existing tools

like question banks or learning analytics systems. By

using external gamiﬁcation tools – even on equipping

them with an interface for data exchange to LMS –

more data protection law issues may arise compared

to an in-house, LMS-integrated solution.

An additional, more socio-scientiﬁc phenomenon

is the raising heterogeneity of students. This leads

to a diversiﬁcation of students’ needs depending on

their age, social background and family responsibil-

ities. Here, a highly extendable software solution is

needed, to address a constantly changing target group.

Considering (i) gamiﬁcation, (ii) affordability,

(iii) extendibility and (iv) integrability of the soft-

ware into university LMS platforms as success fac-

tors for mathematical exercises in e-learning, here we

develop a software architecture for LMS, that allows

lightweight implementation of gamiﬁcation into ex-

ercises to support mathematical learning in the early

phase of higher education. In a ﬁrst test run we show,

that this easy-to-implement approach is capable not

only of raising motivation, but also helps new students

revisiting their math knowledge, concluding to a score

progression during exercise accomplishment.

Our contributions are summarized as follows:

• We present a frontend-oriented software archi-

tecture, that allows lightweight gamiﬁcation im-

plementations into universities LMS without any

server-sided changes.

• Focusing on mathematical e-learning, we de-

velop a gamiﬁcation exercise design based on

the frontend-oriented approach and demonstrate a

possible implementation inside the LMS Moodle.

• We analyze the results of a ﬁrst test run with the

given approach and show, how learners are moti-

vated to solve the most challenging exercises and

progress in their score performance.

• We discuss how speciﬁc game elements inﬂuence

learners’ motivation and learning outcomes.

• We propose to test this approach in multiple group

plans to shed more light on the effect of speciﬁc

gamiﬁcation elements for speciﬁc learner groups.

2 RELATED WORK REGARDING

GAMIFICATION

Since its ﬁrst mention in the early 2000s (see Khaitova

(2021) for genesis), gamiﬁcation became a widely

spread phenomenon in various areas, such as market-

ing (Hofacker et al., 2016) or onboarding (Fischer and

Heinz, 2020). There are many studies showing the ef-

fectiveness of gamiﬁcation in higher education in var-

ious ways, using a variety of different game design el-

ements, ranging from points, badges and leaderboards

over competitions to virtual goods, all accompanied

with evident effects (Dicheva et al., 2015).

Although gamiﬁcation research mostly takes

place in higher education (Dicheva et al., 2015), stud-

ies regarding mathematics mostly focus on primary or

secondary school. Mathematics-related gamiﬁcation

studies, that take place in higher education usually

investigate students’ feedback to quiz software solu-

tions like Kahoot!, Socrative or Quizizz or (Zabala-

Vargas et al., 2021; Zainuddin et al., 2020b; Bul-

lon et al., 2018). Those software solutions do not

ﬁt all the success factors mentioned above since they

are commercial (affordability) and they are only inte-

grable into LMS by embedding or sharing them via

an external link (integrability). In contrast to this,

we take the special needs of higher education into ac-

count to offer an affordable, easily integrable and ex-

tendable gamiﬁcation solution.

The few studies focusing on gamiﬁcation of math-

ematical learning in the speciﬁc context of the transi-

tion phase between school and university barely ad-

dress their technical implementations. Gordon et al.

(2013) for example present results of an approach us-

ing different game elements, paying special attention

to the possibility of repeating attempts (which is fur-

ther referred to as the freedom to fail gamiﬁcation de-

sign principle). But the technical aspect of how the

game elements were implemented into the exercises

is not thematized, making this approach hardly re-

producible. In contrast to this, we propose an open-

source solution for web-based LMS, which explicitly

aims at being able to be adapted to the speciﬁc needs

of local students through its extendibility.

3 DERIVING GAMIFICATION

DESIGN PRINCIPLES FOR

MATHEMATICAL

E-LEARNING

For deriving appropriate game elements, we make

use of ﬁndings from behavioral economics and from

Success Factors for Mathematical e-Learning Exercises Focusing First-Year Students

307

psychology of learning. In the context of gamiﬁca-

tion, the self-determination-theory (SDT) (Ryan and

Deci, 2000) is often referenced to explain raising

intrinsic and extrinsic motivation through gamiﬁca-

tion (Zainuddin et al., 2020a). As per this theory, a

raise of intrinsic motivation appears, when three basic

needs are satisﬁed: competence, autonomy and relat-

edness. Game elements bear the potential to tackle

these needs (van Roy and Zaman, 2017).

Besides motivation, our approach aims at facili-

tating students’ learning process. The Fogg Behav-

ior Model (FBM) (Fogg, 2009) considers both mo-

tivation and ability at the same time to explain be-

havioral change. As per the FBM, behavior is seen

as a convergence of motivation, ability and a prompt.

When both, motivation and ability merge to a sufﬁ-

cient degree, a prompt succeeds. Even if a hard task

is prompted, people will follow the prompt when the

motivation is high enough. For our use case, a rise

in motivation through gamiﬁcation is expected. But

for our aim to facilitate learning in higher education

mathematics, solely raising motivation is not sufﬁ-

cient. Additionally, we aim to raise the needed math-

competence, so that previously too difﬁcult tasks be-

come solvable. Both, raising motivation towards ex-

ercise accomplishment and enabling learners to solve

challenging exercises complement each other when

behavioral change is desired.

As per Vygotsky’s model of proximal develop-

ment (Vygotsky, 1978; Podolskiy, 2012), learning

takes place when people go beyond their comfort

zone. In the so-called growth zone, challenging

tasks are accomplished and ﬁnally assimilated into

the comfort zone. Tutoring and repetition are facil-

itators for this process. Since math is highly modular

(Avigad, 2018), math exercises can be built upon each

other, so that learners can learn new things by deploy-

ing established knowledge on new challenges. In this,

their comfort zone increases exercise by exercise. Or

speaking with the FBM: They are more and more en-

abled to accomplish challenging tasks, reducing the

barrier of following the next prompt – which is the

next exercise.

To realize learning this way with the help of e-

learning exercises, learners have to be supplied with

additional material to understand those exercises, that

go beyond their comfort zone. Furthermore, feed-

back on their current performance in general and

on speciﬁc mistakes will support the assimilation of

challenging tasks into their comfort zone. Here we

use the design principles of gamiﬁcation to increase

motivation on the one hand and to enable learning

progress on the other. State-of-the-art gamiﬁcation re-

search demands elucidating the effects of single game

elements instead of giving a proof-of-concept for

an overall gamiﬁcation approach (Behl et al., 2022;

Zainuddin et al., 2020a). Following this demand, we

base our reﬂections about game elements on a tax-

onomy which is derived from a systematic mapping

study for the context of education (Dicheva et al.,

2015). This taxonomy is already well-referenced

(Ayastuy et al., 2021; Jueru et al., 2019; Piteira et al.,

2018).

Out of the 15 so-called gamiﬁcation design prin-

ciples from this taxonomy, it is reasonable to assume

that, based on the theoretical reﬂections above, the

following four principles will raise motivation and

support learning in a mathematical exercise e-learning

design.

1. Immediate Feedback: This principle will supply

learners with the needed information to solve ex-

ercises correctly, after failing them before. Re-

garding the SDT, in this the need of competence

is tackled.

2. Freedom to Fail: Since repetition is an important

facilitator of learning, learners have to be enabled

to repeat exercises without penalty. This allows

them to immediately apply the given feedback and

prove acquired knowledge – if any – to themselves

and to lecturers. The need for autonomy is tackled

here.

3. Freedom of Choice: Enabling learners to freely

move between easier and harder tasks will allow

them to identify gaps on their own and acquire

the needed knowledge. Regarding the SDT, here

again autonomy is enabled and a raise of motiva-

tion is expected.

4. Goals: Regarding the FBM, exercises ﬁll the role

of the prompt. This prompt can be emphasized by

declaring motivating goals towards exercise ac-

complishment, boosting learners’ motivation.

From this, we derive an exercise design in which

learners have the opportunity to repeat exercises with-

out penalty and move freely back and forth through

the exercises. Furthermore, after accomplishing an

exercise, a sample solution and – where applicable –

additional speciﬁc feedback regarding the mistake is

given. On repeating exercises, another variant of the

exercise is presented (randomization) to enable learn-

ing (instead of typewriting the sample solution). Fi-

nally, the exercises are structured by topics and pre-

sented in raising difﬁculty. Solving the last (thus hard-

est) exercises is declared as the goal of this design.

To emphasize this goal, we use game-like wording by

calling the hardest exercises boss questions – marked

by a skull – and the topics math worlds.

CSEDU 2023 - 15th International Conference on Computer Supported Education

308

The button link

changes according

to performance, chal-

lenging learners with

ﬁtting difﬁculty.

Goals,

freedom of

choice:

The exercise

sheet is struc-

tured by clear

goals: Solving

boss exercises.

Immediate feedback:

Additional material

to solve exercise,

adapted to learners

performance (e. g.

feedback on

speciﬁc mistakes).

Questions can be

added through

LMS to ensure

extendibility

Freedom to fail: After attending the question, a

button to repeat the question is presented here.

Gamiﬁcation

Gamiﬁcation system only

affects LMS frontend to ensure

affordability and integrability.

Figure 1: Adaptations of a mathematical exercise inside the LMS Moodle, serving the four success factors (bold). In italics:

The chosen gamiﬁcation design principles.

Figure 1 gives an insight into the appearance in-

side the LMS Moodle.

4 PROPOSED SOFTWARE

SOLUTION AND

IMPLEMENTATION

After comparing different gamiﬁcation software ar-

chitectures, we introduce a frontend-oriented archi-

tecture, to satisfy integrability and extendibility. This

will be presented in section 4.1. In comparison to a

plugin, this solution doesn’t require any server-sided

changes. An example implementation inside the LMS

Moodle will be presented in section 4.2. Finally,

the technical limitations of this approach will be ad-

dressed in section 4.3.

4.1 Gamiﬁcation Software Architecture

Requirements

To ensure the affordability, integrability and ex-

tendibility of a gamiﬁcation implementation in higher

education, different gamiﬁcation software architec-

tures (GSA) can be considered. Herzig et al. (2014)

cluster GSA into four different classes: achievement

systems (AS), generic gamiﬁcation platforms (GGP),

integrated solutions (IG) and others. Assuming, that

extendibility can be understood as a combination of

ﬂexibility, manageability and reusability, comparing

properties of GSA (see Table 1), the GGP achieves

the best results regarding ﬂexibility, manageability,

reusability, and integrability. Nevertheless, this class

is still evaluated as low in performance, highly com-

plex and only a medium degree regarding integrabil-

ity.

Table 1: Comparison of classes (↑: high, →: medium, ↓:

low, ◦: not considered) (Herzig et al., 2014).

Degree of AS GGP IG

Flexibility → ↑ ↓

Invasivity → ↓ ↑

Reusability → ↑ ↓

Integrability ↓ → ◦

Performance → ↓ ↑

Analyzability → ↑ ↑

Manageability → ↑ ↓

Complexity ↓ ↑ ↓

Success Factors for Mathematical e-Learning Exercises Focusing First-Year Students

309

Most higher education institutions are using an

LMS as an information system for their students. It

can be used to overcome the just mentioned disad-

vantages of the GGP. In case of the web-based LMS

Moodle, with the help of the programming language

JavaScript, a gamiﬁcation platform can be imple-

mented right into its frontend (Figure 2). This will

lead to a rise in integrability and performance, while

reducing the complexity, satisfying the demand for

extendibility and integrability.

To tackle affordability, we give an implementation

proposal for the LMS Moodle and publish it under an

open-source license.

Data Storage

Analytics

Rules & Logic

Gamiﬁcation

API

Core Application

Frontend

Script

Learning Managment

System

Figure 2: The suggested frontend-oriented software archi-

tecture.

This frontend-oriented architecture has the addi-

tional beneﬁt that gamiﬁcation can be implemented

without any security risks and without involving the

institution’s IT department, which could be an addi-

tional obstacle in higher education institutions’ infras-

tructure. In contrast to a plugin for example, this solu-

tion can directly be implemented by question authors.

4.2 Moodle Example Implementation

To demonstrate a practical implementation, we show

below how the chosen gamiﬁcation design princi-

ples can be implemented with the help of a frontend-

oriented approach in the LMS Moodle. One reason

for choosing Moodle is that it is used by many lo-

cal partners, which facilitates testing the adaptability

in different universities. Furthermore, adaptations to

Moodle – e. g. with the web-programming language

JavaScript – can be easily transferred into other web-

based LMS (Blackboard, D2L, Canvas, ILIAS, ...).

To apply the gamiﬁcation system inside the fron-

tend of a mathematical exercise in Moodle, as shown

in Figure 2, at ﬁrst, a question element has to be cre-

ated and then the script has to be included inside the

question text as illustrated below:

ALQuiz.setCurrentQuestionId("questionId");

</script>

where alquiz.js and questionId are respectively

the path to the script offered in the repository pre-

sented and the identiﬁer of the question declared in

the last quiz element as described below. Further-

more, the code line

has to be added to the feedback text, which is shown

on success. This will inform the gamiﬁcation system

that the user solved a question correctly.

Unless the question does not stand for itself but

is part of a series of exercises – in Moodle realized

by the quiz element – authors can structure questions

with the help of the proposed gamiﬁcation system by

levels and worlds. In this, the goals principle is em-

phasized. To do this, in the last element of the quiz,

the questions have to be declared by a given syntax,

e. g.:

...

{

id:"fra_a",

needs:1,

onsuccess:"fra_b",

onfailure:"fra_instructions"

{

id:"fra_b",

needs:1,

onsuccess:"fra_c",

onfailure:"fra_a"

{ ...

In this example, two questions are declared identi-

ﬁed by fra_a and fra_b (giving question authors

the hint that it is about the ﬁrst and second ques-

tion of the fractions world). Solving the ﬁrst ques-

tion will lead the user to the question identiﬁed by

fra_b (onsuccess attribute), while failing will lead

them to the instructions page of this math world

(onfailure attribute). To discern failure from suc-

cess, the script needs to know, how many times

the function ALQuiz.incrementSolved() has to be

called to validate an exercise as completely solved.

This is represented by the needs attribute.

Furthermore, we made use of the STACK question

type. This question type enables authors to test users’

input against speciﬁc error patterns to give speciﬁc

feedback. The authored feedback then is presented

automatically to those learners that run into speciﬁc

error patterns. The additional JavaScript moves the

feedback into the speech bubble of the supportive ﬁg-

ure.

Figure 1 demonstrates how the frontend of a Moo-

dle exercise is adapted to implement the chosen gam-

iﬁcation design principles and serve the given success

factors. Enabling moving freely through exercises

CSEDU 2023 - 15th International Conference on Computer Supported Education

310

and being able to repeat exercises without penalty af-

ter failing has to be conﬁgured by the quiz settings in

the backend of the Moodle course. See the repository

for further instructions and explanations.

4.3 Technical Limitations

Besides the advantages of a frontend-oriented soft-

ware architecture – gamiﬁcation through an afford-

able, integrable and extendable approach – coping

without server communication is also accompanied

by limitations.

Social interaction is a well-used element in gami-

ﬁcation approaches. For example, automatically pre-

senting points or badges from other players or ranking

all participating local learners are known as additional

motivators (Majuri et al., 2018). Communicating in-

formation about other players is realized by a server.

A frontend-oriented approach is in itself not capable

of communicating this information to other players.

Coping without a server also comes along with the

impossibility to synchronize data between devices.

The frontend-oriented approach stores the data locally

by default. When users start an exercise on one device

and continue it later on another device, the data of the

gamiﬁcation system is not transferred by default.

Adding an additional server to the architecture

would overcome this problem. However, this would

also lead to greater effort, which was originally in-

tended to be avoided considering higher education in-

stitutions’ infrastructure.

Such an additional server may be acting indepen-

dently of the LMS or can be combined with it. If a so-

cial interaction and/or data synchronization between

devices is desired, a conventional GSA – AS, GGP

or IG – would be more appreciated here, since server

communication is an integrated part of each of these

solutions (Herzig et al., 2014). But facing, that this

would mean to trade-off affordability, extendibility or

integrability, the frontend-oriented approach extended

with an additional server may be a good choice de-

spite the bigger effort.

Among the derived gamiﬁcation design principles

for mathematical e-learning exercises (section 3), no

principle containing social elements was identiﬁed as

relevant. This would have been applied to the com-

petition and cooperation and visible status principles.

Since neither data synchronization nor social interac-

tion is required in this project, the frontend-oriented

approach without any server communication is the

tool of choice.

5 EXPERIMENT & RESULTS

The approach presented above – hereafter called

training area – was tested in two math preparatory

courses. The test aimed to get insight into the follow-

ing questions.

1. How motivated are students to accomplish the

training area? We used a standardized question-

naire and found that students perceive themselves

as motivated during accomplishment and expect

to be motivated to solve training areas like this in

the future. We will elaborate more on this in Sec-

tion 5.2.

2. How do students perceive the use of game ele-

ments in this exercise design? In the given ques-

tionnaire, we also asked students for their evalua-

tion of the used game elements. It shows up that

students overall perceive the usage of game ele-

ments as suitable, but mostly appreciate, that ex-

ercises appear in ascending difﬁculty as shown in

section 5.3.

3. How do students move through the training area?

Here we analyzed students’ usage data and found

that students retry boss questions more often than

other questions. This can be interpreted as a raised

motivation to solve boss questions as described in

section 5.4.

4. How does the tutor feedback affect students be-

havior? Section 5.5 deals with this question. We

conducted a deeper analysis of students’ tries of

the boss questions and found that a considerable

number of students progressed toward the correct

answer.

Furthermore, students were asked about their overall

satisfaction with the current course design. This, and

asking for their improvement suggestions, aimed to

generate ideas for further development of the training

area.

5.1 Experiment Design

The test took place at university in two different loca-

tions in a given time slot of 90 minutes. Overall 115

participants took part in it. For our use case, the ap-

proach consisted of 28 math questions from the top-

ics fractions, binomial formulas, pq formula, power

laws and trigonometry. Furthermore, the approach in-

cluded 9 questions to learn how to enter answers to

be correctly interpreted by the underlying computer

algebra system (CAS).

After ﬁnishing the training area, a standardized

questionnaire awaited each user as the last part of the

training area. This questionnaire aimed to evaluate

Success Factors for Mathematical e-Learning Exercises Focusing First-Year Students

311

the usability of the training area and how motivated

students were by the exercise design. It contains 7

scaled evaluation questions, 2 multiple choice ques-

tions and 2 free text questions.

In the scaled questions, the participants are asked,

to what extent they agree with the given statements

shown in Table 2 from 1 (completely disagree) to 5

(completely agree).

Table 2: Questionnaire evaluation questions (EQ).

EQ1 Compared to solving exercises in

school, I was more motivated to solve

exercises in the just accomplished

training area.

EQ2 The provided support helped me with

solving the exercises.

EQ3 The ascending difﬁculty combined

with the question design helped me to

stay on track.

EQ4 I appreciated that the questions ap-

peared in ascending difﬁculty.

EQ5 I can well imagine to use training ar-

eas like this as accompanying learning

tools for my studies.

EQ6 I perceived the use of gamiﬁcation el-

ements (levels, worlds, bosses) as suit-

able.

EQ7 I think that illustrating the support by

an icon was basically a good idea.

The evaluation questions (EQ) can be divided into

three groups.

• EQ1, EQ3 and EQ5 aim to evaluate the perceived

motivation to accomplish the training area now or

in the future.

• EQ2, EQ4, EQ6, EQ7 aim to get insights into how

satisﬁed students are with the course design and

what adaptations would be welcome in the future.

The multiple-choice questions (MCQ) ask for

the used device during accomplishment (MCQ1) and

where the participants expect to use it in the future

(MCQ2). The free text questions (FTQ) are shown in

Table 3. The answers to these two questions were an-

alyzed using the qualitative content analysis (Fenzl,

2014).

Table 3: Questionnaire free text questions (FTQ).

FTQ1 What general feedback about the

gamiﬁcation elements (level, worlds,

bosses) do you want to provide?

FTQ2 What general feedback regarding the

usability of the training area do you

want to provide?

To get further insights into how the learners used

the training area, the usage data that was automati-

cally logged by the LMS was acquired. In addition

to the common data the Moodle web surface offers to

course administrators, this enables us to see how of-

ten users repeat questions and in what amount users

succeeded in a question after failing it before.

Thanks to the STACK question type (see section

4.2) additionally to the default logged data we were

able to recapitulate what error patterns users pass

through and how the speciﬁc feedback helped learners

to progress in their score performance.

5.2 Students Perceived Motivation

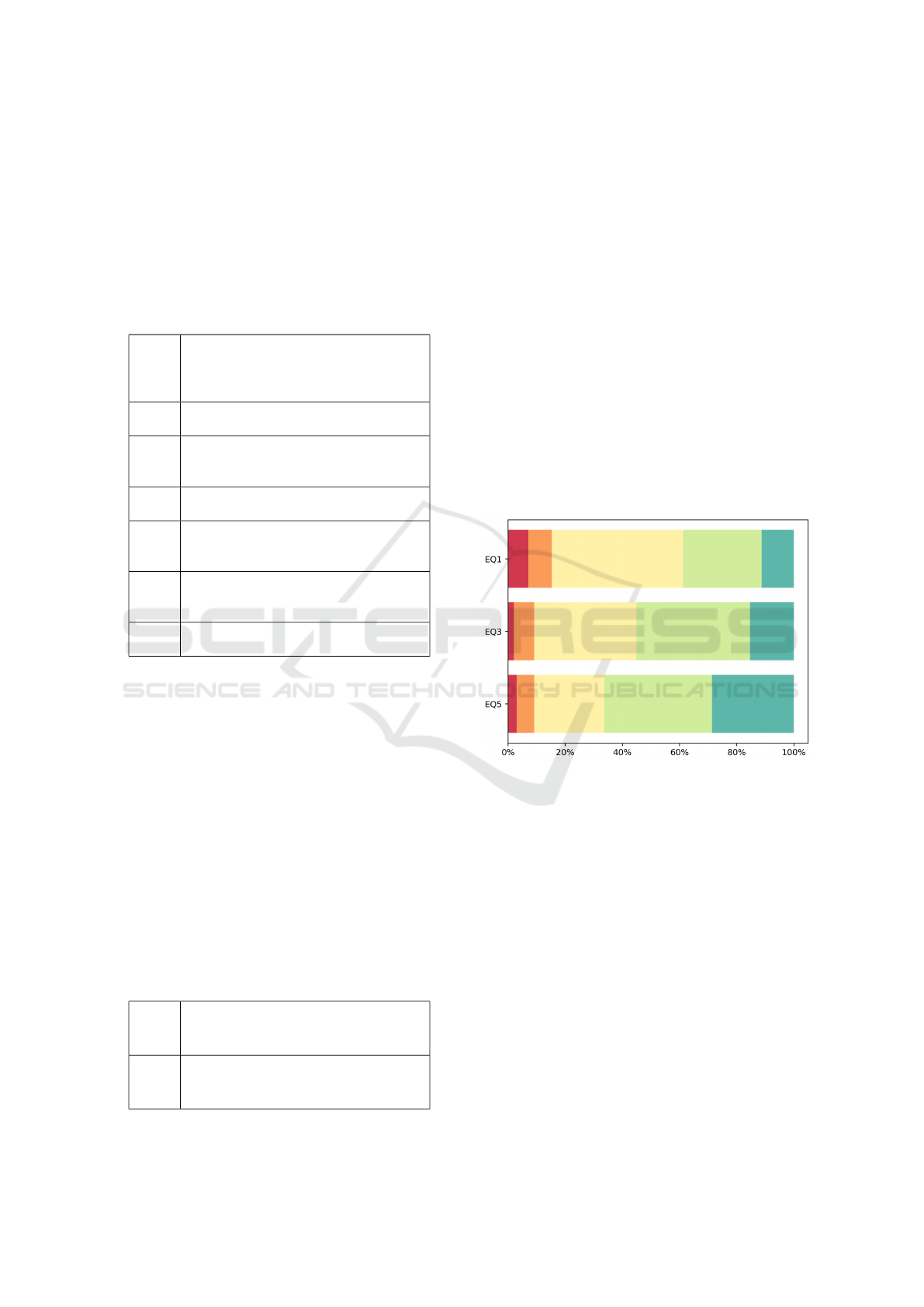
Figure 3 shows different aspects of students’ per-

ceived motivation.

Most users state to be motivated to solve the exer-

cises of the training area during accomplishment com-

pared with solving exercises in school (EQ1).

Figure 3: Users evaluation of their motivation towards the

training area from total disagreement (red) to total agree-

ment (dark green) in percent.

EQ3 asks for the student’s perception, of how the

combination of question design and the raising difﬁ-

culty of questions helped the students to stay on track.

Figure 3 shows, that most students afﬁrm, that this is

the case.

Even more users say, that they can well imagine,

to use training areas like this as accompanying learn-

ing tools for their studies (EQ5).

One can overall say, that the use of this training

area is accompanied by a basic motivation, to solve

exercises like this now and in the future. Unfortu-

nately, there is no comparable data to further prove

that. A control- and test-group research design is ad-

dressed in section 7 to overcome this weakness of this

study.

CSEDU 2023 - 15th International Conference on Computer Supported Education

312

Apart from that, it is important to consider, that

students state to be motivated, although they were un-

satisﬁed with the correct input of math syntax in a

large amount.

On analyzing the answers to the free text ques-

tions, we found 111 entities encoded as described be-

low (amount of entities in brackets).

1. General positive feedback (49),

2. negative feedback regarding the syntax(-input)

(26),

3. general negative feedback (17),

4. negative feedback regarding the input for multi-

plication (15)

5. feedback regarding solution(-paths) (4).

Hence, negative feedback is predominantly re-

lated to the input of math calculations. Especially the

necessity of using the * as a multiplication sign, even

though a multiplication could be implied by the CAS

(like e. g. in 2 x), was noted as “annoying”, “taking

away the pleasure in solving the exercises”. For ex-

ample: users had to write 2 ∗x instead of 2x for a valid

answer. Originally, the question designers intended to

make the users familiar with math input in program-

ming languages or CAS, because these are often used

during the soon to be starting studies of the partici-

pants. Due to the given feedback, it has to be consid-

ered anew, whether this approximation to CAS syntax

is worth the loss of pleasure during exercise solving.

Although this interferes with the unsatisfactory

kind of how math is entered, an overall perceived ba-

sic motivation can be derived from the given answers

of the students. All the more, that students still stated

to be motivated, despite the fact that the input of math

was recognized as annoying, can be interpreted as a

special beneﬁt of this approach. It has to be assumed,

that the perceived motivation is even higher, when the

afﬂiction to enter math forumlas in the same way as

for a programming language or a CAS is removed.

The motivating aspect of the exercise design is

also mirrored in the answers to the free-text questions.

For example, users say about the training area:

• “This makes it a little more motivating to solve the

exercises.”

• “I think the concept is a great idea and incredibly

motivating for learners. It’s notably less boring

and jog-trot than conventional learning.”

Apart from asking for the perceived motivation, ex-

amining the usage data gives further insight into how

learners were motivated to solve the most challenging

exercises. This will be described below.

5.3 Students’ Evaluation of Game

Elements

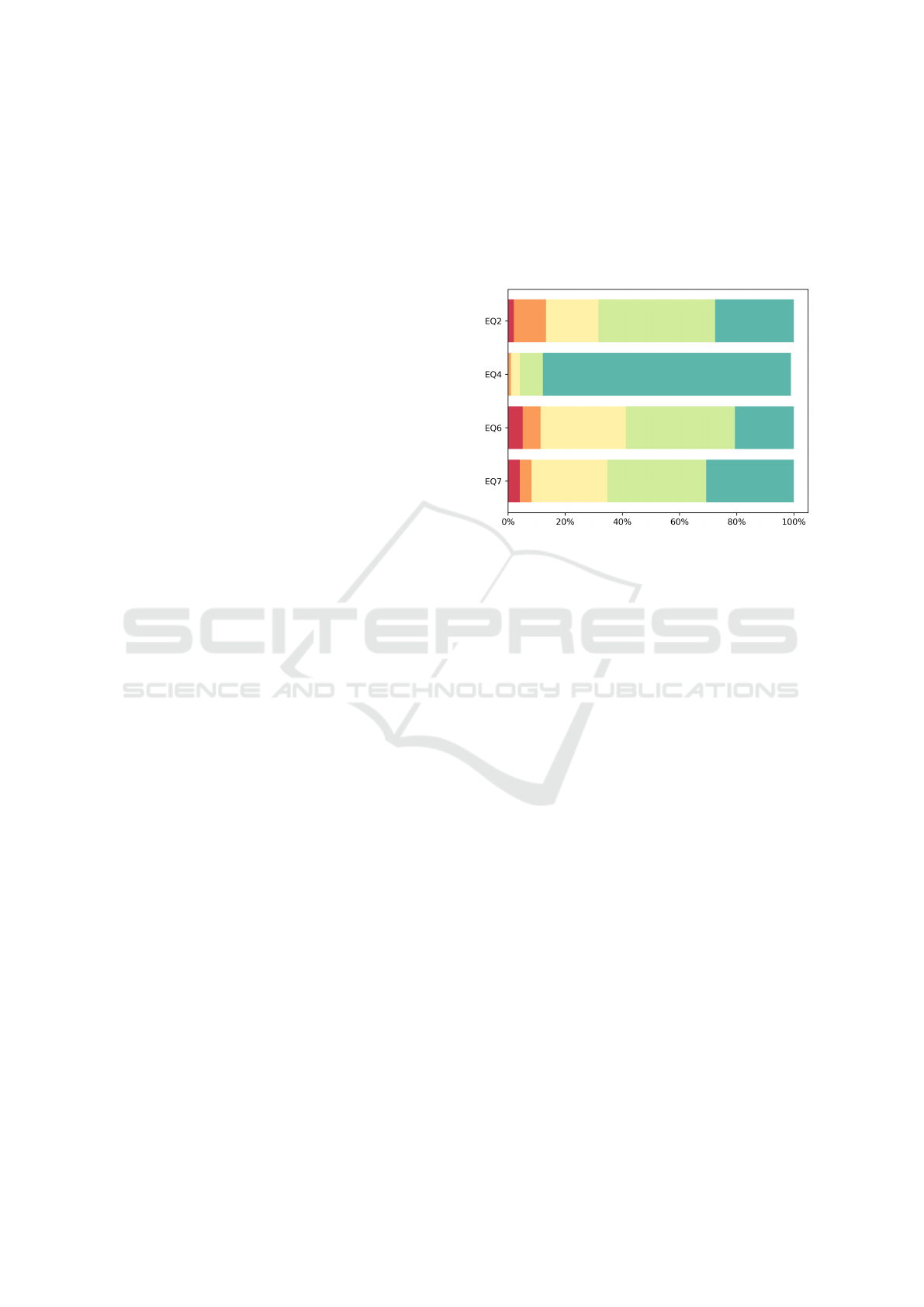
As shown in Figure 4, students evaluate the feedback,

the ascending difﬁculty, the game-like structure (lev-

els, worlds, bosses) and the tutor-icon mainly posi-

tively.

Figure 4: Students’ evaluation of different elements of the

game-like interface from total disagreement (red) to total

agreement (dark green) in percent: Feedback (EQ2), as-

cending difﬁculty (EQ4), game-like structure (EQ6), tutor-

icon (EQ7).

The averages of each statement lie above a neutral

center. Special attention can be paid to the ascending

difﬁculty (EQ4). Here, 87% of learners totally agree

with the statement “I appreciated, that the questions

appeared in ascending difﬁculty.” Obviously, learners

enjoyed especially the challenging aspect of the exer-

cise design.

5.4 Students’ Pathway Decisions

In the given approach students were able to move

freely through the course as described above with

the freedom of choice gamiﬁcation design principle

(section 2). By analyzing students’ pathways, we

found, that people decide more often to visit and retry

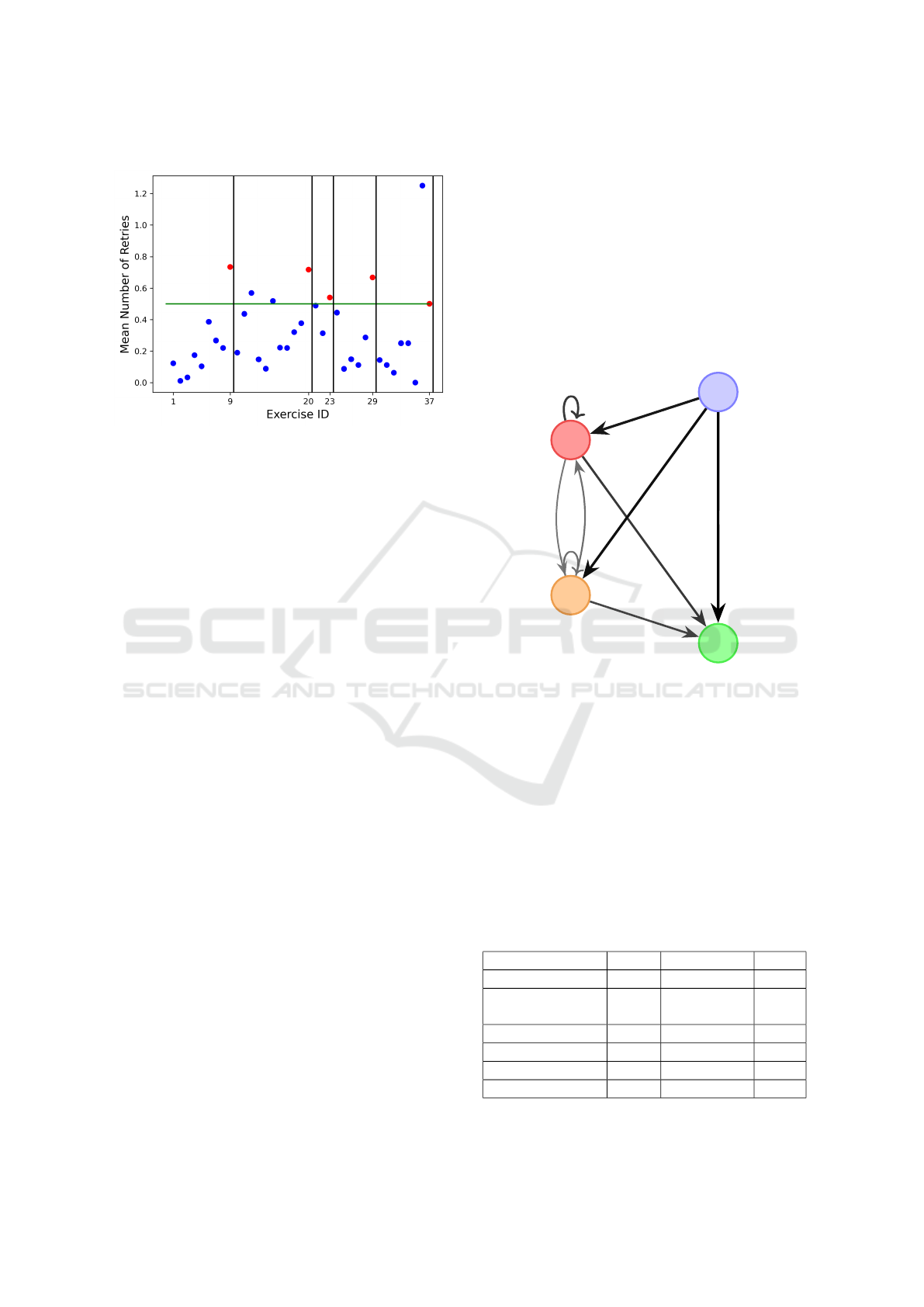
boss questions compared to other questions. Figure 5

shows in what amount users reattend questions after

their ﬁrst try. The ﬁve boss questions (red) all have a

mean number of retry of at least or equal 0.5, which

is signiﬁcantly higher than for most other questions

(r = 3.43, p = 0.0015, t-test).

To clarify the reason for that, the relation between

the mean number of retries to other values was tested

with a person’s correlation test. Beforehand, the last

but one question was removed from the dataset as an

outlier. But neither for question difﬁculty (r = 0.059,

p = 0.752) nor for number of attempters (r = −0.137,

Success Factors for Mathematical e-Learning Exercises Focusing First-Year Students

313

Syntax

Binom. formulas

& fractions

Power

laws

Trigonometry

Figure 5: Mean number of retries by questions after ﬁrst

accomplishment, structured in the ﬁve worlds.

p = 0.418) a signiﬁcant correlation to the mean num-

ber of retries of normal questions was found.

This makes it presumable, that the raised mean

number of retries of boss questions traces back to an

enhanced motivation of students to solve them in ac-

count of the question design. This is supported by

some of the free-text answers of the students from the

accompanying questionnaire. E. g. students say about

the training area:

• “Makes learning more varying and structures it by

clear goals (boss).”

• “I only solved the boss questions, because I was

looking for the greatest challenge. I liked, that I

could directly jump there.”

Furthermore, the boss questions are a recurring part in

the suggestions for improvements. Students suggest:

• “An indicator, that a world is solved after ﬁnishing

the boss.”

• “In the end, you could add a health points bar to

the boss.”

This makes it assumable, that the given gamiﬁca-

tion approach – especially the feature related to the

game attribute goals –, motivates students to confront

themselves with the hardest exercises.

5.5 Feedback Effects

Immediate feedback was identiﬁed as one important

principle in gamiﬁcation approaches in higher educa-

tion mathematics preparatory courses (section 2). To

analyze the effects of this on students and their moti-

vation, we examined the usage data regarding retries

of single questions.

Figure 6 shows for the boss task of the syntax

math world as an example, that at the beginning (0)

34 persons succeeded at the ﬁrst attempt (C), 28 per-

sons failed (W) and 30 persons were partially correct

(P1). If the answer is not correct, a sample solution is

shown to the students. If the answer is partially cor-

rect, the speciﬁc error is described additionally. In the

speciﬁc example of the syntax boss task, the students

will be asked to give two possible solutions, if they

only gave one. The students are then free to skip the

question or to repeat it with different numbers (ran-

domization).

Figure 6: Users progress in the syntax boss question. 0:

Starting point, C: Correct, W: Wrong, P1: Partially correct

(offered only one solution where two were expected). An-

notated arrows represent the amount of movements.

Proceeding from these initial movements, we see

here, that students do not only retry questions in a

notable amount (as already shown in section 5.4),

but that they also progress towards a correct answer.

There are for example 19 movements from wrong (W)

to correct (C) and 15 movements from partially cor-

rect (P) to correct (C).

Table 4: Amount of learners that were initially wrong (W)

or partially correct (P) in boss exercises, mapped onto the

amount of movements toward a correct answer.

World W / P Score-Raise Ratio

Syntax 58 36 62%

Binom. formulas

& fractions

41 23 56%

Pq formula 34 11 32%

Power laws 16 9 56%

Trigonometry 9 1 11%

Sum 158 80 51%

CSEDU 2023 - 15th International Conference on Computer Supported Education

314

Summing up the movements towards a better

score (e. g. 36 movements for the syntax world –

movements from wrong to partially correct included)

divided by the number of learners, that initially failed

or accomplished only partially correct (58 learners),

the amount of progression movements can be ex-

pressed in relation to the learners (62%). Regarding

the boss questions, there is an overall progression of

51% (see Table 4).

6 DISCUSSION

Each of the questions regarding learners’ perceived

motivation is answered positively, on average lying

above neutral. One can say, that learners are overall

motivated to accomplish exercises designed this way.

Surprisingly, this positive result is achieved despite

overall displeasure with the way multiplications have

to be entered to be validated by the CAS.

The answers to the questions regarding spe-

ciﬁc elements of the exercise design are also lying

above neutral. The majority of students evaluate the

feedback-element as helpful. Furthermore, the tutor-

icon and the usage of a game-like structure (levels,

worlds, bosses) are perceived as suitable. The ascend-

ing difﬁculty of exercises is especially appreciated.

The signiﬁcantly higher repetition rate of boss

questions shows, that the high motivation is espe-

cially channeled towards these most challenging ex-

ercises. Obviously, learners focus on accomplishing

these hardest questions, following the prompt derived

by the goals gamiﬁcation design principle.

Taking a closer look at the progress learners make

in repeating boss exercises it shows, that there is an

overall progression towards the correct answer, which

can be expressed by the relation between the number

of learners who don’t solve the exercise at ﬁrst to the

number of learners who raise their score in this ex-

ercise. Here we measured an overall progression of

51%, meaning, that on average half of the learners

that were initially wrong or partially correct in a boss

exercise raised their score in this exercise by retrying

it once, twice or more.

We showed that gamiﬁcation can be implemented

into universities LMS by a frontend-oriented software

architecture. Thus, enabling the implementation of

an affordable, integrable and extendable gamiﬁcation

solution is possible. Independent from the techni-

cal limitations accompanying a such lightweight ap-

proach, a raise of motivation and a learning progress

can be seen.

Combining the gamiﬁcation design principles

goals, immediate feedback, freedom to fail and free-

dom of choice, the given exercise design leads to a

raised motivation, where the highest motivation ap-

plies to the boss exercises. To solve these is the de-

clared goal of the design (goals principle). Unless

there is not enough knowledge yet to solve the boss

exercises, learners are encouraged to ﬁll these gaps,

either by getting immediate feedback (enabled by im-

mediate feedback principle) after failure (enabled by

freedom to fail principle) and/or by skipping back to

easier questions of the same world (enabled by free-

dom of choice principle). In this, the most challenging

tasks are not only attended thanks to a raised motiva-

tion but also solved ﬁnally thanks to a raised under-

standing.

7 CONCLUSION & FUTURE

PROSPECTS

In this work, four success factors to handle differ-

ent competence levels in higher education mathemat-

ical e-learning are identiﬁed. Based on this factors,

a frontend-oriented software approach for mathemat-

ical e-learning exercises is presented, that enables

lightweight gamiﬁcation implementation inside uni-

versities LMS. Four gamiﬁcation design principles

were derived, which led to an exercise design struc-

tured by math worlds and boss exercises, where learn-

ers get immediate feedback and are enabled to move

along and repeat exercises without penalty. This ex-

ercise design was implemented with the help of the

given frontend-oriented software architecture in the

LMS Moodle.

In a ﬁrst test run, we showed: (i) Students fo-

cus on solving the most challenging exercises (boss

exercises). To achieve this, they repeat those ex-

ercises more often or jump back to previous ques-

tions, to acquire the needed knowledge. (ii) Students

progress in their score performance by repeating ex-

ercises when being supplied with additional material

(feedback). (iii) The perceived motivation of students

towards present and future accomplishment of exer-

cises lies above neutral, which indicates a raise in mo-

tivation. (iv) Students perceive the usage of game el-

ements overall as suitable, but especially appreciate,

that exercises appear in ascending difﬁculty.

In the future, this approach has to be tested in a

test- and control-group research design, to give these

ﬁndings more evidence. By additionally applying a

math-skill pre-test, differences in effects regarding

lower- and higher-skilled students can be measured.

By this, more light is shed on how to facilitate a catch-

up of lower-skilled students.

Success Factors for Mathematical e-Learning Exercises Focusing First-Year Students

315

Thanks to its lightweight structure, this approach

is not only extendable by the set of exercises, but also

regarding the overall functionality. Using JavaScript,

other gamiﬁcation principles can be added easily to

this basic implementation. Here, the presented ap-

proach offers possibilities to tackle a demand of re-

cent gamiﬁcation research (Behl et al., 2022; Zain-

uddin et al., 2020a): Elucidating the effects of single

game elements (instead of overall gamiﬁcation prod-

ucts). By adding or removing game elements with

the help of JavaScript, speciﬁc outcomes (motivation,

learning progress) can be mapped onto speciﬁc game

elements (e. g. storytelling), regarding speciﬁc groups

(e. g. lower- vs. higher-skilled students). In this, re-

search regarding the question of how a catch-up of

lower-skilled students regarding math with gamiﬁed

e-learning exercises can be boosted.

ACKNOWLEDGEMENTS

This work is part of the Digital Mentoring project,

which is funded by the Stiftung Innovation in der

Hochschullehre under FBM2020-VA-219-2-05750.

We thank our project partners from the Westphalian

University and the University of Applied Sciences

and Arts Dortmund for their support. We also thank

Ralf Erlebach from the University of Wuppertal. Find

the mentioned repository here: http://bit.ly/3HRpyu0.

REFERENCES

Avigad, J. (2018). Modularity in mathematics. The Review

of Symbolic Logic, 13(1):47–79.

Ayastuy, M. D., Torres, D., and Fern

andez, A. (2021).

Adaptive gamiﬁcation in collaborative systems, a sys-

tematic mapping study. Computer Science Review,

39:100333.

Behl, A., Jayawardena, N., Pereira, V., Islam, N., Giu-

dice, M. D., and Choudrie, J. (2022). Gamiﬁcation

and e-learning for young learners: A systematic lit-

erature review, bibliometric analysis, and future re-

search agenda. Technological Forecasting and Social

Change, 176:121445.

Bullon, J. J., Encinas, A. H., Sanchez, M. J. S., and Mar-

tinez, V. G. (2018). Analysis of student feedback

when using gamiﬁcation tools in math subjects. In

2018 IEEE Global Engineering Education Confer-

ence (EDUCON), pages 1818–1823. IEEE.

uchele, S. and Marten, C. (2022). Math skill growth and

learning differences in higher education. Can lower-

skilled students catch up? MAGKS Joint Discussion

Paper Series in Economics, 15(202236):1–33.

Deterding, S., Dixon, D., Khaled, R., and Nacke, L. (2011).

From game design elements to gamefulness. In Pro-

ceedings of the 15th International Academic MindTrek

Conference on Envisioning Future Media Environ-

ments - MindTrek '11. ACM Press.

Dichev, C. and Dicheva, D. (2017). Gamifying education:

what is known, what is believed and what remains un-

certain: a critical review. International Journal of Ed-

ucational Technology in Higher Education, 14(1).

Dicheva, D., Dichev, C., Agre, G., and Angelova, G. (2015).

Gamiﬁcation in education: A systematic mapping

study. Educational Technology & Society, 18:75–88.

Fenzl, Thomas; Mayring, P. (2014). Qualitative Inhaltsanal-

yse. In Handbuch Methoden der empirischen Sozial-

forschung, pages 543–556. Springer VS.

Fischer, H. and Heinz, M. (2020). Onboarding by gamiﬁ-

cation. Design and evaluation of an online service to

support ﬁrst year students. In EdMedia + Innovate

Learning Conference 2020.

Fogg, B. (2009). A behavior model for persuasive design.

In Proceedings of the 4th International Conference on

Persuasive Technology - Persuasive '09. ACM Press.

Gordon, N., Brayshaw, M., and Grey, S. (2013). Maximis-

ing gain for minimal pain: Utilising natural game me-

chanics. Innovation in Teaching and Learning in In-

formation and Computer Sciences, 12(1):27–38.

Herzig, P., Ameling, M., Wolf, B., and Schill, A. (2014).

Implementing gamiﬁcation: Requirements and gami-

ﬁcation platforms. In Gamiﬁcation in Education and

Business, pages 431–450. Springer International Pub-

lishing.

Hofacker, C. F., de Ruyter, K., Lurie, N. H., Manchanda, P.,

and Donaldson, J. (2016). Gamiﬁcation and mobile

marketing effectiveness. Journal of Interactive Mar-

keting, 34:25–36.

Irfan, M., Kusumaningrum, B., Yulia, Y., and Widodo, S. A.

(2020). Challenges during the pandemic: Use of e-

learning in mathematics learning in higher education.

Inﬁnity Journal, 9(2):147.

Jueru, T., e Silva, R. F., and Ferrao, S. (2019). Success fac-

tors for using gamiﬁcation in language teaching. In

2019 International Symposium on Computers in Edu-

cation (SIIE). IEEE.

Khaitova, N. F. (2021). History of gamiﬁcation and its

role in the educational process. International Jour-

nal of Multicultural and Multireligious Understand-

ing, 8(5):212.

Liang, L., Yeung, K., Lui, R. K. W., Cheung, W. M. Y.,

and Lam, K. F. (2018). Lessons learned from a cal-

culus e-learning system for ﬁrst-year university stu-

dents with diverse mathematics backgrounds. In Dis-

tance Learning, E-Learning and Blended Learning in

Mathematics Education, pages 69–92. Springer Inter-

national Publishing.

Lisnani, L., Putri, R. I. I., Zulkardi, and Somakim (2020).

Designing moodle features as e-learning for learn-

ing mathematics in COVID-19 pandemic. Journal of

Physics: Conference Series, 1657:012024.

Majuri, J., Koivisto, J., and Hamari, J. (2018). Gamiﬁca-

tion of education and learning: A review of empiri-

cal literature. In Proceedings of the 2nd International

GamiFIN conference, pages 11–19. CEUR.

CSEDU 2023 - 15th International Conference on Computer Supported Education

316

Piteira, M., Costa, C. J., and Aparicio, M. (2018). Computer

programming learning: How to apply gamiﬁcation on

online courses? Journal of Information Systems Engi-

neering & Management, 3(2).

Podolskiy, A. I. (2012). Zone of proximal development.

In Encyclopedia of the Sciences of Learning, pages

3485–3487. Springer US.

Ryan, R. M. and Deci, E. L. (2000). Self-determination the-

ory and the facilitation of intrinsic motivation, social

development, and well-being. American Psychologist,

55(1):68–78.

Schulmeister, R. (2004). Diversity of students and the con-

sequences for e- learning. In Proceedings of the 6.

ICNEE.

van Roy, R. and Zaman, B. (2017). Why gamiﬁcation

fails in education and how to make it successful: In-

troducing nine gamiﬁcation heuristics based on self-

determination theory. In Serious Games and Edutain-

ment Applications, pages 485–509. Springer Interna-

tional Publishing.

Vygotsky, L. S. (1978). Mind in Society. Harvard Univer-

sity Press.

Zabala-Vargas, S. A., Garc

ıa-Mora, L. H., Arciniegas-

Hernandez, E., Reina-Medrano, J. I., Benito-Crosetti,

B. D., and Darder-M

esquida, A. (2021). Strengthen-

ing motivation in the mathematical engineering teach-

ing processes – a proposal from gamiﬁcation and

game-based learning. International Journal of Emerg-

ing Technologies in Learning (iJET), 16(06):4.

Zainuddin, Z., Chu, S. K. W., Shujahat, M., and Perera,

C. J. (2020a). The impact of gamiﬁcation on learn-

ing and instruction: A systematic review of empirical

evidence. Educational Research Review, 30:100326.

Zainuddin, Z., Shujahat, M., Haruna, H., and Chu, S. K. W.

(2020b). The role of gamiﬁed e-quizzes on student

learning and engagement: An interactive gamiﬁcation

solution for a formative assessment system. Comput-

ers & Education, 145:103729.

Success Factors for Mathematical e-Learning Exercises Focusing First-Year Students

317