Modelling Adaptive Systems with Nets-Within-Nets in Maude

Lorenzo Capra

1 a

and Michael K

ohler-Bussmeier

2 b

Dipartimento di Informatica, Universit

a degli Studi di Milano, Via Celoria 18, Milan, Italy

University of Applied Science Hamburg, Berliner Tor 7, Hamburg, Germany

Keywords:

Adaptive Systems, Maude, Nets-Within-Nets.

Abstract:

Systems able to dynamically adapt their behaviour gain growing attention to raising service quality by reduc-

ing development costs. On the other hand, adaptation is a major source of complexity and calls for suitable

methodologies during the whole system life cycle. A challenging point is the system’s structural reconﬁgu-

ration in front of particular events like component failure/congestion. This solution is so common in modern

distributed systems that it has led to deﬁning ad-hoc extensions of known formal models (e.g., the pi-calculus)

But even with syntactic sugar, these formalisms differ enough from daily programming languages. This work

aims to bridge the gap between theory and practice by introducing an abstract machine for the “nets-within-

nets” paradigm. Our encoding is in the well-known Maude language, whose rewriting logic semantics ensures

the mathematical soundness needed for analysis and an intuitive operational perspective.

1 INTRODUCTION

Systems with the ability to dynamically adapt/reor-

ganise in front of varying execution environments are

becoming increasingly popular, to raise service qual-

ity without increasing development costs. On the

other hand, system adaptation is complex to manage

and therefore requires suitable models/methodologies

both at design time and runtime. In this context, for-

mal methods can play an important role. (Weyns

et al., 2012), (Hachicha et al., 2019) present a sur-

vey of formal methods for modelling/analysis of self-

adaptive systems. Signiﬁcant examples are (Iglesia

and Weyns, 2015), specifying MAPE-K templates for

a family of self-adaptive systems, and (Weyns and

Iftikhar, 2022), presenting an end-to-end approach for

engineering self-adaptive systems during the life cy-

cle of a feedback loop.

In this paper, we focus on a challenging point,

namely, the structural reconﬁguration of a system

against particular events like component failure/con-

gestion. This solution has become so common in

modern distributed systems, that it has led to a spe-

cialisation of known formalism, e.g. the π-calculus or

nets-within-nets. But even with syntactic sugar, these

formalisms are far enough from ‘daily’ programming

https://orcid.org/0000-0002-1029-1169

https://orcid.org/0000-0002-3074-4145

languages, in which reconﬁguration often boils down

to add- and delete operations.

This work aims to bridge the gap between theory

and practice by presenting an abstract machine for the

nets-within-nets approach, used in the last decade to

model adaptive and mobile processes/agents. Our for-

malisation uses the well-known Maude language since

speciﬁcations given in rewriting logic enjoy the math-

ematical soundness needed for analysis and provide

developers with an intuitive operational perspective

(in (Bruni et al., 2012) Maude has been used to formal-

ize adaptive strategies). We focus on the base class of

nets-within-nets, namely, Elementary Object Systems

(EOS) since they make a reasonable trade-off between

expressivity and analysis complexity. This initial for-

malization, however, fosters further interesting exten-

sions.

We ﬁrst brieﬂy introduce PT nets and Nets within

Nets in Section 2. Section 3 presents (after a short

background) the Maude formalization of EOS, fo-

cusing on the key aspects. Section 4 describes our

running example: the speciﬁcation of an adaptable

production-line system. We sketch the Maude en-

coding (which is annexed) and present a few signif-

icant examples of formal veriﬁcation. Section 5 sum-

marises the lessons learned so far and gives insights

into current research.

Capra, L. and Köhler-Bussmeier, M.

Modelling Adaptive Systems with Nets-Within-Nets in Maude.

DOI: 10.5220/0011860000003464

In Proceedings of the 18th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2023), pages 487-496

ISBN: 978-989-758-647-7; ISSN: 2184-4895

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

487

2 BACKGROUND

Petri Nets. PN are a reference model for concur-

rent systems. We hereafter focus on enriched Place-

Transitions nets (PT). A PT net is a kind of bipartite

multi-graph N := (P,T,I,O,H), where: P and T are

ﬁnite, disjoint sets holding the places –state variables,

drawn as circles– and the transitions –events chang-

ing the state, drawn as bars, respectively; Letting

Bag[P] be the set of multisets on P, {I,O,H} : T →

Bag[P] represent the input/output/inhibitor edges, re-

spectively. The distributed state of a PT, or marking,

is, in turn, m ∈ Bag[P]. PT have intuitive semantics

(in the sequel, we use the operator natural extension

to multisets): t ∈ T is enabled in m if and only if:

I(t) ≤ m ∧ H(t) > m (> is restricted to the support

of H(t)). If t is enabled in m it may ﬁre, leading to

′

= m + O(t) − I(t).

A PT system is a pair ⟨N,m

⟩. Its semantics is a

T -labelled directed graph whose nodes are the mark-

ings reachable from m

and whose edges match direct

state transitions. Enriched PT systems are Turing-

powerful.

Nets-Within-Nets. In recent years, adaptable dis-

tributed systems have been deeply studied in the con-

text of the object-net formalism (K

ohler-Bußmeier

and R

olke, 2004; K

ohler-Bußmeier and Heitmann,

2009), which follows the pioneering nets-within-nets

model proposed by Valk (Valk, 2003). With object-

nets, we mean PN where tokens (graphically denot-

ing a PN marking) are nets in turn, i.e., we have

nested markings. The Maude formalisation we are go-

ing to present refers to elementary object-net systems

(EOS) (K

ohler-Bußmeier and R

olke, 2004), the two-

level specialisation of object-nets (K

ohler-Bußmeier

and R

olke, 2004; K

ohler-Bußmeier and Heitmann,

2009).

HORNETS (K

ohler-Bußmeier, 2009) are a further

extension with algebraic operators making it possible

to modify the structure of net tokens through transi-

tion ﬁring. For complexity studies, elementary HOR-

NETS (K

ohler-Bußmeier and Heitmann, 2013) have

been introduced, which have a two-level nesting in

analogy to EOS. It turns out that elementary HOR-

NETS have greater complexity than EOS, though more

expressive: On the one hand, most problems (in-

cluding reachability and liveness) for safe EOS are

PSPACE-complete (K

ohler-Bußmeier and Heitmann,

2011; K

ohler-Bußmeier, 2014). Namely, safe Eos are

no more complex than PT nets for this kind of prob-

lem. On the other hand, the reachability problem re-

quires exponential space for safe, elementary HOR-

NETS (K

ohler-Bußmeier and Heitmann, 2016).

Elementary Object-Net System. Let’s informally

describe EOS by referring to Figure 1. An EOS con-

sists of a system-net whose places may hold net-

tokens of a certain type. In our encoding, the graph

structure of both the system net and net-tokens is the

same as a PT net. This uniform representation of the

two levels has advantages both in terms of modelling

(e.g., a further extension with an arbitrary nesting of

nets is natural) and analysis (e.g, we can use the same

structural techniques). In the current implementation,

however, net-tokens do not allow a further nesting of

nets, i.e., they are PT systems.

In the example given in Figure 1 there are two dif-

ferent types of net-tokens (that we call net

, net

) cor-

responding to colours yellow and grey; The system-

net and the net-tokens consist of single transitions;

Only weight-one input/output edges are present.

EOS events are nested, accordingly. There may be

three different kinds of events:

1. System-autonomous: A system-net transition (as-

sume t) ﬁres by consistently “moving” net tokens

from its preset places (p

, i : 1 ...3) to its postset

, j : 4 . . .6), without changing the net tokens

marking.

2. Object autonomous: A net-token (assume that of

type net

in the system-net place p

) transition

(e.g., t

) ﬁres by moving (“black”) tokens from

its preset (a

) to its postset (b

). The net token

doesn’t move.

3. Synchronisation (illustrated in Figure 1): When-

ever we add matching synchronisation inscrip-

tions, e.g., between the system-net transition t and

the nested transitions t

, then they ﬁre in a fully

coordinated way: The net-tokens move from the

preset to the postset of t; at the same time, the

black tokens inside nested nets move from the

pre-set to the post-set of nested transitions (t

Transitions involved in a synchronisation cannot

ﬁre autonomously.

Notice that there may be several independent ﬁr-

ing instances for a system-net transition: If many net-

tokens of a certain type are in the transition’s pre/post-

set, their cumulative marking is computed and dis-

tributed on postset places of the same type (possibly

after a nested ﬁring step, in the case of a synchroniza-

tion). Each possible way of distributing the net-tokens

(cumulative) marking results in a separate transition

instance. Therefore, there is another possible instance

of transition t (other than that illustrated in Figure 1)

in which the net-tokens in p

and p

are swapped. We

give further details in Section 3.

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

488

< t1, t2 >

Figure 1: An Elementary Object Net System (EOS).

Maude. Maude (Clavel et al., 2007) is an expres-

sive, purely declarative language with a rewriting

logic semantics (Bruni and Meseguer, 2003). State-

ments are (conditional) equations (eq) and rules (rl).

Both sides of a rule/equation are terms of a given

kind that may contain variables. Rules and equa-

tions have simple rewriting semantics in which in-

stances of the left-hand side are replaced by corre-

sponding instances of the right-hand side. Maude’s

expressivity is achieved through matching modulo as-

sociativity; user-deﬁnable operator syntax/evaluation

strategy; sub-typing; generic types; reﬂection.

A Maude functional module (fmod) contains only

equations and is a functional program deﬁning one

or more operations through equations, used as sim-

pliﬁcation rules. A functional module (with all the

imported modules) speciﬁes an equational theory in

membership equational logic (Bouhoula et al., 2000).

Formally, such a theory is a pair (Σ,E ∪ A), where

Σ is the signature, that is, the speciﬁcation of all the

(sub)sort, kind

, and operator declarations; E is the

set of (conditional) equations and membership ax-

ioms, and A is the set of operator equational attributes

(assoc, comm,..). The model of (Σ, E ∪ A) is the ini-

tial algebra (denoted T

Σ/E∪A

), which is both junk- and

confusion-free and mathematically corresponds to the

quotient of the ground term algebra. Under certain

conditions on E and A, the ﬁnal values (canonical

forms) of all ground terms form an algebra isomor-

phic to the initial algebra, i.e., the denotational and

operational semantics coincide.

A Maude system module (mod) contains rewrite

rules and possibly equations. Rules represent lo-

cal transitions in a concurrent system. Formally, a

system module speciﬁes a generalized rewrite the-

ory (Bruni and Meseguer, 2003), a four-tuple R =

(Σ,E ∪ A,φ,R) where (Σ, E ∪ A) is a membership

equational theory; φ speciﬁes, for each operator in

A kind is an equivalence class grouping sorts directly

or indirectly related by subsort ordering; terms in a kind

without a speciﬁc sort are undeﬁned or error terms.

Σ, the frozen arguments; and R is a set of rewrite

rules A rewrite theory speciﬁes a concurrent system.

(Σ,E ∪ A) deﬁnes the algebraic structure of the states.

R and φ specify the system’s concurrent transitions.

The initial model of R associates to each kind k

a labeled transition system (category) whose states

are T

Σ/E∪A,k

, and whose transitions take the form:

[t]

[α]

→ [t

′

], with [t],[t

′

] ∈ T

Σ/E∪A,k

, and [α] an equiva-

lence class of rewrites modulo the equational theory

of proof-equivalence. Executability of system mod-

ules maps to ground coherence, which ensures that a

rewriting strategy in which terms are ﬁrst reduced to

the canonical form and then rewritten according to the

rules is both sound and complete.

3 MAUDE IMPLEMENTATION OF

EOS

In this section, we describe the Maude formalization

of EOS. It relies on and extends that given in (Capra,

2021; Capra, 2022b), which provides an efﬁcient op-

erational semantics for rewritable PT nets. Accord-

ing to EOS deﬁnition, however, dynamic adaptation

comes down to net-tokens manipulation. Reconﬁgu-

ration of the system net is ongoing work. We use a

few Maude code excerpts and refer to Figure 1 as a

starting example of encoding. The full list of Maude

source ﬁles is available at github.com/lgcapra/rewpt/

new/EOS. We here focus on the non-deterministic ﬁr-

ing rule of EOS.

The PT formalization in (Capra, 2021) relies

on o three generic functional modules, BAG{X},

MAP+{X,Y}, SET+{X} (the last two extensions of

built-in modules). They may be arbitrarily nested

using a ﬂexible mechanism of parameterized views

instantiating the modules’ type parameters. Differ-

ently from other Maude formalizations of PNs (Stehr

et al., 2001; Padberg and Schulz, 2016), bags are not

merely represented as free monoids on sets. Speciﬁc

bag operators guarantee much more abstraction and

Modelling Adaptive Systems with Nets-Within-Nets in Maude

489

efﬁciency: _._, _+_, _[_] _-_, _<=_, _>’_, set,

_*_. The ﬁrst two are constructors, i.e., appear in

canonical forms. We thus conveniently represent a

bag as a commutative/associative weighted sum, e.g.,

3 . a + 1 . b. The module MAP+ deﬁnes a map

term as a “set” of entries built using the associa-

tive/commutative juxtaposition _;_. Sub-sort Entry

of Map has as a unique constructor _|->_. Module

MAP+ supplies, among others, a predicate verifying the

uniqueness of a map’s keys which is widely exploited

in membership equations implementing consistency

checks.

PT nodes are denoted by indexed/labelled terms,

e.g., p(2,"net1"), t(1,"sys"). A transition’s

incidence matrix is a triplet (constructor [_,_,_]

deﬁned in module IMATRIX) of terms of sort

Bag{Place}. The modules PT-NET and PT-SYS

hold the signature of a PT net/system. A net

is a term of sort Map{Tran,Imatrix} (renamed

Net), i.e., a semicolon-separated set of entries

t(k,"lab")|-> [i,o,h], each entry being a term in

subsort ImatrixT < Net. A PT system is the juxta-

position (__ : Net Bag{Place} -> [System]) of

a Net term and Bag{Place} term representing the

marking. Using a kind as the operator’s range means

that it deﬁnes a partial function: the net sub-term must

be a consistent, non-empty map. A membership ax-

iom characterizes well-deﬁned System terms. This

solution is a trade-off between rewriting efﬁciency

and coding elegance.

A system module (PT-EMU) formalizes the opera-

tional semantics of PT systems by exploiting the al-

gebraic representation of PT nets. The conditional

rule firing implements the PT ﬁring rule. All the

involved operators are bag-operators. The matching

equation (t := t’) in rule’s condition ensures com-

pactness.

mod PT−EMU is

pr PT−SYS .

var T : Tran .

vars I O H S : Bag{Place} .

var N N’ : Net .

crl [firing] : N S => N S + O − I if T |−> [I,O,H] ; N’ :=

N /\ I <= S /\ H >’ S .

endm

The model-speciﬁc part consists of a system mod-

ule importing PT-EMU and PT-SYS and containing two

zero-arity operators of range Net and Bag{Place}.

3.1 EOS Speciﬁcation

The EOS speciﬁcation extends and reﬂects in part that

of (rewritable) PT systems. A few functional modules

specify the EOS algebraic structure. A system mod-

ule (EOS-EMU) speciﬁes the (non-trivial) EOS opera-

tion semantics. Some auxiliary operators are needed

to mime the inner steps of transition ﬁring, in particu-

lar, the computation of ﬁring instances of a system-net

transition and the consequent (non-deterministic) dis-

tribution of net-tokens on its post-set. Finally, a spe-

ciﬁc system module instantiates a given EOS model.

For the reader’s convenience, we mix the textual de-

scription with a few code excerpts. We use Figure 1

to illustrate the main concepts.

EOS Net. A term describing an EOS

net (module EOS-NET) is the empty juxta-

position of three sub-terms of sorts Net,

Map{String,Net} (renamed NeTypeS) and

Map{Tran,Map{String,Bag{Tran}}} (renamed

Syncmap). The resulting whole term is of kind

[Sysnet] (because of possible inconsistencies

among its components). The 2nd and 3rd sub-terms

specify the types of net tokens and the synchroniza-

tion between system- and object-net transitions (for

each object-net type), respectively. These sub-terms

are equipped with ad-hoc operators and separately

deﬁned (modules NET-TYPES and SYNCHRO). Note

that, according to EOS deﬁnition, a system-net

transition may synchronize with multiple occurrences

of object-net transitions.

The type of net-tokens a system-net place may

hold is associated with the place’s label in NeTypeS

sub-term. If there is no association, the system-net

place may only hold “black-tokens”. Instead, the

three categories of events possible in a EOS meet the

following conventions.

1. System-autonomous: system transitions not oc-

curring in the Syncmap sub-term.

2. Object autonomous: nested transitions for which

the predicate

op synchronized : Syncmap Tran -> Bool

evaluates to false (this predicate checks that a

given transition appears among the values -that

are maps, in turn- of Syncmap sub-term).

3. Synchronisations: deﬁned implicitly by exclu-

sion.

A membership-axiom connotes well-formed

EOS as terms of sort Sysnet. Predicate

coherent(Sy, Ty) checks that every nested

transition occurring in Syncmap belongs to the

corresponding net-type).

cmb N Ty Sy : Sysnet if welldef(N) and−then welldef(

Ty) and−then not(repeatedKeys(Sy)) and−then

coherent(Sy, Ty)

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

490

Using a uniform syntax for the system-net and net-

tokens is convenient in terms of description/algebraic

manipulation and signiﬁcantly enhances EOS expres-

sivity. Furthermore, the adopted signature may be

easily adapted to support an arbitrary nesting of nets.

EOS System. The EOS dynamics is mimed using

a structured state representation, in which the ba-

sic generic types are reciprocally nested. A term

of sort Map{Place,Bag{Bag{Place}}} speciﬁes an

EOS marking as a map from system-net places to

nested multisets of net-token places: a term of sort

Bag{Place}, indeed, represents a marking of the

net-token type associated to a certain system-net

place, its multiplicity in the top multiset the num-

ber of net-tokens in the system-net place with that

marking. The nil ground term (representing the

empty Bag{Place}) may also denote -without any

ambiguity- anonymous tokens in untyped system-net

places. For example, the EOS marking in Figure 1 is

described by the term ("net1","net2" refer to the

net-token types):

p(1,”net1”) |−> 1 . nil + 1 . (1 . p(1, ”a1”) + 1 . p(2, ”b1

”)) ;

p(2,”net1”) |−> 1 . 1 . p(1, ”a1”) ; p(3,”net2”) |−> 1 . (1

. p(1, ”a2”) + 1 . p(2, ”b2”))

A marked EOS is formally described by the

empty juxtaposition of a Sysnet sub-term and a

Map{Place,Bag{Bag{Place}}} sub-term (module

EOSYS). Due to possible inconsistencies, the opera-

tor’s arity is the kind [Eosystem]. As usual, we

use a membership axiom to connote terms of sort

Eosystem as those in which every system-net place is

a key in the EOS marking sub-term. No check is done

on net-token places, for the sake of efﬁciency and co-

herently with the fact that (in a mutable context) they

may contain isolated places.

var S : Sysnet . var M : Map{Place,Bag{Bag{Place}}} .

cmb S M : Eosystem if not(repeatedKeys(M)) and−then

places(net(S)) subset keySet(M).

In the perspective of allowing an arbitrary nesting

of nets, generalized multisets (whose elements may

be bags in turn) should be used instead of nested bags.

EOS Operational Semantics. According to the ar-

chitecture of EOS, two rewrite rules specify the

ﬁring of system-net transitions –taking account of

synchronizations– and autonomous transitions in

nested nets. Both rely on the PT ﬁring rule.

The former has some trickiness due to the intrinsic

nondeterminism: Similarly to High-Level PN transi-

tions, a system-net transition t may ﬁre in different

instances in a EOS marking m (inhibitor edges cur-

rently have a merely numerical interpretation). An

instance of t has the same algebraic representation as

m, i.e., it is a Map{Place,Bag{Bag{Place}}} term

whose map’s keys are the t’s preset. In other words,

an instance of t is a sub-multiset of m.

The system-net ﬁring rule exploits two main oper-

ators (module EOSYS):

op firingmap : Eosystem −> Map{Tran, Set{Map{

Place,Bag{Bag{Place}}}}} .

op firings : ImatrixT Map{Place, Bag{Bag{Place

}}} Syncmap −> [Set{Map{Place, Bag{Bag{

Place}}}}] .

firingmap computes the enabled ﬁring instances

for every system-net transition, taking account of syn-

chronizations. It builds on a few auxiliary operators

deﬁned in generic modules BAG-SPLIT, MAP-PROD, in

particular:

op split : Bag{X} Nat −> Set{Bag{X}}

op prod : Map{X,Set{Y}} −> [Set{Map{X,Y}}]

The former divides a bag into sub-bags of given

cardinality, the latter performs a kind of Cartesian

product of maps having sets as values. In the event

of synchronization, t’s instances are ﬁltered accord-

ing to the enabled synchronized nested transitions.

The ﬁring of an instance of t may be non-

deterministic, i.e., result in alternative multisets of

net-tokens to distribute on t’s post-set (Sect. 1). Oper-

ator firings calculates this set for a system-net tran-

sition instance (the transition’s incidence matrix and

the synchronization map are the other arguments). It

builds on:

op distribute : Bag{Place} Bag{Place} −> [Set{Map

{Place,Bag{Bag{Place}}}}]

that distributes the (pre-calculated) cumulative mark-

ing obtained by an instance of t (1st arg) to t’s post-

set (2nd arg), assuming that the two arguments refer

to system-net places of the same type. This operation

is tricky and reduces to enumerate the partitions of a

multiset.

The system module EOS-EMU formalizes the EOS

operation semantics.

mod EOS−EMU is

pr EOSYS .

inc PT−EMU .

var FM : Map{Tran, Set{Map{Place,Bag{Bag{Place

}}}}} .

***

whole ﬁring map

var TI : Entry{Tran, Set{Map{Place,Bag{Bag{Place

}}}}} .

***

transition instance

var NeFS : NeSet{Map{Place,Bag{Bag{Place}}}} .

var FS : Set{Map{Place,Bag{Bag{Place}}}} .

***

output ﬁring set

vars I O M M’ : Map{Place,Bag{Bag{Place}}} .

***

ﬁring instance/EOS marking

Modelling Adaptive Systems with Nets-Within-Nets in Maude

491

vars N N’ : Net . var T : Tran . var Ty : NeTypeS . var Sy :

Syncmap .

var Q : Imatrix . var S : String . vars J K : NzNat .

vars B B’ : Bag{Place} . var B2 : Bag{Bag{Place}} .

rl [select] : I U NeFS => I .

***

non−deterministic

extraction of an instance

crl [inst] : N Ty Sy M => N Ty Sy (M − I) + O if N’ ; T |−>

Q := N /\ firingmap(N Ty Sy M)[T] => I /\

firings(T |−> Q, I, Sy) => O .

crl [aut] : SN (p(J,S) |−> K . B + B2) => SN (p(J,S) |−> (

K . B − 1 . B) + 1 . B’ + B2) if N (S |−> (T |−> Q ; N’)

; Ty) Sy := SN /\ not(synchronized(Sy, T)) /\

(T |−> Q) B => (T |−> Q) B’ .

endm

Rules inst and aut encode the ﬁring of a system-

net transition and of an autonomous nested transition,

respectively; inst relies on the auxiliary rule select

which emulates the non-deterministic selection of an

instance (from a set). We exploit the opportunity

that conditional rewrite rules can have very general

conditions involving matching equations, member-

ships and also other rewrites. Rule inst implements

double non-determinism: ﬁrst for selecting an (en-

abled) instance of t, then for choosing one of the

possible output markings generated by that instance.

The rule uses the operators _+_, _-_ deﬁned on

Map{Place,Bag{Bag{Place}}} terms. In the event

of synchronization, the operator firings embeds the

changes to net tokens markings. Rule aut exploits the

synchronized predicate and the PT ﬁring rule.

Example. As a concrete example of Maude for-

malization of EOS, we include the system module

SIMPLE-EOS which speciﬁes the EOS in Figure 1,

where we assume that only the system-net places

}, i : 1...3, are marked.

mod SIMPLE−EOS is

inc EOS−EMU .

ops net type1 type2 : −> Net .

op netype : −> NeTypeS .

op m0 : −> Map{Place,Bag{Bag{Place}}} .

op eosnet : −> Sysnet .

op sync : −> Syncmap .

eq net = t(1,”sys”) |−> [1 . p(1,”net1”) + 1 . p(2,”

net1”) + 1 . p(3,”net2”), 1 . p(4,”net1”) + 1 . p

(5,”net2”) + 1 . p(6,”net2”), nil] .

eq type1 = t(1, ””) |−> [1 . p(1,”a1”), 1 . p(2,”b1”),

nil] .

eq type2 = t(2,””) |−> [1 . p(1,”a2”) + 1 . p(2,”b2”),

1 . p(3,”c2”), nil] .

eq netype = ”net1” |−> type1 ; ”net2” |−> type2 .

eq sync = t(1,”sys”) |−> (”net1” |−> 1 . t(1,””) ; ”

net2” |−> 1 . t(2,””) ) .

eq eosnet = net netype sync .

eq m0 = p(1,”net1”) |−> 1 . nil + 1 . (1 . p(1,”a1”) +

1 . p(2,”b1”)); p(2,”net1”) |−> 1 . 1 . p(1,”a1”) ;

p(3,”net2”) |−> 1 . (1 . p(1,”a2”) + 1 . p(2,”b2”)) .

endm

We refer to the EOS with the term eosnet m0 us-

ing simple aliasing. By running the inline reduce

command of the Maude interpreter

Maude> red firinginstances(eosnet m0, t(1, ”sys”))

we get two enabled instances for the system-net tran-

sition t(1,"sys"), in accordance with the two net-

tokens of type "net1" in place p(1,"net1") (Fig-

ure 1).

The following command searches for reachable ﬁ-

nal (!) states.

Maude> search eosnet m0 =>! X:Eosystem .

The command has four matches which express the

non-determinism of EOS transition ﬁring: For each

instance of t(1,"sys") there are indeed two possi-

ble output-markings, as the ways to distribute the net-

token of type "net2" on places p

, p

4 THE PRODUCTION LINE

We consider a FMS with two production lines as an

example. This scenario has been used as a case study

for Rewritable PT Nets in (Capra, 2021). Here, we

will model the scenario in terms of nets-within-nets.

In the scenario we have raw material and two op-

erations, t1 and t2, working on pieces of those. We

have two production lines (i.e. robots), both being ca-

pable of performing t1 and t2. We assume that the

two lines have different qualities for these operations,

i.e., it is better to execute t1 in line 1 and t2 in line

2. This is the standard production plan. It is possi-

ble that during the execution one of the two lines gets

faulty. A double failure has a negligible probability

and is not modelled here.

The scenario is well suited for a EOS-model as we

have two obvious levels in our model: the production

site and the production plans. The model is speci-

ﬁed in the syntax of the RENEW tool (Kummer et al.,

2004).

The system level shown in Figure 2 describes the

two production lines, the execution life cycle of the

production plan, and the dropout of lines.

In the system net, the place p0 indicates normal

operation. In this mode the transition t0 takes two

tokens (i.e. the raw material) from place p1 and ac-

tivates the normal production plan, i.e. it generates a

net-token of type plan via the inscription x:new plan.

The two production lines are shown as blocks. Their

transitions are side-conditions for the place produc-

tion plan. They synchronise via the channel inscrip-

tions of the form x:line1 t1().

These channels have a counterpart in the net-

tokens (e.g. the net plan – shown in Figure 3 – has

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

492

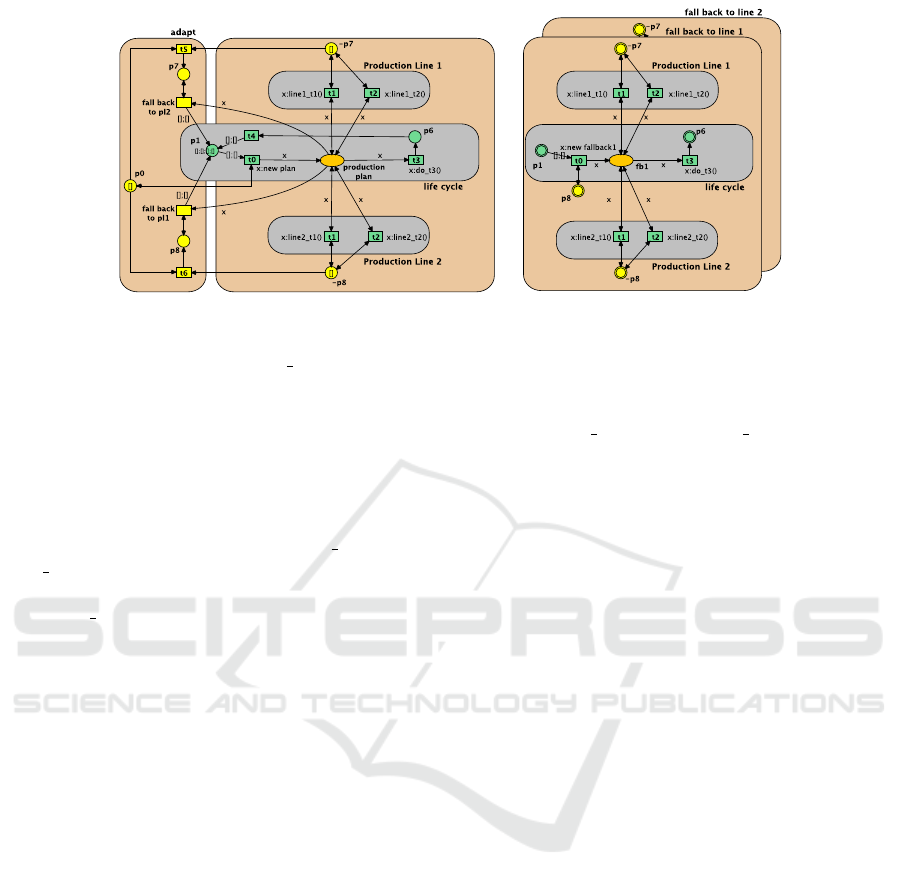
Figure 2: The System Net modelling the Production Lines.

the corresponding inscription line1 t1()). Therefore,

we have a synchronous ﬁring of the transition in the

production line and in the production plan.

Net-tokens describe the different production

plans: That for normal operation is given as the net

plan shown in Figure 3, while we also have two fall

back plans fallback 1 and 2 for the case of dropouts.

Speciﬁcally, the given production plan from Fig-

ure 3 speciﬁes a synchronisation via line1 t1() and via

line2 t2(), so we will execute t1 in line 1 and t2 in line

2. When the production plan is ﬁnished we synchro-

nise via do t3() and delete the net token, i.e. the plan.

For simplicity, the scenario restarts this production

via the transition t4 which regenerates two raw ma-

terials again on place p1. This reset makes the main

loop of the model live.

Now, we will look at the adaption part and how

the model preserves liveness even in the event of

dropouts. On the left part of Figure 2 (the yellow

nodes), we have the adaption part: Transitions t5 and

t6 model the dropout of one production line. When-

ever we have a drop the standard production plan is

not executable anymore. Therefore, the transitions

fall back to production line 1/2 withdraws them. Af-

ter a dropout, the places p7 and p8 indicate which of

the two lines is down. According to this information,

we will select the appropriate fallback plan, i.e. in the

case of a dropout in line one (p7 is marked) we switch

to the fallback plan 2 and vice versa. The two fallback

blocks have almost the same structure as the original

block. The only difference is that we generate a dif-

ferent net-token via x:new fallback1 in the case of the

side condition p8 and via x:new fallback2 in the case

of the side condition p7. To avoid lots of crossing arcs

we use the RENEW feature of so-called virtual places,

i.e., places with a double outer line. They denote a

reference to the original place.

The two fallback plans fallback 1 and 2 are not

shown here as they look almost identical to the ba-

sic plan in Figure 2. The only difference are the used

channels: The plan fallback 1 works only with the

production line 1, which is expressed by using the

channels line1 t1() and via line1 t2(). Analogously

for fallback 2.

The modular Maude speciﬁcation of the adaptable

Production Line may be found in github.com/lgcapra/

rewpt/tree/main/new/EOS. We got it by composing

atomic sub-nets through the associative/commutative

net-juxtaposition operator (’;’).

4.1 Model’s Analysis

Below we give some evidence of formal veriﬁcation

with the only intent of showing the potential of an ap-

proach based on Maude. Since we specify adaptation

in a way to preserve the liveness of the production

process, we focus on this kind of property. We use

the two basic analysis tools, namely the reduce com-

mand, which prints out the canonical form of a ground

term, and the search state-space explorer (both avail-

able inline).

As usual, we manage wordy terms using intu-

itive aliasing. For example, the net term describes

the system-net component of the EOS, whereas the

eosnet term includes the net-token description and

synchronizations. Terms m0 and eosm0 denote the ini-

tial marking of the net (seen as a PT system) and of

the EOS.

We can use the reduce command both to unfold

these aliases and to perform a preliminary formal val-

idation: If it assigns the canonical form a speciﬁc sort

(i.e., Eosystem), it means that the initial term repre-

sents a well-deﬁned EOS speciﬁcation:

re d uce in PLIN E - EOS : eo snet eo s m0 .

re s ult E osyst e m : (.. . un f olded te rm )

The next two searches operate on the PT-system

we obtain from the system-net by replacing net-

tokens with anonymous tokens. One of the advan-

Modelling Adaptive Systems with Nets-Within-Nets in Maude

493

Figure 3: The Object Net plan modelling the standard Production Plan.

tages of EOS, indeed, is that we can separately con-

sider and analyse the two EOS levels.

The ﬁrst one veriﬁes a state invariant which char-

acterizes the production plan’s life-cycle, in a con-

ﬁguration where place p

initially holds four tokens.

The search has indeed no matches (solutions), con-

sistently with the fact that we search for a counter-

example. It is worth noticing two things. An im-

plicit outcome of the command is that the PT system

derived from the system net is bounded because the

state space turns out to be ﬁnite. The invariant is ac-

tually structural, i.e., it holds for any conﬁguration

with 2 ∗ K tokens initially in place p

(K being the

model’s parameter). We cannot prove parametric in-

variants using state-space exploration.

The second search, instead, checks the absence

of ﬁnal (dead) states. Again, there are no matches.

Maud e > s e arc h in pline - SYS : net m0 = >*

X: Sys t em such t hat ma r k i ng ( X :

Sy s tem ) [p (1 ," ") ] + 2 * ma rkin g ( X:

Sy s tem ) [p (2 ," p lan ") ] + 2 * ma r king (

X: Sys t em ) [ p (2 ," fb 1 ") ] + 2 * m arki n g

(X : Syst e m ) [ p (2 ," fb2 ") ] + 2 *

ma r k ing ( X : S yst e m ) [ p (6 ,"" ) ] =/= 4 .

Maud e > s e arc h in pline - SYS : net m0 = >!

X: Sys t em .

Analogously, we can start searching from an

Eosystem term specifying the whole EOS. The fol-

lowing (unmatched) search is much more signiﬁ-

cant than the previous ones because it formally ver-

iﬁes that the whole EOS (including the nested nets)

is deadlock-free (and implicitly, bounded). Both the

state space and the execution time grow up.

Maud e > s e arc h in pline - EOS : e osn e t

eo sm0 =>! E : Eo s yste m .

Table 1 reports the performances of the last

search, as the system’s parameter varies. The data

refer to an Intel Core i7-6700 equipped with 32 GB

of RAM.

Model-checking techniques suffer from the pos-

sible state-space explosion, which may be only al-

leviated using some heuristics, e.g., by carrying out

bounded searches (the search command has a num-

ber of options) or making some abstractions (as we

Table 1: Performance of search command.

K # states # rewrites time (ms)

2 262 19801 38

5 2802 180539 453

10 13932 995724 3192

20 104007 19737494 56090

50 4186132 111564504 906253

did in the ﬁrst two searches). The canonization tech-

nique for rewritable PT systems recently presented in

(Capra, 2022a) might represent an effective approach

to scale the model’s complexity. Using this technique

(which requires a slight adaption to work with EOS)

the state sizes reported in Table 1 would approxi-

mately halve, due to the PL symmetry. Overall, it

would be possible to model-check more realistic con-

ﬁgurations with many PL working in parallel and syn-

chronizing at some point, which would be otherwise

intractable. Another drawback of model-checking is

that, in general, we cannot infer parametric outcomes

(not depending on the initial state).

PT structural analysis, which considers the PT

graph structure, is an effective alternative (comple-

mentary) to state-space inspection. We may use it

to infer parametric outcomes, e.g., structural state-

invariants (semiﬂows). Structural analysis of EOS

looks promising because it may take advantage of the

fact that the types of net tokens ﬂowing through the

system net places are ﬁnite.

5 SUMMARY AND OUTLOOK

In this paper we have deﬁned a Maude representation

of nets-within-nets, more concretely: EOS.

What are the Strengths of the Approach? The

Maude formalization presented here is an extension of

(rewritable) PT speciﬁcation (Capra, 2021). There-

fore a lot of code could be reused, which is beneﬁcial

for the implementation’s reliability and efﬁciency as

well.

The formalisation preserves central design issues

of EOS by supporting a uniform view: The system-

net and net-tokens have the same structure in Maude,

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

494

which is essential as the same is true for EOS. This

aspect is relevant when the architecture is extended

from the two-level case to an unbounded nesting of

net-tokens in a marking (K

ohler-Bußmeier and Heit-

mann, 2009) or HORNETS (K

ohler-Bußmeier, 2009).

Standard Maude facilities for formal veriﬁcation (e.g.,

state-space search and model-checking) may be used

with no additional costs.

Additionally, the EOS ﬁring rule is deﬁned in a

way that moving net-tokens around cannot be distin-

guished from moving ordinary tokens in PT. There-

fore, we can easily deﬁne abstractions on the system’s

state (e.g. forgetting about the marking of net-tokens),

which is essential to perform state space exploration

efﬁciently.

Our approach fosters model extensions. Passing

to Object-nets should be almost for free (using gen-

eral Bags, with an arbitrary nesting). While the ex-

tension from EOS to HORNETS is a rather large step,

which involves new constructs like net-algebra oper-

ators, the formalizing of HORNETS in Maude seems

very simple. We may easily go one step forward, to-

wards “rewritable” EOS, where the structure of both

the system net and of net-tokens may change over

time.

Advantages of the Proposed Approach.

• The approach builds on an existing Maude for-

malization of (rewritable) PT nets: massive code-

reuse, implementation reliability, efﬁciency, uni-

form view (system-nets and net-tokens have the

same structure), easy abstractions (the system-net

may be mimed as an ordinary net)

• The built-in Maude facilities for formal veriﬁca-

tion (e.g., state-space search and model-checking)

may be exploited.

• The approach promotes updates and extensions.

A natural extension is the use of PT nets (with

inhibitor arcs both) at system-net level and at net-

token level. Passing to Object-nets should be al-

most for free (using general Bags, with an arbi-

trary nesting level, would be required). Formaliz-

ing Hornets should be simple as well, even if the

system-net deﬁnition would be closer to an alge-

braic PN.

• We may easily go one step forward, towards

”rewritable” EOS where both the structure of the

system net and that of net-tokens may change over

time.

What Was Complex? The most challenging aspect

of the formalisation was the integration of the so-

called ﬁring modes. Roughly speaking, the ﬁring rule

of a system-autonomous event in an EOS collects the

tokens of all net-tokens coming from the system net

places in the preset. When the system net transition

ﬁres it distributes all these tokens on freshly generated

net-tokens in the postset. The ﬁring rule allows any

of these possible distributions – an aspect which re-

quires some tricky handling of the binding in Maude.

In summary:

• Formalizing the EOS ﬁring mechanism shows

some trickiness.

• The use of nested generic types in Maude requires

some expertise.

Limitations. The current formalisation fulﬁls the

requirement that it provides a link to the world of pro-

gramming. But we have to admit that like in any al-

gebraic speciﬁcation, terms describing EOS may be

wordy, structurally complex and (consequently) difﬁ-

cult to read and manage. A systematic aliasing mech-

anism might greatly help a modeller. Also, syntac-

tic sugar would sweeten the approach. An automated

translation from a high-level (graphical) description

of EOS to the corresponding Maude module would be

highly desirable.

Ongoing Work. In this paper, we were concerned

with the Maude encoding of EOS. Our main motiva-

tion for this is to obtain a representation closer to the

usual programming language world. Our intention is

also to beneﬁt from the advantages of a formal speciﬁ-

cation, i.e. the possibility to apply analysis techniques

more easily. In the case of Maude the ﬁrst idea is to

apply state-space techniques, like LTL model check-

ing. We also like to integrate structural PN techniques

for EOS (K

ohler-Bußmeier and Moldt, 2009).

For the analysis of EOS, we need to struggle with

scalability as the state space of EOS grows even worse

than that of PT nets. Possible approaches are the can-

onization of net-tokens and the use of abstractions to

obtain condensed state spaces. Canonization of net-

tokens allows us to capture symmetries in their be-

haviour. For that purpose, we have slightly adapted

the canonization technique for rewritable PT systems

deﬁned in (Capra, 2022a), fully integrated into Maude.

According to this technique, a PT system is seen as a

coloured graph and put into a “minimal” isomorphic

form by incrementally permuting node indices. The

latter approach (state abstraction) can be expressed

quite easily in Maude by adding additional equations

on markings.

Modelling Adaptive Systems with Nets-Within-Nets in Maude

495

REFERENCES

Bouhoula, A., Jouannaud, J.-P., and Meseguer, J. (2000).

Speciﬁcation and proof in membership equational

logic. Theoretical Computer Science, 236(1):35–132.

Bruni, R., Corradini, A., Gadducci, F., Lluch Lafuente,

A., and Vandin, A. (2012). Modelling and analyz-

ing adaptive self-assembly strategies with maude. In

Dur

an, F., editor, Rewriting Logic and Its Applica-

tions, pages 118–138, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Bruni, R. and Meseguer, J. (2003). Generalized rewrite the-

ories. In Baeten, J. C. M., Lenstra, J. K., Parrow, J.,

and Woeginger, G. J., editors, Automata, Languages

and Programming, pages 252–266, Berlin. Springer-

Verlag.

Capra, L. (2021). A maude implementation of rewritable

petri nets: a feasible model for dynamically reconﬁg-

urable systems. In Gleirscher, M., Pol, J. v. d., and

Woodcock, J., editors, Proceedings First Workshop on

Applicable Formal Methods, virtual, 23rd November

2021, volume 349 of Electronic Proceedings in The-

oretical Computer Science, pages 31–49. Open Pub-

lishing Association.

Capra, L. (2022a). Canonization of reconﬁgurable pt nets

in maude. In Lin, A. W., Zetzsche, G., and Potapov,

I., editors, Reachability Problems, pages 160–177,

Cham. Springer International Publishing.

Capra, L. (2022b). Rewriting logic and petri nets: A natu-

ral model for reconﬁgurable distributed systems. In

Bapi, R., Kulkarni, S., Mohalik, S., and Peri, S.,

editors, Distributed Computing and Intelligent Tech-

nology, pages 140–156, Cham. Springer International

Pub.

Clavel, M., Duran, F., Eker, S., Lincoln, P., Oliet, N. M.,

Meseguer, J., and Talcott, C. (2007). All About Maude

- A High-Performance Logical Framework: How to

Specify, Program, and Verify Systems in Rewriting

Logic. Lecture Notes in Computer Science. Springer.

Hachicha, M., Halima, R. B., and Kacem, A. H. (2019).

Formal veriﬁcation approaches of self-adaptive sys-

tems: A survey. Procedia Computer Science,

159:1853–1862. Proceedings of KES2019.

Iglesia, D. G. D. L. and Weyns, D. (2015). Mape-k for-

mal templates to rigorously design behaviors for self-

adaptive systems. ACM Trans. Auton. Adapt. Syst.,

10(3).

ohler-Bußmeier, M. (2009). Hornets: Nets within nets

combined with net algebra. In Wolf, K. and Frances-

chinis, G., editors, International Conference on Appli-

cation and Theory of Petri Nets (ICATPN’2009), vol-

ume 5606 of LNCS, pages 243–262. Springer-Verlag.

ohler-Bußmeier, M. (2014). A survey on decidability re-

sults for elementary object systems. Fundamenta In-

formaticae, 130(1):99–123.

ohler-Bußmeier, M. and Heitmann, F. (2009). On the

expressiveness of communication channels for object

nets. Fundamenta Informaticae, 93(1-3):205–219.

ohler-Bußmeier, M. and Heitmann, F. (2011). Live-

ness of safe object nets. Fundamenta Informaticae,

112(1):73–87.

ohler-Bußmeier, M. and Heitmann, F. (2013). Complexity

results for elementary Hornets. In Colom, J.-M. and

Desel, J., editors, PETRI NETS 2013, volume 7927 of

LNCS, pages 150–169. Springer-Verlag.

ohler-Bußmeier, M. and Heitmann, F. (2016). An upper

bound for the reachability problem of safe, elementary

hornets. Fundamenta Informaticae, 143:89–100.

ohler-Bußmeier, M. and Moldt, D. (2009). Analysis of

mobile agents using invariants of object nets. Elec-

tronic Communications of the EASST: Special Issue

on Formal Modeling of Adaptive and Mobile Pro-

cesses, 12.

ohler-Bußmeier, M. and R

olke, H. (2004). Properties of

Object Petri Nets. In Cortadella, J. and Reisig, W.,

editors, International Conference on Application and

Theory of Petri Nets 2004, volume 3099 of LNCS,

pages 278–297. Springer-Verlag.

Kummer, O., Wienberg, F., Duvigneau, M., Schumacher, J.,

ohler, M., Moldt, D., R

olke, H., and Valk, R. (2004).

An extensible editor and simulation engine for Petri

nets: Renew. In Cortadella, J. and Reisig, W., editors,

International Conference on Application and Theory

of Petri Nets 2004, volume 3099 of LNCS, pages 484

– 493. Springer-Verlag.

Padberg, J. and Schulz, A. (2016). Model checking recon-

ﬁgurable petri nets with maude. In Echahed, R. and

Minas, M., editors, Graph Transformation, pages 54–

70, Cham. Springer International Publishing.

Stehr, M.-O., Meseguer, J., and

Olveczky, P. C. (2001).

Rewriting Logic as a Unifying Framework for Petri

Nets, pages 250–303. Springer-Verlag.

Valk, R. (2003). Object Petri nets: Using the nets-within-

nets paradigm. In Desel, J., Reisig, W., and Rozen-

berg, G., editors, Advanced Course on Petri Nets

2003, volume 3098 of LNCS, pages 819–848. Sprin-

ger-Verlag.

Weyns, D., Iftikhar, M. U., de la Iglesia, D. G., and Ahmad,

T. (2012). A survey of formal methods in self-adaptive

systems. In Proceedings of the Fifth International C*

Conference on Computer Science and Software En-

gineering, C3S2E ’12, page 67–79, New York, NY,

USA. Association for Computing Machinery.

Weyns, D. and Iftikhar, U. M. (2022). Activforms:

A formally-founded model-based approach to engi-

neer self-adaptive systems. ACM Trans. Softw. Eng.

Methodol.

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

496