HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and

Localization Based on HaloNet

Emilie Mathian

1,4 a

, Huidong Liu

2 b

, Lynnette Fernandez-Cuesta

1 c

, Dimitris Samaras

3 d

Matthieu Foll

1 e

and Liming Chen

4 f

International Agency for Research on Cancer (IARC-WHO), Lyon, France

Amazon, WA, U.S.A.

Stony Brook University, New York, U.S.A.

Ecole Centrale de Lyon, Ecully, France

Keywords:

Anomaly Detection, HaloNet, Transformer, Auto-Encoder.

Abstract:

Unsupervised anomaly detection and localization is a crucial task in many applications, e.g., defect detection

in industry, cancer localization in medicine, and requires both local and global information as enabled by the

self-attention in Transformer. However, brute force adaptation of Transformer, e.g., ViT, suffers from two

issues: 1) the high computation complexity, making it hard to deal with high-resolution images; and 2) patch-

based tokens, which are inappropriate for pixel-level dense prediction tasks, e.g., anomaly localization,and

ignores intra-patch interactions. We present HaloAE, the ﬁrst auto-encoder based on a local 2D version of

Transformer with HaloNet allowing intra-patch correlation computation with a receptive ﬁeld covering 25%

of the input image. HaloAE combines convolution and local 2D block-wise self-attention layers and performs

anomaly detection and segmentation through a single model. Moreover, because the loss function is generally

a weighted sum of several losses, we also introduce a novel dynamic weighting scheme to better optimize the

learning of the model. The competitive results on the MVTec dataset suggest that vision models incorporating

Transformer could beneﬁt from a local computation of the self-attention operation, and its very low computa-

tional cost and pave the way for applications on very large images

The code is available at: https://github.com/IARCbioinfo/HaloAE.

1 INTRODUCTION

Anomaly detection (AD) aims to determine whether a

given image contains an abnormal pattern, given a set

of normal or abnormal images, while its localization

or segmentation need further to determine the subre-

gions containing the anomalies (see Figure 1). Listing

all anomalies is a difﬁcult task because of their low

probability density. Therefore, the problem is usu-

ally addressed via unsupervised learning approaches.

The models use only the defect-free samples during

the learning phase and attempt to identify and local-

https://orcid.org/0000-0001-7175-4318

https://orcid.org/0000-0003-3833-9475

https://orcid.org/0000-0002-0724-6703

https://orcid.org/0000–0002-1373-0294

https://orcid.org/0000-0001-9006-8436

https://orcid.org/0000-0002-7782-9824

ize anomalies at the time of inference.

State of the art has featured two main ap-

proaches on AD: distribution or reconstruction-based.

Distribution-based approaches generally make use of

Deep Convolutional Neural Networks (Deep CNN)

to extract representations of normal images and learn

a parametric distribution of these features (Defard

et al., 2021), (Cohen and Hoshen, 2020a), (Gudovskiy

et al., 2022), (Rudolph et al., 2021), (Roth et al.,

2022). They typically require to learn two models,

one for anomaly detection and another for anomaly

segmentation. Reconstruction-based approaches in-

volve training a convolutional auto-encoder (CAE)

(Bergmann et al., 2019), (Bergmann et al., 2018), (Za-

vrtanik et al., 2021), to reconstruct the normal im-

ages and assume that the model should fail to recon-

struct abnormal images. The advantage of such ap-

proaches is that a single model can be used for both

anomaly detection and segmentation. However, most

Mathian, E., Liu, H., Fernandez-Cuesta, L., Samaras, D., Foll, M. and Chen, L.

HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and Localization Based on HaloNet.

DOI: 10.5220/0011865900003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 5: VISAPP, pages

325-337

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

325

Figure 1: Anomaly localization results from the MVTec AD

dataset. The ﬁrst and third rows show the input images, the

second and fourth rows show the anomaly maps generated

by HaloAE, the ground truth localization is circled with a

pink line.

of them (Bergmann et al., 2019), (Bergmann et al.,

2018), (Akcay et al., 2018) do not perform well as

they generalize strongly and can reconstruct anoma-

lies.

Because spotting anomalous patterns in images

usually requires the combination of local and global

information, promising models have been proposed

either using a full CNN (Zhang et al., 2020), or incor-

porating Transformer’s self-attention (Vaswani et al.,

2017). While CNNs easily capture local translation-

invariant patterns at multiple scales, they are not able

to model long-range content interactions as enabled

by the Transformer through its self-attention. How-

ever, straightforward adaptation of Transformer, e.g.

ViT (Dosovitskiy et al., 2020), for anomaly detec-

tion with an AE (Mishra et al., 2021), (Pirnay and

Chai, 2021), (Yang, 2021), suffers from three issues

of the original design: 1) computational complex-

ity which grows quadratically in image size, prevent-

ing its use for large scale images; 2) tokenization of

image patches which ignores intra-patch correlations

and makes it inappropriate for pixel-wise dense pre-

diction vision tasks as anormaly localization; and 3)

the ViT’s columnar architecture does not enable inter-

actions of multiple scale features.

To overcome the aforementioned deﬁciencies, we

propose in this paper a hybrid AE for anomaly

detection and localization, namely HaloAE, which

combines convolutional layers and a block-based

transformer with local self-attention (i.e., HaloNet

(Vaswani et al., 2021)) to achieve the best of both

worlds (Guo et al., 2022), (Pan et al., 2022). Speciﬁ-

cally, our HaloAE starts by a CNN-based feature ex-

tractor, and integrates a HaloNet as encoder and a

speciﬁcally designed transposed version of HaloNet

as decoder. The CNN-based feature extractor gives

HaloAE access to multi-scale features of an input im-

age as in (Shi et al., 2021), (Yang, 2021), (Mishra

et al., 2021). Thanks to the integrated HaloNet

with its local block-based self attention, HaloAE fur-

ther enables intra-patch correlations and multi-scale

feature interactions. Moreover, the local nature of

the block-based self attention drastically decreases

both memory and computation complexity, making

it possible to achieve a large receptive ﬁeld for self-

attention that covers 25% of the input images. How-

ever, while HaloAE is able to learn to reconstruct

multi-scale feature maps generated by a pre-trained

CNN, it also can strongly generalize and recover

anomaly regions (Mishra et al., 2021). To mitigate the

generalization problem of the proposed HaloAE, we

further incorporate a self-supervised learning (SSL),

and make use of the Cut&Paste framework (Li et al.,

2021), which deﬁnes a proxy classiﬁcation task be-

tween normal and artiﬁcially damaged images. The

combination of classiﬁcation and reconstruction tasks

derives a multi-objective problem (Groenendijk et al.,

2021). As a result, we further propose a novel evolv-

ing weighting scheme that optimizes the learning of

the model in mimicking the human learning strategy

while increasing the importance of complex tasks dur-

ing learning. Finally, unlike most existing methods,

our model does not use image patches for anomaly lo-

calization, which allows for high inference speed, and

thus its use on large histopathological images (70k x

70k pixels resolution) while maintaining pixel-level

localization. The performance of HaloAE was eval-

uated on the challenging MvTec dataset (Bergmann

et al., 2019), an industrial dataset with 15 objects (see

Figure 1).

Our contributions are as follows: we have devel-

oped a new hybrid AE model called HaloAE, which

combines a CNN-based multi-scale feature extractor

with local block-based self-attention to provide a sin-

gle model for both anomaly detection and localiza-

tion. We have introduced a new evolving weighting

scheme (EWS) to optimize the learning process for

dealing with our multi-task loss function. We have

shown that the proposed HaloAE achieves competi-

tive results on the MVTec benchmark, and that local

block-based self-attention outperforms a fully convo-

lutional model. Finally, we have demonstrated the

computational efﬁciency of HaloAE, and shown that

it can be applied to very large histological images.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

326

2 RELATED WORK

2.1 Anomaly Detection and

Localization Models

2.1.1 Reconstruction Based Methods

They are the most commonly used methods for AD

and localization (Bergmann et al., 2019), (Bergmann

et al., 2018), (Zavrtanik et al., 2021). They are usually

based on CAE, trained to reconstruct defect-free im-

ages. At the inference time, the trained models are ex-

pected to fail to reconstruct abnormal regions, as they

differ from the observed training data. Segmentation

maps of abnormal regions are obtained by per-pixel

comparison between input and output images based

on L

deviations (Bergmann et al., 2019), (Zavrtanik

et al., 2021), or SSIM values (Bergmann et al., 2019).

While simple and elegant in design, CAEs suffer from

memory and generalize abnormal regions quite well

(Zavrtanik et al., 2021), (Baur et al., 2018). In order

to regularize the generalization capacity of the AE,

DFR (Shi et al., 2021) shows that the integration of

local and global information is a key point to improve

existing AD methods. They train an AE to recon-

struct multi-scale feature maps, which are themselves

generated by concatenating different layers of a pre-

trained CNN. Our proposed method follows this line

of architecture design.

2.1.2 Distribution Based Methods

An important trend is to use large networks on exter-

nal training datasets such as ImageNet (Deng et al.,

2009) to model the distribution of normal features.

These methods assume that the normal data ﬁts into a

predeﬁned kernel space (Cohen and Hoshen, 2020a),

(Defard et al., 2021), (Cohen and Hoshen, 2020b),

(Roth et al., 2022), (Bergmann et al., 2020). They

then have to deﬁne the distances between the normal

data and the abnormal data, which are assumed to be

located outside this space. While some models use

clustering techniques (Cohen and Hoshen, 2020b),

(Roth et al., 2022), (Bergmann et al., 2019) to de-

tect samples outside the normal distribution of the

data, others model this distribution by Gaussian mod-

els (Defard et al., 2021), (Gudovskiy et al., 2022),

(Bergmann et al., 2020). These models working on

image patches are more powerful than the methods

based on reconstruction, (Defard et al., 2021), (Cohen

and Hoshen, 2020a), (Cohen and Hoshen, 2020b),

(Roth et al., 2022), (Bergmann et al., 2020), but this

leads to a great complexity at the time of the infer-

ence.

2.1.3 Self-Supervised Learning Based Methods

It is now widely accepted that data augmentation

strategies help to regularize CNN. To this end, various

inpainting reconstruction methods have been devel-

oped in the context of AD , (Pirnay and Chai, 2021),

(Zavrtanik et al., 2021). However at the inference

time these methods suffer from high complexity since

an anomaly map is generated via a set of in-painted

versions of an input image. Many SSL-based meth-

ods have shown that the data augmentation strategy

plays a critical role in deﬁning an effective predic-

tive task. Based on this claim, Cut&Paste (Li et al.,

2021) created a data augmentation strategy in which

a patch in an image is copied to another location after

being randomly modiﬁed. This data-driven strategy

outperforms the state of the art in terms of image-level

classiﬁcation. Nevertheless, this method must use im-

age patches to accurately locate anomalies, which re-

sults in high complexity at the time of inference. Our

HaloAE also leverages this data augmentation strat-

egy to regularize the proposed HaloNet-based AE.

2.2 Visual Transformer

Visual Transformer (ViT) is the ﬁrst adaptation of

Transformer to images (Dosovitskiy et al., 2020).

This simple implementation requires a very large

dataset for training, and is very computationally ex-

pensive. In addition, ViT and its adaptations (Touvron

et al., 2021), (Chen et al., 2021) have two other major

limitations for their application to pixel-level tasks:

correlations within patches are not calculated, and the

output feature maps are single scale and low resolu-

tion, due to their columnar architecture (Liu et al.,

2021), (Wang et al., 2021).

To mitigate these drawbacks, two multi-scale ver-

sions of Transformer have recently been proposed.

Pyramidal Vision Transformer (PVT) implemented a

multi-scale transformer, using a strategy of progres-

sive shrinkage to compute attention over increasingly

larger windows, in a way similar to CNNs (Wang

et al., 2021). Swin Transformer (Liu et al., 2021) not

only offers multi-scale patches but also the calculation

of correlations between non-overlapping neighboring

windows, using a strategy of shifted windows.

Another possibility to adapt Transformer to local

tasks is to calculate the self-attention operation locally

within patches (Ramachandran et al., 2019), (Vaswani

et al., 2021). Exactly at the same time as PVT and

Swin, Vaswani et al. proposed HaloNet, where a

block-based local self-attention enable to achieve the

best speed/accuracy trade-off for image classiﬁcation

tasks for both CNN and Transformer based architec-

HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and Localization Based on HaloNet

327

tures (Vaswani et al., 2021). Assuming that neighbor-

ing pixels share most of their neighborhood, HaloNet

extracts a local neighborhood for a block of pixels in

a single run. This block-based strategy allows par-

allelizing the self-attention operation (Vaswani et al.,

2021). Halonet efﬁciency makes the model more

practical and hinting at its adaptation to larger widths,

e.g., very large scale medical images. Finally, un-

like Swin and PVT, Halonet computes self-attention

on 2D matrices, which facilitates its adaptation as a

hybrid model, in order to connect the boundaries of

self-attention blocks with convolutional operations.

The current methods that use the beneﬁts of self-

attention for unsupervised AD have all incorporated

ViT into their models (Zhang et al., 2020), (Mishra

et al., 2021), (Yang, 2021), (Pirnay and Chai, 2021).

Thus, SAAE (Yang, 2021) and Intra (Pirnay and

Chai, 2021) proposed an AE based entirely on ViTs.

SAAE showed no signiﬁcant improvement over an

all-convolutional layer-based architecture (Bergmann

et al., 2020). Intra added an inpainting scheme to the

SAAE architecture, which can be used to hide abnor-

mal regions to further restrict the model’s ability to

reconstruct them (Pirnay and Chai, 2021). However,

this technique is very complex at inference time, as a

set of painted versions of the input is required to lo-

cate the anomaly. In addition, all these models suffer

from inherent limitations in ViT: (1) For example, AD

resolution depends upon the patch size; 2) intra-patch

correlations are not considered, i.e., local informa-

tion; and 3) the feature map from ViT is single-scale,

which is not suitable for the localization task. In this

work, we propose to exploit a block-based local at-

tention, i.e., HaloNet, to deﬁne our AE and achieve a

single model for anomaly detection and segmentation

(Vaswani et al., 2021).

2.3 Multi-Task Learning

Multi-task learning is a paradigm in which different

tasks are learned jointly. This assumes that these tasks

are somehow related to each other and thus that the

parameters used to learn one task can help learn the

others. Usually, the ﬁnal objective function is writ-

ten as a linear combination of the ones of different

tasks, and it is well-known that the weighting can

strongly affect the results (Groenendijk et al., 2021),

(Dosovitskiy and Djolonga, 2019). In general, the

weights are adjusted using an extensive grid search

and stay static during training (Groenendijk et al.,

2021). By mimicking the human learning process,

Li et al. proposed a mechanism to order the tasks

from the easiest one to the hardest one (Li et al.,

2017). They showed that their regularization on tasks

and instances reduces classiﬁcation errors compared

to static weighting methods. Similarly, Galama et

al. showed that gradually increasing the complex-

ity of the input data during learning improves the re-

sults (Galama and Mensink, 2019). Inspired by these

works, we propose a new evolving weighting scheme

(EWS) that gradually increases the importance of the

most difﬁcult tasks while equally weighting the in-

stances, which is an important consideration in unsu-

pervised AD.

3 METHOD

Figure 2 depicts the overall architecture of the pro-

posed HaloAE for AD. It includes 5 blocks: A) data

augmentation for self-supervised learning; B) VGG-

based multi-sacle feature extractor; C) HaloNet-based

autoencoder; D) CNN-based image reconstructor;

and E) the classiﬁer layer. They are explained in the

subsequent subsections.

3.1 Self-Supervised Learning Block

To mimic industrial anomalies on the MVTec dataset

(Bergmann et al., 2019) we make use of the strategy

set up by Cut&Paste. This involves cutting out a piece

of varying shape, size and aspect ratio from an input

image and pasting it back in at a random location, af-

ter undergoing random transformations such as rota-

tions or color variations (Figure 2 - block A). This

framework allows to deﬁne a proxy classiﬁcation task

between normal and artiﬁcially damaged images. Let

IM be the set of training images of size N such that

IM = {im

,...,im

}, where each im

is in R

w×h×c

with w, h and c the input width, height and number

of channels. We deﬁne a classiﬁcation loss function

such as:

cls

∑

i=0

CE(g(

),l = 0)

+ CE(g(CP(

)),l = 1), (1)

where the function CE(.) refers to the binary cross

entropy function, CP(.) to the Cut&Paste data aug-

mentation strategy, and g(.) to the binary classiﬁers,

shown in Figure 2 - block E. This terminal linear layer

takes as input a reconstructed image

associated

with its label l , which is equal to 1 if the image has

been augmented by CP(.) and 0 otherwise.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

328

Original

image

CutPaste

Fixed VGG

Halonet autoencoder:

Feature map reconstruction

Halonet

encoder

Image

reconstruction

Classif.

layer

Linear

layer

B C D E

Halonet

decoder

Multi-scale

feature map

Figure 2: Overview of HaloAE for AD. A) Cut&Paste data augmentation strategy for the SSL module (Li et al., 2021). B)

Multi-scaled feature map extraction via a pretrained VGG19 network (Simonyan and Zisserman, 2014) on ImageNet (Deng

et al., 2009). C) Halonet AE for feature map reconstruction. D) Reconstruction of images via transposed VGG blocks.

E) Linear layer to determine the classiﬁcation loss. Im and

Im, refer to the original image and the reconstructed image

respectively, similarly f m and

f m refer to the feature map and its reconstruction. l and

l refer to the label and its prediction,

0 is associated to the original picture, and 1 to its augmented versions. L

⌋↕∫

, L

Rec

f m

and L

Rec

refer to the classiﬁcation loss

and reconstruction quality of feature maps and images respectively.

3.1.1 Multi-Scale Image Feature Extraction

Following the DFR (Shi et al., 2021) method, we use

a VGG19 (Simonyan and Zisserman, 2014) network

trained on ImageNet (Deng et al., 2009) to extract a

multi-scale feature map of an image. To this end, we

aggregate lower layer feature maps, coding for low-

level patterns, such as texture, and deep layer fea-

ture maps that code for higher-level information, such

as objectness. As reported by PathCore (Roth et al.,

2022), we exclude features from very deep layers to

avoid using overly generic features that are heavily

biased towards ImageNet classiﬁcation. The resulting

multi-scale feature map is denoted f m ∈ R

×h

×c

here w

and h

equal to 64 and c

to 704, (see Figure

2 - block B).

3.2 Reconstruction Based on Halonet

The self-attention operation captures distant relation-

ships between pixels and generates spatially vary-

ing ﬁlters unlike convolutional layers (Ramachandran

et al., 2019), (Vaswani et al., 2021). We make use

of the block-based local self-attention introduced by

HaloNet to create a reconstruction of f m denoted

f m.

f m is divided into a grid of non overlapping blocks

of size

. Every block behaves like a group of

query pixels. The haloing operation combines bands

of hl pixels around each block to obtain the shared

neighborhood from which the keys and values are cal-

culated. In this way, the local self-attention per block

multiplies each pixel in a shared neighborhood,after

they have been transformed by the same linear trans-

formation, by a probability considering both content-

content and content-geometry interactions, resulting

in spatially varying weights ((Vaswani et al., 2021)

eq. 2 and eq. 3). In this work, we set the block size

b to 12 and hl to 2, instead of using the original val-

ues which are 8 and 3 respectively, in order to capture

more contextual information by taking advantage of

the reduced size of the input since h

= h/4.

Halonet proposed architecture (Vaswani et al.,

2021) is modiﬁed while keeping its ResNets-like

structure (He et al., 2016). Speciﬁcally, we have mod-

iﬁed: (a) the head layer, substituting the 7x7 convo-

lution with a stride of 2 by a 5x5 convolutional layer

with a stride of 1, so as not to reduce the spatial di-

mension of the input map again; (b) the number of

blocks per stage is set to 1 instead of 3 or 4 in the

original architecture, in order to create a lighter mem-

ory model with only 18 million of parameters; (c) in

each block the second 1 × 1 convolution is replaced

by a convolution layer with a ﬁlter of size 3 × 3 for

the ﬁrst two stages and 5 × 5 for the last two. This

last modiﬁcation allows both extracting local infor-

mation with the 2D convolution layer and connecting

the edges of the self-attention blocks. All these mod-

iﬁcations are summarized in the supplementary Table

S1.

HaloNet encoder learns a compressed version of

the feature map f m by reducing its channels count.

From these encoded features f m

enc

in R

60×60×58

, f m

is reconstructed by decoder combining both convo-

lutional layers and local block self-attention layers.

The decoder follows a similar architecture as the en-

coder, but all convolutional layers have been replaced

HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and Localization Based on HaloNet

329

by transposed convolutional layers, so as to obtain the

ﬁrst transposed Halonet version (Figure 2 - block C

and supplementary Table S1).

The quality of the reconstructed feature maps is

evaluated by a per-pixel loss L

and by a percep-

tual loss called the structure similarity index SSIM

(Bergmann et al., 2018). Therefore, the loss associ-

ated with feature map reconstruction is given by:

Rec

f m

∑

i=1

∑

j=1

|| f m

i, j

−

f m

i, j

+ (1 − SSIM( f m,

f m))

(i, j)

, (2)

where the SSIM is calculted between patches centered

at (i, j).

To obtain a reﬁned anomaly map at the image

scale, we also implement a small transposed convolu-

tional neural network, which is trained to reconstruct

the input image im from

f m . It consists of ﬁve 2D

convolution layers with ﬁlters of size 3 × 3, followed

by a ReLU activation function (Figure 2 - block D and

supplementary Table S1).

3.3 Loss Function and Evolving

Weighting Scheme

By combining the losses described by eq. 1 and eq.

2 together with the loss associated with image recon-

struction, we deﬁne a multi-objective problem. In-

spired by the fact that humans often learn from an

easy concept to a more difﬁcult one, as pointed out by

Li et al. (Li et al., 2017) and Galama et al. (Galama

and Mensink, 2019), we propose an evolving weight-

ing scheme (EWS) of the total loss function during

learning. This technique can take advantage of the

fact that some losses may conﬂict, such as in our case

the classiﬁcation loss and the reconstruction losses,

while others may beneﬁt from each other, such as

the L

term and the SSIM term in our reconstruction

equations eq. 2 and its adaptation for images. There-

fore, the weighting of different L

terms changes over

the number of epochs t such that:

(t) = α

(t)L

cls

+ α

(t)L

Rec

f m

+ α

(t)L

Rec

. (3)

We assume that the classiﬁcation task is easier

compared to the two reconstruction tasks, since it is

a global decision at the image level while the quality

of the reconstructions is evaluated at the pixel level.

Moreover, since the quality

im depends on the qual-

ity of

f m, we assume that L

Rec

f m

must be optimized

before L

Rec

. To this end, as illustrated in Figure 3,

0.00

0.25

0.50

0.75

1.00

0 50 100 150 200 250

Epoch

: a = 1e+ 1, b = 0.4, c = 80

: a = 1e− 8, b = 1.2, c = 150

: a = 1e− 8, b = 2, c = 300

Figure 3: Evolution of α

α along with the number of

epochs. Each curve is modeled according to the follow-

ing equation, whose parameters are indicated in the legend:

(a−b)

1+exp(x−

)

0.05

+b. The α

α values are then normalized so that

they sum to 1.

we model the evolution of α

by a decreasing logis-

tic function, and α

and α

by two increasing logistic

functions lagged by the number of epochs.

4 EXPERIMENTS

4.1 Experimental Set-up

We evaluated our model on the recent challenging

MVTec AD dataset (Bergmann et al., 2019). The

MVTec images have been resized to 256 × 256 pix-

els. We applied data augmentation by randomly mod-

ulating the color. As explained above, each image is

associated with two artiﬁcially damaged images using

the Cut&Paste approach (Li et al., 2021).

All models have the same training hyperparame-

ters: 250 training epochs, an Adam type optimizer

with a learning rate of 1e

−4

and a weight decay of

−5

, the batch size is 12.

To assess the performance of our method, we cal-

culated the anomaly maps by comparing f m and its

reconstruction

f m via the L

distance such that:

f m

∑

i=1

∑

j=1

|| f m

i, j

−

f m

i, j

. (4)

To obtain an anomaly map from f m at the scale of

im, we upsampled them by linear interpolation. Em-

pirically, we observed that A

f m

gives the best results

in terms of both classiﬁcation and localization tasks.

The classiﬁcation scores according to the values of

cls

and the segmentation scores obtained with A

(i.e. the anomaly maps resulting from the image re-

constructions), are given in supplementary Table S2.

The anomaly maps were post-processed to im-

prove results as explained in the supplementary Fig-

ure S1. They are ﬁrst normalized by the average

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

330

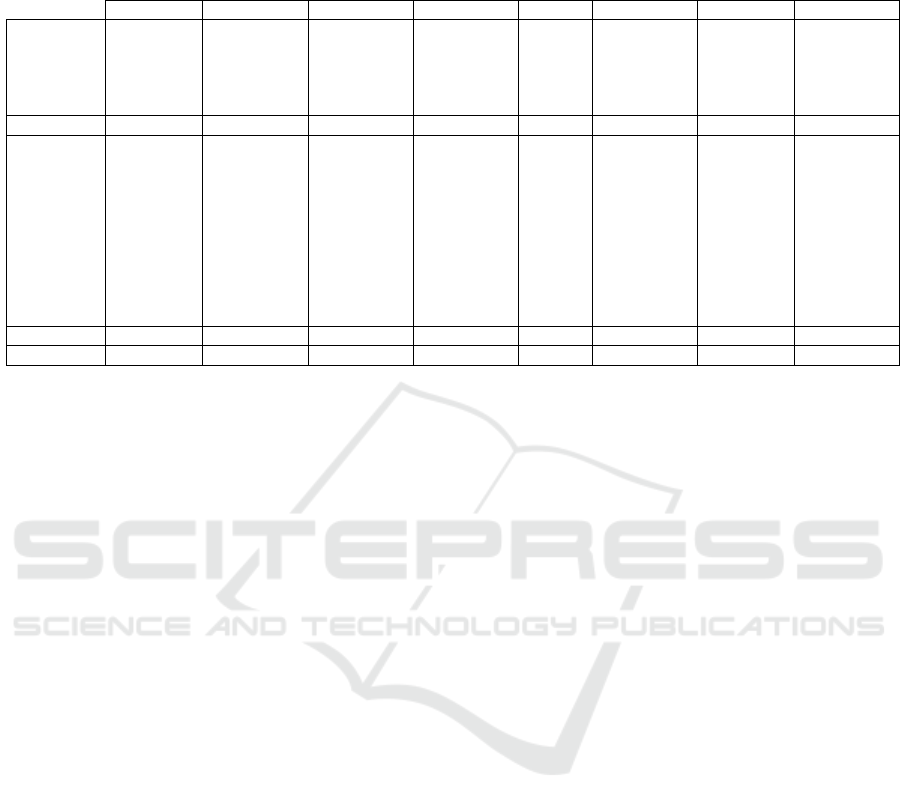
Table 1: Anomaly detection and localization performance on the MVTec dataset. The ﬁrst score in the pair refers to the

image-level AD ROC-AUC score in percent, and the second to the pixel-wise ROC-AUC score in percent. The best score for

each object is highlighted in bold.

AE-l2 P-SVDD DFR Cut&Paste SAAE InTra PatchCore HaloAE

Carpet (-, 59.0) (92.9, 92.6) (95.6, 98.5) (100.0, 98.3) (-, 97.9) (98.8, 99.2) (98.7, 99.1) (69.7, 89.4)

Grid (-, 90.0) (94.4, 96.2) (95.0, 97.4) (96.2, 97.5) (-, 97.9) (100.0, 98.8) (97.9, 98.7) (95.1, 83.1)

Leather (-, 75.0) (90.9, 97.4) (99.4, 99.3) (95.4, 99.5) (-, 99.6) (100.0, 99.5) (100, 99.3) (97.8, 98.5)

Tile (-, 51.0) (97.8, 91.4) (93.1, 90.9) (100.0, 90.5) (-, 97.3) (98.2, 94.4) (98.9, 95.9) (95.7, 78.5 )

Wood (-, 73.0) (96.5, 90.8) (98.9, 95.4) (99.1, 95.5) (-, 97.6) (97.5, 88.7) (99.0, 95.1) (100.0, 91.1)

Mean Text. (-, 69.6) (94.5, 93.8) (96.4, 96.3) (98.1, 96.3) (-, 98.1) (98.9, 96.1) (98.9, 97.6) (91.7, 88.1)

Bottle (-, 86.0) (98.6, 98.1) (99.8, 95.8) (99.9, 97.6) (-, 97.9) (100.0, 97.1) (100, 98.6) (100.0, 91.9)

Cable (-, 86.0) (90.3, 96.8) (78.9, 91.4) (100.0, 90.0) (-, 96.8) (70.3, 91.0) (99.4, 98.5) (84.6, 87.6)

Capsule (-, 88.0) (76.7, 95.8) (96.2, 98.5) (98.6, 97.4) (-, 98.2) (86.5, 97.7) (97.8, 99.1) (88.4, 97.8)

HazelNut (-, 95.0) (92.0, 97.5) (97.0, 92.0) (93.3, 97.3) (-, 98.5) (95.7, 98.3) (100, 98.7) (99.8, 97.8)

MeatalNut (-, 86.0) (94.0, 98.0) (93.1, 93.3) (86.6, 93.1) (-, 97.6) (96.9, 93.3) (100, 98.4) (88.4, 85.2)

Pill (-, 85.0) (86.1, 95.1) (91.9, 96.8) (99.8, 95.7) (-, 98.1) (90.2, 98.3) (96.0, 97.6) (90.1, 91.5)

Screw (-, 96.0) (81.3, 95.7) (94.3,99.0) (90.7, 96.7) (-, 98.9) (95.7, 99.5) (97.0, 99.4) (89.6, 99.0)

Toothbrush (-, 93.0) (100.0, 98.1) (100.0, 98.5) (97.5, 98.1) (-, 98.1) (100.0, 98.9) (99.7, 98.7) (97.2, 92.9)

Transistor (-, 86.0) (91.5, 97.0) (80.6, 79.1) (99.8, 93.0) (-, 96.0) (95.8, 96.1) (100, 96.4) (84.4, 87.5)

Zipper (-, 77.0) (97.9, 95.1) (89.9, 96.9) (99.9, 99.3) (-, 96.9) (99.4, 99.2) (99.5, 98.9) (99.7, 96.0)

Mean Obj. (-, 87.8) (90.8, 96.7) (92.2, 94.1) (96.6, 95.8) (-, 97.7) (93.0, 96.9) (98.9, 98.4) (92.2, 92.7)

Mean (71.0, 81.7) (92.1, 95.7) (93.6, 94.9) (97.1, 96.0) (-, 97.8) (95.0, 96.7) (99.0, 98.1) (92.0, 91.2)

anomaly map of the training data, denoted A

f m

To do so, all the N anomaly maps from the train-

ing set are concatenated before being averaged along

the channel axis of dimension. This operation re-

duces potential noise (supplementary Figure S1). Fi-

nally, the anomaly maps are ﬁltered using a Gaussian

kernel of size 3 × 3, which smoothes the boundaries

of the anomalous regions (supplementary Figure S1).

Image-level AD is reported by the threshold-agnostic

ROC-AUC metric. For the localization we reported

the pixel-wise ROC-AUC.

4.2 Quantitative Results

We compared our method with the methods discussed

in Section 2, ranging from AE L

(Bergmann et al.,

2019), which can be considered the simplest model,

to PatchCore (Roth et al., 2022), which is the best

model according to the state of the art. We have

also included Cut&Paste (Li et al., 2021) and DFR

(Shi et al., 2021) since we have reused parts of their

method. Note that we recomputed the DFR results to

have both the image-level AD ROC-AUC metric and

the per-pixel segmentation ROC-AUC scores that are

not available in the original paper. We also included

P-SVDD (Cohen and Hoshen, 2020a) to refer to an

embedding-similarity based method, as well as SAAE

(Yang, 2021) and InTra (Pirnay and Chai, 2021) to re-

fer to two other techniques using Transformer. The

results are summarized in Table 1.

We can observe that HaloAE obtains satisfactory

results for the detection of anomalies at the image

level with an average ROC-AUC score of 92.0%.

This result is strongly inﬂuenced by the poor perfor-

mance obtained speciﬁcally on the carpet object. As

illustrated in Figure S2, the network seems to be able

to reconstruct the anomalies for this object, so the dis-

tribution of A

f m

means is similar between normal and

abnormal objects. For the pixel-wise segmentation re-

sults, HaloAE obtains an average ROC-AUC score of

91.2%. It is important to note that our model is an all-

in-one model that does not require image patches for

the localization task, unlike P-SVDD, Cut&Paste, In-

Tra or PatchCore, which implies a trade-off between

excellent accuracy and speed, as described in the next

section.

4.3 Inference Time

The inference time is a key criterion to use our

anomaly detection model on very large scale im-

ages. The results in Table 2 have been ob-

tained with the following hardware conﬁguration fol-

lowing hardware conﬁguration: Intel(R) Xeon(R)

Silver 4216 CPU @ 2.10GHz and an NVIDIA

Quadro RTX 5000. We used the ofﬁcial ones

of the models when available, while the code

posted on https://github.com/LilitYolyan/CutPaste,

and https://github.com/jhy12/inpainting-transformer

have been used respectively for Cut&Paste (Li et al.,

2021) and InTra (Pirnay and Chai, 2021). For Patch-

Core, we used a WideResNet50 (Zagoruyko and Ko-

modakis, 2016) with a subsampling of the memory

bank at 10%. For the other models we used the

parameters described in the papers. The speed of

HaloAE can be explained by the fact that our model

does not use patches for the localization task, which

is directly computed on the reconstructed

f m. The

HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and Localization Based on HaloNet

331

efﬁciency of HaloAE compared to DFR, which take

as input images of the same size and have a similar

number of parameters, i.e. ∼ 18M, can be explained

by the depth of the multi-scale feature maps to be re-

constructed of 704 versus 3456 for DFR, and the use

of a Halonet-based architecture.

Table 2: Number of frames per second (FPS) inferred by

the different models and, in parentheses, the speedup ratio

compared to our model.

DFR Cut&Paste InTra PatchCore HaloAE

5.4 (x4) 2.2 (x10) 0.3 (x73) 2.7 (x8) 22.0

4.4 Qualitative Results

We visualize some results of the anomaly localization

in Figure 1. The ﬁrst and third rows show the in-

put images while the second and last rows show the

post-processed anomaly maps. These representations

highlight that HaloAE is capable of locating tiny de-

fects, as illustrated by the screw, capsule or zipper,

and large defects, as illustrated by the hazelnut or the

tile. In addition, HaloAE detects both structural de-

fects, as shown by the wood and the tile, and color

defects, as in the cable example, where the cable in

the lower left corner is supposed to be red.

4.5 Ablation Study

Table 3: Ablation study on loss function. The ﬁrst row

shows the ﬁnal scores of our model, while the other rows

highlight the effects of different L

modiﬁcations. In each

pair, the ﬁrst element refers to the image-level AD ROC-

AUC score in percent and the second to the pixel-wise

ROC-AUC score in percent. The best score is highlighted

in bold.

Mean

(t) equal to eq. 3 (92.0, 91.2)

= L

cls

+ L

Rec

f m

+ L

Rec

(79.0, 86.3)

(t) equal to eq. 5 (88.2, 85.9)

(t) = α

(t)L

cls

+ α

(t)L

Rec

f m

(71.43, 79.1)

(t) = α

(t)L

cls

+ α

(t)L

Rec

(72.5, 82.2)

(t) = L

Rec

f m

+ L

Rec

(76.8, 87.8)

(t) = L

cls

(82.9, 70.6)

(t) = L

Rec

f m

(79.6, 90.3)

To study the efﬁciency of our workﬂow, we per-

formed different ablation experiments exploring our

loss function (eq.3) and the different blocks of the

network (Figure 2). To study the loss function, we

ﬁrst explored the effect of the EWS. We found that

equal weighting of L

terms has a negative impact on

the performance of the classiﬁcation and segmenta-

tion tasks, with an average loss of 12.0 and 4.9 points

respectively (2

row of table 3). To compare our

EWS with other evolving weighting strategies, we im-

plemented the method of Kendall et al. (Kendall et al.,

2018) which takes into account the homoscedastic un-

certainty of each task, with the loss function rewritten

as:

∑

i=1

∑

i=1

log(σ

) (5)

where each loss term is denoted by L

and σ

being the

uncertainty parameter of each task. The results show

that our weighting scheme is better for each of the

two scores, emphasizing the importance of learning

difﬁcult tasks after easy ones (3

row of Table 3).

Then we studied, the importance of image recon-

struction loss (Figure 2 - block D). Removing either

the transposed CNN associated with image recon-

struction (4

row of Table 3, or the loss term asso-

ciated with feature map (5

row of Table 3) had a

signiﬁcant impact on both the classiﬁcation and seg-

mentation scores. Removing the classiﬁcation loss

term to evaluate the effect of the SSL module (Fig-

ure 2 - block A) resulted in a decrease of 14.6 points

in classiﬁcation score and 3.4 points in segmentation

score. However, training the model only on classiﬁ-

cation loss did not yield any improvement in classiﬁ-

cation scores (7

row of Table 3).

Table 4: Ablation study on the architecture. The ﬁrst row

shows the ﬁnal scores of our model. In each pair, the ﬁrst

element refers to the image-level AD ROC-AUC score in

percent and the second to the pixel-wise ROC-AUC score in

percent. The best score per column is highlighted in bold.

Mean Text. Mean Obj. Mean

HaloAE (ﬁnal) (91.7, 88.1) (92.2, 92.7) (91.4, 91.2)

AE-l2 (70.0, 69.2) (88.0, 88.9) (82.0, 82.5)

AE-SSIM (78.0, 78.2) (91.0, 91.2) (87, 86.9)

Block C only (75.6, 67.4) (78.2, 78.8) (77.3, 75.0)

Block C as CNN (89.5, 94.1) (82.7, 90.4) (85.0, 90.4)

Block C as Swin (90.3, 85.8) (82.2, 88.0) (84.9, 86.5)

To evaluate our network architecture, we ﬁrst

compared the performance of HaloNet as a simple AE

dedicated to image reconstruction, retaining only the

C block in Figure 2. HaloNet as an AE does not per-

form as well as CAEs, suggesting that our model is

able to reconstruct abnormal regions through greater

generalization (4

row of Table 4). This justiﬁes

the need for the feature extractor module (Figure 2

- block B). Next, we replaced the HaloNet AE mod-

ule with the CAE from DFR (Shi et al., 2021). In

our architecture, the use of local block self-attention

improves the results with an increase of 6.4 and 0.8

points for classiﬁcation and segmentation respectively

row of Table 4). This important experiment high-

lights that our hybrid model captures more informa-

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

332

tion than a fully convolutional model, emphasizing

that the long-range information extracted by the self-

attentive blocks, covering up to 25% of the feature

map, improves the detection of abnormal regions. Fi-

nally, to compare the attention operations proposed

by Swin Transformer (Liu et al., 2021) and HaloNet,

we designed a Swin AE according to the architecture

proposed by (Lin et al., 2022) and we included it in

block C - Figure 2. Swin AE has a similar number of

parameters to HaloAE, namely 18 million. Our hy-

brid module compared to the model including Swin

Transformer improves the results with an increase of

6.5 and 4.7 points (6

row of Table 4). This sug-

gests that the convolutional operation captures addi-

tional information in comparison to a model including

self-attention only.

4.6 Complementary Experiment

Figure 4: Tumor segmentation experiment. A) Histopatho-

logical image of a lung tumor with KI67 immunostaining.

B) Heatmap of the averages of anomaly scores per tile, the

bluer the tile the more tumorous it is and vice versa for red-

dish tiles.

The use of unsupervised learning techniques is still

little explored in histology (Quiros et al., 2022),

(Cheerla and Gevaert, 2019), even though, contrary

to supervised techniques, they could reveal unknown

morphological characteristics. The efﬁciency and

performance of HaloAE make it a relevant candidate

for very large scale image analysis. Thus, HaloAE

was applied to segment lung tumors from histopatho-

logical images of 70k × 70k pixels. The model was

trained on a set of 7000 tumor patches of 256 × 256

pixels, extracted from 50 patients treated in 11 hospi-

tals. The very promising results presented in Figure

4, highlight the ability of the model to learn what is

supposed to be non-discriminative based on a highly

variable training set, compared to MVTec (see supple-

mentary Figure S3). Indeed, the training set includes

many biases such as hospital of origin, or slide prepa-

ration. This unsupervised approach is innovative for

histopathological image analysis. It can be extended

to many medical problems, such as comparison be-

tween two diseases, since it provides pixel-level inter-

pretation without assumptions or the need to annotate

subregions.

5 DISCUSSION AND

CONCLUSION

To the best of our knowledge, HaloAE is the ﬁrst

model to incorporate a local version of Transformer,

along with HaloNet (Vaswani et al., 2021), to han-

dle an AD problem. Computing intra-patch correla-

tions via the local block self-attention operation im-

proves both detection and localization. The module

optimizing the oversampling of reconstructed feature

maps allows us to obtain an all-in-one model, which

does not require an expansive patch-based process for

anomaly segmentation. We also show that the inte-

gration of an SSL approach leads to a better regu-

larization of the AE, ultimately improving the detec-

tion score at the image level. Finally, the score im-

provement provided by our new evolving loss func-

tion weighting scheme suggests that learning multiple

tasks simultaneously would be facilitated by giving

increasing importance to the most difﬁcult tasks.

Overall, HaloAE performs competitively on the

MVTec dataset (Bergmann et al., 2019). Our hy-

brid AE between CNN and local Transformer outper-

forms both a fully convolutional model and a fully

attentional model implemented according to the Swin

Transformer (Liu et al., 2021) architecture, highlight-

ing the importance of integrating global and local

information at each step of the process, while sug-

gesting the existence of a synergy of both operations

(Zhao et al., 2021), (Fang et al., 2022).

The low memory and computational complexity

of the 2D block-wise self-attention, as proposed by

HaloNet, allows the model to be applied to very large

images, while enabling the calculation of very dis-

tant correlations. This is particularly interesting for

medical applications, where unsupervised models of

anomaly detection are still little explored, although

very promising because they do not require any prior

knowledge of the biological elements that discrimi-

nate different diseases or states. In addition, this ap-

proach offers a pixel-level interpretation, and thus al-

lows the identiﬁcation of the most discriminating bi-

ological elements with respect to the training set.

HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and Localization Based on HaloNet

333

ACKNOWLEDGMENTS

This work for Liming Chen was in part supported

by the 4D Vision project funded by the Partner Uni-

versity Fund (PUF), a FACE program, as well as

the French Research Agency, l’Agence Nationale

de Recherche (ANR), through the projects Learn

Real (ANR-18-CHR3-0002-01), Chiron (ANR-20-

IADJ-0001- 01), Aristotle (ANR-21-FAI1-0009-01),

and the joint support of the French national pro-

gram of investment of the futur and the the regions

through the PSPC FAIR Waste project. This work

has been funded by the Neuroendocrine Tumor Re-

search Foundation (NETRF 2022 investigator award

to Matthieu Foll). This work was granted access to the

HPC resources of IDRIS under the allocation 2022-

[AD011012172R1] made by GENCI.

DISCLAIMER

Where authors are identiﬁed as personnel of the In-

ternational Agency for Research on Cancer/World

Health Organization, the authors alone are responsi-

ble for the views expressed in this article and they

do not necessarily represent the decisions, policy or

views of the International Agency for Research on

Cancer /World Health Organization.

REFERENCES

Akcay, S., Atapour-Abarghouei, A., and Breckon, T. P.

(2018). Ganomaly: Semi-supervised anomaly detec-

tion via adversarial training. In Asian conference on

computer vision, pages 622–637. Springer.

Baur, C., Wiestler, B., Albarqouni, S., and Navab, N.

(2018). Deep autoencoding models for unsupervised

anomaly segmentation in brain mr images. In Inter-

national MICCAI Brainlesion Workshop, pages 161–

169. Springer.

Bergmann, P., Fauser, M., Sattlegger, D., and Steger, C.

(2019). Mvtec ad–a comprehensive real-world dataset

for unsupervised anomaly detection. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 9592–9600.

Bergmann, P., Fauser, M., Sattlegger, D., and Steger,

C. (2020). Uninformed students: Student-teacher

anomaly detection with discriminative latent embed-

dings. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

4183–4192.

Bergmann, P., L

owe, S., Fauser, M., Sattlegger, D., and Ste-

ger, C. (2018). Improving unsupervised defect seg-

mentation by applying structural similarity to autoen-

coders. arXiv preprint arXiv:1807.02011.

Cheerla, A. and Gevaert, O. (2019). Deep learning with

multimodal representation for pancancer prognosis

prediction. Bioinformatics, 35(14):i446–i454.

Chen, C.-F., Fan, Q., and Panda, R. (2021). Crossvit:

Cross-attention multi-scale vision transformer for im-

age classiﬁcation. arXiv preprint arXiv:2103.14899.

Cohen, N. and Hoshen, Y. (2020a). Sub-image anomaly

detection with deep pyramid correspondences. arXiv

preprint arXiv:2005.02357.

Cohen, N. and Hoshen, Y. (2020b). Sub-image anomaly

detection with deep pyramid correspondences. arXiv

preprint arXiv:2005.02357.

Defard, T., Setkov, A., Loesch, A., and Audigier, R. (2021).

Padim: a patch distribution modeling framework for

anomaly detection and localization. In International

Conference on Pattern Recognition, pages 475–489.

Springer.

Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-

Fei, L. (2009). Imagenet: A large-scale hierarchical

image database. In 2009 IEEE conference on com-

puter vision and pattern recognition, pages 248–255.

Ieee.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,

D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,

M., Heigold, G., Gelly, S., et al. (2020). An image is

worth 16x16 words: Transformers for image recogni-

tion at scale. arXiv preprint arXiv:2010.11929.

Dosovitskiy, A. and Djolonga, J. (2019). You only train

once: Loss-conditional training of deep networks. In

International conference on learning representations.

Fang, J., Lin, H., Chen, X., and Zeng, K. (2022). A hybrid

network of cnn and transformer for lightweight im-

age super-resolution. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recogni-

tion, pages 1103–1112.

Galama, Y. and Mensink, T. (2019). Itergans: Iterative gans

to learn and control 3d object transformation. Com-

puter Vision and Image Understanding, 189:102803.

Groenendijk, R., Karaoglu, S., Gevers, T., and Mensink, T.

(2021). Multi-loss weighting with coefﬁcient of vari-

ations. In Proceedings of the IEEE/CVF Winter Con-

ference on Applications of Computer Vision, pages

1469–1478.

Gudovskiy, D., Ishizaka, S., and Kozuka, K. (2022). Cﬂow-

ad: Real-time unsupervised anomaly detection with

localization via conditional normalizing ﬂows. In Pro-

ceedings of the IEEE/CVF Winter Conference on Ap-

plications of Computer Vision, pages 98–107.

Guo, J., Han, K., Wu, H., Tang, Y., Chen, X., Wang, Y.,

and Xu, C. (2022). Cmt: Convolutional neural net-

works meet vision transformers. In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 12175–12185.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Kendall, A., Gal, Y., and Cipolla, R. (2018). Multi-task

learning using uncertainty to weigh losses for scene

geometry and semantics. In Proceedings of the IEEE

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

334

conference on computer vision and pattern recogni-

tion, pages 7482–7491.

Li, C., Yan, J., Wei, F., Dong, W., Liu, Q., and Zha, H.

(2017). Self-paced multi-task learning. In Thirty-First

AAAI Conference on Artiﬁcial Intelligence.

Li, C.-L., Sohn, K., Yoon, J., and Pﬁster, T. (2021). Cut-

paste: Self-supervised learning for anomaly detection

and localization. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recog-

nition, pages 9664–9674.

Lin, A., Chen, B., Xu, J., Zhang, Z., Lu, G., and Zhang,

D. (2022). Ds-transunet: Dual swin transformer u-net

for medical image segmentation. IEEE Transactions

on Instrumentation and Measurement.

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin,

S., and Guo, B. (2021). Swin transformer: Hierarchi-

cal vision transformer using shifted windows. arXiv

preprint arXiv:2103.14030.

Mishra, P., Verk, R., Fornasier, D., Piciarelli, C., and

Foresti, G. L. (2021). Vt-adl: A vision transformer

network for image anomaly detection and localization.

arXiv preprint arXiv:2104.10036.

Pan, X., Ge, C., Lu, R., Song, S., Chen, G., Huang, Z., and

Huang, G. (2022). On the integration of self-attention

and convolution. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recog-

nition, pages 815–825.

Pirnay, J. and Chai, K. (2021). Inpainting transformer for

anomaly detection. arXiv preprint arXiv:2104.13897.

Quiros, A. C., Coudray, N., Yeaton, A., Yang, X., Chiri-

boga, L., Karimkhan, A., Narula, N., Pass, H., Mor-

eira, A. L., Quesne, J. L., Tsirigos, A., and Yuan,

K. (2022). Self-supervised learning in non-small cell

lung cancer discovers novel morphological clusters

linked to patient outcome and molecular phenotypes.

Ramachandran, P., Parmar, N., Vaswani, A., Bello, I.,

Levskaya, A., and Shlens, J. (2019). Stand-alone

self-attention in vision models. arXiv preprint

arXiv:1906.05909.

Roth, K., Pemula, L., Zepeda, J., Sch

olkopf, B., Brox,

T., and Gehler, P. (2022). Towards total recall in

industrial anomaly detection. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 14318–14328.

Rudolph, M., Wandt, B., and Rosenhahn, B. (2021). Same

same but differnet: Semi-supervised defect detec-

tion with normalizing ﬂows. In Proceedings of

the IEEE/CVF Winter Conference on Applications of

Computer Vision, pages 1907–1916.

Shi, Y., Yang, J., and Qi, Z. (2021). Unsupervised anomaly

segmentation via deep feature reconstruction. Neuro-

computing, 424:9–22.

Simonyan, K. and Zisserman, A. (2014). Very deep con-

volutional networks for large-scale image recognition.

arXiv preprint arXiv:1409.1556.

Touvron, H., Cord, M., Douze, M., Massa, F., Sablayrolles,

A., and J

egou, H. (2021). Training data-efﬁcient

image transformers & distillation through attention.

In International Conference on Machine Learning,

pages 10347–10357. PMLR.

Vaswani, A., Ramachandran, P., Srinivas, A., Parmar, N.,

Hechtman, B., and Shlens, J. (2021). Scaling lo-

cal self-attention for parameter efﬁcient visual back-

bones. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

12894–12904.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. In Advances in

neural information processing systems, pages 5998–

6008.

Wang, W., Xie, E., Li, X., Fan, D.-P., Song, K., Liang, D.,

Lu, T., Luo, P., and Shao, L. (2021). Pyramid vi-

sion transformer: A versatile backbone for dense pre-

diction without convolutions. In Proceedings of the

IEEE/CVF International Conference on Computer Vi-

sion, pages 568–578.

Yang, Y. (2021). Self-attention autoencoder for anomaly

segmentation.

Zagoruyko, S. and Komodakis, N. (2016). Wide residual

networks. arXiv preprint arXiv:1605.07146.

Zavrtanik, V., Kristan, M., and Sko caj, D. (2021). Recon-

struction by inpainting for visual anomaly detection.

Pattern Recognition, 112:107706.

Zhang, Y., Gong, Y., Zhu, H., Bai, X., and Tang, W. (2020).

Multi-head enhanced self-attention network for nov-

elty detection. Pattern Recognition, 107:107486.

Zhao, Y., Wang, G., Tang, C., Luo, C., Zeng, W., and Zha,

Z.-J. (2021). A battle of network structures: An empir-

ical study of cnn, transformer, and mlp. arXiv preprint

arXiv:2108.13002.

HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and Localization Based on HaloNet

335

APPENDIX

Figure S1: Post processing workﬂow. A) Input image.

B) Anomaly map (see eq.4 in main text). C) Normalized

anomaly map. D) Normalized anomaly map smoothed with

a Gaussian ﬁlter.

Figure S2: Results of the carpet classiﬁcation. A) Distribu-

tion of the means of the post-processed anomaly maps com-

puted on the feature maps, for defect-free and anomalous

objects. B) Distribution of anomaly scores by defect cate-

gory. Defect-free objects and anomalous objects have simi-

lar distributions. C) Carpet images and their corresponding

anomaly map, 1

and 2

columns defect-free objects, 3

and 4

anomalous objects.

Figure S3: Example of the dataset used for lung tumor seg-

mentation: each 256 × 256 tile is extracted from a KI67-

stained histopathology image of approximately 70k × 70k

pixels. The ﬁrst row shows non-tumor images and the sec-

ond row tumor tiles respectively.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

336

Table S1: Summary of the HaloNet AE architecture: Each brace encloses a block, the number of blocks per stage is indicated

in front of it. The batch normalization operation is denoted by BN, the convolution layers and the transposed convolution

layers are denoted by conv and conv

respectively. Finally, the number of channels at the end of each stage is indicated in the

right-hand column for the encoder and decoder.

Halonet encoder Halonet decoder

5 × 5 conv, BN, relu d

f m

= 704 3 ×







1 × 1 conv

, BN

Attention(b,h),relu

3 × 3 conv

, BN

dec

= 29

dec

= 55

dec

= 118

2 ×







1 × 1 conv, BN

Attention(b,h),relu

3 × 3 conv, BN

enc

= 234

enc

= 117

1 ×







1 × 1 conv

, BN

Attention(b,h),relu

5 × 5 conv

, BN

dec

= 237

2 ×







1 × 1 conv, BN

Attention(b,h),relu

5 × 5 conv, BN

enc

= 58

enc

= 29

1 ×







1 × 1 conv

, BN

Attention(b,h),relu

1 × 1 conv

, BN

dec

= 704

Table S2: Exploring the outputs of HaloAE and the post-processing procedure. The ﬁrst pair score corresponds to the image-

level AD ROC-AUC score in percent, and the second to the pixel-level ROC-AUC score in percent. The best score for each

object is highlighted in bold. A represents the anomaly maps, denoted A

or A

f m

if they are computed on the images or from

the feature maps. A

{im, f m}

represents the normalized anomaly maps. Finnaly, N

f ilter

refers to the Gaussian ﬁlter applied to

the normalized anomaly map.

cls

+ N

f ilter

f m

+ N

f ilter

Carpet (56.9, -) (74.4, 60.7) (54.3, 88.1) (60.7, 88.5) (69.7, 89.4)

Grid (100.0, -) (82.1, 53.4) (94.5, 82.7) (95.2, 83.0) (95.1, 83.1)

Leather (71.0, -) (60.2, 78.3) (97.2, 98.0) (97.8, 98.1) (97.8, 98.5)

Tile (51.5, -) (92.6, 66.1) (93.3, 75.9) (95.2, 76.1) (95.7, 78.5 )

Wood (93.2, -) (99.0, 77.4) (99.7, 90.7) (99.9, 90.3) (100.0, 91.1)

Mean Text. (74.5, -) (81.66, 67.2) (87.8, 87.1) (89.8, 87.2) (89.7, 88.1)

Bottle (98.4, -) (99.9, 86.7) (99.9, 90.0) (100.0, 91.7) (100.0, 91.9)

Cable (100.0, -) (62.8, 76.3) (79.2, 77/9) (84.6, 86.1) (84.6, 87.6)

Capsule (96.8, -) (54.5, 63.6) (83.2, 97.3) (88.4, 97.4) (88.4, 97.8)

HazelNut (99.4, -) (86.3, 76.0) (98.9, 97.9) (99.6, 97.7) (99.8, 97.8)

MeatalNut (98.0, -) (65.2, 69.2) (85.6, 86.3) (88.4, 84.5) (88.4, 85.2)

Pill (100.0, -) (50.8, 77.2) (86.4, 92.8) (90.6, 89.9) (90.1, 91.5)

Screw (100.0, -) (54.6, 78.5) (88.6, 98.8) (89.6, 98.6) (89.6, 99.0)

Toothbrush (58.1. -) (89.7, 81.0) (94.7, 93.0) (97.2, 92.6) (97.2, 92.9)

Transistor (92.3, -) (81.5, 79.9) (80.0, 84.8) (84.4, 85.6) (84.4, 87.5)

Zipper (51.4, -) (99.7, 86.8) (99.7, 95.4) (99.7, 95.3) (99.7, 96.0)

Mean Obj. (89.4, -) (74.5, 77.5) (89.6, 91.6) (92.3, 91.9) (92.2, 92.7)

Mean (84.4, -) (76.9, 74.1) (89.0, 90.0) (91.4, 90.4) (91.4, 91.2)

HaloAE: A Local Transformer Auto-Encoder for Anomaly Detection and Localization Based on HaloNet

337