A Framework for Assessing Decompiler Inference Accuracy of

Source-Level Program Constructs

Jace Kline

and Prasad Kulkarni

Department of Electical Engineering and Computer Science, University of Kansas, Lawrence, Kansas, U.S.A.

Keywords:

Decompilers, Security.

Abstract:

Decompilation is the process of reverse engineering a binary program into an equivalent source code repre-

sentation with the objective to recover high-level program constructs such as functions, variables, data types,

and control ﬂow mechanisms. Decompilation is applicable in many contexts, particularly for security ana-

lysts attempting to decipher the construction and behavior of malware samples. However, due to the loss of

information during compilation, this process is naturally speculative and prone to inaccuracy. This inherent

speculation motivates the idea of an evaluation framework for decompilers. In this work, we present a novel

framework to quantitatively evaluate the inference accuracy of decompilers, regarding functions, variables, and

data types. We develop a domain-speciﬁc language (DSL) for representing such program information from

any “ground truth” or decompiler source. Using our DSL, we implement a strategy for comparing ground truth

and decompiler representations of the same program. Subsequently, we extract and present insightful metrics

illustrating the accuracy of decompiler inference regarding functions, variables, and data types, over a given

set of benchmark programs. We leverage our framework to assess the correctness of the Ghidra decompiler

when compared to ground truth information scraped from DWARF debugging information. We perform this

assessment over all the GNU Core Utilities (Coreutils) programs and discuss our ﬁndings.

1 INTRODUCTION

In an increasingly digital world, cybersecurity has

emerged as a crucial consideration for individuals,

companies, and governments trying to protect their in-

formation, ﬁnancial assets, and intellectual property.

Of the many digital threats, various forms of malware

continue to pervade the digital landscape. Decompi-

lation, the translation from binary code into an ap-

proximate source-level representation, is a key strat-

egy in attempting to understand the construction and

behavior of malware samples. A decompiler is a pro-

gram that performs decompilation. The decompila-

tion process is inherently speculative and error-prone

since high-level information such as function bound-

aries, variables, data types, and control ﬂow mecha-

nisms are lost during program compilation.

Due to this imprecise nature of decompilation,

a generalized and extensible quantitative evaluation

framework for decompilers is critical. Existing work

(Liu and Wang, 2020) proposes an evaluation tech-

https://orcid.org/0000-0003-4442-9776

https://orcid.org/0000-0003-1236-5739

nique to determine whether decompiled programs, af-

ter recompilation, are consistent in behavior to their

original binaries. Another work (Naeem et al., 2007)

proposes a set of metrics for assessing the clarity of

decompiled Java programs with respect to program

size, conditional complexity, identiﬁer complexity,

number of local variables, and expression complex-

ity. These works, although insightful for assessing

decompiler quality, do not measure the recovery ac-

curacy of high-level program constructs such as func-

tions, variables, and data types. The recovery and in-

ference of the these high-level constructs, in conjunc-

tion with clarity and behavioral correctness, is impor-

tant to gain an understanding of decompiled binary

programs.

Targeting the current gap in the literature, this

paper presents a novel framework for quantifying

and assessing the accuracy of decompiler tools with

respect to high-level program constructs, including

functions, variables, and data types. To validate our

concept, we apply our framework to the Ghidra (Na-

tional Security Agency (NSA), 2022) decompiler and

discuss our ﬁndings. The primary objectives achieved

by this work are as follows:

228

Kline, J. and Kulkarni, P.

A Framework for Assessing Decompiler Inference Accuracy of Source-Level Program Constr ucts.

DOI: 10.5220/0011872600003405

In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 228-239

ISBN: 978-989-758-624-8; ISSN: 2184-4356

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

1. We deﬁne a domain-speciﬁc language (DSL),

written in Python, for expressing high-level pro-

gram information including functions, variables,

and data types. This serves as a medium whereby

we can translate program information extracted

from a decompiler or a ground-truth source.

2. We employ our DSL to compare program repre-

sentations from different sources. The primary

use case is to compare ground-truth program in-

formation to that inferred by decompilers.

3. Leveraging the comparison logic in (2), we deﬁne

a set of quantitative metrics to measure the accu-

racy of function, variable, and data type inference.

4. We develop a translation module in Python that

uses DWARF debugging information from a bi-

nary program to generate a ground-truth program

information representation in our DSL.

5. We utilize the Ghidra Python API to implement a

translation module from Ghidra’s decompilation

of a binary program to program information rep-

resentation in our DSL.

6. Using our developed language, metrics, and trans-

lation modules, we quantitatively assess the accu-

racy of the Ghidra decompiler when compared to

ground truth program information obtained from

DWARF debugging information. We perform this

analysis using the set of GNU Coreutils programs

as benchmarks. We present the evaluation results

and discuss additional ﬁndings and takeaways.

The remainder of this paper is outlined as follows: In

Sections 2 and 3, we discuss background concepts and

related research, respectively. Next, in Section 4, we

detail our methodology for developing our evaluation

framework. In Section 5, we present and discuss the

results of applying our evaluation framework to the

Ghidra decompiler. We conclude in Section 6 with a

summary of our results and future research directions.

2 BACKGROUND

DWARF (DWARF Standards Committee, 2022) is a

debugging ﬁle format used by many compilers and

debuggers to support source-level debugging for com-

piled binary programs. When speciﬁed ﬂags (usually

‘-g’) are present at compilation, DWARF-supporting

compilers such as GCC and Clang will augment the

outputted binary program or object ﬁle with DWARF

debugging information. A resulting binary executable

can then be loaded into a DWARF-supporting de-

bugger such as GDB to debug the target binary pro-

gram with references to line numbers, functions, vari-

ables, and types in the source-level program. The

DWARF standard is source language agnostic, but

generally supports equivalent representations for con-

structs present in common procedural languages such

as C, C++, and Fortran. In addition, DWARF is de-

coupled from any architecture or operating system.

The generalizability of DWARF debugging informa-

tion makes it a prime candidate for extracting “ground

truth” information about a particular binary program,

regardless of the speciﬁcs of the source language, ar-

chitecture, or operating system. DWARF is leveraged

in this work to obtain ground truth information about

target binary programs.

Ghidra (National Security Agency (NSA), 2022),

created and maintained by the National Security

Agency (NSA) Research Directorate, is an extensible

software reverse engineering framework that features

a disassembler, decompiler, and an integrated script-

ing environment in both Python and Java. We use the

Ghidra decompiler in this work to demonstrate our

decompiler evaluation framework.

3 RELATED WORK

In a 2020 paper (Liu and Wang, 2020), the authors

present an approach to determine the correctness of

decompilers outputting C source code. They aim

to ﬁnd decompilation errors, recompilation errors,

and behavior discrepancies exhibited by decompil-

ers. To evaluate behavioral correctness, they attempt

to recompile decompiled binaries (after potential syn-

tax modiﬁcations) and use existing dynamic analysis

techniques such as fuzzing to ﬁnd differences in be-

havior between the recompiled and original programs.

The objective of our work differs as we aim to evalu-

ate decompiler inference of high-level structures such

as functions, variables, and data types.

A 2006 technical report (Naeem et al., 2007) pro-

poses a set of metrics for assessing the “cognitive ex-

pressibility” (clarity) of decompiled Java code. This

is achieved through metrics that capture program size,

conditional complexity, identiﬁer complexity, number

of local variables, and expression complexity. Despite

the importance of these aspects in assessing the qual-

ity of a decompiler, this approach does not consider

the “correctness” - either behavioral or structural - of

the decompiled code. In addition, this work only tar-

gets decompiled Java programs.

Several existing works propose methodologies

and frameworks targeting high-level variable and type

inference from binary programs (Balakrishnan and

Reps, 2007; Lee et al., 2011; Caballero et al., 2012;

Lin et al., 2010; ElWazeer et al., 2013; Noonan et al.,

2016). Many of these works contain an evaluation

A Framework for Assessing Decompiler Inference Accuracy of Source-Level Program Constructs

229

of their inference accuracy; however, none of these

works demonstrate evaluation metrics that express a

uniﬁed assessment of function, variable, and data type

recovery.

4 METHODOLOGY

In this section, we discuss the philosophy, design, and

construction of our decompiler evaluation framework.

4.1 Domain-Speciﬁc Language (DSL)

for Program Information

We develop a domain-speciﬁc language (DSL) in

Python to represent program information such as

functions, variables, data types, and addresses, as well

as the relationships between them. This DSL acts

as a bridge linking binary-level information with the

source-level structures such as functions, variables,

and data types. Our DSL is decoupled from the source

of the program information. Any ground truth or de-

compiler source of program information can be trans-

lated into a ProgramInfo construct in this common

language (see Figure 1) and subsequently analyzed or

compared with another source of program informa-

tion.

Binary Program

DSL

ProgramInfo

DWARF

extract

decompile

Ghidra

IDA Pro

JEB3

Figure 1: DSL ProgramInfo extraction from multiple poten-

tial sources (National Security Agency (NSA), 2022; Hex-

Rays, 2022; PNF Software, 2022).

4.2 Capturing Ground Truth Program

Information

With our DSL deﬁned, we need a reliable method to

extract “ground truth” information from a program

and translate this information into our DSL. This

ground truth information is intended to be used in a

comparison with the program information obtained

from a decompiler. Our framework is meant for eval-

uation and therefore we assume that we have access to

the source code of benchmark programs used during

evaluation.

Our approach to extracting ground truth program

information involves leveraging debugging informa-

tion optionally included in the binary by the com-

piler. The primary purpose of debugging information

is to link binary-level instructions and addresses with

source-level structures. We choose the DWARF de-

bugging standard as the assumed debugging format

for our framework; however, deﬁning a translation

module from another debugging format into our DSL

is certainly possible. The DWARF debugging stan-

dard is supported by nearly all major Linux compilers

and may be extended to support any source-level pro-

gramming language. These properties of the DWARF

standard allow it to be used as a “ground truth” source

of program information, decoupled from the source

language or the compiler.

To capture DWARF information from a given

source program, we ﬁrst compile the source pro-

gram with the option to include debugging symbols.

After we compile the program, we then extract the

DWARF debugging information from the resulting bi-

nary. We utilize the pyelftools Python library (Ben-

dersky, 2022) to perform this extraction. The extrac-

tion results in, among other information, a set of de-

bugging information entries (DIEs). Together, these

DIE records provide a description of source-level en-

tities such as functions, variables, and data types in

relation to low-level binary information such as pro-

gram counter (PC) addresses and storage locations.

Using this parsed DWARF information, we deﬁne a

module that translates the DIEs into the equivalent

constructs in our DSL.

4.3 Capturing Decompiler (Ghidra)

Output Information

In addition to capturing a ground-truth program rep-

resentation in our DSL, we must construct a DSL rep-

resentation of the program information obtained from

a decompiler we wish to evaluate. Depending on the

decompiler and the structure of its output, this pro-

cess may take many forms, often involving querying

APIs exposed by the decompiler framework. In all

cases however, this shall involve deﬁning a translation

module from the decompiler output to the constructs

deﬁned in the DSL.

For our analysis of the Ghidra decompiler, we

utilize the Ghidra scripting API to programmatically

scrape and process information about the decompila-

tion of target binary programs. The Ghidra scripting

environment exposes its own collection of data struc-

tures and functions from which we obtain our infor-

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

230

mation.

The strategy employed for the Ghidra translation

is similar to that of our DWARF translation algorithm.

We utilize the Ghidra API to obtain particular infor-

mation about functions, variables, data types, and as-

sociated addresses gathered during the decompilation,

and subsequently translate this information into the

structure of our DSL. Of particular use to our trans-

lation logic is the DecompInterface interface exposed

by the Ghidra API.

4.4 Comparison of Ground Truth and

Decompiler Program Information

With the ability to convert ground truth and decom-

piler (Ghidra) program information into our DSL, we

formulate and implement a strategy to compare the

two resulting ProgramInfo objects. To achieve this,

we create an extension of our DSL that deﬁnes data

structures and functions for capturing comparison in-

formation at different levels.

4.4.1 Data Type Comparison

Given two DataType objects and an offset between

their start locations, we capture nuanced information

about the comparison of the data types.

Deﬁnitions. We deﬁne the metatype of a data type

to be the general “class” of the given data type.

These metatypes include INT, FLOAT, POINTER,

ARRAY, STRUCT, UNION, UNDEFINED, VOID,

and FUNCTION PROTOTYPE. We consider INT,

FLOAT, POINTER, UNDEFINED, and VOID to be

primitive metatypes since they cannot be decomposed

further. ARRAY, STRUCT, and UNION are consid-

ered complex metatypes since these types are formed

via the composition or aggregation of different mem-

bers or subtypes. We consider the ’char’ data type to

be of the INT metatype with size equal to one byte.

Figure 2: The ARTISTE type lattice (Caballero et al., 2012;

Caballero and Lin, 2016).

A primitive type lattice (Caballero and Lin, 2016)

is used to hierarchically relate primitive data types

based on their metatype, size, and signedness (if ap-

plicable). More general types are located higher in

the lattice while more speciﬁc types are located closer

to the leaves. A type lattice may be used to deter-

mine whether two primitive data types are equiva-

lent or share a common parent type. Our framework

leverages a modiﬁed version of the ARTISTE primi-

tive type lattice deﬁned in Caballero et. al (Caballero

et al., 2012) and shown in Figure 2.

We next deﬁne a subset relationship between two

data types. For a given complex data type X and an-

other data type Y with a given offset (possibly 0) be-

tween the location of X and Y in memory, Y is con-

sidered a subset type of X if Y is equivalent to a “por-

tion” of X, consistent with the offset between X and Y.

For example, if X is an array, any sub-array or element

of X such that elements are aligned and the element

types are equivalent to X is considered a subset of X.

If X is a struct or union, any sub-struct or member

with proper alignment and equal constituent elements

is considered a subset of X.

Comparison Logic. Suppose we have two

DataType objects X (ground truth) and Y (decom-

piler) with offset k from the start of X to the start of

Y. The goal is to compute the data type comparison

level for the given comparison. The possible values

for the comparison level are as follows, from lowest

equality to highest equality:

• NO MATCH: No relationship could be found be-

tween X and Y.

• SUBSET: Y is a subset type of complex type X.

• PRIMITIVE COMMON ANCESTOR: In the

primitive type lattice, Y is an ancestor of X. This

indicates that the inferred type Y is a conservative

(more general) form of the ground truth type X.

• MATCH: All properties of X and Y match includ-

ing metatype, size, and possibly subtypes (appli-

cable to pointers, arrays, structs, and unions).

We ﬁrst check the equality of X and Y. If X and Y are

equal, we assign the MATCH comparison code. In the

case that X and Y are both primitive types, we attempt

to compute their shared ancestor in the primitive type

lattice. If Y is an ancestor (more general form) of

X, we assign PRIMITIVE COMMON ANCESTOR. If

X is a complex type, we employ an algorithm to de-

termine whether Y is a subset of X at offset k by

recursively descending into constituent portions of

X starting at offset k (sub-structs, sub-arrays, ele-

ments, members) and checking for equality with Y.

If a subset relationship is found, we assign the SUB-

SET compare level. In all other cases, we assign the

NO MATCH compare level.

A Framework for Assessing Decompiler Inference Accuracy of Source-Level Program Constructs

231

4.4.2 Variable (Varnode) Comparison

There are two main contexts where variable compari-

son occurs. The ﬁrst context is at the top level, where

the set of ground-truth global variables is compared

to the set of decompiler global variables. The second

context for variable comparison is within the context

of a function when we compare local variables be-

tween the ground-truth and the decompiler. In either

case, comparing sets of variables starts with the de-

composition of each Variable object from the DSL

into a set of Varnode objects in our extended DSL.

A Varnode ties a Variable to a speciﬁc storage lo-

cation and the range of PC addresses. The varnodes

for a given variable are directly computed from the

variable’s live ranges discussed previously. In unop-

timized binaries, it is the case that a single Variable

shall decompose into a single Varnode.

With each variable decomposed into its associ-

ated varnodes, we next partition the varnodes from the

ground-truth information and the decompiler based

on the “address space” in which they reside. These

address spaces include the absolute address space, the

stack address space, and the register offset address

space (for a given register). The stack address space

is a special case of the register offset address space

where the offset register is the base pointer which

points to the base of the current stack frame.

For the set of varnodes in each address space, we

ﬁrst order them based on their offset within the ad-

dress space. Next, we attempt to ﬁnd overlaps be-

tween varnodes from the two sources based on their

location and size. If an overlap occurs between two

varnodes, we compute a data type comparison tak-

ing into account the offset between the start locations

of the two varnodes. The data type comparison ap-

proach is described in the previous section. Based

on the overlap status and data type comparison of a

ground-truth varnode X, one of the following varn-

ode comparison levels are assigned (see Figure 3):

• NO MATCH: X is not overlapped with any varn-

odes from the other source.

• OVERLAP: X overlaps with one or more varnodes

from the other space, but the data type compar-

isons are level NO MATCH.

• SUBSET: X overlaps with one or more varn-

odes and each of its compared varnodes has data

type comparison level equal to SUBSET. In other

words, the compared varnode(s) make up a por-

tion of X.

• ALIGNED: For some varnode Y from the other

source, X and Y share the same location and size

in memory; however, the data types of X and Y do

not match. The data types comparison could have

any comparison level less than MATCH.

• MATCH: For some varnode Y from the other

source, X and Y share the same location and size

in memory, and their data types match exactly.

Figure 3: The derivation of varnode comparison level from

varnode recovery status and data type comparison.

The inference of variables with complex data types in-

cluding structs, arrays, and unions proves to be a ma-

jor challenge for decompilers. Recognizing this, we

develop an approach to compare the sets of ground

truth and decompiler variables (varnodes) in their

most “decomposed” forms. An analysis of this sort

helps to recognize how well a decompiler infers the

primitive constituent components of complex vari-

ables. Furthermore, this allows us to recognize the

aggressiveness and accuracy of complex variable syn-

thesis from more primitive components.

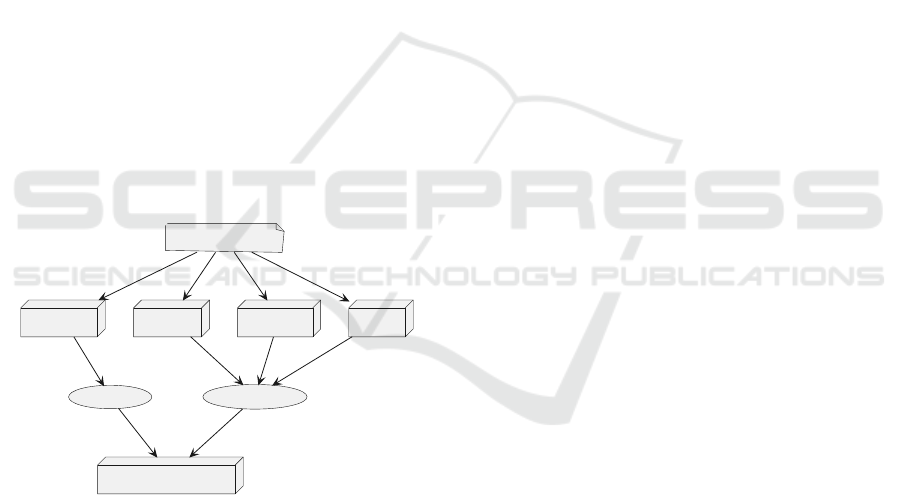
Our approach to recursively decompose complex

types into their primitive components is illustrated in

Figure 4. We ﬁrst implement an approach to recur-

sively strip away the “complex layers” of a varnode

to its most primitive decomposition. This primitive

decomposition produces a set of one or more primi-

tive varnodes as they would appear in memory. For

example, an array of elements is broken down into

a set of its elements (decomposed recursively). A

struct is broken down into a set of varnodes associated

with each of its members (decomposed recursively).

Unions present a special case since the members share

a common, overlapping region of memory. Hence, to

decompose a union, we transform it into an UNDE-

FINED primitive type with the same size as the union.

We apply this primitive decomposition to each

varnode in the sets of ground truth and decompiler

varnodes. With the two sets of decomposed varnodes,

we leverage the same variable comparison approach

described previously to compare the varnodes in these

sets. The resulting comparison information is treated

as a separate analysis from the unaltered varnode sets.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

232

typedef struct {

int day;

int month;

int year;

} Date;

typedef struct {

char* name;

int ssn;

float height;

float weight;

Date dob;

} Person;

Person people[2];

(a) The deﬁnition of a high-

level variable.

(b) The decomposition of a high-level varnode into primitive components.

Figure 4: An example of the recursive decomposition of a high-level varnode.

4.4.3 Function Comparison

The ﬁrst step in function comparison is to deter-

mine whether each ground-truth function is found by

the decompiler. We ﬁrst order the functions from

each source by the start PC address of the function.

Next, we attempt to match the functions from the two

sources based on start address. Any functions from

the ground-truth that are not matched by a decompiler

function are considered “missed”. For any missed

functions, we consider its associated parameters, lo-

cal variables, and data types to also be “missed”.

For each matched function based on start PC ad-

dress, we compute and store information including

the return type, parameter, and local variable com-

parisons. These sub-comparisons leverage the data

type and variable (varnode) comparison techniques

described previously.

5 EVALUATION

To demonstrate our evaluation framework, we target

the Ghidra decompiler (version 10.2). We use all

105 GNU Core Utilities programs (version 9.1) as our

set of benchmarks. For each of the benchmark pro-

grams, we evaluate the accuracy of Ghidra decom-

pilation with the program compiled in three ways:

(1) stripped, (2) standard (not stripped, no debugging

symbols), and (3) DWARF debug symbols included.

We use the results from each of these cases to discern

how the amount of information included in the binary

affects the Ghidra decompiler’s inference accuracy.

To limit the scope of our analysis, we only consider

unoptimized binaries. We use the GCC compiler (ver-

sion 11.1.0) to compile the benchmark programs. The

architecture and operating system of the testing ma-

chine are x86-64 and Ubuntu Linux (version 20.04),

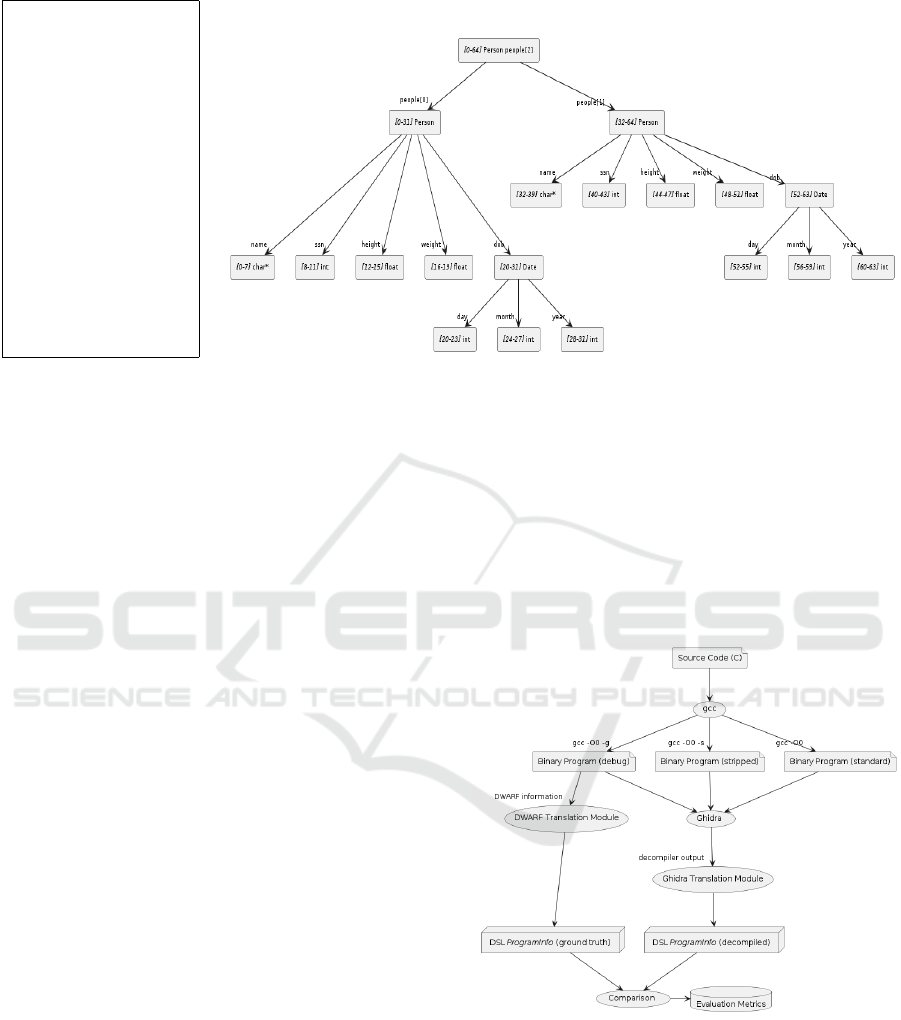
respectively. Figure 5 illustrates our process for gath-

ering evaluation metrics on an individual benchmark

program under each of the compilation conditions.

Figure 5: The process used to gather evaluation metrics on

the Ghidra decompiler for a given benchmark program.

5.1 Function Recovery

Table 1 summarizes of the function recovery statistics

accumulated over all benchmark programs. We ﬁnd

that over the 18139 functions present in the ground

truth, the stripped and standard compilation cases pro-

duce 100% function recovery while the debug case

A Framework for Assessing Decompiler Inference Accuracy of Source-Level Program Constructs

233

fails to recover four functions, resulting in a 99.9%

recovery rate. Upon further examination, we ﬁnd that

all four functions missed are from the factor program.

Table 1: Function recovery by compilation case.

Ground

truth

Functions

found

Functions

missed

Recovery

fraction

strip 18139 18139 0 1.0000

standard 18139 18139 0 1.0000

debug 18139 18135 4 0.9998

To determine the cause of the missed functions,

we further investigate the Ghidra decompilation of

factor and ﬁnd that each of the missed functions re-

sults in a decompilation error, “Low-level Error: Un-

supported data-type for ResolveUnion”. This indi-

cates that an error occurred when attempting to re-

solve a union data type within the decompilation of

these functions. Since this error only occurs in the de-

bug compilation case, it is clear that Ghidra’s parsing

and interpretation of DWARF information contributes

to this error. This same union data type causing the

error is successfully captured and represented in our

ground truth program information and, thus, this is

likely a bug within Ghidra’s resolution logic.

5.2 High-Level Variable Recovery

To evaluate the variable (varnode) recovery accuracy

of the Ghidra decompiler, we ﬁrst measure the in-

ference performance of high-level varnodes, includ-

ing varnodes with complex and aggregate types such

as arrays, structs, and unions. We further measure

the varnode inference accuracy by metatype to deci-

pher which of the metatypes are most and least ac-

curately inferred by the decompiler. This analysis

is performed under each compilation conﬁguration

(stripped, standard, and debug).

In all our varnode evaluation tables, the Varnode

comparison score metric is deﬁned as follows: For

each varnode comparison level, we ﬁrst linearly as-

sign an integer representing the strength of the varn-

ode comparison (NO MATCH = 0, OVERLAP = 1,

SUBSET = 2, ALIGNED = 3, MATCH = 4). We then

normalize these scores to fall within the range zero to

one. Then, for each ground truth varnode, we com-

pute this normalized score. We take the average score

over all ground truth varnodes to obtain the resulting

metric. This metric approximates how well, on aver-

age, the decompiler infers the ground truth varnodes.

In Table 2, we show the high-level varnode recov-

ery metrics for each of the compilation conditions, ag-

gregated from each of the benchmark programs. We

ﬁnd that Ghidra at least partially infers 97.2%, 99.3%,

and 99.6% and precisely infers 36.1%, 38.6%, and

99.7% of high-level varnodes for each of the stripped,

standard, and debug compilation cases, respectively.

In addition, the varnode comparison scores for each

compilation case are 0.788, 0.816, and 0.998, respec-

tively. These metrics indicate that the standard com-

pilation case slightly outperforms the stripped case

in varnode inference while the debug compilation

case results in signiﬁcant improvements over both the

stripped and standard cases, particularly in exact varn-

ode recovery.

In Table 3, we show the inference performance

of high-level varnodes broken down by the metatype

for each compilation conﬁguration. From the stripped

and standard compilation cases, we observe that varn-

odes with metatype INT are most accurately recov-

ered when considering varnode comparison score,

fraction partially recovered, and fraction exactly re-

covered. In the stripped case, the inference of AR-

RAY varnodes shows the worst performance with a

varnode comparison score of 0.315. In the standard

case, varnodes with metatype STRUCT are least ac-

curately recovered with a varnode comparison score

of 0.560, followed closely by ARRAY and UNION.

We see that, for both the stripped and standard compi-

lation cases, the complex (aggregate) metatypes, AR-

RAY, STRUCT, and UNION, show the lowest recovery

accuracy with respect to varnode comparison score.

Among the primitive metatypes, FLOAT shows the

worst recovery metrics for these two cases.

The debug compilation case demonstrates high

relative recovery accuracy across varnodes of all

metatypes when compared to the stripped and stan-

dard cases. Of the primitive metatypes, varnodes of

the FLOAT metatype are perfectly recovered while

varnodes of the INT and POINTER metatypes show

exact recovery percentages of 99.8% and 99.9%, re-

spectively. The complex (aggregate) metatypes, on

average, display slightly lower recovery metrics than

primitive metatypes in the debug compilation case.

The ARRAY metatype reveals the worst varnode com-

parison score at 0.986. The UNION metatype demon-

strates the lowest exact match percentage at 87.5%.

5.3 Decomposed Variable Recovery

In this section, we repeat a similar varnode recovery

analysis over all varnodes; however, we ﬁrst recur-

sively decompose each varnode into a set of primitive

varnodes (see Section 4). We perform this analysis

over all benchmarks for all three compilation cases.

Similar to the high-level varnode analysis, we

show the inference of the decomposed varnodes for

each benchmark and for each compilation conﬁgu-

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

234

Table 2: A summary of high-level varnode recovery by compilation case.

@Level

NO MATCH

@Level

OVER-

LAP

@Level

SUBSET

@Level

ALIGNED

@Level

MATCH

Compare

score

Partial

recovery

fraction

Exact

recovery

fraction

strip 1000 1662 1001 18570 12550 0.788 0.971 0.361

standard 249 1450 613 19029 13442 0.816 0.993 0.386

debug 23 52 24 7 34677 0.998 0.999 0.997

Table 3: A summary of high-level varnode recovery by compilation case and metatype.

@level

NO-

MATCH

@level

OVER-

LAP

@level

SUB-

SET

@level

ALIG-

NED

@level

MATCH

Compare

score

Partial

recovery

fraction

Exact

recovery

fraction

strip

INT 66 48 0 12204 8681 0.850 0.997 0.413

FLOAT 0 56 0 113 22 0.632 1.000 0.115

POINTER 53 4 0 5834 3513 0.839 0.994 0.374

ARRAY 729 597 565 19 228 0.315 0.659 0.107

STRUCT 152 955 432 390 106 0.419 0.925 0.052

UNION 0 2 4 10 0 0.625 1.000 0.000

standard

INT 23 48 0 12248 8680 0.851 0.999 0.413

FLOAT 0 56 0 113 22 0.632 1.000 0.115

POINTER 44 4 0 5836 3520 0.840 0.995 0.374

ARRAY 181 578 352 45 982 0.625 0.915 0.459

STRUCT 1 762 257 777 238 0.560 1.000 0.117

UNION 0 2 4 10 0 0.625 1.000 0.000

debug

INT 13 27 0 4 20955 0.998 0.999 0.998

FLOAT 0 0 0 0 191 1.000 1.000 1.000

POINTER 3 0 0 1 9400 1.000 1.000 1.000

ARRAY 5 17 24 0 2092 0.986 0.998 0.978

STRUCT 2 8 0 0 2025 0.996 0.999 0.995

UNION 0 0 0 2 14 0.969 1.000 0.875

Table 4: A summary of decomposed varnode recovery by compilation case.

@Level

NO MATCH

@Level

OVER-

LAP

@Level

SUBSET

@Level

ALIGNED

@Level

MATCH

Compare

score

Partial

recovery

fraction

Exact

recovery

fraction

strip 139776 31280 0 231267 131593 0.586 0.738 0.246

standard 40187 56605 0 303527 133597 0.703 0.925 0.250

debug 10547 128 0 5 523236 0.980 0.980 0.980

ration in Table 4. Naturally, we expect to see lower

recovery metrics compared to the high-level varnode

analysis since each complex varnode is now analyzed

as a set of its constituent parts. Hence, as a sin-

gle “missed” high-level varnode is translated into a

set of primitive varnodes, each of its constituent is

“missed” in this analysis. As a result, all our scor-

ing metrics, including the varnode comparison score,

varnodes fraction partially recovered, and varnodes

fraction exactly recovered show lower values than in

the high-level analysis. We see that the decomposed

varnode comparison scores for the strip, standard, and

debug compilation cases are 0.586, 0.703, and 0.980,

respectively. The varnodes fraction partially recov-

ered are 73.8%, 92.5%, and 98.0% while the varn-

odes fraction exactly recovered are 24.7%, 25.0%,

and 98.0% across the compilation cases, respectively.

Interestingly, in the stripped compilation case, we ﬁnd

that the number of “missed” decomposed varnodes

(139937) exceeds the number of “exactly matched”

decomposed varnodes (131719). This is largely due

to the quantity of high-level ARRAY and STRUCT

A Framework for Assessing Decompiler Inference Accuracy of Source-Level Program Constructs

235

varnodes that are missed in the stripped case.

We partition the decomposed varnodes by

metatype and show these results in Table 5. The ta-

ble shows that the stripped and standard compilation

cases demostrate the poorest inference performance

in terms of varnode comparison score for varnodes of

metatype FLOAT. However, we ﬁnd that the percent-

age of “missed” INT varnodes is worse than that of

FLOAT in the standard and debug compilation cases,

and is nearly the same in the stripped case. This may

be explained by the prevalence of integer (or charac-

ter) arrays in the Coreutils benchmark programs when

compared to other array types. Recovery accuracy

of the POINTER metatype is comparable to the INT

metatype across the three compilation cases.

5.4 Data Bytes Recovery

Following from our varnode inference analysis, we

next assess the accuracy of the Ghidra decompiler

with regards to the total number of data bytes re-

covered across all varnodes. This analysis provides

an important perspective on data recovery as we can

now correctly account for the size of an improperly in-

ferred varnode. For example, a large array and a sin-

gle character are each represented by a varnode, but

the quantity of data present in the array is often much

greater than that of a character. Hence, it is important

to capture this nuanced view of data recovery.

In Table 6, we show the aggregated data bytes re-

covery metrics across the benchmarks for each com-

pilation case. We see that Ghidra recovers 61.3%,

80.6%, and 99.5% of data bytes in the stripped, stan-

dard, and debug compilation cases, respectively.

5.5 Array Inference Accuracy

The last major analysis we perform targets the array

inference accuracy of the Ghidra decompiler. We aim

to measure the total number of arrays inferred, the

length and size discrepancies, and the similarity of el-

ement types of compared arrays. The descriptions of

the metrics are as follows:

• Ground truth varnodes (metatype=ARRAY): The

number of ground truth varnodes with metatype

of ARRAY.

• Array comparisons: The number of array com-

parisons made when comparing the ground truth

with the decompiler. The decompiler may infer

0 or more array varnodes for each given ground

truth array varnode.

• Array varnodes inferred as array: This measures

how many ground truth array varnodes are com-

pared to at least one decompiler-inferred array

varnode.

• Array varnodes inferred as array fraction: Equiv-

alent to Array varnodes inferred as array divided

by Ground truth varnodes (metatype=ARRAY).

This expresses the fraction of ground truth array

varnodes that are associated with at least one de-

compiler array inference.

• Array length (elements) average error: For each

array comparison, we ﬁnd the absolute difference

in the number of elements inferred by the decom-

piler as compared to the ground truth. We then

average these differences over all array compar-

isons to arrive at this metric.

• Array length (elements) average error ratio: For

each array comparison, we ﬁrst ﬁnd the absolute

difference in the number of elements inferred by

the decompiler as compared to the ground truth.

We then divide this error by the length of the

ground truth array to get the error as a ratio of

the array size. The average of these ratios over all

array comparisons produces this metric.

• Array size (bytes) average error: This metric is

similar to Array length (elements) average error

but measures the error in bytes instead of number

of elements.

• Array size (bytes) average error ratio: This metric

is similar to Array length (elements) average error

ratio but computes the error in bytes instead of

array elements.

• Array dimension match score: This metric is the

number of array comparisons where the decom-

piler inferred the correct number of dimensions

divided by the total number of array comparisons.

• Array average element type comparison score:

Each data type comparison level is ﬁrst mapped

to an integer as follows: NO MATCH = 0, SUB-

SET = 1, PRIMITIVE COMMON ANCESTOR =

2, MATCH = 3. We then normalize these values

such that the range is scaled from 0 to 1. We refer

to this as the data type comparison score. Then,

for each array comparison, we compute the data

type comparison score and subsequently average

the scores across all array comparisons to gener-

ate this metric.

We perform our analysis across all our benchmarks

and for each compilation conﬁguration, resulting in

the data presented in Table 7.

Across all benchmarks, there are 2138 ground

truth arrays present. For each of the stripped, stan-

dard, and debug compilation cases, the number of

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

236

Table 5: A summary of decomposed varnode recovery by compilation case and primitive metatype.

@level

NO-

MATCH

@level

OVER-

LAP

@level

SUB-

SET

@level

ALIG-

NED

@level

MATCH

Compare

score

Partial

recovery

fraction

Exact

recovery

fraction

strip

INT 132910 28812 0 217923 125159 0.586 0.737 0.248

FLOAT 72 73 0 103 22 0.435 0.733 0.081

POINTER 6725 2057 0 13208 6332 0.591 0.763 0.224

standard

INT 40017 46846 0 290436 127505 0.707 0.921 0.253

FLOAT 0 145 0 103 22 0.502 1.000 0.081

POINTER 132 9245 0 12955 5990 0.636 0.995 0.211

debug

INT 10533 124 0 4 494143 0.979 0.979 0.979

FLOAT 0 0 0 0 270 1.000 1.000 1.000

POINTER 14 2 0 1 28305 0.999 1.000 0.999

Table 6: A summary of data bytes recovery.

Ground

truth

Bytes

found

Bytes

missed

Recovery

fraction

strip 1183691 725144 458547 0.613

standard 1183691 954105 229586 0.806

debug 1183691 1177221 6470 0.995

ground truth arrays recognized as arrays by the de-

compiler are 774 (36.2%), 1530 (71.6%), and 2128

(99.5%), respectively. We see that the numbers of ar-

ray comparisons for each compilation case are greater

than these metrics indicating that Ghidra infers some

ground truth arrays to be more than one array.

From the array comparisons, we observe that the

average absolute differential in array length (num-

ber of elements) for the stripped, standard, and de-

bug compilation cases are 134.7, 151.2, and 9.4, re-

spectively. When scaling these errors with respect

to the length of the ground truth arrays in the com-

parisons, the error ratios are 2.84, 5.44, and 0.11

for the compilation cases, respectively. This reveals

that, in the debug case for example, the lengths of

decompiler-inferred arrays are off by an average of

9.4 elements and roughly 11% (greater or less than) of

the size of the ground truth arrays they are compared

to. These metrics, however, fail to capture whether

the decompiler-inferred array has element types of the

correct length. Thus, a similar analysis on the size

(number of bytes) errors yields errors and error ra-

tios of 458.6 (0.91), 239 (0.47), and 9.41 (0.11) for

each compilation case, respectively. This, for exam-

ple, shows that arrays inferred in the standard compi-

lation case have an average absolute byte differential

of 239 and a relative error of 47% compared to the

size of the ground truth array they are compared to.

In this analysis, we also capture a measure of

the array dimension match score for each compila-

tion case. This metric measures the fraction of ar-

ray comparisons where the decompiler-inferred ar-

ray has the same dimensionality (one-dimensional,

two-dimensional, etc.) as the ground truth array.

The stripped and standard compilation cases display

dimensionality match ratios of greater than 97.4%,

while the debug case shows 100% dimensionality in-

ference accuracy.

The last portion of our array recovery analysis fo-

cuses on the element type inference accuracy of the

decompiler-inferred arrays when compared to the el-

ement types of the ground truth arrays. We compute a

data type comparison score between the element types

from each array comparison and average these across

all array comparisons derived from our benchmark

programs. This data type comparison score is sim-

ilar in concept to the varnode comparison score and

is described in Section 4. We ﬁnd that decompiler-

inferred arrays in the stripped, standard, and debug

compilation cases show 0.781, 0.670, and 0.999 av-

erage element type comparison scores, respectively.

The better performance demonstrated in the stripped

case compared to the standard case appears to be a

data artifact resulting from fewer array comparisons

present in the stripped analysis.

5.6 Debug Compilation Case Discussion

Upon examination of our results, the reader may won-

der why the debug compilation case does not produce

100% recovery for varnodes and data bytes across all

benchmarks. The same DWARF information used to

generate the ground truth program information is also

provided to the Ghidra decompiler in this case and

therefore, theoretically, Ghidra should be able to pre-

cisely capture the same program information.

We explore the causes of misses and partial misses

in the debug case across the benchmark programs and

ﬁnd that Ghidra possesses a major limitation in ex-

pressing local variables declared in lexical scopes be-

low the top level of a function. A compiler such

A Framework for Assessing Decompiler Inference Accuracy of Source-Level Program Constructs

237

Table 7: A summary of array recovery by compilation case.

Ground

truth

array

varn-

odes

Array

com-

par-

isons

Array

varn-

odes

in-

ferred

array

Array

varn-

odes

in-

ferred

array

frac-

tion

Array

length

(ele-

ments)

aver-

age

error

Array

length

(ele-

ments)

aver-

age

error

ratio

Array

size

(bytes)

aver-

age

error

Array

size

(bytes)

aver-

age

error

ratio

Array

dimen-

sion

match

score

Array

aver-

age

ele-

ment

type

com-

par-

ison

score

strip 2138 823 774 0.362 134.695 2.845 458.575 0.912 0.979 0.781

standard 2138 1579 1530 0.716 151.156 5.442 239.023 0.475 0.975 0.670

debug 2138 2226 2128 0.995 9.416 0.110 9.416 0.110 1.000 1.000

as GCC may reuse stack address space for variables

associated with disjoint (non-overlapping and non-

nested) lexical scopes. This is a problem for the

Ghidra decompiler as we observe that all variable

declarations are placed at the top level of the func-

tion, ultimately preventing these scope-speciﬁc vari-

ables from being precisely captured. From our man-

ual analysis of the decompiled benchmark programs,

we ﬁnd that this is the cause of the majority of par-

tially missed variables and data bytes in the debug

compilation case. This limitation affects the stripped

and standard compilation cases as well. We consider

this to be a shortcoming and an area of future im-

provement for the Ghidra decompiler.

6 CONCLUSION

In this work, we develop a novel framework for eval-

uating decompiler tools based on the recovery ac-

curacy of high-level program constructs, including

functions, variables, and data types. This framework

includes a domain-speciﬁc language (DSL), devel-

oped in Python, to represent and compare sources of

high-level program information and their association

with binary-level information. In addition, we devise

quantitative metrics for expressing the recovery accu-

racy of high-level program constructs. We leverage

our framework to perform an in-depth evaluation of

the Ghidra decompiler with respect to high-level func-

tion, variable, and data type recovery. This evaluation

is performed over the GNU Core Utilities programs

under three compilation conditions. We also discover

and discuss the implications of two key issues present

in the Ghidra decompiler.

In future work, we will extend our framework to

support the evaluation of optimized binary programs.

We also plan to develop techniques to evaluate be-

havioral correctness and overall clarity of decompiler

output (Liu and Wang, 2020; Naeem et al., 2007). Fi-

nally, we will use our framework to analyze and com-

pare other decompilers.

REFERENCES

Balakrishnan, G. and Reps, T. (2007). Divine: Discovering

variables in executables. In Proceedings of the 8th In-

ternational Conference on Veriﬁcation, Model Check-

ing, and Abstract Interpretation, VMCAI’07, pages

1–28, Berlin, Heidelberg. Springer-Verlag.

Bendersky, E. (2022). pyelftools.

Caballero, J., Grieco, G., Marron, M., Lin, Z., and Urbina,

D. I. (2012). Artiste: Automatic generation of hybrid

data structure signatures from binary code executions.

Caballero, J. and Lin, Z. (2016). Type inference on executa-

bles. ACM Comput. Surv., 48(4).

DWARF Standards Committee (2022). The dwarf debug-

ging standard.

ElWazeer, K., Anand, K., Kotha, A., Smithson, M., and

Barua, R. (2013). Scalable variable and data type de-

tection in a binary rewriter. In Proceedings of the 34th

ACM SIGPLAN Conference on Programming Lan-

guage Design and Implementation, PLDI ’13, pages

51–60.

Hex-Rays (2022). Ida pro.

Lee, J., Avgerinos, T., and Brumley, D. (2011). Tie: Princi-

pled reverse engineering of types in binary programs.

In Network and Distributed System Security Sympo-

sium.

Lin, Z., Zhang, X., and Xu, D. (2010). Automatic reverse

engineering of data structures from binary execution.

In Proceedings of the 11th Annual Information Secu-

rity Symposium, CERIAS ’10.

Liu, Z. and Wang, S. (2020). How far we have come: Test-

ing decompilation correctness of c decompilers. In

Proceedings of the 29th ACM SIGSOFT International

Symposium on Software Testing and Analysis, ISSTA

2020, pages 475–487.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

238

Naeem, N. A., Batchelder, M., and Hendren, L. (2007).

Metrics for measuring the effectiveness of decom-

pilers and obfuscators. In 15th IEEE International

Conference on Program Comprehension (ICPC ’07),

pages 253–258.

National Security Agency (NSA) (2022). Ghidra.

Noonan, M., Loginov, A., and Cok, D. (2016). Polymor-

phic type inference for machine code. In Proceedings

of the 37th ACM SIGPLAN Conference on Program-

ming Language Design and Implementation, PLDI

’16, pages 27–41.

PNF Software (2022). Jeb.

A Framework for Assessing Decompiler Inference Accuracy of Source-Level Program Constructs

239