Anomaly Detection for Multivariate Industrial Sensor Data via

Decoupled Generative Adversarial Network

Chien Wei-Chin and Wang Sheng-De

Department of Electrical Engineering, National Taiwan University, Taipei, Taiwan

Keywords:

Anomaly Detection, Time Series, Deep Learning, Autoencoder, Generative Adversarial Network.

Abstract:

Industrial control systems often contain sensor and actuator devices, which provide monitoring data in the

form of time series, such as bridge vibrations, water distribution systems, and human physiological data. This

paper proposes an anomaly detection model based on autoencoders that can consider time-series relations

of the data. Moreover, the quality of the decoder output is further improved by adding a residual produced

by an extra generator and discriminator. The proposed autoencoder-GAN model and detection algorithm not

only improved the performance but also made the training process of GAN easier. The proposed deep learning

model with the anomaly detection algorithm has been shown to achieve better results on the SWaT, BATADAL,

and Rare Event Classiﬁcation datasets over existing methods.

1 INTRODUCTION

Anomaly detection, i.e outlier detection, has been

an active research area in recent years. The goal

of anomaly detection is to identify the data instance

which is signiﬁcantly different from the majority of

data instances. These data may come in different

forms, for example, image, text or numeric data...etc.

Anomaly detection also has various kinds of applica-

tions, such as Fraud Detection, Cyber-Intrusion De-

tection, Industrial Damage Detection, or even Video

Surveillance.

In recent years, Industrial Control Systems and

IoT applications have been widely deployed in man-

ufacturing factories and our daily lives because of

the advances of hardware technology and computing

power. These devices often contain sensors that keep

track of the monitoring object. For example, a pa-

per manufacturing machine may have sensors moni-

toring the amount of pulp ﬁber or chemicals; power

plants(Zhang et al., 2018a) may have sensors moni-

toring the temperature and pressure; human body may

have smartwatch monitoring functions, such as ECG

or body temperature. These sensors or actuators pro-

duce data in the same period of time continuously.

Consequently, it has become an important issue to de-

tect abnormalities in these data. When abnormalities

occurred in these devices, the corresponding applica-

tions are often accompanied by serious consequences.

For instance, an anomaly occurred in manufacturing

machines can cause the machine to break down, an

ECG anomaly may indicate heart problems of the

smartwatch wearer. Therefore, monitoring or pro-

cessing time series data has been an active research

topic in the past few decades.

In this paper, we mainly focus on anomaly detec-

tion for multivariate time series data. Conventionally,

many domain experts might use hand-crafted rules

to determine a threshold for the monitoring metric

(e.g. temperature, transaction amount). However,

these kinds of methods may be labor-intensive, since

the amount of data keeps growing from time to time.

To deal with this problem, many univariate anomaly

detection methods have been developed, where the

anomalies are determined based on only one metric.

However, a real-world complex system contains lots

of sensors, and these sensors often interact with each

other. Thus, it is often unreasonable to describe a sys-

tem with merely univariate time series data.

This paper focus on MTS data, which can be seen

as a group of univarite times eries data, since MTS

data are more suitable for the real-world complex sys-

tem. We proposed a novel architecture and training

algorithm to predict anomalies in those data. In sum-

mary, our main contributions are:

• We proposed a novel framework to detect anoma-

lies in multi-variate time series (MTS) data, which

uses an LSTM-autoencoder to reconstruct the data

and a generator to produce residuals. The use of

residuals further improves the reconstruction er-

1028

Wei-Chin, C. and Sheng-De, W.

Anomaly Detection for Multivariate Industrial Sensor Data via Decoupled Generative Adversarial Network.

DOI: 10.5220/0011894100003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 1028-1035

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

ror. This model can successfully capture the time-

series dependencies of the data.

• We use a discriminator to calculate anomaly

score, further improving our prediction accuracy.

• GANs are very hard to train. We designed a novel

training algorithm to ease the training of GAN.

• We conduct experiments and evaluation on several

real-world datasets. The proposed method outper-

forms previous autoencoder methods, showing the

effectiveness of our 2 stage training and anomaly

score calculation.

2 RELATED WORK

Anomaly detection is actively and heavily researched

in recent years. Due to the increasing demand and

applications in broad domains, such as risk man-

agement, compliance, security, ﬁnancial surveillance,

health and medical risk, and AI safety, anomaly de-

tection plays increasingly important roles. In anomaly

detection ﬁelds, data can be roughly divided into point

data and time series data. We will discuss which algo-

rithm is suitable for which kind of data type later. In

this chapter, we will divide these algorithms into two

parts, traditional method and deep learning method.

The discussion will be including but not limit to time

series datasets.

2.1 Traditional Method

k-Nearest Neighbor(k-NN) is a machine learning al-

gorithm frequently used for classiﬁcation problems

in data science. It is one of the simplest yet widely

used algorithms with good use cases such as build-

ing recommend systems, face detection applications

and so. Consequently, it has also been widely used in

anomaly detection(Hautamaki et al., 2004). It calcu-

lates the average distance between each samples and

their k nearest neighbors, and uses the average dis-

tance as an anomaly score. However, KNN has the

drawback of its high computation cost and it is often

a challenging problem to determine the value k.

Another common traditional method is Support

Vector Machine(SVM)(Hearst et al., 1998). The ob-

jective of the SVM algorithm is to ﬁnd a decision

boundary that distinctly classiﬁes the data points.

One-Class SVM(Wang et al., 2004) is speciﬁcally

used in anomaly detection. It is a modiﬁcation of

SVM, where algorithm captures the density of the ma-

jority class and classiﬁes examples on the extremes of

the density function as outliers. However, it is often

time consuming for training SVMs on large dataset.

The above mentioned methods do perform well on

point data. However, when it comes to time series

data, those traditional method often lack the ability to

extract temporal dependencies between the data. Fur-

ther experiments have also conducted in this paper to

show that traditional method has relatively low per-

formance.

2.2 Deep Learning Method

In recent years, deep learning has achieved great suc-

cess on many ﬁelds. It has drawn many applications

because of its ability to learn representations from dif-

ferent type of data, such as Image(He et al., 2015),

text(Devlin et al., 2019) or video(Mao et al., 2021)

without hand-coded rules or human domain knowl-

edge. Deep learning also played important roles in

various anomaly detection ﬁelds.

A simple and heuristic way of using deep learning

models for point anomaly detection is by classiﬁca-

tion(Lee et al., 2018). Starting by training the model

on normal data, the model tries to classify each data

to its own class. Later in the testing stage, the abnor-

mal data appears, given that the class has not appeared

in training data, the model tends to produce very low

conﬁdence in every class. Therefore, a threshold can

be set to deﬁne which data is an anomaly. In time

eries data, another simple way is to see this prob-

lem as a forecasting problem. For example, Deep-

AnT (Munir et al., 2019) uses convolutional neural

network (CNN)(Krizhevsky et al., 2012) and history

windows to predict the value of next timestamp. The

data are seen as an anomaly if the Euclidean distance

between the predicted value and the data exceeds a

certain threshold. However, in multivariate time se-

ries data, forecasting may become difﬁcult since there

are multiple variables to predict.

In addition, autoencoder-based deep learning

models(Baldi, 2012) (Bank D., 2021) are widely used

in anomaly detection. The autoencoder model is

trained on normal data and encode input samples to

a smaller dimension. The input is squeezed down to

a lower encoded representation using an encoder net-

work, and then a decoder network decodes the encod-

ing to recreate back the input. Figure 1 shows a sim-

ple illustration of an autoencoder. The aim of an au-

toencoder is to learn a lower-dimensional representa-

tion for higher-dimensional data, typically for dimen-

sional reduction, by training the network to capture

the most important parts of the input data. The target

of this model is such that the Input is equivalent to the

reconstructed output. To achieve this, we minimize

a loss function, namely reconstruction loss, which is

given by the error between the input and the recon-

Anomaly Detection for Multivariate Industrial Sensor Data via Decoupled Generative Adversarial Network

1029

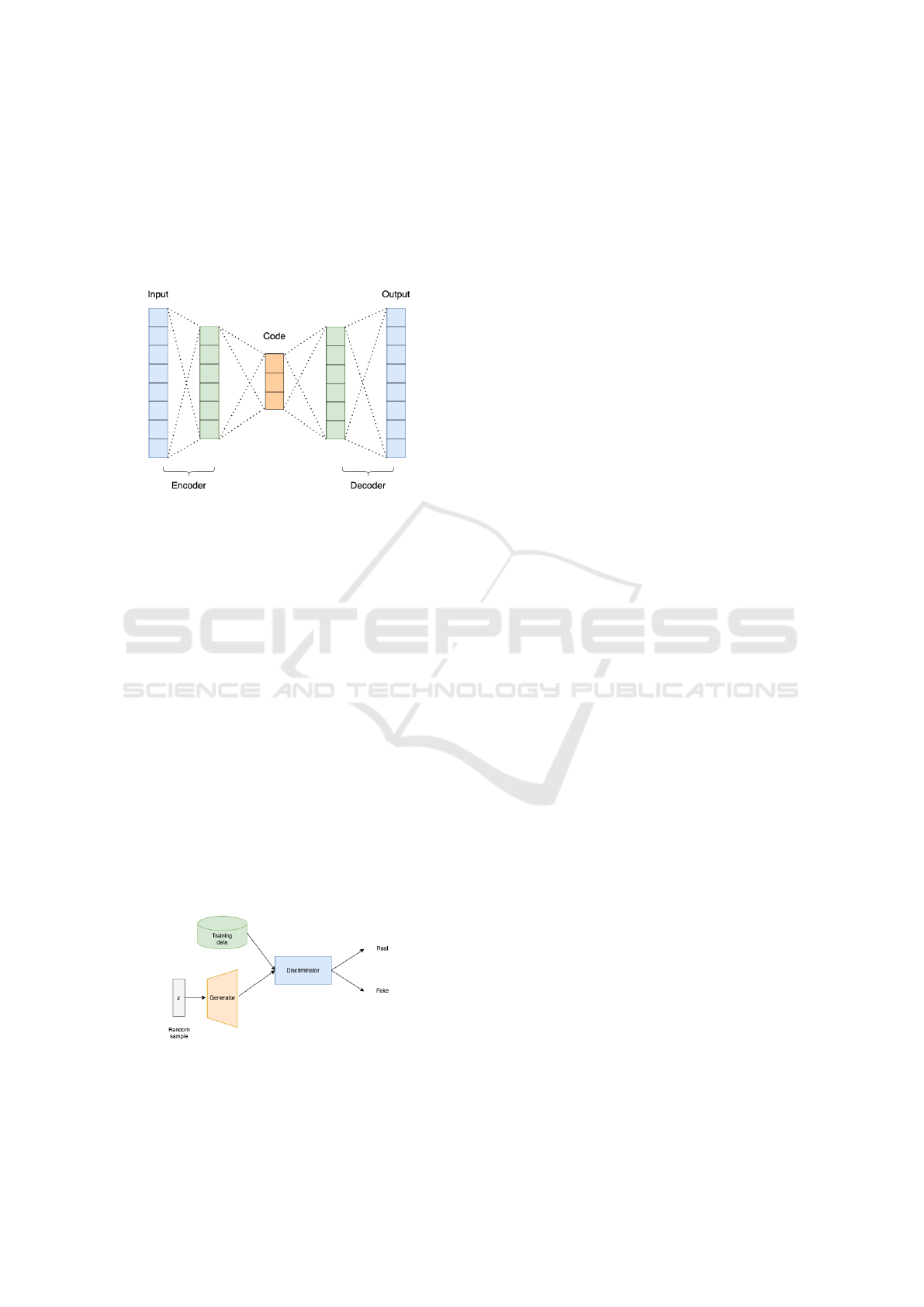
structed output. During an anomaly detection task,

the reconstruction loss is often seen as the anomaly

score. For example, Tung Kieu et.al.(Kieu et al.,

2019) showed the ability of LSTM based autoencoder

models in time series anomaly detection. However,

their work mainly focused on univariate time series

data, which does not consider multivariate data.

Figure 1: A simple illustration of autoencoder.

Generative adversarial networks

(GANs)(Goodfellow et al., 2014) have been driving

signiﬁcant progress in deep learning in recent years.

GANs are neural networks that take random noise as

input and generate outputs that appear to be a sample

from the distribution of the training set. Figure 2

shows a simple structure of GAN. It has also been

used in anomaly detection tasks. AnoGAN(Schlegl

et al., 2017) uses a standard GAN, which trains

only on positive samples. The generator can learn

a mapping from the latent space representation z to

the realistic sample x

′

= G(z) and this learned repre-

sentation is used to map new, unseen, samples back

to the latent space. After training GAN on normal

samples, the generator may learn the distribution

X, which is the normal data. Since the generator

only learns how to generate normal samples, when

an anomalous image is encoded, the reconstruction

can be non-anomalous. During testing time, the

difference between the input and reconstruction data

will be detected as an anomaly.

Figure 2: A simple structure of GAN.

3 PROPOSED APPROACH

3.1 Overview

In this section, we will introduce our proposed

method. The method contains two parts; the ﬁrst part

is the model architecture whereas the second part is

our training and testing algorithm. Before introduc-

ing our method, we’ll ﬁrst describe our problem in

detail in the next section.

3.2 Problem Formulation

The input of multivariate time series data can be for-

mulated as follows:

= [X

t−K

, X

t−K+1

, ..., X

t−1

, X

]

where t is the current timestamp and K is the win-

dow size that we want to look back at from the cur-

rent timestamp. More speciﬁcally, if the sensor pro-

duces a single data every 1 minute and K = 10, that

means we want to consider the data from the previous

10 minutes. X ∈ R

, where m is the dimension of the

data, depending on how many sensors and actuators

the system has.

3.3 Stage 1: Autoencoder

Autoencoders have achieved great performance in the

research of anomaly detection. Therefore, we use

an autoencoder as our backbone model. To further

capture the relation between each timestep, we use

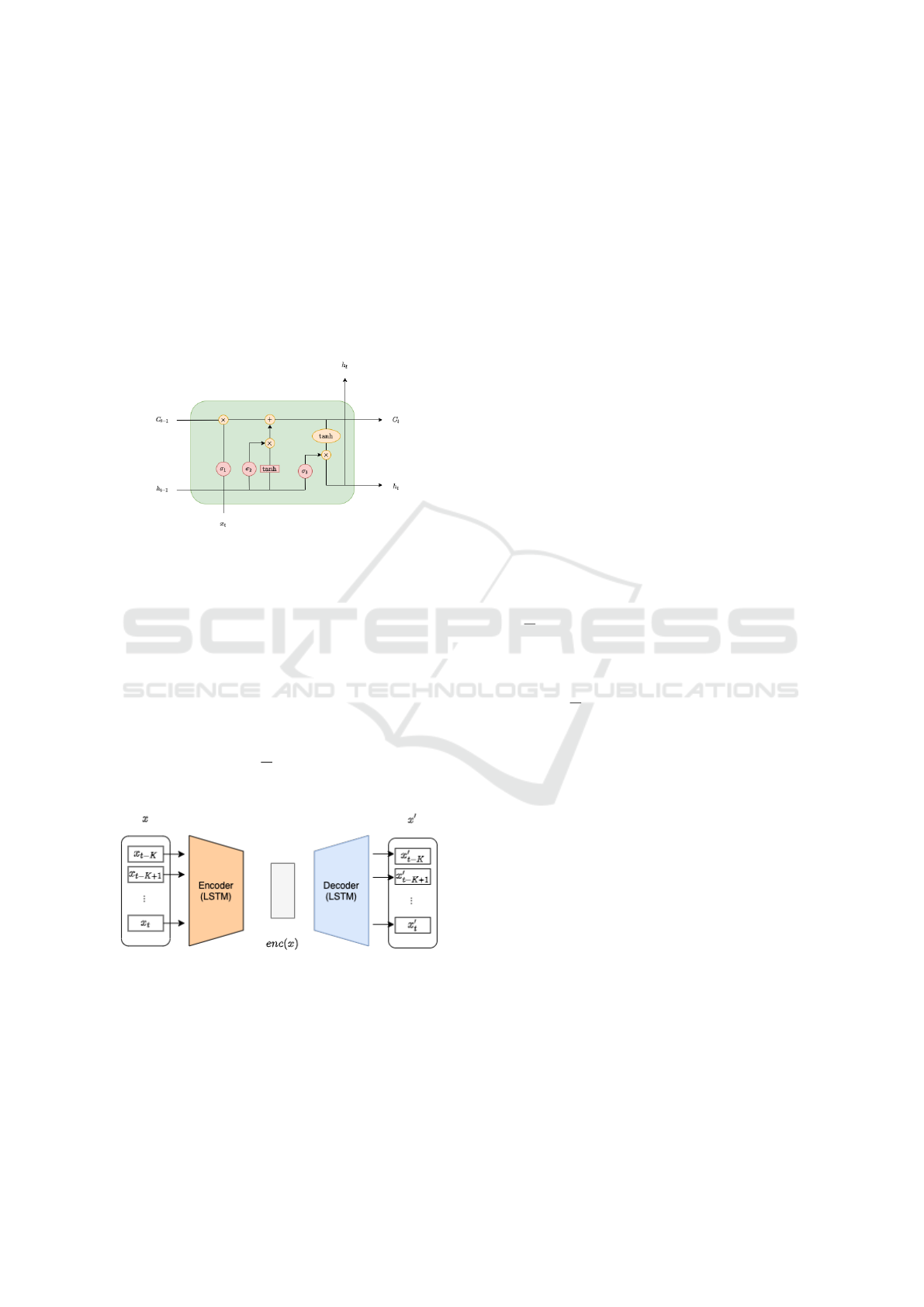
LSTM(Hochreiter and Schmidhuber, 1997) as our en-

coder and decoder model. LSTM network is a vari-

ant of Recurrent Neural Network (RNN). RNN is de-

veloped to deal with complex sequential problems.

LSTM can effectively extracts the long-term tempo-

ral dependencies along with the short-term ones for

time series data by using nonlinear gates. Figure 3 il-

lustrates the typical LSTM structure consisting with a

number of cells. The cell computes the hidden state

∈ R

and the updated cell state c

∈ R

based on

the previous state (c

t−1

, h

t−1

) and the sequential in-

put x

at time step t. Note that the ﬁrst cell uses the

initial states (c

, h

). For each element in the input se-

quence, each layer computes the following function:

= σ(W

i f

+ b

i f

h f

t−1

+ b

h f

)

where f

is the forget gate, a number between 0 and 1

to decide to forget the previous state or not.

The next step is to calculate the current sate. We

ﬁrst calculate the scalar i

to decide the ratio of the

current and previous sate.

= σ(W

+ b

t−1

+ b

)

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

1030

Then we combine them to get the ﬁnal state:

= f

⊙ c

t−1

+ i

⊙ c

Finally, we can get the output h

, which also uses

a scalar o

as an adjusting factor:

= σ(W

+ b

t−1

+ b

)

= o

⊙ tanh(c

)

The above W and b are the weight matrices and

the biases.

Figure 3: A module of LSTM cell.

Consider the input sequence of a multivariate

time series (X

t−K

, X

t−K+1

, ..., X

t−1

, X

) the sequence

is passed into the LSTM encoder, which then is pro-

jected to a low dimension latent vector z. The latent

vector z is then passed to the decoder model to gener-

ate X

′

, which is the reconstructed counterpart of X.

As for the loss function, we use Mean Squared

Error (MSE), where the autoencoder tries to minimize

the objective function:

MSE =

∑

i=1

− x

′

)

(1)

Figure 4: First stage with autoencoder.

4 STAGE 2: GAN

To further improve the reconstruct precision of the

model, in stage 2, we add another pair of generator

and discriminator to guide the output to be more close

to the input. Based on the concept of decoupled learn-

ing(Zhang et al., 2018b), which stabilizes GAN train-

ing by decoupling decoder and generator, we train an-

other generator separately by taking the output of the

encoder as the input of generator. The generator gen-

erates the residual of the data x

′′

as equation (2).

′′

= x

′

+ G(enc(x)) (2)

The parameters of the encoder and the decoder are

ﬁxed in this training stage, which stabilizes the train-

ing process. There are several advantages to doing so.

First, GAN is notoriously hard to train, and the gen-

erator is also hard to learn the reconstruction x

′

from

scratch. With our method, the generator only has to

learn the residual of the reconstruction, which is much

easier. Second, traditional GAN also has the problem

of mode collapse(Thanh-Tung and Tran, 2020). How-

ever, in our training algorithm, the GAN input comes

from the encoder output, which is uniformly sampled

from the data. Further, the generator is trained with a

discriminator in an adversarial network. This discrim-

inator is trained to distinguish whether an input se-

quence, x

′′

, is real or generated by the machine, where

the discriminator tries to minimize function (3):

∑

i=1

[log(D(x

(i)

)) + log(1 − D(G(z

(i)

)] (3)

And the generator minimize the loss function (4)

∑

i=1

[log(1 − D(G(z

(i)

)] (4)

During training, the discriminator will output a like-

lihood of real data in the interval [0, 1]. If D(x

) is

close to 1, it means that the discriminator considers

the input data is real. On the other hand, if D(x

) is

close to 0, the discriminator considers that x is fake

data. The loss of discriminator will be a binary cross-

entropy loss, which is deﬁned as follows:

L = −(y

· log(x

) + (1 − y

) · log(1 − x

) (5)

where y

is the ground-truth answer, with 1 being real

and 0 being fake. Figure 4 and Figure 5 are a sim-

ple illustration of our GAN model, where we use an

LSTM-based autoencoder in the ﬁrst stage and enc(x)

and x

′

are inputs to a GAN in the sencond stage.

5 ANOMALY

DETECTION-TESTING STAGE

At the anomaly detection stage, we use both the au-

toencoder and generator to generate our ﬁnal output.

Anomaly Detection for Multivariate Industrial Sensor Data via Decoupled Generative Adversarial Network

1031

Figure 5: Second stage with autoencoder and GAN.

The time series for anomaly detection is ﬁrst divided

into sub-sequences by a sliding window in the same

step size as the training stage X(x

t−w+1

, ..., x

), which

are input into the encoder. The encoder then trans-

forms the inputs into the latent space and passes the

latent vector to the decoder and generator. The de-

coder outputs the main reconstruction, whereas the

generator outputs the residual. The discriminator out-

puts the possibility of inputs being normal.

The anomaly score utilizes the encoder, the gener-

ator, and the discriminator simultaneously. The score

is composed of reconstruction difference and discrim-

ination results. Since anomalies do not conform to the

distribution of normal data, their anomaly scores will

be relatively high.

Anomaly Score =

∑

i=1

− x

′

) − αDis(x

′

) (6)

Finally, if the anomaly score is larger than a cer-

tain threshold γ, the input is then seen as an anomaly.

We use the validation set to calculate the best thresh-

old for the highest f1 score and apply this threshold at

the testing stage. The equation of the f1 score will be

described in the next section.

6 EXPERIMENTS

6.1 Setup

Dataset: To evaluate our proposed autoencoder-GAN

architecture and the corresponding training algorithm,

we use three different real-world multivariate time se-

ries datasets, as will be reviewed in the following sec-

tion.

6.1.1 SWaT (Secure Water Treatment)

The SWaT(Mathur and Tippenhauer, 2016) dataset is

a small version of a real-world water treatment plant

Algorithm 1: Training and testing algorithm.

Input Time series data (x

(1)

, ..., x

(n)

)

At training Stage 1:

for k training epochs do

sample batch of m examples (x

(1)

, ..., x

(m)

)

from data

Generate z from encoder z = Enc(X)

Generate reconstruction X

′

from decoder X

′

Dec(z)

Update Autoencoder by loss

∑

i=1

− x

′

)

end for

At training Stage 2:

for n training epochs do

sample batch of m examples (x

(1)

, ..., x

(m)

)

from data

Generate z from encoder z = Enc(X)

Generate reconstruction X

′

from decoder X

′

Dec(z)

Generate residual R from generator R = G(z)

Update generator by loss

∑

i=1

[log(1 −

D(X

′

+ R)]

Update discriminator loss

∑

i=1

[log(D(x

(i)

)) + log(1 − D(X

′

+ R)]

end for

At anomaly detection testing stage

Calculate reconstruction X

′

= Enc(Dec(X

test

))

calculate reconstruction residual R =

G(Enc(X

test

)

Calculate discrimination results Dis = Dis(X

′

Calculate anomaly score = MSE(X

test

, (X

′

R)) − αDis(X

′

+ R)

if (score > threshold) then

return anomaly

else

return normal

end if

that produced ﬁltered water. The dataset contains

11 days of continuous operation measured every sec-

ond, where 7 days are collected under normal con-

ditions, and 4 days are collected containing cyber-

attacks. There are a total of 51 variables in the SWaT

dataset, which contains 26 sensors and 25 actuators,

respectively. There are a total of 495000 samples in

the training set (Normal data) and 449919 samples of

testing data (Data with Attack).

6.1.2 BATADAL (BATtle of the Attack Detection

ALgorithms)

BATADAL(Taormina et al., 2018) is a dataset con-

taining hourly measurements of a medium-sized real

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

1032

network, named C-Town. C-Town consists of 388

nodes linked with 429 pipes. There are a total of 43

variables in the dataset, 7 of them are tank water lev-

els, 12 of them are inlet and outlet pressure for actu-

ated valves and pumps.

6.1.3 Rare Event Classiﬁcation

Rare Event Classiﬁcation Dataset (Ranjan et al.,

2019) is a real-world dataset generated from a

pulp-and-paper manufacturing industry. The dataset

records the rare event of paper break 61 sensors ev-

ery two seconds. The dataset starts on May 1st and

ends on May 29th, 1999. Each input sample is la-

beled as “normal” or “break” at each timestamp. For

the data preprocessing, we split the dataset with 80%

of training data with consists of all normal data, 10%

of validation, and 10% of testing data consisting of

data with ”break”.

6.2 Evaluation Metrics

To evaluate our method, we use f1-score as our met-

ric, which is a commonly-used metric in anomaly de-

tection. Since the normal and abnormal might be un-

balanced, it is unnecessary to use accuracy in anomaly

detection. The F1-score is deﬁned as the following:

F1 − Score = 2 ∗

Precision ∗ Recall

Precision + Recall

where Precision is calculated as:

Precision =

T P

T P + FP

and Recall:

Recall =

T P

T P + FN

6.3 Baseline Models for Comparison

OC-SVM. Scholkopf et al.(Sch

olkopf et al., 1999)

propose the kernel-based One-class support vector

machine (OC-SVM) method for outlier detection, the

kernel of the SVM model we use is rbf. We use the

python scikit-learn library to train our model.

FC Autoencoder. Fully connected autoencoder,

which consists of several dense encoding and decod-

ing layer.

Conv 1d Autoencoder. 1d convolution autoencoder

has also been an important method in anomaly detec-

tion(Russo et al., 2020). We expect to use the convo-

lution ﬁlters to capture the time series dependencies.

LSTM Autoencoder. It is also used as our back-

bone model, details are described in section 3. We use

LSTM cells to encode the temporal relation between

the data time sequence.

6.4 Result

In this section, we consider F1 score in comparing

anomaly detection performance. The results of our

proposed anomaly detection of SWaT and BATADAL

are showed in Table 2. As shown in the table, our

proposed method outperforms the LSTM autoencoder

model. The Convolution and vallina autoencoder got

similar results, but not as good as the LSTM autoen-

coder. The One-Class SVM got the worst perfor-

mance. The above result will be further discussed in

the next section.

Table 3 showed our result on the Rare event clas-

siﬁcation dataset. Our propose method also got the

best performance among all compared methods. The

ﬁrst result was provided by the original paper(Ranjan

et al., 2019), which used XGBoost and AdaBoost

models. This method together with OC-SVM didn’t

perform as good as the deep learning based result.

Also, the f1 score is relatively low compared to the

previous two datasets, the reason will also be dis-

cussed in the next section.

6.5 Analysis

As mentioned in the previous section, our proposed

method outperforms other methods. Table 2 shows

the f1 score on SWaT and BATADAL dataset. It can

be seen that the residual generated by generator and

the extra anomaly score calculated by the discrimi-

nator do help in the anomaly detection. The fully-

connected and Conv1d autoencoders have a small per-

formance gap of the LSTM autoencoder. The rea-

son is probably because that the RNN based model

can capture the time series dependencies better than

the convolution and fully-connected models. And

since the fully-connected and convolutional autoen-

coder models have similar results, we assume that the

convolution ﬁlters cannot capture the temporal depen-

dencies of the time series as well as the RNN based

model.

Also, traditional methods such as OC-SVM did

not perform well compared to the DL-based methods.

Moreover, it even took us several times longer to train

OC-SVM models on the SWaT dataset. This showed

that deep learning based models have their advantages

with these kind of data, especially when the data is

large.

Lastly, the performance on Rare Event dataset is

relatively low compared to the other two datasets. Ta-

ble 3 shows the visualization result. The possible rea-

son may be that the dataset is hard to predict, since

the result from the original paper(Ranjan et al., 2019)

also got very low score (with only 0.114 of f1 score).

Anomaly Detection for Multivariate Industrial Sensor Data via Decoupled Generative Adversarial Network

1033

Table 1: Hyperparameters of different methods.

Method Hyperparameter Value

FC AE

Architecture 3 Encoding Layers , 3 Decoding Layers

ReLU for Encoding and Decoding,

Tanh for output

Optimizer, Loss Adam, MSE

Conv AE

Architecture 3 Conv1d Encoding Layers with

max-pooling and ReLU,

3 Conv1d Decoding Layers with

upsampling and ReLU,

Optimizer, Loss Adam, MSE

LSTM AE

Architecture 1 LSTM encoding Layers,

1 LSTM Decoding Layers

1 Dense layer for output projection

Optimizer, Loss Adam, MSE

Proposed

Architecture Same with LSTM AE

Generator 1 LSTM layer,

1 Dense layer for output projection

Discriminator 1 LSTM layer,

1 Dense layer for classiﬁer

Optimizer, Loss Adam, MSE

Table 2: The f1 score on SWaT and BATADAL dataset.

Model SWaT BATADAL

OC-SVM 0.2169 0.163

FC Autoencoder 0.6737 0.425

Conv 1d Autoencoder 0.6771 0.422

LSTM Autoencoder 0.6943 0.435

Proposed Method 0.7182 0.447

Table 3: The f1 score on Rare Event classiﬁcation dataset.

Model Rare Event Classiﬁcation

C. Ranjan et al. 0.114

OC-SVM 0.199

FC Autoencoder 0.2522

Conv 1d Autoencoder 0.2535

LSTM Autoencoder 0.2652

Proposed Method 0.2773

Table 4: Statistics of the datasets.

Dataset Training

size

Testing

size

Anomaly

ratio

SWaT 495000 449919 12%

BATADAL 8756 4177 11%

Rare Event 14718 3680 3.3%

Another possible reason is that the anomaly ratio is

relatively low in the dataset (with only 3 %), com-

pared to SWaT and BATADAL, which has 12% and

11%, respectively, as shown in Table 4. Which makes

the prediction much harder.

7 CONCLUSION

In this paper, we present a novel method combining

autoencoder and generative adversarial network as the

anomaly detection model for multivariate time series,

which use a generator to add residual and discrim-

inator to add an anomaly score. We evaluated our

method on three different datasets with different data

sizes or anomaly ratios. Compared to the LSTM au-

toencoder, our experiments showed that the proposed

method can surely improve the performance on the

multivariate time series datasets. Also, our training al-

gorithms successfully stabilize the GAN training pro-

cess, which made the GAN training process easier. In

the future, we plan to try more complicated models in

our experiments to further improve our performance.

For example, more layers of LSTM encoder and de-

coders, or even Transformer layers (Vaswani et al.,

2017). Also, we expect to examine our method on

more kinds of MTS datasets in the future.

REFERENCES

Baldi, P. (2012). Autoencoders, unsupervised learning, and

deep architectures. In Guyon, I., Dror, G., Lemaire,

V., Taylor, G., and Silver, D., editors, Proceed-

ings of ICML Workshop on Unsupervised and Trans-

fer Learning, volume 27 of Proceedings of Machine

Learning Research, pages 37–49, Bellevue, Washing-

ton, USA. PMLR.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

1034

Bank D., Koenigstein N., G. R. (2021). Autoencoders. [On-

line]. Available: https://arxiv.org/abs/2003.05991

Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K.

(2019). Bert: Pre-training of deep bidirectional trans-

formers for language understanding. [Online]. Avail-

able: https://arxiv.org/abs/1810.04805

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial networks. [On-

line]. Available: https://arxiv.org/abs/1406.2661

Hautamaki, V., Karkkainen, I., and Franti, P. (2004). Out-

lier detection using k-nearest neighbour graph. In Pro-

ceedings of the 17th International Conference on Pat-

tern Recognition, 2004. ICPR 2004., volume 3, pages

430–433 Vol.3.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep resid-

ual learning for image recognition. [Online]. Avail-

able: https://arxiv.org/abs/1512.03385

Hearst, M., Dumais, S., Osuna, E., Platt, J., and Scholkopf,

B. (1998). Support vector machines. IEEE Intelligent

Systems and their Applications, 13(4):18–28.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural computation, 9(8):1735–1780.

Kieu, T., Yang, B., Guo, C., and Jensen, C. S. (2019).

Outlier detection for time series with recurrent au-

toencoder ensembles. In Proceedings of the Twenty-

Eighth International Joint Conference on Artiﬁcial In-

telligence, IJCAI-19, pages 2725–2732. International

Joint Conferences on Artiﬁcial Intelligence Organiza-

tion.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).

Imagenet classiﬁcation with deep convolutional neu-

ral networks. In Pereira, F., Burges, C. J. C., Bottou,

L., and Weinberger, K. Q., editors, Advances in Neu-

ral Information Processing Systems 25, pages 1097–

1105. Curran Associates, Inc.

Lee, K., Lee, H., Lee, K., and Shin, J. (2018). Train-

ing conﬁdence-calibrated classiﬁers for detecting

out-of-distribution samples. [Online]. Available:

https://arxiv.org/abs/1711.09325

Mao, F., Wu, X., Xue, H., and Zhang, R. (2021). Hi-

erarchical video frame sequence representation with

deep convolutional graph network. Computer Vision

– ECCV 2018 Workshops, page 262–270.

Mathur, A. P. and Tippenhauer, N. O. (2016). Swat: a wa-

ter treatment testbed for research and training on ics

security. In 2016 International Workshop on Cyber-

physical Systems for Smart Water Networks (CySWa-

ter), pages 31–36.

Munir, M., Siddiqui, S. A., Dengel, A., and Ahmed, S.

(2019). Deepant: A deep learning approach for un-

supervised anomaly detection in time series. IEEE

Access, 7:1991–2005.

Ranjan, C., Reddy, M., Mustonen, M., Paynabar, K., and

Pourak, K. (2019). Dataset: Rare event classiﬁca-

tion in multivariate time series. [Online]. Available:

https://arxiv.org/abs/1809.10717

Russo, S., Disch, A., Blumensaat, F., and Villez, K. (2020).

Anomaly detection using deep autoencoders for in-

situ wastewater systems monitoring data. [Online].

Available: https://arxiv.org/abs/2002.03843

Schlegl, T., Seeb

ock, P., Waldstein, S. M., Schmidt-

Erfurth, U., and Langs, G. (2017). Unsupervised

anomaly detection with generative adversarial net-

works to guide marker discovery. [Online]. Available:

https://arxiv.org/abs/1703.05921

Sch

olkopf, B., Williamson, R. C., Smola, A. J., Shawe-

Taylor, J., Platt, J. C., et al. (1999). Support vector

method for novelty detection. In NIPS, volume 12,

pages 582–588. Citeseer.

Taormina, R., Galelli, S., Tippenhauer, N. O., Salomons,

E., Ostfeld, A., Eliades, D. G., Aghashahi, M., Sun-

dararajan, R., Pourahmadi, M., Banks, M. K., et al.

(2018). Battle of the attack detection algorithms: Dis-

closing cyber attacks on water distribution networks.

Journal of Water Resources Planning and Manage-

ment, 144(8):04018048.

Thanh-Tung, H. and Tran, T. (2020). On catas-

trophic forgetting and mode collapse in genera-

tive adversarial networks. [Online]. Available:

https://arxiv.org/abs/1807.04015

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, L., and Polosukhin, I.

(2017). Attention is all you need. [Online]. Available:

https://arxiv.org/abs/1706.03762

Wang, Y., Wong, J., and Miner, A. (2004). Anomaly in-

trusion detection using one class svm. In Proceedings

from the Fifth Annual IEEE SMC Information Assur-

ance Workshop, 2004., pages 358–364.

Zhang, C., Song, D., Chen, Y., Feng, X., Lumezanu,

C., Cheng, W., Ni, J., Zong, B., Chen, H., and

Chawla, N. V. (2018a). A deep neural network

for unsupervised anomaly detection and diagnosis in

multivariate time series data. [Online]. Available:

https://arxiv.org/abs/1811.08055

Zhang, Z., Song, Y., and Qi, H. (2018b). Decoupled learn-

ing for conditional adversarial networks. [Online].

Available: https://arxiv.org/abs/1801.06790

Anomaly Detection for Multivariate Industrial Sensor Data via Decoupled Generative Adversarial Network

1035