Accuracy Assessment of Direct Georeferencing Using UAV Matrice

210 RTK V2 on Gully Santiš, Island of Pag (Croatia)

Katarina Glavačević

, Ivan Marić

and Ante Šiljeg

Independent Researcher, Ludwigshafen am Rhein, Germany

Department of Geography, University of Zadar, Zadar, Croatia

Keywords: Direct Georeferencing, Matrice 210 RTK V2, Absolute Accuracy, D-RTK 2, UAV Photogrammetry.

Abstract: Rapid development and increased availability of unmanned aerial vehicles (UAVs) resulted in the exponential

use of these systems in many scientific fields and activities. However, the application of photogrammetric

models derived using the Structure from Motion (SfM) technique largely depends on the use of ground control

points (GCPs). Since the acquisition of the GCPs requires the use of high-quality total stations or GNSS-RTK

receivers, these procedures generally take up a lot of time. Execution of a photogrammetric process without

using the GCPs is called direct georeferencing, and it is becoming an increasingly popular method. In this

research, we tested three methods of RTK positioning using the system of the Matrice 210 RTK V2 and D-

RTK 2 mobile station. The following methods were tested: (a) D-RTK 2 as a base station; (b) D-RTK 2

correction with the third-party base station; (c) network NTRIP corrections CROPOS. An absolute accuracy

assessment of each RTK positioning mode was done using 10 check points (CPs). By calculating the total

RMSE, it was determined that (b) and (c) RTK positioning modes have a centimeter level of accuracy (<10

cm). In this research, it is determined that the tested UAV system for direct georeferencing can be used in a

wide range of geographical applications and other disciplines where absolute accuracy of centimeter-level is

required.

1 INTRODUCTION

The knowledge of accurate information about the

Earth's surface has always played a key role in the

development of scientific disciplines and activities

(Guptill and Morrison, 1995, Šiljeg et al., 2018).

Obtaining reliable spatial data is primarily based on

the development of modern geospatial technologies

(GST) (Linder, 2009). Accurate, precise, and fast

collection of topographic data is becoming the basis

of physical geography (Smith et al., 2016), other

sciences, and sub-disciplines (Pike et al., 2009).

Aerial, UAV and terrestrial photogrammetry is

becoming a dominant technology in the study of

various spatio-temporal changes. In recent years,

obtaining high-resolution topographic models has

been based on the application of UAV

photogrammetry (Stott et al., 2020) and the SfM

technique, which significantly accelerated the

photogrammetric process (Masiero et al., 2017). The

fundamental task of all photogrammetric techniques

is to derive the geometric features of a certain object

or scene (Dittrich et al., 2017). However, the

dominance of UAV/SfM photogrammetry is limited

by the need to mark and collect ground control points

(GCPs) and check points (CPs) using quality and

expensive GNSS receivers (Carbonneau and Dietrich,

2016). The GCPs and CPs need to be marked and

measured according to the optimal distribution, which

can be an extremely long and expensive process

(Sanz-Ablanedo et al., 2018). It is generally

considered that increasing the number of GCPs

results in better model accuracy (Oniga et al., 2018).

In the context of spatio-temporal analysis, additional

problems arise due to the fact that GCPs can move or

disappear due to surface deformations or weather

conditions. Ultimately, a major limitation of this

classic aerial photogrammetry approach is that

sometimes it is not possible to achieve optimal GCPs

and CPs distribution due to security or practical

reasons (e.g. landslides, flood, frozen or swampy

areas, etc.) (Zhang et al., 2019), the unavailability of

the GNSS receiver, high energy relief, shortage of

time, etc. Although the „classical“ way of performing

aerial photogrammetry is recognized as the most

important data collection method in the creation of

topographic maps, it has obvious disadvantages in

long production time, inefficiency, and dependence

184

Glava

cevi

c, K., Mari

c, I. and Šiljeg, A.

Accuracy Assessment of Direct Georeferencing Using UAV Matrice 210 RTK V2 on Gully Santiš, Island of Pag (Croatia).

DOI: 10.5220/0011933700003473

In Proceedings of the 9th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2023), pages 184-191

ISBN: 978-989-758-649-1; ISSN: 2184-500X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

on GCPs, etc. (Yuan and Zhang, 2008). A new

acceleration of the photogrammetric process comes

with the appearance of the direct georeferencing (DG)

method (Bláha et al., 2011, Rehak et al., 2013). The

DG method does not require GCPs acquisition and

aerotriangulation (AT) in the process of model

derivation (Rizaldy and Firadus, 2012). DG

represents a photogrammetric process in which

modeling is based on the direct measurement of six

exterior orientation (EO) parameters, that is, the

position (XYZ) of the camera, which is measured by

the GNSS receiver, and the orientation/inclination of

the camera (pitch, roll, and yaw), which is measured

by the inertial measurement unit (IMU), in real-time

(Rizaldy and Firadus, 2012). However, the absence of

GCPs represents a significant challenge in assessing

the model’s quality. The development of more

affordable UAV platforms capable of producing

models using the DG approach has begun in recent

years. Therefore, the research about accuracy and

suitability of such an approach as a full-fledged

topographic imaging method is currently increasing

(Liu et al., 2022, Zeybek, 2021, Carbonneau and

Dietrich, 2016). Therefore, this research examines the

accuracy of the DG approach using the popular UAV

(Matrice 210 RTK V2 and D-RTK2) platform. The

camera Zenmuse X7 DL-S 16mm F2.8 was used. The

main goal of the research was to assess the accuracy

of the DG method using the different modes of RTK

positioning: (a) D-RTK 2 as a base station; (a

) D-

RTK 2 as a base station with the addition of a few

GCPs; (b) D-RTK 2 correction with the third-party

base station STONEX S10; (c) Network NTRIP

corrections CROPOS.

Also, the following scenarios were tested:

(d) a classical photogrammetric approach using

GCP and CP; (e) method using embedded navigation

sensors (GPS/GNSS and IMU-MEMS) in UAVs.

The purpose of the research was to provide

guidelines for the use of this setup at various scale

(resolution). In this case study, the testing was not

performed under the best possible conditions, because

such conditions, especially in the case where the

application of direct georeferencing is required, are

not always possible. Therefore, the goal was to

determine whether this sensor system corresponds to

the manufacturer's claims in conditions (light wind,

vertically dissected terrain) that are not ideal.

1.1 Gully Santiš (Pag Island)

The research area is gully Santiš (1163 m²), located

on the southeastern coast of the Island of Pag

(Croatia) (Figure 1). The island is dominated by

Cretaceous-Paleogene carbonate deposits of

limestone and dolomite, smaller parts of Paleogene

flysch, and younger Quaternary deposits (Magaš,

2011). The gully was formed on accumulated thick

brown soil, the deposits of which are prone to surface

loss of material. The dimensions of the gully Santiš

are 80 x 15 m, with an area of 1163 m

and a drainage

basin with an area of 0.18 km

(Šiljeg et al. 2021).

Figure 1: Location of gully Santiš in Croatia, Pag.

2 MATERIALS AND METHODS

The research methodology is divided into three main

steps that include: (A) marking and measurement of

ground control and check points (GCPs and CPs)

within the research area; (B) derivation of digital

surface models (DSM) and digital orthophoto (DOP)

using: (b

) classical photogrammetric image

workflow process (with GCPs and CPs) and (b

)

through different ways of RTK positioning (1 - D-

RTK2 as base station; 2 - D-RTK2 correction with a

third party base station; 3- network NTRIP correction

with CROPOS); (C) accuracy assessment of the

derived models.

2.1 Connection of the UAV System

The D-RTK 2 mobile station was placed on an open,

elevated area and was stabilized by a tripod using the

built-in level. Open space means an environment

without obstacles within a >200 m from the source of

high-power radio emissions. After installation D-

RTK 2 was not moved. The mobile station was turned

on, and a constant green light on the power indicator

Accuracy Assessment of Direct Georeferencing Using UAV Matrice 210 RTK V2 on Gully Santiš, Island of Pag (Croatia)

185

indicated that D-RTK2 was connected to ≥10

satellites. Then the (4th) operating mode was

selected, which is intended for work with Matrice 210

RTK V2. Successful connection is done if the

orientation and positioning status of the is in FIX

mode. The UAV takeoff location had to be visible

from the base station location. The selected location

in the middle of the gully was visible from the D-

RTK2 mobile station. UAV mission planning was

done in the DJI Pilot application, single-grid missions

were planned with a front and side photo overlap of

80%. The flight height was set at 30 m. The flight

speed in the mission was 2 m/s.

2.1.1 D-RTK 2 as Base Station

The first tested method of RTK positioning was the

D-RTK2 as base station. This method uses only the

D-RTK2 base station to transmit RTK information

directly to the UAV (Fig. 2). The base station is

turned on and it connects to the controller and the

UAV. The primary benefit of this method is very easy

set up. This workflow does not require an internet

connection. If the default coordinates measured with

D-RTR2 are used in the Z value, the height of the base

station does not have to be added. The D-RTK2

measures long. and lat. in decimal degrees (DD), and

altitude as height above ellipsoidal height (HAE

Figure 2: D-RTK2 as a base station.

2.1.2 D-RTK 2 Coordinate Correction with

a Stonex S10

In the second method of RTK positioning, the precise

determination of the D-RTK2 coordinates was

performed by using the STONEX S10 GNSS

receiver, which was mounted using a suitable tripod

on the same location as D-RTK2 (Fig. 3).

Height Above Ellipsoid

Figure 3: D-RTK2 coordinate correction with a STONEX

S10.

After the initialization of the receiver, the

measurement of the point where the D-RTK2 was

mounted lasted 2 min (10 measurement epochs). The

measured coordinates, using STONEX S10 and

NRTK modality, were entered in the DJI GO

application. The precision of the measurement was in

accordance with the official specifications of the

STONEX S10. Since there is no place in the

application to enter the height of the base station, the

measured coordinates representing the antenna phase

center (APC) of the D-RTK2 were entered (1.802 m)

(Buonanno, 2019). The height of the antenna is

calculated as follows: the tripod provided by DJI has

a height of 1,660 m from the end to the bottom of the

antenna. Adding the distance between the base of the

antenna and the phase center of the antenna (0.1419

m) gives a value of 1.802 m, which is added to the

reference height in the DJI GS RTK settings. In

summary, the measured coordinates representing the

phase center of the antenna (APC) D-RTK 2 are

entered. Table 1 shows the differences in the

coordinates of the location where the D-RTK 2

mobile station was mounted, measured by the

STONEX S10 and the D-RTK2 mobile station. The

D-RTK2 measured the height of the antenna almost

40 cm lower. The differences for longitude are about

73.3 cm and for latitude 43.9 cm. Therefore, the

assumption was that the model generated by RTK

positioning using the first operating mode, i.e. where

only D-RTK2 is used as a base station, will deviate

from the model derived by the classic approach in

similar values (long. ≈ 73.3 cm, lat. ≈ -43.869 cm,

elev. ≈ 38,60 cm).

GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management

186

Table 1: Differences in base station coordinates measured

with D-RTK2 (mode 1) and Stonex S10 (mode 2).

WGS84 X (dd) Y (dd) Z (m)

D-RTK2 15.19281974 44.37452990 69.331

Stonex S10 15.19281054 44.37453387 69.717

Diff. (cm) 73.366 -43.869 -38.60

2.1.3 Network NTRIP Correction with

CROPOS

In the third method of RTK positioning, the

Networked Transport of RTCM via the Internet

Protocol (NTRIP) connection option was used (Fig.

4). This methodology uses NTRIP without a base

station of any kind and provides live RTK data using

an NTRIP stream connected to the Internet. This

process requires an internet connection at the

recording location via local Wi-Fi, hotspot, or

dedicated 5G connection to the controller. The

advantage of this method is that using a networked

workflow requires the least amount of physical

equipment at the recording location. The biggest

disadvantage is the need for an active, reliable

internet connection. Even a brief interruption of the

Internet connection can cause problems.

Figure 4: Network NTRIP correction with CROPOS.

2.2 Marking and Acquisition of GCPs

and CPs

The arrangement of GCPs/CP was determined by the

type of shallow brown soil, extremely dynamic and

subject to erosion that prevails in the research area.

Furthermore, certain parts of the gully are extremely

vertically dissected with a large slope, which

complicates the process of marking and acquisition of

GCPs and CPs. The majority of points were marked

on limited rocky surfaces, which are characterized by

small surface slopes. A total of 10 points were marked

and collected in the research area in order to verify

the accuracy of the derived models. The coordinates

were collected using a STONEX S10 GNSS receiver

which in RTK mode has a horizontal accuracy of 0.8

cm and a vertical accuracy of 1.5 cm. After the

initialization, the points were measured in one

independent measurement, and each point was

measured for 2 min (10 measurement epochs) (Fig.

5). The coordinates of the marked points were

collected in the WGS84 coordinate system in decimal

degrees (DD), while the altitude was collected as

ellipsoidal height (HAE).

Figure 5: Acquisition of GCPs and CPs.

2.3 Processing of UAV Images

In each mission about 240 images were collected.

Flight time of each mission was 14 minutes. UAV

images were processed using Agisoft Metashape

1.5.1. software. The process consisted of seven

commonly known steps in the SfM photogrammetry

process (Marić et al., 2019): (1) image quality

checking; (2) camera accuracy settings; (3) align

photos; (4) gradual selection and optimization of the

camera position; (5) adding GCPs and/or; (6) build a

dense cloud, mesh, and texture; (7) build and export

digital surface model (DSM), and digital orthophoto

(DOP). The quality of all photos was assessed. Those

photos with a quality value < 0.5 were deleted. In the

first step (align photos) about 20 million tie points

were generated. The accuracy parameter in align

photos is set to high, and the key point limit and ie

point limit are set to 40000 and 8000. Interior camera

calibration parameters were determined

automatically after alignment. Using the gradual

selection, all tie points with reprojection error greater

than 0.2 and reconstruction uncertainty greater than

20 were deleted. The GCPs and CPs were added to

the reconstructed sparse point cloud. In some models,

all points served as GCPs, while in others, all points

served as CPs. In cases where GCPs/ CPs were added,

and the reconstructed model was updated, it was

observed that certain camera locations (photos) have

a significant positioning error (e.g. >40 cm).

Therefore, a smaller number of these photos were

Accuracy Assessment of Direct Georeferencing Using UAV Matrice 210 RTK V2 on Gully Santiš, Island of Pag (Croatia)

187

deleted, which were mostly located at the edges of the

mission. This process decreased the model error.

DSM and DOP were derived from the point cloud,

which had approximately 101 million points (Fig. 6).

Figure 6: Derived dense point cloud.

3 RESULTS

3.1 GCP and Check Points

All points were collected using GNSS Stonex S10

and NRTK modality, and the precision of the

measurement was calculated from 10 measurements

collected at each point. Table 2 shows the mean range

value for XYZ coordinates. The precision of the

collected points corresponds to the specified factory

precision of the receiver. The X coordinate deviates

on average by 0.83 cm, the Y coordinate the same,

and the Z coordinate slightly higher (Table 2).

Table 2: The average range of XYZ coordinate values.

Range (cm)

GCP/CP X Y Z

A 0.61 0.69 0.90

B 0.73 0.77 1.80

D 0.37 0.80 0.7

E 0.90 1.06 1.00

F 1.18 0.80 0.90

G 0.71 0.88 1.2

H 1.13 0.74 1.30

I 1.01 0.91 0.50

J 0.97 0.91 1.00

0.72 0.70 0.70

MEAN 0.83 0.83 1.00

3.2 The Classical Photogrammetric

Methods

The classic method refers to the dominant way of

performing the UAV photogrammetry process (Fig.

7). In this image processing workflow, the D-RTK 2

mobile station was not used. The collected GCPs

(n=6) were used to position the reconstructed model

in a global coordinate system, while the CPs (n=4)

were used to check the accuracy of the model.

The recorded surface area was 0.0143 km². The

ground samplig distance (GSD) of the DOP was 6.62

mm, and the DSM was 1.32 cm. Point density was

5700 points/m². From the added CPs the root mean

square error (RMSE) was calculated. The RMSE for

the X coordinate

was 1.33 cm, for the Y 1.28 cm, and

for the Z 2.76 cm. The total RMSE of this model was

3.32 cm.

Figure 7: Derived DOP and DSM (classical method).

3.3 Direct Georeferencing

3.3.1 D-RTK 2 as Base Station

In this method of RTK positioning the D-RTK 2

mobile station was used. All collected points were

used as CP (n=10) (Fig. 8). The RMSE for the X

coordinate was 75.89 cm, for the Y 34.98 cm, and for

the Z 26.94 cm. The total RMSE was 87.80 cm. The

large total RMSE is not surprising the difference in

the coordinates of the mobile station location

measured by D-RTK 2 itself and those by Stonex S10

is known (Table 1). The total RMSE was extremely

large (87.809 cm) due to the incorrect measurement

of the location of D-RTK 2. In this reconstructed

model, a smaller number of GCPs were added, with

the aim of determining their impact on model

accuracy. An iterative assessment of the accuracy of

the model was performed (Table 3), first with one,

then two, and finally with three GCP added. Thus, in

the 1

scenario, nine CPs were used, in the 2

eight,

and in the 3

seven CPs.

Table 3: The accuracy of different scenarios (D-RTK +

GCPs).

X error

(cm)

Y error

(cm)

Z error

(cm)

Total

(cm)

D-RTK2

+1GCP

20.37 11.68 31.99 39.68

D-RTK2

+2GCP

21.57 9.36 23.05 32.93

D-RTK2

+3GCP

15.10 7.36 9.08 19.09

It can be seen that the total RMSE decreases with

the addition of GCPs. By adding just one GCP, the

total RMSE decreased by 48.129 cm. The second

GCP reduced the RMSE by 6.75 cm, and the third by

GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management

188

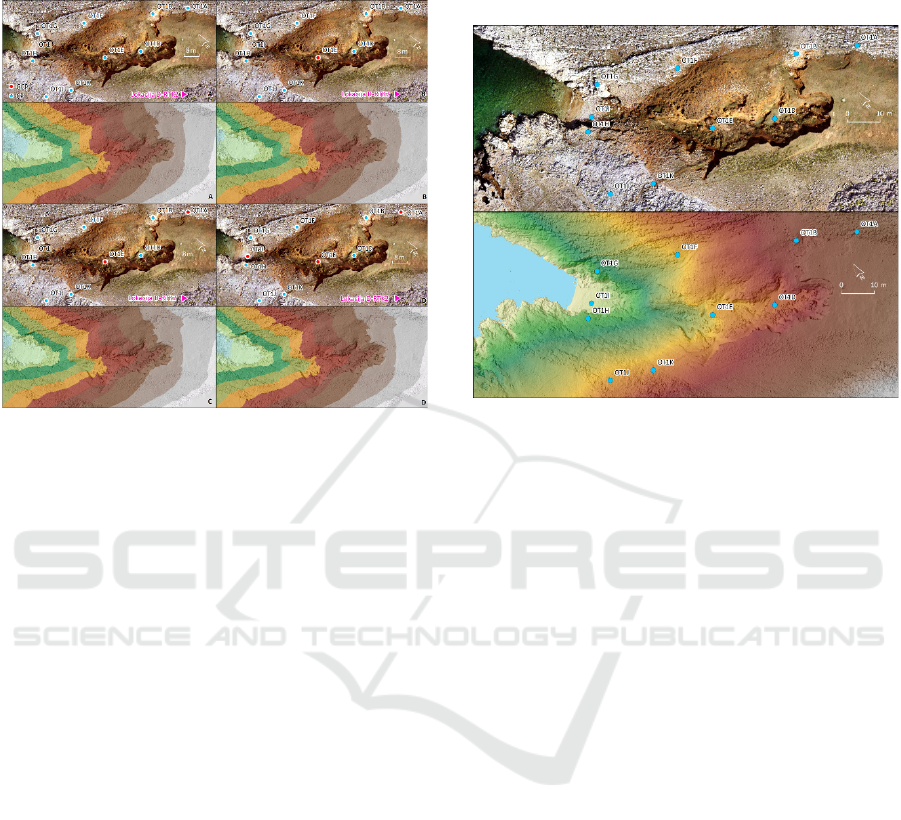
13.84 cm. The total RMSE was reduced by 68.719 cm

by adding only three GCPs.

Figure 8: Derived DOPs and DSMs. (A) D-RTK; (B) D-

RTK+1GCP; (C) D-RTK+2GCP; (D) D-RTK+3GCP.

3.3.2 D-RTK 2 Coordinate Correction with

STONEX S10

In this method of RTK positioning a GNSS receiver,

Stonex S10 was used in measuring the exact

coordinates of the location of the D-RTK 2 mobile

station. As in the first scenario on all acquired points

were used as CPs (n=10). The RMSE for the X

coordinate was 4.09 cm, for the Y 2.69 cm, and for

the Z 5.97 cm. The total RMSE of this model was 7.72

cm. The points “OT1A” and “OT1B”, which were

located on the least number of photos, had the highest

total RMSE. If these two points were excluded from

the analysis, the total RMSE of the model derived by

RTK positioning using the Stonex S10 correction

would amount to 5.99 cm.

3.3.3 Network NTRIP Corrections with

CROPOS

In this method of RTK positioning the NTRIP

connection option with CROPOS (Croatian

Positioning System) was used, providing real-time

RTK data without a base station on the site. All

collected points were used as CPs (n=10) (Fig. 9). The

RMSE for the X coordinate was 4.044 cm, for the Y

2.228 cm, and for the Z 4.488 cm. The total RMSE of

this model is 6.44 cm. The points “OT1A” and

“OT1B”, which were located on the least number of

photos (15 and 25), had the highest total RMSE. If

these two points were excluded from the analysis, the

total RMSE of the model derived from RTK

positioning using the network NTRIP correction

would be 5.31 cm.

Figure 9: Derived DOP and DSM (NTRIP connection with

CROPOS).

3.4 Absolute Accuracy of Tested RTK

Positioning Modes

The official specifications that can be found for many

sensor systems are usually tested and determined

under best-case scenarios. In this case, the testing was

not performed under best-case scenarios precisely

because such conditions, especially in the case where

the application of direct georeferencing is required,

are not always possible. In general, the goal was to

determine if this sensor system corresponds to the

manufacturer's own claims in conditions that are not

ideal. It was found that the accuracy of direct

georeferencing using the Matrice 210 RTK V2 and

the D-RTK 2 depends on the selected mode of

operation. Three modes of RTK positioning were

tested. Table 4 shows the summary results of XYZ

and total RMSE for the derived models. The highest

accuracy, as expected, was achieved in scenario (d)

with the application of GCP and CP resulting in a

total RMSE of 3.22 cm. Furthermore, the centimeter

level of accuracy (<10 cm) was achieved in the

operating mode where the (c) NTRIP connection

option with CROPOS was used, which enables the

positioning of the UAV in real-time, and in the

operating mode where the (b) corrective coordinates

collected by the Stonex S10 receiver were used

(Table 4). These two methods give similar results,

which is expected considering that the STONEX S10

uses the CROPOS system of base stations. The

Accuracy Assessment of Direct Georeferencing Using UAV Matrice 210 RTK V2 on Gully Santiš, Island of Pag (Croatia)

189

advantage of the first method is, that using a network

NTRIP connection option, requires the least amount

of equipment at the recording location. The biggest

disadvantage is the need for an active, reliable

Internet connection. In the second method, another

high-precision GNSS receiver is needed, which could

measure the coordinate on which the D-RTK 2

mobile station was mounted.

Table 4: Summary data on the accuracy of all tested RTK

positioning methods.

Scenario

X error

(cm)

Y error

(cm)

Z error

(cm)

Total

(cm)

D 1.33 1.28 2.76 3.32

C 4.04 2.23 4.49 6.44

B 4.06 2.69 5.97 7.72

A1 +3GCP 15.10 7.36 9.08 19.09

A1 +2 GCP 21.57 9.36 23.05 32.93

A1 +1 GCP 20.37 11.68 31.99 39.68

A 75.90 34.98 26.94 87.81

E 75.48 70.78 93.78 139.7

(a) D-RTK 2 as a base station; (a

) D-RTK 2 with the addition of

few GCPs; (b) D-RTK 2 correction with the Stonex S10; (c)

network NTRIP corrections CROPOS; (d) classical approach using

GCP and CP; (e) method using embedded navigation sensors into

UAVs.

The large total RMSE of 87.81 cm which is recorded

for D-RTK 2 is not surprising considering the

differences in the location coordinates of the mobile

station measured by D-RTK 2 itself and those by

STONEX S10 (Table 1). Therefore, the deviation in

the location of D-RTK 2 contributed to this error

(Table 4). Namely, in the official specifications, it is

stated that the accuracy of RTK positioning is

centimeters (horizontal = 1 cm, vertical = 2 cm). This

means that, in ideal recording conditions (absence of

wind), the relative accuracy of the positioning of the

cameras (photos location) will be in centimeters.

However, the single point (absolute) accuracy is 1.5

m horizontally and 3 m vertically. Therefore, this

result is not surprising. By including a smaller

number of GCPs (n=3) there is a significant reduction

in model error (87.81 cm - 19.09 cm). However, the

final total RMSE is still too large (19.09 cm) to justify

the use of XYZ coordinates of the photos in model

orientation. Based on this research, it can be

concluded that, if the D-RTK 2 mobile station retains

this level of absolute accuracy in reading its own

location (≈ 1 m), it is not worth using a smaller

number of GCPs in the orientation of the model,

because ultimately, in order to obtain satisfactory

accuracy, a larger number of them should be added (>

3), which would make the very application of D-RTK

2 senseless if it is about the smaller surface. In

scenario (E), the D-RTK 2 mobile station was not

used for positioning, and GCPs were not used in the

photogrammetric process. The RTK positioning

mode was turned off, and only the XYZ coordinates

of the photos from the UAV's GNSS receiver were

used. In this case, all 10 points were used to check the

accuracy of the model (CP=10). The RMSE for the X

coordinate was 75.5 cm, for the Y 70.8 cm, and for

the Z 93.8 cm. The total RMSE of this model was

139.7 cm. Nevertheless, the accuracy of positioning

is satisfactory considering that only XYZ data of the

photos, collected with the UAV's GNSS receiver,

were used in the process of model orientation.

4 CONCLUSIONS

The research tested three modes of RTK positioning

using the Matrice 210 RTK V2 system and D-RTK 2

mobile station. An assessment of the absolute

accuracy of the photogrammetric models was carried

out through the marking and collection of GCPs/ CPs

(n=10).

By calculating the total RMSE, it was determined

that two (NTRIP network correction with CROPOS

and STONEX S10 correction) of the three tested RTK

positioning modes have a centimeter level of

accuracy. It was found that the accuracy of RTK

positioning using the Matrice 210 RTK V2 and the D-

RTK 2 mobile station depends on the selected mode

of operation. These two methods give similar results,

which is expected given that the STONEX S10 uses

the CROPOS system of base stations. The third

method of RTK positioning, where the D-RTK

determines its location by itself, generates a large

absolute error. This error is not surprising,

considering the differences in the location

coordinates of the mobile station read by D-RTK 2

itself and those read by STONEX S10. This research

established that the tested UAV system for direct

georeferencing can be used in a wide range of

geographic sciences and other disciplines where

absolute centimeter accuracy of different models is

required.

ACKNOWLEDGEMENTS

This work has been supported in part by Croatian

Science Foundation under the project UIP-2017-

05-2694 and conducted within Center for

Geospatial Technology.

GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management

190

REFERENCES

Bláha, M., Eisenbeiss, H., Grimm, D., & Limpach, P.

(2011). Direct georeferencing of UAVs, In Proceedings

of the International Conference on Unmanned Aerial

Vehicle in Geomatics (UAV-g) (Vol. 38, pp. 131-136).

Copernicus.

Buonanno, M. (2019): D-RTK2 - User Notes - rev_200417,

CNR-ISAFOM, Italy.

Carbonneau, P. E., Dietrich, J. T. (2016): Cost‐effective

non‐metric photogrammetry from consumer‐grade

sUAS: implications for direct georeferencing of

structure from motion photogrammetry, Earth Surface

Processes and Landforms, 42(3), 473-486.

Dittrich, A., Weinmann, M., Hinz, S. (2017): Analytical

and numerical investigations on the accuracy and

robustness of geometric features extracted from 3D

point cloud data. ISPRS journal of photogrammetry

and remote sensing, 126, 195-208.

Guptill, S. C., Morrison, J. L. (1995). Looking ahead. In

Elements of spatial data quality (pp. 189-197).

Pergamon

Linder, W. (2009). Digital photogrammetry (Vol. 1).

Berlin: Springer.

Liu, X., Lian, X., Yang, W., Wang, F., Han, Y., Zhang, Y.

(2022): Accuracy assessment of a UAV direct

georeferencing method and impact of the configuration

of ground control points. Drones, 6(2), 30.

Magaš, D. (2011). Zemljopisna obilježja otoka Paga u

funkciji upoznavanja njegove toponimije. Toponimija

otoka Paga, 5-49.

Marić, I., Šiljeg, A., Domazetović, F. (2019): Geoprostorne

tehnologije u 3D dokumentaciji i promociji kulturne

baštine–primjer utvrde Fortica na otoku Pagu.

Geodetski glasnik, 50, 19-44.

Masiero, A., Fissore, F., Vettore, A. (2017). A low-cost

UWB based solution for direct georeferencing UAV

photogrammetry, Remote Sensing, 9(5), 414.

Oniga, V. E., Breaban, A. I., Statescu, F. (2018).

Determining the optimum number of ground control

points for obtaining high precision results based on

UAS images. In Multidisciplinary Digital Publishing

Institute Proceedings (Vol. 2, No. 7, p. 352).

Pike, R. J., Evans, I. S., Hengl, T. (2009).

Geomorphometry: a brief guide. Developments in Soil

Science, 33, 3-30.

Rehak, M., Mabillard, R., Skaloud, J. (2013): A micro-UAV

with the capability of direct georeferencing,

International Archives of the Photogrammetry, Remote

Sensing and Spatial Information Sciences, Volume XL-

1/W2, 4 – 6 September 2013, Rostock, Germany.

Rizaldy, A., Firdaus, W. (2012). Direct georeferencing: A

new standard in photogrammetry for high accuracy

mapping, International Archives of the

Photogrammetry, Remote Sensing and Spatial

Information Sciences, Volume XXXIX-B1, XXII

ISPRS Congress, 25 August – 01 September 2012,

Melbourne, Australia

Sanz-Ablanedo, E., Chandler, J. H., Rodríguez-Pérez, J. R.,

Ordóñez, C. (2018): Accuracy of unmanned aerial

vehicle (UAV) and SfM photogrammetry survey as a

function of the number and location of ground control

points used, Remote Sensing, 10(10), 1606.

Šiljeg, A., Barada, M., Marić, I. (2018): Digitalno

modeliranje reljefa, Alfa d.d., Sveučilište u Zadru,

Zadar.

Šiljeg, A., Domazetović, F., Marić, I., Lončar, N., Panđa, L.

(2021). New Method for Automated Quantification of

Vertical Spatio-Temporal Changes within Gully Cross-

Sections Based on Very-High-Resolution Models.

Remote Sensing, 13(2), 321.

Smith, M. W., J. L. Carrivick, D. J. Quincey (2016):

"Structure from motion photogrammetry in physical

geography." Progress in Physical Geography 40.2 247-

275.

Stott, E., Williams, R. D., Hoey, T. B. (2020): Ground

control point distribution for accurate kilometre-scale

topographic mapping using an RTK-GNSS unmanned

aerial vehicle and SfM photogrammetry. Drones, 4(3),

55.

Yuan, X., Zhang, X. P. (2008): Theoretical accuracy of

direct georeferencing with position and orientation

system in aerial photogrammetry. The International

Archives of the Photogrammetry, Remote Sensing and

Spatial Sciences, 617-622.

Zeybek, M. (2021). Accuracy assessment of direct

georeferencing UAV images with onboard global

navigation satellite system and comparison of

CORS/RTK surveying methods. Measurement Science

and Technology, 32(6), 065402.

Zhang, H., Aldana-Jague, E., Clapuyt, F., Wilken, F.,

Vanacker, V., Van Oost, K. (2019): Evaluating the

Potential of PPK Direct Georeferencing for UAV-SfM

Photogrammetry and Precise Topographic Mapping.

Earth Surf. Dyn. Discuss, 1-34.

Accuracy Assessment of Direct Georeferencing Using UAV Matrice 210 RTK V2 on Gully Santiš, Island of Pag (Croatia)

191