A Recent Publications Survey on Reinforcement Learning for Selecting

Parameters of Meta-Heuristic and Machine Learning Algorithms

Maria Chernigovskaya, Andrey Kharitonov and Klaus Turowski

Faculty of Computer Science, Otto von Guericke University, Magdeburg, Germany

Keywords:

Reinforcement Learning, Deep Reinforcement Learning, Hyper-Parameter Optimization.

Abstract:

Nowadays, meta-heuristic and machine learning algorithms are often used for a variety of tasks in cloud

computing operations. The choice of hyper-parameter values has a direct impact on the performance of

these algorithms, making Hyper-Parameter Optimization (HPO) an important research ﬁeld for facilitating

the widespread application of machine learning and meta-heuristics for problem-solving. Manual parameter-

ization of these algorithms is an inefﬁcient method, which motivates researchers to look for a new and more

efﬁcient approach to tackle this challenge. One such innovative approach is Deep Reinforcement Learning

(DRL), which has recently demonstrated a lot of potential in solving complex problems. In this work, we

aim to explore this topic more thoroughly and shed light on the application of DRL-based techniques in HPO,

speciﬁcally for Machine Learning and Heuristics/Meta-heuristics-based algorithms. We approach the problem

by conducting a systematic literature review of the recently published literature and summarizing the results

of the analysis. Based on the conducted literature review, within the selected sources, we identiﬁed 14 relevant

publications and a clear research gap in the cloud-speciﬁc use case for HPO via DRL.

1 INTRODUCTION

Modern cloud computing offers a multitude of op-

timization challenges for both providers and clients,

such as various size enterprises. These challenges in-

clude the pursuit of cost, performance, service, and

energy efﬁciency. These can be tackled with the use

of state-of-the-art meta-heuristics (e.g., virtual ma-

chine consolidation (Pourghebleh et al., 2021)) and

machine learning (ML) (e.g., cloud instance selection

(Samreen et al., 2016)).

Proper selection of the parameter values for such

algorithms is important for both meta-heuristics (Liao

et al., 2015) and ML (Mantovani et al., 2016), because

it can directly inﬂuence the quality of the solution and

algorithm’s performance. Manual selection of these

parameters is often difﬁcult and time-consuming (Qi

and Xu, 2022) as it requires an understanding of

both, the algorithm’s internal workings and the prob-

lem. This, in turn, can potentially be a limiting factor

(Paleyes et al., 2022) for the application of these tech-

niques outside of the research community. Numer-

ous ways to tackle this challenge are proposed in the

form of various automatic hyper-parameter optimiza-

tion (HPO) for meta-heuristics (Huang et al., 2020;

Eryoldas¸ and Durmus¸oglu, 2022) and ML (Yang and

Shami, 2020). However, the application of these HPO

techniques does not fully alleviate the challenge of us-

ing state-of-the-art algorithms in real-world business

environments (Paleyes et al., 2022), which warrants

further investigation and research.

This aspect has stimulated increased investiga-

tion into novel methods for the automated optimiza-

tion of hyper-parameter values. Many researchers

have turned their attention to various techniques in

an attempt to identify more efﬁcient ways to tackle

this challenge. Deep Reinforcement Learning (DRL)

is among such techniques as it have been demon-

strated to be successful in handling various optimiza-

tion problems (Zhang et al., 2022b).

Investigation of DRL-based techniques for tun-

ing hyper-parameters is a promising research topic

for enhancing application efﬁciency of ML and meta-

heuristics. Especially interesting is the possibility of

exploiting the ability of DRL to instantly infer solu-

tions (Tian et al., 2022), which can signiﬁcantly in-

crease the efﬁciency and applicability of HPO in cer-

tain real-world scenarios.

To the best of our knowledge, there are no pub-

lished surveys that offer a thorough overview of the

DRL application for HPO of ML and meta-heuristic

algorithms. The available recent surveys that study

236

Chernigovskaya, M., Kharitonov, A. and Turowski, K.

A Recent Publications Survey on Reinforcement Learning for Selecting Parameters of Meta-Heuristic and Machine Learning Algorithms.

DOI: 10.5220/0011954300003488

In Proceedings of the 13th International Conference on Cloud Computing and Services Science (CLOSER 2023), pages 236-243

ISBN: 978-989-758-650-7; ISSN: 2184-5042

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

HPO, do not cover the perspectives of the appli-

cation of DRL (Huang et al., 2020; Eryoldas¸ and

Durmus¸oglu, 2022; Yang and Shami, 2020). To ad-

dress this research gap, we present a systematic liter-

ature analysis to summarize the current stand of the

research in this domain and highlight the existing ap-

plications.

Additionally, we outline the selected approaches

and compare their main insights based on the type of

algorithms used and how the key concepts, such as

action space and reward functions, are deﬁned.

2 BACKGROUND

In this chapter, we provide the theoretical background

on the concepts and deﬁnitions that are relevant to

our work. In subsection 2.1 we shed light on Hyper-

parameter Optimization (HPO) and its current stand

and challenges. In subsection 2.2 we provide key

deﬁnitions of Machine Learning (ML). In subsec-

tion 2.3, we outline the fundamentals behind the con-

cept of Deep Reinforcement Learning (DRL) and give

a brief description of its key components. We con-

clude this section with deﬁnitions of Heuristics and

Meta-heuristics in subsection 2.4.

2.1 Hyper-Parameter Optimization

HPO could be deﬁned as the task of ﬁnding optimal

hyper-parameter values within a search space com-

prised of valid parameter values in order to improve

the performance of a certain algorithm (Motz et al.,

2022). The process of optimizing, also often referred

to as tuning, hyper-parameters varies amongst differ-

ent algorithms due to the numerous types of hyper-

parameter values, which can be categorical, discrete,

or continuous. Manual parameter value selection is

typical in research but it is a challenging and time-

consuming process, thus automated hyper-parameter

selection became an active research ﬁeld(Yang and

Shami, 2020).

The primary goal of automated HPO is to sim-

plify the hyper-parameter tuning process and enable

users to efﬁciently apply parameterized algorithms to

practical problems. Since many HPO problems are

non-convex or non-differentiable optimization prob-

lems, conventional optimization techniques may not

be suited for them and may provide a local rather than

a global optimum. DRL and RL-based techniques are

shown to be effective in solving optimization prob-

lems (N. Xu et al., 2022) and therefore there are at-

tempts to use these for HPO.

2.2 Machine Learning

Machine learning (ML) incorporates algorithms that

make decisions or predictions, often based on speciﬁc

data, without a need for every detail of such decision-

making to be predeﬁned explicitly. These are par-

ticularly sensitive to the selection of hyper-parameter

values (Yang and Shami, 2020). Depending on the

kind of problem that has to be solved, machine learn-

ing algorithms can be divided into three subcategories

(Agrawal, 2021): Supervised, Unsupervised, and Re-

inforcement Learning.

Supervised learning in ML uses labeled datasets to

train algorithms to precisely categorize inputs or pre-

dict outcomes. It is called supervised because these

algorithms rely on labeled training data to build a

model. In contrast to supervised learning, unsuper-

vised machine learning employs algorithms to an-

alyze and classify unlabeled data. Without human

oversight, these algorithms may ﬁnd hidden patterns

in data and infer relationships between different fea-

tures in the data. The third type of ML is Reinforce-

ment Learning. Reinforcement Learning (RL) algo-

rithm learns from its environment and generally does

not require training data. Hyperparameters in ML are

diverse and vary from algorithm to algorithm.

Important subclass of ML approaches, called

Deep Learning (DL) (LeCun et al., 2015), is worth

mentioning speciﬁcally since it presents particular

HPO problems. DL is an area of ML, based on the

use of artiﬁcial neural networks, and is speciﬁcally

concerned with deep neural networks (DNN), which

can be used in all three aforementioned ML types.

Number of hidden neuron layers and the number of

neurons in each layers, are primary hyper-parameters

examples of DL models (Yang and Shami, 2020).

Each type of ML algorithm has different key

hyper-parameters that must be tuned. For super-

vised Learning algorithms such as k-nearest neigh-

bors (KNN), the number of considered nearest neigh-

bors, k is the most important hyper-parameter. In

Unsupervised Learning, many clustering algorithms

like k-means, the expectation-maximization (EM) al-

gorithm, and hierarchical clustering — the number of

clusters is the most crucial hyper-parameter to tune

(Yang and Shami, 2020). For RL algorithms, the crit-

ical hyper-parameters to tune are Learning rate (α)

and Gamma (γ). The ﬁrst one, α, allows the agent

to learn faster about its environment, but it may pre-

vent it from exploring the space of possibilities, γ, on

the other hand, helps agent to develop optimal ac-

tion strategies by teaching it to prioritize immediate

rewards versus future rewards (Sun, 2017).

A Recent Publications Survey on Reinforcement Learning for Selecting Parameters of Meta-Heuristic and Machine Learning Algorithms

237

2.3 Deep Reinforcement Learning

The goal of RL is to determine the best behavior for

an agent while it is exploring a given environment by

interacting with it (Asadulaev et al., 2020). The en-

vironment can be an interface or a representation of

a system or an optimization problem. Recently RL

gained interest in research due to a number of ad-

vancements in the area, speciﬁcally in the subset of

RL algorithms commonly named as Deep Reinforce-

ment Learning (Alves and Mateus, 2020).

Deep Reinforcement Learning (DRL) is an ML

technique that combines RL and DL. The fundamen-

tal DRL mechanism is, in principle, identical to RL

and consists of an iterative process in which the agent

observes the state of the environment within its ob-

servation space and acts in accordance with the state,

the environment transitions to a new state as a result

of the agent’s action, and the agent receives feedback

(reward). The agent’s goal is to maximize the reward

(Alves and Mateus, 2020).

DRL implementations may be classiﬁed into three

categories based on the type of supported action

space: discrete action space, continuous action space,

and discrete-continuous (hybrid) action space (Zhu

et al., 2021). In the discrete action space, we can pre-

cisely quantify the number of possible options. The

number of options in the continuous action space is

not pre-deﬁned as a closed set, but deﬁned as a value

range. For discrete-continuous (hybrid) action spaces,

the algorithm should generate discrete actions as well

as the continuous parameters performed by the dis-

crete actions (Zhu et al., 2021). This distinction is

important for HPO problems because the nature of

the tuned parameters can fall into any of these three

categories.

Published surveys (Arulkumaran et al., 2017;

Wang et al., 2022b) discuss various speciﬁc examples

of algorithms that fall into the aforementioned cate-

gories. Q-Learning and Q-learning-based algorithms

such as Deep Q-Network (DQN) are well suited for

discrete action spaces. Proximal Policy Optimization

(PPO) and Policy Gradient methods (e.g., Deep De-

terministic Policy Gradient (DDPG)) handle continu-

ous action spaces. Algorithms such as Asynchronous

Advantage Actor Critic (A3C) and Advantage Actor

Critic (A2C) belong to the hybrid type.

2.4 Heuristics and Meta-Heuristics

Heuristics are optimization methods that are designed

for a speciﬁc problem and try to exploit problem-

speciﬁc knowledge. They do not attempt to ﬁnd an

optimal solution but focus on producing optimum so-

lution procedures. Two types of heuristics are de-

ﬁned in the literature(Rothlauf, 2011): Construction

and Improvement heuristics.

Construction heuristics develop a solution from

the ground up step-wise, where components of the so-

lution are ﬁxed at every step. Improvement heuristics

start with a complete solution and iteratively aim to

enhance it (Rothlauf, 2011).

Meta-heuristic algorithms are a set of techniques

used to address complicated optimization problems.

Usually, researchers distinguish three types of meta-

heuristic techniques: based on the local search algo-

rithm (Tabu search, simulated annealing), evolution-

ary computing (genetic algorithms), or swarm intelli-

gence (Ant colony optimization, particle swarm opti-

mization (PSO)) (Pereira et al., 2021). Each of these

meta-heuristic algorithms has critical parameters that

need to be tuned in order for these algorithms to work

optimally. In the case of the GA, three numeric pa-

rameters are usually considered of the most impor-

tance: population size, mutation rate, and crossover

rate (Eryoldas¸ and Durmus¸oglu, 2022). For PSO, crit-

ical hyper-parameters are particle number m, acceler-

ate constant c

and c

, inertia weight w, and maxi-

mum limited velocity v

max

(He et al., 2016).

3 LITERATURE SURVEY

The core of this study is a systematic literature review

that gives an overview of recent publications that ap-

ply DRL-based (or RL-based) approaches to address

HPO concerns. We begin this section with a descrip-

tion of the applied literature survey methodology in

subsection 3.1. As a result, a number of relevant stud-

ies is identiﬁed and evaluated to provide a summary

of the current state of the research in subsection 3.2.

Additionally, in subsection 3.3, we discuss a couple

of publications that fall outside of the survey’s criteria

but still present concepts potentially relevant to HPO

with DRL.

3.1 Methodology

To identify the current state of the research on hyper-

parameter tuning using DRL and RL, we conduct a

systematic literature review. The search for the rel-

evant papers is performed using the following aca-

demic research databases: ScienceDirect

, Springer

ACM

and IEEE

. We focus on the publications that

https://www.sciencedirect.com

https://link.springer.com

https://dl.acm.org

https://ieeexplore.ieee.org

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

238

apply DRL or RL for hyper-parameter tuning for ML

and Meta-heuristics (or Heuristics). The focus of this

work is recent research on DRL in HPO; therefore,

only works published since 2017 were considered for

all DRL-related queries. The range for RL-based

approaches is extended to include works published

since 2015. In our research, we also applied forward

and backward searches. Additionally, only accessi-

ble, peer-reviewed publications written in the English

language were considered.

To conduct a systematic literature analysis for the

selected topic, four categories of the research were

deﬁned:

• DRL for HPO of Heuristics and Meta-heuristics

• RL for HPO of Heuristics and Meta-heuristics

• DRL for HPO of ML

• RL for HPO of ML

To narrow down the most relevant papers, three ﬁlter-

ing phases were carried out for each category. First,

all papers with relevant titles were selected for each

category. Secondly, the abstract relevance of the

remaining papers was examined. Lastly, we thor-

oughly researched the entire contents of the remain-

ing papers to select the relevant candidates. Addition-

ally, the differences in spelling of terms like hyper-

parameters (e.g., hyperparameters or hyper parame-

ters) and meta-heuristics (e.g., metaheuristics or meta

heuristics) are considered. Worth mentioning that all

variations of spelling are present in the published lit-

erature.

For each deﬁned category, we came to the follow-

ing results:

• DRL for HPO of Heuristics and Meta-heuristics -

Out of the 28 papers that were initially taken into

consideration, 3 were deemed relevant

• RL for HPO of Heuristics and Meta-heuristics -

Out of the 21 papers that were initially taken into

consideration, 1 was deemed relevant

• DRL for HPO of ML - Out of the 50 papers

that were initially taken into consideration, 8 were

deemed relevant

• RL for HPO of ML - Out of the 19 papers that

were initially taken into consideration, 2 were

deemed relevant

Furthermore, in the process of assessing the relevance

of publications, the inclusion and exclusion criteria

are deﬁned.

All publications, where the authors implement

concepts of DRL (RL) in HPO for meta-heuristics and

ML algorithms and demonstrate their results, were in-

cluded. Likewise, the authors that present more con-

ceptual and theoretical background on the HPO con-

cept and provide in-depth deﬁnitions of relevant DRL

components like state space (observation space), ac-

tion space, and reward function, those papers are also

considered in the literature analysis, since they may

offer interesting insights for our research.

If the key concepts such as DRL, RL, and HPO

were not presented and important deﬁnitions such as

state space, action space, and reward function were

missing – those papers were excluded. Moreover,

publications with HPO approaches, which are not

based on DRL (RL) algorithms or where no HPO ap-

proach is implemented, were not considered by us.

The same exclusion strategy we follow with the pa-

pers whose main topic was irrelevant to our litera-

ture survey, therefore they don’t offer any valuable

insights.

3.2 Literature Analysis

In this section, we summarise the results of the con-

ducted literature analysis. The reviewed publications

are divided into four categories in order to discuss the

ﬁndings methodically. The presented categorization

is based on two factors, particularly, which solution

approach was used in chosen publications, whether it

is a DRL-based or RL-based approach and to what

type of algorithms were these solutions applied: to

ML algorithms or heuristics and meta-heuristics al-

gorithms.

In the analyzed literature, various approaches have

been used to tune the parameters of meta-heuristic,

heuristics, and ML algorithms using DRL or RL. Re-

sults of the literature are summarized in the Table 1,

including mentioning type of the action space and

used base algorithm.

For instance, (Zhang et al., 2022b) in their work

propose a DRL-based framework in order to solve

combinatorial problems. The presented framework

is based on a heuristic method that uses a Dou-

ble Deep Q-network (DDQN) algorithm (Marchesini

et al., 2019). The authors deﬁne the action space

as a set of parameterized heuristics that could be ad-

justed in order to get the desired performance. A sim-

ilar approach takes (Dong et al., 2021), which uses

Deep Q-Learning (DQN) (Mnih et al., 2015) to op-

timize hyper-parameters of the proposed heuristics-

based framework for visual object tracking. The au-

thors deﬁne the action space as the adjustment of the

hyper-parameter numeric values in a continuous man-

ner. The author’s proposed approach demonstrates

high accuracy of the performance in comparison with

chosen methods. A further example of applying DRL

to optimizing parameters of meta-heuristics is pre-

A Recent Publications Survey on Reinforcement Learning for Selecting Parameters of Meta-Heuristic and Machine Learning Algorithms

239

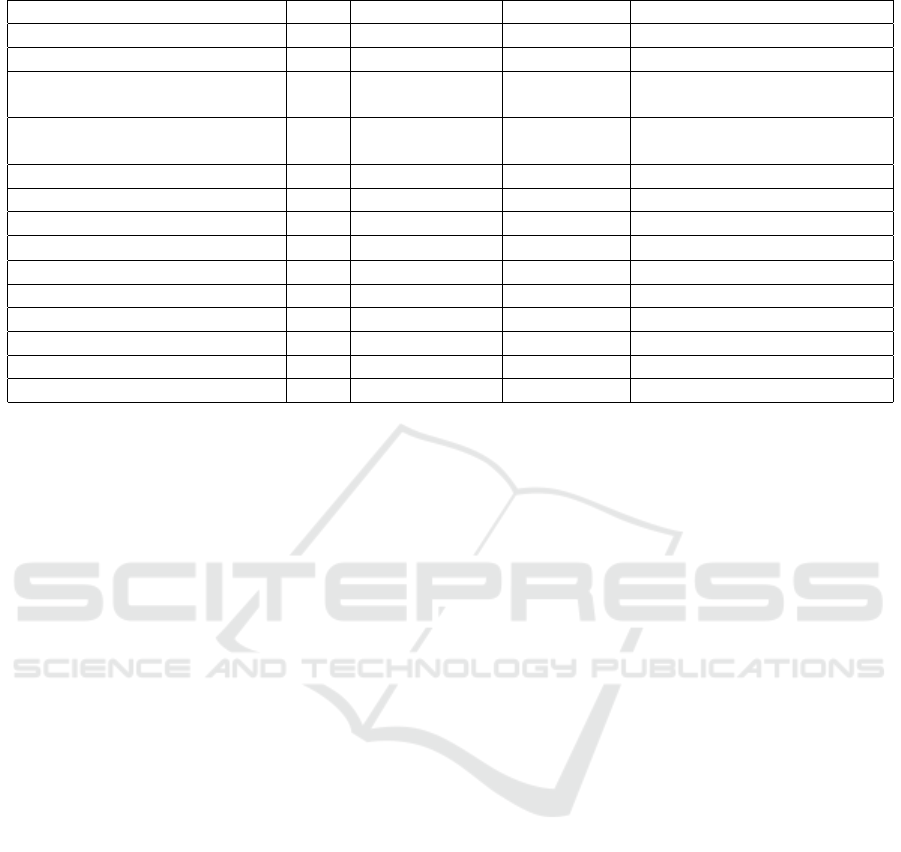
Table 1: Literature analysis summary.

Publication Type Tuning Action space Base algorithm

(Zhang et al., 2022b) DRL Heuristics Discrete Double Deep Q-network

(Qi and Xu, 2022) RL ML Discrete Q-learning

(N. Xu et al., 2022) DRL ML Discrete

Attention and Memory

Enhancement

(Zhang et al., 2022a) DRL ML Discrete

Twin Delayed Deep

Deterministic Policy Gradient

(Wang et al., 2022a) RL ML Discrete Q-learning

(Dong et al., 2021) DRL Heuristics Continuous Continuous Deep Q-learning

(Wan et al., 2021) DRL ML Continuous Double Deep Q-network

(Mills et al., 2021) DRL ML Continuous L

NAS

(de Santiago J

unior et al., 2020) RL Meta-Heuristics Not deﬁned Not deﬁned

(Liu et al., 2020) RL ML Continuous Proximal Policy Optimization

(S. Chen et al., 2019) DRL ML Discrete Policy Gradient

(Sharma et al., 2019) DRL Meta-Heuristics Discrete Double Deep Q-Learning

(WU et al., 2019) DRL ML Discrete Policy Gradient

(P. Neary, 2018) RL ML Discrete Not deﬁned

sented by the authors of (Sharma et al., 2019) for con-

trolling mutation strategies of an evolutionary algo-

rithm.

RL-based approaches can also be successfully ap-

plied to heuristics and meta-heuristics algorithms for

solving HPO problems. For example, (de Santiago

unior et al., 2020) presents an innovative approach

for solving parameter optimization problems by com-

bining meta-heuristics and RL-based algorithms. The

action space is deﬁned by authors as a set of low-

level heuristics and reward is designed as as reward

or penalties based on its performance.

A good example of the RL application for ML al-

gorithms would be the work of (Qi and Xu, 2022). In

their research, authors apply a Q-learning-based al-

gorithm (Sun, 2017) to optimize the hyper-parameter

tuning strategy in a Deep Learning approach. They

deﬁne action space as discrete, where only one hyper-

parameter is tuned at a time, and the reward func-

tion as the difference between the evaluation metric of

neural network models before hyper-parameter tun-

ing and the current one. A further example (Wang

et al., 2022a) of HPO in ML optimization is also rely-

ing on Q-Learning but for selecting optimal Spatial-

Temporal Graph Convolutional Network models for a

given problem. For this purpose, the authors present

a way to construct a network model from predeﬁned

blocks and attempt to automate the construction pro-

cess by employing an RL algorithm.

An illustration of applying DRL to ML models

would be the work of (S. Chen et al., 2019). The au-

thors propose an architecture based on DRL, which

should be able to optimize hyper-parameters for any

ML model using Policy Gradient Algorithm (Parisi

et al., 2014). They approach the problem by creat-

ing a DRL agent which can automatically select the

optimal hyper-parameters for ML models on a given

dataset. Another approach takes (Wan et al., 2021),

where the authors propose an HPO method based on

DRL, which is used to balance image service quality

and privacy protection. The authors present a method

where a Neural Network is trained as an agent to ﬁnd

the best hyper-parameter adjustment. To tackle the

problem, they use the Double Deep Q-network al-

gorithm (DDQN). Another example of searching for

optimal neural network hyper-parameters is presented

in (Mills et al., 2021). In that work, authors present

a DRL-based L

NAS algorithm, which employs an

actor neural network to automatically optimize and

update architecture hyper-parameters within an actor-

critic algorithm. For the presented approach, authors

deﬁne an action as a continuous architecture hyper-

parameter, which is then deterministically mapped

into a discrete one. An interesting approach in au-

tomatically determining the best clustering parame-

ters take (Zhang et al., 2022a). The authors propose

a parameter search framework based on the Twin De-

layed Deep Deterministic strategy gradient algorithm

(TD3), where a DRL agent attempts to ﬁnd the best

parameter values of a classic ML-based clustering al-

gorithm by taking discrete actions for increasing or

decreasing individual continuous values of the algo-

rithm’s parameters. Another instance of DRL being

applied to ML models is the work of (WU et al.,

2019). In their research, the authors present a DRL-

based architecture where they create an agent that se-

lects a set of hyper-parameters and uses the accuracy

of an ML model as a reward signal to update its pa-

rameters. The authors deﬁne the action space as a

set of decisions where each decision corresponds to a

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

240

selection of a hyper-parameter. A similar approach is

taken by authors of (N. Xu et al., 2022). In their work,

the authors introduce a conﬁguration searcher to se-

lect appropriate hyper-parameters for ML models. To

enhance the performance of the proposed searcher, a

new Attention and Memory Enhancement (AME) al-

gorithm is developed to tackle the problem of opti-

mizing all types of hyper-parameters. Similarly to

previous work, this is also a DRL-based algorithm.

The authors deﬁne the action space for the problem

as a set of new conﬁgurations, one of which the agent

picks from search space and the reward function as

the evaluation of the taken action.

The RL-based approaches can also be successfully

used for tuning ML models. An interesting exam-

ple of it would be the work of (Liu et al., 2020).

The authors in their research present a model-based

Reinforcement Learning for solving HPO problems.

The action space for the designed research objective

is deﬁned as a set of hyper-parameter conﬁgurations

to tune. The authors describe the reward function as

the accuracy of a validation set. A similar approach

takes (P. Neary, 2018). The authors present an Asyn-

chronous Reinforcement Learning algorithm to set

optimal neural network conﬁgurations by adjusting its

hyper-parameters. The authors deﬁne the state space

for the presented problem as a network architecture,

the action space as a set of hyper-parameters to tune,

and the reward function as the accuracy achieved by

changing a single hyper-parameter while keeping all

others ﬁxed.

3.3 Conceptually Related Research

In addition to the previously discussed works, we dis-

covered two publications that are dedicated to the

optimization of parameterization in real-world sys-

tems. While these papers are not directly connected

to the application of DRL for HPO for ML and Meta-

heuristics, the insights they provide are potentially in-

teresting within the scope of our research.

(Lindstah and Lan, 2020) in their work combine

Imitation and Reinforcement Learning in order to ef-

ﬁciently tune hyper-parameters of cavity ﬁlters. The

action space is deﬁned as a set of screw adjustments

in a speciﬁc range. Therefore the adjustments are rep-

resented as continuous values. The reward is deﬁned

by the authors as a heuristic function of the error after

the adjustment.

(Tom

e De Andrade e Silva, Manuel and Azevedo,

2022) in their research investigating the potential of

dynamical adjustment of work in process (WIP) cap

limits. The authors approach the problem by applying

the PPO algorithm to minimize the WIP levels with-

out reducing production’s throughput performance.

The action space is discrete and deﬁned as the set of

natural numbers, which represent the WIP cap(limit)

to be applied to the production system.

4 CONCLUSION

Based on the ﬁndings of our research, we can con-

clude that the number of publications attempting to

use DRL-based techniques is quite low, especially for

HPO for Heuristics and Meta-heuristics. In fact, only

14 papers are considered relevant as they address the

topic of selection of optimal parameter values within

meta-heuristic, conventional ML, and deep learning

algorithms, as well as a selection of the most appro-

priate parameterized heuristics. Discovered relevant

publications present various approaches for parame-

terization of the algorithms to ﬁt an optimization or

data processing problem at hand, including the ways

to tackle the challenge of discretization of continu-

ous parameter values to ﬁt speciﬁc RL and DRL tech-

niques.

Additionally, the reviewed publications demon-

strate that various DRL-based algorithms may be suit-

able for solving HPO problems. Within the discov-

ered relevant publications, the authors demonstrate

that it can be advantageous to use DRL techniques

in HPO to achieve higher performance in comparison

with the conventional techniques (e.g., Bayesian opti-

mization and Random Search), which they chose as

a baseline. This, coupled with the relatively small

amount of discovered relevant publications, merits

further systematic investigation of the DRL applica-

tion in HPO problems. The discovered publications

do not concentrat on optimization problems oriented

to cloud operations or any speciﬁc use-case, which

indicates a research gap.

Another interesting observation is that the action

space is often deﬁned by the authors as a set of hyper-

parameters to adjust for ML algorithms and as a set of

heuristics (meta-heuristics) for Heuristics and Meta-

heuristics algorithms. Additionally, in the case of

ML, the Reward function is commonly characterized

as the accuracy gained by each adjustment of the

hyper-parameters.

5 FUTURE WORK

The next step of the research is the formulation of

observation spaces, action spaces, and reward func-

tions for DRL to solve HPO problems for algorithms

typically present in cloud operations research. These

A Recent Publications Survey on Reinforcement Learning for Selecting Parameters of Meta-Heuristic and Machine Learning Algorithms

241

include, but are not limited to, virtual machine con-

solidation (Varasteh and Goudarzi, 2017) and cloud

service composition (Vakili and Navimipour, 2017)

based on heuristic or meta-heuristic algorithms, cloud

security enhancement via machine learning (Nassif

et al., 2021). DRL implementations of HPO for such

problems are then to be compared against the tra-

ditional HPO approaches (Yang and Shami, 2020;

Huang et al., 2020) in order to determine the advan-

tages and disadvantages of applying one or another

in the cloud operations-related HPO problems. At

the same time, it would be prudent to investigate ap-

plying a tuning technique to the DRL approach used

for HPO itself to increase training efﬁciency in look-

ing for optimal deep neural network architecture, and

hyper-parameters (Wang et al., 2021).

REFERENCES

Agrawal, T. (2021). Hyperparameter Optimization in Ma-

chine Learning. Apress, Berkeley, CA.

Alves, J. C. and Mateus, G. R. (2020). Deep reinforcement

learning and optimization approach for multi-echelon

supply chain with uncertain demands. In Lalla-Ruiz,

E., Mes, M., and Voss, S., editors, Computational Lo-

gistics, volume 12433 of Lecture Notes in Computer

Science, pages 584–599. Springer, Cham.

Arulkumaran, K., Deisenroth, M. P., Brundage, M., and

Bharath, A. A. (2017). Deep reinforcement learning:

A brief survey. IEEE Signal Processing Magazine,

34(6):26–38.

Asadulaev, A., Kuznetsov, I., Stein, G., and Filchenkov, A.

(2020). Exploring and exploiting conditioning of re-

inforcement learning agents. IEEE Access, 8:211951–

211960.

de Santiago J

unior, V. A.,

Ozcan, E., and de Carvalho,

V. R. (2020). Hyper-heuristics based on reinforcement

learning, balanced heuristic selection and group deci-

sion acceptance. Applied Soft Computing, 97:106760.

Dong, X., Shen, J., Wang, W., Shao, L., Ling, H., and

Porikli, F. (2021). Dynamical hyperparameter opti-

mization via deep reinforcement learning in tracking.

IEEE transactions on pattern analysis and machine

intelligence, 43(5):1515–1529.

Eryoldas¸, Y. and Durmus¸oglu, A. (2022). A literature sur-

vey on ofﬂine automatic algorithm conﬁguration. Ap-

plied Sciences, 12(13):6316.

He, Y., Ma, W., and Zhang, J. (2016). The parame-

ters selection of pso algorithm inﬂuencing on perfor-

mance of fault diagnosis. MATEC Web of Confer-

ences, 63:02019.

Huang, C., Li, Y., and Yao, X. (2020). A survey of

automatic parameter tuning methods for metaheuris-

tics. IEEE Transactions on Evolutionary Computa-

tion, 24(2):201–216.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. Nature, 521(7553):436–444.

Liao, T., Molina, D., and St

utzle, T. (2015). Performance

evaluation of automatically tuned continuous optimiz-

ers on different benchmark sets. Applied Soft Comput-

ing, 27:490–503.

Lindstah, S. and Lan, X. (2020). Reinforcement learn-

ing with imitation for cavity ﬁlter tuning. In 2020

IEEE/ASME International Conference on Advanced

Intelligent Mechatronics (AIM), pages 1335–1340,

[Piscataway, NJ]. IEEE.

Liu, X., Wu, J., and Chen, S. (12/14/2020 - 12/16/2020). Ef-

ﬁcient hyperparameters optimization through model-

based reinforcement learning and meta-learning. In

2020 IEEE 22nd International Conference on High

Performance Computing and Communications; IEEE

18th International Conference on Smart City; IEEE

6th International Conference on Data Science and

Systems (HPCC/SmartCity/DSS), pages 1036–1041.

IEEE.

Mantovani, R. G., Horv

ath, T., Cerri, R., Vanschoren, J.,

and Carvalho, A. C. d. (2016). Hyper-parameter

tuning of a decision tree induction algorithm. In

2016 5th Brazilian Conference on Intelligent Systems

(BRACIS), pages 37–42.

Marchesini, E., Corsi, D., Benfatti, A., Farinelli, A., and

Fiorini, P. (2019). Double deep q-network for trajec-

tory generation of a commercial 7dof redundant ma-

nipulator. In 2019 Third IEEE International Confer-

ence on Robotic Computing (IRC), pages 421–422.

Mills, K. G., Han, F. X., Salameh, M., Changiz Rezaei,

S. S., Kong, L., Lu, W., Lian, S., Jui, S., and Niu,

D. (2021). L2nas: Learning to optimize neural archi-

tectures via continuous-action reinforcement learning.

In Proceedings of the 30th ACM International Con-

ference on Information & Knowledge Management,

CIKM ’21, page 1284–1293, New York, NY, USA.

Association for Computing Machinery.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,

J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-

jeland, A. K., Ostrovski, G., et al. (2015). Human-

level control through deep reinforcement learning.

Nature, 518(7540):529–533.

Motz, M., Krauß, J., and Schmitt, R. H. (2022). Bench-

marking of hyperparameter optimization techniques

for machine learning applications in production. Ad-

vances in Industrial and Manufacturing Engineering,

5:100099.

N. Xu, J. Chang, X. Nie, C. Huo, S. Xiang, and C. Pan

(2022). Ame: Attention and memory enhancement

in hyper-parameter optimization. In 2022 IEEE/CVF

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 480–489.

Nassif, A. B., Talib, M. A., Nasir, Q., Albadani, H., and

Dakalbab, F. M. (2021). Machine learning for cloud

security: A systematic review. IEEE Access, 9:20717–

20735.

P. Neary (2018). Automatic hyperparameter tuning in deep

convolutional neural networks using asynchronous re-

inforcement learning. In 2018 IEEE International

Conference on Cognitive Computing (ICCC), pages

73–77.

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

242

Paleyes, A., Urma, R.-G., and Lawrence, N. D. (2022).

Challenges in deploying machine learning: A survey

of case studies. ACM Comput. Surv., 55(6).

Parisi, S., Pirotta, M., Smacchia, N., Bascetta, L., and

Restelli, M. (2014). Policy gradient approaches for

multi-objective sequential decision making: A com-

parison. In 2014 IEEE Symposium on Adaptive

Dynamic Programming and Reinforcement Learning

(ADPRL), pages 1–8.

Pereira, I., Madureira, A., Costa e Silva, E., and Abraham,

A. (2021). A hybrid metaheuristics parameter tun-

ing approach for scheduling through racing and case-

based reasoning. Applied Sciences, 11(8):3325.

Pourghebleh, B., Aghaei Anvigh, A., Ramtin, A. R., and

Mohammadi, B. (2021). The importance of nature-

inspired meta-heuristic algorithms for solving vir-

tual machine consolidation problem in cloud environ-

ments. Cluster Computing, 24(3):2673–2696.

Qi, X. and Xu, B. (2022). Hyperparameter optimization of

neural networks based on q-learning. Signal, Image

and Video Processing.

Rothlauf, F. (2011). Application and Adaptation of

Heuristic Optimization Methods. Natural Computing.

Springer Berlin Heidelberg, Berlin, Heidelberg.

S. Chen, J. Wu, and X. Chen (2019). Deep reinforcement

learning with model-based acceleration for hyperpa-

rameter optimization. In 2019 IEEE 31st International

Conference on Tools with Artiﬁcial Intelligence (IC-

TAI), pages 170–177.

Samreen, F., Elkhatib, Y., Rowe, M., and Blair, G. S.

(2016). Daleel: Simplifying cloud instance selec-

tion using machine learning. In NOMS 2016 -

2016 IEEE/IFIP Network Operations and Manage-

ment Symposium, pages 557–563.

Sharma, M., Komninos, A., L

opez-Ib

nez, M., and Kaza-

kov, D. (2019). Deep reinforcement learning based

parameter control in differential evolution. In Pro-

ceedings of the Genetic and Evolutionary Computa-

tion Conference, GECCO ’19, page 709–717, New

York, NY, USA. Association for Computing Machin-

ery.

Sun, C. (2017). Fundamental q-learning algorithm in ﬁnd-

ing optimal policy. In 2017 International Conference

on Smart Grid and Electrical Automation (ICSGEA),

pages 243–246.

Tian, Y., Chao, M. A., Kulkarni, C., Goebel, K., and Fink,

O. (2022). Real-time model calibration with deep re-

inforcement learning. Mechanical Systems and Signal

Processing, 165:108284.

Tom

e De Andrade e Silva, Manuel and Azevedo, A. (2022).

Self-adapting wip parameter setting using deep re-

inforcement learning. Computers & Operations Re-

search, 144:105854.

Vakili, A. and Navimipour, N. J. (2017). Comprehen-

sive and systematic review of the service composition

mechanisms in the cloud environments. Journal of

Network and Computer Applications, 81:24–36.

Varasteh, A. and Goudarzi, M. (2017). Server consolidation

techniques in virtualized data centers: A survey. IEEE

Systems Journal, 11(2):772–783.

Wan, J., Cao, Z., Ma, Y., Zhao, G., and Sun, Z. (2021).

A parameter selection method based on reinforce-

ment learning: The qos-privacy trade-off for adver-

sarial training framework. In Sun, X., editor, Ad-

vances in artiﬁcial intelligence and security, volume

1422 of Communications in computer and informa-

tion science, 1865-0929, pages 338–350. Springer,

Cham, Switzerland.

Wang, C., Zhang, K., Wang, H., and Chen, B. (2022a).

Auto-stgcn: Autonomous spatial-temporal graph con-

volutional network search. ACM Trans. Knowl. Dis-

cov. Data. Just Accepted.

Wang, X., Wang, S., Liang, X., Zhao, D., Huang, J., Xu, X.,

Dai, B., and Miao, Q. (2022b). Deep reinforcement

learning: A survey. IEEE Transactions on Neural Net-

works and Learning Systems, pages 1–15.

Wang, Z., Zhang, J., Li, Y., Gong, Q., Luo, W., and Zhao,

J. (2021). Automated reinforcement learning based

on parameter sharing network architecture search. In

2021 6th International Conference on Robotics and

Automation Engineering (ICRAE 2021), pages 358–

363, Piscataway, NJ. IEEE.

WU, J., CHEN, S., and CHEN, X. (2019). Rpr-bp: A deep

reinforcement learning method for automatic hyper-

parameter optimization. In 2019 International Joint

Conference on Neural Networks (IJCNN), pages 1–8.

Yang, L. and Shami, A. (2020). On hyperparameter opti-

mization of machine learning algorithms: Theory and

practice. Neurocomputing, 415:295–316.

Zhang, R., Peng, H., Dou, Y., Wu, J., Sun, Q., Li, Y.,

Zhang, J., and Yu, P. S. (2022a). Automating db-

scan via deep reinforcement learning. In Proceed-

ings of the 31st ACM International Conference on

Information & Knowledge Management, CIKM ’22,

page 2620–2630, New York, NY, USA. Association

for Computing Machinery.

Zhang, Y., Bai, R., Qu, R., Tu, C., and Jin, J. (2022b). A

deep reinforcement learning based hyper-heuristic for

combinatorial optimisation with uncertainties. Euro-

pean Journal of Operational Research, 300(2):418–

427.

Zhu, J., Wu, F., and Zhao, J. (2021). An overview of the ac-

tion space for deep reinforcement learning. In 2021

4th International Conference on Algorithms, Com-

puting and Artiﬁcial Intelligence (ACAI 2021), ICPS,

pages 1–10, New York, New York. The Association

for Computing Machinery.

A Recent Publications Survey on Reinforcement Learning for Selecting Parameters of Meta-Heuristic and Machine Learning Algorithms

243