Handling Data Heterogeneity in Federated Learning with Global Data

Distribution

C Nagaraju

1 a

, Mrinmay Sen

2 b

and C Krishna Mohan

1 c

Deparment of Computer Science, IIT Hyderabad,, India

Department of Artiﬁcial Intelligence, IIT Hyderabad, India

Keywords:

Data Heterogeneity in Federated Learning, Global Data Distribution with Gaussian Mixture Model.

Abstract:

Federated learning, a different direction of distributed optimization, is very much important when there are re-

strictions of data sharing due to privacy and communication overhead. In federated learning, instead of sharing

raw data, information from different sources are gathered in terms of model parameters or gradients of local

loss functions and these information is fused in such way that we can ﬁnd the optima of average of all the local

loss functions (global objective). Exiting analyses on federated learning show that federated optimization gets

slow convergence when data distribution across all the clients or sources are not homogeneous. Heterogeneous

data distribution in federated learning causes objective inconsistency which means global model converges to

a another stationary point which is not same as the optima of the global objective which results in poor per-

formance of the global model. In this paper, we propose a federated Learning(FL) algorithm in heterogeneous

data distribution. To handle data heterogeneity during collaborative training, we generate data in local clients

with the help of a globally trained Gaussian Mixture Models(GMM). We update each local model with the

help of both original and generated local data and then perform the similar operations of the most popular

algorithm called FedAvg. We compare our proposed method with exiting FedAvg and FedProx algorithms

with CIFAR10 and FashionMNIST Non-IID data. Our experimental results show that our proposed method

performs better than the exiting FedAvg and FedProx algorithm in terms of training loss, test loss and test

accuracy in heterogeneous system.

1 INTRODUCTION

Federated learning (FL) (McMahan et al., 2017) is

the part of distributed training where instead of tak-

ing raw data from different sources or clients, lo-

cally trained models or local gradients are commu-

nicated to the server to build a globally representative

model. Server ﬁnds the global model by aggregat-

ing all the local information (either model parame-

ters or gradients) in such way that the global objec-

tive function (average of all local loss functions) is

optimized. The main challenge associated with fed-

erated optimization is the data across the clients. The

most popular federated learning algorithm named Fe-

dAvg (McMahan et al., 2017) uses weighted aver-

age of all the local information which performs well

when data across all the clients are homogeneous or

https://orcid.org/0000-0003-4468-6895

https://orcid.org/0000-0001-9550-7709

https://orcid.org/0000-0002-7316-0836

slightly heterogeneous. Exiting analyses on federated

learning (Li et al., 2020b; Zhu et al., 2021; Karim-

ireddy et al., 2020; Wang et al., 2020) shows that

FedAvg suffers from very slow convergence when

data are highly heterogeneous. Heterogeneous data

distribution across all the clients causes client drift

(Global model gets biased towards some part of the

client’s models) which results in objective inconsis-

tency (Wang et al., 2020; Karimireddy et al., 2020;

Tan et al., 2021). Due to heterogeneous data distribu-

tion, the global model gets converged to a point which

is away from the optima of the global loss function.

According to the survey of (Tan et al., 2021), there are

two types of approaches to handle data heterogene-

ity in FL system. One is model based and another

is data based. Model based approaches are based on

regularization of loss function (Li et al., 2020a; Wang

et al., 2020; Karimireddy et al., 2020; Li et al., 2021;

Deng et al., 2020), meta learning (Fallah et al., 2020)

and transfer learning (Li and Wang, 2019). Model

based approaches are easy to implement but these are

Nagaraju, C., Sen, M. and Mohan, C.

Handling Data Heterogeneity in Federated Learning with Global Data Distribution.

DOI: 10.5220/0011955400003497

In Proceedings of the 3rd International Conference on Image Processing and Vision Engineering (IMPROVE 2023), pages 121-125

ISBN: 978-989-758-642-2; ISSN: 2795-4943

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

121

not suitable for signiﬁcantly high degree of heteroge-

neous data distribution (Tan et al., 2021) which mo-

tivates us to use data based approach. The exiting

data based approaches (Jeong et al., 2018; Duan et al.,

2021; Wu et al., 2022) are either computationally ex-

pensive (as they are using generative complex models

like Generative Adversarial Network or deep learn-

ing based auto-encoder) or associated with local data

down sampling (which results in signiﬁcant informa-

tion loss) or less privacy concerned (Due to sending

some raw data from clients to server).

To overcome the above mentioned issues in feder-

ated learning, we propose a new data based approach.

In our proposed method, we ﬁnd the global data dis-

tribution by using aggregated locally trained Gaussian

Mixture Models (GMMs) (Reynolds, 2009) which is

comparatively less complex and easy to train. To han-

dle data heterogeneity across all the clients, we gen-

erate data in all the local clients with the help of these

global GMMs.

The rest of the paper is organized as follows. We

ﬁrst formulate the problem of heterogeneous feder-

ated optimization, then we show the exiting works

on heterogeneous FL. Next we discuss about our pro-

posed method. Next sections cover the experimental

setup, results discussion and conclusions of our whole

work.

2 PROBLEM FORMULATION

In federated learning, all the participating clients par-

allelly train local models by optimizing their own loss

function and the server aggregates all the local models

to ﬁnd the optima of the global loss function. Global

loss function is found by taking weighted average of

all the local loss functions. Let total m number of

clients are jointly involved in federated optimization.

Each client contains N

number of samples. Then the

global objective function is deﬁned as

F(w) =

∑

i=1

(w) (1)

Where, F

and N

are the loss function and num-

ber of samples of i

client respectively, p

∑

(w)=

∑

ς∈D

(w;ς), Where ς are the samples of

clients which is taken from the distribution D

Our goal is to ﬁnd the optima of the global loss func-

tion F(w) ∀w ∈ R

Algorithm 1: Proposed Federated Algorithm.

0: Input: T , w

, η=η

, ψ

1: {(µ

, Σ

)}

i=1

← Global-GMM(m) {ﬁnd data dis-

tribution across all the clients}

2: Server sends Global-GMM to all the participating

clients

3: All the clients generate data with the help of this

Global GMM to overcome data heterogeneity

4: for t = 1 to T do

5: Server sends w

to all clients

6: Clients update w

with locally available data

and SGD optimizer and ﬁnd w

7: Server receives all the locally updated models

and aggregate these and ﬁnd w

t+1

8: Update learning rate η=(1 − ψ)η

9: end for

3 RELATED WORKS

Many works has been done to mitigate the problem

of data heterogeneity in FL system. The most related

works of this paper can be viewed in two directions

((Tan et al., 2021)). One is model based approaches

and another one is data based approaches. Model

based approaches include regularization of loss func-

tion, meta learning and transfer learning. Some ex-

amples of model based approches are FedProx (Li

et al., 2020a), FedNova (Wang et al., 2020), SCAF-

FOLD (Karimireddy et al., 2020), pFedMe (Dinh

et al., 2020), MOON (Li et al., 2021), APFL (Deng

et al., 2020) etc. To handle problem of client drift

due to Non-IID data, FedProx add proximal term

||w − w

with the local loss functions. FedNova

uses normalized averaging (Wang et al., 2020) to han-

dle objective inconsistency. SCAFFOLD uses vari-

ance reduction to correct the client drift in local mod-

els. pFedMe uses Moreau envelopes as the local reg-

ularized objective. MOON uses model label con-

stractive learning to handle Non-IID data. APFL in-

troduces mixing concept of local and global models

with an adaptive weight to handles client drift. (Fal-

lah et al., 2020) use meta learning (MAML) to eas-

ily adapt the local information with one or few steps

of gradient descent. Even all the model based ap-

proaches perform better than FedAvg, these methods

suffer from tight convergence when there is high de-

gree of heterogeneity (Tan et al., 2021) which mo-

tivates us to jump into data based approach. The

exiting data based approaches (Jeong et al., 2018;

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

122

Duan et al., 2021; Wu et al., 2022) are either com-

putationally expensive (due to use of complex models

like Generative Adversarial Network (GAN) or deep

learning based auto-encoder) or associated with lo-

cal data down sampling (which results in signiﬁcant

information loss) or less privacy concerned (Due to

sending some raw data from clients to server).

4 PROPOSED METHOD

Algorithm- 1 shows one global iteration of our pro-

posed method. In our proposed method we ﬁrst col-

lect locally trained GMMs and aggregate these in

server to ﬁnd the global data distribution. Then the

aggregated GMMs is sent to all the available clients

and then clients generate data with the help of these

globally trained GMMs which results in transforma-

tion of data distribution across all the clients from het-

erogeneous to nearly homogeneous. After data gen-

eration, server sends global model w

is randomly

initialized) to all the clients and clients update this

global model with the help of locally available data

(original data and generated data). Clients use SGD

optimizer (with learning rate scheduler, momentum

and weight decay) (Ruder, 2016) to optimize the lo-

cal loss functions with only one local epoch per client

per global iteration. Then server collects all the lo-

cally updated models and aggregate these to ﬁnd the

global model w

t+1

. To get faster convergence, we use

learning rate decay (Li et al., 2020b) ψ ∈ [0, 1).

4.1 Data Distributions

To ﬁnd the overall data distributions across all the

clients, we train GMMs ((Reynolds, 2009)) with local

data and aggregate these in server. To reduce compu-

tational complexity, instead of using full covariance

matrix, we use diagonal covariance matrix with the

assumption that each class samples are coming from

5 number of Gaussian components.

5 EXPERIMENTAL SETUP

We validate our proposed method with CIFAR10 and

FashionMNIST Non-IID data. The CIFAR-10 dataset

contains of 60000 RGB images (3 x 32 x 32) with

10 number of classes (50000 training samples and

10000 test samples). Each class has 6000 number of

samples. FashionMNIST contains gray scale images

of size 28 × 28 with 10 number of classes. In our

experiment (60000 training samples and 10000 test

samples). To get Non-IID data partitions, we use the

same data partition concept of the paper (McMahan

et al., 2017). We divide whole training samples into

80 shards (size of each shard is 625 for CIFAR10 and

750 for FashionMNIST) and divide these shards into

20 clients in such way that each client gets only two

shards i.e. Each client gets samples of 4 classes only.

Instead of taking into account of all device partici-

pation, we assume that only 50% of total number of

clients of available at each global iteration. We com-

pare our proposed method with the most popular FL

algorithms named FedAvg ((McMahan et al., 2017))

and FedProx ((Li et al., 2020a)).

We evaluate the performance of FedAvg, Fed-

Prox and our proposed method with learning rate

∈ [0.1, 0.01, 0.001], weight decay ∈ [1e − 4, 1e − 8] ,

fedprox proximal term µ ∈ [0.1, 0.01], learning rate

decay (ψ)= 0.02, momentum = 0.9 and batch size =

128. We ﬁnd the best performing model for each al-

gorithm by considering minimum train and test loss.

We use Resnet18 model and categorical cross entropy

loss function for our experiments. To ﬁnd global data

distributions, we train GMMs locally with diagonal

covariance matrix and 5 number of components per

class samples. Server receives all the locally trained

GMMs and aggregates these to ﬁnd global GMMs.

Each client receives these global GMMs and gener-

ates data in such a way that after generation, number

of samples for all the classes become same.

Figure 1: CIFAR10 average train loss VS Global epoch.

Figure 2: CIFAR10 average test loss VS Global epoch.

5.1 Results

Figure- 1, 2, 3, 4, 5, 6 show our experimental re-

sults. We ﬁnd average train loss, average test loss and

test accuracy for FedAvg, FedProx and our proposed

Handling Data Heterogeneity in Federated Learning with Global Data Distribution

123

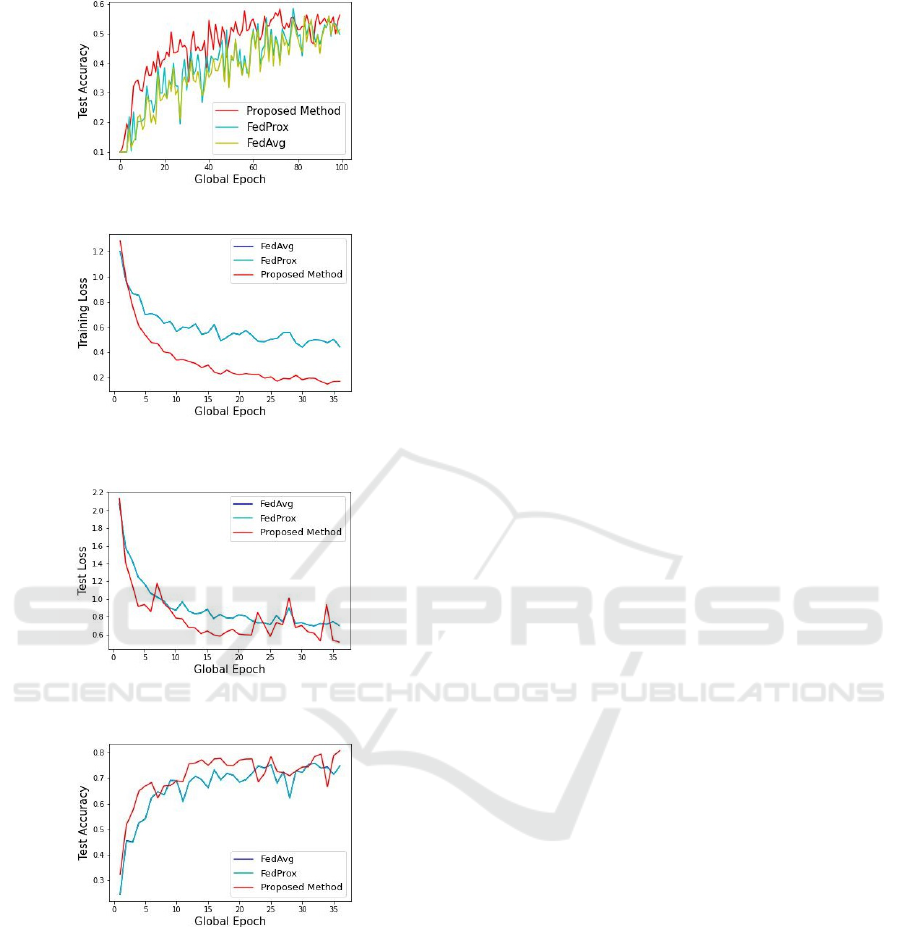
Figure 3: CIFAR10 test accuracy VS Global epoch.

Figure 4: FashionMNIST average train loss VS Global

epoch.

Figure 5: FashionMNIST average test loss VS Global

epoch.

Figure 6: FashionMNIST test accuracy VS Global epoch.

method in the same FL system. In heterogeneous

data, experimental results show that our proposed al-

gorithm performs better than FedAvg and FedProx in

terms of average train loss, average test loss and test

accuracy. For CIFAR10, to acheive 55% of test accu-

racy, FedAvg, FedProx and our proposed method take

95, 84 and 57 number of global epochs respectively.

For FashionMNIST, to acheive 75% of test accuracy,

FedAvg, FedProx and our proposed method take 25,

25 and 12 number of global epochs respectively. We

observed that for FashionMNIST Non-IID data, Fed-

prox performs similar to FedAvg.

6 CONCLUSIONS

In federated learning, data heterogeneity across all the

participating clients is one of the critical challenge.

Data heterogeneity causes client drift which results

in degradation of the performance of FL model in

terms of higher loss (both train and test) and lower

test accuracy. To mitigate this problem, we proposed

a GMM based approach where we handle data hetero-

geneity by generating new local samples from glob-

ally trained GMMs. Our experimental results show

that our proposed method handles data heterogene-

ity in FL system better than exiting FedAvg and Fed-

Prox algorithm. We show that the performance of FL

model is improved in terms of train loss, test loss and

test accuracy by our proposed method.

REFERENCES

Deng, Y., Kamani, M. M., and Mahdavi, M. (2020).

Adaptive personalized federated learning. CoRR,

abs/2003.13461.

Dinh, C. T., Tran, N. H., and Nguyen, T. D. (2020). Person-

alized federated learning with moreau envelopes. In

Advances in Neural Information Processing Systems

33: Annual Conference on Neural Information Pro-

cessing Systems 2020, NeurIPS 2020, December 6-12,

2020, virtual.

Duan, M., Liu, D., Chen, X., Liu, R., Tan, Y., and Liang, L.

(2021). Self-balancing federated learning with global

imbalanced data in mobile systems. IEEE Trans. Par-

allel Distributed Syst., 32(1):59–71.

Fallah, A., Mokhtari, A., and Ozdaglar, A. E. (2020). Per-

sonalized federated learning with theoretical guaran-

tees: A model-agnostic meta-learning approach. In

Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.,

and Lin, H., editors, Advances in Neural Information

Processing Systems 33: Annual Conference on Neural

Information Processing Systems 2020, NeurIPS 2020,

December 6-12, 2020, virtual.

Jeong, E., Oh, S., Kim, H., Park, J., Bennis, M., and Kim, S.

(2018). Communication-efﬁcient on-device machine

learning: Federated distillation and augmentation un-

der non-iid private data. CoRR, abs/1811.11479.

Karimireddy, S. P., Kale, S., Mohri, M., Reddi, S. J., Stich,

S. U., and Suresh, A. T. (2020). SCAFFOLD: stochas-

tic controlled averaging for federated learning. In Pro-

ceedings of the 37th International Conference on Ma-

chine Learning, ICML 2020, 13-18 July 2020, Virtual

Event, volume 119 of Proceedings of Machine Learn-

ing Research, pages 5132–5143. PMLR.

Li, D. and Wang, J. (2019). Fedmd: Heterogenous

federated learning via model distillation. CoRR,

abs/1910.03581.

Li, Q., He, B., and Song, D. (2021). Model-contrastive

federated learning. In IEEE Conference on Computer

Vision and Pattern Recognition, CVPR 2021, virtual,

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

124

June 19-25, 2021, pages 10713–10722. Computer Vi-

sion Foundation / IEEE.

Li, T., Sahu, A. K., Zaheer, M., Sanjabi, M., Talwalkar,

A., and Smith, V. (2020a). Federated optimization in

heterogeneous networks. In Proceedings of Machine

Learning and Systems 2020, MLSys 2020, Austin, TX,

USA, March 2-4, 2020. mlsys.org.

Li, X., Huang, K., Yang, W., Wang, S., and Zhang, Z.

(2020b). On the convergence of fedavg on non-iid

data. In 8th International Conference on Learning

Representations, ICLR 2020, Addis Ababa, Ethiopia,

April 26-30, 2020.

McMahan, B., Moore, E., Ramage, D., Hampson, S., and

y Arcas, B. A. (2017). Communication-efﬁcient learn-

ing of deep networks from decentralized data. In Pro-

ceedings of the 20th International Conference on Ar-

tiﬁcial Intelligence and Statistics, AISTATS 2017, 20-

22 April 2017, Fort Lauderdale, FL, USA, volume 54,

pages 1273–1282. PMLR.

Reynolds, D. A. (2009). Gaussian mixture models. Ency-

clopedia of biometrics, 741(659-663).

Ruder, S. (2016). An overview of gradient descent opti-

mization algorithms. CoRR, abs/1609.04747.

Tan, A. Z., Yu, H., Cui, L., and Yang, Q. (2021).

Towards personalized federated learning. CoRR,

abs/2103.00710.

Wang, J., Liu, Q., Liang, H., Joshi, G., and Poor, H. V.

(2020). Tackling the objective inconsistency prob-

lem in heterogeneous federated optimization. In Ad-

vances in Neural Information Processing Systems 33:

Annual Conference on Neural Information Processing

Systems 2020, NeurIPS 2020, December 6-12, 2020,

virtual.

Wu, Q., Chen, X., Zhou, Z., and Zhang, J. (2022).

Fedhome: Cloud-edge based personalized federated

learning for in-home health monitoring. IEEE Trans.

Mob. Comput., 21(8):2818–2832.

Zhu, H., Xu, J., Liu, S., and Jin, Y. (2021). Federated

learning on non-iid data: A survey. Neurocomputing,

465:371–390.

Handling Data Heterogeneity in Federated Learning with Global Data Distribution

125