Fuzzy Inference System in a Local Eigenvector Based Color Image

Smoothing Framework

Khleef Almutairi

1,2 a

, Samuel Morillas

1 b

, and Pedro Latorre-Carmona

3 c

Instituto Universitario de Matem

atica Pura y Aplicada, Universitat Polit

ecnica de Val

encia,

Camino de Vera s/n, Valencia, 46022, Spain

Mathematics Department, Faculty of Science, Albaha University, Suadi Arabia

Departmento de Ingenier

ıa Inform

atica, Universidad de Burgos, Avda. Cantabria s/n, Burgos, 09006, Spain

Keywords:

Colour Image Smoothing, Fuzzy Inference System, Gaussian Noise, Noise Reduction, Eigenvector Analysis.

Abstract:

Noise ﬁltering in colour images is a complex task since it is essential to distinguish between structural and

noise information in the image. It would therefore be important to simultaneously remove noise while keeping

the original image details. This paper proposes a method based on a fuzzy inference system to eliminate noise

and retrieve original image details. Images are transformed from an RGB space to an eigenvector based space

and this transformation is fed to the fuzzy system. Results conﬁrm the validity of the approach, its superior

performance when compared to the eigenvector based framework it is based on, and its competitive behaviour

when compared to other state-of-the-art methods.

1 INTRODUCTION

Digital image processing and computer vision ﬁelds

have experienced sustained and intensive growth due

to the importance digital image processing have had

in the last decade. One of the research scopes that

brought scientist attention is image denoising (ﬁlter-

ing), since this research line has played a prominent

role in computer vision. Focus has been given to im-

age denoising to help suppress unwanted noise and

improve the quality of reconstructed (transmitted) im-

ages.

Noise is deﬁned as the random changes appear-

ing in the pixel colour information or image bright-

ness (Hong and Thanh, 2020). A well-known noise

source is the so-called thermal noise, which is caused

by the sensor charge-coupled device (CCD) malfunc-

tion. This type of noise can be modelled as addi-

tive white Gaussian noise, and it can be simulated by

adding a random amount of zero-mean Gaussian dis-

tributed values to those in the image, on a channel-

independent basis (Plataniotis and Venetsanopoulos,

2000).

Many Gaussian noise ﬁltering methods have

https://orcid.org/0000-0003-3167-5708

https://orcid.org/0000-0001-9262-6139

https://orcid.org/0000-0001-6984-5173

shared the same aim of maximizing the smoothing

of homogeneous regions. The structure of the im-

ages should be preserved and avoid mixing the tex-

ture of the image with noise. Finally, the denois-

ing method should not introduce any colour artifacts.

That is, once the denoising process is done, no addi-

tional colours that are different from the image’s orig-

inal colours should appear. (Hong and Thanh, 2020).

The ﬁrst ﬁltering methods, which appeared more

than twenty years ago, were of linear nature. We

can mention, for instance, the arithmetic mean ﬁl-

ter (AMF) (Plataniotis and Venetsanopoulos, 2000).

Despite its noise-suppressing capability, taking ad-

vantage of its zero-mean property, AMF added un-

wanted blur to the image details and structure. This

drawback, which is inherent to its linear nature,

motivated the development of many non-linear ap-

proaches. Some of them overcame the blur effect that

was added to the edges, by detecting the details and

the structure, in order to smooth them less than the

rest of the image.

A number of non-linear methods use the advan-

tage of the zero-mean property. The well-known

bilateral ﬁlter (BF) method (Tomasi and Manduchi,

1998) is one example. Not only using the average may

successfully minimize the noise, but other approaches

can also improve noise suppression. The eigenvector

142

Almutairi, K., Morillas, S. and Latorre-Carmona, P.

Fuzzy Inference System in a Local Eigenvector Based Color Image Smoothing Framework.

DOI: 10.5220/0011966900003497

In Proceedings of the 3rd International Conference on Image Processing and Vision Engineering (IMPROVE 2023), pages 142-149

ISBN: 978-989-758-642-2; ISSN: 2795-4943

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

analysis ﬁlter (EIG) (Latorre-Carmona et al., 2020),

for instance, uses the technique of weighted pixel av-

eraging to be used in colour images smoothing prob-

lems based on linear algebra. This approach will be

thoroughly discussed in the next section.

In addition, wavelet theory has been used for im-

age ﬁltering. An example is the collaborative wavelet

ﬁlter (CWF), originally proposed in (Dabov et al.,

2007). Another method named the graph method for

simultaneous smoothing and sharpening (GMS

) and

its normalized version (NGMS

) is based on the anal-

ysis of local graphs structure, obtained at every pixel,

using its neighbour (P

erez-Benito et al., 2020). On

the other hand, fuzzy logic has recently contributed

to the design of systems that may be able to smooth

images.

In this study, we use a fuzzy inference system

(FIS) to adapt the ﬁlter denoising capability to the

amount that might be needed for each image region.

The image is ﬁrst transformed from the RGB space to

a local eigenvector space in order to analyse the corre-

lation among the colour image channels, and then to

extract three descriptive statistic features, which are

therefore used as input data for FIS. Extracting the

statistics is also an inherent part of the EIG ﬁltering

process.

Our proposal is different from EIG in some as-

pects. One of them is that EIG uses the so-called

normalized standard deviation to perform smoothing,

whereas FIS uses the local standard deviation of each

EIG channel component as an input value. The mem-

bership functions as well as the set FIS rules, are used

to infer the degree of smoothing in the three image

channels, depending on the channel information.

Hence, if the channel has details that should be

preserved, the system will perform a gentle smooth-

ing in that channel. Otherwise, in the homogeneous

regions where no information needs to be kept intact

in the channel, FIS will smooth with the highest po-

tential intensity. When smoothing has already been

applied, the image is returned to the original RGB

space. Experimental results for FIS are promising

when compared to the method it is based on and with

others consdiered here.

This paper is organized as follows: Section 2 re-

views the EIG ﬁlter. Section 3 illustrates the proposed

method. Section 4 shows the experimental results

and compares this method with other state-of-the-art

methods. Section 5 presents the conclusions and fu-

ture work.

2 EIGENVECTOR ANALYSIS

METHOD, REVIEWED

This section highlights the process of Eigenvector

analysis shown in (Latorre-Carmona et al., 2020) that

has been used in this study. Assume F is an RGB

colour image. Let us consider a sliding window of

size N × N where N = 2N + 1 and n = 1,2,.... Each

pixel to be processed is in the centre in the sliding

window, denoted as F

, and deﬁned as (F

The neighbour pixels are denoted as F

, where i =

1,...N

− 1. The data matrix, called D of the size

− 1, is built using the pixel colour channel val-

ues. A proper analysis of this matrix D may allow for

processing the correlation of the colour image chan-

nels and also to preserve the edges of the image under

processing. Based on principal component analysis

(PCA) (Dillon and Goldstein, 1984) and using the in-

formation of the D matrix, we can ﬁnd the eigenvector

of D

D, where T is the matrix transpose. Since D is a

symmetric matrix, it can be reduced to a diagonal ma-

trix L by pre-multiplication and post multiplication by

an orthonormal matrix O. The diagonal elements of

L are called the eigenvalues, and the columns of the

matrix O are called the eigenvector of the D

D. A

vector v is called an eigenvector of D

D if it satisﬁes

the condition of the eigenvector of a matrix that can

compress or stretch without affecting the direction.

We may then transform the original data into a

group of uncorrelated data employing the coordinate

axis given by the direction of each one of the inferred

eigenvectors. Thus, if V is an orthonormal matrix of

size 3 × 3 that has the three eigenvectors of D

D as

columns, named as V

, and V

, the transformation

process is given by the following equation:

U = DV (1)

where U is the score matrix that has the trans-

formed data, since V is orthonormal. The whole pro-

cess is completely invertible:

= D (2)

We can now consider applying any component-

wise method on U, which is a set of uncorrelated vari-

ables U

, U

, and U

, each of them associated with

the eigenvalues V

, V

, and V

. Now, we apply a de-

noising method taking advantage of the information

from the eigenvector analysis stated previously.

Due to the sample variance maximization, we can

associate the new variable U

with how many corre-

lated changes in the data they represent. We may have

that σ(U

) >> σ(U

) and σ(U

) >> σ(U

) where σ

is the sample standard deviation. In this case, while

the variable U

is associated with a correlated colour

Fuzzy Inference System in a Local Eigenvector Based Color Image Smoothing Framework

143

variance, most probably representing edges of the im-

age which means we should smooth this variable gen-

tly. However, in the absence of edges and correlated

information in the images where we expect the vari-

ance of U

, U

and U

to be similar, which means

safely smoothing. In order to smooth each compo-

nent independently, we apply a weighted averaging

operation

−1

∑

p=0

−1

∑

p=0

,i = 1,2,3. (3)

where i is the colour channels and p are the pixel

numbers around the central pixel. Where W

needs

to be set depending on the desired smoothing. Us-

ing this information and a decreasing function repre-

senting that U

close to U

receive high weight, EIG

computes

= exp

−

−U

|σ

)

, (4)

where D is the ﬁlter parameter which is experi-

mentally optimized, and it has been set to be D =

(5/6) × s for the window of the size 3 × 3 where s

is the value of noise standard deviation, and that can

be quite accurately estimated.

In the last stage, the processed data should be re-

turned back to RGB space, and this can be done by

multiplying the data by the matrix V

EIG exhibits a good performance when preserv-

ing image details while removing unwanted noise. In

the following section, we propose how this smooth-

ing effect can be enhanced using a fuzzy system with

an appropriate setting to take non-normalized stan-

dard deviation as an input of the system to determine

three smoothing coefﬁcients that replace the normal-

ized standard deviations used by EIG the ﬁlter.

3 DENOISING COLOUR IMAGES

USING A FUZZY INFERENCE

SYSTEM

Fuzzy logic was introduced by Zadeh (Zadeh, 1965)

with the idea of extending the classical logical frame-

work. This means including ﬂexibility for reason-

ing with uncertain data so that it is closer to human

thinking instead of being restricted to either true or

false statements (Nov

ak et al., 2012). Illustrating that,

there are other propositions that have a range of po-

tential responses, such as those that arise when ask-

ing a group of individuals to name a colour. When

this happens, the sampled answers are mapped on a

spectrum, and it appears that the truth can be deduced

based on incomplete or imperfect knowledge. For this

fact, fuzzy logic has been used in diverse research ar-

eas covering almost all disciplines in technology and

science.

In the image processing ﬁeld, several articles

pointed out that the beneﬁts of using a fuzzy in-

ference were particularly important in two main as-

pects (Qidwai and Chen, 2009): (i) The fuzzy ap-

proach is a powerful tool for representing and pro-

cessing knowledge, and (ii) Vagueness and ambiguity

can be effectively managed using fuzzy approaches.

Some studies, (Schulte et al., 2007a) and (Schulte

et al., 2007b) showed the feasibility to use a fuzzy ap-

proach to minimize the noise in colour images. On the

other hand, (Van De Ville et al., 2003) uses a 2-steps

fuzzy method to remove white additive noise (Gaus-

sian noise). Moreover, (Shen and Barner, 2004) and

(Lukac et al., 2005) showed the advantages of using

fuzzy logic in other particular image ﬁltering opera-

tions.

In this work, we study whether or not the use of

a fuzzy inference system may improve the EIG ﬁlter

performance in terms of noise reduction while keep-

ing the details preservation ability.

Any fuzzy inference system usually consists of

three major components: Fuzzyﬁcation, Inference

and Defuzzyﬁcation (Mendel, 1995), as shown in Fig-

ure 1.

In our case, we propose to use the σ(u

), σ(u

)

values as the crisp inputs for FIS, and compute σ(u

)

as described in Section 2. In the fuzziﬁcation stage,

the transformation of numerical inputs to linguistic

variables with the help of membership functions is

done. We consider different linguistic variables for

each input, as their ranges are different. Then, they

are ranked so that σ(U

) < σ(U

). In each

case, we consider low, medium, and high fuzzy sets.

The membership functions that are used in the input

and the output are chosen to be Gaussian membership

functions.

Each function has two parameters (location and

width), which are then multiplied by three linguistic

variables for three different inputs, for a total amount

of 36 parameters. Other functions could be used in-

deed, but we prefer to keep the number of total pa-

rameters as low as possible. Subsection 3.1 explains

the optimization process for this set of parameters.

The next stage is the inference process. Here, the

system applies the set of linguistic rules built with

expert knowledge that implements the expected be-

haviour of the process. The set of rules takes the form

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

144

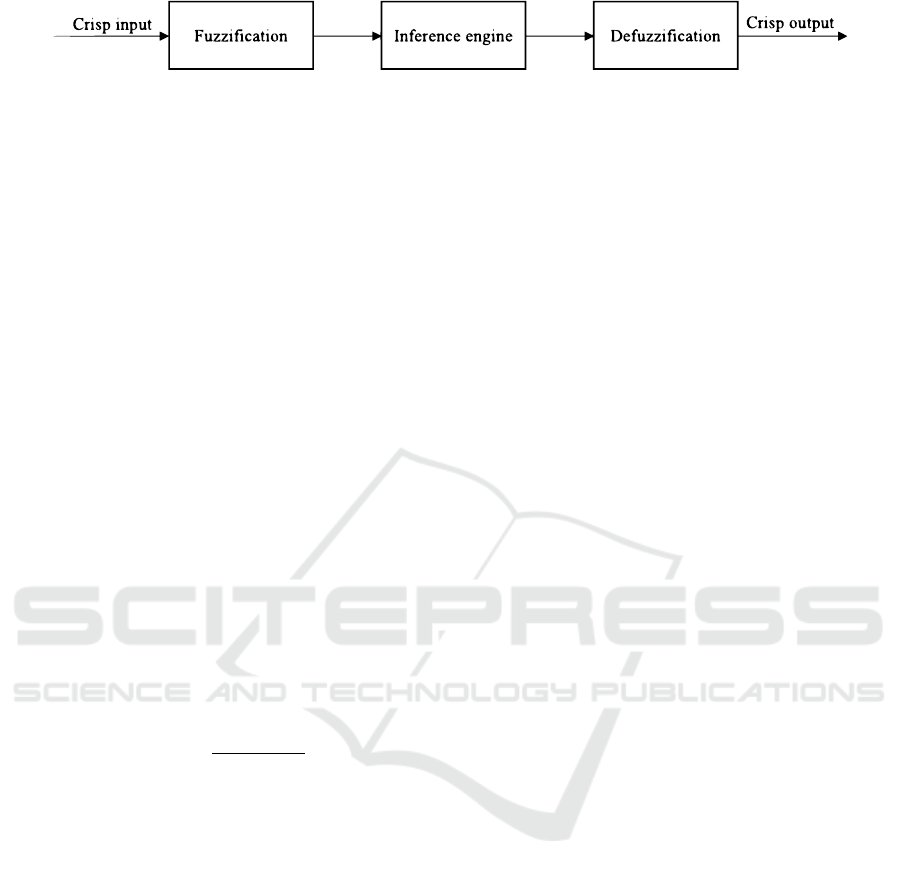
Figure 1: The general structure of any fuzzy inference system.

of IF-THEN implication rules. The inference system

transforms the fuzzy input linguistic certainty values

into fuzzy output linguistic certainty values. The set

of rules that are speciﬁed for this system process in-

cludes 3 rules for each input i = 1,2,3, described as

follows:

1. IF σ(u

) is low, Then the smoothing coefﬁcient C

is low.

2. IF σ(u

) is medium, Then the smoothing coefﬁ-

cient C

is medium.

3. IF σ(u

) is high, Then the smoothing coefﬁcient

is high.

Therefore, we have 9 rules overall because we

consider that the linguistic variables are different for

each input because each input takes values in different

ranges, taking into account that: σ(U

) < σ(U

) <

σ(U

The Last part is the defuzziﬁcation process, where

processing done by the linguistic terms will be de-

fuzziﬁed again to three numerical values called C

, and C

, through membership functions. Those co-

efﬁcients will be used for smoothing the noisy image,

replacing the normalized standard deviation used in

EIG in Eq. (8), so that:

= exp

−

−U

. (5)

3.1 Membership Functions

Optimization

Regardless of the method employed to create the

fuzzy inference system, its numerical accuracy can

be improved by optimizing its parameters. This

goal should be accomplished without compromis-

ing the system’s interpretation (Casillas et al., 2003).

Many strategies allow us to deal with these types of

problems: Genetic algorithms (GA) (Moallem et al.,

2015), for instance, are used effectively to optimize

the fuzzy inference system for both categories; (i) The

structure dealing with the deﬁnition and the fuzzy sys-

tem rule (ii) The parameters deﬁning the membership

function in each FIS subset. In this study, we focus

on parameter optimization using a GA approach.

GAs are global stochastic optimization methods.

They are based on structures developed primarily

employing Darwin’s ”survival of the ﬁttest” concept

and natural selection and evolutionary theories. The

aforementioned approach is commonly used as an ef-

fective optimization technique for difﬁcult real-world

optimization issues, such as design and combinatorial

problems (Abualigah and Hanandeh, 2015). When

using GAs to solve a speciﬁc problem, a deﬁned num-

ber of people are produced at random for each gener-

ation to form the initial population of people or can-

didate solutions. The variation, selection, and inher-

itance principles are used to build the population of

candidate solutions in question.

GAs can be simpliﬁed into the following seven

steps (Moallem et al., 2015):

• Start with an n chromosome population that was

produced randomly.

• Compute the ﬁtness for each chromosome.

• From the original population, choose a set of

parental chromosomes.

• Preform crossover to create two offspring with the

probability of P

cross

• The two offspring should be mutated with the

probability of P

mut

• Replace the offspring among the population.

• Check for the end or back to point two.

In this paper, GA is used to optimize the mem-

bership functions for the inputs and the outputs of

the fuzzy inference system separately, as each input

and output is taking values in different ranges. In

other words, the low subset for instance, is different

for each input. The ﬁtness function is deﬁned as the

minimization of the mean square error between the

denoised pixel and the original one. The maximum

number of generations is set to be 100. The bound-

aries of the membership functions for the inputs are

0 −200 for the input centre and 5− 100 for the width.

For the output boundaries, the settings are 0 − 1 and

0.01 − 1 for the centre and width of the membership

functions, respectively. Figure 2 graphically shows

the FIS membership functions using the optimized pa-

rameters for noise level s = 10. The ﬁrst row has the

input membership functions, and the second row rep-

resents the corresponding output membership func-

tions.

Table 1 summarizes the result of the optimization

process for each level of Gaussian noise studied and

input and output membership functions, respectively.

To compute this, we have used the image training

Fuzzy Inference System in a Local Eigenvector Based Color Image Smoothing Framework

145

dataset explained in Section 4. By looking at Table

1 we can see that location parameters agree with the

meaning of each linguistic variable. Also, when noise

is increased, we can see that in general, the location

of the membership functions increases in value. This

happens because the higher the noise is, the higher the

standard deviation in all the channels is as well. How-

ever, there are some exceptions to this behaviour that

we need to analyze in more detail. For instance, the

introduction of noise affects more the ﬁrst input than

the rest. This may be explained because inputs two

and three are related to more correlated data variations

meaning that noise will affect them less. Worth point-

ing out that, by looking at Table 1, we see that loca-

tion of functions is increased by the addition of noise.

This means that output coefﬁcients tend to be higher

in these cases, which means that smoothing will be

higher, which is what it is needed for higher noise.

Therefore, this behaviour is what one would expect it

to happen.

4 EXPERIMENTAL RESULTS

We divided a set of images into training and valida-

tion sets, and performed the optimization and vali-

dation of the fuzzy inference system using the train-

ing images set, which are Pills 50 × 50, Head-phone

100 × 100, and Parrot 80 × 80. We tested the sys-

tem with the optimized parameters, using the vali-

dation set of images formed by Beach 100 × 100,

Lena 90 × 90, and Grass 200 × 200. The train-

ing and validation image sets are shown in Figure

3. Those sets of images have been corrupted with

different Gaussian noise levels. We used ﬁve differ-

ent measures, each of which accounts for a different

point of view when evaluating the performance of a

ﬁltering process: (a) The mean absolute error (MAE)

(Plataniotis and Venetsanopoulos, 2000) to estimate

the ability of details preservation; (b) The peak signal

to noise ratio (PSNR) (Plataniotis and Venetsanopou-

los, 2000) for the ability of noise-cancelling; (c) The

normalized colour difference (NCD) (Plataniotis and

Venetsanopoulos, 2000) to measure the colourimetric

preserving; (d) The Fuzzy colour structural similar-

ity (FCSS) (Gre

cova and Morillas, 2016); and lastly

(d) The perceptual difference inspired in the image

colour appearance model iCAM (iCAMd) (Fairchild

and Johnson, 2004). We then compared the perfor-

mance of the proposed method with state-of-art meth-

ods, which are: Collaborative Wavelet Filter (CWF)

(Dabov et al., 2007), Eigenvector analysis method

(EIG) (Latorre-Carmona et al., 2020), Graphs based

methods for simultaneous smoothing and sharpening

(GMS

), and Normalized graph-method for simulta-

neous smoothing and sharpening (NGMS

) (P

erez-

Benito et al., 2020). Each ﬁlter was applied to a

3× 3 ﬁlter window, and the parameter settings recom-

mended by the respective authors were used for each

approach. It is worth pointing out that the sharpen-

ing process in the methods (GMS

) and (GMS

) has

been ignored for a fair comparison with the proposed

method.

All experimental results of the methods are shown

in Table 2. In this table, the best result is highlighted

in blue, and the second best, in red. Several images

that were denoised using these ﬁlters are presented in

the second row of the Figure 4. It can be seen that the

images given by the proposed method give good re-

sults in terms of suppressing the noise, while keeping

the structure and details of the image.

It has therefore been shown that the proposed

method achieves effective noise reduction without

adding colour artifacts, and it does so while main-

taining image features, colours, and structures. In

the larger images with more homogeneous areas, the

proposed method is performing better than the EIG

ﬁlter, which was one of its drawbacks. CWF, how-

ever, has the best results in these kinds of images

and this makes sense as the block matching method

used in CWF ﬁnds more matches in these types of

images, allowing for better denoising efﬁciency. In

relation to the high-spatial frequencies content, the

proposed approach performance is more efﬁcient than

CWF which means the latter fails in preserving tex-

ture and small details. Nevertheless, in these cases,

our proposal is not as good as the EIG ﬁlter, and

hence we still have some room for future improve-

ment. This potential (future) improvement may come

from changing the system settings (The number of

subsets of membership functions and rules) and also

by increasing the number of images under the test.

Overall, it should be noted that the proposed method

works competitively with different types of images.

5 CONCLUSION AND FUTURE

WORK

In this paper, a fuzzy inference system, on top of an

eigenvector-based image denoising strategy, was ap-

plied in order to ﬁlter Gaussian noise in colour im-

ages. The complete system infers, on a pixel-by-pixel

basis, the amount of noise that should be smoothed.

This method performs competitively in terms of both

noise reduction image structure and details preserva-

tion, without the introduction of artifacts in the im-

age. However, in order to increase the efﬁciency of

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

146

Table 1: Optimized parameters of the membership functions of the input and the output of the fuzzy inference system.

Optimized parameters for the inputs

SD First input \output Second input \output Third input \output

MF Low Med. High Low Med. High Low Med. High

Params. Loc. Wid. Loc. Wid. Loc. Wid. Loc. Wid. Loc. Wid. Loc. Wid. Loc. Wid. Loc. Wid. Loc. Wid.

Noise 10 31.54 75.30 84.91 11.86 150.12 79.90 89.80 15.68 179.98 44.58 198.85 11.72 11.85 12.13 101.80 67.30 160.67 48.00

Noise 20 49.47 15.55 113.18 25.97 191.86 15.38 69.58 5.79 149.80 98.76 150.58 12.99 60.85 73.64 117.51 35.60 195.31 36.54

Noise 30 68.89 91.65 136.88 14.38 154.47 18.10 11.96 67.85 153.51 25.49 168.22 11.97 53.66 92.86 100.82 32.59 196.52 63.81

Optimized parameters for the output

Noise 10 0.10 0.07 0.30 0.08 0.60 0.94 0.10 0.01 0.17 0.25 0.97 0.20 0.03 0.15 0.91 0.01 0.95 0.07

Noise 20 0.03 0.06 0.26 0.57 0.33 0.69 0.02 0.02 0.03 0.14 0.46 0.04 0.23 0.07 0.95 0.33 0.97 0.43

Noise 30 0.06 0.03 0.16 0.94 0.92 0.77 0.06 0.01 0.06 0.47 0.67 0.41 0.30 0.08 0.87 0.18 0.91 0.26

the method and to generalize it for any level of noise

we need to ﬁnd out a way to adjust one set of param-

eters to be valid for every case in the colour images.

This ﬁltering method could be improved by train-

ing the system from data extracted from the images

themselves.

ACKNOWLEDGEMENTS

S. Morillas acknowledges the support of the research

project PID2019-107790RB-C22, funded by MCIN/

AEI/10.13039/501100011033/

REFERENCES

Abualigah, L. M. Q. and Hanandeh, E. S. (2015). Applying

genetic algorithms to information retrieval using vec-

tor space model. International Journal of Computer

Science, Engineering and Applications (IJCSEA) Vol,

Casillas, J., Cord

on, O., Herrera, F., and Magdalena, L.

(2003). Interpretability improvements to ﬁnd the bal-

ance interpretability-accuracy in fuzzy modeling: an

overview. Interpretability issues in fuzzy modeling,

pages 3–22.

Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.

(2007). Color image denoising via sparse 3d collabo-

rative ﬁltering with grouping constraint in luminance-

chrominance space. In 2007 IEEE International Con-

ference on Image Processing, volume 1, pages I–313.

IEEE.

Dillon, W. R. and Goldstein, M. (1984). Multivariate anal-

ysis: Methods and applications. New York (NY): Wi-

ley, 1984.

Fairchild, M. D. and Johnson, G. M. (2004). icam frame-

work for image appearance, differences, and quality.

Journal of Electronic Imaging, 13(1):126–138.

Gre

cova, S. and Morillas, S. (2016). Perceptual similarity

between color images using fuzzy metrics. Journal

of Visual Communication and Image Representation,

34:230–235.

Hong, N. M. and Thanh, N. C. (2020). Distance-based mean

ﬁlter for image denoising. In Proceedings of the 4th

International Conference on Machine Learning and

Soft Computing.

Latorre-Carmona, P., Mi

nana, J.-J., and Morillas, S. (2020).

Colour image denoising by eigenvector analysis of

neighbourhood colour samples. Signal, Image and

Video Processing, 14(3):483–490.

Lukac, R., Plataniotis, K. N., Smolka, B., and Venet-

sanopoulos, A. N. (2005). cdna microarray image pro-

cessing using fuzzy vector ﬁltering framework. Fuzzy

Sets and Systems, 152(1):17–35.

Mendel, J. M. (1995). Fuzzy logic systems for engineering:

a tutorial. Proceedings of the IEEE, 83(3):345–377.

Moallem, P., Mousavi, B., and Naghibzadeh, S. S. (2015).

Fuzzy inference system optimized by genetic algo-

rithm for robust face and pose detection. Int. J. Artif.

Intell, 13(2):73–88.

Nov

ak, V., Perﬁlieva, I., and Mockor, J. (2012). Mathemat-

ical principles of fuzzy logic, volume 517. Springer

Science & Business Media.

erez-Benito, C., Jord

an, C., Conejero, J. A., and Morillas,

S. (2020). Graphs based methods for simultaneous

smoothing and sharpening. MethodsX, 7:100819.

Plataniotis, K. N. and Venetsanopoulos, A. N. (2000).

Companion image processing software. In Color

Image Processing and Applications, pages 349–352.

Springer.

Qidwai, U. and Chen, C.-h. (2009). Digital image process-

ing: an algorithmic approach with MATLAB. Chap-

man and Hall/CRC.

Schulte, S., De Witte, V., and Kerre, E. E. (2007a). A fuzzy

noise reduction method for color images. IEEE Trans-

actions on image Processing, 16(5):1425–1436.

Schulte, S., Witte, V. D., Nachtegael, M., M

elange, T., and

Kerre, E. E. (2007b). A new fuzzy additive noise re-

duction method. In International Conference Image

Analysis and Recognition, pages 12–23. Springer.

Shen, Y. and Barner, K. E. (2004). Fuzzy vector median-

based surface smoothing. IEEE Transactions on Visu-

alization and Computer Graphics, 10(3):252–265.

Tomasi, C. and Manduchi, R. (1998). Bilateral ﬁltering for

gray and color images. In Sixth international confer-

ence on computer vision (IEEE Cat. No. 98CH36271),

pages 839–846. IEEE.

Van De Ville, D., Nachtegael, M., Van der Weken, D.,

Kerre, E. E., Philips, W., and Lemahieu, I. (2003).

Noise reduction by fuzzy image ﬁltering. IEEE trans-

actions on fuzzy systems, 11(4):429–436.

Zadeh, L. A. (1965). Fuzzy sets. Information and control,

8(3):338–353.

Fuzzy Inference System in a Local Eigenvector Based Color Image Smoothing Framework

147

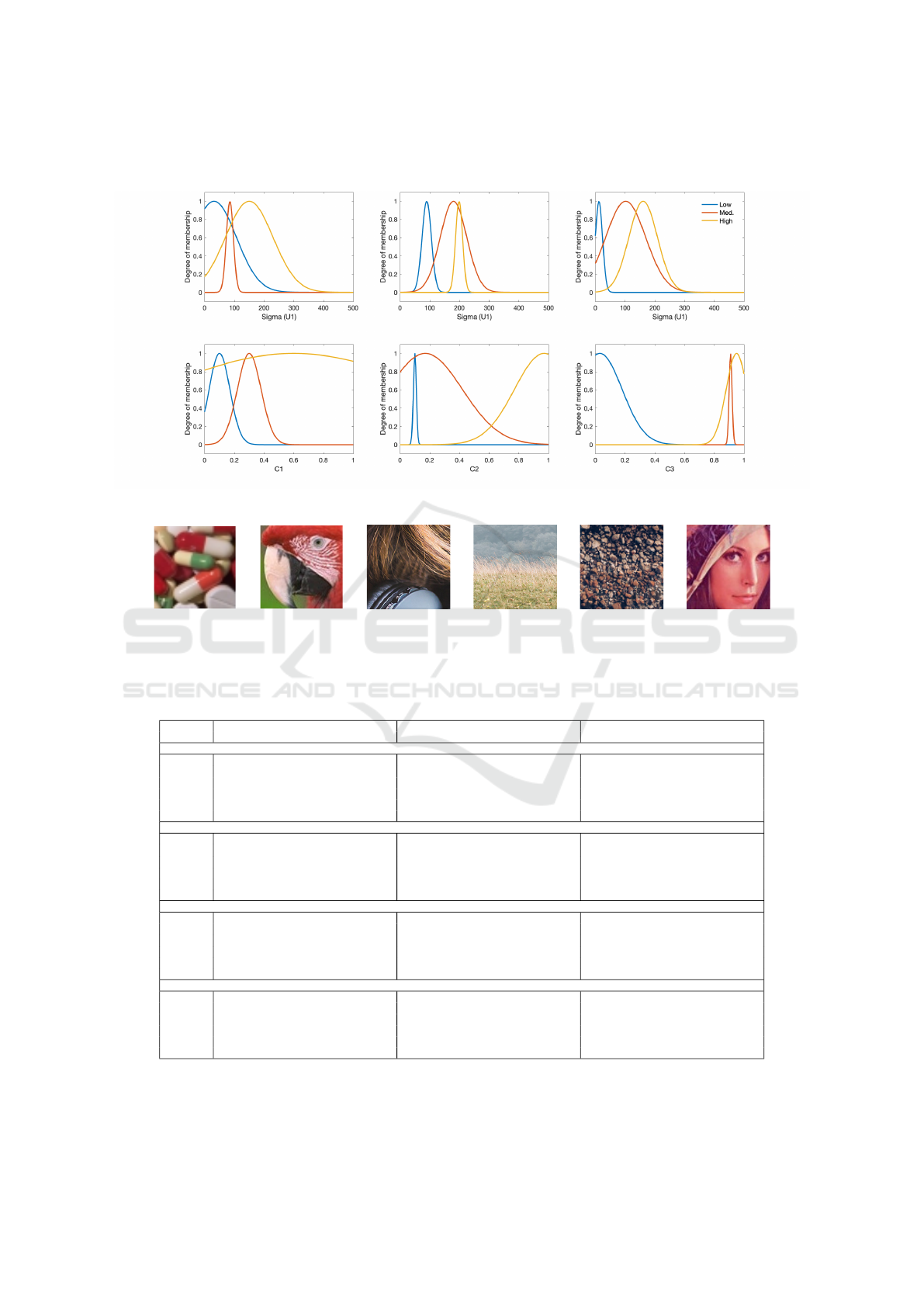
APPENDIX

Figure 2: Membership functions that are optimized to use for images with noise level 10 of the fuzzy inference system: The

ﬁrst row represents the input subsets and the second row shows the output subsets.

Pills 50 × 50 Parrot 80 × 80 Headphone 100 × 100 Grass 200 × 200 Beach 100 × 100 Lenna 90 × 90

Figure 3: The ﬁrst three images are the training images set, and the last three images are the validation images set.

Table 2: Performance for each one of the methods, in terms of MAE, PSNR, NCD (×10

), FCSS (×10) and iCAMd using

different images with different sizes contaminated with various standard deviation s of Gaussian noise. In the table, the best

result for each noise level and performance measure is highlighted in blue, the second best is highlighted in red.

Filter s = 10 s = 20 s = 30

MAE PSNR NCD FCSS iCAMd MAE PSNR NCD FCSS iCAMd MAE PSNR NCD FCSS iCAMd

The results of Grass image (200 × 200)

None 7.82 28.22 5.37 9.38 3.38 15.56 22.24 10.75 8.69 6.71 23.23 18.79 16.16 7.97 10.04

GMS

5.23 31.16 2.91 9.51 2.72 8.94 26.71 5.65 9.19 4.93 14.68 22.53 9.85 8.70 7.70

NGMS

5.52 30.59 2.88 9.48 2.80 8.11 27.35 4.66 9.18 4.72 10.92 24.96 6.86 8.98 6.70

CWF 3.82 33.90 1.82 9.63 1.91 5.80 30.08 2.48 9.38 2.93 7.35 27.92 2.97 9.14 3.76

EIG 4.82 32.24 2.80 9.58 2.56 8.64 27.20 5.33 9.27 4.82 12.21 24.22 7.85 8.98 7.02

Proposed 4.76 32.19 2.58 9.51 2.58 7.76 28.11 4.56 9.30 4.57 11.71 24.55 7.37 9.01 6.85

The results of Beach image (200 × 200)

None 7.59 28.39 15.22 9.42 4.78 14.91 22.52 29.16 8.93 8.92 21.82 19.20 41.55 8.51 12.79

GMS

7.23 28.73 10.26 9.19 4.96 11.31 24.81 17.63 8.94 7.96 16.45 21.53 26.50 8.68 11.15

NGMS

9.17 26.55 11.23 8.98 5.89 12.47 23.88 16.39 8.68 8.61 15.53 21.94 21.38 8.48 10.98

CWF 5.62 31.01 8.26 9.49 4.01 9.64 26.30 12.35 9.14 6.67 12.99 23.66 15.67 8.83 8.91

EIG 5.61 30.97 8.94 9.47 4.14 10.03 25.92 15.08 9.08 7.29 14.05 23.00 20.55 8.76 10.09

Proposed 5.69 30.85 8.94 9.44 4.14 9.99 25.96 14.34 9.01 7.30 13.78 23.16 19.61 8.76 9.94

The results of Beach image (100 × 100)

None 3.88 34.35 6.88 9.68 3.33 7.61 28.51 13.12 9.42 6.31 11.22 25.13 18.90 9.17 8.91

GMS

6.51 29.62 6.70 9.16 4.60 7.87 28.08 9.27 9.07 5.89 9.70 26.32 12.41 8.95 7.41

NGM

10.94 24.86 9.52 8.68 6.72 11.90 24.27 11.30 8.61 7.58 13.21 23.47 13.44 8.49 8.81

CWF 4.23 33.40 6.29 9.66 3.52 8.40 27.25 10.75 9.30 6.37 12.74 23.61 14.59 8.79 9.10

EIG 3.69 34.60 4.94 9.65 3.02 6.33 30.00 8.06 9.34 5.01 9.04 26.90 11.11 9.02 6.83

Proposed 3.80 34.27 4.99 9.63 2.96 7.50 28.42 8.73 9.14 5.54 9.78 26.19 11.45 8.89 7.16

The results of Lenns image (90 × 90)

None 7.64 28.33 9.11 9.34 5.19 14.88 22.54 17.49 8.63 10.25 21.85 19.17 25.75 7.95 15.39

GMS

4.87 31.62 4.95 9.49 3.31 8.53 26.99 9.18 9.20 6.24 13.72 22.89 15.25 8.68 10.26

NGMS

5.08 31.16 4.90 9.45 3.31 7.71 27.62 7.74 9.22 5.47 10.45 25.07 11.01 8.98 8.01

CWF 3.38 35.23 3.01 9.64 2.17 5.07 31.51 4.25 9.47 3.19 6.87 28.91 5.91 9.30 4.24

EIG 4.56 32.64 4.67 9.56 3.20 8.17 27.57 8.48 9.24 5.96 11.40 24.63 12.14 8.95 8.72

Proposed 4.28 33.10 4.29 9.56 2.95 7.29 28.55 7.38 9.31 5.32 10.85 25.04 11.38 9.00 8.30

IMPROVE 2023 - 3rd International Conference on Image Processing and Vision Engineering

148

Figure 4: Filtering methods output for visual comparison. The ﬁrst column contains the Grass images in size (200 x 200)

with noise level s = 10. The second column contains the images of Lenna in size (90 x 90) with noise level s = 20. The last

column contains the images of the Beach in size of (200 x 200) with noise level s = 30. The ﬁrst row has the original images.

The second row has noisy images with different levels of noise. The third row is the output images from the CWF ﬁlter. The

fourth row has the output images from the EIG method. The ﬁfth row has the output images from the GMS

ﬁlter. The last

row has the output images from the proposed method.

Fuzzy Inference System in a Local Eigenvector Based Color Image Smoothing Framework

149