Exploring Potential Causal Models for Climate-Society-Conﬂict

Interaction

Weisi Guo

1,2 a

, Schyler Sun

1 b

and Alan Wilson

2 c

Cranﬁeld University, Bedford, U.K.

Alan Turing Institute, London, U.K.

Keywords:

Conﬂict, Climate Change, Causal Models.

Abstract:

Climate change affects human liveability and may increase the likelihood of armed violence. However, the

precise repercussions on social cohesion and conﬂict are difﬁcult to model, and several socio-economic mech-

anisms exist between local climate changes and conﬂict, and are often hidden to us. Nonetheless, we offer an

exploratory data analysis in this paper at a global scale, on the relationship between diverse climate indicators

and conﬂict. Here we investigate potential basic causal models between climate change and conﬂict, including

the causal direction, causal lag, and causal strength. We use historical climate and extreme environmental

event data from the past 50 years across the world to identify geographic region-speciﬁc causal indicators.

The initial broad ﬁndings are: (1) rainfall is a reasonably general indicator of conﬂict, (2) there are fragile

regions which exhibit a strong causal link between extreme climate variations and conﬂict (predominantly in

Africa and South Asia), and 3. there exists a common time lag of the causality between the climate variations

and the conﬂict in many regions, which is worth further study.

1 INTRODUCTION

Among the most worrying of the mooted impacts of

climate change is an increased risk in armed conﬂict.

As people compete for diminishing resources, such as

arable land and water (Homer-Dixon, 2010), forced

migration and labour changes can introduce politi-

cal tensions and create conﬂict in fragile states. Re-

search over the past decade has established that cli-

mate variability and extreme change may inﬂuence

the risk of violent conﬂict (including political vio-

lence, terrorism, civil and inter-state wars) (Burke

et al., 2009; Hsiang et al., 2011). Authors in (Hsiang

and Burke, 2014) examined 50 quantitative empirical

studies and found a remarkable convergence in ﬁnd-

ings and strong support for a causal association be-

tween climatological changes and conﬂict at all scales

and across all major regions of the world. How-

ever, under various hypothesis, different methodolo-

gies and datasets applied, the results in different re-

gions are divergent or even contradictory (Mach et al.,

2019; Buhaug, 2010; Slettebak, 2012). Although the

https://orcid.org/0000-0003-3524-3953

https://orcid.org/0000-0001-8465-8448

https://orcid.org/0000-0002-7495-6617

relationship between climate and conﬂict has been

empirically tested in a wide variety of studies, the lit-

erature has yet to converge on a commonly accepted

set of causal mechanisms (Salehyan, 2014). For ex-

ample, some states may experience an irreversible

labour transformation from agricultural economy to

urban organised crime, whereas others may see mi-

gratory sources of violence.

1.1 Review of Causal Analysis in

Complex Systems

Causal analysis in complex systems with no existing

explicit mathematical models is challenging. On the

one hand, an end-to-end data analysis between cli-

mate change and conﬂict might exhibit certain results,

but one cannot be certain they are reasonable and re-

late to known socioeconomic mechanisms. We of-

fer a brief review of existing data-driven causal infer-

ence approaches and then go on to explain our dual

approach of verifying data analysis with a toy causal

model.

Guo, W., Sun, S. and Wilson, A.

Exploring Potential Causal Models for Climate-Society-Conﬂict Interaction.

DOI: 10.5220/0011968400003485

In Proceedings of the 8th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2023), pages 69-76

ISBN: 978-989-758-644-6; ISSN: 2184-5034

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

1.1.1 Stationary to Nonlinear State Space

Approaches

Granger causality test is the ﬁrst proposed station-

ary approach to detect causality based on statis-

tical hypothesis test. Two time series are given

and under Granger’s theory, the causality (the al-

ternative hypothesis) is deﬁned as that time series

[..., X(t − 1), X(t)] provide signiﬁcant information

about [Y (t),Y (t + 1), ...] (Granger, 1969). It is valid

in stationary linear systems rather than dynamic sys-

tems. The predictability improvement (PI) causal-

ity test is proposed in response to this issue, where

(Krakovska, 2017; Krakovska and Hanzely, 2016;

Krakovska et al., 2018) reconstruct the time series in

multi-dimensional state spaces, which try to convert

the non-linear dynamic system into a linear manifold,

where the Granger causality test can then be applied.

Conditional mutual information (CMI)

(Hlavackova-Schindler et al., 2007) is based on

transfer entropy. Discrete random variables (X,Y, Z)

with support sets (X, Y, Z) are given, and the CMI

I(X,Y |Z) estimates the directed information ﬂow

from a variable X to another variable Y under the

condition of Z. Different from PI hypothesis test, the

CMI approach can yield the value of predictability

improvement. CMI does not depend on any assump-

tions in its formulation compared to other directed

information ﬂow measures like Granger causality,

which makes this method capable of assessing both

linear and non-linear interactions. In time series

causality detection application, with a causation lag

τ, I(X(n),Y (n +τ)|Y (n)) is normally used to evaluate

the causality with directionality (Li and Ouyang,

2010; Wen et al., 2019).

In (Sugihara et al., 2012; Tsonis et al., 2018), Con-

vergent Cross Map (CCM) is proposed to detect the

causal relationships in nonlinear dynamical systems.

The key idea of CCM lies on the fundamental princi-

ple of Takens’s theorem, which states that in a time se-

ries dynamical system with multi-variables, any sin-

gle series of one variable of the system can be re-

covered by the historical series of another variable by

high dimensional state space reconstruction. In prac-

tical terms of CCM, two time series X ,Y is given,

and the causality is deﬁned as the extent to which

the time series [X(t −Eτ), ..., X(t −2τ), X(t −τ)] can

be encoded into time series Y (t). The parameter τ

here is the time step for the reconstruction while E is

the dimension of the reconstruction. CCM has been

successfully applied in various climate change ﬁelds,

such as the soil moisture-precipitation interaction in

environment (Wang et al., 2018), the sensitivity of the

carbon cycle to tropical temperature variations (Wang

et al., 2014) and the relationship between temperature

and green-house gases (Nes et al., 2015) in climate

research.

1.1.2 Neural Approaches

Long Short-Term Memory (LSTM) is an artiﬁcial re-

current neural network (RNN) architecture, which is

capable of learning order dependence in series. The

training process in LSTM can be considered as an

adaptive non-linear regression from the input series to

the output series. Owing to the non-linear expressive

power of the neurons and the characteristics of RNN,

LSTM has the following advantages (Krakovska and

Jakubik, 2020): (a) able to store information for an

arbitrary duration; (b) resistant to noise (i.e., ﬂuctu-

ations of the inputs that are random or irrelevant for

regression); (c) trainable in a reasonable time. In our

practice, two time series X,Y is given, we set X (t)

and Y (t) as the inputs while Y (t + 1) as the output.

Then, we can evaluate the causality of X (t) by vali-

dating the regression error in LSTM. Other variations

of this include the Neural Point Process (NPP), where

a given time-series process is established (e.g., point

process), and the neural network models a non-linear

function that maps diverse variables to the intensity

of the PP. This has been quite successful in our recent

modeling of climate conﬂict interactions (Sun et al.,

2022).

1.1.3 Summary & Innovation

In summary, methods such as PI gives the non-linear

Granger causality between two series through hypoth-

esis testing at the most basic binary level, whereas

CMI model the causality strength using the mutual in-

formation between two series, and CCM reconstructs

one series into another and evaluates the causality us-

ing the correlation between reconstructed series and

raw series. Neural method such as LSTM and neu-

ral point process (NPP) does an adaptive nonlinear

regression from one series to another and assess the

causality by prediction error. These methods increas-

ingly contribute towards AI algorithms in understand-

ing complex climate social interactions and predicting

conﬂict (Guo et al., 2018). However, without an un-

derlying multi-staged causal model, we have no way

of knowing how reasonable these approaches are. Cli-

mate change can cause multi-staged social transfor-

mations (e.g., agricultural, supply chain, labour mar-

kets, migration....etc.) with different dynamical pro-

cesses and lag times.

As such, this paper ﬁrst introduces a basic causal

toy model to verify ﬁrst that these approaches can or

cannot evaluate artiﬁcial data successfully. We then

evaluate the real end-to-end data to draw disaggre-

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk

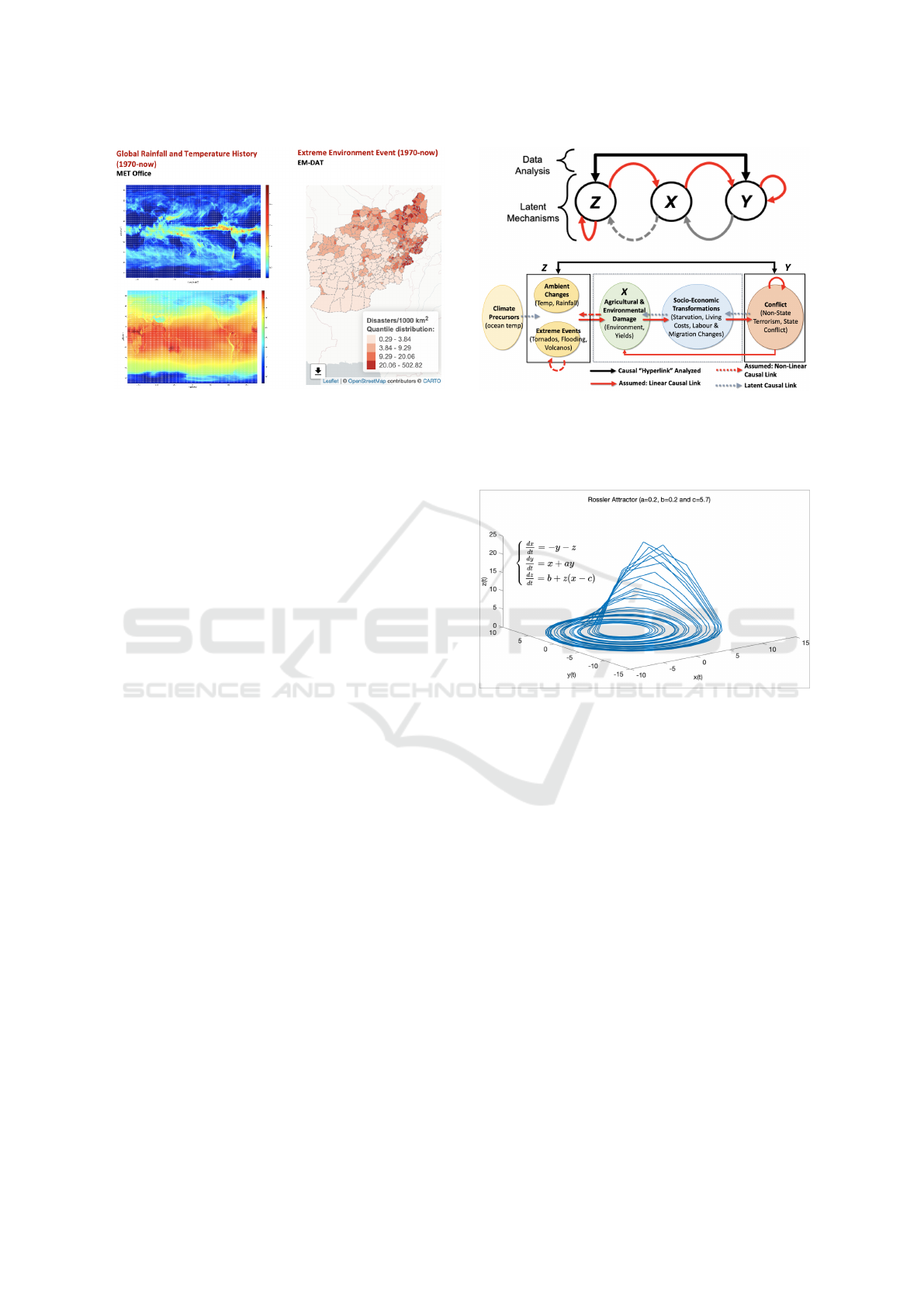
Figure 1: Example data of weather and natural disasters.

gated and general conclusions.

2 DATA & CAUSAL MODEL

2.1 Data

In this paper, temperature and rainfall data

are used to represent the general climate

conditions. We used the ERA5 dataset

(https://www.ecmwf.int/en/forecasts/datasets/reanaly-

sis-datasets/era5), which records the global temper-

ature and rainfall gridded in 0.5 degree resolution

(grid size is 56-79 sqkm depending on latitude),

and monthly in scope, spanning 1970-present. For

natural disaster events (including tsunami, drought,

tornado and etc.) we use the Emergency Events

Database (EM-DAT, https://www.emdat.be), which

records these events around the world with the dates

and locations, spans 1900-present. In this paper,

data from Global Terrorism Database (GTD) are

selected as the indicator of conﬂict, which dominate

the majority of violent events. GTD is the most

comprehensive database of terrorist attacks in the

world, which contains over 200k terrorist attacks

with the dates and locations, spans 1970-2018.

In our experiments, in order to keep data’s at-

tributes consistency in causality tests, the data are pre-

processed as follow:

• Data series spans 1970-2018 are selected,

• Data series are uniﬁed into monthly resolution,

• For natural disasters and terrorist attacks, we

quantify it in terms of its counting times per

month

• Data series for the following 12 regions are se-

lected: (i) Northern Africa (AfricaN), (ii) South-

ern Africa (AfricaS), (iii) Central America (Amer-

Figure 2: Our assumptions of the overall causal mecha-

nisms between climate change, social transformation, and

conﬂict. End-to-end causal data analysis (top) between Z

and Y will be validated by artiﬁcial data generated by a

causal toy model (bottom).

Figure 3: Rossler toy model and underlying equations and

parameters.

icaC), (iv) Northern America (AmericaN), (v)

Southern America (AmericaS), (vi) Central Asia

(AsiaC), (vii) Eastern Asia (AsiaE), (viii) South-

ern Asia (AsiaS), (ix) Southeastern Asia (Asi-

aSE), (x) Eastern Europe (EuropeE), (xi) Western

Europe (EuropeW) and (xii) Oceania.

Example of data is shown in Fig.1.

2.2 Toy Causal Model

We develop a toy causal model as the simplest step

one can take to test if causal detection would work.

Fig.2 shows the assumptions we used. We assume

the climate system (i.e. RainFall (x

), Temperature

) and Natural Disaster (x

)) is an autonomous sys-

tem which has linear and nonlinear internal causal-

ity to each other, while there is a unidirectional lin-

ear causal link from climate system to the agriculture

). The agriculture has a bidirectional linear causal

link with the socio-economic (y

) while also a uni-

directional linear causal link from conﬂict (y

) to it.

Exploring Potential Causal Models for Climate-Society-Conﬂict Interaction

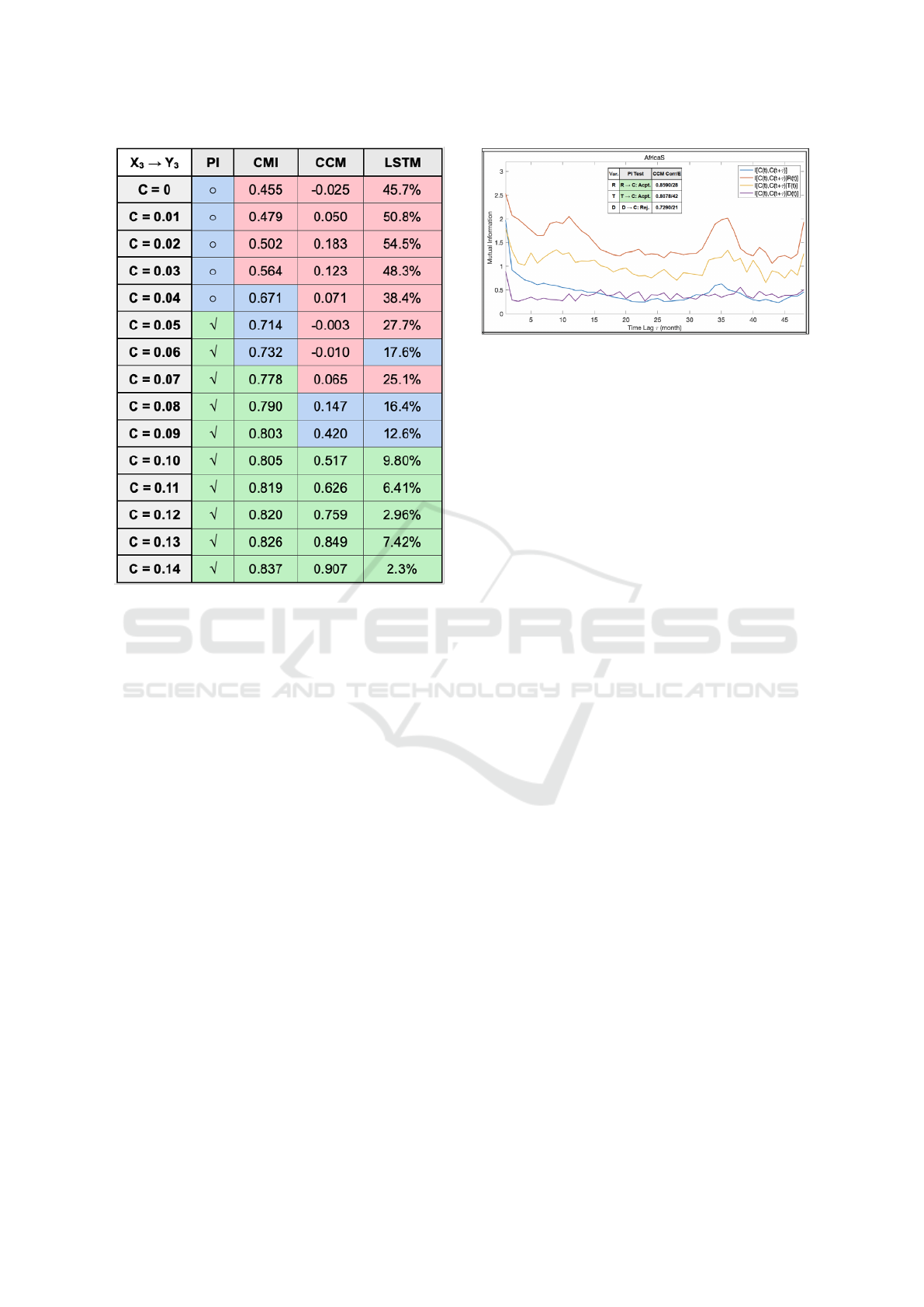
Figure 4: Causal analysis veriﬁcation in the toy model:

green is acceptance, blue is borderline, and red is rejection

of null hypothesis.

Then, our key assumption is that the agriculture has

a nonlinear causal link to the conﬂict. Based on our

assumptions, we establish a toy model using two uni-

directional coupled Rossler systems (Fig.3) with an

adjustable coupling strength parameter C. The initial

conditions can be arbitrary, in our experiments, we

set the initial conditions of ω

= 1.015, ω

= 0.985

and x

= y

= [1, 1, 0]. With our initial conditions,

two systems would be synchronized when the cou-

pling strength C is about 0.14. An example of the

Rossler model is in Fig.3.

2.3 Validation Using Toy Model

Firstly, we test classical causal methods (i.e., PI,

CCM and CMI) on the aforementioned theoretical toy

model, in order to verify the validity of these meth-

ods in detecting our assumed causality mechanism be-

tween climate and conﬂict. Fig.4. gives the causality

results in our theoretical toy model with the coupling

strength from 0 to 0.14 before the synchronization.

The values in PI give the hypothesis test results on

whether X

cause the Y

; The outcome in the CMI

model give the amount of mutual information given

by X

to Y

; The values in CCM give the correlation

between the reconstructed Y

using X

and Y

itself;

Figure 5: Sub-Sahara causal results of PI, CCM, and CMI

by region. The abbreviations are: Var = variable, Acpt. =

Acceptance, Rej. = Rejection, Corr = Correlation, RTS =

Reconstruction Time Steps, C = Conﬂict, R = Rainfall, T =

Temperature, D = Natural Disaster, R ⇒ C = R cause C.

The values in LSTM give the regression error in per-

centage.

The result shows that all methods can detect the

causality link before the synchronization of two sys-

tems. However, it can be observed that PI method

has the most sensitivity to the causality among all our

proposed methods, while CCM and LSTM require the

longest lags to reliably detect causality. Another no-

table thing is that LSTM is not consistent in perfor-

mance. PI, CMI and CCM always give better result

when the coupling strength goes up while LSTM does

not. Due to it is unexplainable, the result come from

LSTM is more blackbox than the others and we will

analyze the LSTM result separately.

3 GLOBAL RESULTS

3.1 Overall Causality Results by Region

The raw quantitative overall causality results of PI,

CCM and CMI by region are shown in Fig.6, with a

speciﬁc highlighted example of Sub-Sahara in Fig.5.

In each sub-ﬁgure, we show the CMI results for dif-

ferent cause in different time lags with the coloured

lines, and the PI and CCM results in the table at-

tached on. For CCM, we have two values in the grid,

the ﬁrst value is the correlation value between the re-

constructed conﬂict data and raw conﬂict data, while

the second one is the corresponding reconstruction di-

mension.

In order to have more intuitive interpretation and

analysis, we convert these results into qualitative rep-

resentations with the following rules:

(1) For PI hypothesis test, we use

√

(coloured

in green) to represent the accepted positive causal-

ity from the variables series towards terrorism series,

◦ (coloured in blue) to represent no causality, and

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk

Figure 6: Overall causal results of PI, CCM, and CMI by region. The abbreviations are: Var = variable, Acpt. = Acceptance,

Rej. = Rejection, Corr = Correlation, RTS = Reconstruction Time Steps, C = Conﬂict, R = Rainfall, T = Temperature, D =

Natural Disaster, R ⇒ C = R cause C.

× (coloured in red) to represent reversed anti-nature

causality from terrorism series towards climate series

(2) For correlation degree in CCM, we deﬁne ρ > 0.7

as strong correlated (coloured in green), 0.4 < ρ ≤0.7

as moderate correlated (coloured in blue), and 0.2 <

ρ ≤ 0.4 as weak correlated (coloured in red), ρ ≤ 0.2

as none correlated (3) For causality mechanism com-

plexity degree in CCM, we deﬁne E < 13 as low com-

plexity, 13 < E ≤ 24 as moderate complexity, E > 24

as high complexity (4) There are no absolute stan-

dards for CMI which makes the inter-comparison of

CMI between different regions’ datasets meaningless,

thus we use the CMI mean difference over MI of ter-

rorism series:

E(CMI −MI) =



I[C(t),C(t +τ) −MI|Var(t)] −I[C(t),C(t +τ)]



(1)

to demonstrate the assistance of climate series causal-

ity in one region and internally compare this causal-

ity. The larger the difference between CMI and MI

appears, the more causality effect the corresponding

condition has. We set the self-mutual information as

the baseline and calculate the addition mutual infor-

mation given by the condition. We coloured the value

larger than 0.5 in green, 0-0.5 in blue and negative

value in red for clearer demonstrating results.

Fig.7 shows the processed qualitative interpreta-

tion of the causality results both in region domain and

methods domain according to our rules. We are going

to analyse these results in both domains:

3.1.1 Region Domain

It can be observed that the regions of AfricaN,

AfricaS, AsiaS and AsiaSE give the strongest causal-

ity evidence of climate series affects terrorism series

from the results of all these three methods. However,

although the result for other regions is ambiguous, it

does not necessarily mean that the causality does not

exist in these regions, it is also possible that our meth-

ods cannot detect the causality completely.

Another notable issue is the inconsistency in re-

sults from different methods. The representative ex-

amples are AmericaC and AsiaC, causality of natural

disaster series results given from PI, CCM and CMI

are conﬂicting with each other. The reason for this

would be that the real mechanism in these regions is

beyond our assumptions.

3.1.2 Method Domain

PI: With PI hypothesis test, terrorism series in each

region shows the predictability improvement from

the corresponding rainfall series. However, temper-

ature series act as a cause to terrorism series in just

some speciﬁc regions, while natural disaster series af-

fect only one region (i.e., AsiaC). Based on this PI

method, the rainfall series can be concluded as a uni-

versal causation factor to the terrorism series.

CCM: The correlation offered by CCM is always

contiguous with climate series in each region, there

is no case where one variable series has strong CCM

correlation while others have it weak. This result in-

dicates that the climate variables in our experiments

can be considered as an autonomous system which

the terrorism system is coupled on.

Exploring Potential Causal Models for Climate-Society-Conﬂict Interaction

Figure 7: (a) Qualitative interpretation of PI, CCM, and CMI in each region (region domain), (b) Parallel comparison of

qualitative interpretations in each region (method domain).

CMI: In CMI method, the condition of rainfall and

temperature series offers the positive mutual informa-

tion between the terrorism series C(t) and C(t + τ) in

all of the regions except for AmericaC. However, the

mutual information given by the condition of natural

disaster series is ambiguous over these regions, which

match the results in (Slettebak, 2012) - natural disas-

ters are not the factors to be blamed for conﬂict.

3.2 LSTM Causality Result

We analyze the LSTM result separately since it is un-

explainable, which makes its result not guaranteed to

be true. In our experiments, we establish a LSTM net-

work with two LSTM layers with 128 hidden nodes

and three full connect layers with 64,128,16 hidden

nodes respectively. There maybe other architectures

featuring attention and mixed with graph neural net-

works we have not considered yet and is left for future

work.

We applied one-step prediction along the last ten

years (1998-2018), which means for each month in

each region, an independent LSTM is applied, while

the average prediction percentage error is considered

as the causality indicator. Fig.8 shows the results from

LSTM. In AmericaC, AmericaS, AsiaE and Ocea-

nia, the causality between climate and conﬂict is am-

biguous from a LSTM regression sight, while oth-

ers shows climate series may help in the conﬂict pre-

diction which indicates the causality between climate

and conﬂict. However, we can also observe the in-

stability of the algorithm from the results, e.g. in

AfricaN, AsiaC, EuropeE and Oceania, the prediction

with inputs of C&D is worse than that with only C.

This means LSTM has learned some odd mechanisms

which actually does not exist and cause an overﬁtting.

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk

Figure 8: LSTM results.

Figure 9: Global result summary by region.

In this report, we will only take the LSTM results as

a reference, not as a decisive factor.

3.3 Temporal Lag

Back to Fig.8, we ﬁnd an interesting phenomenon in

CMI(τ) results. Obviously, when temporal lag τ = 0,

the mutual information between terrorism series C(t)

and C(t +τ) reaches the maximum. Nevertheless, the

rainfall and temperature series CMI(τ) reaches an-

other peek when the temporal lag τ is around 10-14

months (1 year) and around 34-38 months (3 years) in

the regions of AfricaN, AfricaS, AsiaE, AsiaS, Asi-

aSE and EuropeE. This indicates that in these re-

gions, the climate series may have the same causa-

tion mechanism in climate ⇒ agriculture ⇒ socioe-

conomic ⇒ conﬂict under our assumptions. A possi-

ble preliminary answer would be that, in low socioe-

conomic development and low capabilities regions,

or regions dominated by agriculture, the climate has

a distinct causation to the region conﬂict/terrorism

with the time lag of one year and three year (Mach

et al., 2019). However, the mechanism lay in this

phenomenon is still an open question and becomes a

further issue for us.

4 CONCLUSIONS AND NEXT

STEPS

Climate change affects human liveability and may in-

crease the likelihood of armed violence. However, the

precise repercussions on social cohesion and conﬂict

are difﬁcult to model, and several socio-economic

mechanisms exist between local climate changes and

conﬂict, and are often hidden to us. Nonetheless, we

offer an exploratory data analysis in this paper at a

global scale, on the relationship between diverse cli-

mate indicators and conﬂict. Here we investigate po-

tential basic causal models between climate change

and conﬂict, including the causal direction, causal lag,

and causal strength. We use historical climate and

extreme environmental event data from the past 50

years across the world to identify geographic region-

speciﬁc causal indicators. The initial broad ﬁnd-

ings shown in Fig.9 are: (1) rainfall is a reasonably

general indicator of conﬂict, (2) there are fragile re-

Exploring Potential Causal Models for Climate-Society-Conﬂict Interaction

gions which exhibit a strong causal link between ex-

treme climate variations and conﬂict (predominantly

in Africa and South Asia), and 3. there exists a com-

mon time lag of the causality between the climate

variations and the conﬂict in many regions, which is

worth further study. In order to identify the spurious

causality in our results from pure data analysis per-

spective, we proposed to embed the knowledge from

social science into our initial assumptions about the

mechanisms within climate and conﬂict.

ACKNOWLEDGEMENTS

We acknowledge funding from the Alan Turing In-

stitute via the Defence and Securities Program, and

valuable advice and help given by the previous pro-

gram director Prof. Mark Briers.

REFERENCES

Buhaug, H. (2010). Climate not to blame for african civil

wars. In Proc. National Academy of Sciences (PNAS).

Burke, M. B., Miguel, E., Satyanath, S., Dykema, J. A.,

and Lobell, D. B. (2009). Warming increases the risk

of civil war in africa. In Proc. National Academy of

Sciences (PNAS).

Granger, C. W. (1969). nvestigating causal relations by

econometric models and cross-spectral methods. In

Econometrica: journal of the Econometric Society.

Guo, W., Gleditsch, K., and Wilson, A. (2018). Retool AI

to forecast and limit wars. In Nature.

Hlavackova-Schindler, K., Palus, M., Vejmelka, M., and

Bhattacharya, J. (2007). Causality detection based on

information-theoretic approaches in time series analy-

sis. In Physical Reports.

Homer-Dixon, T. (2010). Environment, scarcity, and vio-

lence. Princeton University Press.

Hsiang, S. M. and Burke, M. (2014). Climate, conﬂict, and

social stability: what does the evidence say? In Cli-

matic Change.

Hsiang, S. M., Meng, K. C., and Cane, M. A. (2011). Civil

conﬂicts are associated with the global climate. In

Nature.

Krakovska, A. (2017). Predictability improvement as a tool

to detect causality. In International Conference on

Measurement.

Krakovska, A. and Hanzely, F. (2016). Testing for causality

in reconstructed state spaces by an optimized mixed

prediction method. In Physical Review E.

Krakovska, A. and Jakubik, J. (2020). Implementation of

two causal methods based on predictions in recon-

structed state space. In Physical Review E.

Krakovska, A., Jakubik, J., Chvostekova, M., Coufal, D.,

Jajcay, N., and Palus, M. (2018). Comparison of six

methods for the detection of causality in a bivariate

time series. In Physical Review E.

Li, X. and Ouyang, W. (2010). Estimating coupling direc-

tion between neuronal populations with permutation

conditional mutual information. In NeuroImage.

Mach, K. J., Kraan, C. M., Adger, W. N., Buhaug, H.,

Burke, M., Fearon, J. D., Field, C., Maystadt, J.-F.,

and O’Loughlin, J. (2019). Climate as a risk factor for

armed conﬂict. In Nature.

Nes, E. H. V., Scheffer, M., Brovkin, V., Lenton, T. M., Ye,

H., Deyle, E., and Sugihara, G. (2015). Causal feed-

backs in climate change. In Nature Climate Change.

Salehyan, I. (2014). Climate change and conﬂict: Making

sense of disparate ﬁndings. In Political Geography.

Slettebak, R. T. (2012). Don?t blame the weather! climate-

related natural disasters and civil conﬂict. In Journal

of Peace Research.

Sugihara, G., May, R., Ye, H., h. Hsieh, C., Deyle, E., Fog-

arty, M., and Munch, S. (2012). Detecting causality in

complex ecosystems. In Science.

Sun, S. C., Jin, B., Wei, Z., and Guo, W. (2022). Revealing

the excitation causality between climate and political

violence via a neural forward-intensity poisson pro-

cess. In International Joint Congress on AI (IJCAI).

Tsonis, A., Deyle, E. R., Ye, H., and Sugihara, G. (2018).

Convergent cross mapping: theory and an example. In

Advances in nonlinear geosciences.

Wang, X., Piao, S., Ciais, P., Friedlingstein, P., Myneni,

R. B., Cox, P., Heimann, M., Miller, J., Peng, S., and

Wang, T. (2014). A two-fold increase of carbon cy-

cle sensitivity to tropical temperature variations. In

Nature.

Wang, Y., Yang, J., Chen, Y., P. De Maeyer, Z. L., and Duan,

W. (2018). Detecting the causal effect of soil moisture

on precipitation using convergent cross mapping. In

Nature Scientiﬁc reports.

Wen, D., Jia, P., Hsu, S.-H., Zhou, Y., Lan, X., Cui, D., Li,

G., Yin, S., and Wang, L. (2019). Estimating coupling

strength between multivariate neural series with mul-

tivariate permutation conditional mutual information.

In Neural Networks.

COMPLEXIS 2023 - 8th International Conference on Complexity, Future Information Systems and Risk