The Generalization of the Solution Process in a Mathematical

Problem-Solving Activity with an Advanced Computing Environment

Cecilia Fissore

, Valeria Fradiante

and Marina Marchisio

Department of Foreign Languages, Literatures and Modern Culture, Via Giuseppe Verdi, 10, 10124 Turin, Italy

Department of Molecular Biotechnology and Health Sciences, University of Turin, Via Nizza 52, 10126, Turin, Italy

Keywords: Advanced Computing Environment, Generalization, Mathematics, Problem Solving.

Abstract: In a problem-solving activity, generalizing is an important process by which the specifics of a solution are

examined. Technologies support this process, making it possible to create interactive explorations that allow

to see how the result changes as the initial data vary. In this article we focus on the generalization of the

solution process during a mathematical problem-solving activity using an Advanced Computing Environment

(ACE). Our research questions are: how can we analyze the skills students develop while generalizing a

problem? What are the most frequent difficulties? We analyzed the solution of a problem-solving activity

with an ACE submitted by 75 students using a model specially developed by us for studying generalization

using interactive components. The model considers three phases: design and choice of interactive components,

programming of the system and control stages of generalization of a problem. For each stage we established

a set of indicators to understand the competences achieved by each student. The results show that the students

generalized the problem using different strategies, with some difficulty in the programming and control phase.

The model developed allows to reflect on the skills achieved by students in the various phases of the

generalization process.

1 INTRODUCTION

Generalization in Mathematics is a recurring topic in

literature; in particular it is often studied how to

extend a mathematical object, such as a formula, from

a particular situation to a general one. In a problem-

solving activity, generalizing is an important process

by which the specifics of a solution are examined and

questions as to why it worked are investigated

(Liljedahl et al., 2016). Technology can be an

amplifier of a generalization activity of the solution

of a problem. In our previous research we started

studying the development of students’ problem-

solving skills and the generalization processes during

a mathematical problem-solving activity through the

creation of animated graphs (Barana et al., 2020a).

Our intent is to continue to explore the whole process

that students develop when they have to generalize

the solution process of a problem. In particular, our

research analyzes students’ processes of

https://orcid.org/0000-0001-8398-265X

https://orcid.org/0000-0001-7647-1050

https://orcid.org/0000-0003-1007-5404

generalization in solving mathematical problems

contextualized in real life with an Advanced

Computing Environment (ACE). An ACE is a system

that allows to perform numerical and symbolic

calculation, make graphical representations in 2 and

3 dimensions and create mathematical simulations

through interactive components. Our research

questions are: how can we analyze the skills students

develop while generalizing a problem? What are the

most frequent difficulties of students? Our first

research objective is to study how students generalize

a contextualized problem with an ACE. For this

purpose, first we did some research to clearly define

what generalization means in Mathematics, in

particular in problem solving, and how technologies

can support this process. Then we analyzed the

solution of a problem-solving activity with an ACE

submitted by 75 students participating in the Digital

Math Training (DMT) project proposed by the

University of Turin (Barana et al., 2017; Barana &

426

Fissore, C., Fradiante, V. and Marchisio, M.

The Generalization of the Solution Process in a Mathematical Problem-Solving Activity with an Advanced Computing Environment.

DOI: 10.5220/0011986200003470

In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023) - Volume 2, pages 426-433

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Marchisio, 2016). In order to analyze how students

generalize a problem using interactive components,

we have developed and used a model which considers

three different phases: design and choice of

interactive components, programming of a system of

interactive components, and control stages of

generalization of a problem. For each stage we

established a set of indicators to understand the

competences achieved by each student. Our model

can be a useful tool to understand all different ways

of generalizing the solution of a problem used by the

students and their difficulties in the generalization

process.

2 STATE OF THE ART

2.1 Generalization in Mathematics

According to Radford, one of the characteristics of

Mathematics is that its objects are general (Radford,

2005). The term “process of generalization” includes

“a series of acts of thought which lead a subject to

recognize, by examining individual cases, the

occurrence of common characteristic elements. The

focus of the process consists in shifting attention from

single cases to all possible ones and in extending and

adapting the identified model to any one of them”

(Malara, 2013). In particular, Dörfler (1991) reflects

on the means used in a process of generalization: he

considers the representation of the process to be

crucial through the use of perceptible objects, such as

written signs, characteristic elements, steps and

results of actions. In this regard, Radford (2001)

identifies 3 levels of generalization on the basis of

means employed in this process:

 Factual: generalization is manifested through

concrete actions on specific cases in the form

of an operational scheme that remains

numerically confined.

 Contextual: it takes the form of a general

scheme which is learned at a more abstract

level, whose arguments possess the spatial and

temporal characteristics of the situation from

which it derives.

 Symbolic: it expects a shift towards the

relationships between constant and variable

elements (numbers and letters). For this

purpose, “it requires a desubjectification

process ensuring the disembodiment of spatial-

temporal embodied mathematical experience”.

In literature, most authors agree upon giving

generalization a central role in Mathematics. In this

sense, Mason (1996) sees generalization as the

centerpiece of Mathematics and his kind of

generalization expects students not only to reach the

universal from the particular, but also to see the

particular situation into the universal. Radford (2005)

agrees that awareness is an important achievement in

the process of generalization.

2.2 Generalization in Problem Solving

Polya in “How to solve it” (1945) states that problems

have a central role in Mathematics since they

stimulate concept building and students’ process of

learning. By solving mathematical problems, students

acquire ways of thinking, habits of persistence,

curiosity, and confidence in unfamiliar situations

(Leong & Janjaruporn, 2015). Problem solving

includes multiple steps: understanding the problem,

developing a mathematical model, developing the

solving process, and interpreting the obtained

solution. It also includes the process of

generalization, which consists in the use of

recognized regularities to make predictions or to

solve more general problems (Barana et al., 2020b).

The generalization of problems is fundamental, since

it represents the moment in which the process of

mathematical abstraction begins and it leads students

to the identification and solution of a variety of

similar problems (Malara, 2013). At the same time,

“the specifics of a solution are examined thought

generalization and questions as to why it worked are

investigated”. Generalization may also include a final

phase of review that is similar to Pólya’s looking back

(Liljedahl et al., 2016).

2.3 Use of Technology in Problems

Generalization

The research in the last decades has emphasized how

technologies can support and encourage the process

of generalization and exploration in Mathematics.

Among the various technologies that support the

learning of Mathematics (Brancaccio et al., 2015;

Barana et al., 2021), there are tools such as Multi-

Representational Technological (MRT)

environments which allow students to view multiple

representations of mathematical objects (Clark-

Wilson & Timotheus, 2022). In problem-solving

activities with the use of technologies there is a

“paradigm shift constituted by the transition from

solving problems to making problem solving”

(Barana et al., 2020b). Clark-Wilson and Timotheus

(2022) identify seven questions to analyze how

generalization can emerge in a task for students:

The Generalization of the Solution Process in a Mathematical Problem-Solving Activity with an Advanced Computing Environment

427

 What is the generalizable property within the

Mathematics topic under investigation?

 What forms of interaction with the MRT will

reveal the desired manifestation?

 What labeling and referencing notations will

support the articulation and communication of

the generalization that is being sought?

 What might the flow of mathematical

representations (with and without technology)

look like as a means to illuminate and make

sense of the generalization?

 What forms of interaction between the students

and the teacher will support the generalization

to be more widely communicated?

 How can the environment be amplified to

include a larger generalization?

ACE is a computer system which allows its user

to perform numeric and symbolic computations,

graphical representations in 2 and 3 dimensions, to

write procedures in a simple language, to program

and connect all the different registers of

representation in a single interactive worksheet

(Barana et al., 2017). The use of an ACE in problem

solving can support students in reasoning processes,

in the formulation of solving strategies and in the

generalization of solutions (Barana et al., 2020a). For

example, an ACE enables students to use different

types of representations depending on the chosen

strategy and to display the whole reasoning together

with verbal explanation in the same page (Barana et

al., 2017). The use of interactive components

represents a way to generalize a solving process with

an ACE (Barana et al., 2020a). There are different

types of interactive components (text areas,

mathematical containers, buttons and sliders) through

which it is possible to insert input data and to view

the output. The generalization of a problem though

the use of interactive components takes place in three

stages (Barana et al., 2020b):

 Creation of a system of interactive

components: students choose the interactive

components that best suit problem data and

demands;

 Programming: students program the interactive

component system to process the input data and

return the outputs;

 Control: students check that the system of

interactive component works in order to solve

the initial problem, and that it fits all cases

considered.

Through interactive components, students can

visualize how results change when the input

parameters are modified, making the generalization

of the solving process of a problem possible. In this

way, technology represents “an amplifier of a

mathematical activity” and enables to extend to “a

new dimension of problem posing, solving”

(Barana et al., 2019).

3 HOW TO USE AN ACE FOR

GENERALIZATION

Within Maple it is possible to program interactive

components through different tools. The use of these

components allows to compute and to obtain different

outputs according to different parameters, in order to

generalize mathematical concepts and resolution

processes. Suppose, to give an example, we solve the

following problem: "Calculate the area of a rectangle

with a base of 10 cm and a height of 3 cm and then

draw it. Create a system of interactive components to

calculate the area of a generic rectangle in which the

base and height can vary". We chose a simple

example in order to focus on generalization process

with an ACE . In next section we show an example of

a real life contextualized problem. Figure 1 shows a

possible resolution of the first two requests. The first

two commands are used to initialize two variables

(one for the base and one for the height). The third

command is for calculating the area and the fourth is

for drawing the rectangle.

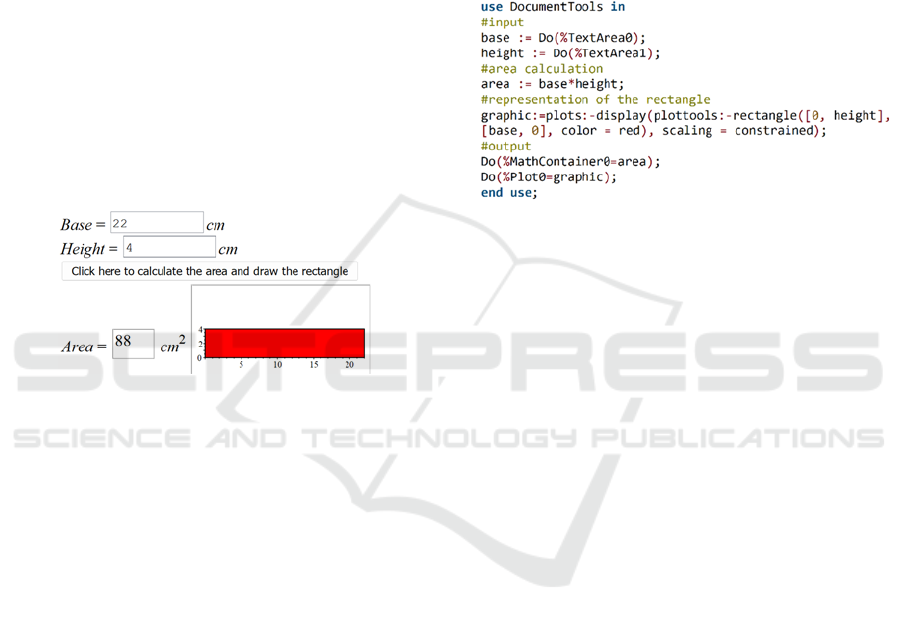
Figure 1: Example of resolution of the problem.

To generalize the resolution of the problem, it is

necessary to vary the initial data (the measurement of

the base and height of the rectangle) and see how the

value of the area and the representation change. The

first step is the choice of the interactive components

to use. The most complex choice concerns the input

data. You can insert: text areas in which the user

enters values, sliders to let the user choose the value

within a pre-set range, radio buttons to let the user

choose from a limited number of preset values. For

the output values, it is necessary to insert a math

container to display the value of the area and a graphic

CSEDU 2023 - 15th International Conference on Computer Supported Education

428

component to display the representation of the

rectangle. Finally, it may be necessary to insert a

button for the user to click to view the result, creating

a link between the input data and the output data. The

functioning of the system of interactive components

will be programmed inside the button. Figure 2 shows

the example of generalization with text areas. In

generalization design, it is not enough to insert the

appropriate interactive components to answer all the

questions of the problem, but it is also necessary to

discuss the process to explain to the user how to use

the system of interactive components. For example,

you can use the phrase "Enter the value of the base in

the text area" or "Click here to calculate the area and

draw the rectangle". This helps to properly

distinguish input and output, explaining the required

actions to the user. In this type of design, static

feedback on the generalization is obtained: by

changing the initial data, the result does not vary

dynamically but it is possible to see one case at a time.

Figure 2: Example of generalization of the problem.

The next step of the generalization process is the

programming of the system of interactive

components, in this case by inserting the commands

inside the button. Figure 3 shows the commands in

the button. While writing the code, the generalization

process takes place, which can happen starting from

the commands used to solve the problem. The

"Do(%TextArea0)" command is used to take the

value inserted in the first text area (in this case 22).

By doing so, the input values are generalized to the

(potentially infinite) values that the user will enter.

The third and fourth commands concern the

calculation of the area and the representation of the

rectangle. The last two commands are used to insert

the results respectively in the math container and in

the graphical component, so that the user can view

them. When programming the interactive component

system, a clear distinction between input and output

helps students write code. Comments can also be used

to discuss the process of generalizing and writing

code. This is particularly important in the DMT

project, the context of our research, because the

students receive an evaluation on this. The last step is

to check and verify the generalization process. This

step involves checking the correct functioning of the

component (which involves not only making sure that

it works, but also that it gives the correct results) and

of the input data. This last step is not mandatory for

the functioning of the interactive component system,

but it can be very important in the case of

contextualized problems. For this, it is possible to use

two strategies: explaining to the user the

characteristics of the values to be inserted and

warning them about possible meaningless results, or

inserting checks on the input values in the code.

Figure 3: Code inside the button.

This process of generalization can be combined

with a factual generalization, following Radford’s

definition (2001), because it manifests itself through

concrete actions on specific cases, but also

contextual, because it takes the form of a general

scheme that can be learned at a more abstract level. In

this instance, the students can see how to solve the

problem with generic base and height values, but

always taking on one pair of values at a time. As

explained by the author, students often fail to reach a

higher level of generalization because even a clear

intention is not always expressed satisfactorily

without recourse to concrete examples, typical of the

conceptual level of factual generalization. This type

of generalization is also in agreement with Clark-

Wilson & Timotheus’ (2022) theory on

generalization in a task performed through an MRT

environment. The generalizable property within the

mathematical topic under investigation changes

depending on the problem, but this type of process

can be applied to any type of problem. Within the

ACE, different representation registers can be used

for solving the problem and therefore for

generalization. The forms of interaction with the

MRT that reveal the desired manifestation are the

three phases of the generalization process: design,

programming, verification, and feedback. The

labeling and referencing notations supporting the

articulation and communication of the generalization

consist of the argumentation foreseen in each of the

three phases of the generalization process. The 'flow'

of mathematical representations which gives meaning

The Generalization of the Solution Process in a Mathematical Problem-Solving Activity with an Advanced Computing Environment

429

to the generalization can be seen mainly in the

programming phase, in which the input data is taken,

the results are processed and the outputs are returned.

In the case of a problem-solving activity with an ACE

done by students in the classroom, forms of

interaction between students and teachers can be

encouraged. As shown in the example, in this type of

generalization task, the original problem is expanded

in order to solve (potentially infinite) similar

situations. By choosing the data to insert in the

interactive components, students write new problems.

4 RESEARCH CONTEXT AND

METHODOLOGY

4.1 Research Context

The context of our research is the Digital Math

Training (DMT) project funded by the Fondazione

CRT within the Diderot Project and organized by the

University of Turin. Every year the project engages

about 150 classes of students from grade 9 to grade

13. The project is aimed at students, from Piemonte

and Valle d’Aosta, developing mathematical and

computer science competences through resolution of

real-world mathematical problems using the ACE

Maple (Barana et al., 2019). The main part of the

project is the “online training” attended by a

maximum of 5 selected students for class. In this

stage students are divided into 5 online courses,

depending on their scholar grade. They are asked to

solve 8 non-standard problems in a Digital Learning

Environment and for each problem they receive an

assessment by trained tutors. The last question of each

problem demands a generalization of the problematic

situation by using a system of interactive

components. Before the beginning of the training the

students did not know how to use the ACE. In fact

for the whole training they can participate in online

tutoring on the use of the ACE and explanation files

are at their disposal. To understand how students

generalize a contextualized problem with an ACE, we

have analyzed the grade 12 online training of the

2021/22 DMT edition. We analyzed all the 75

solutions of the fifth problem, which is a medium

difficult problem proposed to students in the middle

of online training. At this stage of the training

students’ competences in problem solving and in

using the ACE start to be good. The problem asks

students to help Pietro to evaluate a life insurance

which includes the following conditions:

 Pietro has to pay a premium of €1,500 every

year from his 51th birthday;

 From his 51th birthday to his 70 birthday the

amount at the end of the payment period

corresponds to the sum of the instalments, plus

a certain annual percentage (1%);

 From his 71th birthday to his 100th birthday the

company will give Pietro an annual amount

(the first one on his 71th birthday and the last

one on his 100

birthday). This amount is

calculated as follows: the sum gained during

the 20 years of payment before is divided by 30

(i.e. the number of years of life up to Pietro’s

100

birthday. This amount is then multiplied

by (1+probability of death)*n, where n is the

number of years since his 70th birthday. The

probability of death will be calculated as

follows: every year Pietro has a 2% chance of

dying more than the year before. The

probability that Piero will die from his 70th to

his 100th birthday is 1.

The request of the problems are:

 At the end of the 20 years, how much will

Pietro have paid in total?

 Which function can estimate the probability of

death?

 How far Pietro has to live in order to receive an

annual amount greater than €1,500?

 Create a system of interactive components that

helps Pietro to evaluate the different options of

the insurance. It must allow Pietro to change

the instalment of the premium paid every year

starting from the 51st year of age and to choose

the age until Pietro has to pay the instalment.

As a result, Pietro wants to know when the

annual amount will be greater than the paid

premium instalment.

Last request asks students to generalize the

problem to different situations by changing the initial

data and evaluating the obtained results. We

considered the last request focused on generalization,

which was developed by 42 of the 75 students, to

investigate how students generalize a problem.

4.2 Research Methodology

On the basis of the theoretical framework, we

developed a model to understand how students

generalize a contextualized problem with an ACE.

We considered three stages of generalization of a

problem through the use of interactive components:

creation and design, programming, and control. In

each stage we established some indicators to study

how students developed them. In particular, we

CSEDU 2023 - 15th International Conference on Computer Supported Education

430

assigned a value for each stage: “1” if the request of

the indicator was satisfied and “0 otherwise. Creation

and design stage contains the following indicators:

 Right choice of a system of interactive

components: students choose the interactive

components that best suit problem data and

demands;

 Argumentation of the process: students well

explain how their system of interactive

components works and why they choose that

kind of component;

 Clear input-output distinction: the system of

interactive components allows everyone who

uses it to understand where to insert inputs and

where to receive the outputs;

 Argumentation of the result: students explain

what the system of components allows to

achieve from the data given in input;

 Kind of feedback: static or dynamic;

 Answer given to all problem requests: the

system of interactive components answers to

the problem requests;

 Use of different registers of representation: for

example, algebraic, symbolic, graphic.

The indicators of the programming stage are:

 Adding more commands: students experience

new and original commands compared to the

ones employed in previous problem requests;

 Clear input-output distinction: the

programming code clearly distinguishes input

elements from outputs;

 Functional interactive component system: the

system of interactive components works;

 Argumentation of generalization process:

students explain through comments in the

programming code how they build the system

of interactive components to generalize one or

more parts of the problem;

 Comments within the code: students insert

comments inside the code.

The Control stage includes the following

indicators:

 Correct answers to the problem: the system of

interactive components correctly answers the

problem;

 Consistency with the context: students insert

context-related controlling elements;

 Argumentation of the control: students insert

comments and remarks related to the context.

To analyze the 42 submissions, we used peer

review: first we evaluated the 42 submissions

individually following the indicators mentioned

above, then we compared our evaluations and we

discussed any differences to find an agreement. In

most cases there were no particular disagreements in

evaluations; the only differences were related to the

clear input-output distinction in programming stage:

according to one reviewer, inputs and outputs had to

be precisely specified, while according to the others

inputs and outputs could be inferred from the type of

commands used. At the end all reviewers agreed with

the last position.

5 RESULTS

Table 1 shows the percentage of students who scored

“1” or “0” for each indicator. The first column

contains the three stages of generalization of a

problem through the use of interactive components:

design and choice of interactive components,

programming of a system of interactive components

and control stages of generalization of a problem. The

second column refers to the indicators of each stage.

The third and the fourth columns show the percentage

of students who obtained respectively a “0”and “1”

evaluation in a specific indicator.

Table 1: Percentage of students who scored “1” or “0” for

each indicator.

Stages Indicators 0 1

DESIGN

AND

CHOICE

Right choice of a system of

interactive components

10% 90%

Argumentation of the

rocess

7% 93%

Clear input-output

distinction

21% 79%

Argumentation of the

result

21% 79%

Static feedback 24% 76%

Dynamic feedback 76% 24%

Answer to all problem

requests

19% 81%

Use of different registers

of representation

7% 93%

PROGRAM

MING

Adding more commands 95% 5%

Clear input-output

distinction

17% 83%

Functional interactive

component system

2% 98%

Argumentation of

generalization process

76% 24%

Comments within the code 76% 24%

CONTROL Correct answers to the

roblem

31% 69%

Consistency with the

contex

74% 26%

Argumentation of the

control

86% 14%

The Generalization of the Solution Process in a Mathematical Problem-Solving Activity with an Advanced Computing Environment

431

Most of the students (more than 70% in all

indicators) had no problems in the design phase of the

generalization process. Almost all the students (90%)

correctly chose the interactive components to use and

explained the process in order to help the user

understand how to use the interactive component

system. Students well explained how their systems of

interactive components work and why they chose

those kinds of components. A null score was given

for these two indicators in cases where the system of

interactive components was not complete or in cases

where the interactive components were simply

inserted without an explanation. These cases also

received a null score in the indicator "clear input-

output distinction". The design of almost all the

students (81%) answered all the questions of the

problem and almost all of the students (93%) knew

how to use different registers of representation, as

also required by the problem. The indicator on which

they had the greatest difficulty in this phase was

"Argumentation of the result", which was performed

correctly by 79% of the students. This aspect may be

due to the fact that students thought that the result of

the problem may have been implicit for those readers

who know the problem. However, especially in the

case of contextualized problems, discussing the result

obtained is very important. As we have seen,

generalization depends on the solution process used

to solve the problem, and students can use different

strategies and models to solve the problem. Most

students (76%) preferred static feedback instead of a

dynamic one in the generalization of a problem. In the

generalization process the use of dynamic feedback,

mainly through a slider, has the advantage of seeing

how the result varies dynamically as the initial data

varies, and this certainly favors mathematical

exploration and the formulation of conjectures. On

the other hand, it limits the values that can be used for

the generalization. As shown in Table 1, some

difficulties arise in the programming and control

stages. As expected, most students (95%) used the

same commands employed to solve the problem,

generalizing them and adapting them in the

programming phase. Students who used extra

commands did so to add insights to their solution or

to check the code. In this phase the students had no

difficulty in programming the code. Almost all

students (83%) structured the code clearly by

distinguishing input, process, and output; and almost

all (98%) of them created a functioning system of

interactive components (which took input data and

returned output data). A few students (24%) inserted

comments into the code and these comments were

used to explain

how they programmed the system of

interactive components to generalize one or more

parts of the problem. This step was not necessarily

required of students, but we believe it is important to

study since discussing the code certainly helps them

in the generalization process. This also helps trainers

and teachers to understand the reasoning and then to

evaluate it and give effective feedback.

Same difficulties characterize the argumentation

of the control stage, in fact only 14% of students

inserted comments and remarks related to the context.

For example, advising the user what data could be

entered as input into the interactive component

system or arguing an acceptable or not acceptable

result based on the context of the problem. Only 26%

of the students inserted controlling elements in order

to relate solutions to the context of the problem. Most

students provided a graphical representation in their

system of interactive components. In using the graph

explanatory graph of the problematic situation. Not

all the students have correctly created an argument

graph, for example by inserting the variables on the

axes, the legend and the title of the graph, etc. In this

analysis we have investigated the presence or absence

of multiple registers of representation but not how

they were used. In future analyses, this may be an

aspect to consider. Another goal of future research is

to correlate generalization processes of the students

with their level of programming skills. For example,

if only few of them know how to plot a function, this

fact will not display a higher level of generalization

only a lack of programming skills.

6 CONCLUSIONS

In our opinion, dividing the generalization process

into three main stages and identifying the related

process indicators helps to evaluate the processes

implemented by the students and the skills they have

developed. Even if students may not distinguish

between the three stages and probably develop them

in a single time, these are crucial steps in the process

of generalization. In each stage, different strategies

of generalization emerge in the choice of interactive

components and commands employed. Students’

main difficulties are related to the programming of a

system of interactive components and to the control

stages. The first difficulty may depend on the fact that

the generalization of a problem requires students also

to know the specific language of the ACE. The

students' results in the generalization process were

very positive and they showed good generalization

skills. This gave the students the opportunity to

CSEDU 2023 - 15th International Conference on Computer Supported Education

432

extend the problematic situation to more cases and to

reflect critically on the significance of the results

obtained based on the context of the problem. The use

of contextualized and real-life problems was made

with the goal of creating a bridge between school and

extracurricular Mathematics, bringing out realistic

considerations and developing modeling skills. This

also helps students to understand the role of

Mathematics in daily life. The results show students’

difficulties in the argumentation of the various phases

of the generalization process. It would be important

to analyze this aspect also in the problem-solving

phase and train students more on this. Even if the

study is limited to a sample of 42 mathematically

gifted students, it could be a starting point for

extending the research to a bigger sample and to a

different students and problems. For example, it

would be possible to analyze other DMT online

training courses from different grades and extend the

analysis to more problems to understand if and how

much the difficulty in solving the problem and in

programming affects the generalization process.

REFERENCES

Barana, A., Fioravera, M., Marchisio, M. (2017).

Developing Problem Solving Competences through the

Resolution of Contextualized Problems with an

Advanced Computing Environment. In Proceedings of

the 3

International Conference on Higher Education

Advances, 1015–1023.

Barana, A., Brancaccio, A., Conte, A., Fissore, C.,

Floris, F., Pardini, C., Marchisio, M. (2019). The Role of an

Advanced Computing Environment in Teaching and

Learning Mathematics through Problem Posing and

Solving. 15th International Scientific Conference

eLearning and Software Education, 2, 11-18.

Barana, A., Conte, A., Fissore, C., Floris, F., Marchisio,

M., Sacchet, M. (2020a). The Creation of Animated

Graphs to Develop Computational Thinking and

Support STEM Education. Communications in

Computer and Information Science, 1125 CCIS, 189–

204.

Barana, A., Conte, A., Fissore, C., Marchisio, M., &

Roman, F. (2020b). Problem solving and generalization

with an Advanced Computing Environment. In 14

International Congress on Mathematics Education

(ICME 14), 1–4.

Barana, A., & Marchisio, M. (2016). Dall’esperienza di

Digital Mate Training all’attività di Alternanza Scuola

Lavoro. Mondo Digitale, 15 (64), 63-82.

Barana, A., Marchisio, M., & Sacchet, M. (2021).

Interactive feedback for learning mathematics in a

digital learning environment. Education Sciences,

11(6), 279.

Brancaccio, A., Marchisio, M., Meneghini, C., & Pardini,

C. (2015). More SMART Mathematics and Science for

teaching and learning. Mondo Digitale, 14(58), 1-8.

Clark-Wilson, A., & Timotheus, J. (2022). Designing tasks

within a multi-representational technological

environment: An emerging rubric. In C. Margolinas

(Ed.), Task Design in Mathematics Education.

Proceedings of ICMI Study. Oxford, United Kingdom,

45–52. Retrieved from: https://hal.archives-

ouvertes.fr/hal-00834054v3.

Dörfler, W. (1991). Forms and means of generalization in

mathematics. In A. Bishop (Ed.), Mathematical

Knowledge: Its growth through teaching. Erlbaum, 63–

85.

Leong, Y. H., & Janjaruporn, R. (2015). Teaching of

Problem Solving in School Mathematics Classrooms.

In S. J. Cho (Ed.), The Proceedings of the 12

International Congress on Mathematical Education.

645–648.

Liljedahl, P., Santos-Trigo, M., Malaspina, U., & Bruder,

R. (2016). Problem solving in mathematics education.

Springer Berlin Heidelberg. New York, NY

Malara, N.A. (2013). Processi di generalizzazione

nell’insegnamento/apprendimento dell’algebra. In

Annali online formazione docente, 4(4), 13–35.

Mason, J. (1996). Future for Arithmetic & Algebra:

Exploiting Awareness of Generality. In J. Gimenez, R.

Lins & B. Gomez (Eds.), Arithmetics and Algebra

Education, Searching for the future. Barcelona:

Universitat Rovira y Vir gili, 16–3.

Pólya, G. (1945). How to solve it. Princeton NJ: Princeton

University.

Radford, L. (2001). Factual, Contextual and Symbolic

Generalizations in Algebra. In Proceedings of the 25

Conference of the International Group for the

Psychology of Mathematics Education, 4, 81–89.

Radford, L. (2005). La generalizzazione matematica come

processo semiotico. La matematica e la sua didattica,

2, 191–213.

The Generalization of the Solution Process in a Mathematical Problem-Solving Activity with an Advanced Computing Environment

433