ASMS: A Metrics Suite to Measure Adaptive Strategies of

Self-Adaptive Systems

Koen Kraaijveld

and Claudia Raibulet

1,2 a

Vrije Universiteit Amsterdam, Computer Science Department, De Beolelaan 1111, 1081HV, Amsterdam, The Netherlands

University of Milano-Bicocca, DISCo-Dip. di Informatica, Sistemistica e Comunicazione, Viale Sarca 336, Milan, Italy

Keywords:

Self-Adaptive System, Evaluation, Software Metrics, Adaptive Strategy, Architecture-based Self-Adaptation.

Abstract:

In the last two decades, research in Self-Adaptive Systems (SAS) has proposed various approaches for induc-

ing a software system with the ability to change itself at runtime in terms of self-adaptation strategies. For the

wider adoption of these strategies, there is a need for a framework and tool support to enable their analysis,

evaluation, comparison, and eventually their selection in overlapping cases. In this paper, we take a step in

this direction by proposing a comprehensive metric suite, i.e., the Adaptive Strategies Metric Suite (ASMS), to

measure the design and runtime properties of the adaptive strategies for SAS. ASMS consists of metrics that

can be applied through both static and dynamic code analysis. The metrics pertaining to static code analysis

have been implemented as a plugin for Understand tool.

1 INTRODUCTION

Self-adaptive systems (SAS) have represented an ac-

tive research in the past twenty years, with the overall

goal to make systems more robust to runtime faults

and threats, as well as to optimize their performances

while running (Cheng et al., 2009). Several adapta-

tion strategies have been proposed following different

paradigms, e.g., search-based, optimization, control-

theory, architecture-based (Krupitzer et al., 2015).

Despite this progress, it is still a challenge to eval-

uate whether an adaptation strategy brings the ex-

pected beneﬁts that outweigh the costs of designing

and implementing it (Gerostathopoulos et al., 2022),

(Raibulet et al., 2017). For the same reason, it is

hard to compare strategies based on their design and

runtime properties. Having a framework that guides

such evaluation and comparison is important for the

maturity of the ﬁeld and in particular for the indus-

trial adoption of the proposed self-adaptation strate-

gies (Masciadri and Raibulet, 2009).

With the overall goal of providing a framework for

the evaluation and comparison of adaptation strate-

gies, in this paper we focus on measuring their de-

sign and runtime properties after they they have been

implemented. Our approach can be seen as comple-

mentary to the top-down evaluation approaches that

https://orcid.org/0000-0002-7194-3159

measure e.g., how well a strategy satisﬁes an adap-

tation goal (e.g., minimize response time). Our ap-

proach also acknowledges that adaptive strategies are

software programs and can be analyzed for their qual-

ity using proven techniques for software evaluation.

This paper focuses on producing high-level com-

putable metrics targeted towards adaptive strategies.

Metrics capture a particular design or runtime prop-

erty. The research question (RQ) this paper centers

around asks:

In what meaningful ways can we measure the

design and runtime properties of the adaptive

strategies belonging to a SAS?

Towards answering this RQ, we propose the

Adaptive Strategies Metric Suite (ASMS): a compre-

hensive metrics suite that measures different design

and runtime features of a SAS adaptive strategies.

ASMS blends static and dynamic code analysis ap-

proaches that are split into 5 categories, each of which

focuses on a particular facet of an adaptive strategy’s

operation. Each ASMS metric is supported by a con-

crete formulae or method for their computation.

Our approach to ASMS leverages several different

methodologies. First, we conduct a case study analy-

sis of various SAS that implement one or more adap-

tive strategies. In order to limit the scope of which

case studies have been examined, we have speciﬁcally

chosen systems programmed in the smart mobility ap-

238

Kraaijveld, K. and Raibulet, C.

ASMS: A Metrics Suite to Measure Adaptive Strategies of Self-Adaptive Systems.

DOI: 10.5220/0011992800003464

In Proceedings of the 18th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2023), pages 238-249

ISBN: 978-989-758-647-7; ISSN: 2184-4895

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

plication domain. Second, observations made from

the case studies are used in the design of the metric

suite. Third, these metrics are implemented into a

plugin

designed for the static code analysis tool Un-

derstand, provided by Scientiﬁc Toolworks.

For the purposes of this paper, we focus on sys-

tems that employ architecture-based self-adaptation.

The architecture of SAS consists of two components:

managing system and managed system (Weyns et al.,

2010). The managing system decides which adaptive

changes need to be executed to achieve adaptation. It

does this by adapting them into the controllable man-

aged system, which then in turn effects these changes

into the surrounding, non-controllable environment.

To decide the changes to be performed, the managing

system uses a MAPE-K feedback loop that consists

of four steps: Monitor, Analyze, Plan and Execute,

which operate on a pool of shared Knowledge (Gar-

lan et al., 2009), (Weyns and Iftikhar, 2019).

The paper is structured as follows. Section 2 in-

troduces the examined case studies and their self-

adaptation. Section 3 covers the guidelines and con-

straints under which the metrics have been designed.

Section 4 presents the metric suite by explaining its

design. Section 5 covers the key parts behind the

implementation of the plugin. Section 6 outlines the

evaluation of the plugin by presenting and discussing

its results after being applied to an exemplar. Section

7 discusses the current and future developments of

ASMS. Related work is addressed in Section 8. Sec-

tion 9 summarizes the conclusions and future work.

2 CASE STUDIES

Various case studies have been examined to explore

which design and runtime properties occur frequently

in the adaptive strategies of several SAS. They have

been analyzed on the basis of their code (through the

Understand tool) and their respective papers. In par-

ticular, we have considered the following SAS (pre-

sented in alphabetical order):

• ATRP (Automated Trafﬁc Routing Problem)

(Wuttke et al., 2012) presents a trafﬁc routing sim-

ulator that enables the evaluation and comparison

of different self-adaptive methods that try to solve

the automated trafﬁc routing problem. Several ve-

hicles traverse across a map and try to reach a

target destination given a starting point. During

their travel, they may be restricted by complica-

tions such speed limits or trafﬁc accidents. Adap-

tivity is related to how vehicles can deal with these

ASMS-https://github.com/Koen-Kraaijveld/ASMS

imposed restrictions to reliably reach their desti-

nation in a minimal amount of time.

• Dragonﬂy (Maia et al., 2019) focuses on the self-

adaptive behaviour of drones. Speciﬁcally, it is

centered around how a drone can reliably reach its

destination when under pressure from limited re-

sources and environmental hazards. This includes

factors such as monitoring battery life or analyz-

ing safe locations where the drone may potentially

land. Adaptivity is related to how a drone maxi-

mizes reliability in response to travel issues.

• TRAPP (Trafﬁc Reconﬁgurations via Adaptive

Participatory Planning) (Gerostathopoulos and

Pournaras, 2019) is focused on the optimization

of a city’s trafﬁc ﬂow. As ATRP, it provides a de-

centralized approach for vehicles that must each

make decisions on how to best navigate a city.

Adaptivity is related to how an individual vehi-

cle can optimize itself to improve upon different

factors, such as trip travel times.

2.1 Self-Adaptation Details

Table 1 provides details of each case study in rela-

tion to their self-adaptation details by highlighting the

main steps from MAPE-K loops.

Table 1: Case Study Self-Adaptation Details.

Exemplar

Main steps of the MAPE-K loop

Monitor Analyze Plan Execute

ATRP Trafﬁc

status

Resource

con-

sump-

tion

Quality

service

(perfor-

mance,

depend-

ability,

safety)

Adaptive

changes

planned

routes

Adapted

navigation

Dragonﬂy Remain-

ing

battery

life

Distance

to desti-

nation

Single

reference

values

Predeﬁ-

ned

adaptive

changes

Flying

direction

TRAPP Trafﬁc

status

Street

utiliza-

tion

Trip

travel

times

Quality

service

(perfor-

mance,

depend-

ability,

safety)

Adaptive

strategy

parameter

tuning

Adapted

naviga-

tion

Adaptive

plan-

ning

fre-

quency

ASMS: A Metrics Suite to Measure Adaptive Strategies of Self-Adaptive Systems

239

2.2 Observations and Considerations

Several key observations can be made when examin-

ing how exemplars execute their adaptive strategies.

Small vs. Large Impact. Executing certain adap-

tive strategies may result in more behavioural changes

in the system over other strategies, or may require a

larger degree of computational effort from the sys-

tem. Carrying out a low-impact strategy would not

need, for example, to spend a signiﬁcant amount of

resources on adapting the managed system, or would

result in minimal changes in the system’s behaviour.

By contrast, the execution of a high impact strategy

may, for example, need to analyze greater amounts of

sensor data before formulating a plan, or the strategy

may need to perform signiﬁcantly more changes in

the managed system to achieve the adaptation goals.

In this sense, impact is observed as the repercussions

imposed on the system during the execution of an

adaptive strategy.

Sequential vs. Concurrent. If any two adap-

tive strategies do not interfere with each other, they

may be executed concurrently. However, when a

clash arises between the two, they are performed se-

quentially. The conﬂicts that threaten the possibility

for concurrent execution between two strategies may

stem from various factors, e.g.,. incompatible depen-

dencies on certain system states, or resource costs that

exceed what a system can feasibly handle altogether.

Dependent vs. Independent. Dependencies between

two adaptive strategies form when one depends on

the functionality of the other. In the case studies

where this notion applies, adaptive strategies would

be programmed as classes, from which another strat-

egy could use inheritance to assume some of the func-

tionality given by other strategies. By contrast, strate-

gies that do not inherit from others do not form any

dependencies and can be considered as independent.

Dependencies on Time. Several properties related

to adaptive strategies can be observed over time, e.g.,

how often an adaptive strategy needs to be performed

(e.g., frequent vs. infrequent) or the preferred range

of strategies that a system tends to execute over a

given period of time.

3 METRIC DESIGN GUIDELINES

Before going into detail on the design behind ASMS,

we discuss preliminary information that shows un-

der which circumstances the metrics have been con-

structed. We do this by outlining the requirements

behind the metrics, the role that static and dynamic

code analysis plays, and the application of subtypes.

3.1 Requirements

Each of the proposed metrics in this work should sat-

isfy the following requirements (Rawat et al., 2012),

(Reinecke et al., 2010):

Comparability. The metric suite should enable the

comparison between any two or more given self-

adaptive systems. It should be able to express the ex-

istence of an equality relation between these systems.

Validity. The metric suite should clearly measure

what it is intended to measure.

Robustness. The computational output of the metric

should not be vulnerable to being signiﬁcantly altered

when small changes are implemented into the system

that the metric running on.

Computational Efﬁciency. The metric calculation

should not result in high resource costs or take a sig-

niﬁcant amount of time to process.

3.2 Static vs. Dynamic Code Analysis

To capture relevant design and runtime properties, we

present a metrics suite that blends static and dynamic

code analysis. The type of analysis used deﬁnes the

resources and tools at a metric’s disposal with which

it can compute its output. Each type presents several

advantages and disadvantages, which we now outline.

Static Code Analysis is useful when measuring var-

ious design properties. This type of analysis is per-

formed without the execution of the source code,

meaning that the extracted data can only come from

the scripting language ﬁles themselves (Hande and

Rao, 2017). One of its main advantages is the ex-

haustive analysis of code.

The ﬁrst advantage that we focus on when using

static code analysis is its ability to examine the struc-

tural elements of a codebase. The static approach of-

fers various resources to aid in this, such as control-

ﬂow and data-ﬂow analysis, which are useful when

trying to understand how the components of a system

are composed (Kritzinger, 2017). These resources

may take into account the entirety of a system’s code-

base, whereas dynamic analysis can only analyze the

code it is executing. The second advantage is that

it can also provide generalized information on how

code fragments behaves, e.g., count its number of ex-

ecutable statements (Gomes et al., 2009). The ASMS

metrics exploit the beneﬁts of both these advantages.

Dynamic Code Analysis is useful when examin-

ing the runtime properties of a system. Contrary to

static analysis, the dynamic analysis is possible dur-

ing the execution of code, which means that measur-

ing the features of a system is performed in a runtime

environment (Gomes et al., 2009). The main bene-

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

240

ﬁt of this type of analysis is being able to use re-

sources such as memory snapshots and runtime API

data, which enables a deeper and more accurate study

of how the system operates (Hande and Rao, 2017).

However, a disadvantage is the non-deterministic na-

ture of sequential code executions. There is no guar-

antee that the results produced by dynamic code anal-

ysis will be the same for all future executions (Gomes

et al., 2009). The metrics we devise using dynamic

analysis focus on the properties of adaptive strategies

that can only be measured reliably during runtime.

3.3 Subtypes

For a subset of the our metrics, we split them into

subtypes that represent slight variations on the general

method used to calculate their outputs. This is done

in an effort to foster additional customizability and

extendability to future developments of metrics.

4 ASMS

We now present the metrics and how they operate.

They are divided into 5 categories, each focusing on

a design or runtime property. The categories are Lo-

cality, Concentration of Impact, Elementarity, Main-

tainbility and Time-related.

4.1 Locality Metrics

The metrics in Locality category, i.e., Impact Radius

and Concurrency Capacity, are designed to measure

the impact-related properties of an individual strategy.

4.1.1 Impact Radius

This metric calculates the computational effort re-

quired by the system when an adaptive strategy will

be executed. We do this by counting the total num-

ber of executable statements that the system will pro-

cess. Using executable statements over other types of

statements to quantify impact is preferred because ex-

ecutable statements may include behavioural changes

in the system since it requires the processing of an ac-

tion (Pollack and Cytron, 2003). Counting the num-

ber of executable statements for a given code frag-

ment is a process that can be done without code exe-

cution, therefore this metrics needs static analysis.

The main source that the Impact Radius uses to

compute its output is the call graph of an adaptive

strategy. In the codebase of a system, if a given strat-

egy is programmed as a function, we traverse each

node in its call graph and then sum up the number

of executable statements. In cases where the strategy

is programmed as a class, we perform the same op-

eration, but instead applied to each of the strategy’s

methods and summing up their outputs instead.

We differentiate the metric’s calculation based on

two subtypes: Local and Global. When counting the

number of executable statements in the call graph of a

given strategy, the Local Impact Radius (LIR) is inter-

ested in nodes that are directly connected to the root

node (i.e., the strategy the metric is running on). The

Global Impact Radius (GIR) is interested in all the

nodes of a strategy’s call graph. Fig. 1 shows the

distinction between these subtypes using a call graph.

Figure 1: Diagram showing a call graph, starting from an

adaptive strategy called Strategy A1. The red color denotes

all the methods that are locally reachable, while the blue

color denotes all the methods that are globally reachable.

In more formal terms, the general formula used

to derive the Impact Radius and its subtypes is as fol-

lows. Let E(m) return the number of executable state-

ments belonging to a function f and let L( f ) return

the set of methods that are directly connected to a

function f in its call graph. Then, the Local Impact

Radius (LIR) of a strategy s can be deﬁned as:

LIR(s) = E(s) +

∑

f ∈L(s)

E( f ) (1)

By contrast, the Global Impact Radius (GIR) can

be deﬁned as follows. Let G( f ) return the set of func-

tions in which a path can be formed from f to any

other function in the call graph of f . Then, the GIR

of a strategy s can be deﬁned as:

GIR(s) = E(s) +

∑

f ∈G(s)

E( f ) (2)

4.1.2 Concurrency Capacity

This metric measures the extent to which adaptive

strategies may be performed concurrently. Since this

is a task that can best be measured during execution,

this metric is designed for dynamic analysis. We de-

ﬁne the metric using two subtypes: Index and Ratio.

The Concurrency Capacity Index (CCI) computes

the number of adaptive strategies in a set of strategies

that can be performed concurrently with others. It can

be deﬁned as the following. Let C(s, S) be a function

ASMS: A Metrics Suite to Measure Adaptive Strategies of Self-Adaptive Systems

241

that returns true if an individual input strategy s can

be performed concurrently with any other strategy in

the set of adaptive strategies S. Then, for a given set

of adaptive strategies S, we have.

CCI(S) = | {s | C(s, S), ∀s ∈ S} | (3)

The Concurrency Capacity Ratio (CCR) com-

putes the ratio of the number of adaptive strategies

that can be performed concurrently, over the total

number of available strategies. It is deﬁned as the fol-

lowing. For a set of adaptive strategies S, we have:

CCR(S) =

| {s | C(s, S), ∀s ∈ S} |

| S |

(4)

4.2 Concentration of Impact Metrics

The Concentration of Impact metrics make use of el-

ements from the Impact Radius, but differ in that they

are designed to measure impact-related properties in

a group of adaptive strategies, rather than individual

ones. In particular, these included the Global Impact

Radius Distribution (GIRD) and Global Impact Ra-

dius Statistics (GIRS).

4.2.1 Global Impact Radius Distribution

This metric takes advantage of the Impact Radius

metric by computing the GIR of each adaptive strat-

egy. Using this information, it is possible to produce a

distribution used to compare the impact of each strat-

egy. For a set of adaptive strategies that belong to a

system, each value in the distribution corresponds to a

strategy in the set. The value is calculated as the ratio

of an adaptive strategy’s GIR to the summed total of

each adaptive strategy’s GIR in the set.

In more formal terms, we deﬁne the GIRD as the

following. We ﬁrst deﬁne a function R(s, S) that cal-

culates the ratio of the GIR of an adaptive strategy s

to the total GIR of all adaptive strategies in the set S.

This is written as:

R(s, S) =

GIR(s)

∑

′

∈S

GIR(s

′

)

(5)

Then, for the set of adaptive strategies S on which

the metric will run, we have:

GIRD(S) = {R(s, S) | ∀s ∈ S} (6)

4.2.2 Global Impact Radius Statistics

By performing statistical analysis on the GIRD, we

can obtain more insights into how adaptive strategies

relate to each other in regards to their impact. This is

what the GIRS metric tries to do by computing several

statistics on the distribution from the GIRD metric.

The metric consists of ﬁve subtypes, each corre-

sponding to commonly calculated statistics. They are

deﬁned as follows:

• Maximum. This metric subtype returns the adap-

tive strategy which has the largest GIRD value.

This can be deﬁned as the following, where the

function R is established in (5).

GIRS

max

(S) =

s∈S

R(s, S) (7)

• Minimum. By contrast, this metric subtype re-

turns the adaptive strategy which has the smallest

value in the GIRD. We deﬁne it as the following:

GIRS

min

(S) =

s∈S

R(s, S) (8)

• Mean. This metric subtype may be expressed

through following formula, where S is a set of

adaptive strategies:

GIRS

mean

(S) =

∑

r∈GIRD(S)

| GIRD(S) |

(9)

• Median. This metric subtype may deﬁned through

following formula, where S is a set of adaptive

strategies and n is the number of elements in the

set GIRD(S). If n is odd, then:

GIRS

med,odd

(S) = GIRD(S)

n+1

(10)

If n is even, then we have:

GIRS

med,even

(S) =

GIRD(S)

+ GIRD(S)

(11)

• Standard Deviation. Lastly, with regards to the

Standard Deviation subtypes, its calculation is

based on the sample standard deviation. It may

be deﬁned as the following for a set of adaptive

strategies S:

GIRS

std

(S) =

∑

r∈GIRD(S)

(r − GIRS

mean

(S))

| GIRD(S) | −1

(12)

4.3 Elementarity Metrics

The metrics in the Elementarity category follow the

idea of measuring how elementary an adaptive strat-

egy is relative to others in the system. This is done by

computing the dependencies between strategies, i.e.,

the Dependency Degree.

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

242

4.3.1 Dependency Degree

In this metric, we can measure the dependencies

that form between the adaptive strategies of a sys-

tem. We deﬁne a dependency as any strategy that

assumes the functionality of another through means

such as class inheritance. Since we detect dependen-

cies through data-ﬂow analysis, this metric is imple-

mented in static code analysis.

Using this notion, it is possible to construct a tree

where each node represents an adaptive strategy in

a system. Edges connecting any two nodes indicate

a dependency between the strategies associated with

those nodes. Parent nodes show which strategies a

given strategy depend on, while child nodes show

which strategies a given strategy are depended on by.

Fig. 2 shows such a tree for an example set of adap-

tive strategies belonging to a SAS.

Figure 2: A tree visualization of the Dependency Degree

metric from an example set of adaptive strategies.

There are two subtypes that the Dependency De-

gree metric consists of, which are named Bottom-up

and Top-down. Both of these base their calculation

on the constructed tree. For a given input adaptive

strategy that corresponds to a node in the tree, the

Bottom-up Dependency Degree subtype counts the to-

tal number of edges it takes to reach the root from the

given node. This output represents the total number

of strategies that the given strategy depends on. The

Top-down Dependency Degree subtype calculates its

total number of child nodes. This output represents

the total number of strategies that a given strategy is

depended on by.

To illustrate this with greater clarity, we give an

example that uses the tree in Fig. 2. Lets calcu-

late both Dependency Degree subtypes for Strategy 1.

We can see that the node for Strategy 1 has six child

nodes, which means that it is depended on by six other

strategies. This would be the output for the Top-down

Dependency Degree subtype. Oppositely, Strategy 1

has no parent node (being the root) and would depend

on zero strategies, so the output for the Bottom-up

Dependency Degree subtype would be zero.

4.4 Maintainability Metrics

The Maintainability metrics are designed to measure

the properties pertaining to the complexity and mod-

iﬁability of an adaptive strategy. They leverage sev-

eral established metrics often employed in static code

analysis (Turetken, 2013): Complexity and Modiﬁa-

bility metrics.

4.4.1 Complexity

This metric measures the complexity of an adaptive

strategy in relation to its control-ﬂow; it does this by

calculating its Cyclomatic Complexity. It consists of

two subtypes: Cyclomatic (CC) and Strict Cyclomatic

(SCC). Since these metrics can be measured using

control-ﬂow analysis, this metric is implemented in

static code analysis.

The CC metric, which corresponds to the ﬁrst sub-

type, counts the number of linearly independent paths

through the control ﬂow graph of a code (McCabe,

1976). It treats conditional statements as a singu-

lar branching path that contributes to the ﬁnal sum.

By contrast, the second subtype (SCC) performs the

same calculation, but treats the variables involved in

the conditional’s boolean expression as their own in-

dependent paths. The code below shows an example

of a basic if-else statement. The CC of this code is 1,

while its SCC is 3.

Begin

if (a AND b OR c) {

...

}

End.

4.4.2 Modiﬁability

The Modiﬁability metric measures the extent to which

the adaptive strategies can be changed to ensure mini-

mal conﬂicts occur with other components of the sys-

tem. In particular, we focus on how well the adaptive

strategy is connected internally and externally. These

include calculations based on two subtypes: the Class

Coupling (CCM) and the Lack of Cohesion (LCOM).

Since these metrics focus on structural properties of

strategies, they are implemented using static analysis.

The LCOM subtype on the other hand, calcu-

lates how an adaptive strategy is internally connected.

Given an adaptive strategy that is implemented in the

code as a class, LCOM calculates the percentage of

the average number of the strategy’s instance vari-

ables that are not used by any of that strategy’s meth-

ods. The formula for this metric is as follows.

Let I(c) return the set of instance variables be-

longing to a class c and let M(c) return the set of

ASMS: A Metrics Suite to Measure Adaptive Strategies of Self-Adaptive Systems

243

methods that belong to a class c. Let Uses(c, i) re-

turn the set of all methods belonging to a class c and

that use an instance variable i belonging to c. Then,

for a class c, we have,

LCOM(c) = 100 · (1 −

∑

i∈I(c)

|Uses(c,i)|

|M(c)|

| I(c) |

) (13)

4.5 Time-Related Metrics

The Time-related metrics involve measuring the prop-

erties of an adaptive strategy with respect to time.

These metrics are the Frequency, Volatility Ratio, Av-

erage Duration, and Uptime. They all require the use

of dynamic code analysis due to their focus on time.

1) Frequency (F) is designed to calculate how

many times an adaptive strategy is executed in a sys-

tem over a period of time. In this instance, the metric

treats the ‘execution’ of an adaptive strategy as any

strategy that has started executing or is currently be-

ing executed over a speciﬁed time period. Since a

strategy may take a signiﬁcant amount of time to per-

form fully, it does not have to ﬁnish its execution in

order for it to be counted in the metric. The general

calculation for this metric takes as input a time period

t and can be expressed through the following.

F(t) =

Number of strategies executed during t

(14)

2) Volatility Ratio (VR) is designed to calculate

how many unique adaptive strategies are executed

over a speciﬁed period of time. It can show if a system

relies mostly on a small or large number of strategies,

depending on the value of t.

The metric takes as input a time period t and can

be expressed through the following.

V R(t) =

Number of unique strategies executed during t

Total number of available strategies

(15)

3) Average Duration (AD) is designed to calculate

the average amount of time that adaptive strategies are

being performed over a period of time. This includes

the time from when a strategy starts executing to when

it has ﬁnished executing.

The way a strategy may be executed depends on

the system. For example, it may be carried instantly,

for a period of time or for the lifetime of the system

(Cheng et al., 2009). The AD metric can help illus-

trate what a system looks like in this regard. It can be

expressed using the following formula.

Let S be the set of adaptive strategies executed

over the course of a time period t. Let D(s) return

the duration of the execution of an adaptive strategy

s. Then, for an input time period of t, we have,

AD(t) =

∑

s∈S

D(s)

| S |

(16)

4) Adaptation Uptime (AU) is designed to calcu-

late how much time a system spends on performing

adaptive strategies over a period of time. The met-

ric can show how much a system relies on its adaptive

strategies. It can be expressed using the following for-

mula using an input time period of t.

AU(t) =

Time spent executing strategies during t

(17)

5 IMPLEMENTATION

We now cover the relevant details to the Understand

tool as well as some of the details behind the plugin

that implements the designed metrics from Section 4.

5.1 The Understand Tool and Its API

Understand, developed by Scientiﬁc Toolworks, is a

static code analysis tool that allows users to analyze

their code through source code comprehension, graph

visualizations, and software metrics. It supports up

to 12 different programming languages, e.g., Java,

Python and C/C++. It boasts a comprehensive and

easy to use API that allows users to implement their

own metrics, graphs and code style scripts.

5.2 Understand API: Relevant Details

Understand offers several ways for users to program

their own scripts that take advantage of its API. Our

implemented plugin uses the Interactive Reports (IRe-

port) feature because it provides an accessible and in-

tuitive means to display information. When executing

an IReport, Understand renders a UI box containing

data based on the plugin script, which can be pre-

sented in various formats. An IReport can also be

programmed through many languages, with the most

comprehensive API languages being Perl and Python.

For each, Understand uses a simpliﬁed compiler and

a different ﬁle format.

5.3 Understand vs. Other Tools

The other considered candidate for the development

of the plugin was SonarQube. This is a program that

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

244

is capable of competing with Understand in its func-

tionality and provides a rich library of plugins to draw

from. It is also a program that has already been used

in other studies related to SAS (Raibulet et al., 2020).

However, Understand was chosen due to its enhanced

data visualizations, expansive software metrics and

broad, yet accessible options offered by the API.

5.4 Technical Details of the Plugin

The plugin has been implemented in Python. While

this decision has been made in part due to its familiar-

ity, it also proved to be the more stable choice over

Perl, with development suffering from less crashes

and technical issues. As mentioned previously, the

plugin has been implemented using Understand’s

IReport feature. This is due to its simplicity and com-

prehensiveness, as it enables quickly getting started

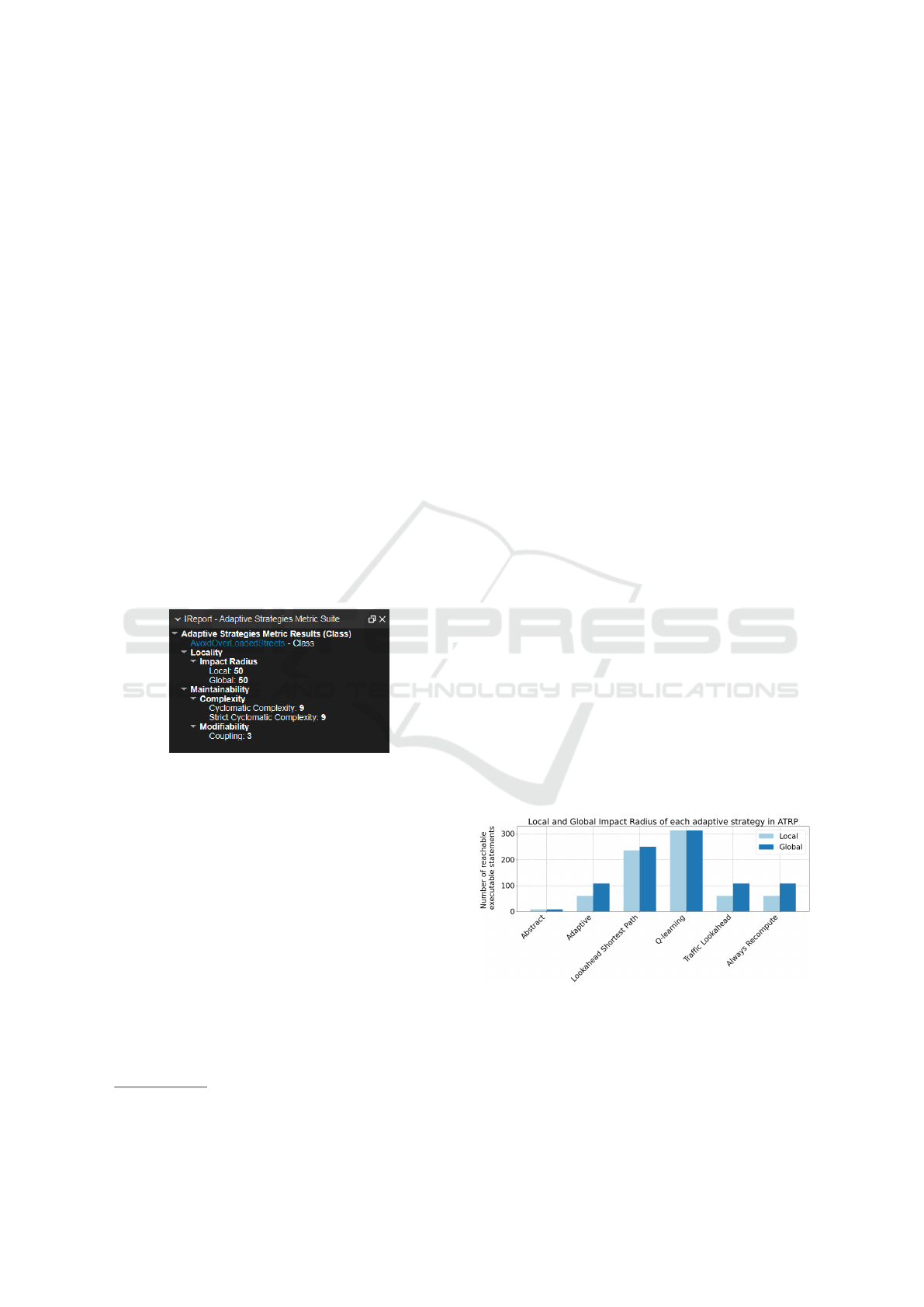
with development. Fig. 3 shows the output that

Understand produces when running the plugin on an

adaptive strategy from the TRAPP exemplar. This

particular output only generates the results that apply

to metrics designed for an individual adaptive strat-

egy. The code for the plugin and the instructions on

how to run it are available at the GitHub repository

Figure 3: TRAPP exemplar: metric results when running

the pugin on an adaptive strategy.

6 EVALUATION

We now focus on the evaluation of the metrics suite

by applying them to an exemplar, thereby giving a

grounded understanding in the value and limitations

that the metrics can offer. We ﬁrst delineate the setup

for the evaluation and then move on the to its results.

6.1 Setup

The exemplar that has been selected to evaluate on is

ATRP. The adaptive strategies of ATRP are all pro-

grammed in Java and are implemented as classes.

ASMS repository: https://github.com/

Koen-Kraaijveld/ASMS

These strategies are named as follows: Abstract,

Adaptive, Lookahead Shortest Path, Q-learning, Traf-

ﬁc Lookahead, Always Recompute.

In ATRP, the strategies represent the options that

the cars have in navigating the city to reach their des-

tination. These incorporate self-adaptation to tell the

managed system on how to respond to incoming en-

vironmental and internal changes at runtime, such as

trafﬁc accidents or congestion.

The justiﬁcation for why ATRP has been picked

to evaluate on is because it uses the largest number

of adaptive strategies from the examined case studies.

Additionally, all strategies in ATRP are programmed

as classes, which allows metrics that need to run on

classes to be included in the evaluation. These reasons

allow the evaluation to cover a diverse set of scenar-

ios in which the metrics can operate, which can then

highlight of their potential value and limitations.

The evaluation is based on the following metrics

designed for static code analysis that are implemented

in the plugin for the Understand tool. They include

all their respective subtypes and will be presented in

the following order: Impact Radius (Locality), Global

Impact Radius Distribution and Statistics (Concentra-

tion of Impact), Dependency Degree (Elementarity),

and Complexity and Modiﬁability (Maintainability).

The following sections present the results from

each of these listed metrics when applied to the adap-

tive strategies of the ATRP exemplar.

6.2 Locality Metric Results

6.2.1 Impact Radius Results

This experiment applies the Local and Global Impact

Radius to ATRP using the methods discussed in Sec-

tion 4.1. The results are shown in Fig. 4.

Figure 4: Double bar chart for the Local and Global Impact

Radius of each adaptive strategy in ATRP, with the num-

ber of reachable executable statements on the y-axis and the

adaptive strategies on the x-axis.

From Fig. 4, it is clear that the Q-learning strat-

egy is able to reach the most executable statements,

followed by Lookahead Shortest Path. This tells us

ASMS: A Metrics Suite to Measure Adaptive Strategies of Self-Adaptive Systems

245

that both of these have the greatest potential to effect

change in the system. Other outstanding properties

may be observed in the discrepancies between the LIR

and GIR of an adaptive strategy. For example, Adap-

tive (among others) has a clear difference between the

number of executable statements that may be reached

locally versus globally. This indicates that the strat-

egy has a much greater impact on the more distant

parts of the system. By contrast, Q-learning has no

difference between its LIR and GIR, which means its

impact is restricted to the parts of the system that are

closely associated with it.

6.3 Concentration of Impact Metric

Results

6.3.1 Global Impact Radius Distribution

This experiment applies the GIRD metric to ATRP

using the methods discussed in Section 4.2. Results

are shown as a pie chart in Fig. 5.

Figure 5: Pie chart showing the results from Global Impact

Radius Distribution metric involving all adaptive strategies

in ATRP, expressed as a percentage.

In contrast to the Locality metrics, this approach

can provide an alternate view on how much impact an

adaptive strategy has on a system relative to others.

However, many of the same observations made in the

section above apply here as well.

6.3.2 Global Impact Radius Statistics

The usefulness of the GIRD metric can be exempli-

ﬁed in how we can use it to calculate statistics, which

is provided by the GIRS metric. This includes statis-

tics that show the adaptive strategy with the maximum

and minimum GIR, as well as the mean, median and

standard deviation of the GIRD. Table 2 shows the

outputs for this metric.

From this table, we can see how GIRS provides

some unique interpretations to the GIRD’s data. First,

it can concretely give the adaptive strategy that has

the maximum or minimum GIR through the ﬁrst two

statistics. Second, the Mean and Median subtypes

Table 2: Global Impact Radius Statistics of ATRP, includ-

ing the Maximum, Minimum, Mean, Median and Standard

Deviation subtypes.

GIRS Subtype ATRP

Maximum Q-learning

Minimum Abstract

Mean 0.17

Median 0.12

Standard Deviation 0.12

can show around which values the GIRD of the adap-

tive strategies tend to exist. The difference between

these two values is also particularly useful in getting

an idea of how the strategies are distributed in regards

to their GIR, since the Mean may be greatly affected

by extreme values, while the Median is not. Third, it

can show how spread out the GIR are of the adaptive

strategies. If this statistic is high, it may point to the

existence of one or more adaptive strategies that can

reach signiﬁcantly more executable statements rela-

tive to the other strategies in the system.

6.4 Elementarity Metrics Results

6.4.1 Dependency Degree Results

This experiment applies the Dependency Degree met-

ric to ATRP using the methods discussed in Section

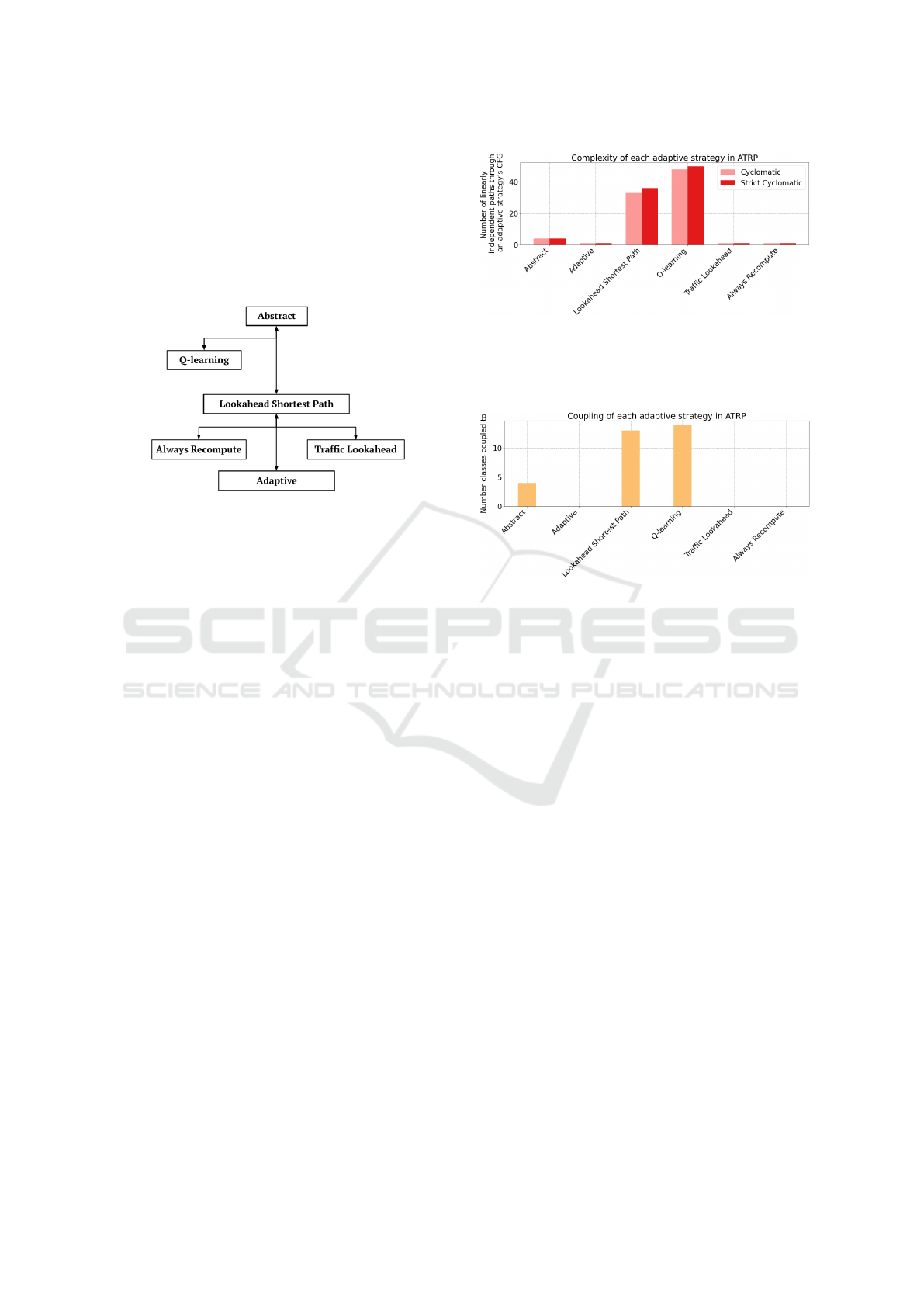
4.3. Fig. 6 shows the results for this metric. From

these results, we can see that Abstract is depended on

by most of the strategies, while several others depend

on none. On the other hand, few strategies depend on

the most of the other strategies.

Figure 6: Double bar chart showing the Top-down and

Bottom-up subtypes when applied to ATRP, with the num-

ber of dependency relations a given adaptive strategy has on

the y-axis and the adaptive strategies on the x-axis.

There are a number of properties implied by this

data. First, since Abstract depends on zero strategies,

while being depended on by 5 (i.e., all other strate-

gies), it indicates that it has inﬂuence over all other

strategies in the set. Since each strategy in this set is a

class, this means that each extends functionality from

Abstract through inheritance. Second, every strategy

that is depended on by zero others, but does depends

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

246

on at least one, constitutes a strategy that is not inher-

ited from. These two notions are reﬂected in Fig. 7,

which shows the tree representation of all the depen-

dency relations between each of the adaptive strate-

gies. The strategy that is depended on by all others,

but does not depend on any, forms the root of the tree.

The strategy that is not depended on by any, but does

depend on at least one forms a leaf in the tree.

Figure 7: The Dependency Degree tree of the ATRP adap-

tive strategies, with parent nodes representing the strategy

a given strategy depends and child nodes representing the

strategies a given strategy are depended on by.

6.5 Maintainbility Results

6.5.1 Complexity

This experiment applies the Complexity metric to

ATRP using the methods discussed in Section 4.4 (see

Fig. 8). From Fig. 8, it is clear that Q-learning and

Lookahead Shortest Path are the most complex out of

all the adaptive strategies. One indication that this ob-

servation provides is that these strategies will require

signiﬁcantly more effort to test appropriately. By con-

trast, all other strategies have a CC and SCC of less

than 5, which will be less costly to test. On closer in-

spection of this result, it can be observed when com-

paring the results of this metric to that of the Local

and Global Impact Radius (Fig. 8 compared to Fig.

4). Putting both these results side by side, we can see

that there are similarities and overlaps between them.

This can be explained in part due to the fact that more

complex classes and functions have a greater chance

to contain executable statements, since there will be

more branching paths that may be followed.

6.5.2 Modiﬁability Results

This ﬁnal experiment applies the Modiﬁability metric

of the ATRP exemplar, as shown in Fig. 9.

From Fig. 9, Lookahead Shortest Path and Q-

learning are the adaptive strategies in ATRP that have

the highest coupling. For these strategies, it indicates

Figure 8: Double bar chart showing the Cyclomatic and

Strict Cyclomatic Complexities of the ATRP adaptive

strategies; y-axis represents the number of linearly indepen-

dent paths through an adaptive strategy’s control ﬂow graph

and x-axis represents the names of the adaptive strategies.

Figure 9: Graph showing the Coupling of each ATRP adap-

tive strategy, with the y-axis representing the number of

components in the system it is coupled to and the x-axis

representing the names of the adaptive strategies.

that some of them are externally more connected than

others. When it comes to the modiﬁability of a self-

adaptive system, it would be optimal for its adaptive

strategies to score low in this metric, since a change

in one of them would require less changes in other

components in the system (Kukreja, 2015).

Additionally, Fig. 10 presents the LCOM of each

adaptive strategy in ATRP. The same strategies that

score high on Coupling also score high on Lack of

Cohesion. Similar to Coupling, it is considered bet-

ter to score low in this metric, since it implies that

a given class is internally well-connected and there-

fore more cohesive (Kukreja, 2015). The reason why

some strategies have 0% LCOM is because their cor-

responding classes do not have any instance variables.

7 DISCUSSION

ASMS provides metrics for the practitioners to ana-

lyze adaptive strategies (1) from the design point of

view through static analysis of code, and (2) from the

runtime point of view through dynamic analysis. The

current version of ASMS is implemented as a plug-in

for Understand, which is widely used both in industry

ASMS: A Metrics Suite to Measure Adaptive Strategies of Self-Adaptive Systems

247

Figure 10: The Lack of Cohesion of each ATRP adaptive

strategy; y-axis represents the average number of class in-

stance variables that are not used by its methods; x-axis rep-

resents the names of the adaptive strategies.

and academia for software quality assessment.

A subset of the proposed metrics rely on classes,

hence on the object-oriented paradigm. This may be

considered a limitations, since not all the metrics de-

ﬁned by ASMS may be applied to adaptive strategies

written in non object-oriented languages.

The ASMS plugin analyzes Java software. How-

ever, Understand supports other programming lan-

guages. Therefore, we plan to extend ASMS to

analyze software written in other programming lan-

guages (e.g., C++, Python used by other SEAMS ex-

emplars). The current version of ASMS implements

those metrics which can be computed through a static

analysis of code. One of the next steps is to proceed

with the implementation of the metrics requiring the

dynamic analysis of self-adaptive strategies.

8 RELATED WORK

Several works focus on the main features and devel-

opment aspects of SAS. They provide insights into

the various design and runtime properties of a self-

adaptive system that this paper has applied to adap-

tive strategies. For example, Cheng et. al (Cheng

et al., 2009) provides a comprehensive summary in

how state-of-the-art self-adaptive systems are engi-

neered today. Most notably, the authors have included

a number of different modeling dimensions that cor-

respond to the possible properties that a self-adaptive

system may have. Their list provides a basis to iden-

tify what kind of metrics may be developed to capture

these properties. The authors, however, do not pro-

vide a means to calculate such properties. Salehie and

Tahvildari (Salehie and Tahvildari, 2009) provide an

overview on self-adaptive software and a taxonomy of

self-adaptation which may inspire analysis and eval-

uation approaches for SAS. Raibulet (Raibulet, 2018)

proposes a taxonomy for the evaluation approaches

of SAS by considering what (e.g., scope, perspective,

level), how (e.g., mechanisms, type) and when (e.g.,

time, recativity) should it be evaluated. Turetken

(Turetken, 2013) provides a thorough summary of

the SIG Maintainability Model, which is used to map

source code properties onto the maintainability char-

acteristic of the ISO/IEC 9126 software quality at-

tributes. This is useful in determining which prop-

erties belonging to a piece of code have an inﬂuence

on the maintainability of software. In particular, the

author details how the model relates code complexity

and coupling to software testability and modiﬁability.

On the other hand, there are several papers fo-

cusing on the evaluation of SAS. For example, some

of the available evaluation approaches are summa-

rized in (Raibulet and Fontana, 2017). They con-

sider static and/or dynamic aspects of SAS. Perez-

Palacin et al. (Perez-Palacin et al., 2014) evaluates

architectural aspects at design time through the Sys-

tem Adaptability and Adaptability of Services metrics

in component-based systems. While, Reinecke et al.

(Reinecke et al., 2010) evaluate behavioural aspects

of SAS through the Adaptive metric, which collects

various performance aspects at rumtime. Kaddoum

et. al (Kaddoum et al., 2010) proposes a metric suite

based on four categories: methodological, architec-

tural, intrinsic, and runtime evaluation. Part of the

metrics identify ways to measure the quality of a SAS

design. For several of these metrics, they provide con-

crete formulas, methods or examples in how to cal-

culate them, but do not provide tool support. Ex-

cept (Perez-Palacin et al., 2014), none of the cited

approaches provides tool support for the computation

of the proposed evaluation approaches. This may be

considered a limitation in the adoption and applica-

tion of the proposed metrics in practice.

In this paper, we propose (1) a novel set of metrics

complementary to the existent ones, and (2) a plug-in

for a well known and spread tool in software devel-

opment (i.e., Understand) for the computation of our

proposed metrics requiring static code analysis.

9 CONCLUSIONS AND FUTURE

WORK

This paper centered around answering the question In

what meaningful ways can we measure the design and

runtime properties of the adaptive strategies belong-

ing to a self-adaptive system?. We have provided an

answer to this question through the proposal the new

ASMS metrics suite, which consists of ﬁve different

categories of metrics capturing various aspects of the

self-adaptive strategies. The proposed metrics requir-

ing static code analysis have been implemented in the

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

248

Understand tool. The plugin is used to gather the re-

sults for the evaluation, which involved applying the

metrics to one of the SAS exemplars.

In regards to future work, combining the ap-

proaches of static and dynamic code analysis could

lead to a more fruitful space in which to design met-

rics. Tackling the RQ with hybrid code analysis, for

example, could accomplish this. In addition to this,

further developing and implementing the metrics that

are based on dynamic code analysis would make the

suite more comprehensive and complete.

REFERENCES

Cheng, B. H. C., de Lemos, R., Giese, H., Inverardi, P.,

Magee, J., Andersson, J., Becker, B., Bencomo, N.,

Brun, Y., Cukic, B., Serugendo, G. D. M., Dustdar, S.,

Finkelstein, A., Gacek, C., Geihs, K., Grassi, V., Kar-

sai, G., Kienle, H. M., Kramer, J., Litoiu, M., Malek,

S., Mirandola, R., M

uller, H. A., Park, S., Shaw, M.,

Tichy, M., Tivoli, M., Weyns, D., and Whittle, J.

(2009). Software engineering for self-adaptive sys-

tems: A research roadmap. In Software Engineering

for Self-Adaptive Systems, LNCS 5525, pages 1–26.

Garlan, D., Schmerl, B., and Cheng, S.-W. (2009). Soft-

ware Architecture-Based Self-Adaptation, pages 31–

55. Springer.

Gerostathopoulos, I. and Pournaras, E. (2019). Trapped in

trafﬁc? a self-adaptive framework for decentralized

trafﬁc optimization. In Intl Symposium on Sw Eng for

Adaptive and Self-Managing Systems, pages 32–38.

Gerostathopoulos, I., Raibulet, C., and Alberts, E. (2022).

Assessing self-adaptation strategies using cost-beneﬁt

analysis. In 19th Intl Conference on Software Archi-

tecture Companion (ICSA-C), pages 92–95.

Gomes, I. V., Morgado, P., Gomes, T., and Moreira, R. M.

L. M. (2009). An overview on the static code analysis

approach in software development.

Hande, N. and Rao, P. V. (2017). A comparative study of

static, dynamic and hybrid analysis techniques for an-

droid malware detection. International Journal of En-

gineering Development and Research, 5:1433–1436.

Kaddoum, E., Raibulet, C., Georg

e, J.-P., Picard, G., and

Gleizes, M.-P. (2010). Criteria for the evaluation of

self-* systems. In ICSE Workshop on Software Eng

for Adaptive and Self-Managing Systems, page 29–38.

Kritzinger, D. (2017). 9 - development assurance. In

Kritzinger, D., editor, Aircraft System Safety, pages

193–324. Woodhead Publishing.

Krupitzer, C., Roth, F. M., VanSyckel, S., Schiele, G.,

and Becker, C. (2015). A survey on engineering ap-

proaches for self-adaptive systems. Pervasive Mob.

Comput., 17:184–206.

Kukreja, N. (2015). Measuring software maintainability,

https://quandarypeak.com/2015/02/measuring-

software-maintainability/.

Maia, P., Vieira, L., Chagas, M., Yu, Y., Zisman, A., and

Nuseibeh, B. (2019). Dragonﬂy: a tool for simulat-

ing self-adaptive drone behaviours. In Intl Sympo-

sium on Software Engineering for Adaptive and Self-

Managing Systems (SEAMS).

Masciadri, L. and Raibulet, C. (2009). Frameworks for

the development of adaptive systems: Evaluation of

their adaptability feature through software metrics. In

4th International Conf on Software Engineering Ad-

vances, pages 309–312. IEEE Computer Society.

McCabe, T. (1976). A complexity measure. IEEE Transac-

tions on Software Engineering, SE-2(4):308–320.

Perez-Palacin, D., Mirandola, R., and Merseguer, J. (2014).

On the relationships between qos and software adapt-

ability at the architectural level. Journal of System and

Software, 87:1–17.

Pollack, S. V. and Cytron, R. K. (2003). Executable State-

ment, page 683–684. John Wiley and Sons Ltd., GBR.

Raibulet, C. (2018). Towards a taxonomy for the evaluation

of self-* software. In 3rd Intl Workshops on Founda-

tions and Applications of Self* Systems, pages 22–23.

Raibulet, C., Arcelli Fontana, F., Capilla, R., and Carrillo,

C. (2017). Chapter 13 - an overview on quality evalu-

ation of self-adaptive systems. pages 325–352.

Raibulet, C., Arcelli Fontana, F., and Carettoni, S. (2020). A

preliminary analysis of self-adaptive systems accord-

ing to different issues. In Software Quality Journal,

volume 28, pages 1213–1243.

Raibulet, C. and Fontana, F. A. (2017). Evaluation of self-

adaptive systems: a women perspective. In 11th Euro-

pean Conference on Software Architecture, pages 23–

30.

Rawat, M. S., Mittal, A., and Dubey, S. K. (2012). Sur-

vey on impact of software metrics on software quality.

Journal of Advanced CS and Applications, 3(1).

Reinecke, P., Wolter, K., and van Moorsel, A. (2010). Eval-

uating the adaptivity of computing systems. Perfor-

mance Evaluation Journal, 67(8):676–693.

Salehie, M. and Tahvildari, L. (2009). Self-adaptive soft-

ware: Landscape and research challenges. Trans on

Autonomous and Adaptive Systems, 4(2):14:1–14:42.

Turetken, O. (2013). Towards a maintainability model for

business processes: Adapting a software maintainabil-

ity model. In Workshop on Communicat., pages 1–4.

Weyns, D. and Iftikhar, M. U. (2019). Activforms: A

model-based approach to engineer self-adaptive sys-

tems. ACM TOSEM, 10(10):1–59.

Weyns, D., Schmerl, B. R., Grassi, V., Malek, S., Mi-

randola, R., Prehofer, C., Wuttke, J., Andersson, J.,

Giese, H., and G

oschka, K. M. (2010). On patterns for

decentralized control in self-adaptive systems. In Soft-

ware Engineering for Self-Adaptive Systems, pages

76–107.

Wuttke, J., Brun, Y., Gorla, A., and Ramaswamy, J. (2012).

Trafﬁc routing for evaluating self-adaptation. In Intl

Symposium on Software Engineering for Adaptive and

Self-Managing Systems, pages 27–32.

ASMS: A Metrics Suite to Measure Adaptive Strategies of Self-Adaptive Systems

249